1 Introduction

Thermodynamics of black holes always provide important clues to study the properties of quantum gravity. The research of asymptotically AdS black holes has been a fascinating area because of the AdS/CFT correspondence [1,2,3]. Especially, after interpreting the cosmological constant \(\Lambda \) as thermodynamic pressure \(P=-\frac{\Lambda }{8\pi }\) [4,5,6,7,8,9], the thermodynamic properties of AdS black holes behave similarly qualitatively to a Van der Waals fluid [10]. The analogy is generalized to the reentrant phase transition for multi-component fluids [11], triple point [12] and “\(\lambda \)-line phase transition characterizing the superfluidity [13]. (See the recent reviews in [14, 15].) These reveal that AdS black holes can be treated as an ordinary thermodynamical system, which is a good theoretical laboratories for studying the microscopic structure of black holes. For example, some papers focus on this subject, including the possible black hole molecules [16] and microscopic origin of the black hole reentrant phase transition [17].

The quantitative analogy between black holes with an ordinary thermodynamical system is introduced firstly in [18, 19], which obtain the Van der Waals (VdW) black holes containing the precisely same thermodynamical phase space with the classical VdW fluid. However, the VdW solutions are near horizon metric, and physically unacceptable in the global spacetime. Recently, the study extends to construct the quantitative analogy between black holes with an quantum thermodynamical system, i.e. anyons system [20]. Anyons follow the fractional statistics in two spatial dimensions [21,22,23,24], which is actually intermediate statistics between Fermi–Dirac and Bose–Einstein statistics [23, 25]. The authors declare that, under the small effective pressure limit, there is physical anyon black hole solutions taking the same thermodynamic properties with the anyon VdW fluid exhibiting a quasi Bose–Einstein statistics [20].

In this paper, we study the exact anyon solutions, and find some different but interesting results. After considering the energy conditions, we find that the exact anyon VdW solutions with \(b>0\) are physically un-acceptable. Especially for the reduced case \(b=0\), after carefully studying its energy conditions, geometric quantities and horizon structure, we conclude that there is an anyon black hole taking the precisely same thermodynamical phase space with the gas of “interacting point particle” (IPP), which should exhibit a quasi Fermi–Dirac statistics and have an upper bound of mass. The anyon IPP black hole can contain 1 or 2 horizons. This is the first physical VdW-like black hole solution in the global spacetime. Moreover, there exist the Hawking–Page phase transition between the anyon IPP black holes and the pure thermal radiation phase.

The paper is organized as follows: we revisit the equation of state (EOS) for anyons in next section. In Sect. 3, we present the exact anyon Van Der Waals solutions. In Sect. 3, we obtain the anyon “interacting point particle” black holes and discuss their physical properties, including the, degenerated “perfect gas” black holes and Hawking–Page transition. Finally some concluding remarks are given.

2 EOS for anyons

In this section, we revisit the EOS for anyons, which follow the fractional statistics in two spatial dimensions [23, 25]. As the fractional statistics is actually intermediate statistics between Fermi–Dirac and Bose–Einstein statistics, we can begin with the number of quantum states for N bosons or fermions which occupy G state, i.e.

$$\begin{aligned} W_b=\frac{(G+N-1)!}{N!(G-1)!},\quad \,W_f=\frac{G!}{N!(G-N)!}, \end{aligned}$$

respectively. It is generalized to the fractional statistics with the following form

$$\begin{aligned} W=\frac{\bigg (G+(N-1)(1-\alpha )\bigg )!}{N!\bigg (G-\alpha \,N-(1-\alpha )\bigg )!}, \end{aligned}$$
(1)

where the fraction statistical parameter \(\alpha =0\) corresponds to the bosons and \(\alpha =1\) corresponds to the fermions, while \(0<\alpha <1\) represents the anyons taking the intermediate statistics. Especially for \(\alpha <\frac{1}{2}\), the anyons follow a quasi Bose–Einstein statistics; while for \(\alpha >\frac{1}{2}\), there is a quasi Fermi–Dirac statistics.

As usual in quantum statistical mechanics, one can introduce the fixed particle number and energy, i.e.

$$\begin{aligned} N=\sum \,N_i,\quad \,E=\sum \,N_i\varepsilon _i, \end{aligned}$$
(2)

with \(\varepsilon _i\) identified as the energy of each one of the \(N_i\) particles. Then the grand partition function is determined as [23, 25]

$$\begin{aligned} Z=\sum _{N_i}W(N_i)\exp \bigg (\sum _{i}N_i(\mu _i-\varepsilon _i)/T\bigg ), \end{aligned}$$
(3)

where \(\mu \) and T are the chemical potential and the temperature, respectively. By some straightforward calculations, one can obtain the famous Wu relations [23], which result in the EOS of anyons

$$\begin{aligned} PV=NT\bigg (1+\frac{(2\alpha -1)N\lambda ^2}{4V}\bigg ), \end{aligned}$$
(4)

in the Boltzmann limit (\(\exp (\mu /kT)\ll 1\)). Here

$$\begin{aligned} \lambda =\sqrt{\frac{2\pi }{mT}}, \end{aligned}$$
(5)

P is the pressure, V is the conjugate volume for pressure, and m is the mass of the particle. Note that we use the convention \(\hbar =c=k=1\).

In this paper, we favor another form of EOS of anyons, namely,

$$\begin{aligned} Pv=T\bigg (1+\frac{(2\alpha -1)\lambda ^2}{4v}\bigg ), \end{aligned}$$
(6)

where \(v=\frac{V}{N}\) is the specific volume and N is the degree of freedom. For this EOS, one can easily generalize it to that for an anyon VdW fluid which should have the following form

$$\begin{aligned} \bigg (P+\frac{a}{v^2}\bigg )(v-b)=T\bigg (1+\frac{(2\alpha -1)\lambda ^2}{4v}\bigg ), \end{aligned}$$
(7)

where the parameter \(a>0\) measures the intermolecular attraction between the fluid constituents, and the parameter \(b>0\) measures their volume. Similarly, \(\alpha =\frac{1}{2}\) is the boundary between the quasi Bose–Einstein and the quasi Fermi–Dirac statistics of the fluid. Especially, the critical value \(\alpha =\frac{1}{2}\) represents the exact VdW fluid from the above EOS.

3 Exact anyon Van Der Waals solutions

In this section, we present the exact anyon VdW solutions. As anyons is introduced in two spatial dimensions, we will focus on the discussion in three dimensional spacetime. Actually, it can be also generalized to higher dimensions, because of the existence of Haldane fractional statistics [23, 25].

3.1 General solutions

We start with the BTZ-like metric

$$\begin{aligned} \mathrm {d} s^2=-f(r)\mathrm {d}t^2+\frac{\mathrm {d}r^2}{f(r)}+r^2\mathrm {d}\theta ^2, \end{aligned}$$
(8)

with the metric function

$$\begin{aligned} f(r)&=\frac{r^2}{\ell ^2}-\mu -h(r,\ell ),\nonumber \\&=8\pi \,P_{\Lambda }r^2-\mu -h(r,P_{\Lambda }) \end{aligned}$$
(9)

where \(P_{\Lambda }\) is interpreted as thermodynamic pressure [4,5,6,7,8,9] with the form

$$\begin{aligned} P_{\Lambda }=-\frac{\Lambda }{8\pi }=\frac{1}{8\pi \ell ^2}. \end{aligned}$$
(10)

Parameter \(\mu \) is related to the black hole mass as

$$\begin{aligned} M=\frac{\mu }{8}. \end{aligned}$$
(11)

Thus the conjugated thermodynamic volume is

$$\begin{aligned} V=\left( \frac{\partial M}{\partial P_{\Lambda }}\right) \bigg |_{S}. \end{aligned}$$
(12)

For simplicity, we follow [18, 19] to assume that \(h(r,P_{\Lambda })=A(r)-B(r)P_{\Lambda }\). Under this ansatz, one will find the specific volume is independent of thermodynamic pressure, i.e.

$$\begin{aligned} v_{\Lambda }=\frac{kV}{\mathcal {A}}=4r_++\frac{B(r_+)}{2\pi \,r_+}, \end{aligned}$$
(13)

with \(k=\frac{4(d-1)}{(d-2)}\), d being the dimensions of the spacetime, as the area \({\mathcal {A}}=2\pi \,r_+\) counting the degrees of freedom of black holes. This is similar as the specific volume of classical fluid, i.e \(v=\frac{V}{N}\) as N counting the degrees of freedom of the fluid. Here \(r_+\) denotes the event horizon, which is the biggest positive root of \(f(r)=0\).

The solutions must satisfy the equation of gravitational field

$$\begin{aligned} G^{\mu \nu }+\Lambda \,g^{\mu \nu }=T^{\mu \nu }. \end{aligned}$$
(14)

Here \(T^{\mu \nu }\) is the energy momentum tensor of an anisotropic fluid sources, which takes the following form

$$\begin{aligned} T^{\mu \nu }=\rho e^{\mu }_{0}e^{\nu }_{0}+\sum _{i}P_{i}e^{\mu }_{i}e^{\mu }_{i}, \end{aligned}$$
(15)

where \(e^{\mu }_{i}\) are the components of the vielbein and \(i=1,2\). It is easy to derive that

$$\begin{aligned} \rho&=-P_r=-\frac{f'(r)}{2r}+8\pi \,P_{\Lambda }, \nonumber \\ P_{\theta }&=\frac{f''(r)}{2}-8\pi \,P_{\Lambda }, \end{aligned}$$
(16)

where the convention \(G_{N}=\frac{1}{8\pi }\) is used.

Then in the extended black hole thermodynamics phase space, it is easy to check the first law

$$\begin{aligned} \mathrm {d} M=T\mathrm {d}S+V\mathrm {d}P_{\Lambda }, \end{aligned}$$
(17)

where the black hole mass should be treated as enthalpy H other than the internal energy U. The thermodynamic quantities are

$$\begin{aligned} M&=P_{\Lambda }\pi \,r_{+}^2-\frac{1}{8}\bigg (A(r_+)-B(r_+)P_{\Lambda }\bigg ),\nonumber \\ T&=\frac{f'(r_+)}{4\pi }=-\frac{1}{4\pi } \bigg (A'(r_+)-B'(r_+)P_{\Lambda }\bigg )+4P_{\Lambda }r_+,\nonumber \\ S&=\frac{{\mathcal {A}}}{4}=\frac{\pi \,r_{+}}{2}. \end{aligned}$$
(18)

Finally, we construct the \((2+1)\) dimensional solution whose thermodynamics is exactly similar to that of an Anyon VdW fluid, with the exactly same EOS in Eq. (7), i.e.

$$\begin{aligned} \bigg (P_{\Lambda }+\frac{a}{v_{\Lambda }^2}\bigg )(v_{\Lambda }-b)=T\bigg (1+\frac{(2\alpha -1)\lambda ^2}{4v_{\Lambda }}\bigg ). \end{aligned}$$
(19)

This leads to the following differential equation

$$\begin{aligned} F_1(r)&+P_{\Lambda }F_2(r)=0,\nonumber \\ F_1(r)&=r\bigg (-m(8\pi \,r^2+B(r))^2A'(r)\nonumber \\&\quad +4\pi ^2r(-2am+2\pi \alpha -\pi )B(r)\nonumber \\&\quad +16\pi ^3r^2(am(b-4r)+2\pi \,r(2\alpha -1))\bigg ),\nonumber \\ F_2(r)&=\bigg (8\pi \,r^2+B(r)\bigg )^2\bigg (-2B(r) +4b\pi \,r+B'(r)r\bigg )m. \end{aligned}$$
(20)

As the functions \(F_1(r)\) and \(F_2(r)\) should vanish independently, we can obtain two differential equations \(F_1(r)=F_2(r)=0\), which result in the solutions

$$\begin{aligned} A(r)&=\frac{(-2am+2\pi \alpha -\pi )\pi }{(C_{\ell }+2)m}\nonumber \\&\quad \times \bigg (\ln \bigg (4\pi ((C_{\ell }+2)r+b)\bigg )-C_0\bigg )\nonumber \\&\quad -\frac{ab\pi }{(C_{\ell }+2)(C_{\ell }r+2r+b)},\nonumber \\ B(r)&=4\pi \,r(C_{\ell }r+b), \end{aligned}$$
(21)

where \(C_{\ell },C_0\) are constants.

Thus, we find the general Anyon VdW solutions

$$\begin{aligned} f(r)&=-8M+4\pi \,(C_{\ell }+2)P_{\Lambda }r^2+4\pi \,bP_{\Lambda }r \nonumber \\&\quad -\frac{(-2am+2\pi \alpha -\pi )\pi }{(C_{\ell }+2)m} \ln \bigg (r+\frac{b}{(C_{\ell }+2)}\bigg )\nonumber \\&\quad +\frac{ab\pi }{(C_{\ell }+2)(C_{\ell }r+2r+b)}. \end{aligned}$$
(22)

As the constant \(C_0\) only contributes to the black hole mass term, we have chosen \(C_0=\ln (4\pi (C_{\ell }+2))\), which keeps the black hole mass term still being M. This is shown by studying the \(r=+\infty \) behaviour of f(r), i.e.

$$\begin{aligned} f(r)&=-8M+4\pi \,(C_{\ell }+2)P_{\Lambda }r^2+4\pi \,bP_{\Lambda }r\nonumber \\&\quad -\frac{(-2am+2\pi \alpha -\pi )\pi }{(C_{\ell }+2)m}\ln (r)\nonumber \\&\quad +{\mathcal {O}}(r^{-1}). \end{aligned}$$
(23)

On other hand, the effective cosmological constant should be

$$\begin{aligned} \Lambda _{eff}=\left( \frac{C_{\ell }}{2}+1\right) \Lambda =-\left( \frac{C_{\ell }}{2}+1\right) \frac{1}{\ell ^2}. \end{aligned}$$
(24)

Therefore, the AdS spacetime provides the following constraint:

$$\begin{aligned} C_{\ell }>-2, \end{aligned}$$
(25)

which is also the requirement of the existence of a smooth event horizon [26].

3.2 Energy conditions

For physical solutions, energy conditions of source should be hold. For this case, the energy conditions are given by [27]

  • Weak energy condition (WEC): \(\rho \ge 0,\rho +P_{i}\ge 0\), which could be reduced to \(\rho \ge 0,\rho +P_{\theta }\ge 0\);

  • Null energy condition (NEC): \(\rho +P_{i}\ge 0\), namely \(\rho +P_{\theta }\ge 0\);

  • Strong energy condition (SEC): \(\rho +\sum _{i}P_{i}\ge 0,\rho +P_{i}\ge 0\), which could be simplified as \(P_{\theta }\ge 0,\rho +P_{\theta }\ge 0\), as \(\rho +P_{r}=0\);

  • Dominant energy condition (DEC): \(\rho \ge |P_{i}|\), i.e. \(\rho \pm \,P_{\theta }\ge 0\);

Actually, one would always expect that the energy conditions only hold outsider the black hole event horizon, because of the Cosmic Censorship Conjecture [28, 29], for which the static observer will never find these physically un-acceptable properties. Considering the minimum requirement of energy conditions, NEC \(\rho +P_{\theta }>0\) should be hold. This can be easy to check by inspecting the large r behaviour, i.e.

$$\begin{aligned} \rho +P_{\theta }&=-\frac{bP_{\Lambda }}{4r} +\frac{(-2am+2\pi \alpha -\pi )}{8(C_{\ell }+2)mr^2}\nonumber \\&\quad +\mathcal {O}(r^{-3}),\,as\quad \, r\rightarrow +\infty , \end{aligned}$$
(26)

from which, one can find that the NEC is always negative for sufficiently large r. Therefore, one can conclude that the anyon VdW solutions with \(b>0\) are physically un-acceptable. This is consistent with the small effective pressure limit [20] and the standard VdW case [19]. Similarly, one can construct the consistent anyon VdW solutions as a near horizon metric [19], which satisfies the energy conditions at least in a region close to the horizon. This is left for a future considerations. Here we take the case with \(a=0,b\ne 0\) as an example to take a glance at this kind of local solutions. The corresponding NEC Eq. (26) reduces to

$$\begin{aligned} \rho +P_{\theta }&=-\frac{bP_{\Lambda }}{4r}+\frac{(2\alpha -1)\pi }{8(C_{\ell }+2)mr^2}\nonumber \\&\quad +{\mathcal {O}}(r^{-3}),\,as\quad \, r\rightarrow +\infty . \end{aligned}$$
(27)

For sufficiently large r, one can find that the NEC always breaks, hence the solution is physically un-acceptable in the global spacetime. On the other hand, mathematically it follows that there always exists a region of metric parameters where these energy conditions are satisfied close to the horizon. In this sense, the metric with \(a=0,b\ne 0\) should be thought as a near horizon solution, as it is always valid locally near the horizon.

Especially, from Eq. (26), one can see that it is possible for the solutions \(b=0\) to satisfy the energy conditions. Actually, it is really true as shown in the following paper. The case \(b=0\) is the solution for the IPP. We will study the physical properties of the anyon IPP black hole solutions, including the energy conditions, geometric quantities, horizon structure, degenerated cases and thermodynamics. The existence of anyon IPP black holes are more interesting than the un-physical VdW solutions in [19].

4 Anyon “interacting point particle” black holes

In this section, we study the anyon IPP black holes, with the reduced metric function (\(b=0\))

$$\begin{aligned} f(r)&=-8M+4\pi \,(C_{\ell }+2)P_{\Lambda }r^2\nonumber \\&\quad -\frac{(-2am+2\pi \alpha -\pi )\pi }{(C_{\ell }+2)m}\ln (r). \end{aligned}$$
(28)

We note that when \((-2am+2\pi \alpha -\pi )=0\), the solution reduces to the famous AdS\(_{3}\) vacuum in three dimensions, which is trivial.

4.1 Energy conditions

The matter source density and pressure are reduced as

$$\begin{aligned} \rho&=-\frac{1}{2}P_{\Lambda }C_{\ell }+\frac{(-2am+2\pi \alpha -\pi )}{16(C_{\ell }+2)mr^2},\nonumber \\ P_{\theta }&=\frac{1}{2}P_{\Lambda }C_{\ell }+\frac{(-2am+2\pi \alpha -\pi )}{16(C_{\ell }+2)mr^2}. \end{aligned}$$
(29)

For the NEC,

$$\begin{aligned} \rho +P_{\theta }=\frac{(-2am+2\pi \alpha -\pi )}{8(C_{\ell }+2)mr^2}, \end{aligned}$$
(30)

its validity indicates

$$\begin{aligned} (-2am+2\pi \alpha -\pi )>0, \end{aligned}$$
(31)

where the AdS condition Eq. (25) is used. Noting that the case \((-2am+2\pi \alpha -\pi )=0\) corresponds to valid NEC as well, which is actually the AdS vacuum solution and out of our discussion. The NEC is the minimum requirement of energy conditions, which is actually a constraint on the mass of particle, i.e.

$$\begin{aligned} m<\frac{\pi }{2a}(2\alpha -1). \end{aligned}$$
(32)

As \(m>0\), one can find

$$\begin{aligned} \alpha >\frac{1}{2}, \end{aligned}$$
(33)

which indicates that the anyon IPP solutions only exhibit a quasi Fermi–Dirac statistics, while the quasi Bose–Einstein statistics case are invalid and corresponding to physically un-acceptable matter source. Especially for the classical IPP solutions, i.e. \(b=0,\alpha =\frac{1}{2}\), the NEC is simplified as \(\rho +P_{\theta }=-\frac{a}{4(C_{\ell }+2)r^2}\), which is always negative for \(a>0\). Thus it is invalid, which is consistent with the conclusions in [19].

Considering other energy conditions, one also study directly the large r behaviour. It is easy to obtain that valid the WEC leads to Eq. (32) and \(-2<C_{\ell }\le 0\); the SEC corresponds to Eq. (32) and \(C_{\ell }\ge 0\); the DEC requires Eq. (32) and \(-2<C_{\ell }\le 0\). Especially for the case \(C_{\ell }=0\), as \(\rho =P_{\theta }=\frac{(-2am+2\pi \alpha -\pi )}{32mr^2}\), ALL energy conditions reduce to \(\rho >0\), i.e. the inequality Eq. (31). Then when the condition Eq. (32) holds, ALL energy conditions hold.

Totally, under the condition Eq. (32), one can find:

  • When \(-2<C_{\ell }<0\): the NEC, WEC and DEC hold;

  • When \(C_{\ell }>0\): the NEC, SEC are valid;

  • When \(C_{\ell }=0\): ALL energy conditions hold.

Besides, one can conclude that there is only a quasi Fermi–Dirac anyon IPP solutions.

4.2 Horizon structure

Before discussing the black hole solutions in three dimensions, we should firstly calculate some associated geometric quantities to further characterize the geometry of the solutions. The Ricci scalar takes the form

$$\begin{aligned} R=-6\Lambda _{eff}+\frac{(-2am+2\pi \alpha -\pi )\pi }{(C_{\ell }+2)mr^2}, \end{aligned}$$
(34)

which corresponds to a curvature singularity at \(r=0\) if \((-2am+2\pi \alpha -\pi )\ne 0\). For the black hole solutions, there should exist a event horizon according to the Cosmic Censorship Conjecture [28, 29]. The Cotton tensor \(C_{\mu \nu \sigma }=\nabla _\sigma R_{\mu \nu }-\nabla _\nu R_{\mu \sigma } +\frac{1}{4}(\nabla _\nu R g_{\mu \sigma } - \nabla _\sigma R g_{\mu \nu })\) contains some non-vanishing components, and we only list a simple one below:

$$\begin{aligned} C_{\theta \,r\theta }=\frac{(-2am+2\pi \alpha -\pi )\pi }{2(C_{\ell }+2)mr}. \end{aligned}$$

When \((-2am+2\pi \alpha -\pi )\ne 0\), the non-vanishing Cotton tensor signifies that the metric is not conformally flat [30].

The event horizon \(r=r_+\) is the biggest positive root of \(f(r)=0\). Under the condition Eq. (31) and considering the behaviour of

$$\begin{aligned}&f'(r)=8\pi \,(C_{\ell }+2)P_{\Lambda }r\bigg (1-\frac{r_{ex}^2}{r^2}\bigg ),\nonumber \\&r_{ex}=\frac{1}{(C_{\ell }+2)}\sqrt{\frac{(-2am+2\pi \alpha -\pi )}{8\,P_{\Lambda }m}}, \end{aligned}$$
(35)

it is easy to obtain that f(r) always decrease from \(+\infty \) to the minimum \(f(r_{ex})\), and then increase to \(+\infty \). Here the minimum can be simplified as

$$\begin{aligned}&f(r_{ex})=-8(M-M_{ex}),\nonumber \\&M_{ex}=\frac{\pi \bigg (1-2\ln (r_{ex})\bigg )(-2am+2\pi \alpha -\pi )}{16(C_{\ell }+2)m}. \end{aligned}$$
(36)

Then there are three cases:

  • If \(M<M_{ex}\), f(r) will always be positive, indicating that the solution corresponds to an asymptotically AdS\({}_3\) spacetime with a naked singularity, which is a physically unacceptable;

  • If \(M=M_{ex}\), i.e. \(f(r_{ex})=0\), it is evident that \(r_{ex}\) is a double root of f(r). Thus this case corresponds to a three dimensional extremal anyon IPP AdS black hole;

  • If \(M>M_{ex}\), f(r) will have two positive zeros, which both correspond to the black hole horizon, with the outer one being the event horizon. This solution corresponds to a non-extremal anyon IPP AdS black hole.

In conclusion, when \(m<\frac{\pi }{2a}(2\alpha -1),M\ge \,M_{ex}\), there is a quasi Fermi–Dirac anyon IPP black holes in three dimensions, while the one taking Bose–Einstein statistics is physically acceptable.

Fig. 1
figure 1

The free energy F of anyon IPP black hole relates to the temperature T when \(C_{\ell }=0,m=\frac{1}{10},a=\frac{1}{10},\alpha =\frac{4}{5},P=10\). The zero located in \(T_c\) indicates Hawking–Page transition between the anyon IPP black holes and the pure thermal radiation

Full size image

When \(a=0\), the solution degenerates into an anyon perfect gas black hole, which reads as

$$\begin{aligned}&f(r)=-8M+4\pi \,(C_{\ell }+2)P_{\Lambda }r^2-\frac{(2\pi \alpha -\pi )\pi }{(C_{\ell }+2)m}\ln (r),\nonumber \\&\rho =-\frac{1}{2}P_{\Lambda }C_{\ell } +\frac{(2\pi \alpha -\pi )}{16(C_{\ell }+2)mr^2},\nonumber \\&P_{\theta }=\frac{1}{2}P_{\Lambda }C_{\ell } +\frac{(2\pi \alpha -\pi )}{16(C_{\ell }+2)mr^2}, \end{aligned}$$

with the Ricci scalar Eq. (34) reduced to \(R=-6\Lambda _{eff}+\frac{(2\pi \alpha -\pi )\pi }{(C_{\ell }+2)mr^2}\). As the valid NEC Eq. (31) reduces to \((2\alpha -1)\pi >0\), the above one characterizes the solution exhibiting Bose–Einstein statistics with arbitrary particle mass m.

4.3 Hawking–Page phase transition

The thermodynamic quantities of anyon IPP black holes are list here:

$$\begin{aligned}&M=\frac{\pi }{2}(C_{\ell }+2)P_{\Lambda }r_+^2 -\frac{(-2am+2\pi \alpha -\pi )\pi }{8m(C_{\ell }+2)}\ln (r), \quad \,\nonumber \\&S =\frac{\pi \,r_+}{2},\nonumber \\&T=2(C_{\ell }+2)P_{\Lambda }r_+-\frac{(-2am+2\pi \alpha -\pi )}{4m(C_{\ell }+2)r_+},\quad \,\nonumber \\&V=\frac{\pi }{2}(C_{\ell }+2)\,r_+^2. \end{aligned}$$
(37)

Now we examine the behavior of free energy the free energy, which characterizing the global stability and can be calculated as

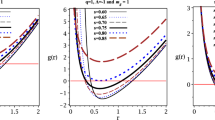
$$\begin{aligned} F&=H-TS-P_{\Lambda }V=M-TS-P_{\Lambda }V\nonumber \\&=-\pi (C_{\ell }+2)P_{\Lambda }r_+^2\nonumber \\&\quad -\frac{(-2am+2\pi \alpha -\pi )\pi }{8m(C_{\ell }+2)}\bigg (\ln (r)-1\bigg ). \end{aligned}$$
(38)

As F always decreases from \(+\infty \) to \(-\infty \), it is sure that there is a black hole horizon \(r+=r_c\) corresponding to vanishing free energy. The critical temperature should be \(T_c=T|_{r=r_c}\). From Fig. 1, it is easy to find that the free energy changes its sign at Hawking temperature \(T=T_c\). Namely, there exist the Hawking–Page phase transition between the anyon IPP black holes and the pure thermal radiation phase [31].

5 Conclusion

In this paper, we present the exact anyon solutions, and find some different but interesting results comparing with the so-called small effective pressure limit anyon black hole [20] and standard VdW solutions [19], including:

  • The exact anyon VdW solutions with \(b>0\) are physically un-acceptable in the global spacetime. However they are acceptable near the horizon, which is consistent with the small effective pressure limit [20] and the standard VdW case [19].

  • Especially for the reduced case \(b=0\), there is an anyon black hole taking the precisely same thermodynamical properties with the gas of “interacting point particle” (IPP). Besides, the IPP should only exhibit a quasi Fermi–Dirac statistics and have an upper bound of mass. This is the first physical VdW-like global black hole solution in the global spacetime, as the small effective pressure limit [20] and the standard VdW case [19] are both the near horizon metric and physical unacceptable in the global spacetime.

  • The anyon IPP black hole can contain 1 or 2 horizons. Moreover, there exist the Hawking–Page phase transition between the anyon IPP black holes and the pure thermal radiation phase.

For the future tasks, we will construct the black holes corresponding to thermodynamics of particles taking the fractional statistics in four and high dimensions [23, 25]. It is also interesting and important to explore the microscopic structure of black holes, in order to interpret the thermodynamics of this kind of black holes by quantum statistics viewpoints.