1 Introduction

The historical trajectory of studies on the dynamics of two-body systems can be traced back to the early investigations following the introduction of the Dirac equation [1]. The initial attempts to theoretically analyze fermion–antifermion (\(f{\overline{f}}\)) systems led to the formulation of a two-body equation by Breit, where the velocities were replaced with Dirac matrices, and the modified Darwin potential served as the inter-particle interaction potential [2]. While effective in weak-coupling scenarios, this equation faced limitations in addressing long-range interactions and high velocities due to retardation effects. Subsequently, Bethe and Salpeter proposed a novel formalism rooted in quantum field theory to overcome these challenges [3]. However, this approach introduced a relative time problem, prompting the exploration of alternatives, including the instantaneous-interaction approximation. Barut extended the quest for a Dirac-Coulomb type two-body equation, seeking a solution in 3+1 dimensions with exact solvability. His pursuit included the incorporation of retardation effects, precise spin algebra, and accommodation of general electromagnetic potentials. From quantum electrodynamics, Barut derived such an equation through the action principle [4]. Despite providing a covariant framework and yielding a set of coupled equations in 3+1 dimensions, Barut’s equation remained unsolvable for well-known systems like one-electron atoms or positronium-like \(f{\overline{f}}\) systems. This is because Barut’s equation yields a system of coupled second-order wave equations in 3+1 dimensions [5]. Notably, the exact solubility of this equation has been demonstrated in three-dimensional flat spaces [6] as well as in curved spaces [7,8,9,10] for specific coupled \(f{\overline{f}}\) systems. However, applying this covariant two-body Dirac equation to interacting fermions in a black hole (BH) background poses challenges, and despite new approaches [11], achieving precise results in such scenarios remains elusive, necessitating reliance on numerical methods even for associated one-body fields.

On the other hand, it is well-established that the near-horizon (\({\mathcal {N}}_{h}\)) background of a BH encodes crucial information pertaining to the Kerr/CFT (conformal field theory) correspondence’s key outcomes [12]. In this context, investigating the ramifications of the interaction between a \(f{\overline{f}}\) pair within the \({\mathcal {N}}_{h}\) of the Banados–Teitelboim–Zanelli (BTZ) BH [13] becomes particularly intriguing. The BTZ BH, originally introduced as a one-body solution to the Einstein field equations in \(2+1\) dimensions with a negative cosmological constant (\(\Lambda =-1/\ell ^2\)), can be described by three parameters: mass, charge, and angular momentum, closely resembling \(3+1\) dimensional BHs. However, it resides locally and asymptotically in \(2+1\) dimensional anti-de Sitter (AdS) spacetime. The corresponding background is neither asymptotically flat nor does it exhibit curvature singularities at the origin [14]. The \({\mathcal {N}}_{h}\) background of the BTZ BH was introduced in Ref. [15], opening the possibility of analyzing the evolution of a composite particle formed by an interacting \(f{\overline{f}}\) pair in this background spacetime. Consideration of a strongly coupled \(f{\overline{f}}\) pair in this context involves analyzing the pair’s evolution through a Cornell-type non-minimal interaction, commonly known as the generalized Dirac oscillator (\(g\mathcal{D}\mathcal{O}\)) interaction. The \(\mathcal{D}\mathcal{O}\) system, introduced by modifying the momentum operator(s) of the free Dirac Hamiltonian, results in a non-relativistic harmonic oscillator with strong spin-orbit coupling in the non-relativistic limit [16]. The \(\mathcal{D}\mathcal{O}\) system’s super-potential was derived, demonstrating its description of the coupling of the anomalous (chromo) magnetic moment with a linearly growing electric field [17]. The \(\mathcal{D}\mathcal{O}\) system serves as an alternative confinement potential for heavy quarks in quantum chromodynamics, with applications in describing the dynamics of quarks in mesons and baryons [6, 7, 16, 17]. The \(g\mathcal{D}\mathcal{O}\) represents a generalized form of the \(\mathcal{D}\mathcal{O}\), investigated through Cornell-type non-minimal coupling into the Dirac Hamiltonian. Although Moshinsky et al. [18] initially studied the \(\mathcal{D}\mathcal{O}\) system as a coupling term between an interacting \(f{\overline{f}}\) pair in \(3+1\) dimensions, only perturbative solutions were obtained. In contrast, in \(2+1\) dimensions, exact results were derived [6]. These results suggest that the relativistic dynamics of an \(f{\overline{f}}\) pair, bound together by the \(g\mathcal{D}\mathcal{O}\) coupling, may be exactly solvable in certain \(2+1\) dimensional curved spaces [7]. However, despite research on the evolution of relativistic oscillators [19, 20], there is a notable absence of studies exploring the evolution of a composite system composed of interacting \(f{\overline{f}}\) pairs in a BH background. This manuscript aims to bridge this gap by investigating the effects of the interaction between particles on the evolution of a \(f{\overline{f}}\) pair coupled through the \(g\mathcal{D}\mathcal{O}\) interaction in the \({\mathcal {N}}_{h}\) of the BTZ BH.

This paper is arranged as follows: in Sect. 2, we present the generalized form of the covariant two-body equation for a \(f{\overline{f}}\) pair interacting through the \(g\mathcal{D}\mathcal{O}\) interaction in the \({\mathcal {N}}_{h}\) of the BTZ BH and then we attempt to derive a set of coupled equations for the relative motion of the considered pair. In Sect. 3, we showcase non-perturbative results for such a static spinless composite system. Subsequently, we provide a summary and discuss the results in Sect. 4. In this work, we will use the units \(G=1=\hbar =c\).

2 System of coupled equations

Here, let us begin by introducing the fully-covariant two-body Dirac equation in a \(2+1\) dimensional curved background spacetime [7, 8]

(2.1)

in which Greek indice(s) refers the coordinates of the curved spacetime. In this equation, \(\gamma ^{\mu }\) are the space-dependent Dirac matrices that can be determined by the relation: \(\gamma ^{\mu }=e^{\mu }_{(k)}\gamma ^{(k)}\) in which \(e^{\mu }_{(k)}\) are the inverse tetrad fields and \(\gamma ^{(k)}\), where \(k=0,1,2.\), are the space-independent Dirac matrices that may be chosen in terms of the Pauli matrices, \((\sigma ^{x}, \sigma ^{y}, \sigma ^{z} )\) as follows: \(\gamma ^{0}=\sigma ^{z}\), \(\gamma ^{1}=i\sigma ^{z}\), \(\gamma ^{2}=i\sigma ^{y}\) if one considers a \(2+1\) dimensional metric with negative signature, for which the Minkowski tensor (\(\eta _{(k)(l)}\)) is \(\eta _{(k)(l)}=\text {diag}(+,-,-)\). The inverse tetrad fields can be found by using \(e^{\mu }_{(k)}=g^{\mu \tau }e_{\tau }^{(l)}\eta _{(k)(l)}\) expression [20]. Here, \(g^{\mu \tau }\) is the contravariant metric tensor and \(e_{\tau }^{(l)}\) are the tetrad fields determined through \(g_{\mu \tau }=e_{\mu }^{(k)}e_{\tau }^{(l)}\eta _{(k)(l)}\) in which \(g_{\mu \tau }\) is the covariant metric tensor. Spinorial affine connections are represented by \(\Gamma _{\mu }\) in the Eq. (2.1) and components of the \(\Gamma _{\mu }\) are obtained by using \(\Gamma _{\lambda }=\frac{1}{8}\left[ e^{(k)}_{\nu _{,\lambda }}e^{\tau }_{(k)}-\Gamma _{\nu \lambda }^{\tau } \right] \left[ \gamma ^{\mu },\gamma ^{\nu }\right] \), in which \(\Gamma _{\nu \lambda }^{\tau }\) are the Christoffel symbols that can be found via the following relation: \(\Gamma _{\nu \lambda }^{\tau }=\frac{1}{2}g^{\tau \epsilon }\left[ \partial _{\nu } g_{\lambda \tau }+\partial _{\lambda } g_{\epsilon \nu }-\partial _{\epsilon } g_{\nu \lambda } \right] \). In addition, the notation \(I_2\) denotes a two-dimensional identity matrix, and \(f ({\overline{f}})\) refers a fermion (antifermion) in our context. Specifically, we are considering a pair of fermions, \(f{\overline{f}}\), each with an equal mass denoted as \(m^{f}=m^{{\overline{f}}}=m\). Moving forward, we aim to introduce the spacetime interval that characterizes the \({\mathcal {N}}_{h}\) background of the BTZ BH. The construction of this background aligns with the methodology introduced in [15]. Adhering to the conventions of negative signature, the expression for the spacetime interval can be redefined as follows:

$$\begin{aligned} ds^2 \approx \frac{\alpha ^2\rho ^2}{\ell ^2}dt^2-d\rho ^2-\alpha ^2\ell ^2d\phi ^2, \end{aligned}$$
(2.2)

in which, as is customary, the parameter \(\ell \) is associated with the cosmological constant, while the parameter \(\alpha \) (where \(\alpha >0\)) is linked to the BH mass. In this context, it is essential to highlight that the time is identified with the period \(\beta =2\pi \frac{\ell }{\alpha }\) so that Euclidean continuation in the \((t,\rho )\)-plane becomes singularity-free [15]. At first look, one can write the covariant form of the metric tensor for the line element (2.2) as the following: \(g_{\mu \nu }=\text {diag}(\alpha ^2\rho ^2/\ell ^2, -1, -\alpha ^2\ell ^2)\) and one can easily determine its contravariant form, since \(g_{\mu \nu }g^{\mu \nu }=I_{3}\). Accordingly, we can obtain the following results (see also [20])

$$\begin{aligned} e^{\mu ^{f({\overline{f}})}}_{(k)}= & {} \text {diag}\left( \frac{\ell }{\alpha \rho ^{f({\overline{f}})}}, 1, \frac{1}{\alpha \ell } \right) ,\nonumber \\ \gamma ^{t^{f({\overline{f}})}}= & {} \frac{\ell }{\alpha \rho ^{f({\overline{f}})}}\sigma ^{z},\quad \gamma ^{\rho ^{f({\overline{f}})}}=i\sigma ^{x},\quad \gamma ^{\phi ^{f({\overline{f}})}}=\frac{1}{\alpha \ell }i\sigma ^{y},\nonumber \\ \Gamma _{t\rho }^{t^{f({\overline{f}})}}= & {} \frac{1}{\rho ^{f({\overline{f}})}}, \quad \Gamma _{t t}^{\rho ^{f({\overline{f}})}}=\frac{\alpha ^2 \rho ^{f({\overline{f}})}}{\ell ^2},\quad \Gamma _{t}^{^{f({\overline{f}})}}=\frac{\alpha }{2\ell }\sigma ^{y},\nonumber \\ e_{\mu }^{(k)^{f({\overline{f}})}}= & {} \text {diag}\left( \frac{\alpha \rho ^{f({\overline{f}})}}{\ell }, 1, \alpha \ell \right) . \end{aligned}$$
(2.3)

Here, it is clear that the tetrad fields satisfy the orthogonality and orthonormality conditions. Additionally, it is observed that \(\gamma ^{\mu ^{^{f({\overline{f}})}}}\Gamma ^{^{f({\overline{f}})}}_{\mu }=-i\frac{1}{\rho ^{f({\overline{f}})}}\sigma ^{x}\) due to the presence of only one non-vanishing component, \(\Gamma ^{^{f({\overline{f}})}}_{t}\), in the spinorial affine connections. To further clarity, let us express the fully-covariant two-body Dirac equation explicitly in the form \(\hat{{\mathcal {M}}}\Theta =0\), where \(\hat{{\mathcal {M}}}\) is

(2.4)

Now, by examining the spacetime interval under consideration, we can express the spacetime-dependent bi-spinor \(\Theta (t,r,R)\) as a factorized form, \(\Theta =e^{-i\omega t}\theta (r,R)\), where \(\omega \) represents the relativistic frequency, and r and R denote the relative motion coordinates and center of mass motion coordinates, respectively, introduced through

$$\begin{aligned} r_{\mu }= & {} x_{\mu }^{f}-x_{\mu }^{{\overline{f}}},\quad R_{\mu }=\frac{x_{\mu }^{f}+x_{\mu }^{{\overline{f}}}}{2},\quad x_{\mu }^{f}=\frac{1}{2}r_{\mu }+R_{\mu },\nonumber \\ x_{\mu }^{{\overline{f}}}= & {} -\frac{1}{2}r_{\mu }+R_{\mu }, \partial _{x_{\mu }}^{f}=\partial _{r_{\mu }}+\frac{1}{2}\partial _{R_{\mu }},\nonumber \\ \partial _{x_{\mu }}^{{\overline{f}}}= & {} -\partial _{r_{\mu }}+\frac{1}{2}\partial _{R_{\mu }}, \end{aligned}$$

for two fermions with identical masses. Here, it should be noted that \(\partial _{x_{\mu }}^{f}+\partial _{x_{\mu }}^{{\overline{f}}}=\partial _{R_{\mu }}\). The evolution of the system, linked to the relativistic frequency \(\propto \omega \), is governed in relation to the proper time, denoted as \(\partial _{R_{t}}\). In Eq. (2.4), we express the partial derivatives with respect to the radial coordinate as , allowing for the substitution of the Cornell-type non-minimal coupling into each free Dirac Hamiltonian. This is crucial as the generalized Dirac oscillator coupling is introduced by altering the free Dirac Hamiltonian in accordance with the method outlined in [7]

Here, m denotes the rest mass of each particle, while \(\omega _{o}\) is employed to signify the oscillator frequency or coupling strength. In the context of the \(f{\overline{f}}\) system coupled through the \(g\mathcal{D}\mathcal{O}\) interaction, it is important to highlight that \(\omega _{o}^{f}=-\omega _{o}^{{\overline{f}}}=\omega _{o}\), as discussed in references [6, 7, 18]. Here, our focus lies in examining the relative motion of the \(f{\overline{f}}\) pair, which can be elucidated by assuming the center of mass of the system is stationary at the origin. At that rate, one can factorise the spatial part of the spinor \(\theta (\rho ,\phi )=e^{is\phi }(\psi _{1},\psi _{2},\psi _{3},\psi _{4})^{T}\), in which s is the total spin of the considered composite system. At that rate, we can derive the following coupled equations governing this static composite system without spin (\(s=0\))

$$\begin{aligned}{} & {} \varpi (\rho )\chi _{3}(\rho )+{\hat{\Lambda }}\chi _{2}(\rho )+{\tilde{f}}(\rho )\chi _{1}(\rho )-m\chi _{4}(\rho )=0,\nonumber \\{} & {} \varpi (\rho )\chi _{1}(\rho )+{\tilde{f}}(\rho )\chi _{3}(\rho )=0,\nonumber \\{} & {} \varpi (\rho )\chi _{2}(\rho )-{\hat{\Lambda }}\chi _{3}(\rho )=0,\nonumber \\{} & {} \varpi (\rho )\chi _{4}(\rho )-m \chi _{3}(\rho )=0, \end{aligned}$$
(2.5)

where

$$\begin{aligned}{} & {} \varpi (\rho )=\frac{\omega \ell }{\alpha \rho },\quad {\hat{\Lambda }}=\left[ \partial _{\rho }+\frac{1}{\rho } \right] ,\\{} & {} \quad {\tilde{f}}(\rho )=\frac{\ell }{\alpha }\kappa \left[ \frac{a}{2}\rho +\frac{2b}{\rho }\right] , \end{aligned}$$

\(\kappa =m\omega _{o}\), provided \(\chi _{1}(\rho )=\psi _{1}(\rho )+\psi _{4}(\rho )\), \(\chi _{2}(\rho )=\psi _{1}(\rho )-\psi _{4}(\rho )\), \(\chi _{3}(\rho )=\psi _{2}(\rho )+\psi _{3}(\rho )\) and \(\chi _{4}(\rho )=\psi _{2}(\rho )-\psi _{3}(\rho )\). Here, we have defined new components to transform some concluding equations into algebraic forms. Notably, all remaining components can be represented in relation to the component \(\chi _{3}(\rho )\), enabling the derivation of a second-order non-perturbative wave equation (Table 1).

Table 1 A report on the decay time of damped modes for a composite system, comprising a pair of \(f{\overline{f}}\) interacting through the \(g\mathcal{D}\mathcal{O}\) coupling in the \({\mathcal {N}}_{h}\) region of the BTZ BH. Here, \(m=0.2\), \(a=0.1\), \(b=0.1\), \(\alpha =0.9\), \(\ell =1\)
Full size table

3 Exact solution

In this section, our aim is to derive a non-perturbative solution for the system of equations outlined in Eq. (2.5). By solving this set of equations in favor of \(\chi _{3}(\rho )\), we can express the outcome through the following equation

$$\begin{aligned} \chi _{3_{,\rho \rho }}+\frac{3}{\rho }\chi _{3_{,\rho }}+\left[ \varpi (\rho )^2+\frac{1}{\rho ^2}-{\tilde{f}}(\rho )^2-m^2 \right] \chi _{3}=0, \nonumber \\ \end{aligned}$$
(3.1)

where \(_{,\rho }\) denotes the derivative with respect to the variable \(\rho \). Introducing a new variable transformation, \(\xi =\frac{\ell }{2\alpha }\kappa a \rho ^2\) (note that \(\xi \rightsquigarrow 0 (\infty )\) as \(\rho \rightsquigarrow 0 (\infty )\)), leads to a wave equation governing \(\chi _{3}(\xi )\). By employing an ansatz function, \(\chi _{3}(\xi )=\xi ^{-1}\chi (\xi )\), this wave equation can be simplified into a more recognizable form,

$$\begin{aligned} \left[ \partial _{\xi }^2+\frac{{\tilde{\mu }}}{\xi }+\frac{\frac{1}{4}-{\tilde{\nu }}^2}{\xi ^2}-\frac{1}{4} \right] \chi (\xi )=0, \end{aligned}$$
(3.2)

in which

$$\begin{aligned} {\tilde{\mu }}=-\frac{2ab\kappa ^2\ell ^2+m^2\alpha ^2}{2a\alpha \ell \kappa },\quad {\tilde{\nu }}=\frac{\ell }{2\alpha }\sqrt{4b^2\kappa ^2-\omega ^2}. \end{aligned}$$

Now, providing the following clear formulations, specifically in relation to the variable \(\xi \), for the identified components could prove beneficial

$$\begin{aligned} \chi (\xi )= & {} \xi \chi _{3}(\xi ),\quad \chi _{1}(\xi )=-\frac{\kappa }{\omega }\left[ \frac{\alpha \xi }{\kappa \ell }+2b \right] \chi _{3}(\xi ),\nonumber \\ \chi _{2}(\xi )= & {} \frac{\alpha }{\omega \ell }\left[ 2\kappa \xi \partial _{\xi }+1 \right] \chi _{3}(\xi ), \ \chi _{4}(\xi )=\frac{m\alpha }{\omega \ell }\sqrt{\frac{2\alpha \xi }{\kappa \ell a}}\chi _{3}(\xi ). \end{aligned}$$

Solution function of the Eq. (3.2) can be expressed in terms of the confluent hypergeometric function, \(\chi (\xi )=e^{-\frac{\xi }{2}}\xi ^{\frac{1}{2}+{\tilde{\nu }}}\ _1F_{1}(\frac{1}{2}+{\tilde{\nu }}-{\tilde{\mu }}, 1+2{\tilde{\nu }}; \xi )\). In this context, it is essential to highlight that the analyzed system is confined within the \({\mathcal {N}}_{h}\) region, and the corresponding wave function(s) should asymptotically approach zero as the spatial coordinate extends to infinity, expressed as \(\chi (\xi )\propto e^{-\xi }\). However, it is known that the asymptotic form of the function \( _1F_{1}(\frac{1}{2}+{\tilde{\nu }}-{\tilde{\mu }}, 1+2{\tilde{\nu }}; \xi )\)

$$\begin{aligned} \approx \frac{\Gamma (1+2{\tilde{\nu }})}{\Gamma (\frac{1}{2}+{\tilde{\nu }}-{\tilde{\mu }})}\frac{e^{\xi }}{\xi ^{(\frac{1}{2}+{\tilde{\nu }}+{\tilde{\mu }})}}\left[ 1+{\mathcal {O}}(|\xi |^{-1}) \right] , \end{aligned}$$

is divergent when \(\xi \rightsquigarrow \infty \). In seeking the regular solution for the wave equation, we aim to establish it by imposing the condition \(\frac{1}{2}+{\tilde{\nu }}-{\tilde{\mu }}=-n\), where n represents the overtone number \((n=0,1,2...)\). This leads to the derivation of the relativistic frequency expression for the analyzed system

$$\begin{aligned} \omega _{n}=-i\sqrt{\frac{4\alpha ^2}{\ell ^2}\left[ n^{{\textbf {*}}}+\frac{m^2\alpha ^2+2ab\kappa ^2\ell ^2}{2a\alpha \ell \kappa } \right] ^2 -4b^2\kappa ^2}, \nonumber \\ \end{aligned}$$
(3.3)
Fig. 1
figure 1

Influence of parameters \(\alpha \), \(\omega _{o}\), b and m on the decay time of damped modes

Full size image

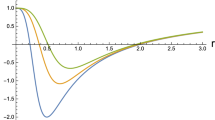
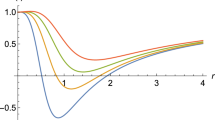
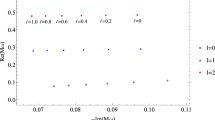
in which \(n^{{\textbf {*}}}=n+\frac{1}{2}\). It is clear that the lowest mode (\(n=0\)) becomes \(\omega _{0}\rightsquigarrow -i\alpha /\ell \) when \(m\rightsquigarrow 0\). Through this way, we can derive the formal Hawking temperature for the background, consistent with earlier findings as documented in [15]. At first look, it is evident that these identified states lack stability and the corresponding modes decay exponentially over time. Moreover, the alteration in decay rates manifests as a consequence of the interplay between the spacetime parameters intrinsic to the surrounding environment and the intensity of the particle-particle coupling. These findings necessitate an analysis into the impact of the background conditions on the evolution of the \(f{\overline{f}}\) pair, owing to the unequivocal correlation between non-perturbative frequency modes and both background parameters (\(\alpha , \ell \)) and parameters (\(a, b, \omega _{o}\)) associated with inter-particle interaction. Furthermore, the decay rates undergo modification influenced by both the background spacetime parameters and the strength of the coupling between the particles. To derive insights from the expression presented in Eq. (3.3), a formula can be established for the practical computation of the decay time (\(\tau _{n}\propto |\omega _{{\mathcal {I}}m}|^{-1}\)) of the damped modes

$$\begin{aligned} \tau _{n}=\left[ \frac{4\alpha ^2}{\ell ^2}\left[ n^{{\textbf {*}}}+\frac{m^2\alpha ^2+2ab\kappa ^2\ell ^2}{2a\alpha \ell \kappa } \right] ^2 -4b^2\kappa ^2 \right] ^{-1/2},\nonumber \\ \end{aligned}$$
(3.4)

since \(\Theta \propto e^{-i\omega t}\). Upon initial examination, it appears that the modes exhibit relatively prolonged lifetimes as \(\alpha \) approaches zero (where \(\alpha > 0\)); nevertheless, a notable observation emerges, wherein all modes experience accelerated decay with higher values of \(\alpha \). Furthermore, an intriguing pattern unfolds, elucidating that damped modes manifest swifter decay rates with increasing parameters b and m, especially within the excited states of the system. Notably, an examination of the decay time reveals a nuanced behavior, with modes exhibiting an initial increase in decay time up to a specific \(\omega _{o}\) value for each possible quantum state, beyond which they undergo accelerated decay for larger \(\omega _{o}\) values (see Fig. 1).

4 Summary and discussions

In this work, we conducts an analysis of the evolution of a composite particle comprised of a \(f{\overline{f}}\) pair, interacting through the \(g\mathcal{D}\mathcal{O}\) interaction in the \({\mathcal {N}}_{h}\) region of the BTZ BH. Our analysis involves deriving a non-perturbative solution for the fully-covariant one-time two-body Dirac equation corresponding to the system. Initially, we formulate the two-body equation for two fermions in the \({\mathcal {N}}_{h}\) background, introducing the \(g\mathcal{D}\mathcal{O}\) coupling through Cornell-type non-minimal interaction terms incorporated into each free Dirac Hamiltonian. Subsequently, by separating relative motion and center of mass motion coordinates, we arrive at a set of coupled equations governing the relative motion of the interacting particles, assuming the center of mass to be stationary at the spatial origin. For such a spinless static composite system, the resultant set of equations yields an exactly soluble wave equation, and we successfully obtain an exact solution. Notably, our findings reveal that the composite particle undergoes temporal decay devoid of any real oscillatory behavior. Furthermore, the decay rates are found to be contingent on both the background parameters and the strength of the coupling between particles. Our investigation yields a precise result (3.4), simplifying the computation of decay times for damped modes and illustrating their sensitivity to background parameters and inter-particle interaction parameters in Fig. 1. In the initial segment (a) of this figure, we observe that the decay time of the lowest mode (\(n=0\)) surpassed that of the other excited states, with all modes exhibiting faster decay rates for larger values of the parameter \(\alpha \) (where \(\alpha \propto \) BH mass). Clearly, relatively long-lived modes are discernible for smaller \(\alpha \) values. Segment (b) of the figure shows the possibility of relatively long-lived modes, particularly for the lowest damped mode, associated with specific values of the coupling strength (\(\propto \omega _{o}\)). Nevertheless, all modes exhibits faster decay for larger values of the oscillator frequency \(\omega _{o}\). The third segment of Fig. 1 illustrate the impact of the Coulombic term coefficient (\(\propto b\)) in Cornell-type coupling on the damped modes, revealing rapid decay, particularly for larger values of the parameter b. Additionally, we observe that the decay time of damped modes could be relatively prolonged for smaller rest masses (m) of the particles, while larger rest masses led to faster decay. Here, it is pertinent to note that our exact results were confined to the evolution of a spinless static composite particle (e.g., a meson) formed by an interacting \(f{\overline{f}}\) pair in the \({\mathcal {N}}_{h}\) region of the BTZ BH. Although the derivation appears intricate, the prospect of obtaining exact results for interacting particles in a complete BH or other non-trivial topologies remains a promising avenue for our future research (see also [21]). Here, it is worth mentioning that the existing literature presents compelling findings by applying the principles of simulating gravitational effects in condensed matter systems, particularly emphasizing 2+1 dimensions and the Weyl symmetry in defining the massless Dirac field. A notable research approach is the use of graphene as a tangible representation of quantum field theory in curved spacetimes [22, 23]. However, in our research, it is crucial to emphasize that the intricate interplay between the considered \(f{\overline{f}}\) pair is closely tied to the masses of the particles involved. When the mass is zero, the system transforms into a two-body problem with no interaction between the particles, since \(\kappa =m\omega _{o}\). It is noteworthy, however, that such a reduction may not make any sense within the specific context under consideration. On the other hand, the AdS/CFT correspondence serves as a powerful tool in theoretical physics, linking specific gravitational theories in AdS space to conformal field theories in one lower dimension [24,25,26]. In alignment with the AdS/CFT correspondence, the exact outcomes derived for systems analogous to exciton-like configurations or Weyl pairs, subjected to external electromagnetic fields within this spacetime region, may offer an avenue for establishing an analogy and exploring intriguing condensed matter phenomena. By imposing appropriate boundary conditions, scenarios involving the \({\mathcal {N}}_{h}\) region of black holes can be systematically investigated across diverse limits, thereby exploring new aspects of holographic superconductivity within the corresponding dual field theory. Although the presence of external magnetic fields or magnetization adding complexity to the system, investigating the evolution of mutually-interacting \(f{\overline{f}}\) pairs in magnetized \({\mathcal {N}}_{h}\) region of BHs may allow the “observation” of novel results, in principle. This can be very interesting because such a system can be mapped to mutually-interacting massless charge carriers within a superconductor influenced by external magnetic fields. This line of inquiry holds promise in contributing to the understanding of a spectrum of condensates and statistical properties of many-body systems. We believe that a comprehensive analysis of the aforementioned study could yield profound insights across various domains of modern physics. Therefore, within this context, our objective is to conduct an in-depth and thorough analysis in the near future.