1 Introduction

The LHC record energy, as well as the good resolution in azimuthal angles of the particle detectors, offer a unique opportunity to test a wide class of predictions of perturbative QCD. These include the so called Mueller–Navelet jet production [1], i.e. the inclusive production of two jets featuring a large rapidity separation between them, for which a wealth of theoretical analyses were produced in the last years [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16], and the somewhat related process where two identified, charged light hadrons well separated in rapidity are inclusively produced [17, 18], instead of jets.

A common feature to these two processes is that their high-energy behavior is dominated by those final-state configurations where the produced particles are strongly ordered in rapidity, the tagged objects (jets or identified hadrons) being the two extrema in the rapidity tower, thus yielding a number of energy logarithms growing with the number of produced particles. Such energy logarithms are so large to compensate the smallness of the coupling \(\alpha _s\), so the perturbative series must be properly resummed.

The theoretical framework for the resummation of energy logs for these two processes, as well as for any semi-hard process in perturbative QCD, is provided by the Balitsky–Fadin–Kuraev–Lipatov (BFKL) approach [19,20,21,22], whereby the resummation of all terms proportional to \((\alpha _s\ln (s))^n\), the so called leading logarithmic approximation or LLA, and that of all terms proportional to \(\alpha _s(\alpha _s\ln (s))^n\), the next-to-leading approximation or NLA, can be systematically carried out. The bottom line of the BFKL formalism is that azimuthal coefficients of the Fourier expansion of the cross section differential in the variables of the tagged objects over the relative azimuthal angle take the very simple form of a convolution between two impact factors, describing the transition from each colliding proton to the respective final state tagged object, and a process-independent Green’s function. The BFKL Green’s function obeys an integral equation, whose kernel is known at the next-to-leading order (NLO) both for forward scattering (i.e. for \(t=0\) and color singlet in the t-channel) [23, 24] and for any fixed (not growing with energy) momentum transfer t and any possible two-gluon color state in the t-channel [25,26,27,28,29,30,31].

The impact factors for the proton to forward jet transition (the so called “jet vertices”) are known up to the NLO for several jet selection algorithms [32,33,34,35,36]. The jet vertex, in its turn, can be expressed, within leading-twist collinear factorization, as the convolution of the parton distribution function (PDF) of the colliding proton, obeying the standard DGLAP evolution [37,38,39], with the hard process describing the transition from the parton emitted by the proton to the forward jet in the final state. Two such jet vertices must be convoluted with the BFKL Green’s function to theoretically describe the Mueller–Navelet jet production. The main aim is to calculate cross sections and azimuthal angle correlations [40, 41] between the two measured jets, i.e. average values of \(\cos {(n \phi )}\), where n is an integer and \(\phi \) is the angle in the azimuthal plane between the direction of one jet and the direction opposite to the other jet, and ratios of two such cosines [42, 43].

Also the impact factors for the proton to identified hadron transition are known up to the NLO [44] and can be expressed, within leading-twist collinear factorization, as the convolution of the parton distribution function (PDF) of the colliding proton with the hard process describing the transition from the parton emitted by the proton to a final-state parton and with the fragmentation function (FF) for that parton to the desired hadron. Two such hadron vertices must be convoluted with the BFKL Green’s function to theoretically describe the above-mentioned inclusive hadron-hadron production and finally get predictions for cross sections and azimuthal angle correlations, similarly to the case of jets.

Within the same formalism, other interesting processes have been proposed as a testfield for BFKL dynamics at the LHC, namely the inclusive production of three or four jets, well separated in rapidity from each other [45,46,47,48,49], the inclusive detection of two heavy quark–antiquark pairs, separated in rapidity, in the collision of two real (or quasi-real) photons [50], and the inclusive tag of a forward \(J/\Psi \)-meson and a very backward jet at the LHC [51].

On the experimental side the situation is as follows: the CMS Collaboration [52] has presented the first measurements of the azimuthal correlation of the Mueller–Navelet jets at \(\sqrt{s}=7\) TeV, but further experimental studies of the Mueller–Navelet jets are expected at higher LHC energies and larger rapidity intervals, including also the effects of using asymmetrical cuts for the jet transverse momenta. No experimental analyses have yet appeared on azimuthal correlation between two rapidity-separated identified light hadrons. The reason for that could be that events with identified hadrons in the final state, carrying transverse momenta of the order of, say, 5 GeV or larger, fall into the class of what experimentalists call “minimum bias events”, which represent the main background in high-luminosity runs at a collider. They would be better studied in low-luminosity, dedicated, runs.

In this paper we want to introduce a new process which could serve as a probe of BFKL dynamics: the inclusive hadron-jet production in proton-proton collisions,

$$\begin{aligned} {\mathrm{proton}}(p_1) + {\mathrm{proton}}(p_2)\rightarrow & {} {\mathrm{hadron}}(k_H, y_H) + \mathrm{X}\nonumber \\&+\, {\mathrm{jet}}(k_J, y_J), \end{aligned}$$
(1)

when a charged light hadron: \(\pi ^{\pm }, K^{\pm }, p \left( \bar{p}\right) \) and a jet with high transverse momenta, separated by a large interval of rapidity, are produced together with an undetected hadronic system X (see Fig. 1 for a schematic view). The process (1) has many common features with the inclusive \(J/\Psi \)-meson plus backward jet production, considered recently in Ref. [51]. From the experimental side, the detection of the \(J/\Psi \)-meson looks rather appealing. But, from the theory side, there are more uncertainties in this case in comparison to our proposal. The \(J/\Psi \)-meson production impact factor was considered in LO; moreover, several production mechanisms in the frame of NRQCD were discussed. Instead, the light hadron impact factor is well defined in collinear factorization and it is known in NLO. Previous experience in BFKL calculations for various processes at LHC shows that the account of NLO corrections to the impact factors leads both to a considerable change of predictions and to a big reduction of the theoretical uncertainties.

The theoretical task to build predictions for cross section and azimuthal correlations for our process is embarrassingly simple: one should simply replace one of the two jet impact factor entering the Mueller–Navelet formulas with the vertex for the proton-to-hadron transition. From the theoretical point of view, this process is definitely an easy target, since all the needed building blocks are available, with NLO accuracy.

Yet, we believe that there are some good reasons for building numerical predictions for this process and submitting them to the attention of both experimentalists and theorists:

  • the BFKL resummation implies certain factorization structure for the predicted observables: the latter are calculated as a convolution of the universal BFKL Green’s function with the process dependent impact factors, which resembles the factorization in Regge theory. It is important to test this picture experimentally, considering all possible processes for which the full NLO BFKL description is available.

  • In Refs. [9, 10, 13, 53] it was discussed, in the context of Mueller–Navelet jet production, that using asymmetric cuts for the transverse momenta of the tagged jets suppresses the Born term, present only for back-to-back jets, thus enhancing the effects of the additional undetected hard gluon radiation and making therefore more visible the impact of the BFKL resummation, with respect to the fixed-order (DGLAP) contribution. For the process we are considering here this kind asymmetry would be naturally imposed by the completely different nature of the two tagged objects: the identified jet should have transverse momentum not smaller than 20 GeV or so, whereas the minimum hadron transverse momentum can be as small as 5 GeV.

  • For the process under consideration only one hadron in the final state should be identified, instead of two as in the hadron-hadron inclusive production, the other identified object being a jet with a typically much larger transverse momentum. This should facilitate the mining of these events out of the minimum-bias ones.

  • From the theoretical point of view one can use this process to compare models for FFs or for jet algorithms, handling expressions which are linear in the corresponding functions and not quadratic as it would be, respectively, in the hadron-hadron and in the Mueller–Navelet jet case.

Fig. 1
figure 1

Inclusive hadroproduction of a charged light hadron and of a jet

Full size image

The summary of the paper is as follows: in Sect. 1 we present the theoretical framework and sketch the derivation of our predictions; in Sect. 2 we show and discuss the results of our numerical analysis; finally, in Sect. 3, we draw our conclusions and give some outlook.

2 Theoretical framework

The final state configuration of the inclusive process under consideration is schematically represented in Fig. 1, where a charged light hadron \((k_H, y_H)\) and a jet \((k_J, y_J)\) are detected, featuring a large rapidity separation, together with an undetected system of hadrons. For the sake of definiteness, we will consider the case where the hadron rapidity \(y_H\) is larger than the jet one \(y_J\), so that \(Y\equiv y_H-y_J\) is always positive. This implies that, for most of the considered values of Y, the hadron is forward and the jet is backward.

The hadron and the jet are also required to possess large transverse momenta, \(\vec k_H^2\sim \vec k_J^2 \gg \Lambda ^2_{\mathrm{QCD}}\). The protons’ momenta \(p_1\) and \(p_2\) are taken as Sudakov vectors satisfying \(p^2_1= p^2_2=0\) and \(2 (p_1p_2) = s\), so that the momenta of the final-state objects can be decomposed as

$$\begin{aligned} k_H= & {} x_H p_1+ \frac{\vec k_H^2}{x_H s}p_2+k_{H\perp }, \quad k_{H\perp }^2=-\vec k_H^2, \nonumber \\ k_J= & {} x_J p_2+ \frac{\vec k_J^2}{x_J s}p_1+k_{J\perp }, \quad k_{J\perp }^2=-\vec k_J^2. \end{aligned}$$
(2)

In the center-of-mass system, the hadron/jet longitudinal momentum fractions \(x_{H,J}\) are connected to the respective rapidities through the relations \(y_H=\frac{1}{2}\ln \frac{x_H^2 s}{\vec k_H^2}\), and \(y_J=\frac{1}{2}\ln \frac{\vec k_J^2}{x_J^2 s}\), so that \(dy_H=\frac{dx_H}{x_H}\), \(dy_J=-\frac{dx_J}{x_J}\), and \(Y=y_H-y_J=\ln \frac{x_Hx_J s}{|\vec k_H||\vec k_J|}\), here the space part of the four-vector \(p_{1\parallel }\) being taken positive.

In QCD collinear factorization the cross section of the process (1) reads

$$\begin{aligned}&\frac{d\sigma }{dx_Hdx_Jd^2k_Hd^2k_J}\nonumber \\&\quad =\sum _{r,s=q,{\bar{q}},g} \int _0^1 dx_1 \int _0^1 dx_2\ f_r\left( x_1,\mu _F\right) \ f_s\left( x_2,\mu _F\right) \nonumber \\&\qquad \times \, \frac{d{\hat{\sigma }}_{r,s} \left( \hat{s},\mu _F\right) }{dx_Hdx_Jd^2k_Hd^2k_J}\;, \end{aligned}$$
(3)

where the r, s indices specify the parton types (quarks \(q = u, d, s, c, b\); antiquarks \(\bar{q} = {\bar{u}}, \bar{d}, \bar{s}, \bar{c}, \bar{b}\); or gluon g), \(f_{r,s}\left( x, \mu _F \right) \) denote the initial proton PDFs; \(x_{1,2}\) are the longitudinal fractions of the partons involved in the hard subprocess, while \(\mu _F\) is the factorization scale; \(d\hat{\sigma }_{r,s}\left( \hat{s} \right) \) is the partonic cross section and \(\hat{s} \equiv x_1x_2s\) is the squared center-of-mass energy of the parton-parton collision subprocess.

In the BFKL approach the cross section can be presented (see Ref. [4] for the details of the derivation) as the Fourier sum of the azimuthal coefficients \(\mathcal{C}_n\), having so

$$\begin{aligned}&\frac{d\sigma }{dy_Hdy_J\, d|\vec k_H| \, d|\vec k_J|d\phi _H d\phi _J}\nonumber \\&\quad =\frac{1}{(2\pi )^2}\left[ \mathcal{C}_0+\sum _{n=1}^\infty 2\cos (n\phi )\, \mathcal{C}_n\right] , \end{aligned}$$
(4)

where \(\phi =\phi _H-\phi _J-\pi \), with \(\phi _{H,J}\) the hadron/jet azimuthal angles, while \(y_{H,J}\) and \(\vec k_{H,J}\) are their rapidities and transverse momenta, respectively. The \(\phi \)-averaged cross section \(\mathcal{C}_0\) and the other coefficients \(\mathcal{C}_{n\ne 0}\) are given byFootnote 1

$$\begin{aligned} \mathcal{C}_n\equiv & {} \int _0^{2\pi }d\phi _H\int _0^{2\pi }d\phi _J\, \cos [n(\phi _H-\phi _J-\pi )]\times \,\frac{d\sigma }{dy_Hdy_J\, d|\vec k_H| \, d|\vec k_J|d\phi _H d\phi _J}\;\nonumber \\= & {} \frac{e^Y}{s} \int _{-\infty }^{+\infty } d\nu \, \left( \frac{x_H x_J s}{s_0} \right) ^{\bar{\alpha }_s(\mu _R)\left\{ \chi (n,\nu )+\bar{\alpha }_s(\mu _R) \left[ \bar{\chi }(n,\nu ) +\frac{\beta _0}{8 N_c}\chi (n,\nu )\left[ -\chi (n,\nu ) +\frac{10}{3}+2\ln \left( \frac{\mu _R^2}{\sqrt{\vec k_H^2\vec k_J^2}}\right) \right] \right] \right\} }\nonumber \\&\times \,\alpha _s^2(\mu _R) c_H(n,\nu ,|\vec k_H|, x_H) [c_J(n,\nu ,|\vec k_J|,x_J)]^*\,\times \left\{ 1 +\alpha _s(\mu _R)\left[ \frac{c_H^{(1)}(n,\nu ,|\vec k_H|, x_H)}{c_H(n,\nu ,|\vec k_H|, x_H)}+\left[ \frac{c_J^{(1)}(n,\nu ,|\vec k_J|, x_J)}{c_J(n,\nu ,|\vec k_J|, x_J)}\right] ^*\right] \right. \nonumber \\&\left. +\, \bar{\alpha }_s^2(\mu _R) \ln \left( \frac{x_H x_J s}{s_0}\right) \frac{\beta _0}{4 N_c}\chi (n,\nu )f(\nu )\right\} \;. \end{aligned}$$
(5)

Here \(\bar{\alpha }_s(\mu _R) \equiv \alpha _s(\mu _R) N_c/\pi \), with \(N_c\) the number of colors,

$$\begin{aligned} \beta _0=\frac{11}{3} N_c - \frac{2}{3}n_f \end{aligned}$$
(6)

is the first coefficient of the QCD \(\beta \)-function, where \(n_f\) is the number of active flavors,

$$\begin{aligned} \chi \left( n,\nu \right)= & {} 2\psi \left( 1\right) -\psi \left( \frac{n}{2} +\frac{1}{2}+i\nu \right) \nonumber \\&-\psi \left( \frac{n}{2}+\frac{1}{2}-i\nu \right) \end{aligned}$$
(7)

is the leading-order (LO) BFKL characteristic function, \(c_H(n,\nu )\) is the LO forward hadron impact factor in the \(\nu \)-representation, given as an integral in the parton fraction x, containing the PDFs of the gluon and of the different quark/antiquark flavors in the proton, and the FFs of the detected hadron,

$$\begin{aligned}&c_H(n,\nu ,|\vec k_H|,x_H)= 2 \sqrt{\frac{C_F}{C_A}} (\vec k_H^2)^{i\nu -1/2}\,\int _{x_H}^1\frac{dx}{x} \left( \frac{x}{x_H}\right) ^{2 i\nu -1} \nonumber \\&\quad \times \left[ \frac{C_A}{C_F}f_g(x)D_g^h\left( \frac{x_H}{x}\right) +\sum _{r=q,\bar{q}}f_r(x)D_r^h\left( \frac{x_H}{x}\right) \right] , \end{aligned}$$
(8)

\(c_J(n,\nu )\) is the LO forward jet vertex in the \(\nu \)-representation,

$$\begin{aligned} c_J(n,\nu ,|\vec k_J|,x_J)= & {} 2\sqrt{\frac{C_F}{C_A}} (\vec k_J^{\,2})^{i\nu -1/2}\nonumber \\&\times \left( \frac{C_A}{C_F}f_g(x_J) +\sum _{s=q,\bar{q}}f_s(x_J)\right) \end{aligned}$$
(9)

and the \(f(\nu )\) function is defined by

$$\begin{aligned} i\frac{d}{d\nu }\ln \left( \frac{c_H}{[c_J]^*}\right) =2\left[ f(\nu ) -\ln \left( \sqrt{\vec k_H^2 \vec k_J^2}\right) \right] \;. \end{aligned}$$
(10)

The remaining objects are the hadron/jet NLO impact factor corrections in the \(\nu \)-representation, \(c_{H,J}^{(1)}(n,\nu ,|\vec k_{H,J}|, x_{H,J})\), their expressions being given in Eqs. (4.58)–(4.65) of Ref. [44] and in Eq. (36) of Ref. [4], respectively.

3 Results and discussion

Fig. 2
figure 2

Y-dependence of \(C_0\) for \(\mu _R = \mu _N = \sqrt{|\vec k_H||\vec k_J|}\), \((\mu _F)_{1,2} = |\vec k_{H,J}|\), for \(\sqrt{s}= 7\) TeV (left) and \(\sqrt{s} = 13\) TeV (right), and \(Y \le 7.1\) (CMS-jet configuration)

Full size image
Fig. 3
figure 3

Y-dependence of \(C_0\) and of several ratios \(C_m/C_n\) for \(\mu _F = \mu _R^{\mathrm{BLM}}\), \(\sqrt{s} = 7\) TeV, and \(Y \le 7.1\) (CMS-jet configuration)

Full size image
Fig. 4
figure 4

Y-dependence of \(C_0\) and of several ratios \(C_m/C_n\) for \(\mu _F = \mu _R^{\mathrm{BLM}}\), \(\sqrt{s} = 13\) TeV, and \(Y \le 7.1\) (CMS-jet configuration)

Full size image
Fig. 5
figure 5

Y-dependence of \(C_0\) and of several ratios \(C_m/C_n\) for \(\mu _F = \mu _R^{\mathrm{BLM}}\), \(\sqrt{s} = 13\) TeV, and \(Y \le 9\) (CASTOR-jet configuration)

Full size image
Fig. 6
figure 6

Comparison of the \(\phi \)-averaged cross section \(C_0\) in different NLA BFKL processes: Mueller–Navelet jet, hadron-jet and dihadron production, for \(\mu _F = \mu _R^{\mathrm{BLM}}\), \(\sqrt{s} = 7\) and 13 TeV, and \(Y \le 7.1\) (CMS-jet configuration)

Full size image

3.1 Integration over the final-state phase space

In order to match the actual LHC kinematic cuts, we integrate the coefficients over the phase space for two final-state objects and keep fixed the rapidity interval, Y, between the hadron and the jet:

$$\begin{aligned} C_n= & {} \int _{y^{\mathrm{min}}_H}^{y^{\mathrm{max}}_H}dy_H \int _{y^{\mathrm{min}}_J}^{y^{\mathrm{max}}_J}dy_J\int _{k^{\mathrm{min}}_H}^{k^{\mathrm{max}}_H}dk_H \int _{k^{\mathrm{min}}_J}^{{k^{\mathrm{max}}_J}}dk_J\nonumber \\&\times \,\delta \left( y_H - y_J - Y \right) \, \mathcal{C}_n \left( y_H,y_J,k_H,k_J \right) . \end{aligned}$$
(11)

We consider two distinct ranges for the final-state objects:

  • both the hadron and the jet tagged by the CMS detector in their typical kinematic configurations, i.e.: \(k^{\mathrm{min}}_H=5\) GeV, \(k^{\mathrm{min}}_J=35\) GeV, \(y^{\mathrm{max}}_H=-y^{\mathrm{min}}_H=2.4\), \(y^{\mathrm{max}}_J=-y^{\mathrm{min}}_J=4.7\) [52]. For the sake of brevity, we will refer to this choice as the CMS-jet configuration;  

  • a hadron always detected inside CMS in the range given above, together with a very backward jet tagged by CASTOR. In this peculiar, CASTOR-jet configuration, the jet lies in the typical range of the CASTOR experimental analyses, i.e. \(k^{\mathrm{min}}_J=5\) GeV, \(y^{\mathrm{max}}_J=-5.2\), \(y^{\mathrm{min}}_J=-6.6\)  [54],

The value of \(k_H^{\mathrm{max}}\) is constrained by the lower cutoff of the adopted FF parametrizations (see below) and is always fixed at 21.5 GeV. The value of \(k_J^{\mathrm{max}}\) is instead constrained by the requirement that \(x_J \le 1\) which implies \(k_J^{\mathrm{max}} \simeq 60\) GeV for \(\sqrt{s} = 7\) TeV and \(|y_J| < 4.7\) (CMS-jet) and \(k_J^{\mathrm{max}} \simeq 17.68\) GeV for \(\sqrt{s} = 13\) TeV (CASTOR-jet).

The rapidity interval, Y, is taken to be positive: \(0 < Y \le y^{\mathrm{max}}_H - y^{\mathrm{min}}_J\). Two center-of-mass energies, \(\sqrt{s} = 7\) and 13 TeV, are taken into account in the CMS-jet configuration, while we give predictions for \(\sqrt{s} = 13\) TeV in the CASTOR-jet case.

In our calculations we use the MMHT 2014 NLO PDF set [55] with two different NLO parametrizations for hadron FFs: AKK 2008 [56] and HKNS 2007 [57] (see Sect. 3.3 for a related discussion). In the results presented below, we sum over the production of forward charged light hadrons: \(\pi ^{\pm }, K^{\pm }, p,\bar{p}\).

3.2 Scale optimization

To fix the renormalization scale \(\mu _R\), which can be arbitrarily chosen within the NLA, we adopt the BLM [58,59,60,61] approach, which has become a quite common choice for semihard processes. We first perform a finite renormalization from the \(\overline{\mathrm{MS}}\) to the physical MOM scheme, whose definition is related to the 3-gluon vertex being a key ingredient of the BFKL approach and get

$$\begin{aligned} \alpha _s^{\overline{\mathrm{MS}}}=\alpha _s^{{\mathrm{MOM}}}\left( 1+\frac{\alpha _s^{{\mathrm{MOM}}}}{\pi }T \right) \;, \end{aligned}$$
(12)

with \(T=T^{\beta }+T^{\mathrm{conf}}\),

$$\begin{aligned} T^{\beta }= & {} -\frac{\beta _0}{2}\left( 1+\frac{2}{3}I \right) ,\\ T^{{\mathrm{conf}}}= & {} \frac{3}{8}\left[ \frac{17}{2}I +\frac{3}{2}\left( I-1\right) \xi +\left( 1-\frac{1}{3}I\right) \xi ^2-\frac{1}{6}\xi ^3 \right] ,\nonumber \end{aligned}$$
(13)

where \(I=-2\int _0^1dx\frac{\ln \left( x\right) }{x^2-x+1}\simeq 2.3439\) and \(\xi \) is the gauge parameter of the MOM scheme, fixed at zero in the following. Then, the “optimal” BLM scale \(\mu _R^{\mathrm{BLM}}\) is the value of \(\mu _R\) that makes the \(\beta _0\)-dependent part in the expression for the observable of interest vanish. In Ref. [12] some of us showed that terms proportional to the QCD \(\beta _0\)-function are present not only in the NLA BFKL kernel, but also in the expressions for the NLA impact factor. This leads to a non-universality of the BLM scale and to its dependence on the energy of the process.

Finally, the condition for the BLM scale setting was found to be

$$\begin{aligned}&C^{\beta }_n \propto \!\! \int _{y^{\mathrm{min}}_H}^{y^{\mathrm{max}}_H}dy_H \int _{y^{\mathrm{min}}_J}^{y^{\mathrm{max}}_J}dy_J\int _{k^{\mathrm{min}}_H}^{k^{\mathrm{max}}_H}dk_H \int _{k^{\mathrm{min}}_J}^{k^{\mathrm{max}}_J}dk_J \!\! \int \limits ^{\infty }_{-\infty } \!\!d\nu \nonumber \\&\quad \times \,e^{Y \bar{\alpha }^{{\mathrm{MOM}}}_s(\mu ^{\mathrm{BLM}}_R)\chi (n,\nu )} c_H(n,\nu )[c_J(n,\nu )]^*\nonumber \\&\quad \times \left[ \frac{5}{3} +\ln \frac{(\mu ^{\mathrm{BLM}}_R)^2}{|\vec k_H| |\vec k_J|} +f(\nu )-2\left( 1+\frac{2}{3}I \right) \right. \nonumber \\&\quad \left. +\,\bar{\alpha }^{\mathrm{MOM}}_s(\mu ^{\mathrm{BLM}}_R) Y \, \frac{\chi (n,\nu )}{2} \left( -\frac{\chi (n,\nu )}{2}\right. \right. \nonumber \\&\quad \left. \left. +\,\frac{5}{3}+\ln \frac{(\mu ^{\mathrm{BLM}}_R)^2}{|\vec k_H| |\vec k_J|} +f(\nu )-2\left( 1+\frac{2}{3}I \right) \right) \right] =0.\nonumber \\ \end{aligned}$$
(14)

The term in the r.h.s. of Eq. (14) (proportional to \(\alpha ^{{\mathrm{MOM}}}_s\)) originates from the NLA part of the kernel, while the remaining ones come from the NLA corrections to the hadron/jet vertices.

In order to find the values of the BLM scales, we introduce the ratios of the BLM to the “natural” scale suggested by the kinematic of the process, \(\mu _N=\sqrt{|\vec k_H||\vec k_J|}\), so that \(m_R=\mu _R^{\mathrm{BLM}}/\mu _N\), and look for the values of \(m_R\) which solve Eq. (14).

We finally plug these scales into our expression for the integrated coefficients in the BLM scheme (for the derivation see Ref. [12]):

$$\begin{aligned} C_n= & {} \int _{y^{\mathrm{min}}_H}^{y^{\mathrm{max}}_H}dy_H \int _{y^{\mathrm{min}}_J}^{y^{\mathrm{max}}_J}dy_J\int _{k^{\mathrm{min}}_H}^{k^{\mathrm{max}}_H}dk_H \int _{k^{\mathrm{min}}_J}^{k^{\mathrm{max}}_J}dk_J \, \int \limits ^{\infty }_{-\infty } d\nu \nonumber \\&\times \,\frac{e^Y}{s}\, e^{Y \bar{\alpha }^{\mathrm{MOM}}_s(\mu ^{\mathrm{BLM}}_R)\left[ \chi (n,\nu ) +\bar{\alpha }^{\mathrm{MOM}}_s(\mu ^{\mathrm{BLM}}_R)\left( \bar{\chi }(n,\nu ) +\frac{T^{\mathrm{conf}}}{3}\chi (n,\nu )\right) \right] }\nonumber \\&\times \left( \alpha ^{\mathrm{MOM}}_s (\mu ^{\mathrm{BLM}}_R)\right) ^2 \nonumber \\&\times \, c_H(n,\nu )[c_J(n,\nu )]^* \left\{ 1+\bar{\alpha }^{\mathrm{MOM}}_s(\mu ^{\mathrm{BLM}}_R)\left[ \frac{\bar{c}^{(1)}_H(n,\nu )}{c_H(n,\nu )}\right. \right. \nonumber \\&\left. \left. +\left[ \frac{\bar{c}^{(1)}_J(n,\nu )}{c_J(n,\nu )}\right] ^* +\frac{2T^{\mathrm{conf}}}{3} \right] \right\} . \end{aligned}$$
(15)

The coefficient \(C_0\) gives the \(\phi \)-averaged cross section, while the ratios \(R_{n0} \equiv C_n/C_0 = \langle \cos (n\phi )\rangle \) determine the values of the mean cosines, or azimuthal correlations, of the produced hadron and jet. In Eq. (15), \(\bar{\chi }(n,\nu )\) is the eigenvalue of NLA BFKL kernel [62] and its expression is given, e.g. in Eq. (23) of Ref. [4], whereas \(\bar{c}^{(1)}_{H,J}\) are the NLA parts of the hadron/jet vertices (see Ref. [12]).

We set the factorization scale \(\mu _F\) equal to the renormalization scale \(\mu _R\), as assumed by the MMHT 2014 PDF.

All calculations are done in the MOM scheme. For comparison, we present results for the \(\phi \)-averaged cross section \(C_0\) in the \(\overline{\mathrm{MS}}\) scheme, as implemented in Eq. (11). In the latter case, we choose natural values for \(\mu _R\), i.e. \(\mu _R = \mu _N \equiv \sqrt{|\vec k_H||\vec k_J|}\), and two different values of the factorization scale, \((\mu _F)_{1,2} = |\vec k_{H,J}|\), depending on which of the two vertices is considered. We checked that the effect of using natural values also for \(\mu _F\), i.e. \(\mu _F = \mu _N\), is negligible with respect to our two-value choice.

3.3 Used tools and uncertainty estimation

All numerical calculations were done using JETHAD, a Fortran code we recently developed, suited for the computation of cross sections and related observables for two-body final-state processes, and offering also support in the study of multi-body final-state reactions. In order to perform numerical integrations, we interfaced JETHAD with specific CERN program libraries [63] and with Cuba library integrators [64, 65]. We made extensive use of the CERNLIB routines Dadmul and WGauss, while the Cuba ones were mainly used for crosschecks. A two-loop running coupling setup with \(\alpha _s\left( M_Z\right) =0.11707\) and five quark flavors was chosen. It is known that potential sources of uncertainty could be due to the particular PDF and FF parametrizations used. For this reason, we did preliminary tests by using three different NLO PDF sets, expressly: MMHT 2014 [55], CT 2014 [66] and NNPDF3.0 [67], and convolving them with the four following NLO FF routines: AKK 2008 [56], DSS 2007 [68, 69], HKNS 2007 [57] and NNFF1.0 [70]. All PDF sets and the NNFF1.0 FF parametrization were used via the Les Houches Accord PDF Interface (LHAPDF) 6.2.1 [71]. Our tests have shown no significant discrepancy when different PDF sets are used in our kinematic range. In view of this result, in the final calculations we selected the MMHT 2014 PDF set, together with the FF interfaces mentioned above. We do not show the results with DSS 2007 and NNFF1.0 FF routines, since they would be hardly distinguishable from those with the HKNS 2007 parametrization.

The most relevant uncertainty comes from the numerical 4-dimensional integration over the two transverse momenta \(|\vec k_{H,J}|\), the hadron rapidity \(y_H\), and over \(\nu \). Its effect was directly estimated by Dadmul integration routine [63]. The other three sources of uncertainty, which are respectively: the one-dimensional integration over the parton fraction x needed to perform the convolution between PDFs and FFs in the LO/NLO hadron impact factors, the one-dimensional integration over the longitudinal momentum fraction \(\zeta \) in the NLO hadron/jet impact factor corrections, and the upper cutoff in the numerical integrations over \(|\vec k_{H,J}|\) and \(\nu \), are negligible with respect to the first one. For this reason the error bands of all predictions presented in this work are just those given by the Dadmul routine.

3.4 Discussion

In Fig. 2 we present our results at natural scales for the \(\phi \)-averaged cross section \(C_0\) at \(\sqrt{s} = 7\) and 13 TeV in the CMS-jet kinematic configuration. We can see that the NLO corrections become larger and larger at increasing Y, an expected phenomenon in the BFKL approach.

In Figs. 3 and 4, predictions with the BLM scale optimization for \(C_0\) and several \(R_{nm} \equiv C_n/C_m\) ratios with the jet tagged inside the CMS detector are shown for \(\sqrt{s} = 7\) and 13 TeV, respectively. Here the benefit of the use of BLM optimization appears, since the LLA and NLA predictions for \(C_0\) are now comparable, a sign of stabilization of the perturbative series. The trend of ratios of the form \(R_{n0}\) is the standard one and indicates increasing azimuthal decorrelation between the jet and the hadron as Y goes up, with the NLA predictions systematically above the LLA ones, as it was also observed in Mueller–Navelet jets and in the hadron-hadron case. The ratios \(R_{21}\) and \(R_{32}\) seem to be almost insensitive to the NLO corrections.

Panels in Fig. 5 show results with BLM scale optimization for \(C_0\) and several \(R_{nm}\) ratios in the CASTOR-jet configuration at \(\sqrt{s} = 13\) TeV. They exhibit some new and, to some extent, unexpected features: (i) the two parametrizations for the FFs lead to clearly distinct predictions, (ii) \(\langle \cos \phi \rangle \) exceeds one at the smaller values for Y, a clearly unphysical effect. The reason for these phenomena could reside in the fact that, the lower values for Y in the CASTOR-jet case are obtained for negative values of the hadron rapidity, i.e. in final-state configurations where both jet and hadron are backward.

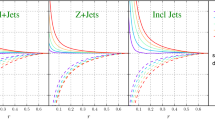
Finally, in Fig. 6 we compare the \(\phi \)-averaged cross section \(C_0\) in different NLA BFKL processes: Mueller–Navelet jet, hadron-jet and hadron-hadron production, for \(\mu _F = \mu _R^{\mathrm{BLM}}\), at \(\sqrt{s} = 7\) and 13 TeV, and \(Y \le 7.1\) in the CMS-jet case. The hadron-hadron cross section, with the kinematical cuts adopted, dominates over the jet-jet one by an order of magnitude, with the hadron-jet cross section lying, not surprisingly, in-between.

4 Summary

In this paper we have proposed a new candidate probe of BFKL dynamics at the LHC in the process for the inclusive production of an identified charged light hadron and a jet, separated by a large rapidity gap.

We have given some arguments that this process, though being a naive hybridization of two already well studied ones, presents some own characteristics which can make it worthy of consideration in future analyses at the LHC.

In view of that, we have provided some theoretical predictions, with next-to-leading accuracy, for the cross section averaged over the azimuthal angle between the identified jet and hadron and for ratios of the azimuthal coefficients.

The trends observed in the distributions over the rapidity interval between the jet and the hadron are not different from the cases of Mueller–Navelet jets and hadron-hadron, when the jet is detected by CMS, whereas some new features have appeared when the jet is seen by CASTOR, which deserve further investigation.