Weak decays of doubly heavy charm $\Omega _{cc}^{+}$ baryon

Abstract

We investigate the two-body non-leptonic decays of doubly charm strange, $\Omega _{cc}^{+}$, baryon. The branching ratios of the $\Omega _{cc}^{+}$ baryon decays involving a pseudoscalar meson for CKM-favored and -suppressed modes are determined by employing the pole model and the factorization hypothesis. We give the first estimates of the non-factorizable W-exchange contributions of $\Omega _{cc}^{+}$ decay in the pole model. We find that the branching ratios of some decays receive contributions, exclusively from the W-exchange diagrams, are as large as $\sim \mathcal {O}(10^{-2})$. The non-spectator contributions in doubly charmed decays are comparable to the factorizable contributions in most of the cases.

1 Introduction

The LHCb collaboration has been quite active, with recently several new observations in heavy flavor spectroscopy [1, 2]. The heavy baryon physics has taken the center stage with the announcement of various results including exotic states, the observation of $\Omega _c$ resonances and the discovery of doubly heavy charm baryon, $\Xi _{cc}^{++}$ [3,4,5,6,7,8,9]. The newly discovered baryon, $\Xi _{cc}^{++}$, is one of the three weakly decaying ground states ($J^P ={\frac{1}{2}}^{+}$ spin–parity) containing two valence charm quarks, namely, an iso-doublet: $\Xi _{cc}^{+}(ccd)$ and $\Xi _{cc}^{++}(ccu)$ baryons, and an iso-singlet: $\Omega _{cc}^{+}(ccs)$ baryon. As regards the LHCb future prospects, one will continue to work on the search and analyses of the doubly heavy baryons with prime focus on the states $\Xi _{cc}^{+}$ and $\Omega _{cc}^{+}$ [1,2,3, 9]. Thus one can expect the confirmation of these states in the near future. The extensive current experimental searches in the sector of heavy flavor baryons provide the motivation for the theoretical efforts. Tremendous theoretical and phenomenological activities related to the doubly heavy baryon mass spectroscopy, magnetic moments, strong and electromagnetic decays etc. have been reported in the literature in the recent past [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. All these years, the efforts to carry out investigations on the non-leptonic decays of heavy baryons [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71] have been moderate due to several reasons, but most importantly due to: (a) the lack of experimental focus on the heavy baryon sector, (b) the non-existence of reliable theoretical and phenomenological approaches to study the weak decays of heavy baryons. The recent LHCb results has brought the focus back on the non-leptonic weak decays of heavy baryons. The non-leptonic decays of doubly and triply heavy baryons are studied mainly using the SU(3) symmetry, perturbative QCD, the factorization hypothesis in the light front approach and in nonrelativistic quark models [72,73,74,75,76,77,78,79,80]. It is worth remarking here that the W-exchange contributions in the meson decays are susceptible to the helicity and color-suppression; however, it has been shown that in the charm baryon decays these contributions are found to be large [43,44,45,46,47,48,49,50,51,52, 81]. The color non-suppression of baryon decays is contrary to naive color-suppression of the internal W-emission diagrams in heavy mesons decays, where the non-factorizable contributions deprecate the color-suppression [44,45,46, 81]. At first glance, the W-exchange terms in baryon decays appear to be suppressed by a factor of $1/N_c$ relative to the external W-emission. However, it is balanced by the fact that baryons contain $N_c$ quarks in the large $N_c$ limit, thus making the W-exchange contributions equally important [43]. In a recent attempt [82], the weak decays of $\Xi _{cc}$ baryon were studied using the factorization and taking the short- and long-distance contributions in the final-state interaction (FSI) rescattering to highlight the importance of W-exchange contributions. Also in our previous work [83], we have highlighted the importance of non-factorizable W-exchange contributions in $\Xi _{cc}$ decays in a more systematic way using both the factorization hypothesis and the pole model approach.

In the present work, we extend our analysis to a study of the non-leptonic weak decays of the $\Omega _{cc}^{+}$ baryon. We give first estimates of W-exchange (pole) contribution using the pole model [44]. We evaluate the factorization contributions based on the form factors calculated in two different models, namely, the nonrelativistic quark model (NRQM) [53] and heavy quark effective theory (HQET) [56]. The reason for this choice is that these models have worked reasonably well in explaining the weak decays of singly heavy (charm and bottom) baryons. Here again, the W-exchange contributions are calculated by employing the pole model approach using the nonrelativistic approximation [54] to evaluate the weak matrix element. It may be noted that in the present analysis we have ignored $\frac{1}{2}^-$-intermediate pole terms and used ground state $\frac{1}{2}^+$-intermediate baryon pole terms alone to get a preliminary estimate of the W-exchange (pole) contributions. We wish to emphasize that the calculation of the $\frac{1}{2}^-$-intermediate pole terms is non-trivial and little is known about the strong-coupling constants of the $\frac{1}{2}^-$ baryons involved. Conventionally, the meson–baryon strong couplings involved in the pole contributions are calculated using the SU(4) symmetry. However, the SU(4) symmetry being badly broken can lead to a substantial correction in the results [44, 52]. We induce the SU(4) symmetry breaking effects in a calculation of the meson–baryon strong couplings, using a more accurate method [84]. Furthermore, the SU(4) symmetry breaking effects could be included in the evaluation of the weak decay amplitude (baryon-to-baryon matrix elements) via the variation of the spatial baryon wave function overlap ($|\psi (0)|^2$) [51, 60, 71, 83]. We find that such flavor-dependent effects significantly enhance the W-exchange contributions, resulting in larger branching ratios for the decays involving pole terms. We observe that the branching ratios of several $\Omega _{cc}^{+}$ decays are well within the reach of current experiments.

The layout of the present work is as follows. In Sect. 2, we give the weak Hamiltonian and the decay amplitudes. We discuss our numerical results in Sect. 3 and summarize our major findings Sect. 4.

2 Hamiltonian and decay amplitudes

The effective weak Hamiltonian for the charm changing two-body non-leptonic decays emitting pseudoscalar (P) meson is given by

$$\begin{aligned} \mathcal{H}_{W}^{\text {eff}}\!=\! & {} \frac{G_{F}}{ \sqrt{2}} \Bigg \{ V_{ud} V_{cs}^{*} \Big [ c_{1} (\bar{u}d)_{V-A}(\bar{c}s)_{V-A}\nonumber \\&+c_{2} (\bar{s}d)_{V-A}(\bar{u}c)_{V-A}\Big ] \nonumber \\&+V_{ud} V_{cd}^{*} \Big [ c_{1} \{(\bar{s}c)_{V-A}(\bar{u}s)_{V-A}-(\bar{d}c)_{V-A}(\bar{u}d)_{V-A}\} \nonumber \\&+c_{2}\{ (\bar{u}c)_{V-A}(\bar{s}s)_{V-A}-(\bar{u}c)_{V-A}(\bar{d}d)_{V-A}\}\Big ] \nonumber \\&-V_{us} V_{cd}^{*} \Big [ c_{1} (\bar{d}c)_{V-A}(\bar{u}s)_{V-A}\nonumber \\&+c_{2} (\bar{u}c)_{V-A}(\bar{d}s)_{V-A}\Big ]\Bigg \} , \end{aligned}$$

(1)

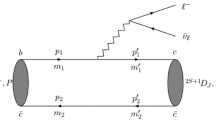
where the $V_{ij}$ denote the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements resulting in CKM-favored, $\Delta C =\Delta S= -1$, CKM-suppressed, $\Delta C = -1,~ \Delta S = 0$, and CKM-doubly-suppressed, $\Delta C =-\Delta S= -1$ modes. $(\bar{q}_{i} q_{j} )_{V-A}$ is written $\bar{q}_{i} \gamma _{\mu } (1-\gamma _{5} )q_{j}$ and denotes the weak V–A current. $c_1~\text {and}~c_2$ are the QCD coefficients and we use $c_{1} (\mu )=1.2$, $c_{2} (\mu )=-0.51$ at $\mu \approx m_{{c}}^{2}$ in the large $N_{c}$ limit for our analysis [85]. The transition amplitude, $\mathcal{A}(B_{{i}} (\frac{1}{2}^{+},~ p_{ i} )\rightarrow B_{{f}} (\frac{1}{2}^{+},~ p_{ f} )+P_{k} (0^{-},~q ))$, can be expressed in terms of the reduced matrix element:

$$\begin{aligned} \langle B_{{f}} (p_{{f}} )P_{k} (q)\vert \mathcal{H}_{W}^{\text {eff}} \vert B_{i} (p_{{i}} )\rangle = i\bar{u}_{B_{{f}} } (p_{{f}} ) (A + B \gamma _{5})u_{B_{{i}} } (p_{{i}} ). \end{aligned}$$

(2)

Here the $u_{B_k}$ represent Dirac spinors for the initial and final ($\frac{1}{2}^+$) baryons, $B_{ i}$ and $B_{ f}$. A and B are the parity-violating (PV) s-wave and parity-conserving (PC) p-wave amplitudes, respectively.

The decay width for the $B_{ i}\rightarrow B_{{f}}P$ decays are

$$\begin{aligned} {\Gamma (B_{ i}\rightarrow B_{{f}}P) \!=\!\frac{p_{ c} }{8\pi } \frac{E_{{f}} +m_{{f}} }{m_{{i}} } \Big [ |A|^{2} +\frac{E_{{f}} -m_{{f}} }{E_{{f}} +m_{{f}} } (|B|^{2} )\Big ] }.\nonumber \\ \end{aligned}$$

(3)

The magnitude of the three-momentum, $p_{ c}$, in the rest frame of $B_{ i}$, is

$$\begin{aligned} p_{{c}} = \frac{1}{2m_i}\sqrt{[m_{i}^{2} -(m_{{f}} -m_{{P}} )^{2} ][m_{{i}}^{2} -(m_{{f}} +m_{{P}} )^{2} ]} , \end{aligned}$$

where $m_{{i}}$ and $m_{{f}}$ are the masses of the initial- and final-state baryons and $m_{{P}}$ is the mass of the emitted pseudoscalar meson, and

$$\begin{aligned} E_{{f}} \pm m_{{f}}= \frac{(m_{{i}} \pm m_{{f}})^{2} -m_{{P}}^{2}}{2m_{ i}}. \end{aligned}$$

The corresponding asymmetry parameter is given by

$$\begin{aligned} \alpha =\frac{2~\frac{p_{ c}}{E_{ f} + m_{ f} }~\text{ Re }[A*B]}{ \left( |A|^{2} + \frac{p_{ c}^2}{(E_{ f} + m_{ f} )^2}|B|^{2} \right) }. \end{aligned}$$

(4)

2.1 Decay amplitudes

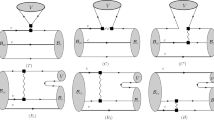
In general, the hadronic matrix element for the $B_{ i} \rightarrow B_{ f} +P_{ k}$ process can receive dominant contributions from the pole and factorization terms; thus it can be given as follows:

$$\begin{aligned} \langle B_{{f}} P_{{k}}\vert H_{{W}} \vert B_{{i}} \rangle \equiv \mathcal {A}_{{P}} + \mathcal {A}_{{F}} , \end{aligned}$$

(5)

where $\mathcal {A}_{{P}}$ and $\mathcal {A}_{{F}}$ denote the pole and factorization amplitudes, respectively. Conventionally, the contributions from these terms, the pole and factorization, are discussed in terms of PV and PC amplitudes.

The decay amplitude, $\mathcal {A}_{{P}}$, can be calculated from the reduced matrix element,

$$\begin{aligned} \langle B_{ f} \vert H \vert B_{ i} \rangle = \bar{u}_{B_{{i}}} (A +\gamma _{5} B )u_{B_{{f}}}, \end{aligned}$$

(6)

between the two $J^P=\frac{1}{2}^+$ baryon states expressed in terms of PV and PC amplitudes, A and B, respectively. Thus, the decay amplitude can simply be expressed in terms of masses, strong couplings and weak matrix elements. The pole amplitude consisting of contributions of the s- and u-channels for the positive-parity intermediate baryon $\frac{1}{2}^+$ poles are denoted by $A_{{\mathrm{pole}}}$ and $B_{{\mathrm{pole}}}$:

$$\begin{aligned} A_{{\mathrm{pole}}} =\mathop {\Sigma }\limits _{n} \left[ \frac{g^{B_{{f}} B_{{n}}}_{P_{{k}}} b_{{ni}} }{m_{{i}} +m_{{n}} } +\frac{ g^{B_{{n}} B_{{i}} }_{P_{{k}} } b_{{fn}}}{m_{{f}} +m_{{n}} } \right] , \end{aligned}$$

(7)

$$\begin{aligned} B_{{\mathrm{pole}}} =\mathop {-\Sigma }\limits _{n} \left[ \frac{g^{B_{{f}} B_{{n}} }_{P_{{k}} } a_{{ni}} }{m_{{i}} -m_{{n}} } +\frac{ g^{B_{{n}} B_{{i}} } _{P_{{k}}}a_{{fn}}}{m_{{f}} -m_{{n}} } \right] ; \end{aligned}$$

(8)

here $g^{ij}_k$ are the strong meson–baryon coupling constants. The weak baryon–baryon matrix elements, $a_{ij}$ and $b_{ij}$, are defined as

$$\begin{aligned} \langle B_{{i}} \vert H_{W} \vert B_{{j}} \rangle = \bar{u}_{B_{{i}} } (a_{ij} +\gamma _{5} b_{ij} )u_{B_{{j}} } . \end{aligned}$$

(9)

2.2 Weak transitions

The SU(4) flavor symmetric and the quark model weak Hamiltonian [48, 59] involved in weak transitions for the quark level process $q_{i} +q_{j} \rightarrow q_{l} +q_{m}$ is given by

$$\begin{aligned} H_{{W}} \cong V_{il} V_{jm}^* c_{-}(m_c)\left[ \bar{B}^{[i,j]k} B_{[l,m]k} H_{[i,j]}^{[l,m]} \right] , \end{aligned}$$

(10)

where $c_{-} = c_1 + c_2$, and the antisymmetrization among the indices is represented by the brackets, [ , ]. The weak Hamiltonian can further be written as

$$\begin{aligned} H_{{W}} \cong a_{ W}\left[ \bar{B}^{[i,j]k} B_{[l,m]k} H_{[i,j]}^{[l,m]} \right] . \end{aligned}$$

(11)

Here, $a_{{W}}$ is the weak amplitude for CKM-favored and CKM-suppressed modes. However, the SU(4) symmetry being badly broken ignores QCD enhancements due to the hard gluon exchanges, coming through $c_{-}$, at corresponding mass scales which will affect the weak transition.

As discussed in Ref. [51, 52, 54], a rough estimate of $a_W$ can be made based on the symmetry arguments. In order to calculate the numerical values of the pole terms, we follow Riazuddin and Fayyazuddin [54], who have shown that the weak matrix element $\langle B_{{f}}\vert H_{{W}}^{{PC}} \vert B_{{i}} \rangle$ can safely be treated in leading nonrelativistic approximation. Thus we acquired the weak Hamiltonian for the charm baryons as a first approximation:

$$\begin{aligned} H^{{PC}}_{ W}= \frac{G_{ F}}{\sqrt{2}}V_{{du}} V_{{cs}} \sum _{i\ne j}\alpha ^{+}_{ i} \gamma ^{-}_{ j} (1-\sigma _{ i}\cdot \sigma _{ j})\delta ^3(r), \end{aligned}$$

(12)

which gives a first estimate of the pole contributions in terms of the flavor invariant spatial baryon wave function overlap. We assumed

$$\begin{aligned} \langle \psi _{ f}|\delta ^3(r)|\psi _{ i}\rangle _{{c}} \approx \langle \psi _{ f}|\delta ^3(r)|\psi _{ i}\rangle _{{s}}. \end{aligned}$$

(13)

Equation (13) connects the non-leptonic charmed baryon decays with the hyperon decays in SU(4) symmetry, which is considered to be badly broken due to the large mass difference between the s- and c-quarks [52]. In the present analysis, we follow our previous work [83] by treating $|\psi (0)|^2$ (based on a dimensionality argument) as a flavor-dependent quantity. It may be noted that a reliable estimate of the baryon ground state wave function at the origin (at charm mass scale) can be obtained from the precisely known experimental masses of the baryons using the hyperfine splitting, which in turn yields

$$\begin{aligned} \frac{m_{\Sigma _{{c}}} -m_{\Lambda _{{c}}}}{m_{\Sigma } -m_{\Lambda } } =\frac{\alpha _{{s}} (m_{{c}} )}{\alpha _{{s}} (m_{{s}} )} \frac{m_{{s}} (m_{{c}} -m_{{u}} )|\psi (0)|_{{c}}^{2} }{m_{{c}} (m_{{s}} -m_{{u}} )|\psi (0)|_{{s}}^{2} }. \end{aligned}$$

(14)

Thus, we get

$$\begin{aligned} \frac{|\psi (0)|_{{c}}^{2} }{|\psi (0)|_{{s}}^{2} } \approx 2.1, \end{aligned}$$

(15)

for $\frac{\alpha _{{s}} (m_{{c}} )}{\alpha _{{s}} (m_{{s}} )}\approx 0.53$ [51, 83]. The variation of the flavor-dependent baryon spatial wave function overlap would lead to a substantial correction in the branching ratios of doubly heavy baryons. The numerical results are discussed in Sect. 3.

Table 1 The expressions of strong-coupling constants and their absolute numerical values

As mentioned above, we adopt the relatively accurate method given by Khanna and Verma [84] to calculate the Baryon–Baryon–Pseudoscalar (${BB^{\prime }P}$) couplings with SU(4) breaking effects:

$$\begin{aligned} g^{BB^{'}}_{P}\text{(SB) }\! =\! \frac{M_{ B} +M_{ B}^{'}}{2M_N} \left( \sqrt{\frac{8}{3}}\frac{m_{ s}-m_{ u}}{m_{ c}-m_{ u}}\right) g^{BB^{'}}_{P}\text{(Sym) }, \end{aligned}$$

(16)

where $g^{BB^{'}}_{P}$(Sym) is the value of SU(4) symmetric couplings [84, 85]. We obtained the absolute numerical values and expressions of the relevant $g^{BB^{'}}_{P} (\mathrm{SB})$ strong meson–baryon coupling constants, as shown in Table 1. $g^{BB^{'}}_{P} (\mathrm{SB})$ are expressed in terms of $g_{ D} (=8.4)$ and $g_{ F} (=5.6)$ [59, 86].

2.3 Factorization

The factorizable decay amplitudes (ignoring the scale factors) can be expanded in terms of the following reduced matrix elements:

$$\begin{aligned}&\mathcal {A}^{\mathrm{Fac}}(B_{ i} \rightarrow B_{ f} +P_{ k})\nonumber \\&\quad \equiv \left<P_{k} (q)|A_{\mu } |0\right>\, \left<B_{{f}} (p_{{f}} )|V^{\mu } +A^{\mu } |B_{{i}} (p_{{i}} )\right>. \end{aligned}$$

(17)

The baryon–baryon matrix elements of the weak currents can be expressed in terms of the form factors, $f_{ i}$ and $g_{ i}$ (as functions of $q^2$) [43, 44] as

$$\begin{aligned}&\left<B_{{f}} (p_{{f}} )|V_{\mu } |B_{{i}} (p_{{i}} )\right>\, \nonumber \\&\quad =\bar{u}_{{f}} (p_{{f}} )\left[ f_{1} \gamma _{\mu } -\frac{f_{2} }{m_{{i}} } i\sigma _{\mu \nu } q^{\nu } +\frac{ f_{3} }{m_{{i}} } q_{\mu } \right] u_{{i}} (p_{{i}} ), \end{aligned}$$

(18)

$$\begin{aligned}&\left<B_{{f}} (p_{{f}} )|A_{\mu } |B(p_{{i}} )\right>\, \nonumber \\&\quad =\bar{u}_{{f}} (p_{{f}} )\left[ g_{1} \gamma _{\mu } \gamma _{5} -\frac{g_{2} }{m_{i} } i\sigma _{\mu \nu } q^{\nu } \gamma _{5} +\frac{g_{3} }{m_{{i}} } q_{\mu } \gamma _{5} \right] u_{{i}} (p_{{i}} ).\nonumber \\ \end{aligned}$$

(19)

The decay constant $f_{{P}}$ of the emitted pseudoscalar meson, $P_{{k}}$, is defined as

$$\begin{aligned} \left<P_{{k}} (q)|A_{\mu } |0\right> = if_{{P}} m_{{P}}. \end{aligned}$$

(20)

The factorizable amplitudes could be simplified to

$$\begin{aligned} A_{1}^{\mathrm{fac}}= & {} -\frac{G_{{F}} }{\sqrt{2} } F_{{C}} f_{{P}} c_{{k}} \left[ (m_{{i}} -m_{{f}})f_{1}^{B_{{i}} ,B_{{f}} } (m_{{P}}^{2} )\right] ,\\ B_{1}^{\mathrm{fac}}= & {} \frac{G_{{F}} }{\sqrt{2} } F_{{C}} f_{{P}} c_{{k}} \left[ (m_{{i}} +m_{{f}})g_{1}^{B_{{i}} ,B_{{f}} } (m_{{P}}^{2} ) \right] , \end{aligned}$$

where the factor $F_{ C}$ is a product of the appropriate CKM factors and Clebsch–Gordan (CG) coefficients, and the $c_{ k}$ are the corresponding QCD coefficients. The nonrelativistic quark model (NRQM) [53] and the heavy quark effective theory (HQET) [56] are used to calculate the $\Omega _{cc}^{+}$ (baryon–baryon) transition form factors, $f_{{i}}$ and $g_{{i}}$. The obtained transition form factors are given in Table 2.

Table 2 The $\Omega _{cc}^{+}$ transition form factors in NRQM [53] and HQET [56]

Table 3 The decay amplitudes (in units of $\frac{G_{{F}}}{ \sqrt{2}} V_{uq} V_{cq}^{*}$) for CKM-favored ($\Delta C =\Delta S= -1$) mode

We use the following mixing scheme for the $\eta$ and $\eta ^{'}$ mesons:

$$\begin{aligned} \eta ^{'}(0.958)= & {} \frac{1}{\sqrt{2} } (u\overline{u}+d\overline{d})\cos \phi _{{P}} +(s\overline{s})\sin \phi _{{P}}, \nonumber \\ \eta (0.547)\,= & {} \frac{1}{\sqrt{2} } (u\overline{u}+d\overline{d})\sin \phi _{{P}} -(s\overline{s})\cos \phi _{{P}}, \end{aligned}$$

(21)

where $\phi _{ P} = \theta _{{\mathrm{ideal}}}-\theta _{ P} ^{\mathrm{phy}}$ and $\theta _P ^{\mathrm{phy}} = -15.4^{\circ }$ [87]. The relevant decay constants [87, 88] for the present analysis are given by

$$\begin{aligned} f_{\pi }&\!=\!131~\mathrm{MeV},~~ f_{\eta }=133~\mathrm{MeV},~~ f_{\eta ^{'}}=126~\mathrm{MeV},\\ f_{{K}}&\!=\!160~\mathrm{MeV},\quad f_{{D}} =207.4~\mathrm{MeV}~~ \mathrm{and}~~ f_{{D}_{{s}}}\!=\!255~~\mathrm{MeV}. \end{aligned}$$

Table 4 The decay amplitudes (in units of $\frac{G_{{F}}}{ \sqrt{2}} V_{uq} V_{cq}^{*}$) for CKM-suppressed ($\Delta C = -1, \Delta S= 0$) mode

3 Numerical results and discussions

The preliminary results for the various decay channels of the $\Omega _{cc}^{+}$ baryon are obtained as a sum of factorization and pole contributions to the corresponding PV and PC amplitudes. We also include the SU(4) breaking effects in evaluating the strong meson–baryon coupling constants as well the weak baryon–baryon transitions. First, we evaluate the factorizable amplitudes using the NRQM- and HQET-based form factors for CKM-favored, CKM-suppressed and CKM-doubly-suppressed modes as listed in columns 3 and 4 of Tables 3, 4, 5 and 6. We calculate the pole amplitudes by using the SU(4) broken strong-coupling constants (ignoring flavor dependence through the spatial wave function overlap) as shown in column 5 of Tables 3, 4, 5 and 6. In our calculations, we use $m_{\Omega _{cc}^{+}}\simeq 3.7$ GeV [38] and $\tau _{\Omega _{cc}^{+}}=300$ ps [75].

Later, we shall introduce the flavor-dependent effects in weak transition amplitudes through the hyperfine splitting. The variation of the spatial baryon wave function overlap, $|\psi (0)|^{2}$, with flavor results in increased pole contributions. The numerical values of the flavor-dependent pole amplitudes of the $\Omega _{cc}^{+}$ baryon decays in CKM-favored, CKM-suppressed and CKM-doubly-suppressed modes are given in column 6 of Tables 3, 4, 5 and 6. It is evident from (15) that the pole contribution are enhanced by a factor of $\sim 2$ due to the flavor-dependent effects caused by the SU(4) breaking. Moreover, the increment in the pole amplitudes could be viewed as a variation of scale (charm to strange) by 2.

Table 5 The decay amplitudes (in units of $\frac{G_{{F}}}{ \sqrt{2}} V_{uq} V_{cq}^{*}$) for CKM-suppressed ($\Delta C = -1, \Delta S= 0$) mode

Table 6 The decay amplitudes (in units of $\frac{G_{{F}}}{ \sqrt{2}} V_{uq} V_{cq}^{*}$) for CKM-doubly-suppressed ($\Delta C =-\Delta S= -1$) mode

Table 7 The branching ratios$^{\mathrm{a}}$ for CKM-favored ($\Delta C =\Delta S= -1$) mode with factorization and pole contributions

Table 8 The branching ratios for CKM-suppressed ($\Delta C =-1\Delta S= 0$) mode with factorization and pole contributions

Table 9 The branching ratios for CKM-doubly-suppressed ($\Delta C =-\Delta S= -1$) mode with factorization and pole contributions

After adding the factorizable and pole contributions, we obtain the branching ratios (BRs) and asymmetry ($\alpha$) parameters for the two-body weak decays of the doubly heavy, $\Omega _{cc}^{+}$, baryon for the flavor-independent and flavor-dependent cases. In order to emphasize the importance of the W-exchange contribution to $\Omega _{cc}^{+}$ decays, we present our prediction for the branching ratios receiving contributions from: (a) the pole amplitudes alone, (b) both the factorization and the pole amplitudes, and (c) the factorization amplitudes alone. The corresponding results are given in Tables 7, 8 and 9 for CKM-favored, CKM-suppressed and CKM-doubly-suppressed modes, respectively. We observe the following:

• 1. As expected, a large number of $\Omega _{cc}^{+}$ decay channels receive contributions from the W-exchange processes. Comparison with the factorizable contributions reveals that the pole amplitudes are not only of equivalent magnitude but are also dominant in some decay channels.

• 2. The pole and factorizable amplitudes can interfere constructively or destructively in the decays comprising both the factorizable and pole contributions. The pole and factorization amplitudes interfere constructively in the $\Omega _{cc}^{+}\rightarrow \Xi _c^+ \bar{K}^0$, $\Omega _{cc}^{+}\rightarrow \Xi _c^+ \eta$, $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime +} \eta$, $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime +} K^0$ and $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime 0} K^+$ decay channels. However, they interfere destructively in the $\Omega _{cc}^{+}\rightarrow \Xi _c^+ \pi ^0$, $\Omega _{cc}^{+}\rightarrow \Xi _c^+ \eta ^{'}$, $\Omega _{cc}^{+}\rightarrow \Xi _c^0 \pi ^+$, $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime +} \pi ^0$, $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime +} \eta ^{'}$, $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime 0} \pi ^+$, $\Omega _{cc}^{+}\rightarrow \Omega _c^0K^+$, $\Omega _{cc}^{+}\rightarrow \Xi _c^+ K^0$ and $\Omega _{cc}^{+}\rightarrow \Xi _c^0 K^+$ decays.

• 3. The factorization contribution obtained from the NRQM and HQET differs owing to the different form factors. The factorization amplitude based on HQET, in general, yields larger values.

• 4. In the CKM-favored $(\Delta C = \Delta S = -1)$ decay mode, one of the decays comes from the pole diagram alone; two of the decays come from the factorization alone and the remaining decay receives contributions from both the pole and the factorization amplitudes. The flavor-dependent branching ratio of the most dominant decay is $B(\Omega _{cc}^{+}\rightarrow \Xi _c^+ \bar{K}^0)$ = $19\%$, which makes it the best candidate to look for in experimental searches.

• 5. It is interesting to note that, among the flavor-independent (factorization alone) decays, the color-favored decay channel $\Omega _{cc}^{+}\rightarrow \Omega _c^0\pi ^+$ has the largest branching ratio, it being $\mathcal {O}(10^{-1})$. However, the color-suppressed decay channel $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime +} \bar{K}^0$ has a branching ratio of $\mathcal {O}(\%)$. As mentioned before, we have used the large $N_c$ limit in our calculations. We wish to point out that for heavy meson decays the discrepancy between theory and experiments greatly improves in the large $N_{ c}$ limit [89, 90]. On the other hand, for baryon decays the theoretical studies, supported by the experimental data, indicate that the color suppression seems to be nonoperative in factorizable amplitudes [44,45,46, 81]. Furthermore, the question of $N_{ c}$ for the factorizable contribution is settled by investigating the Cabibbo suppressed $\Lambda _c^{+}\rightarrow p\phi$ decay, which is contributed to only by factorization [43, 44]. The most recent analysis of $\Lambda _c^{+}\rightarrow p\phi$ decay yields $|a_2|= 0.45 \pm 0.03$ for $N^{\mathrm{eff}}_{ c} \simeq 7$ [81]. The experimental observation of such color-suppressed decays could provide more insight into baryon decay dynamics.

• 6. The decay $\Omega _{cc}^{+}\rightarrow \Xi _c^+ \bar{K}^0$ gets contributions from constructive interference of the pole and factorization amplitudes. Moreover, the W-exchange (pole) contribution in this decay is dominant as compared to the color-suppressed factorization amplitude. Inclusion of the flavor-dependent effect enhances the pole contribution, consequently, increasing the branching ratio.

• 7. In the CKM-suppressed $(\Delta C = -1, \Delta S = 0)$ decay mode, all the decays receive contributions either from both the pole and the factorization amplitudes or from the pole amplitude only. The most dominant decay, $\Omega _{cc}^{+}\rightarrow \Omega _c^0K^+$, receives contributions via destructive inference, while the second largest branching ratio for the decay mode $\Omega _{cc}^{+}\rightarrow \Lambda _c^{+}\bar{K}^0$ appears via the pole amplitude only. In general, the flavor-dependent branching ratios of these decay channels are larger than in the flavor-independent case; however, in some cases destructive interference may suppress the flavor-dependent enhancement, yielding smaller branching ratios. The factorization contributions of the color-favored $\Omega _{cc}^{+}\rightarrow \Omega _c^0K^+$, $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime 0} \pi ^+$ and $\Omega _{cc}^{+}\rightarrow \Xi _c^{0} \pi ^+$ decays are either dominant or comparable to the pole contributions. The flavor-independent branching ratios for decays affected by the interference are $\mathcal {O} (10^{-2})~ \sim \mathcal {O}( 10^{-5})$. However, the pole-only decays have branching ratios $\mathcal {O} (10^{-2})~ \sim \mathcal {O}( 10^{-4})$ for the flavor-dependent case.

• 8. In CKM-doubly-suppressed $(\Delta C = \Delta S = -1)$ mode, the flavor-independent decays have branching ratios, $\mathcal {O} (10^{-4})$ $\sim \mathcal {O}( 10^{-7})$ and in the flavor-dependent case the order of the branching ratios are of $\mathcal {O} (10^{-4})$ $\sim \mathcal {O}( 10^{-6})$. Decays with the pole-only contributions have branching ratios comparable to the decays receiving contributions from both the pole and the factorization amplitudes. The dominant (color-favored) decays in the doubly-suppressed mode are $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime 0} K^+/\Xi _c^{0} K^+$.

• 9. It is interesting to note that in the CKM-suppressed and CKM-doubly-suppressed decay modes, none of the decays receives a contribution from the factorization approach alone. We also wish to point out that the flavor-dependent results enhance the contribution of the pole terms roughly by a factor of 4, consequently, giving larger branching ratios. Thus, the results based on the flavor-dependent and flavor-independent analysis provide a useful domain for the experimental searches.

We also compared our results with the decays (CKM-suppressed and CKM-doubly-suppressed modes) calculated by the recent factorization based analysis by the Wang et al. [75] in the quark–diquark picture using the light front approach. Their predictions are of the same order and compare well with our results. Note that all the decay processes predicted in their analysis receive contributions from the factorizable as well as the non-factorizable W-exchange amplitudes. Especially, the $\Omega _{cc}^{+}\rightarrow \Xi _c^0 \pi ^+$ decay gets a dominant pole amplitude contribution as compared to the factorizable amplitude, where they interfere destructively. Similarly, the rest of their results would also receive W-exchange contributions that cannot be ignored. Interestingly, the factorization amplitude dominates in the $\Omega _{cc}^{+}\rightarrow \Omega _c^0K^+$ decay channel but interferes constructively with the pole amplitude, resulting in a larger branching ratio, in the present case, as compared to their result, as expected.

We wish to remark that in addition to the non-factorizable W-exchange/annihilation contributions, the penguin diagrams may also affect the heavy baryon decays. However, to establish the CP-symmetries one requires a huge amount of experimental data. Moreover, it would be a difficult task to establish CP-violation in charm baryon decays, as the CP-symmetries originating from the Standard Model are very small or even zero [91].

4 Summary

In the light of future prospects of LHCb, we further extended our analysis with focus on the study of non-leptonic weak decays of the doubly charmed baryon, $\Omega _{cc}^{+}$. In the factorization model, we obtained the form factors, $f_i$ and $g_i$, using the approaches based on the nonrelativistic quark model [53] and heavy quark effective theory [56]. The non-factorizable W-exchange diagrams are calculated using the pole model approach involving $\frac{1}{2}^+$-intermediate states only. The pole diagrams mainly involve the W-exchange contributions that are evaluated using the pole model framework. In the pole model, the weak and strong vertices are separated by the introduction of a set of intermediate states into the decay process. It is worth mentioning that the factorization may be considered as a correction to the pole contributions where the t-channel pole process is equivalent to the tree-level diagram i.e. we have a factorizable process. The contributions of both the pole and the factorization processes can be summed up in terms of s-wave (PV) and p-wave (PC) amplitudes. We have obtained the branching ratios of $\Omega _{cc}^{+}$ decay for CKM-favored, CKM-suppressed and CKM-doubly-suppressed modes in the factorization and in the pole model approaches. Since it was well established that the W-exchange contributions are comparable to the factorization amplitudes, the purpose of the present work is to give the first estimates of the W-exchange terms in $\Omega _{cc}^{+}$ decay to get a more comprehensive picture. Furthermore, we include the SU(4) breaking effects in the meson–baryon strong couplings as well as in the weak amplitudes, following which the results are presented in two scenarios, namely, the flavor-independent and the flavor-dependent scenarios. The results can be summarized as follows:

• 1. The W-exchange contributions in $\Omega _{cc}^{+}$ decays cannot be ignored. These amplitudes contribute to the majority of $\Omega _{cc}^{+}$ decays. In contrast to the factorization contributions, the pole contributions are not only comparable but are also dominant in many decay channels.

• 2. In the CKM-favored mode, the most dominant decay channels, $\Omega _{cc}^{+}\rightarrow \Xi _c^+ \bar{K}^0$ and $\Omega _{cc}^{+}\rightarrow \Omega _c^0\pi ^+$, could be of immediate experimental interest. The $\Omega _{cc}^{+}\rightarrow \Xi _c^+ \bar{K}^0$ decay receives a contribution from the W-exchange as well as the factorization amplitudes. The observation of the color-suppressed factorizable decay $\Omega _{cc}^{+}\rightarrow \Xi _c^{\prime +} \bar{K}^0$ could provide a useful test of the factorization hypothesis in heavy baryon decays. The overall branching ratio in this mode ranges from $10^{-1}$ to $10^{-3}$ in the flavor-dependent case.

• 3. None of the decays, in the CKM-suppressed and CKM-doubly-suppressed modes, appears from the factorization amplitudes alone. Owing to the W-exchange contributions, the branching ratios of several decays, $\mathcal {O}(10^{-2}) \sim \mathcal {O}(10^{-3})$, highlight the importance of W-exchange processes in heavy baryon decays.

• 4. The amplitudes can interfere constructively and destructively for the pole and factorization contributions depending on their signs. The search of these decays could prove to be a useful test of the theoretical models.

• 5. The flavor-dependent factor enhances the pole contribution appreciably. Thus, the present results based on both the NRQM and the HQET approaches with flavor-dependent W-exchange contributions provide a functional range to search for the experimental authentications.

The experimental hunt for such decays of the $\Omega _{cc}^{+}$ baryon could help theorists to understand the underlying dynamics of the W-exchange processes. New measurements of the doubly heavy baryons are planned by several on-going experiments at Fermilab and CERN. There is an exciting time ahead and we hope that the present analysis could prove to be handy and expedient in the experimental searches for these decay modes. The present work’s result can be regarded as a start-off towards wide understanding of the weak decays of such a doubly heavy baryon, $\Omega _{cc}^{+}$.