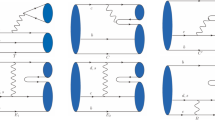
Appendix A: Expressions of amplitudes The expressions of amplitudes for all the \(\mathcal{B}_{cc}\rightarrow \mathcal{B}_{c}V\) decays are collected in the section. In order to make the expressions simpler, we define function \(\mathcal{M}(P1,P2,P3,P4,P5,P6)\) as the absorptive part of a triangle diagram shown in Fig. 4 . The isospin factors of external particles are already included. The absorptive part in Eq. (11 ) is related to this function as
$$\begin{aligned} \mathcal{A}bs\,M_{a2}(\pi ^+;\Xi _c^0;\pi ^-)=\mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^0, \pi ^-, \rho ^0,\Xi _c^{+}). \end{aligned}$$
(A1)
Amplitudes of all \(\mathcal{B}_{cc} \rightarrow \mathcal{B}_c V\) decays are given as follows with the help of this function.
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} \bar{K}^{*0}) =C_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} \bar{K}^{*0})\nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^+, K^-, \bar{K}^{*0},\Sigma _c^{++}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+,\Xi _c^+, K^{*-}, \bar{K}^{*0},\Sigma _c^{++}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{\prime +}, K^-, \bar{K}^{*0},\Sigma _c^{++}) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+,\Xi _c^{\prime +}, K^{*-}, \bar{K}^{*0},\Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{ +}, \Lambda _c^+,\Sigma _c^{++}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+,\Xi _c^{ +}, \Lambda _c^+,\Sigma _c^{++}, \bar{K}^{*0}) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{ +}, \Sigma _c^+,\Sigma _c^{++}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+,\Xi _c^{ +}, \Sigma _c^+,\Sigma _c^{++}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{\prime +}, \Lambda _c^+,\Sigma _c^{++}, \bar{K}^{*0}) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+,\Xi _c^{\prime +}, \Lambda _c^+,\Sigma _c^{++}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{\prime +},\Sigma _c^+,\Sigma _c^{++},\bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+,\Xi _c^{\prime +}, \Sigma _c^+,\Sigma _c^{++}, \bar{K}^{*0})], \end{aligned}$$
(A2)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Xi _c^+\rho ^+) =T_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Xi _c^{+} \rho ^+)\nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{ +}, \pi ^0, \rho ^+, \Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{ +}, \rho ^0, \rho ^+, \Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{'+}, \pi ^0, \rho ^+, \Xi _c^{+}) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{'+}, \rho ^0, \rho ^+, \Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{ +}, \Xi _c^{0}, \Xi _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{ +}, \Xi _c^{0}, \Xi _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{ +}, \Xi _c^{'0}, \Xi _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{ +}, \Xi _c^{'0}, \Xi _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{'+}, \Xi _c^{ 0}, \Xi _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{'+}, \Xi _c^{ 0}, \Xi _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{'+}, \Xi _c^{'0}, \Xi _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{'+}, \Xi _c^{'0}, \Xi _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^0, \Sigma _c^{++}, K^+, \rho ^+, \Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^{*0}, \Sigma _c^{++}, K^{*+}, \rho ^+, \Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^0, \Sigma _c^{++}, \Lambda _c^+, \Xi _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^{*0}, \Sigma _c^{++}, \Lambda _c^+, \Xi _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^0, \Sigma _c^{++}, \Sigma _c^{+}, \Xi _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^{*0}, \Sigma _c^{++}, \Sigma _c^{+}, \Xi _c^{+}, \rho ^+)], \end{aligned}$$
(A3)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Xi _c^{'+} \rho ^+) =T_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Xi _c^{'+} \rho ^+)\nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{ +}, \pi ^0, \rho ^+, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{ +}, \rho ^0, \rho ^+, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{'+}, \pi ^0, \rho ^+, \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{'+}, \rho ^0, \rho ^+, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{ +}, \Xi _c^{0}, \Xi _c^{'+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{ +}, \Xi _c^{0}, \Xi _c^{'+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{ +}, \Xi _c^{'0}, \Xi _c^{'+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{ +}, \Xi _c^{'0}, \Xi _c^{'+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{'+}, \Xi _c^{ 0}, \Xi _c^{'+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{'+}, \Xi _c^{ 0}, \Xi _c^{'+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Xi _c^{'+}, \Xi _c^{'0}, \Xi _c^{'+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Xi _c^{'+}, \Xi _c^{'0}, \Xi _c^{'+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^0, \Sigma _c^{++}, K^+, \rho ^+, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^{*0}, \Sigma _c^{++}, K^{*+}, \rho ^+, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^0, \Sigma _c^{++}, \Lambda _c^+, \Xi _c^{'+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^{*0}, \Sigma _c^{++}, \Lambda _c^+, \Xi _c^{'+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^0, \Sigma _c^{++}, \Sigma _c^{+}, \Xi _c^{'+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \bar{K}^{*0}, \Sigma _c^{++}, \Sigma _c^{+}, \Xi _c^{'+}, \rho ^+)], \end{aligned}$$
(A4)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{+} \rho ^+) =T_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{+} \rho ^+)+ i [ \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \pi ^0, \rho ^+, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \rho ^0, \rho ^+, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \Sigma _c^{0}, \Sigma _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \Sigma _c^{0}, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, \Sigma _c^{0}, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^{+}, \Sigma _c^{0}, \Sigma _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^0, \Sigma _c^{++}, \pi ^+, \rho ^+, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^0, \Sigma _c^{++}, \rho ^+, \rho ^+, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^0, \Sigma _c^{++}, \Lambda _c^+, \Sigma _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^0, \Sigma _c^{++}, \Lambda _c^+, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \eta _8, \Sigma _c^{++}, \Sigma _c^+, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \omega , \Sigma _c^{++}, \Sigma _c^+, \Sigma _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \bar{K}^0, \rho ^+, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \bar{K}^{*0}, \rho ^+, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Xi _c^{'+}, \bar{K}^ 0 , \rho ^+, \Sigma _c^{+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \bar{K}^{*0}, \rho ^+, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Xi _c^{ +}, \Xi _c^{ 0}, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{ +}, \Xi _c^{ 0}, \Sigma _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{ +}, \Xi _c^{'0}, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{ +}, \Xi _c^{'0}, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Xi _c^{'+}, \Xi _c^{ 0}, \Sigma _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c^{ 0}, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Xi _c^{'+}, \Xi _c^{'0}, \Sigma _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c^{'0}, \Sigma _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \eta _1, \Sigma _c^{++}, \Sigma _c^+, \Sigma _c^{+}, \rho ^+)],\nonumber \\ \end{aligned}$$
(A5)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Lambda _c^{+} \rho ^+) =T_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Lambda _c^{+} \rho ^+)+ i [ \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, \pi ^0, \rho ^+, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, \rho ^0, \rho ^+, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \Sigma _c^{0}, \Lambda _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \Sigma _c^{0}, \Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, \Sigma _c^{0}, \Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, \Sigma _c^{0}, \Lambda _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^0, \Sigma _c^{++}, \pi ^+, \rho ^+, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^0, \Sigma _c^{++}, \rho ^+, \rho ^+, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^0, \Sigma _c^{++}, \Sigma _c^{+}, \Lambda _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^0, \Sigma _c^{++}, \Sigma _c^{+}, \Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \eta _8, \Sigma _c^{++}, \Lambda _c^{+},\Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \omega , \Sigma _c^{++}, \Lambda _c^{+},\Lambda _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{+}, \bar{K}^0, \rho ^+, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{+}, \bar{K}^{*0}, \rho ^+, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \bar{K}^0, \rho ^+, \Lambda _c^{+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \bar{K}^{*0}, \rho ^+, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{ +}, \Xi _c^{0}, \Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{ +}, \Xi _c^{0}, \Lambda _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{ +}, \Xi _c^{'0}, \Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{ +}, \Xi _c^{'0}, \Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Xi _c^{ 0}, \Lambda _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c^{ 0}, \Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Xi _c^{'0}, \Lambda _c^{+}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c^{'0}, \Lambda _c^{+}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{++}, \eta _1, \Sigma _c^{++}, \Lambda _c^{+},\Lambda _c^{+}, \rho ^+)],\nonumber \\ \end{aligned}$$
(A6)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} \rho ^{0}) =C_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} \rho ^{0+} )\nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \pi ^-, \rho ^0, \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \rho ^-, \rho ^0, \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^{+}, \pi ^-, \rho ^0, \Sigma _c^{++}) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^{+}, \rho ^-, \rho ^0, \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^{+}, \Sigma _c^{+}, \Sigma _c^{++},\rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^{+}, \Sigma _c^{+}, \Sigma _c^{++},\rho ^0 ) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^{+}, \Lambda _c^{+},\Sigma _c^{++},\rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^{+}, \Lambda _c^{+},\Sigma _c^{++},\rho ^0 ) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{+}, K^-, \rho ^0, \Sigma _c^{++}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{+}, K^{*-}, \rho ^0, \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, K^-, \rho ^0, \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, K^{*-}, \rho ^0, \Sigma _c^{++}) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{+}, \Xi _c^{+}, \Sigma _c^{++}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{+}, \Xi _c^{+}, \Sigma _c^{++}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Xi _c^{+}, \Sigma _c^{++}, \rho ^0 ) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c^{+}, \Sigma _c^{++}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{+}, \Xi _c^{'+}, \Sigma _c^{++}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{+}, \Xi _c^{'+}, \Sigma _c^{++}, \rho ^0 ) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Xi _c^{'+}, \Sigma _c^{++}, \rho ^0 ) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c^{'+}, \Sigma _c^{++}, \rho ^0 )], \end{aligned}$$
(A7)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} \omega ) =C_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} \omega ) \nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \Lambda _c^+, \Sigma _c^{++}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \Lambda _c^+, \Sigma _c^{++}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, \Sigma _c^+, \Sigma _c^{++}, \omega ) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, \Sigma _c^+, \Sigma _c^{++}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, K^-, \omega , \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, K^{*-}, \omega , \Sigma _c^{++}) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, K^-, \omega , \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, K^{*-}, \omega , \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \Xi _c{0}, \Sigma _c^{++}, \omega ) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \Xi _c{0}, \Sigma _c^{++}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Xi _c{0}, \Sigma _c^{++}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c{0}, \Sigma _c^{++}, \omega ) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \Xi _c{'0}, \Sigma _c^{++}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \Xi _c{'0}, \Sigma _c^{++}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Xi _c{'0}, \Sigma _c^{++}, \omega ) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c{'0}, \Sigma _c^{++}, \omega )],\nonumber \\ \end{aligned}$$
(A8)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} \phi ) =C_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} \phi )+ i [ \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, K^-, \phi , \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, K^{*-}, \phi , \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, K^-, \phi , \Sigma _c^{++}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, K^{*-}, \phi , \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \Xi _c^+, \Sigma _c^{++}, \phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \Xi _c^+, \Sigma _c^{++}, \phi ) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \Xi _c^{'+}, \Sigma _c^{++}, \phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \Xi _c^{'+}, \Sigma _c^{++}, \phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Xi _c^+, \Sigma _c^{++}, \phi ) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c^+, \Sigma _c^{++}, \phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Xi _c^{'+}, \Sigma _c^{++}, \phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Xi _c^{'+}, \Sigma _c^{++}, \phi )], \end{aligned}$$
(A9)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Xi _c^+ K^{*+}) =T_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Xi _c^+ K^{*+}) \nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \pi ^0, K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \rho ^0 , K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \eta _8, K^{*+}, \Xi _c^+) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \omega , K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \pi ^0 , K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \rho ^0, K^{*+}, \Xi _c^+) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \eta _8, K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \pi ^0 , K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \omega , K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \Omega _c, \Xi _c^+, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \Omega _c, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Omega _c, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Omega _c, \Xi _c^+, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \eta _8, \Xi _c^{++}, K^+, K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \phi , \Xi _c^{++}, K^{*+}, K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \eta _8, \Xi _c^{++}, \Xi _c^+, \Xi _c^+, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \phi , \Xi _c^{++}, \Xi _c^+, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \eta _8, \Xi _c^{++}, \Xi _c^{'+}, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \phi , \Xi _c^{++}, \Xi _c^{'+}, \Xi _c^+, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, K^{ 0}, K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, K^{*0}, K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, K^{ 0}, K^{*+}, \Xi _c^+) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, K^{*0}, K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \Xi _c^{ 0}, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \Xi _c^{ 0}, \Xi _c^+, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, \Xi _c^{ 0}, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, \Xi _c^{ 0}, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \Xi _c^{'0}, \Xi _c^+, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \Xi _c^{'0}, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, \Xi _c^{'0}, \Xi _c^+, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, \Xi _c^{'0}, \Xi _c^+, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \eta _8, K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \phi , K^{*+}, \Xi _c^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \eta _8, K^{*+}, \Xi _c^+) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \phi , K^{*+}, \Xi _c^+) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \eta _1, \Sigma _c^{++}, \Xi _c^+, \Xi _c^+, K^{*+})], \end{aligned}$$
(A10)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Xi _c^{'+} K^{*+}) =T_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Xi _c^{'+} K^{*+}) \nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \pi ^0, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \rho ^0 , K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \eta _8, K^{*+}, \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \omega , K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \pi ^0, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \rho ^0, K^{*+}, \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \eta _8, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \omega , K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \Omega _c, \Xi _c^{'+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \Omega _c, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \Omega _c, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \Omega _c, \Xi _c^{'+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \eta _8, \Xi _c^{++}, K^+, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \phi , \Xi _c^{++}, K^{*+}, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \eta _8, \Xi _c^{++}, \Xi _c^+, \Xi _c^{'+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \phi , \Xi _c^{++}, \Xi _c^+, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \eta _8, \Xi _c^{++}, \Xi _c^{'+}, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \phi , \Xi _c^{++}, \Xi _c^{'+}, \Xi _c^{'+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, K^{ 0}, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, K^{*0}, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, K^{ 0}, K^{*+}, \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, K^{*0}, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \Xi _c^{ 0}, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \Xi _c^{ 0}, \Xi _c^{'+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, \Xi _c^{ 0}, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, \Xi _c^{ 0}, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Lambda _c^+, \Xi _c^{'0}, \Xi _c^{'+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Lambda _c^+, \Xi _c^{'0}, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \pi ^+, \Sigma _c^+, \Xi _c^{'0}, \Xi _c^{'+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \rho ^+, \Sigma _c^+, \Xi _c^{'0}, \Xi _c^{'+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^+, \eta _8, K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^+, \phi , K^{*+}, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Xi _c^{'+}, \eta _8, K^{*+}, \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Xi _c^{'+}, \phi , K^{*+}, \Xi _c^{'+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, \eta _1, \Sigma _c^{++}, \Xi _c^{'+}, \Xi _c^{'+}, K^{*+})], \end{aligned}$$
(A11)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{ +} K^{*+}) =T_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Xi _c^{'+} K^{*+}) \nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, K^+, \Lambda _c^+, \pi ^0, K^{*+}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^+, \rho ^0, K^{*+}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Sigma _c^+, \eta _8, K^{*+}, \Sigma _c^{+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^+, \omega , K^{*+}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Lambda _c^+, \Xi _c^{ 0}, \Sigma _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^+, \Xi _c^{ 0}, \Sigma _c^{+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Lambda _c^+, \Xi _c^{'0}, \Sigma _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^+, \Xi _c^{'0}, \Sigma _c^{+}, K^{*+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Sigma _c^+, \Xi _c^{ 0}, \Sigma _c^{+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^+, \Xi _c^{ 0}, \Sigma _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Sigma _c^+, \Xi _c^{'0}, \Sigma _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^+, \Xi _c^{'0}, \Sigma _c^{+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^0, \Sigma _c^{++}, \pi ^+, K^{*+}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*0}, \Sigma _c^{++}, \rho ^+, K^{*+}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^0, \Sigma _c^{++}, \Xi _c^{ +}, \Sigma _c^{+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*0}, \Sigma _c^{++}, \Xi _c^{ +}, \Sigma _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^0, \Sigma _c^{++}, \Xi _c^{'+}, \Sigma _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*0}, \Sigma _c^{++}, \Xi _c^{'+}, \Sigma _c^{+}, K^{*+})], \end{aligned}$$
(A12)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Lambda _c^{ +} K^{*+}) =T_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Xi _c^{'+} K^{*+})\nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, K^+, \Lambda _c^+, \eta _8, K^{*+}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^+, \omega , K^{*+}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Sigma _c^+, \pi ^0, K^{*+}, \Lambda _c^{+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^+, \rho ^0, K^{*+}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Lambda _c^+, \Xi _c^{ 0}, \Lambda _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^+, \Xi _c^{ 0}, \Lambda _c^{+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Lambda _c^+, \Xi _c^{'0}, \Lambda _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^+, \Xi _c^{'0}, \Lambda _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Sigma _c^+, \Xi _c^{ 0}, \Lambda _c^{+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^+, \Xi _c^{ 0}, \Lambda _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^+, \Sigma _c^+, \Xi _c^{'0}, \Lambda _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^+, \Xi _c^{'0}, \Lambda _c^{+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^0, \Sigma _c^{++}, \pi ^+, K^{*+}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*0}, \Sigma _c^{++}, \rho ^+, K^{*+}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^0, \Sigma _c^{++}, \Xi _c^{ +}, \Lambda _c^{+}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{++}, K^{*0}, \Sigma _c^{++}, \Xi _c^{ +}, \Lambda _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^0, \Sigma _c^{++}, \Xi _c^{'+}, \Lambda _c^{+}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*0}, \Sigma _c^{++}, \Xi _c^{'+}, \Lambda _c^{+}, K^{*+})], \end{aligned}$$
(A13)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} K^{*0}) =C_\mathrm{SD}(\Xi _{cc}^{++} \rightarrow \Sigma _c^{++} K^{*0}) \nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Lambda _c^+, \pi ^-, K^{*0}, \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^+, \rho ^-, K^{*0}, \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Sigma _c^{+}, \pi ^-, K^{*0}, \Sigma _c^{++}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^{+}, \rho ^-, K^{*0}, \Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Lambda _c^{+}, \Xi _c^{ +}, \Sigma _c^{++}, K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^{+}, \Xi _c^{ +}, \Sigma _c^{++}, K^{*0}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Lambda _c^{+}, \Xi _c^{'+}, \Sigma _c^{++}, K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Lambda _c^{+}, \Xi _c^{'+}, \Sigma _c^{++}, K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Sigma _c^{+}, \Xi _c^{ +}, \Sigma _c^{++}, K^{*0}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^{+}, \Xi _c^{ +}, \Sigma _c^{++}, K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{ +}, \Sigma _c^{+}, \Xi _c^{'+}, \Sigma _c^{++}, K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{++}, K^{*+}, \Sigma _c^{+}, \Xi _c^{'+}, \Sigma _c^{++}, K^{*0})], \end{aligned}$$
(A14)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _c^{ +}\bar{K}^{*0}) =C_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Sigma _c^{ +} \bar{K}^{*0}) \nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _c^{ 0}, K^{ -}, \bar{K}^{*0}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Xi _c^{ 0}, K^{*-}, \bar{K}^{*0}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _c^{'0}, K^{ -}, \bar{K}^{*0}, \Sigma _c^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Xi _c^{'0}, K^{*-}, \bar{K}^{*0}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _c^{ 0}, \Sigma _c^{0}, \Sigma _c^{+}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Xi _c^{ 0}, \Sigma _c^{0}, \Sigma _c^{+}, \bar{K}^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _c^{'0}, \Sigma _c^{0}, \Sigma _c^{+}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Xi _c^{'0}, \Sigma _c^{0}, \Sigma _c^{+}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^{+}, \pi ^0, \bar{K}^{*0}, \Sigma _c^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^{+}, \rho ^0, \bar{K}^{*0}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^{+}, \eta _8 , \bar{K}^{*0}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^{+}, \omega , \bar{K}^{*0}, \Sigma _c^{+})], \end{aligned}$$
(A15)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Lambda _c^{ +}\bar{K}^{*0}) =C_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Lambda _c^{ +} \bar{K}^{*0}) + i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _c^{ 0}, K^{ -}, \bar{K}^{*0}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Xi _c^{ 0}, K^{*-}, \bar{K}^{*0}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _c^{'0}, K^{ -}, \bar{K}^{*0}, \Lambda _c^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Xi _c^{'0}, K^{*-}, \bar{K}^{*0}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _c^{ 0}, \Sigma _c^{0}, \Lambda _c^{+}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Xi _c^{ 0}, \Sigma _c^{0}, \Lambda _c^{+}, \bar{K}^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _c^{'0}, \Sigma _c^{0}, \Lambda _c^{+}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Xi _c^{'0}, \Sigma _c^{0}, \Lambda _c^{+}, \bar{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^{+}, \eta _8, \bar{K}^{*0}, \Lambda _c^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^{+}, \omega , \bar{K}^{*0}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^{+}, \pi ^0 , \bar{K}^{*0}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^{+}, \rho ^0, \bar{K}^{*0}, \Lambda _c^{+})], \end{aligned}$$
(A16)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _c^{ 0}\rho ^+) =T_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Xi _c^{ 0} \rho ^+) + i [ \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^{+}, K^{ +}, \rho ^+, \Xi _c^{ 0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^{+}, K^{*+}, \rho ^+, \Xi _c^{ 0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^{+}, K^{ +}, \rho ^+, \Xi _c^{ 0}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^{+}, K^{*+}, \rho ^+, \Xi _c^{ 0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^{+}, \Sigma _c^{0}, \Xi _c^{ 0}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^{+}, \Sigma _c^{0}, \Xi _c^{ 0}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^{+}, \Sigma _c^{0}, \Xi _c^{ 0}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^{+}, \Sigma _c^{0}, \Xi _c^{ 0}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \pi ^0, \rho ^+, \Xi _c^{ 0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \rho ^0, \rho ^+, \Xi _c^{ 0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \pi ^0, \rho ^+, \Xi _c^{ 0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \rho ^0 , \rho ^+, \Xi _c^{ 0})], \end{aligned}$$
(A17)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _c^{'0}\rho ^+) =T_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Xi _c^{'0} \rho ^+) + i [ \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^{+}, K^{ +}, \rho ^+, \Xi _c^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^{+}, K^{*+}, \rho ^+, \Xi _c^{' 0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^{+}, K^{ +}, \rho ^+, \Xi _c^{'0}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^{+}, K^{*+}, \rho ^+, \Xi _c^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^{+}, \Sigma _c^{0}, \Xi _c^{'0}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^{+}, \Sigma _c^{0}, \Xi _c^{'0}, \rho ^+) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^{+}, \Sigma _c^{0}, \Xi _c^{'0}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^{+}, \Sigma _c^{0}, \Xi _c^{'0}, \rho ^+)\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \pi ^0, \rho ^+, \Xi _c^{'0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \rho ^0, \rho ^+, \Xi _c^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \pi ^0, \rho ^+, \Xi _c^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \rho ^0 , \rho ^+, \Xi _c^{' 0})], \end{aligned}$$
(A18)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _c^{ +}\rho ^0) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \pi ^{ -}, \rho ^0, \Xi _c^{ +})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \rho ^{-}, \rho ^0, \Xi _c^{ +})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \pi ^{ -}, \rho ^0, \Xi _c^{ +})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \rho ^{-}, \rho ^0, \Xi _c^{ +}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \Xi _c^{ 0}, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \Xi _c^{ 0}, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \Xi _c^{'0}, \Xi _c^{ +}, \rho ^0 ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \Xi _c^{'0}, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \Xi _c^{ 0}, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{ 0}, \Xi _c^{ +}, \rho ^0 ) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Xi _c^{ 0}, K^{ 0}, \rho ^0, \Xi _c^{ +}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Xi _c^{ 0}, K^{*0}, \rho ^0, \Xi _c^{ +})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Xi _c^{'0}, K^{ 0}, \rho ^0, \Xi _c^{ +})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Xi _c^{'0}, K^{*0}, \rho ^0, \Xi _c^{ +}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^+, \Sigma _c^+, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^+, \Sigma _c^+, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^+, \Lambda _c^+, \Xi _c^{ +}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^+, \Lambda _c^+, \Xi _c^{ +}, \rho ^0 )], \end{aligned}$$
(A19)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _c^{'+}\rho ^0) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \pi ^{ -}, \rho ^0, \Xi _c^{'+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \rho ^{-}, \rho ^0, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \pi ^{ -}, \rho ^0, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \rho ^{-}, \rho ^0, \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \Xi _c^{ 0}, \Xi _c^{'+}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \Xi _c^{ 0}, \Xi _c^{'+}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \Xi _c^{'0}, \Xi _c^{'+}, \rho ^0 ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \Xi _c^{'0}, \Xi _c^{'+}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \Xi _c^{ 0}, \Xi _c^{'+}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{ 0}, \Xi _c^{'+}, \rho ^0 ) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{'+}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{'+}, \rho ^0(d))\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Xi _c^{ 0}, K^{ 0}, \rho ^0, \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Xi _c^{ 0}, K^{*0}, \rho ^0, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Xi _c^{'0}, K^{ 0}, \rho ^0, \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Xi _c^{'0}, K^{*0}, \rho ^0, \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^+, \Sigma _c^+, \Xi _c^{'+}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^+, \Sigma _c^+, \Xi _c^{'+}, \rho ^0 )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^+, \Lambda _c^+, \Xi _c^{'+}, \rho ^0 ) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^+, \Lambda _c^+, \Xi _c^{'+}, \rho ^0 )],\nonumber \\ \end{aligned}$$
(A20)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _c^{+}\omega ) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \Xi _c^{ 0}, \Xi _c^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \Xi _c^{ 0}, \Xi _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \Xi _c^{'0}, \Xi _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \Xi _c^{ 0}, \Xi _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{ 0}, \Xi _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^+, K^{ 0}, \omega , \Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^+, K^{*0} , \omega , \Xi _c^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^+, K^{ 0}, \omega , \Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^+, K^{*0}, \omega , \Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^+, \Lambda _c^+, \Xi _c^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^+, \Lambda _c^+, \Xi _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^+, \Sigma _c^+, \Xi _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^+, \Sigma _c^+, \Xi _c^{+}, \omega )], \end{aligned}$$
(A21)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _c^{'+}\omega ) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \Xi _c^{ 0}, \Xi _c^{'+}, \omega ) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{ 0}, \Xi _c^{ 0}, \Xi _c^{'+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{ 0}, \Xi _c^{'0}, \Xi _c^{'+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{'+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \Xi _c^{ 0}, \Xi _c^{'+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{ 0}, \Xi _c^{'+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{'+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^+, \Xi _c^{'0}, \Xi _c^{'0}, \Xi _c^{'+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^+, K^{ 0}, \omega , \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^+, K^{*0} , \omega , \Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^+, K^{ 0}, \omega , \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^+, K^{*0}, \omega , \Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Lambda _c^+, \Lambda _c^+, \Xi _c^{'+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Lambda _c^+, \Lambda _c^+, \Xi _c^{'+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{ 0}, \Sigma _c^+, \Sigma _c^+, \Xi _c^{'+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \bar{K}^{*0}, \Sigma _c^+, \Sigma _c^+, \Xi _c^{+'}, \omega )], \end{aligned}$$
(A22)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{+}\rho ^{0}) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \pi ^{-}, \rho ^{0}, \Sigma _{c}^{+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \rho ^{-}, \rho ^{0}, \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0}, \Sigma _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \Lambda _{c}^{+}, \Sigma _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, \Lambda _{c}^{+}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \rho ^{0}, \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \rho ^{0}, \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \rho ^{0}, \Sigma _{c}^{+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \rho ^{0}, \Sigma _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Lambda _{c}^{+}, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \rho ^{0} )],\nonumber \\ \end{aligned}$$
(A23)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Lambda _{c}^{+}\rho ^{0}) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \pi ^{-}, \rho ^{0}, \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \rho ^{-}, \rho ^{0}, \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0}, \Lambda _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, \Sigma _{c}^{+}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, \Sigma _{c}^{+}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \rho ^{0} ) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \rho ^{0}, \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \rho ^{0}, \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \rho ^{0}, \Lambda _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \rho ^{0}, \Lambda _{c}^{+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Sigma _{c}^{+}, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \rho ^{0} )], \end{aligned}$$
(A24)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{+}\omega ) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0}, \Sigma _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \Sigma _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \omega , \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \omega , \Sigma _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \omega , \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \omega , \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \omega )], \end{aligned}$$
(A25)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Lambda _{c}^{+}\omega ) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0}, \Lambda _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, \Sigma _{c}^{+}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \omega ) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \omega , \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \omega , \Lambda _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \omega , \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \omega , \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \Lambda _{c}^{+}, \omega )], \end{aligned}$$
(A26)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{0}\rho ^{+}) =T_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{+}\rho ^{+})+ i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, \pi ^{+}, \rho ^{+},\Sigma _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, \rho ^{+}, \rho ^{+},\Sigma _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \pi ^{+}, \rho ^{+},\Sigma _{c}^{0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, \rho ^{+}, \rho ^{+},\Sigma _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \pi ^{0}, \rho ^{+},\Sigma _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \rho ^{0}, \rho ^{+},\Sigma _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \overline{K}^{0}, \rho ^{+},\Sigma _{c}^{0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \overline{K}^{*0}, \rho ^{+},\Sigma _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \overline{K}^{0}, \rho ^{+},\Sigma _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \overline{K}^{*0}, \rho ^{+},\Sigma _{c}^{0}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Lambda _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Sigma _{c}^{+}, \Sigma _{c}^{0}, \Sigma _{c}^{0},\rho ^{+})], \end{aligned}$$
(A27)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{+}\phi ) =C_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{+}\phi )+ i [ \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \phi ,\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \phi ,\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \phi ,\Sigma _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \phi ,\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+},\phi ) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _{c}^{+},\phi ) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _{c}^{+},\phi ) ], \end{aligned}$$
(A28)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Lambda _{c}^{+}\phi ) =C_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Lambda _{c}^{+}\phi )+ i [ \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \phi ,\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \phi ,\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \phi ,\Lambda _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \phi ,\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+},\phi ) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _{c}^{+},\phi ) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _{c}^{+},\phi ) ], \end{aligned}$$
(A29)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _{c}^{0}K^{*+}) =T_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Xi _{c}^{0}K^{*+})+ i [ \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, K^{+}, K^{*+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, K^{*+}, K^{*+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, K^{+}, K^{*+},\Xi _{c}^{0}) + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, K^{*+}, K^{*+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, K^{0}, K^{*+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, K^{*0}, K^{*+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0} , \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8 , \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \eta _8, K^{*+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \phi , K^{*+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \eta _8, K^{*+},\Xi _{c}^{0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \phi , K^{*+},\Xi _{c}^{0})\nonumber \\&\quad +\, \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},K^{*0})], \end{aligned}$$
(A30)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _{c}^{'0}K^{*+}) =T_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Xi _{c}^{'0}K^{*+})\nonumber \\&\quad + i [ \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, K^{+}, K^{*+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, K^{*+}, K^{*+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, K^{+}, K^{*+},\Xi _{c}^{'0}) + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, K^{*+}, K^{*+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, K^{0}, K^{*+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, K^{*0}, K^{*+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \eta _8, K^{*+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \phi , K^{*+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \eta _8, K^{*+},\Xi _{c}^{'0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \phi , K^{*+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},K^{*0})], \end{aligned}$$
(A31)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _{c}^{+}K^{*0}) =i [ \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \pi ^{-}, K^{*0},\Xi _{c}^{+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \rho ^{-}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \pi ^{-}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \rho ^{-}, K^{*0},\Xi _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Omega _{c}^{0}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Omega _{c}^{0}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Omega _{c}^{0}, \Xi _{c}^{+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Omega _{c}^{0}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, K^{*0}, K^{*+},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Lambda _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Sigma _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},K^{*0}) ], \end{aligned}$$
(A32)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _{c}^{'+}K^{*0}) =i [ \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \pi ^{-}, K^{*0},\Xi _{c}^{'+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \rho ^{-}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \pi ^{-}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \rho ^{-}, K^{*0},\Xi _{c}^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Omega _{c}^{0}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Omega _{c}^{0}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Omega _{c}^{0}, \Xi _{c}^{'+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Omega _{c}^{0}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, K^{*0}, K^{*+},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{'+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \phi , \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Lambda _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0}, \Sigma _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Lambda _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Lambda _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _8, \Sigma _{c}^{+}, K^{0}, K^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \omega , \Sigma _{c}^{+}, K^{*0}, K^{*0},\Xi _{c}^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Sigma _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+}, \Sigma _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \eta _1, \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},K^{*0})], \end{aligned}$$
(A33)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{0}K^{*+}) =T_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{0}K^{*+})+ i [ \mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \pi ^{+}, K^{*+},\Sigma _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \rho ^{+}, K^{*+},\Sigma _{c}^{0})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \pi ^{+}, K^{*+},\Sigma _{c}^{0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \rho ^{+}, K^{*+},\Sigma _{c}^{0})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Sigma _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \Xi _{c}^{0}, \Sigma _{c}^{0},K^{*+}) +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{0},K^{*+})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Sigma _{c}^{0},K^{*+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Sigma _{c}^{+}, \Xi _{c}^{0}, \Sigma _{c}^{0},K^{*+})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Sigma _{c}^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{0},K^{*+}) ], \end{aligned}$$
(A34)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{+}K^{*0}) =C_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Sigma _{c}^{+}K^{*0})+ i [ \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Sigma _{c}^{0}, \pi ^{-}, K^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Sigma _{c}^{0}, \rho ^{-}, K^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Sigma _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Sigma _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Sigma _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Sigma _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+},K^{*0}) +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \pi ^{0}, K^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \rho ^{0}, K^{*0},\Sigma _{c}^{+})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Sigma _{c}^{+}, \eta _8, K^{*0},\Sigma _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Sigma _{c}^{+}, \omega , K^{*0},\Sigma _{c}^{+})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \Xi _{c}^{+}, \Sigma _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \Xi _{c}^{+}, \Sigma _{c}^{+},K^{*0}) +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Sigma _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Sigma _{c}^{+},K^{*0})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Sigma _{c}^{+}, \Xi _{c}^{+}, \Sigma _{c}^{+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Sigma _{c}^{+}, \Xi _{c}^{+}, \Sigma _{c}^{+},K^{*0})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Sigma _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Sigma _{c}^{+},K^{*0})], \end{aligned}$$
(A35)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Lambda _{c}^{+}K^{*0}) =C_\mathrm{SD}(\Xi _{cc}^{+} \rightarrow \Lambda _{c}^{+}K^{*0})+ i [ \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Sigma _{c}^{0}, \pi ^{-}, K^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Sigma _{c}^{0}, \rho ^{-}, K^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Sigma _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Sigma _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+}, \Sigma _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+}, \Sigma _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+},K^{*0}) +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \eta _8, K^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \omega , K^{*0},\Lambda _{c}^{+})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Sigma _{c}^{+}, \pi ^{0}, K^{*0},\Lambda _{c}^{+}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Sigma _{c}^{+}, \rho ^{0}, K^{*0},\Lambda _{c}^{+})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \Xi _{c}^{+}, \Lambda _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \Xi _{c}^{+}, \Lambda _{c}^{+},K^{*0}) +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Lambda _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Lambda _{c}^{+}, \Xi _{c}^{'+}, \Lambda _{c}^{+},K^{*0})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Sigma _{c}^{+}, \Xi _{c}^{+}, \Lambda _{c}^{+},K^{*0}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Sigma _{c}^{+}, \Xi _{c}^{+}, \Lambda _{c}^{+},K^{*0})\nonumber \\&\quad +\mathcal{M}(\Xi _{cc}^{+}, K^{0}, \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Lambda _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*0}, \Sigma _{c}^{+}, \Xi _{c}^{'+}, \Lambda _{c}^{+},K^{*0})], \end{aligned}$$
(A36)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}\overline{K}^{*0}) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}\overline{K}^{*0})\nonumber \\&\quad + i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Omega _{c}^{0}, K^{-}, \overline{K}^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Omega _{c}^{0}, K^{*-}, \overline{K}^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Omega _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Omega _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Omega _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Omega _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\overline{K}^{*0}) +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, \eta _8, \overline{K}^{*0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, \phi , \overline{K}^{*0},\Xi _{c}^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, \eta _8, \overline{K}^{*0},\Xi _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, \phi , \overline{K}^{*0},\Xi _{c}^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, \Lambda _{c}^{+}, \Xi _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, \Lambda _{c}^{+}, \Xi _{c}^{+},\overline{K}^{*0}) +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, \Sigma _{c}^{+}, \Xi _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, \Sigma _{c}^{+}, \Xi _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, \Lambda _{c}^{+}, \Xi _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, \Lambda _{c}^{+}, \Xi _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, \Sigma _{c}^{+}, \Xi _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, \Sigma _{c}^{+}, \Xi _{c}^{+},\overline{K}^{*0}) ], \end{aligned}$$
(A37)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}\overline{K}^{*0}) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}\overline{K}^{*0})\nonumber \\&\quad + i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Omega _{c}^{0}, K^{-}, \overline{K}^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Omega _{c}^{0}, K^{*-}, \overline{K}^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Omega _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Omega _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Omega _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Omega _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\overline{K}^{*0}) +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, \eta _8, \overline{K}^{*0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, \phi , \overline{K}^{*0},\Xi _{c}^{'+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, \eta _8, \overline{K}^{*0},\Xi _{c}^{'+}) + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, \phi , \overline{K}^{*0},\Xi _{c}^{'+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, \Lambda _{c}^{+}, \Xi _{c}^{'+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, \Lambda _{c}^{+}, \Xi _{c}^{'+},\overline{K}^{*0}) +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, \Sigma _{c}^{+}, \Xi _{c}^{'+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, \Sigma _{c}^{+}, \Xi _{c}^{'+},\overline{K}^{*0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, \Lambda _{c}^{+}, \Xi _{c}^{'+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, \Lambda _{c}^{+}, \Xi _{c}^{'+},\overline{K}^{*0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, \Sigma _{c}^{+}, \Xi _{c}^{'+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, \Sigma _{c}^{+}, \Xi _{c}^{'+},\overline{K}^{*0}) ], \end{aligned}$$
(A38)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Omega _{c}^{0}\rho ^{+}) =T_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Omega _{c}^{0}\rho ^{+})+ i [ \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, K^{+}, \rho ^{+},\Omega _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, K^{*+},\rho ^{+},\Omega _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, K^{+},\rho ^{+},\Omega _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, K^{*+},\rho ^{+},\Omega _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, \Xi _{c}^{0}, \Omega _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, \Xi _{c}^{0}, \Omega _{c}^{0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{+}, \Xi _{c}^{'0}, \Omega _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{+}, \Xi _{c}^{'0}, \Omega _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, \Xi _{c}^{0}, \Omega _{c}^{0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{0}, \Omega _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'0}, \Omega _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \overline{K}^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{'0}, \Omega _{c}^{0},\rho ^{+}) ], \end{aligned}$$
(A39)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Sigma _{c}^{+}\overline{K}^{*0}) =i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, K^{-}, \overline{K}^{*0},\Sigma _{c}^{+}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, K^{*-},\overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, K^{-}, \overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, K^{*-},\overline{K}^{*0},\Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Sigma _{c}^{0}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Sigma _{c}^{0}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{0}, \Sigma _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{0}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \overline{K}^{0}, \overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \overline{K}^{*0},\overline{K}^{*0},\Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \overline{K}^{0}, \overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{+}, \overline{K}^{*0},\overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \overline{K}^{0}, \overline{K}^{*0},\Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \overline{K}^{*0},\overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \overline{K}^{0}, \overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{'+}, \overline{K}^{*0},\overline{K}^{*0},\Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \Lambda _{c}^{+}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \Lambda _{c}^{+},\Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Sigma _{c}^{+}, \Sigma _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{+}, \Sigma _{c}^{+},\Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \Lambda _{c}^{+}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \Lambda _{c}^{+},\Sigma _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Sigma _{c}^{+}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{'+}, \Sigma _{c}^{+},\Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \overline{K}^{0}, \overline{K}^{*0},\Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \overline{K}^{*0},\overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \overline{K}^{0}, \overline{K}^{*0},\Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \overline{K}^{*0},\overline{K}^{*0},\Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \Xi _{c}^{0}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \Xi _{c}^{'0}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Sigma _{c}^{+}, \Sigma _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Sigma _{c}^{+}, \Sigma _{c}^{+},\overline{K}^{*0})], \end{aligned}$$
(A40)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Lambda _{c}^{+}\overline{K}^{*0}) =i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, K^{-}, \overline{K}^{*0},\Lambda _{c}^{+}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, K^{*-},\overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, K^{-}, \overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, K^{*-},\overline{K}^{*0},\Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Sigma _{c}^{0}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Sigma _{c}^{0}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{0}, \Lambda _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{0}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \overline{K}^{0}, \overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \overline{K}^{*0},\overline{K}^{*0},\Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \overline{K}^{0}, \overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{+}, \overline{K}^{*0},\overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \overline{K}^{0}, \overline{K}^{*0},\Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \overline{K}^{*0},\overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \overline{K}^{0}, \overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{'+}, \overline{K}^{*0},\overline{K}^{*0},\Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Lambda _{c}^{+}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{+}, \Lambda _{c}^{+},\Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \Sigma _{c}^{+}, \Lambda _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \Sigma _{c}^{+},\Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Lambda _{c}^{+}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{'+}, \Lambda _{c}^{+},\Lambda _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \Sigma _{c}^{+}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \Sigma _{c}^{+},\Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \overline{K}^{0}, \overline{K}^{*0},\Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \overline{K}^{*0},\overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \overline{K}^{0}, \overline{K}^{*0},\Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \overline{K}^{*0},\overline{K}^{*0},\Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \Xi _{c}^{0}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+},\overline{K}^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \Xi _{c}^{'0}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Lambda _{c}^{+}, \Lambda _{c}^{+},\overline{K}^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Lambda _{c}^{+}, \Lambda _{c}^{+},\overline{K}^{*0}) ], \end{aligned}$$
(A41)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}\rho ^{0}) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}\rho ^{0} )+ i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \pi ^{-}, \rho ^{0} ,\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \rho ^{-},\rho ^{0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \pi ^{-}, \rho ^{0},\Xi _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \rho ^{-},\rho ^{0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Xi _{c}^{+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, K^{-}, \rho ^{0},\Xi _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, K^{*-},\rho ^{0},\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{+},\rho ^{0} ) ], \end{aligned}$$
(A42)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}\rho ^{0}) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}\rho ^{0} )+ i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \pi ^{-}, \rho ^{0} ,\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \rho ^{-},\rho ^{0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \pi ^{-}, \rho ^{0},\Xi _{c}^{'+}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \rho ^{-},\rho ^{0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{'+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, K^{-}, \rho ^{0},\Xi _{c}^{'+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, K^{*-},\rho ^{0},\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\rho ^{0} ) ], \end{aligned}$$
(A43)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}\omega ) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}\omega )+ i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Xi _{c}^{+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, K^{-}, \omega ,\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, K^{*-},\omega ,\Xi _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{+},\omega ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{+},\omega ) ], \end{aligned}$$
(A44)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}\omega ) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}\omega )+ i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Xi _{c}^{'+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{'+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{+}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{+}, \Xi _{c}^{'+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\omega ) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, K^{-}, \omega ,\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, K^{*-},\omega ,\Xi _{c}^{'+}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\omega ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\omega ) ], \end{aligned}$$
(A45)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{0}\rho ^{+}) =T_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{0}\rho ^{+})+ i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \pi ^{+}, \rho ^{+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \rho ^{+},\rho ^{+},\Xi _{c}^{0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \pi ^{+}, \rho ^{+},\Xi _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \rho ^{+},\rho ^{+},\Xi _{c}^{0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+}) +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+}) +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \pi ^{0}, \rho ^{+},\Xi _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \rho ^{0},\rho ^{+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \pi ^{0}, \rho ^{+},\Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \rho ^{0} ,\rho ^{+},\Xi _{c}^{0}) +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+}) +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \overline{K}^{0}, \rho ^{+},\Xi _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \overline{K}^{*0},\rho ^{+},\Xi _{c}^{0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{0},\rho ^{+})], \end{aligned}$$
(A46)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'0}\rho ^{+}) =T_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'0}\rho ^{+})+ i [ \mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \pi ^{+}, \rho ^{+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \rho ^{+},\rho ^{+},\Xi _{c}^{'0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \pi ^{+}, \rho ^{+},\Xi _{c}^{'0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \rho ^{+},\rho ^{+},\Xi _{c}^{'0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+}) +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+}) +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \omega , \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \pi ^{0}, \rho ^{+},\Xi _{c}^{'0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \rho ^{0},\rho ^{+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \pi ^{0}, \rho ^{+},\Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \rho ^{0} ,\rho ^{+},\Xi _{c}^{'0}) +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+}) +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \overline{K}^{0}, \rho ^{+},\Xi _{c}^{'0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \overline{K}^{*0},\rho ^{+},\Xi _{c}^{'0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\rho ^{+})], \end{aligned}$$
(A47)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}\phi ) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}\phi )+ i [ \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, K^{-}, \phi ,\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, K^{*-},\phi ,\Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \Omega _{c}^{0},\Xi _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \Omega _{c}^{0},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{+},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{+},\Xi _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'+},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{'+},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{+},\Xi _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{+},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'+},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{'+},\Xi _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Xi _{c}^{+},\phi ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Xi _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Xi _{c}^{+},\phi ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Xi _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},\Xi _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},\Xi _{c}^{+},\phi ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Xi _{c}^{+},\Xi _{c}^{+},\phi ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Xi _{c}^{+},\Xi _{c}^{+},\phi )], \end{aligned}$$
(A48)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}\phi ) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}\phi )+ i [ \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, K^{-}, \phi ,\Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, K^{*-},\phi ,\Xi _{c}^{'+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \Omega _{c}^{0},\Xi _{c}^{'+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \Omega _{c}^{0},\Xi _{c}^{'+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{+},\Xi _{c}^{'+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{+},\Xi _{c}^{'+},\phi ) +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Xi _{c}^{'+},\Xi _{c}^{'+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Xi _{c}^{'+},\Xi _{c}^{'+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{+},\Xi _{c}^{'+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{+},\Xi _{c}^{'+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Xi _{c}^{'+},\Xi _{c}^{'+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Xi _{c}^{'+},\Xi _{c}^{'+},\phi ) +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Xi _{c}^{'+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Xi _{c}^{'+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Xi _{c}^{'+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Xi _{c}^{'+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Xi _{c}^{'+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Xi _{c}^{'+},\phi ) +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},\Xi _{c}^{'+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},\Xi _{c}^{'+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Xi _{c}^{'+},\Xi _{c}^{'+},\phi ) \nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Xi _{c}^{'+},\Xi _{c}^{'+},\phi ) ], \end{aligned}$$
(A49)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Omega _{c}^{0}K^{*+}) =T_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Omega _{c}^{0}K^{*+})+ i [ \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, K^{+}, K^{*+}, \Omega _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, K^{*+}, K^{*+}, \Omega _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, K^{+}, K^{*+}, \Omega _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, K^{*+}, K^{*+}, \Omega _{c}^{0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, K^{0}, K^{*+}, \Omega _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, K^{*0}, K^{*+}, \Omega _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, K^{0}, K^{*+}, \Omega _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, K^{*0}, K^{*+}, \Omega _{c}^{0}) +\mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+}) + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \eta _8, K^{*+}, \Omega _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \phi , K^{*+}, \Omega _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _1, \Xi _{c}^{'+}, \Omega _{c}^{0},\Omega _{c}^{0},K^{*+})], \end{aligned}$$
(A50)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}K^{*0}) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{+}K^{*0})+ i [ \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \pi ^{-}, K^{*0}, \Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \rho ^{-}, K^{*0}, \Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \pi ^{-}, K^{*0}, \Xi _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \rho ^{-}, K^{*0}, \Xi _{c}^{+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Omega _{c}^{0},\Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Omega _{c}^{0},\Xi _{c}^{+},K^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Omega _{c}^{0},\Xi _{c}^{+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Omega _{c}^{0},\Xi _{c}^{+},K^{*0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \eta _8, K^{*0}, \Xi _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \phi , K^{*0}, \Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \eta _8, K^{*0}, \Xi _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \phi , K^{*0}, \Xi _{c}^{+})], \end{aligned}$$
(A51)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}K^{*0}) =C_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'+}K^{*0})\nonumber \\&\quad + i [ \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \pi ^{-}, K^{*0}, \Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \rho ^{-}, K^{*0}, \Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \pi ^{-}, K^{*0}, \Xi _{c}^{'+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \rho ^{-}, K^{*0}, \Xi _{c}^{'+})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Omega _{c}^{0},\Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Omega _{c}^{0},\Xi _{c}^{'+},K^{*0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Omega _{c}^{0},\Xi _{c}^{'+},K^{*0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Omega _{c}^{0},\Xi _{c}^{'+},K^{*0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \eta _8, K^{*0}, \Xi _{c}^{'+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \phi , K^{*0}, \Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \eta _8, K^{*0}, \Xi _{c}^{'+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \phi , K^{*0}, \Xi _{c}^{'+})], \end{aligned}$$
(A52)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Sigma _{c}^{+}\phi ) =i [ \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \phi , \Sigma _{c}^{+}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \phi , \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \phi , \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \phi , \Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Sigma _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Sigma _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},\Sigma _{c}^{+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \bar{K}^{ 0}, \phi , \Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \bar{K}^{*0}, \phi , \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \bar{K}^{ 0}, \phi , \Sigma _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \phi , \Sigma _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{+},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{+},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{'+},\Sigma _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{'+},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{+},\Sigma _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{+},\Sigma _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\Sigma _{c}^{+},\phi ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\Sigma _{c}^{+},\phi )], \end{aligned}$$
(A53)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Lambda _{c}^{+}\phi ) =i [ \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \phi , \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \phi , \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \phi , \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \phi , \Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Lambda _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Lambda _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0},\Lambda _{c}^{+},\phi )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \bar{K}^0, \phi , \Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \bar{K}^{*0}, \phi , \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \bar{K}^0, \phi , \Lambda _{c}^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \phi , \Lambda _{c}^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{+},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{+},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{'+},\Lambda _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{'+},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{+},\Lambda _{c}^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{+},\Lambda _{c}^{+},\phi ) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\Lambda _{c}^{+},\phi ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{'+},\Lambda _{c}^{+},\phi )], \end{aligned}$$
(A54)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{0}K^{*+}) =T_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{0}K^{*+})+ i [ \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \pi ^{+}, K^{*+}, \Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \rho ^{+}, K^{*+}, \Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \pi ^{+}, K^{*+}, \Xi _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \rho ^{+}, K^{*+}, \Xi _{c}^{0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Omega _{c}^{0},K^{*+}, \Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Omega _{c}^{0},K^{*+}, \Xi _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Omega _{c}^{0},K^{*+}, \Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Omega _{c}^{0},K^{*+}, \Xi _{c}^{0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \eta _8, K^{*+}, \Xi _{c}^{0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \phi , K^{*+}, \Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \eta _8, K^{*+}, \Xi _{c}^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \phi , K^{*+}, \Xi _{c}^{0})], \end{aligned}$$
(A55)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'0}K^{*+}) =T_\mathrm{SD}(\Omega _{cc}^{+} \rightarrow \Xi _{c}^{'0}K^{*+})+ i [ \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \pi ^{+}, K^{*+}, \Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \rho ^{+}, K^{*+}, \Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \pi ^{+}, K^{*+}, \Xi _{c}^{'0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \rho ^{+}, K^{*+}, \Xi _{c}^{'0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Omega _{c}^{0},K^{*+}, \Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Omega _{c}^{0},K^{*+}, \Xi _{c}^{'0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Omega _{c}^{0},K^{*+}, \Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Omega _{c}^{0},K^{*+}, \Xi _{c}^{'0})\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \eta _8, K^{*+}, \Xi _{c}^{'0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \phi , K^{*+}, \Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \eta _8, K^{*+}, \Xi _{c}^{'0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \phi , K^{*+}, \Xi _{c}^{'0})], \end{aligned}$$
(A56)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _c^{++}K^{*-}) =i [ \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Lambda _{c}^{+},\pi ^{-},K^{*-},\Sigma _c^{++}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Lambda _{c}^{+},\rho ^{-}, K^{*-},\Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Sigma _{c}^{+}, \pi ^{-}, K^{*-},\Sigma _c^{++}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Sigma _{c}^{+}, \rho ^{-},K^{*-},\Sigma _c^{++}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Lambda _{c}^{+},\Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{0}, \Lambda _{c}^{+},\Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Lambda _{c}^{+},\Sigma _c^{++}, K^{*-}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{'0}, \Lambda _{c}^{+},\Sigma _c^{++}, K^{*-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Sigma _{c}^{+},\Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{0}, \Sigma _{c}^{+},\Sigma _c^{++},K^{*-}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0},\Sigma _{c}^{+},\Sigma _c^{++},K^{*-}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{'0},\Sigma _{c}^{+},\Sigma _c^{++},K^{*-})], \end{aligned}$$
(A57)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _c^{+}\phi ) =i [ \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Lambda _{c}^{+}, K^{0},\phi ,\Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Lambda _{c}^{+}, K^{*0}, \phi ,\Xi _c^{+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Sigma _{c}^{+}, K^{0}, \phi ,\Xi _c^{+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Sigma _{c}^{+}, K^{*0},\phi ,\Xi _c^{+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Xi _c^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{0}, \Xi _{c}^{0},\Xi _c^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Xi _c^{+}, \phi ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{'0}, \Xi _{c}^{0},\Xi _c^{+}, \phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Xi _c^{+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{0}, \Xi _{c}^{'0},\Xi _c^{+}, \phi ) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\Xi _c^{+}, \phi ) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{'0},\Xi _{c}^{'0},\Xi _c^{+}, \phi )], \end{aligned}$$
(A58)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Xi _c^{'+}\phi ) =i [ \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Lambda _{c}^{+}, K^{0},\phi ,\Xi _c^{'+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Lambda _{c}^{+}, K^{*0}, \phi ,\Xi _c^{'+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Sigma _{c}^{+}, K^{0}, \phi ,\Xi _c^{'+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Sigma _{c}^{+}, K^{*0},\phi ,\Xi _c^{'+}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{0},\Xi _c^{'+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{0}, \Xi _{c}^{0},\Xi _c^{'+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0},\Xi _c^{'+}, \phi ) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{'0}, \Xi _{c}^{0},\Xi _c^{'+}, \phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0},\Xi _c^{'+},\phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{0}, \Xi _{c}^{'0},\Xi _c^{'+}, \phi ) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0},\Xi _{c}^{'0},\Xi _c^{'+}, \phi )\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{'0},\Xi _{c}^{'0},\Xi _c^{'+}, \phi )], \end{aligned}$$
(A59)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Omega _c^{0} K^{*+}) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, K^{0}, K^{*+},\Omega _c^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{0}, K^{*0}, K^{*+},\Omega _c^{0})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, K^{0}, K^{*+},\Omega _c^{0}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Xi _{c}^{'0}, K^{*0}, K^{*+},\Omega _c^{0}) + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Lambda _c^{+}, \Xi _{c}^{0},\Omega _c^{0}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Lambda _c^{+}, \Xi _{c}^{0},\Omega _c^{0}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Sigma _c^{+}, \Xi _{c}^{0},\Omega _c^{0}, K^{*+}) + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Sigma _c^{+}, \Xi _{c}^{0},\Omega _c^{0}, K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Lambda _c^{+}, \Xi _{c}^{'0},\Omega _c^{0},K^{*+})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Lambda _c^{+}, \Xi _{c}^{'0},\Omega _c^{0}, K^{*+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{0}, \Sigma _c^{+},\Xi _{c}^{'0},\Omega _c^{0},K^{*+}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \overline{K}^{*0},\Sigma _c^{+},\Xi _{c}^{'0},\Omega _c^{0}, K^{*+})], \end{aligned}$$
(A60)
$$\begin{aligned}&\mathcal{A}(\Xi _{cc}^{+} \rightarrow \Sigma _c^{++} \rho ^{-}) =i [ \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Lambda _{c}^{+}, \pi ^{-}, \rho ^{-},\Sigma _c^{++}) \nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0} ,\Lambda _{c}^{+},\rho ^{-}, \rho ^{-},\Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{0}, \Sigma _{c}^{+}, \pi ^{-}, \rho ^{-},\Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{0},\Sigma _{c}^{+},\rho ^{-}, \rho ^{-},\Sigma _c^{++}) + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+},\Sigma _{c}^{0},\Lambda _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Sigma _{c}^{0},\Lambda _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, \pi ^{+},\Sigma _{c}^{0},\Sigma _{c}^{+}, \Sigma _c^{++},\rho ^{-}) + \mathcal{M}(\Xi _{cc}^{+}, \rho ^{+},\Sigma _{c}^{0},\Sigma _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+},\Xi _{c}^{0},\Xi _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+},\Xi _{c}^{0},\Xi _{c}^{+}, \Sigma _c^{++},\rho ^{-}) + \mathcal{M}(\Xi _{cc}^{+}, K^{+},\Xi _{c}^{'0},\Xi _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+},\Xi _{c}^{'0},\Xi _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+},\Xi _{c}^{0},\Xi _{c}^{'+}, \Sigma _c^{++},\rho ^{-}) + \mathcal{M}(\Xi _{cc}^{+}, K^{*+},\Xi _{c}^{0},\Xi _{c}^{'+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{+},\Xi _{c}^{'0},\Xi _{c}^{'+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Xi _{cc}^{+}, K^{*+},\Xi _{c}^{'0},\Xi _{c}^{'+}, \Sigma _c^{++},\rho ^{-}) ], \end{aligned}$$
(A61)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Sigma _c^{++} K^{*-}) =i [ \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{+}, K^{-}, K^{*-},\Sigma _c^{++}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{+}, K^{*-}, K^{*-},\Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \eta _8, \Xi _{c}^{'+}, K^{-}, K^{*-},\Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \phi , \Xi _{c}^{'+},K^{*-}, K^{*-},\Sigma _c^{++}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \Xi _{c}^{+}, \Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \Xi _{c}^{+}, \Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Omega _{c}^{0}, \Xi _{c}^{'+}, \Sigma _c^{++},K^{*-}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Omega _{c}^{0}, \Xi _{c}^{'+}, \Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Lambda _{c}^{+}, \Sigma _c^{++},K^{*-}) + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Lambda _{c}^{+}, \Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \Sigma _c^{++},K^{*-}) + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{0}, \Sigma _{c}^{+}, \Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \pi ^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \Sigma _c^{++},K^{*-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, \rho ^{+}, \Xi _{c}^{'0}, \Sigma _{c}^{+}, \Sigma _c^{++},K^{*-})], \end{aligned}$$
(A62)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Sigma _c^{++} \rho ^{-}) =i [ \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, K^{-}, \rho ^{-},\Sigma _c^{++}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, K^{*-}, \rho ^{-},\Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, K^{-}, \rho ^{-},\Sigma _c^{++})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+},K^{*-}, \rho ^{-},\Sigma _c^{++}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'+}, \Sigma _c^{++},\rho ^{-}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{+}, \Sigma _c^{++},\rho ^{-})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'+}, \Sigma _c^{++},\rho ^{-}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'+}, \Sigma _c^{++},\rho ^{-})],\nonumber \\ \end{aligned}$$
(A63)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Sigma _c^{+}\rho ^{0}) =i [ \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \bar{K}^{*0}, \rho ^{0} ,\Sigma _c^{+}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \bar{K}^{*0}, \rho ^{0},\Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \rho ^{0},\Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \rho ^{0},\Sigma _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{+}, \Sigma _c^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{+}, \Sigma _c^{+},\rho ^{0} )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Sigma _c^{+},\rho ^{0} ) +\mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Sigma _c^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Sigma _c^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Sigma _c^{+},\rho ^{0} ) +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Sigma _c^{+},\rho ^{0} )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Sigma _c^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \rho ^{0}, \Sigma _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \rho ^{0}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \rho ^{0}, \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \rho ^{0} , \Sigma _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _c^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _c^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _c^{+}, \rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _c^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _c^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _c^{+}, \rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _c^{+}, \rho ^{0} ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _c^{+}, \rho ^{0} ) ], \end{aligned}$$
(A64)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Lambda _c^{+}\rho ^{0}) =i [ \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \bar{K}^{*0}, \rho ^{0} ,\Lambda _c^{+}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \bar{K}^{*0}, \rho ^{0},\Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \rho ^{0},\Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \rho ^{0},\Lambda _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{+}, \Lambda _c^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{+}, \Lambda _c^{+},\rho ^{0} )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Lambda _c^{+},\rho ^{0} ) +\mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Lambda _c^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Lambda _c^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Lambda _c^{+},\rho ^{0} ) +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Lambda _c^{+},\rho ^{0} )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Lambda _c^{+},\rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \rho ^{0}, \Lambda _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \rho ^{0}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \rho ^{0}, \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \rho ^{0} , \Lambda _c^{+} ) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _c^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _c^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _c^{+}, \rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _c^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _c^{+}, \rho ^{0} )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _c^{+}, \rho ^{0} ) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _c^{+}, \rho ^{0} ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _c^{+}, \rho ^{0} ) ], \end{aligned}$$
(A65)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Sigma _c^{+}\omega ) =i [ \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \bar{K}^{*0}, \omega ,\Sigma _c^{+}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \bar{K}^{*0}, \omega ,\Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \omega ,\Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \omega ,\Sigma _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{+}, \Sigma _c^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{+}, \Sigma _c^{+},\omega )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Sigma _c^{+},\omega ) +\mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Sigma _c^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Sigma _c^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Sigma _c^{+},\omega ) +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Sigma _c^{+},\omega )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Sigma _c^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \omega , \Sigma _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \omega , \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \omega , \Sigma _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \omega , \Sigma _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Sigma _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _c^{+}, \omega ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Sigma _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Sigma _c^{+}, \omega ) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _c^{+}, \omega ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Sigma _c^{+}, \omega ) ], \end{aligned}$$
(A66)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Lambda _c^{+}\omega ) =i [ \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \bar{K}^{*0}, \omega ,\Lambda _c^{+}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \bar{K}^{*0}, \omega ,\Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \omega ,\Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \bar{K}^{*0}, \omega ,\Lambda _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{+}, \Lambda _c^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{+}, \Lambda _c^{+},\omega )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Lambda _c^{+},\omega ) \nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{'+}, \Lambda _c^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Lambda _c^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{+}, \Lambda _c^{+},\omega ) +\mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Lambda _c^{+},\omega )\nonumber \\&\quad +\mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{'+}, \Lambda _c^{+},\omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{-}, \omega , \Lambda _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, K^{*-}, \omega , \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{-}, \omega , \Lambda _c^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, K^{*-}, \omega , \Lambda _c^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{0}, \Lambda _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _c^{+}, \omega ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \Xi _{c}^{'0}, \Lambda _c^{+}, \omega ) + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _c^{+}, \omega )\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{0}, \Lambda _c^{+}, \omega ) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _c^{+}, \omega ) + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \Xi _{c}^{'0}, \Lambda _c^{+}, \omega ) ],\nonumber \\ \end{aligned}$$
(A67)
$$\begin{aligned}&\mathcal{A}(\Omega _{cc}^{+} \rightarrow \Sigma _c^{0} \rho ^{+}) =i [ \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{0}, K^{0}, \rho ^{+},\Sigma _c^{0}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{0}, \bar{K}^{*0}, \rho ^{+},\Sigma _c^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{+}, \Xi _{c}^{'0}, K^{0}, \rho ^{+},\Sigma _c^{0})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*+}, \Xi _{c}^{'0}, \bar{K}^{*0}, \rho ^{+},\Sigma _c^{0}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{0}, \Sigma _c^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{0}, \Sigma _c^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{+}, \Xi _{c}^{'0}, \Sigma _c^{0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{+}, \Xi _{c}^{'0}, \Sigma _c^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{0}, \Sigma _c^{0},\rho ^{+})\nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{0}, \Sigma _c^{0},\rho ^{+}) + \mathcal{M}(\Omega _{cc}^{+}, K^{0}, \Xi _{c}^{'+}, \Xi _{c}^{'0}, \Sigma _c^{0},\rho ^{+}) \nonumber \\&\quad + \mathcal{M}(\Omega _{cc}^{+}, K^{*0}, \Xi _{c}^{'+}, \Xi _{c}^{'0}, \Sigma _c^{0},\rho ^{+})]. \end{aligned}$$
(A68)
Appendix B: Strong coupling constants In this section we list all the strong coupling constants used in our calculation. Some of these values are taken from Refs. [36 , 51 ,52 ,53 ,54 ,55 ,56 ,57 ]. For those that can not be found directly in the literatures, we calculate them under the assumption of SU (3) symmetry. In calculation we perform SU (2) transformation prior to SU (3) ones.
According to which SU (3) multiplets do the particles belong to, the vertices in this paper can be divided into 8 types: VPP , VVV , \(\mathcal{B}_{c3}\mathcal{B}_{c3}P\) , \(\mathcal{B}_{c6}\mathcal{B}_{c6}P\) , \(\mathcal{B}_{c6}\mathcal{B}_{c3}P\) , \(\mathcal{B}_{c3}\mathcal{B}_{c3}V\) , \(\mathcal{B}_{c6}\mathcal{B}_{c6}V\) , and \(\mathcal{B}_{c6}\mathcal{B}_{c3}V\) . P denotes a light pseudoscalar meson, and V represents a light vector meson. The singly charm baryons can be classified into two SU (3) multiplets: a triplet labeled by \(\mathcal{B}_{c3}\) and a sextet by \(\mathcal{B}_{c6}\) . With these label-definitions one can know the meaning of our symbols for each vertices whose coupling constants are collected in Tables 5 , 6 , 7 .
Table 5 Strong coupling constants of VPP and VVV vertices Table 6 Strong coupling constants of \(\mathcal{B}_{c3}\mathcal{B}_{c3}P\) , \(\mathcal{B}_{c3}\mathcal{B}_{c6}P\) and \(\mathcal{B}_{c6}\mathcal{B}_{c6}P\) vertices Table 7 Strong coupling constants of \(\mathcal{B}_{c3}\mathcal{B}_{c3}V\) , \(\mathcal{B}_{c3}\mathcal{B}_{c6}V\) and \(\mathcal{B}_{c6}\mathcal{B}_{c6}V\) vertices 



















 when \(\eta =2\), which is hopeful to be observed.
when \(\eta =2\), which is hopeful to be observed.