1 Introduction

In general relativity (GR), where the corresponding graviton is a massless spin-2 particle, is the current description of gravitation in physics and has importantly astrophysical implications. One of the alternating theory of gravity, which follows a very simple idea of generalization to GR, is known as massive gravity where interaction terms, corresponding to graviton mass, are added into GR. The result of such an introduction is that the model of gravity is modified significantly at a large scale so that, from the cosmological point of view, a system like our universe can enter the cosmic accelerating expansion phase. Not only that; the gravity at smaller scale is not altered much by such a modification to ensure the same predictions as GR makes.

However, adding generic mass terms for the graviton on given background usually brings about various instabilities and ghosts for the gravitational theories. To avoid the appearance of the ghost in massive gravity suggested by Boulware and Deser [1], the set of possible interaction terms is constructed accordingly by de Rham, Gabadadze and Tolley (dRGT) [2, 3]. In particular, the interaction terms are constructed in a specific way to ensure that the corresponding equations of motion are at most second order differential equations so that there is no ghost field. The allowed interaction terms for the four-dimensional theory consist of three kinds of combination; the quadratic, the cubic, and the quartic orders of the metric. Unfortunately, such nonlinearities involve complexities in the calculation as a price to pay for eliminating the ghost and usually make it cumbersome to find an exact solution. Nevertheless, there have been plenty interesting approaches to tackle the complexity to obtain spherical symmetric solutions in massive gravity theories [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. In particular, it was found by Vegh [4] that a spherically symmetric black hole with a Ricci flat horizon is a solution to the four-dimensional massive gravity and then the solution was studied in the aspect of thermodynamical properties and phase transition structure [5, 6]. The spherically symmetric solutions for dRGT were also considered in [9, 10]. The extension of the solution in terms of electric charge was found in [11, 12]. Moreover, the bi-gravity extension of the solution was found in [13] which covers the previously known spherically symmetric solutions (see [14,15,16] for reviews on black holes in massive gravity). Recently, other extensions of the dRGT massive gravity solution were explored [27,28,29,30,31,32,33,34,35,36].

In astrophysics, it is commonly known that black holes can be created by the gravitational collapse of massive stars. However, the famous Thorne [37] hoop conjecture states that gravitational collapse of a massive star will yield a black hole only if the mass M is compressed to a region with circumference \( C <4 \pi M \) in all directions. If the hoop conjecture is true, cylindrical matter will not form a black hole. However, the hoop conjecture was given for a spacetime with a zero cosmological constant. When a negative cosmological constant is introduced, the spacetime will become an asymptotically anti-de Sitter spacetime. Indeed, Lemos [38] has shown a possibility of cylindrical black holes from the gravitational collapse with cylindrical matter distribution in an anti-de Sitter spacetime, violating in this way the hoop conjecture. This cylindrically static black hole solutions in an anti-de Sitter spacetime are called black strings. The pioneering work on the black string is due to Lemos [39,40,41], and soon its charged and rotating [42] counterpart were also obtained.

The main purpose of this paper is to present an exact black string solution, including its generalization to the charge case in dRGT massive gravity, and also to discuss their thermodynamical properties with a focus on thermodynamic stability. The possibility to obtain a Hawking–Page phase transition is explored. We use units which fix the speed of light and the gravitational constant via \(G = c = 1\), and use the metric signature (\(-,\;+,\;+,\;+\)).

2 dRGT massive gravity

In this section we review an important ingredient of dRGT massive gravity theory, which is a well-known nonlinear generalization of a massive gravity and is free of the Boulware–Deser ghost by incorporating higher order interaction terms into the Lagrangian. The dRGT massive gravity action is the well-known Einstein–Hilbert action plus suitable nonlinear interaction terms as given by [3]

$$\begin{aligned} S = \int \mathrm{{d}}^4x \sqrt{-g}\; \frac{1}{2} \left[ R(g) +m_g^2\,\, \mathcal {U}(g, f)\right] , \end{aligned}$$
(1)

where R is the Ricci scalar and \(\mathcal {U}\) is a potential for the graviton which modifies the gravitational sector with the parameter \(m_g\) interpreted as the graviton mass. The effective potential \(\mathcal {U}\) in four-dimensional spacetime is given by

$$\begin{aligned} \mathcal {U}(g, \phi ^a) = \mathcal {U}_2 + \alpha _3\mathcal {U}_3 +\alpha _4\mathcal {U}_4 , \end{aligned}$$
(2)

where \(\alpha _3\) and \(\alpha _4\) are dimensionless free parameters of the theory. The terms \(\mathcal {U}_2\), \(\mathcal {U}_3\) and \(\mathcal {U}_4\) can be written in terms of the physical metric \(g_{\mu \nu }\) and the reference (or fiducial) metric \(f_{\mu \nu }\) as

$$\begin{aligned} \mathcal {U}_2\equiv & {} [\mathcal {K}]^2-[\mathcal {K}^2] , \end{aligned}$$
(3)
$$\begin{aligned} \mathcal {U}_3\equiv & {} [\mathcal {K}]^3-3[\mathcal {K}][\mathcal {K}^2]+2[\mathcal {K}^3] , \end{aligned}$$
(4)
$$\begin{aligned} \mathcal {U}_4\equiv & {} [\mathcal {K}]^4-6[\mathcal {K}]^2[\mathcal {K}^2]+8[\mathcal {K}][\mathcal {K}^3]+3[\mathcal {K}^2]^2-6[\mathcal {K}^4],\nonumber \\ \end{aligned}$$
(5)

where

$$\begin{aligned} \mathcal {K}^\mu _\nu = \delta ^\mu _\nu -\sqrt{g^{\mu \nu }f_{\mu \nu }}, \end{aligned}$$
(6)

where the rectangular brackets denote the traces, namely \([\mathcal {K}]=\mathcal {K}^\mu _\mu \) and \([\mathcal {K}^n]=(\mathcal {K}^n)^\mu _\mu \). Note that we choose the unitary gauge in our consideration [4]. One can see that there are no kinetic terms for the fiducial metric. It seems to play the role of the Lagrange multiplier to help us to construct the suitable form of the mass term. Conveniently, we redefine the two parameters \(\alpha _3\) and \(\alpha _4\) of the graviton potential in Eq. (2) by introducing two new parameters \(\alpha \) and \(\beta \), as follows:

$$\begin{aligned} \alpha _3 = \frac{\alpha -1}{3}, \quad \alpha _4 = \frac{\beta }{4}+\frac{1-\alpha }{12}. \end{aligned}$$
(7)

The equation of motion of the theory can be obtained by varying the action with respect to the dynamical metric \(g_{\mu \nu }\) as

$$\begin{aligned} G_{\mu \nu } +m_g^2 X_{\mu \nu } = 0, \end{aligned}$$
(8)

where \(X_{\mu \nu }\) is obtained by varying the potential term with respect to \(g_{\mu \nu }\) known as the effective energy-momentum tensor. This effective energy-momentum tensor can be written explicitly as

$$\begin{aligned} X_{\mu \nu }= & {} \mathcal {K}_ {\mu \nu } -\mathcal {K}g_ {\mu \nu } -\alpha \left( \mathcal {K}^2_{\mu \nu }-\mathcal {K}\mathcal {K}_{\mu \nu } +\frac{\mathcal {U}_2}{2}g_{\mu \nu }\right) \nonumber \\&+\,3\beta \left( \mathcal {K}^3_{\mu \nu } -\mathcal {K}\mathcal {K}^2_{\mu \nu } +\frac{\mathcal {U}_2}{2}\mathcal {K}_{\mu \nu } - \frac{\mathcal {U}_3}{6}g_{\mu \nu } \right) , \,\,\,\,\,\, \end{aligned}$$
(9)

and it obeys a constraint by using the Bianchi identities as follows:

$$\begin{aligned} \nabla ^\mu X_{\mu \nu } = 0, \end{aligned}$$
(10)

where \(\nabla ^\mu \) denotes the covariant derivative which is compatible with \(g_{\mu \nu }\). In the next section, we will find the solution to this equation of motion by imposing the static and axial symmetry.

3 Black string solution in dRGT massive gravity

In this section, we will look for a static and axially symmetric solution of the modified Einstein equations (8) with the following physical metric ansatz:

$$\begin{aligned} \mathrm{d}s^2 = -n(r)\mathrm{d}t^2 + 2d(r) \mathrm{d}t \mathrm{d}r +\frac{\mathrm{d}r^2}{f(r)} + L(r)^2 \mathrm{d}\varOmega ^2, \end{aligned}$$
(11)

and with the Minkowski flat fiducial metric,

$$\begin{aligned} \mathrm{d}s^2 = -\mathrm{d}t^2 + \mathrm{d}r^2 + r^2 \mathrm{d}\varOmega ^2. \end{aligned}$$
(12)

Here \(\mathrm{d}\varOmega ^2 =\mathrm{d}\varphi ^2 + \alpha _g^2 \mathrm{d}z^2\) is a metric on the 2-D surface. The 2-D surface is chosen to be compatible with the black string solution [40, 43]. The solutions in this ansatz can be classified into two branches: \(d(r) = 0\) or \(L(r) = l_0 r\), where \(l_0\) is a constant, in terms of the parameters \(\alpha \) and \(\beta \) as

$$\begin{aligned} l_0 = \frac{ \left( \alpha +3 \beta \pm \sqrt{\alpha ^2-3 \beta } \right) }{2 \alpha +3 \beta +1}. \end{aligned}$$
(13)

From this stage, it is convenient to investigate the branch \(d = 0\). Even though we choose to investigate the simple branch, the equation is still difficult to investigate analytically. Since the fiducial metric seems to play the role of a Lagrange multiplier to eliminate the BD ghost, one can choose an appropriate form to simplify the calculation. Indeed, the suitable form of the fiducial metric significantly provides the analytical form of the physical metric, for example [4] for a spherically symmetric solution and [44] for a cosmological solution. In the present work, we choose the fiducial metric to be

$$\begin{aligned} f_{\mu \nu }=\text {diag}(0,0,h(r)^2 ,\alpha _f^2 h(r)^2 ), \end{aligned}$$
(14)

where h(r) is an arbitrary function. The line element of the corresponding physical metric in this branch can be written as

$$\begin{aligned} \mathrm{d}s^2 = -n(r)\mathrm{d}t^2 +\frac{\mathrm{d}r^2}{f(r)} +L(r)^2 \mathrm{d}\varOmega ^2. \end{aligned}$$
(15)

From this ansatz, the components of the Einstein tensor can be written as

$$\begin{aligned} G^{t}_{t}= & {} \frac{L f' L'+2 f L L''+f L'^2}{L^2}, \end{aligned}$$
(16)
$$\begin{aligned} G^{r}_{r}= & {} \frac{f L' \left( n L'+L n'\right) }{L^2 n}, \end{aligned}$$
(17)
$$\begin{aligned} G^{\varphi }_{\varphi } {=}\, G^{z}_{z}= & {} \frac{n f' \left( 2 n L'{+}L n'\right) {+}f \left( 4 n^2 L''{+}2 n L' n'{+}2 L n n''{-}L n'^2\right) }{4 L n^2}. \nonumber \\ \end{aligned}$$
(18)

Computing the effective energy-momentum tensor in Eq. (9) with this ansatz, the tensor \(X_{\mu \nu }\) can be written as

$$\begin{aligned} X^{t}_{t} = X^{r}_{r}= & {} \frac{h \alpha _f}{L \alpha _g }-\frac{3 L-h}{L}+ \alpha \left( \frac{h \alpha _f (2 L-h)}{L^2 \alpha _g }-\frac{3 L-2 h}{L}\right) \nonumber \\&+\beta \left( \frac{3 h \alpha _f (L-h)}{L^2 \alpha _g }-\frac{3 (L-h)}{L}\right) , \end{aligned}$$
(19)
$$\begin{aligned} X^{\varphi }_{\varphi }= & {} \frac{h \alpha _f}{L \alpha _g }-3 +\alpha \left( \frac{2 h \alpha _f}{L \alpha _g }-3\right) +\beta \left( \frac{3 h \alpha _f}{L \alpha _g }-3\right) , \nonumber \\\end{aligned}$$
(20)
$$\begin{aligned} X^{z}_{z}= & {} -\left( \frac{h-3 L}{L}+\frac{\alpha (2 h-3 L)}{L}+\frac{3 \beta (h-L)}{L}\right) . \end{aligned}$$
(21)

By substituting these components into the modified equation in Eq. (8) and then using the equations for the (t, t) and (r, r) components, we found the constraint

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{f L'^2}{n}\right) =0. \end{aligned}$$
(22)

In order to obtain the black hole solution with \(f =n\), the function L(r) must be proportional to r. Therefore, we can set \(L =r\) for the following investigation. By using this setting, we have only two independent functions, f and h. The two independent equations for these two functions are the conservation of the energy-momentum tensor in Eq. (10) and the (t, t) component of the modified Einstein equation in Eq. (8), which can be expressed, respectively, as

$$\begin{aligned}&\frac{h' (r (1+2 \alpha +3 \beta ) (\alpha _f+\alpha _g )-2 h \alpha _f(\alpha +3 \beta ))}{\alpha _g r^2}= 0 , \nonumber \\\end{aligned}$$
(23)
$$\begin{aligned}&\frac{r f'+f}{r^2} = -m_{g}^2 \Bigg (\frac{h \alpha _f}{\alpha _g r}-\frac{3 r-h}{r} \nonumber \\&+\,\alpha \left( \frac{h \alpha _f (2 r-h)}{\alpha _g r^2}-\frac{3 r-2 h}{r}\right) \nonumber \\&+\, \beta \left( \frac{3 h \alpha _f (r-h)}{\alpha _g r^2}-\frac{3 (r-h)}{r}\right) \Bigg ). \end{aligned}$$
(24)
Fig. 1
figure 1

The left panel shows the horizon structure of the AdS solution for specific values of the parameters where \(\alpha _m^2 = 4, c_0 = 6, c_1=5\). The right panel shows the horizon structure of the dS solution for the value of the parameters as \(\alpha _m^2 = -4, c_0 = -3, c_1=1\)

Full size image

From Eq. (23), two exact solutions of h can be written as

$$\begin{aligned} h(r)= & {} \frac{ r (1+2 \alpha +3 \beta )(\alpha _f+\alpha _g )}{2 \alpha _f (\alpha +3 \beta )}, \quad \end{aligned}$$
(25)
$$\begin{aligned} h(r)= & {} h_0 = \text {constant}, \end{aligned}$$
(26)

and with these solutions of h(r), Eq. (24) admits the following two solutions:

$$\begin{aligned} f_1(r)= & {} \left( -\frac{m_{g}^2 \left( 1+\alpha +\alpha ^2-3 \beta \right) }{3 (\alpha +3 \beta ) }\right) r^2-\frac{b}{\alpha _g r}, \end{aligned}$$
(27)
$$\begin{aligned} f_2(r)= & {} -\frac{b}{\alpha _g r} +m_{g}^2 \left( (1+\alpha +\beta )r^2 \right. \nonumber \\&\left. - h_0 (1+2 \alpha +3 \beta )r + h_0^2 (\alpha +3 \beta ) \right) , \end{aligned}$$
(28)

where b is an integration constant. Note that we have used the component \((\varphi ,\varphi )\) of the modified Einstein equation in Eq. (8) to obtain the constraint \(\alpha _f = \alpha _g\). The first solution in Eq. (27) coincides with the black string solution in general relativity [39, 40, 43] with an effective cosmological constant \(\varLambda \) as

$$\begin{aligned} \varLambda = -\frac{m_{g}^2 \left( 1+\alpha +\alpha ^2-3 \beta \right) }{3 (\alpha +3 \beta ) }. \end{aligned}$$
(29)

Note that in [39, 40, 43], the constant \(\alpha _g^2\) is chosen to be \(\alpha _g^2 = - \varLambda /3\), and

$$\begin{aligned} \alpha _g^2 = \frac{m_{g}^2 \left( 1+\alpha +\alpha ^2-3 \beta \right) }{ (\alpha +3 \beta ) }. \end{aligned}$$
(30)

The integration constant b can be obtained by using the solutions in the Newtonian limit which can be expressed as \(b = 4M\), where M is the ADM mass per unit length in z direction. Mathematically, the solution (27) is exactly the same as the one in general relativity which is already widely investigated. Moreover, its charged and rotating counterparts, and their properties including thermodynamics, have also widely been investigated [37,38,39,40,41,42]. Although the solution (27) coincides mathematically with that of Lemos [39, 40, 43], the dRGT solution naturally generates the cosmological-constant-like term from the graviton mass while for Lemos’ black string solution [39] the cosmological constant is introduced by hand. Hence, the properties of the solution (27) can be analyzed as in the previously mentioned cases, and hence we shall not address them here. The second solution in Eq. (28) is new. We can redefine the variables and parameters as follows:

$$\begin{aligned} f_2({r})= & {} \alpha _{m}^2r^2-\frac{4M}{\alpha _g r}-\alpha _{m}^2c_1 r +\alpha _{m}^2c_0, \end{aligned}$$
(31)

where

$$\begin{aligned} \alpha _{m}^2\equiv & {} m^2_g \left( 1+\alpha +\beta \right) ,\qquad c_1 \equiv \frac{h_0 (1+2 \alpha +3 \beta )}{1+\alpha +\beta },\nonumber \\ c_0\equiv & {} \frac{h_0^2 (\alpha +3 \beta )}{1+\alpha +\beta }. \end{aligned}$$
(32)

The solution in Eq. (31) is an exact black string solution in dRGT massive gravity which, in the limit \(\alpha _m = \alpha _g\) and \(c_0=c_1=0\), naturally goes over to Lemos’ [39] black string in general relativity. Henceforth, for definiteness, we shall call this massive gravity solution (31) a dRGT black string. In particular, it incorporates the cosmological-constant term naturally in terms of the graviton mass \(m_g\), which should not be surprising since the graviton mass serves as the cosmological constant in the self-expanding cosmological solution in massive gravity. The graviton mass also generates a constant term which is known as the so-called global monopole term.

It is important to note that the strong coupling scale of the dRGT massive gravity theory is \(\varLambda _3 = (m_g^2 M_{Pl})^{1/3}\). This is fixed by the construction of the mass terms of the theory [45], which may not be obvious from the action in Eq. (2). However, this scale can be simply seen through this solution. From this solution, the nonlinear scale known as the Vainshtein radius can be written as

$$\begin{aligned} r_V = \left( \frac{M}{\alpha _g m_g^2}\right) ^{1/3} = \left( \frac{M}{\alpha _g M_{Pl}}\right) ^{1/3} \frac{1}{\varLambda _3}. \end{aligned}$$
(33)

The parameter M is dimensionful with mass per unit length scaled by \(\alpha _g^{-1}\). Therefore, \(M/\alpha _g\) is the mass of the black string. By taking the values within the solar system and \(m_g \sim H\), one found that \(r_V \sim 10^{16} \text {km} \gg \varLambda _3^{-1} \sim 10^{3} \text {km}\). In particular, this indicates that we do not have to worry about the strong coupling issue in dRGT massive gravity for a system of scale below \(\varLambda _3\) (or of length scale beyond \(\sim 10^3\) km). The same situation also occurs in the spherically symmetric case [45].

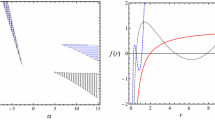
One can see that the horizon structure depends on the sign of \(\alpha _m^2\). If \(\alpha _m^2>0\), corresponding to an anti-de Sitter-like solution, the maximum number of horizons is three. If \(\alpha _m^2<0\), corresponding to de Sitter-like solution, the maximum number of horizons is two. The generic behavior of the horizon structure is shown in Fig. 1. This solution modifies the black string solution in general relativity with cosmological constant [39] by the three parameters \(c_0, c_1\) and \(\alpha _m^2\).

3.1 Thermodynamics of dRGT black string

Now, we analyze the thermodynamics of the new dRGT black string (31). By definition, the horizons are zeros of \(f(r_+)=0\). Depending on the parameters, there may exist up to three real roots. The horizon radius (\(r_+\)) and black string mass (\(M_+\)) are related via

$$\begin{aligned} M_+ = \frac{1}{4} \alpha _g \alpha ^2_m r_+ \left( r^2_+ -c_1 r_+ + c_0\right) . \end{aligned}$$
(34)

The mass \(M_+\) depends on the parameters \(c_0,\; c_1,\; \alpha ^2_m\) and \(\alpha ^2_g\). To have a positive definite mass, one may require the term \(\alpha ^2_m r_+ \left( r^2_+ -c_1 r_+ + c_0\right) \) to be positive. Such a consideration yields the following conditions:

$$\begin{aligned} \alpha ^2_m > 0, \quad c_1^2-4c_0<0. \end{aligned}$$
(35)

The second condition is obtained from the requirement that \(r^2_+ -c_1 r_+ + c_0\) cannot be factorized so that, including the condition \(\alpha ^2_m > 0\), the term \(\alpha ^2_m r_+ \left( r^2_+ -c_1 r_+ + c_0\right) \) will be positive definite. The Hawking temperature of the dRGT black string can be obtained by using \(T = \kappa /(2\pi )\), where \(\kappa = f'(r)/2|_{r=r_+}\) is the surface gravity of the black string. As a result, the temperature can be written as

$$\begin{aligned} T_+=\frac{\alpha _m^2}{4\pi r_+}\left( 3r_+^2-2c_1 r_+ +c_0\right) . \end{aligned}$$
(36)

We can determine a condition for a positive definite temperature by using the same procedure as we did for the mass. Consequently, we obtain

$$\begin{aligned} c_1^2-3c_0<0. \end{aligned}$$
(37)

These positivity conditions for both the mass and the temperature can narrow down the parameter space. The minimum temperature can be found at \(r_+ = \sqrt{c_0/3}\). At this point, the temperature can be written as

$$\begin{aligned} T_\mathrm{min} = \frac{\alpha _m^2}{2\pi }\left( \sqrt{3c_0}-c_1\right) . \end{aligned}$$
(38)

The square root of \(c_0\) is well defined through the conditions in Eq. (35) and/or in Eq. (37). Next, we can find its entropy via the first law of thermodynamics, \(\mathrm{{d}}M_+=T_+\mathrm{{d}}S\); it reads

$$\begin{aligned} S&= \frac{1}{2}\pi \alpha _g r_+^2 = \frac{A}{4}, \end{aligned}$$
(39)
$$\begin{aligned} A&= 2\pi \alpha _g r_+^2, \end{aligned}$$
(40)

and it turns out to satisfy the area law. Now we find the thermodynamical stability of the black string. For the local thermodynamical stability, we find the heat capacity of the system, which can be expressed as

$$\begin{aligned} C = \left( T \frac{\mathrm{d}S}{\mathrm{d}T}\right) _{r=r_+} = \frac{\pi \alpha _g r_+^2\left( 3r_+^2 -2c_1 r_+ +c_0\right) }{3r_+^2-c_0}. \end{aligned}$$
(41)

There exists a minimum temperature; C diverges at that temperature, where the corresponding radius obeys \(r_+ = \sqrt{c_0/3}\). Moreover, the heat capacity is negative when \(r_+ < \sqrt{c_0/3}\) and positive when \(r_+ > \sqrt{c_0/3}\). This suggests that the local thermodynamical stability of the black string requires the condition \(r_+ > \sqrt{c_0/3}\). Apart from the local one, the global thermodynamical stability can be analyzed by considering the Helmholtz potential

$$\begin{aligned} F&= M-TS \end{aligned}$$
(42)
$$\begin{aligned}&= \frac{\alpha _g \alpha _m^2 r_+}{8}\left( c_0-r_+^2\right) . \end{aligned}$$
(43)

The black string will be stable if the Helmholtz potential is negative. Thus, the global thermodynamical stability condition can be expressed as

$$\begin{aligned} r_+ > r_c = \sqrt{c_0}. \end{aligned}$$
(44)

Note that this condition also satisfies the local stability condition. As a result, the Hawking–Page phase transition, the transition from the hot flat space state to the black hole or black string state [46], occurs at the critical point, \(r_+=r_c=\sqrt{c_0}\). It is interesting to note that the phase transition can be realized only for the asymptotic AdS solution. Moreover, the existence of the phase transition depends only on the graviton mass. This can be seen clearly when we consider the case \(c_1 = c_0 = 0\). In this case, the Helmholtz potential does not change sign, which means that the Lemos black string is always thermodynamically stable.

4 Charged dRGT black string

Even though the astronomical objects are neutral, the charged black holes are intensively investigated. For spherically symmetric solutions, the charged black hole is a useful toy model since the structure of the horizon usually differs that of the neutral one in a quite drastic way. Moreover, study of thermodynamics of the charged black holes can be significantly extended, since it usually involves an open system such as a grand canonical system where the charge can play the role of the chemical potential. In this section, we extend our consideration by adding the electric charge to the theory. As a result, the action can be obtained by adding a gauge field term as follows:

$$\begin{aligned} S = \int \mathrm{{d}}^4x \sqrt{-g} \Bigg [\frac{1}{2}\left[ R +m_g^2 \mathcal {U}(g, \phi ^a)\right] -\frac{1}{16\pi }F_{\mu \nu }F^{\mu \nu }\Bigg ], \nonumber \\ \end{aligned}$$
(45)

where \(F_{\mu \nu }\equiv \left( \nabla _\mu A_\nu -\nabla _\nu A_\mu \right) \), \(A_\mu =(a(r),0,0,0)\) and a(r) is an arbitrary function. By using the same procedure as in the non-charged case, the solutions still can be divided into two branches according to Eqs. (25) and (26). The equations of motion of the electric field, the Maxwell equations, provide the constraint to the function a(r) of

$$\begin{aligned} a(r) =- \frac{ \gamma }{\alpha _g r}, \end{aligned}$$
(46)

where \(\gamma \) is an integration constant. In order to reduce the theory to the electromagnetic theory in flat spacetime, the integration constant can be written in terms of the linear charge density, q, in the z direction as \(\gamma ^2 = 4 q^2\). By solving the modified Einstein equations, the solutions for both branches can be written as

$$\begin{aligned} f^{(q)}_1(r)= & {} \left( -\frac{m_{g}^2 \left( 1+\alpha +\alpha ^2-3 \beta \right) }{3 (\alpha +3 \beta ) }\right) r^2 \nonumber \\&-\frac{b}{\alpha _g r}+\frac{\gamma ^2}{\alpha _g^2 r^2} , \end{aligned}$$
(47)
$$\begin{aligned} f^{(q)}_2(r)= & {} \frac{\gamma ^2}{\alpha _g^2 r^2}-\frac{b}{\alpha _g r} +m_{g}^2 \left( (1+\alpha +\beta )r^2 \right. \nonumber \\&\left. -\,\, h_0 (1+2 \alpha +3 \beta )r + h_0^2 (\alpha +3 \beta ) \right) . \end{aligned}$$
(48)

As we have mentioned before, we will focus on the second branch of the solutions which can be written in terms of the parameters in Eq. (32) as

$$\begin{aligned} f(r)= & {} \alpha _m^2 r^2-\frac{4 M}{\alpha _g r}+\frac{4 q^2}{\alpha _g^2 r^2}- \alpha _m^2 c_1 r + \alpha _m^2 c_0. \end{aligned}$$
(49)

The solution (49) is the charged dRGT black string solution. The linear mass density M can be expressed by solving \(f(r_+) = 0\) as follows:

$$\begin{aligned} M^{(q)} = \frac{1}{4} \alpha _g \alpha _m^2 r_+ \left( r_+^2-c_1 r_+ + c_0\right) + \frac{q^2}{\alpha _g r_+}. \end{aligned}$$
(50)

For a charged dRGT black string, it can be treated as two kinds of thermodynamical systems; grand canonical and canonical systems. We will separate our considerations into the two following subsections.

4.1 Grand canonical black string

In this aspect of treatment, a charged dRGT black string is considered to be an open system where charge transfer or creation/annihilation are allowed. The energy gain/loss from the increase/decrease of charge is determined by the chemical potential,

$$\begin{aligned} \mu = \frac{2 q}{\alpha _g r}, \end{aligned}$$
(51)

evaluating at the horizon. The charged dRGT black string mass and the Hawking temperature can be written as

$$\begin{aligned} M^{(q)}_G= & {} \frac{1}{4} \alpha _g \alpha _m^2 r_+ \left( r_+^2-c_1 r_+ + c_0\right) +\frac{1}{4}\alpha _g r_+ \mu ^2 , \end{aligned}$$
(52)
$$\begin{aligned} T^{(q)}_G= & {} \frac{\alpha _m^2\left( 3r^2_+-2c_1 r_+ +c_0\right) -\mu ^2}{4\pi r_+}. \end{aligned}$$
(53)

The positive definite of both mass and temperature can be found by following the same step as done in the non-charge case. As a result, the condition can be expressed as

$$\begin{aligned} \alpha _m^2 >0, \quad c_1^2 - 3 \left( c_0 -\frac{\mu ^2}{\alpha _m^2}\right) < 0. \end{aligned}$$
(54)

From these thermodynamic quantities, one found that they satisfy the first law of thermodynamics and the area law in which the entropy of the charged dRGT black string in the grand canonical system can be written as

$$\begin{aligned} S^{(q)}_G&= \frac{1}{2}\pi \alpha _g r_+^2 = \frac{A}{4}. \end{aligned}$$
(55)

For the thermodynamical stability of the system, one can proceed finding the heat capacity and the Gibbs potential. By following the same strategy as done in the non-charge case, the heat capacity and the Gibbs potential can be found as

$$\begin{aligned} C^{(q)}_G&= \left( T \frac{\mathrm{d}S}{\mathrm{d}T}\right) _{r=r_+}= \frac{\pi \alpha _g r^2_+\left[ \alpha _m^2\left( 3r^2_+-2c_1 r_+ +c_0\right) -\mu ^2\right] }{\alpha _m^2\left( 3r^2_+-c_0\right) +\mu ^2}, \end{aligned}$$
(56)
$$\begin{aligned} G^{(q)}&= M-TS-\mu Q=-\frac{\alpha _g r_+}{8}\left[ \alpha _m^2\left( r^2_+ -c_0\right) +\mu ^2\right] . \end{aligned}$$
(57)

The thermodynamical stability conditions can be found by requiring \(C^{(q)}_G > 0\) and \( G^{(q)} < 0\). The resulting condition can be expressed as

$$\begin{aligned} r_+ > r_c = \sqrt{ \left( c_0 -\frac{\mu ^2}{\alpha _m^2}\right) }. \end{aligned}$$
(58)

This suggests that it is possible to obtain the Hawking–Page phase transition for charged dRGT black string in massive gravity theory, when considered in the grand canonical aspect. Note that this phase transition cannot be provided by using a Lemos black string solution. This issue can be seen by setting \(c_1=c_0=0\), from which it turns out that the Gibbs potential is always negative for AdS solution while the dS solution does not satisfy the requirement of positive definite of the charged dRGT black string mass and temperature.

4.2 Canonical black string

For the canonical aspect of the black string, charge transfer or charge creation/annihilation are not allowed. The Hawking temperature can be found as

$$\begin{aligned} T^{(q)}_C = \frac{1}{4\pi r_+}\left[ \alpha _m^2\left( 3r^2_+ -2c_1 r_+ +c_0\right) - \frac{4q^2}{\alpha _g^2 r^2_+}\right] . \end{aligned}$$
(59)

From this expression, we found that one of requirements to obtain the positive definite of the black string temperature is \(\alpha _m^2 >0\). This corresponds to the asymptotic AdS solution. By following the strategy as done before, we found that the system still obeys the first law of thermodynamics and the area law in which the entropy of the black string can be written as

$$\begin{aligned} S^{(q)}_C&= \frac{1}{2}\pi \alpha _g r^2_+ = \frac{A}{4}. \end{aligned}$$
(60)

For the stability issue of this thermodynamic system, the local stability can be analyzed by considering the heat capacity which can be found as

$$\begin{aligned} C^{(q)}_C = \frac{\pi \alpha _g r^2_+\left[ \alpha _m^2\left( 3r^2_+-2c_1 r_+ +c_0\right) -\frac{4q^2}{\alpha _g^2 r^2_+}\right] }{\alpha _m^2\left( 3r^2_+ -c_0\right) +\frac{12q^2}{\alpha _g^2 r^2_+}}. \end{aligned}$$
(61)

By using \(T^{(q)}_C >0\), the positivity of the heat capacity will be guaranteed by requiring

$$\begin{aligned} r_+ > \sqrt{ \frac{c_0}{6}\left( 1 + \left[ 1 - \frac{144 q^2}{\alpha _g^2\alpha _m^2 c_0^2}\right] ^{1/2}\right) }. \end{aligned}$$
(62)

The Helmholtz potential of the system can be written as

$$\begin{aligned} F^{(q)} = -\frac{\alpha _g r_+}{8}\left[ \alpha _m^2\left( r^2_+ -c_0\right) -\frac{12q^2}{\alpha _g^2 r^2_+}\right] . \end{aligned}$$
(63)

To investigate the global thermodynamical stability, one requires that \(F^{(q)} < 0\). The condition turns out to be as follows:

$$\begin{aligned} r_+ > r_c = \sqrt{ c_0\left( 1 + \left[ 1 + \frac{144 q^2}{\alpha _g^2\alpha _m^2 c_0^2}\right] ^{1/2}\right) }, \end{aligned}$$
(64)

which is stronger than the one for the local stability condition. This suggests that, for the canonical system, it is possible to provide the Hawking–Page phase transition for the charged black string in massive gravity theory. However, for this system, the AdS black string solution can also provide the phase transition. This can be seen by setting \(c_1 = c_0 = 0\), from which it turns out that the phase transition occurs when \(r_+^2 = \sqrt{\frac{2 q}{\sqrt{3\alpha _m^2\alpha _g^2}}}\).

5 Concluding remarks

The dRGT massive gravity describes nonlinear interaction terms as a generalization of the Einstein–Hilbert action when the graviton is massive. It is believed that dRGT massive gravity may provide a possible explanation for the accelerating expansion of the universe that does not require any dark energy or cosmological constant. In this paper, we have presented a class of black strings, both charged and uncharged, in dRGT massive gravity where the effective cosmological constant is negative, and we studied the thermodynamics and phase structure of the solutions in both the grand canonical and the canonical ensembles. The black string obtained is immensely simplified due to the choice of the fiducial metric. As expected the solution contains the Lemos solutions [39] as a particular case. Our dRGT black string solution can be identified, e.g., as a monopole-black string of general relativity for a suitable choice of the parameters of the theory where the graviton mass in massive gravity naturally generates the cosmological constant and the global monopole term.

We have also analyzed the thermodynamical properties of the dRGT black string solution. The thermodynamic quantities have also been found to contain corrections from the graviton mass except for the black string entropy which is unaffected by massive gravity and still obeys the area law. By analyzing the thermodynamical properties of the black string solution, we found that it is possible to obtain the Hawking–Page phase transition in the dRGT black string case, while this is not possible for Lemos solution. The conditions to provide such a transition were explored. In fact, we determined the phase transition in both charged and non-charged case by analyzing the sign of the potential at \(r=r_c\), with the stable (unstable) branch for \(r > (<) r_c\).

The results presented here are a generalization of previous discussions of Lemos [39,40,41], on the black string, in a more general setting. The possibility of a further generalization of these results to higher dimensions is an interesting problem for future research. The rotating dRGT black string solution is also interesting, since most astronomical objects are rotating. We leave this investigation for further work.