All spherically symmetric charged anisotropic solutions for compact stars

Abstract

In the present paper we develop an algorithm for all spherically symmetric anisotropic charged fluid distributions. Considering a new source function $\nu (r)$ we find a set of solutions which is physically well behaved and represents compact stellar models. A detailed study specifically shows that the models actually correspond to strange stars in terms of their mass and radius. In this connection we investigate several physical properties like energy conditions, stability, mass–radius ratio, electric charge content, anisotropic nature and surface redshift through graphical plots and mathematical calculations. All the features from these studies are in excellent agreement with the already available evidence in theory as well as observations.

1 Introduction

Historically the possibility that self-gravitating stars could actually contain a non-vanishing net charge was first pointed out by Rosseland [1] and later on by several other researchers [2,3,4] with different view points. The general relativistic analog for charged dust stars were discussed by Majumdar [5] and Papapetrou [6]. However, in his pioneering work Bonnor [7] further discussed this issue and also several investigators considered the problem later on in detail in connection to stability and other aspects [3, 8,9,10,11,12,13,14].

Following Treves and Turolla [15], to justify the present work with a charged fluid distribution, Ray and Das [16, 17] argue that even though the astrophysical systems are by and large electrically neutral, recent studies do not rule out the existence of massive astrophysical systems that are not electrically neutral. The mechanism is mainly related to acquiring a net charge by accretion from the surrounding medium or even by a compact star during its collapse from the supernova stage. In this connection it is interesting to note that to study the effect of electric charge in compact stars Ray et al. [18] by assuming an ansatz have shown that in order to see any appreciable effect on the phenomenology of the compact stars, the total electric charge is to be $\sim$ $10^{20}$ C.

It has been pointed out by Ivanov [14] that substantial analytical difficulties associated with self-gravitating, static, isotropic fluid spheres when pressure explicitly depends on matter density. However, it is also observed that simplification can be achieved with the introduction of electric charge. One is to note that charged, self-gravitating anisotropic fluid spheres have been investigated by Horvat et al. [19] in studies of gravastars and also recently Thirukkanesh and Maharaj [20] found solutions for the charged anisotropic fluid.

In connection to the stability of the stellar model Stettner [21] argued that a fluid sphere of uniform density with a net surface charge is more stable than without charge. Therefore, as pointed out by Rahaman et al. [22], a general mechanism has been adopted to overcome the singularity due to gravitationally collapsing of a static, spherically symmetric fluid sphere one is to include charge to the neutral system. It is observed that in the presence of charge several features may arise: (i) gravitational attraction is counter balanced by the electrical repulsion in addition to the pressure gradient [23], (ii) it inhibits the growth of space-time curvature which has a great role to avoid singularities [24] and (iii) the presence of the charge function serves as a safety valve, which absorbs much of the fine tuning, necessary in the uncharged case [14].

One can notice that since the breakthrough idea of a white dwarf by Chandrasekhar [25] the study of compact stars was tremendously motivated in the field of ultra-dense objects. In this line of research the other dense compact stars are neutron stars, quark stars, strange stars, boson stars, gravastars and so on. As far as composition is concerned in the compact stars the matter is found to be in a stable ground state where the quarks are confined inside the hadrons. It is argued by several workers [26,27,28,29] that if it is composed of de-confined quarks then also a stable ground state of matter, known as ‘strange matter’, is achievable, which leads to a ‘strange star’. There are two aspects of this assumption behind the strange star: (i) theoretically to explain the exotic phenomena of gamma ray bursts and soft gamma ray repeaters [30, 31], and (ii) observational confirmation of $\textit{SAX}\,{J}{1808.4}{\text {-}}3658$ as one of the candidates for a strange star by the Rossi X-ray Timing Explorer [32].

It was Ruderman [33] who investigated the idea that nuclear matter may have anisotropic features at least in certain very high density ranges ( $10^{15}$ gm/cm$^3$), where the nuclear interaction must be treated relativistically. However, later on Bowers and Liang [34] showed specifically that anisotropy might have non-negligible effects on such parameters like maximum equilibrium mass and surface redshift. We notice that recently an anisotropic matter distribution has been considered by several authors in connection to compact stars [22, 35,36,37,38,39,40,41].

Studies have shown that at the center of the fluid sphere the anisotropy vanishes. However, for a small radial increase the anisotropy parameter increases, and after reaching a maximum in the interior of the star, it becomes a decreasing function of the radial distance [42, 43]. So there are several possibilities of expressions for charge functions and pressure anisotropy. It is also indicated by Varela et al. [38] that inward-directed fluid forces caused by pressure anisotropy may allow equilibrium configurations with larger net charges and electric field intensities than those found in studies of charged isotropic fluids.

The algorithm for a perfect fluid and an anisotropic uncharged fluid has already been published by others [44,45,46]. In his work Lake [44, 45] has considered an algorithm based on the choice of a single monotone function which generates all regular static spherically symmetric perfect as well as anisotropic fluid solutions of Einstein’s equations. On the other hand, Herrera et al. [46] have extended the algorithm to the case of locally anisotropic fluids. Therefore, there remains a natural choice of an algorithm so as to apply to a more general case with the inclusion of charge along with an anisotropic fluid distribution.

Against the above background and with the above motivation, in the present paper, we have carried out an investigation for a relativistic stellar model with charged anisotropic fluid sphere. The schematic format of this study is as follows: we provide the Einstein–Maxwell field equations for a charged anisotropic stellar source in Sect. 2, whereas an allied algorithm has been constructed in Sect. 3. The general solutions are shown in Sect. 4, along with a special example for the index $n=1$ and matching of the interior solution with the exterior Reissner–Nordström solution. In Sect. 5 we explore several interesting properties of the physical parameters which include density, pressure, stability, charge, anisotropy and redshift. Special case studies are conducted in Sect. 6 to verify (i) the mass–radius ratio and (ii) the density of the star, both of which clearly indicate that the model represents a stable configuration of a strange compact star. Section 7 is meant as a platform for providing some salient features and concluding remarks.

2 The field equations for charged and anisotropic matter distribution

In this work we intend to study a static and spherically symmetric matter distribution whose interior metric is given in Schwarzschild coordinates [47, 48] $x^i=(r, \theta , \phi , t)$ as follows:

$$\begin{aligned} \mathrm{d}s^2 = - \mathrm{e}^{\lambda (r)} \mathrm{d}r^2 - r^2(\mathrm{d}\theta ^2 + \mathrm{sin}^2\theta \mathrm{d}\phi ^2) + \mathrm{e}^{\nu (r)} \mathrm{d}t^2. \end{aligned}$$

(1)

The Einstein–Maxwell field equations are as usual given by

$$\begin{aligned} {R^i}_j - \frac{1}{2} R\, {g^i}_j = \kappa ({T^i}_j + {E^i}_j), \end{aligned}$$

(2)

where $\kappa = 8\pi$ is the Einstein constant with $G=1=c$ in relativistic geometrized unit, G and c, respectively, being the Newtonian gravitational constant and velocity of photon in vacua.

The matter within the star is assumed to be locally anisotropic fluid in nature and consequently ${T^i}_j$ and ${E^i}_j$ are the energy-momentum tensor of fluid distribution and electromagnetic field defined by [49]

$$\begin{aligned} {T^i}_j = [(\rho + p_\mathrm{t})v^iv_j - p_\mathrm{t}{\delta ^i}_j + (p_\mathrm{r} - p_\mathrm{t}) \theta ^i \theta _j], \end{aligned}$$

(3)

$$\begin{aligned} {E^i}_j = \frac{1}{4}\left( -F^{im}F_{jm} + \frac{1}{4}{\delta ^i}_jF^{mn}F_{mn}\right) \!, \end{aligned}$$

(4)

where $v^i$ is the four-velocity as $v^i=\mathrm{e}^{\nu (r)/2}{\delta ^i}_4$, $\theta ^i$ is the unit space like vector in the direction of radial vector as $\theta ^i = \mathrm{e}^{\lambda (r)/2}{\delta ^i}_1$, $\rho$ is the energy density, $p_\mathrm{r}$ is the pressure in the direction of $\theta ^i$ (normal or radial pressure) and $p_\mathrm{t}$ is the pressure orthogonal to $\theta _i$ (transverse or tangential pressure), while ${T^1}_1=-p_\mathrm{r}$,  ${T^2}_2={T^3}_3=-p_\mathrm{t}$,  ${T^4}_4=\rho$ and ${E^1}_1=-{E^2}_2=-{E^3}_3={E^4}_4=\frac{1}{8\,\pi }\,\frac{q^2(r)}{r^4}$.

Now, anti-symmetric electromagnetic field tensor $F_{ij}$ can be defined by

$$\begin{aligned} F_{ij} = \frac{\partial A_j}{\partial x_i} - \frac{\partial A_i}{\partial x_j}, \end{aligned}$$

(5)

which satisfies the Maxwell equations

$$\begin{aligned} F_{ik,j} + F_{kj,i} + F_{ji,k} = 0, \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial }{\partial x^k}({\sqrt{-}g} F^{ik}) = -4\pi {\sqrt{-}g} J^i, \end{aligned}$$

(7)

where g is the determinant of quantities $g_{ij}$ in Eq. (2) defined by

$$\begin{aligned} g = \left( \begin{array}{cccc} \mathrm{e}^{\nu } &{} 0 &{} 0 &{} 0\\ 0 &{}-\mathrm{e}^{\lambda } &{} 0 &{} 0\\ 0 &{} 0 &{} -r^2 &{} 0\\ 0 &{} 0 &{} 0 &{} -r^2\mathrm{sin}^2\theta \end{array} \right) = - \mathrm{e}^{\nu +\lambda }r^4 \mathrm{sin}^2\theta , \end{aligned}$$

(8)

where $A_j=(\phi (r), 0, 0, 0)$ is the four-potential and $J^i$ is the four-current vector defined by

$$\begin{aligned} J^i = \frac{\sigma }{\sqrt{g}_{44}} \frac{\mathrm{d}x^i}{\mathrm{d}x^4} = \sigma v^i, \end{aligned}$$

(9)

where $\sigma$ is the charged density.

For static matter distribution the only non-zero component of the four-current is $J^4$. Because of spherical symmetry, the four-current component is only a function of radial distance, r. The only non-vanishing components of electromagnetic field tensor are $F^{41}$ and $F^{14}$, related by $F^{41} = - F^{14}$, which describe the radial component of the electric field. From Eqs. (7) and (9), one obtains the following expression for the component of the electric field:

$$\begin{aligned} \mathrm{e}^{(\nu +\lambda )/2}\,r^2\,F^{41}= & {} -4\pi \,\int _0^r {\frac{\sigma \, r^2\, \mathrm{e}^{(\lambda +\nu )/2}}{\sqrt{g_{44}}}\, \mathrm{d}r}\nonumber \\= & {} -4\pi \,\int _0^r {{\sigma r^2 \mathrm{e}^{\lambda /2}}\,\mathrm{d}r}, \end{aligned}$$

(10)

where $\sqrt{g_{44}}=\mathrm{e}^{\nu /2}$ and if q(r) represents the total charge contained within the sphere of radius r, then it can be defined by the relativistic Gauss law as

$$\begin{aligned} q(r) = 4\pi \int _0^r \sigma r^2 \mathrm{e}^{\lambda /2} \mathrm{d}r = r^2 \sqrt{-F_{14}F^{14}}. \end{aligned}$$

(11)

From Eqs. (10) and (11), we obtain the electric charge q(r) as

$$\begin{aligned} q(r)=- \mathrm{e}^{(\nu +\lambda )/2}\,r^2\,F^{41}. \end{aligned}$$

(12)

For the spherically symmetric metric (1), the Einstein–Maxwell field equations may be expressed as the following system of ordinary differential equations [49]:

$$\begin{aligned} -\kappa ({T^1}_1+{E^1}_1)= & {} \frac{{\nu }^{\prime }}{r} \mathrm{e}^{-\lambda } - \frac{(1 - \mathrm{e}^{-\lambda })}{r^2} = \kappa p_\mathrm{r} - \frac{q^2}{r^4},\nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned} -\kappa ({T^2_2}+{E^2}_2)= & {} -\kappa ({T^3}_3+{E^3}_3)\nonumber \\= & {} \left[ \frac{{\nu }^{\prime \prime }}{2} - \frac{{\lambda }^{\prime }{\nu }^{\prime }}{4} + \frac{{{\nu }^{\prime }}^2}{4} + \frac{{\nu }^{\prime } - {\lambda }^{\prime }}{2r}\right] \mathrm{e}^{-\lambda } \nonumber \\= & {} \kappa p_\mathrm{t} + \frac{q^2}{r^4}, \end{aligned}$$

(14)

$$\begin{aligned} \kappa ({T^4}_4+{E^4}_4)= & {} \frac{{\lambda }^{\prime }}{r} \mathrm{e}^{-\lambda } + \frac{(1 - \mathrm{e}^{-\lambda })}{r^2} = \kappa \rho + \frac{q^2}{r^4}, \end{aligned}$$

(15)

where the prime denotes differential with respect to r.

If the mass function for electrically charged fluid sphere is denoted by m(r), then it can be defined by the metric function $\mathrm{e}^{\lambda (r)}$ as

$$\begin{aligned} \mathrm{e}^{-\lambda (r)} = 1 - \frac{2m(r)}{r} + \frac{q^2}{r^2}. \end{aligned}$$

(16)

If R represents the radius of the fluid spheres then it can be showed that m is constant $m(r = R) = M$ outside the fluid distribution where M is the gravitational mass. Thus the function m(r) represents the gravitational mass of the matter contained in a sphere of radius r. The gravitational mass M of the fluid distribution is defined as

$$\begin{aligned} M = \mu (R) + \xi (R), \end{aligned}$$

(17)

where $\mu (R) = \frac{\kappa }{2} \int _0^R\rho \, r^2\, \mathrm{d}r$ is the mass inside the sphere, $\xi (R) = \frac{\kappa }{2} \int _0^R \sigma \, r\, q\, \mathrm{e}^{\lambda /2}\,\mathrm{d}r$ is the mass equivalence of the electromagnetic energy of distribution and q(R) is the total charge inside the fluid spheres [50].

Now using Eqs. (17) and (11), we can write the mass m(r) of the fluid spheres of radius r in terms of energy density and charge function as

$$\begin{aligned} m(r)= \frac{\kappa }{2} \int \rho r^2 \mathrm{d}r +\frac{1}{2} \int \frac{q^2}{r^2}\mathrm{d}r + \frac{q^2}{2r}, \end{aligned}$$

(18)

whereas from Eqs. (13) and (16) we obtain

$$\begin{aligned} \nu ^{\prime } = \frac{\left( \kappa r p_\mathrm{r} + \frac{2m}{r^2} - \frac{2q^2}{r^3}\right) }{\left( 1 - \frac{2m}{r} + \frac{q^2}{r^2}\right) }. \end{aligned}$$

(19)

We suppose here that the radial pressure is not equal to the tangential pressure i.e. $p_\mathrm{r} \ne p_\mathrm{t}$, otherwise if the radial pressure is equal to the transverse pressure i.e. $p_\mathrm{r} = p_\mathrm{t}$, which corresponds to isotropic or perfect fluid distribution. Let the measure of anisotropy $\Delta = p_\mathrm{t} - p_\mathrm{r}$ and is called the anisotropy factor [51]. The term $2(p_\mathrm{t} - p_\mathrm{r})/r$ appears in the conservation equations ${T^i}_{j;i} = 0$ (where a semi-colon denotes the covariant derivative) which is representing a force due to anisotropic nature of the fluid. When $p_\mathrm{t} > p_\mathrm{r}$ then direction of force to be outward and inward when $p_\mathrm{t} < p_\mathrm{r}$. However, if $p_\mathrm{t} > p_\mathrm{r}$, then the force allows construction of more compact object for the case of anisotropic fluid than isotropic fluid distribution [52].

By using Eqs. (13)–(16) and also Eqs. (18) and (19) the expression of pressure gradient in terms of mass, charge, energy density and radial pressure read

$$\begin{aligned} \frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}= & {} - \frac{\left( p_\mathrm{r} + \frac{2m^{\prime }}{r^2} - \frac{q}{r^3}\frac{\mathrm{d}q}{\mathrm{d}r}\right) \left( \kappa r p_\mathrm{r} + \frac{2m}{r^2} - \frac{2q^2}{r^3}\right) }{2\left( 1 - \frac{2m}{r} + \frac{q^2}{r^2}\right) }\nonumber \\&+\,\frac{q}{4\pi r^4} \frac{\mathrm{d}q}{\mathrm{d}r} + \frac{2\Delta }{r}, \end{aligned}$$

(20)

where $m^{\prime } \equiv \frac{\mathrm{d}m}{\mathrm{d}r}$ i.e. variation of mass with radial coordinate r. The above Eq. (20) represents the charged generalization of the well-known Tolman–Oppenheimer–Volkoff (TOV) equation of hydrostatic for anisotropic stellar structure [47, 48].

3 The algorithm for constructing all possible anisotropic charged fluid solutions

The Einstein equations (13), (14) and (15) in terms of mass function reduce to

$$\begin{aligned} -\frac{2m(1+r{\nu }^{\prime })}{r^3} + \frac{{\nu }^{\prime }}{r}+\frac{q^2(1+r{\nu }^{\prime })}{r^4}+ \frac{q^2}{r^4}=\kappa p_\mathrm{r}, \end{aligned}$$

(21)

$$\begin{aligned}&-\,\frac{m^{\prime }(2+r{\nu }^{\prime })}{2r^2} - \frac{m(2r^2{\nu }^{\prime \prime } +r^2{{\nu }^{\prime }}^2 +r{\nu }^{\prime } -2)}{2r^3} \nonumber \\&\quad +\,\frac{2rqq^{\prime }{\nu }^{\prime }-2q^2{\nu }^{\prime }+4qq^{\prime } +(r^2+q^2)(2r{\nu }^{\prime \prime } +r{{\nu }^{\prime }}^2+2{\nu }^{\prime })}{4r^3}\nonumber \\&\quad -\, \frac{2q^2}{r^4}=\kappa p_\mathrm{t}, \end{aligned}$$

(22)

$$\begin{aligned} \frac{2m^{\prime }}{r^2} - \frac{2qq^{\prime }}{r^3}= \kappa \rho , \end{aligned}$$

(23)

Using Eqs. (21) and (22), we obtain a Riccati equation in the first derivative of $\nu (r)$. However, after the re examination of the differential equation we come across a linear differential equation of first order in m(r) [53].

The first order linear differential equation of m(r) in terms of $\nu (r)$, anisotropy $\Delta = (p_\mathrm{t} - p_\mathrm{r})$ and charge function q(r) can be provided as follows:

$$\begin{aligned}&m^{\prime }+ \frac{(2r^2{\nu }^{\prime \prime } + r^2{{\nu }^{\prime }}^2 - 3r{\nu }^{\prime } -6)}{r(r{\nu }^{\prime } + 2)}m \nonumber \\&\quad = \frac{(2r^2{\nu }^{\prime \prime } + r^2{{\nu }^{\prime }}^2 - 2{\nu }^{\prime }r)}{2(r{\nu }^{\prime } + 2)} + f(r), \end{aligned}$$

(24)

where

$$\begin{aligned} f(r)= & {} \frac{2rq^2{\nu }^{\prime \prime } + q^2{\nu }^{\prime }(r{\nu }^{\prime } - 4) + 2qq^{\prime }(r{\nu }^{\prime } + 2)}{2r(r{\nu }^{\prime } + 2)}\nonumber \\&-\, \frac{2r^2}{(r{\nu }^{\prime } + 2)} \left( \Delta + \frac{4q^2}{r^4}\right) . \end{aligned}$$

(25)

Equation (24) gives the mass m(r) as follows:

$$\begin{aligned} m(r)= \mathrm{e}^{-\int g(r) \mathrm{d}r} \left[ \int \left\{ h(r) + f(r)\right\} (\mathrm{e}^{\int g(r)\mathrm{d}r}) \mathrm{d}r + A \right] ,\nonumber \\ \end{aligned}$$

(26)

where

$$\begin{aligned} g(r) = \frac{(2r^2{\nu }^{\prime \prime } + r^2{{\nu }^{\prime }}^2 - 3r{\nu }^{\prime } -6)}{r(r{\nu }^{\prime } + 2)}, \end{aligned}$$

(27)

$$\begin{aligned} h(r) = \frac{(2r^2{\nu }^{\prime \prime } + r^2{{\nu }^{\prime }}^2 - 2{\nu }^{\prime }r)}{2(r{\nu }^{\prime } + 2)}, \end{aligned}$$

(28)

where we have used the symbol $\prime \equiv \frac{d}{\mathrm{d}r}$.

At this point we would like to construct useful algorithm to generate solutions for any known generic function $\nu (r)$. Now from Eqs. (21) and (23), we get

$$\begin{aligned} \kappa \rho = \frac{2m^{\prime }}{r^2} - \frac{2qq^{\prime }}{r^3} \ge 0, \end{aligned}$$

(29)

$$\begin{aligned} \kappa p_\mathrm{r} = \frac{r[\nu ^{\prime }(r^2+q^2 - 2rm) - 2m] + 2q^2}{r^4} \ge 0. \end{aligned}$$

(30)

Note that the inequalities in (29) and (30) are to be viewed from reality or energy conditions which will impose the restrictions on $\nu (r)$. At the center of symmetry $(r = 0)$ the regularity of the Ricci invariants requires that energy density $\rho (r)$, radial pressure $p_\mathrm{r}(r)$ and tangential pressure $p_\mathrm{t}(r)$ at origin should be finite. The regularity of Weyl invariants requires that mass m(r) and charge q(r) at $r=0$ should satisfy $m(0)= m^{\prime }(0)=m^{\prime \prime }(0)=0$, $q(0)= q^{\prime }(0)=0$ and $m^{\prime \prime \prime }(0)=\kappa \rho (0) + (q^{\prime \prime }(0))^2$.

Now the metric function $\nu (0)$ is a finite constant, $q(0)= 0$ and it follows from (30) that $\nu ^{\prime }(0)=0$ and $\nu ^{\prime \prime }(0)=\frac{\kappa }{3}[\rho (0)+3p_\mathrm{r}(0)]-(q^{\prime \prime }(0))^2 > 0$. Since $\rho \ge 0$ and continuous, and also since $p_\mathrm{r} > 0$ is finite, it follows that $r > 2m(r)$ [54, 55]. With $r > 2m(r)$ for $r > 0$. It also follows from (30) for $p_\mathrm{r} > 0$ that $\nu ^{\prime }(r)\ne 0$. As a result, the source function $\nu (r)$ must be a monotone increasing function with a regular minimum at $r = 0$.

4 A class of new solutions for charged anisotropic stellar models

For a class of new anisotropic charged stellar models we consider the following suitable source function in the form of the metric potential:

$$\begin{aligned} \nu (r) = -n~\mathrm{log}~B^{-1/n} (1-Cr^2), \end{aligned}$$

(31)

where n, B and C are positive integers. It is suitable in the sense that the source function given by Eq. (31) is monotonic increasing with a regular minimum at $r=0$. It is to note that charged and uncharged perfect fluid of this source function with different electric intensity has already been carried out [56, 57] where it was proved that the above kind of source function with increasing and non-singular behavior provides physically valid solutions.

In terms of the source function expressed in Eq. (31) we consider the electric charge distribution and anisotropic pressure distribution are in the following forms:

$$\begin{aligned} \frac{2q^2}{Cr^4}= & {} K(Cr^2)^{1+N}[1+(n-1)Cr^2]^{\frac{n+1}{n-1}}\nonumber \\&\times \,(1-Cr^2)^{n+1}(a-bCr^2)^m, \end{aligned}$$

(32)

$$\begin{aligned} \frac{\Delta }{C} = \beta (Cr^2)^{n}[1+(n-1)Cr^2]^{n-1}, \end{aligned}$$

(33)

where K, N and $\beta$ are positive constants, a and b are positive real numbers and m is a positive integer. The electric field intensity and anisotropy are vanishing at the center and remains continuous, regular and bounded in the inside of the fluid sphere for certain range of values of the parameters. Also these forms of the electric intensity and anisotropy function allow us to integrate Eq. (26). Thus these choices may be physically reasonable and useful in the study of the gravitational behavior of anisotropic charged stellar models.

It is observed that Durgapal and Pandey [58], Ishak et al. [59], Lake [44], Pant [60] and Maurya et al. [61] have proposed solutions via the ansatz (31) with some particular values of n. After that Maurya and Gupta [62, 63] showed that the same ansatz for the metric function (1) by taking n is a negative integer, $C<0$ and $C>0$, $0<n<1$ and it produces an infinite family of analytic solutions of the self-bound type (see details in the Tables 7 and 8 of Appendix). Recently Maurya and Gupta [64] have also obtained infinite family of anisotropic solutions for the same ansatz. But recently Murad [65] obtained charged stellar model for $n=-2$ and $C<0$, however, neutral solutions of this are irregular in the behavior of $\mathrm{d}p/\mathrm{d}\rho$ (Durgapal and Fuloria [66], Delgaty and Lake [67], Pant [60], Maurya and Gupta [63]). Hence the solution is not suitable for application to a neutron star model because the equations of state for nuclear matter show a regular behavior of $\mathrm{d}p/\mathrm{d}\rho$ [66]. So in the present problem we have started with regular behavior of $\mathrm{d}p/\mathrm{d}\rho$ in the same ansatz by taking the value of $n=1$ and 3. Recently Maurya et al. [68] argued that neutral solutions for these cases have the regular behavior of $\mathrm{d}p/\mathrm{d}\rho$ and it may be suitable for application to a neutron star model.

By using Eqs. (31), (32) and (33), Eq. (26) gives m(r) in the following form:

$$\begin{aligned} m(r)= \mathrm{e}^{-\int G(r) \mathrm{d}r} \left[ \int \left\{ H(r) + F(r)\right\} (\mathrm{e}^{\int G(r)\mathrm{d}r}) \mathrm{d}r + A \right] ,\nonumber \\ \end{aligned}$$

(34)

where

$$\begin{aligned} G(r) = \frac{2(2n^2 + 5n - 3)C^2r^4 + (12-n)Cr^2 - 6}{2r(1 - Cr^2)[1+(n-1)Cr^2]}, \end{aligned}$$

(35)

$$\begin{aligned} H(r) = \frac{n(n + 2)C^2r^4}{(1 - Cr^2)[1+(n-1)Cr^2]}, \end{aligned}$$

(36)

$$\begin{aligned} F(r)= & {} \frac{2K(Cr^2)^{N+2}(1 - Cr^2)^{n+1}(a-bCr^2)^m [F_1(r)+ [1+(n-1)Cr^2]F_2(r)]}{4(1 - Cr^2)[1+(n-1)Cr^2]}\nonumber \\&- F_3(r), \end{aligned}$$

(37)

where

$$\begin{aligned} F_1(r)= [1+(n-1)Cr^2]^{\frac{n+1}{n-1}}[4nC^2r^4 - 2nCr^2], \end{aligned}$$

(38)

$$\begin{aligned} F_2(r)= & {} 1 - 2Cr^2 + (2+N)(1 - Cr^2) \nonumber \\&-\, \frac{bmCr^2(1-Cr^2)}{(a-bCr^2)}+ \frac{(1+n)Cr^2(1 - Cr^2)}{[1+(n-1)Cr^2]},\nonumber \\ \end{aligned}$$

(39)

$$\begin{aligned}&F_3(r)= \frac{\beta (Cr^2)^{n+1}[1+(n-1)Cr^2]^{n-1}}{(1 - Cr^2)^{-n-1}[1+(n-1)Cr^2]} \nonumber \\&\quad +\,\frac{2K(Cr^2)^{N+2}[1+(n-1)Cr^2]^{\frac{n+1}{n-1}}(1-Cr^2)(a-bCr^2)}{(1 - Cr^2)^{-n-1}[1+(n-1)Cr^2]}.\nonumber \\ \end{aligned}$$

(40)

In the absence of electric field intensity $(K =0)$ and pressure anisotropy $(\beta = 0)$, Eqs. (21), (22) and (23) reduce to the equations obtained by Maurya et al. [68]. Corresponding solutions belongs to the solutions of Maurya et al. [62, 63, 68] for the values of n being all negative integers, all positive fractional values between 0 and 1 and some positive integers ($n=1$, 2 and 3) and solutions for particular values of n to the well-known Tolman [47] for $n =-1$, Wyman [69], Kuchowicz [70], Adler [71], Adams and Cohen [72] all for $n =- 2$, Heintzmann [73] for $n =-3$, Durgapal [74] for $n = -4, - 5$ and Pant [60] for $n = -6, - 7$ for the ansatz (31).

4.1 An example: physical parameters of charged anisotropic model for $n=1$

We calculate mass of the charged anisotropic fluid sphere as

$$\begin{aligned} \frac{2m_1(r)}{r}= & {} 1 - K(1 - Cr^2)^2 \mathrm{e}^{2Cr^2}\nonumber \\&\times \,\Bigg [-\frac{1}{2}(Cr^2)^{N+2}(a-bCr^2)^m\nonumber \\&+ Cr^2(1 - Cr^2) \Pi _{a,b,C,m,i,N}(r)\Bigg ] \nonumber \\&+\, 2(\beta +3)Cr^2(1 - Cr^2)^3\mathrm{e}^{2Cr^2-2}\nonumber \\&\times \,[\phi _{C,j}(r) + \psi _{C,j}(r)] \nonumber \\&-\, A(1 - Cr^2)^3 Cr^2 \mathrm{e}^{2Cr^2}\nonumber \\&- [1+(\beta -2)Cr^2](1 - Cr^2)^2, \end{aligned}$$

(41)

where

$$\begin{aligned}&\phi _{C,j}(r) = \Sigma _{j=1}^{\infty }(-1)^{j-1} \frac{(1 - 2Cr^2)^j}{j}\nonumber \\&\qquad =\mathrm{log}(2-2Cr^2),\\&\psi _{C,j}(r) = \Sigma _{j=1}^{\infty }\frac{2(1 - Cr^2)^j}{j!j}\nonumber \\&\qquad =Ei(2-2Cr^2)-\mathrm{log}(2-2Cr^2),\\&\Pi _{a,b,C,m,i,N}(r) = \Sigma _{i=0}^{m}(-1)^i a^{m-i} b^i \left( \begin{array}{c} m\\ i \end{array}\right) \left[ \frac{(Cr^2)^{N+i+1}}{N+i+1}\right] . \end{aligned}$$

The expressions for energy density, radial pressure and tangential pressure are (by taking $x=Cr^2$) given by

$$\begin{aligned} \frac{\kappa \rho (r)}{C}= & {} A(4x^3-3x^3-7x^2-1)\mathrm{e}^{2x}\nonumber \\&+\, (6-11x^2+2x^3) - \beta (3-10x+7x^2) \nonumber \\&+\, (6+\beta )(1-x)^2(3-5x-4x^2)\nonumber \\&\times \,\mathrm{e}^{2x-2}[\phi _{j}(x) + \psi _{j}(x)]\nonumber \\&-\,2\beta x \mathrm{e}^{2x-2} (1-x)^2[1+(1-x)\theta _j(x)]\nonumber \\&-\,K(1-x)^2(3-5x-4x^2)\nonumber \\&\times \,\mathrm{e}^{2x} \Pi _{a,b,C,m,i,N}(x) \nonumber \\&-\,\frac{K}{2}(x)^{N+1}(1 - x)(a-bx)^m\nonumber \\&\times \,[4\mathrm{e}^{2x} + \mathrm{e}^{2x}(1-x)], \end{aligned}$$

(42)

$$\begin{aligned} \frac{\kappa p_\mathrm{r}}{C}= & {} A(1-x-x^2-x^3)\mathrm{e}^{2x} + (2-10x+7x^2-2x^3)\nonumber \\&+\, \frac{K}{2}\mathrm{e}^{2x}(x)^{N+1}(1 - x)^2(a-bx)^m \nonumber \\&-\, 2(6+\beta )(1+x-5x^2+3x^3)\mathrm{e}^{2x-2}\nonumber \\&\times \,\bigg [\phi _{j}(x) + \psi _{j}(x)]+\beta (1-x^2)\nonumber \\&+\,\frac{K(1-6x^2+8x^3-3x^4)\mathrm{e}^{2x}}{(1 + x)} \nonumber \\&\times \,\Pi _{a,b,C,m,i,N}(x)\bigg ], \end{aligned}$$

(43)

$$\begin{aligned} p_\mathrm{t} = p_\mathrm{r} + \Delta , \end{aligned}$$

(44)

where $\Delta$ is the measure of anisotropy as defined earlier and also

$$\begin{aligned}&\phi _{j}(x) = \sum _{j=1}^{\infty }(-1)^{j-1} \frac{(1 - 2x)^j}{j},\\&\psi _{j}(x) = \sum _{j=1}^{\infty }\frac{2(1 - x)^j}{j!j},\\&\Pi _{a,b,C,m,i,N}(x) = \sum _{i=0}^{m}(-1)^i a^{m-i} b^i \left( \begin{array}{c} m\\ i \end{array}\right) \left[ \frac{(x)^{N+i+1}}{N+i+1}\right] ,\\&\theta _{j}(x) = 2\sum _{j=1}^{\infty }\frac{2(1 - x)^{j-1}}{j!}. \end{aligned}$$

In a similar way one can calculate the mass m(r) of charged anisotropic model for $n=3$ and other permissible cases.

4.2 Matching and boundary conditions

The metric or first fundamental form of the boundary surface should be the same whether obtained from the interior or exterior metric, guarantees that for some coordinate system the metric components $g_{ij}$ will be continuous across the surface. The requirements of matching condition for metric (1) that the above system of equations is to be solved subject to the boundary condition that radial pressure $p_\mathrm{r} =0$ at $r=R$ (which is the outer boundary of the fluid sphere). It is clear that $m (r=R)=M$ is a constant and, in fact, the interior metric (1) can be joined smoothly at the surface of spheres $(r=R)$ to an exterior Reissner–Nordström metric whose mass is the same as $m(r=R)=M$ [75]. Thus one can get

$$\begin{aligned} \mathrm{d}s^2= & {} - \left( 1 - \frac{2M}{r} + \frac{Q^2}{r^2}\right) ^{-1} \mathrm{d}r^2-\, r^2(\mathrm{d}\theta ^2 + \mathrm{sin}^2\theta \mathrm{d}\phi ^2)\nonumber \\&+\, \left( 1 - \frac{2M}{r} + \frac{Q^2}{r^2}\right) \mathrm{d}t^2, \end{aligned}$$

(45)

which requires the continuity of $\mathrm{e}^{\lambda (r)}$, $\mathrm{e}^{\nu (r)}$ and q across the boundary $r=R$

$$\begin{aligned} \mathrm{e}^{-\lambda (R)}=\mathrm{e}^{\nu (R)}= 1 - \frac{2M}{R} + \frac{Q^2}{R^2}, \end{aligned}$$

(46)

$$\begin{aligned} q(R)=Q, \end{aligned}$$

(47)

where M and Q are called the total mass and charge inside the fluid sphere, respectively.

The continuity of $\mathrm{e}^{\lambda (r)}$ and $\mathrm{e}^{\nu (r)}$ on the boundary is $\mathrm{e}^{-\lambda (R)}=\mathrm{e}^{\nu (R)}$, which gives the constant B in the following form:

$$\begin{aligned} B = (1-X)^n \mathrm{e}^{-\lambda (R)} = (1-X)^n \left( 1 - \frac{2M}{R} + \frac{Q^2}{R^2}\right) , \end{aligned}$$

(48)

where $X = CR^2$.

On the other hand, the arbitrary constant A will be determined from the boundary conditions by putting radial pressure $p_\mathrm{r} =0$ at $r = R$ for the case $n=1$ as follows:

$$\begin{aligned} A= & {} \frac{-\mathrm{e}^{2X}}{(1 - X)^2(1 + X)}\bigg [(2-10X+7X^2-2X^3)\nonumber \\&+\, \frac{K}{2}\mathrm{e}^{2X}(X)^{N+1}(1 - X)^2(a-bX)^m \nonumber \\&- 2(6+\beta )(1+X-5X^2+3X^3)\mathrm{e}^{2X-2}\nonumber \\&\times \,[\phi _{j}(X) + \psi _{j}(X)] + \beta (1-X^2) \nonumber \\&+ \frac{K(1-6X^2+8X^3-3X^4)\mathrm{e}^{2X}}{(1 + X)}\nonumber \\&\times \,\Pi _{a,b,C,m,i,N}(X)\bigg ]. \end{aligned}$$

(49)

Hence the total charge inside the star, central density and surface density can, respectively, be evaluated for the case $n=1$ as follows:

$$\begin{aligned} Q (q_{r=R}) = R \sqrt{\frac{K}{2}\mathrm{e}^{2X}(X)^{N+2}(1 - X)^2(a-bX)^m}. \end{aligned}$$

(50)

$$\begin{aligned} \rho _0 = \frac{C}{\kappa }[-A +6 -3\beta +3(6+\beta )\mathrm{e}^{-2}\{\phi _{j}(0) + \psi _{j}(0)\}],\nonumber \\ \end{aligned}$$

(51)

$$\begin{aligned} \rho _\mathrm{R}= & {} \frac{X}{\kappa R^2}\bigg [\Omega _{11}(X) + \Omega _{12}(X) + \beta \Omega _{13}(X) - 2\beta \Omega _{14}(X)\nonumber \\&-\, \frac{K}{2} \Omega _{15}(X) + A\Omega _{16}(X)\bigg ], \end{aligned}$$

(52)

where

$$\begin{aligned} \phi _{j}(0)= & {} \sum _{j=1}^{\infty } \frac{(-1)^{j-1}}{j},\\ \psi _{j}(0)= & {} \sum _{j=1}^{\infty }\frac{2^j}{j!j},\\ \Omega _{11}(X)= & {} (6+\beta )(1-X)^2(3-5X-4X^2)\\&\times \,\mathrm{e}^{2(X-1)}\{\phi _{j}(X) + \psi _{j}(X)\}],\\ \Omega _{12}(X)= & {} (6-11X^2+2X^3),\\ \Omega _{13}(X)= & {} \beta (-3+10X-7X^2),\\ \Omega _{14}(X)= & {} X\mathrm{e}^{2X-2}(1 - X)^2[1 + (1 - X)\theta _j(X)]\\&-\, K\mathrm{e}^{2X}(1 - X)^2(3-5X-4X^2)\Pi _{a,b,C,m,i,N}(X),\\ \Omega _{15}(X)= & {} (X)^{N+1}(1 - X)(a-bX)^m\\&\times \,[4 \mathrm{e}^{2X} + \mathrm{e}^{2X}(1 - X)],\\ \Omega _{16}(X)= & {} \mathrm{e}^{2X}(-1 - 7X -7X^2-3X^3+4X^4). \end{aligned}$$

5 Physical acceptability conditions for anisotropic stellar models

In order to be physically meaningful, the interior solution for static fluid spheres of Einstein’s gravitational-field equations must satisfy some general physical requirements. Because the Einstein field equation (2) is highly nonlinear in nature, not many realistic physical solutions are known for the description of static spherically symmetric perfect fluid spheres. Out of 127 solutions only 16 were found to be physically meaningful [67]. The following conditions have been generally recognized to be crucial for anisotropic fluid spheres [76].

5.1 Regularity and reality conditions

5.1.1 Case 1

The solution should be free from physical and geometrical singularities i.e. pressure and energy density at the center should be finite and metric potentials $\mathrm{e}^{-\lambda (r)}$ and $\mathrm{e}^{\nu (r)}$ should have non-zero positive values in the range $0 \le r \le R$. At origin Eq. (17) provides $\mathrm{e}^{-\lambda (0)}=1$ whereas from Eq. (32) we obtain $\mathrm{e}^{\nu (0)}=B$. So it is clear that metric potentials are positive and finite at the center (Fig. 1).

Fig. 1

Behavior of the metric potentials $\nu$ and $\lambda$ with respect to fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting this figure, the numerical values of the parameters are taken as follows: $n=1$, $m=5$, $N=11$, $a=1$, $b=0.25$, $K=0.11$, $\beta =4.2395$,  $A=1.1426$, $B=0.4798$, $C=2.3113 \times 10^{-3}$ (Table 5)

5.1.2 Case 2

The density $\rho$ and radial pressure $p_\mathrm{r}$ and tangential pressure $p_\mathrm{t}$ should be positive inside the star.

5.1.3 Case 3

The radial pressure $p_\mathrm{r}$ must be vanishing at the boundary of sphere $r=R$ but the tangential pressure $p_\mathrm{t}$ may not vanish at the boundary $r=R$ of the fluid sphere and may follow $p_\mathrm{t}>0$ at $r=R$. However, the radial pressure is equal to the tangential pressure at the center of the fluid sphere.

5.1.4 Case 4

$(\mathrm{d}p_\mathrm{r}/\mathrm{d}r)_{r=0}= 0$ and $(\mathrm{d}^2p_\mathrm{r}/\mathrm{d}r^2)_{r=0} < 0$ so that pressure gradient $\mathrm{d}p_\mathrm{r}/\mathrm{d}r$ is negative for $0 \le r \le R$.

5.1.5 Case 5

$(\mathrm{d}p_\mathrm{t}/\mathrm{d}r )_{r=0} = 0$ and $(\mathrm{d}^2p_\mathrm{t}/ \mathrm{d}r^2)_{r=0} < 0$ so that pressure gradient $\mathrm{d}p_\mathrm{t}/\mathrm{d}r$ is negative for $0 \le r \le R$.

5.1.6 Case 6

$(\mathrm{d}{\rho }/\mathrm{d}r )_{r=0} = 0$ and $(\mathrm{d}^2\rho /\mathrm{d}r^2)_{r=0} < 0$ so that density gradient $\mathrm{d}\rho /\mathrm{d}r$ is negative for $0 \le r \le R$.

Fig. 2

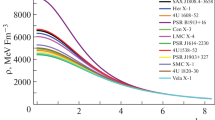
Behavior of the effective matter–energy density $\rho _i=8\pi \,\rho /C$ with respect to fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Fig. 1

Fig. 3

Behavior of the effective radial and tangential pressures $P_\mathrm{r}=8\pi \,p_\mathrm{r}/C$ and $P_\mathrm{t}=8\pi \,p_\mathrm{t}/C$ with respect to the fractional radial distance r / R for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1 and 2

Conditions (5.1.4)–(5.1.6) imply that pressure and density should be maximum at the center and monotonically decreasing towards the surface (Figs. 2, 3).

5.2 Causality and well-behaved conditions

5.2.1 Case 1

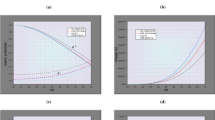
Inside the fluid ball the speed of sound should be less than the speed of light i.e. $0 \le \sqrt{\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }} <1$, $0 \le \sqrt{\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }} <1$ i.e. both $\sqrt{\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }}$ and $\sqrt{\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }}$ are lies between 0 and 1 which can be observed from Fig. 4 as well as from Table 1.

5.2.2 Case 2

The velocity of sound monotonically decreasing away from the center and it is increasing with the increase of density i.e. $\frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }\right) <0$ or $\frac{\mathrm{d}^2p_\mathrm{r}}{\mathrm{d}\rho ^2}>0$ and $\frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}\rho }\right) <0$ or $\frac{\mathrm{d}^2p_\mathrm{t}}{\mathrm{d}\rho ^2}>0$ for $0 \le r \le R$ (see Fig. 4). In this context it is worth mentioning that the equation of state at ultra-high distribution has the property that the sound speed is decreasing outwards [77].

Fig. 4

Behavior of the sound speed V with respect to the fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1, 2 and 3

Table 1 Values of different physical parameters $P_\mathrm{r}=8\pi \,p_\mathrm{r}/C$,  $P_\mathrm{t}=8\pi \,p_\mathrm{t}/C$,  $\rho _i=8\pi \,\rho /C$,  $V_\mathrm{r}=\sqrt{\mathrm{d}p_\mathrm{r}/\mathrm{d}\rho }$,  $V_\mathrm{t}=\sqrt{\mathrm{d}p_\mathrm{t}/\mathrm{d}\rho }$  for $RXJ 1856{\text {-}}37$ with the values of different parameters and constants: $n=1$, $m=5$, $N=11$,  $a=1$, $b=0.25$, $K=0.11$, $\beta =4.2395$

5.2.3 Case 3

The ratios of the pressure to density, $p_\mathrm{r}/\rho$ and $p_\mathrm{t}/\rho$ (as can easily be obtained from Table 1), should be monotonically decreasing with the increase of r, i.e. $\frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{p_\mathrm{r}}{\rho }\right) _{r=0}=0$ and $\frac{\mathrm{d}^2}{\mathrm{d}r^2}\left( \frac{p_\mathrm{r}}{\rho }\right) _{r=0}<0$, $\frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{p_\mathrm{t}}{\rho }\right) _{r=0}=0$ and $\frac{\mathrm{d}^2}{\mathrm{d}r^2}\left( \frac{p_\mathrm{t}}{\rho }\right) _{r=0}<0$. Then $\frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{p_\mathrm{r}}{\rho }\right)$ and $\frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{p_\mathrm{t}}{\rho }\right)$ are negative valued function for $r>0$. These behavior can be observed from Fig. 5. Also note from Table 1 which indicates the ratios via the data of $p_\mathrm{r}$, $p_\mathrm{t}$ and $\rho$.

Fig. 5

Behavior of the ratios of pressure to density, $p_\mathrm{r}/\rho$ and $p_\mathrm{t}/\rho$ with respect to the fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1, 2, 3 and 4

5.3 Energy conditions

A physically reasonable energy-momentum tensor has to obey the following energy conditions [78]:

$$\begin{aligned} \mathrm{(i)}~\mathrm{NEC}{:}\,\rho +E^2 \ge 0, \end{aligned}$$

$$\begin{aligned} \mathrm{(ii)}~\mathrm{WEC}{:} \,\rho +p_\mathrm{r} \ge 0,~\rho +p_\mathrm{t}+2E^2 \ge 0, \end{aligned}$$

$$\begin{aligned} \mathrm{(iii)}~\mathrm{SEC}{:}\, \rho +p_\mathrm{r}+2p_\mathrm{t}+2E^2 \ge 0. \end{aligned}$$

Now we check whether all the energy conditions are satisfied or not. For this purpose, numerical values of these energy conditions are given in Table 2 and accordingly their behavior are shown in Fig. 6. This figure indicates that in our model all the energy conditions are satisfied throughout the interior region.

5.4 Stability of the stellar models

5.4.1 Method 1

In order to have an equilibrium configuration the matter must be stable against the collapse of local regions. This requires Le Chatelier’s principle, also known as the local or microscopic stability condition, that the radial pressure $p_\mathrm{r}$ must be a monotonically non-decreasing function of $\rho$ [79].

With the energy-momentum tensor of the form (3), the relativistic first law of thermodynamics may be expressed as

$$\begin{aligned} \frac{\mathrm{d}\rho }{p_\mathrm{r}+\rho } = \frac{\mathrm{d}\rho _\mathrm{m}}{\rho _\mathrm{m}}, \end{aligned}$$

(53)

where $p_\mathrm{r}$ is the radial pressure, $\rho$ is the total energy density and $\rho _\mathrm{m}$ is that part of the mass density which satisfies a continuity equation and is therefore conserved throughout the motion.

We let the pressure change with density as

$$\begin{aligned} p_\mathrm{r} \propto (\rho _\mathrm{m})^{\gamma }. \end{aligned}$$

(54)

From Eq. (54) we have

$$\begin{aligned} \gamma = \left( \frac{\rho _\mathrm{m}}{p_\mathrm{r}}\right) \left( \frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho _\mathrm{m}}\right) . \end{aligned}$$

(55)

By Eqs. (53) and (55) we have

$$\begin{aligned} \gamma = \left( \frac{\rho +p_\mathrm{r}}{p_\mathrm{r}}\right) \left( \frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}\rho }\right) , \end{aligned}$$

(56)

where $\gamma$ is a parameter called the adiabatic index. Matter obeying these equations is stable to gravitational collapse if the pressure times the surface area increases more rapidly than $R^{-2}$. Because the density is proportional to $R^{-3}$, the force exerted by the pressure is proportional to $R^{2-3\gamma }$. This force increases more rapidly than the gravitational force when $\gamma > 4/3$.

Table 2 Values of the energy conditions for the constants $n=1$, $m=5$, $N=11$, $a=1$, $b=0.25$, $K=0.11$, $\beta =4.2395$ and $CR^2 = 0.0829$

Fig. 6

Plot for the energy conditions with respect to the fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting of this figure we have employed the same data set of numerical values as used in Figs. 1, 2, 3, 4 and 5

Fig. 7

Behavior of the adiabatic index $\gamma$ with respect to the fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs.  1, 2, 3, 4, 5 and 6

The latter condition is, however, necessary but not sufficient to obtain a dynamically stable model [80]. Heintzmann and Hillebrandt [81] also proposed that a neutron star with an anisotropic equation of state is stable for $\gamma > 4/3$. Also it is well known that Newton’s theory of gravitation has no upper mass limit if the equation of state has an adiabatic index $\gamma > 4/3$.

The behavior of adiabatic index ($\gamma$) is shown in Fig. 7. It is clear from the figure that the value of $\gamma$ is higher than 4 / 3. So our model is stable.

5.4.2 Method 2

For this case let us write the generalized Tolman–Oppenheimer–Volkoff (TOV) equation in the following form:

$$\begin{aligned}&-\frac{M_\mathrm{G}(\rho +p_\mathrm{r})}{r^2}\mathrm{e}^{(\lambda -\nu )/2}-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}+ \sigma \frac{q}{r^2}\mathrm{e}^{\lambda /2}\nonumber \\&\quad + \frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})=0, \end{aligned}$$

(57)

where $M_\mathrm{G}$ is the gravitational mass within the radius r and is given by

$$\begin{aligned} M_\mathrm{G}(r)=\frac{1}{2}r^2 \nu ^{\prime }\mathrm{e}^{(\nu - \lambda )/2}. \end{aligned}$$

(58)

Substituting the value of $M_\mathrm{G}(r)$ in the above equation we get

$$\begin{aligned} -\frac{1}{2} \nu ^{\prime }(\rho +p_\mathrm{r})-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}+ \sigma \frac{q}{r^2}\mathrm{e}^{\lambda /2}+\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})=0.\nonumber \\ \end{aligned}$$

(59)

The above TOV equation describes the equilibrium condition for a charged anisotropic fluid subject to gravitational ($F_\mathrm{g}$), hydrostatic ($F_\mathrm{h}$), electric ($F_\mathrm{e}$) and anisotropic stress ($F_\mathrm{a}$) so that

$$\begin{aligned} F_\mathrm{g}+F_\mathrm{h}+F_\mathrm{e}+F_\mathrm{a}=0, \end{aligned}$$

(60)

where

$$\begin{aligned} F_\mathrm{g}=-\frac{1}{2} \nu ^{\prime }(\rho +p_\mathrm{r}), \end{aligned}$$

(61)

$$\begin{aligned} F_\mathrm{h}=-\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}, \end{aligned}$$

(62)

$$\begin{aligned} F_\mathrm{e}=\sigma \frac{q}{r^2}\mathrm{e}^{\lambda /2}, \end{aligned}$$

(63)

$$\begin{aligned} F_\mathrm{a}=\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r}). \end{aligned}$$

(64)

Now, the above forces can be expressed in the explicit forms as follows:

$$\begin{aligned} F_\mathrm{g}= -\frac{1}{2} \nu ^{\prime }(\rho +p_\mathrm{r})=-\frac{C r}{1-x}(\rho +p_\mathrm{r}), \end{aligned}$$

(65)

$$\begin{aligned} F_\mathrm{h}= & {} -\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r} = -\frac{2C^2r}{8\pi }\Bigg [A(1-4x+x^2+2x^3)\mathrm{e}^{2x}\nonumber \\&\left. +\, (10-14x+6x^2)+ K\mathrm{e}^{2x}(x)^N (1 - x)^3(a-bx)^m \right. \nonumber \\&\left. -2[(6+\beta )(1-x)(1+3x)\right. \nonumber \\&-\,3(5-12x-3x^2+10x^3)]\nonumber \\&\left. \times \mathrm{e}^{2x-2} (1+(1-x)\theta _j(x)) \right. \nonumber \\&\left. - \beta [-2x+\mathrm{e}^{2x-2}(-2+5x-3x^2)\{\phi _{j}(x) + \psi _{j}(x)\}] \right. \nonumber \\&\left. -K\left( \frac{(1-x)^2(1-8x-11x^2-6x^3)\mathrm{e}^{2x}\Pi _{a,b,C,m,i,N}(x)}{(1 + x)^2}\right. \right. \nonumber \\&\left. + \frac{\Psi _{a,b,C,m,i,N}(x)}{2}\right) \Bigg ], \end{aligned}$$

(66)

$$\begin{aligned} F_\mathrm{e}= & {} \frac{K}{8\pi r^3}\Bigg [\mathrm{e}^{2x} (1-x)(x)^{N+2}(a-bx)^m \Bigg \{(N+3)(1-x)\nonumber \\&-2x+2(1-x)x - \frac{bmx(1-x)}{(a-bx)}\Bigg \}\Bigg ], \end{aligned}$$

(67)

$$\begin{aligned} F_\mathrm{a}=\frac{2}{r}(p_\mathrm{t}-p_\mathrm{r})=\frac{2\beta C}{8\pi r}x, \end{aligned}$$

(68)

with $x=Cr^2$ as mentioned earlier.

Fig. 8

Feature of the static equilibrium under different forces for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1, 2, 3, 4, 5, 6 and 7

We have shown the plot for TOV equation in Fig. 8. From the figure it is observed that the system is in static equilibrium under four different forces, e.g. gravitational, hydrostatic, electric and anisotropic to attain overall equilibrium. However, a strong gravitational force is counter balanced jointly by hydrostatic and anisotropic forces. The electric force, it seems, has a negligible effect on this balancing mechanism.

5.4.3 Method 3

In our anisotropic model, to verify stability we plot the radial ($V_\mathrm{sr}^2=\mathrm{d}p_\mathrm{r}/\mathrm{d}t$) and transverse ($V_\mathrm{st}^2=\mathrm{d}p_\mathrm{t}/\mathrm{d}\rho$) sound speeds in Fig. 9. It is observed that these parameters satisfy the inequalities $0\le V_\mathrm{sr}^2 \le 1$ and $0\le V_\mathrm{st}^2 \le 1$ everywhere within the stellar object which obeys the anisotropic fluid models [82, 83].

Fig. 9

Behavior of the square of the sound speed $V^2$ for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1, 2, 3, 4, 5, 6, 7 and 8

Fig. 10

Behavior of the difference of sound speeds $V^2_\mathrm{st}-V^2_\mathrm{sr}$ and $\mid V_\mathrm{st}^2 - V_\mathrm{sr}^2 \mid$ for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1, 2, 3, 4, 5, 6, 7, 8 and 9

Again, to check whether local anisotropic matter distribution is stable or not, we use the proposal of Herrera [82], known as cracking (or overturning), which states that the potentially stable region is where the radial speed of sound is greater than the transverse speed of sound. From the left panel of Fig. 10, we can easily say that $V^2_\mathrm{st}-V^2_\mathrm{sr}\le 1$. Since $0\le V_\mathrm{sr}^2 \le 1$ and $0\le V_\mathrm{st}^2 \le 1$, we have $|V_\mathrm{st}^2 - V_\mathrm{sr}^2| \le 1$ as can be seen from the right panel of Fig. 10. Hence, we can conclude that our compact star model provides a stable configuration.

5.5 Electric charge

From the present model it is observed that in units of Coulomb, the charge on the boundary is $1.5151 \times 10^{13}$ C and at the center it is as usual zero. In Table 3 we have put the data for charge q in the relativistic units km. However, to convert these values to Coulomb one has to multiply every value by a factor $1.1659 \times 10^{20}$. The graphical plot is shown in Fig. 11 where the charge profile is such that starting from a minimum it acquires a maximum value at the boundary.

Table 3 Values of charge, anisotropy and redshift for $n=1$, $m=5$, $N=11$, $a=1$, $b=0.25$, $K=0.11$, $\beta =4.2395$. The related plots are shown, respectively, in Figs. 11, 12 and 13

Fig. 11

Distribution of charge with respect to fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10

Let us now justify this feature of the charge from the available literature. It was shown by Varela et al. [38] that spheres with vanishing net charge contain fluid elements with unbounded proper charge density located at the fluid-vacuum interface and net charges can be huge ($10^{19}$ C). On the other hand, Ray et al. [18] have analyzed the effect of charge in compact stars considering the limit of the maximum amount of charge they can hold and they have shown through numerical calculation that the global balance of the forces allows a huge charge ($10^{20}$ C) to be present in a neutron star. Thus we see that the net amount of charge has less effect to balance the mechanism of the force in our model.

5.6 Pressure anisotropy

For the present model we calculate the measure of pressure anisotropy as follows:

$$\begin{aligned} \Delta \equiv (p_\mathrm{t}-p_\mathrm{r})= \beta C x. \end{aligned}$$

(69)

It is in general argued that the ‘anisotropy’ will be directed outward for the condition $p_\mathrm{t} > p_\mathrm{r}$ i.e. $\Delta > 0$, and inward for the condition $p_\mathrm{t} < p_\mathrm{r}$ i.e. $\Delta < 0$. This special feature can be observed from Fig. 12 related to our model. This kind of repulsive ‘anisotropic’ force allows for construction of a more massive compact stellar configuration [84].

One can also calculate variation of the radial and transverse pressures which are, respectively, given by $\frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r}$, as can be obtained from Eq. (20), and $\frac{\mathrm{d}p_\mathrm{t}}{\mathrm{d}r}= \frac{\mathrm{d}p_\mathrm{r}}{\mathrm{d}r} + \frac{2C^2{\beta } r}{8\pi }$.

Fig. 12

Anisotropic behavior ($\Delta _i=\Delta /C$) at the stellar interior with respect to fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11

5.7 Surface redshift

The effective gravitational mass in terms of the energy density can be written as

$$\begin{aligned} M_\mathrm{eff}=4\pi \int _{0}^{R}\left( \rho +\frac{E^2}{8\pi }\right) r^2 \mathrm{d}r= \frac{1}{2}R[1-\mathrm{e}^{-\lambda (R)}], \end{aligned}$$

(70)

where $\mathrm{e}^{-\lambda (R)}$ is given by Eq. (46).

One can therefore provide the compactness of the star as

$$\begin{aligned} u= \frac{M_\mathrm{eff}}{R}= \frac{1}{2}[1-\mathrm{e}^{-\lambda (R)}] . \end{aligned}$$

(71)

Again we define the surface redshift corresponding to the above compactness factor as follows:

$$\begin{aligned} Z = [1-2u]^{-1/2} - 1 = \mathrm{e}^{\lambda (R)/2} - 1. \end{aligned}$$

(72)

Fig. 13

Redshift of the stellar model with respect to fractional radial distance (r / R) for $RXJ 1856{\text {-}}37$. For plotting this figure we have employed the same data set of numerical values as used in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12

We plot the redshift in Fig. 13 from which it is evident that it shows a gradual decrease. This feature also can be observed from Table 3. The maximum surface redshift for the present stellar configuration of radius 6.0 km turns out to be $Z = 0.3826$.

In this connection it is worth to mention that for the isotropic case and in the absence of the cosmological constant the surface redshift is constrained: $Z \le 2$ [85,86,87]. Again for an anisotropic star in the presence of a cosmological constant the constraint on the surface redshift is $Z \le 5$ [88], whereas Ivanov [14] put the bound $Z \le 5.211$. Based on the above discussion we therefore conclude that for an anisotropic star without cosmological constant the value for our model $Z = 0.3826$ is in good agreement.

Fig. 14

Plot for mass-to-radius ratio M / R with respect to radius R for $RXJ 1856{\text {-}}37$

Table 4 Values of lower and upper bounds of mass for the values $n=1$, $m=5$, $N=11$, $a=1$, $b=0.25$, $K=0.11$ and $\beta =4.2395$

Table 5 Values of the model parameters A, B, m etc. for different strange stars

Table 6 Energy densities and pressure for different strange star candidates for the above parameter values of Table 1

6 Some case studies: comparison of present stellar model with compact stars

6.1 Allowable mass-to-radius ratio

Buchdahl [85] has proposed an absolute constraint on the maximally allowable mass-to-radius ratio (M / R) for isotropic fluid spheres of the form $2M/R \le 8/9$ (in units $c = G = 1$) which states that for a given radius a static isotropic fluid sphere cannot be arbitrarily massive. Böhmer and Harko [87] proved that for a compact object with charge, $Q (<M)$, there is a lower bound for the mass–radius ratio

$$\begin{aligned} \frac{3Q^2}{2R^2} \left( \frac{1+\frac{Q^2}{18R^2}}{1+\frac{Q^2}{12R^2}}\right) \le \frac{2M}{R}. \end{aligned}$$

(73)

The upper bound of the mass of charged sphere was generalized by Andréasson [89] and it was proved that

$$\begin{aligned} \sqrt{M} \le \frac{\sqrt{R}}{3} + \sqrt{\frac{R}{9} + \frac{Q^2}{3R}}. \end{aligned}$$

(74)

By substituting the following data: mass $M= 0.9693 M_{\odot }$ and radius $R=6.0$ km, we find that $M/R=0.238 < 4/9$ and also $2M/R=0.4760$, which satisfy the Buchdahl condition of a stable configuration [85]. We also note from Fig. 14 and Table 4 that the charged stars have large mass and radius, as we should expect due to the effect of the repulsive Coulomb force with the M / R ratio increasing with charge [18]. However, unlike Ray et al.’results [18] where in the limit of the maximum charge the mass goes up to 10, which is much higher than the maximum mass allowed for a neutral compact star, our model seems very satisfactory.

6.2 Validity with strange star candidates

We have presented two tables here (Tables 5, 6) from which it can be observed that the mass and radius exactly correspond to the strange stars $RXJ~1856{\text {-}}37$ and $Her~X{\text {-}}1$. What we did in the tables is as follows: by considering the mass and radius of the above mentioned stars we have figured out data for the model parameters, and in the next step we evaluated the data for the different physical parameters, e.g. central density, surface density and central pressure, of those strange stars. One can observe that these data are in good agreement with the available observational data.

In this connection we would like to mention that previously Gupta and Maurya [90] showed a similar result for $PSR~J~1614{\text {-}}2230$ with an isotropic fluid distribution and the charge generalization of Durgapal [66]. We also note that like the models presented by Kalam et al. [41], Hossein et al. [84] and Kalam et al. [91] our models provide significantly promising results as regards observational evidence.

7 Conclusion

In this work we have presented a set of new solutions for an anisotropic charged fluid distribution in the framework of General Theory of Relativity. To solve the Einstein–Maxwell field equations we construct a general algorithm for all possible anisotropic charged fluid spheres. As an additional condition which simplifies the physical system of space-time we consider a special source function in terms of the metric potential $\nu$. We further adopt the exterior solution of Reissner–Nordström, so that our interior solution can be matched smoothly as a consequence of the junction conditions at the surface of spheres $(r=R)$.

The solutions thus obtained exhibit regular physical behavior as can be observed from the figures and tables for different parameters. We specifically discuss (i) regularity and reality conditions (applied for metric potentials $\mathrm{e}^{-\lambda (r)}$ and $\mathrm{e}^{\nu (r)}$, energy density $\rho$, fluid pressures $p_\mathrm{r}$ and $p_\mathrm{t}$, pressure gradients $\mathrm{d}p_\mathrm{r}/\mathrm{d}r$ and $\mathrm{d}p_\mathrm{t}/\mathrm{d}r$, and density gradient $\mathrm{d}\rho /\mathrm{d}r$), and (ii) causality and well-behaved conditions (applied for speed of sound $\mathrm{d}p_\mathrm{r}/\mathrm{d}\rho$ and ratios of pressure to densities $p_\mathrm{r}/\rho$ and $p_\mathrm{t}/\rho$). Beside all these general physical properties the solution set shows the desirable and essential features for energy condition, stability condition, charge distribution, pressure anisotropy and surface redshift. Among these physical parameters as a special case, regarding the electric charge distribution of our model, we note that the charge on the boundary is $1.5151 \times 10^{13}$ C and at the center it is as usual zero. Other features of charge are also available in the literature [18, 38, 65] in connection to a stable configuration of compact stars where it has been shown that the global balance of the forces allows a huge charge ($\sim$ $10^{20}$ C) to be present in a neutron star.

We also observe some special and interesting features for our stellar models, which are related to compact stars as follows.

• 1. Allowable mass-to-radius ratio: the condition of Buchdahl [85] related to the maximally allowable mass-to-radius ratio for isotropic fluid spheres is of the form $2M/R \le 8/9$. By substituting the following data: mass $M= 0.9693~M_{\odot }$ and radius $R=6.0$ Km, we find that $2M/R=0.4760$, which satisfies the Buchdahl condition of a stable configuration [85] as mentioned above.

• 2. Validity with strange stars: we have prepared several data sets from which it is observed that the mass and radius exactly correspond to the strange stars $RXJ~1856{\text {-}}37$ and $Her~X{\text {-}}1$. Therefore, one can note that like the models of Kalam et al. [41], Hossein et al. [84] and Kalam et al. [91] our models also provide significantly promising results as regards observational evidence.

In this work we have studied the case for $n=1$ only in the source function because of the fact that this value is more relevant for exploring existence and properties of strange stars. There is, however, scope for further study with other values of n also as follows: (1) for integer values of $n= 2,~3,~5$ (not possible for all other positive integer values), and (2) for fractional values of n there are two possibilities: (i) if n lies between 0 and 1 then exact solutions are possible for all fractional values, and (ii) if n is greater than 1 then they are possible for all fractional values of n except the values of $n=p/(p-1)$ and $n=p/(p-2)$, where p is a positive integer ($p \ne 1$ and $p \ne 2$). However, the specific value 3 / 2 is not allowed for these factors to study the solutions for the present model.

As a final comment we would like to mention that Tiwari and Ray [92] proved that any relativistic solution for spherically symmetric charged fluid sphere has an electromagnetic origin and hence it provides an electromagnetic mass model [93,94,95,96]. Therefore, it would be an interesting task to verify whether our model also represents an electromagnetic mass or not and this is to be studied elsewhere in a future project.

Appendix

In this appendix we present Tables 7 and 8.

Table 7 List of regular behavior of $\mathrm{d}p/\mathrm{d}\rho$ for the ansatz $\mathrm{e}^{\nu (r)} = B(1+x)^n$, with $x=Cr^2$ where p in the table is a positive integer

Table 8 List of regular behavior of $\mathrm{d}p/\mathrm{d}\rho$ for the ansatz $\mathrm{e}^{\nu (r)} = B(1-x)^{-n}$