1 Introduction

Strong field gravitational lensing by a black hole has generated considerable recent research interest, which is being enhanced by a growing number of efforts to directly image the supermassive black hole at the Galactic center, Sgr A* [1–3]. It was demonstrated by Darwin [4] that light rays can be significantly deflected in the vicinity of a black hole, resulting relativistic images. Those images are unique features presented by the strong gravitational field of a black hole. By making use of the strong deflection limit (SDL), which requires the light ray to be very close to the photon sphere [5–7], an analytical approach can be employed to describe the strong field lensings by the Schwarzschild spacetime [4, 8–12], by the Reissner–Nordström spacetime [12, 13], and by a static and spherically symmetric spacetime [14]. With the SDL method, astronomical observables can easily be obtained, including the positional separations, the brightness differences, and time delays among the relativistic images. The strong field lensings by static and spherically symmetric spacetimes were also considered in various contexts with different methods [6, 15–44]. Strong field lensings of rotating black holes were discussed [45–58]. Relativistic images might be able to provide new hints for the possible existence of naked singularities [30, 59–62] as well as wormholes [63–66]. Reviews of strong gravitational field lensing can be found in [67, 68].

The underlying reason of gravitational lensing is the interaction between electromagnetic and gravitational fields. Beyond the standard Einstein–Maxwell theory, the authors of [69] investigated the local propagation of photons after considering the effects of one-loop vacuum polarization on the photon effective action for quantum electrodynamics. It was found [69] that the properties of light propagation could be changed by tidal gravitational forces introduced by these quantum corrections, and a photon might be able to travel “faster than light” in some cases. These “superluminal” photons were also found in various gravitational contexts [70–79]. However, the strength of the effects is immeasurably small because its coupling constant is inversely proportional to \(\lambda ^2_e\), where \(\lambda _e\) is the Compton wavelength of an electron [69]. Motivated by some physical circumstances, extended theoretical models without this limit on the coupling were investigated for primordial magnetic fields [80–85] and new coupling between gravity and photons [86–96].

Another way to couple the electromagnetic and gravitational fields can be realized through the Weyl tensor in the effective action, which has been widely investigated in the cases of holographic conductivity and superconductors [97–105] and the dynamical evolution of electromagnetic field in the black hole spacetime [106–109]. The authors of [110] studied the strong field gravitational lensing for the photons coupled to Weyl tensor in the Schwarzschild black hole, and they obtained the strong deflection angle, angular separations, and brightness difference between the resulting relativistic images. Complementary to these observables, the time delays between these images are important observables as well. They can be used to measure the distance of the black hole [111] and can also be probe of cosmic censorship [61] and the Gauss–Bonnet correction [112].

In this work, as an extension of the previous work [110], we will focus on the strong field time delays between relativistic images when such a coupling of the Weyl tensor is taken into account. In Sect. 2, the effective metric for the Weyl tensor coupled photons is briefly reviewed for completeness. The strong field time delay is investigated in Sect. 3. The observables of such delays between relativistic images are discussed in Sect. 4 by taking Sgr A* as an example. A practical problem about the determination of the polarization direction for the coupling of the Weyl tensor by observations is also investigated. Finally, in Sect. 5, we summarize our results.

2 Effective metric for Weyl tensor coupled photons

The effective metric for the Weyl tensor coupled photons will be briefly reviewed for completeness in this section, which only covers necessary information for our following work. More details can be found in [69, 105, 110]. We consider the electromagnetic field coupled to the Weyl tensor in the curved spacetime (in the units \(G=c=1\)) [97]:

$$\begin{aligned} S = \int \sqrt{-g}\mathrm {d}^4x\bigg [\frac{R}{16\pi }-\frac{1}{4}\bigg (F_{\mu \nu }F^{\mu \nu }-4\alpha C^{\mu \nu \rho \sigma }F_{\mu \nu }F_{\rho \sigma }\bigg )\bigg ], \end{aligned}$$

where the 4-dimensional Weyl tensor \(C_{\mu \nu \rho \sigma }\) of the spacetime metric \(g_{\mu \nu }\) is defined by

$$\begin{aligned} C_{\mu \nu \rho \sigma } = R_{\mu \nu \rho \sigma }-(g_{\mu [\rho }R_{\sigma ]\nu }-g_{\nu [\rho }R_{\sigma ]\mu }) \,{+}\,\frac{1}{3}Rg_{\mu [\rho }g_{\sigma ]\nu }. \end{aligned}$$
(1)

The square brackets around indices are used to denote the antisymmetric parts. \(F_{\mu \nu }\equiv A_{\nu ;\mu }-A_{\mu ;\nu }\) is the electromagnetic tensor. \(\alpha \) is the coupling constant with dimension of [Length]\(^2\). Variation of the above action with respect to \(A_{\mu }\) gives the Weyl tensor corrected Maxwell equation as

$$\begin{aligned} \bigg (F_{\mu \nu }-4C^{\mu \nu \rho \sigma }F_{\rho \sigma }\bigg )_{;\mu }=0. \end{aligned}$$
(2)

With the geometric optics approximation that \(\lambda _e<\lambda <L\), where \(\lambda \) is the wavelength of the photon and L is the typical curvature length scale, we can set [69]

$$\begin{aligned} F_{\mu \nu }=f_{\mu \nu }\exp (i\theta ) \end{aligned}$$
(3)

and regard \(f_{\mu \nu }\) to be slowly varying compared with \(\theta \). Putting \(k_{\mu }=\theta _{;\mu }\) and using the electromagnetic Bianchi identity, we have [69]

$$\begin{aligned} k_{\rho }f_{\mu \nu }+k_{\mu }f_{\nu \rho }+k_{\nu }f_{\rho \mu }=0, \end{aligned}$$
(4)

which leads to

$$\begin{aligned} f_{\mu \nu } = k_{\mu }a_{\nu }-k_{\nu }a_{\mu }. \end{aligned}$$
(5)

Here, \(a_{\mu }\) is the polarization vector which satisfies \(k_{\mu }a^{\mu }=0\). After rewriting Eq. (2) with Eqs. (3) and (5), we obtain the equations of motion for a photon which couples to the Weyl tensor [105, 110]:

$$\begin{aligned} k_{\mu }k^{\mu }a^{\nu }+8\alpha C^{\mu \nu \rho \sigma }k_{\sigma }k_{\mu }a_{\rho }=0. \end{aligned}$$
(6)

If considering a 4-dimensional static and spherically symmetric spacetime as the background for the photon’s propagation, i.e.,

$$\begin{aligned} \mathrm {d}s^2=-f(r)\mathrm {d}t^2+\frac{\mathrm {d}r^2}{f(r)}+r^2(\mathrm {d}\theta ^2+\sin ^2{\theta }\mathrm {d}\varphi ^2), \end{aligned}$$
(7)

we introduce the orthonormal tetrad [69]

$$\begin{aligned} e^{a}_{\mu }=\bigg (\sqrt{f},\frac{1}{\sqrt{f}},r,r\sin \theta \bigg ) \end{aligned}$$
(8)

and the bivectors [69]

$$\begin{aligned} U^{ab}_{\mu \nu } = e^a_{\mu }e^b_{\nu }-e^{a}_{\nu }e^{b}_{\mu }. \end{aligned}$$
(9)

In order to simplify the equations of motion for the coupled photon, three independent vectors can be defined as [69]

$$\begin{aligned} l_{\nu } = k^{\mu }U^{01}_{\mu \nu },\quad n_{\nu }=k^{\mu }U^{02}_{\mu \nu },\quad m_{\nu } = k^{\mu }U^{23}_{\mu \nu }, \end{aligned}$$
(10)

which are all orthogonal to the vector \(k_{\nu }\). Therefore, the light-cone conditions can be found [105, 110]:

$$\begin{aligned} (g_{00}k^0k^0+g_{11}k^1k^1)+W(g_{22}k^2k^2+g_{33}k^3k^3)=0, \end{aligned}$$
(11)

where W depends on polarization of the photon. When the polarization is along the direction of \(l_{\mu }\) (PPL), it is

$$\begin{aligned} W(r)=\frac{r^3-8\alpha M}{r^3+16\alpha M}; \end{aligned}$$
(12)

when the polarization is along \(m_{\mu }\) (PPM), then it is

$$\begin{aligned} W(r)=\frac{r^3+16\alpha M}{r^3-8\alpha M}. \end{aligned}$$
(13)

Although these light-cone conditions demonstrate that the coupled photon no longer travels as null geodesic worldline in the Schwarzschild spacetime, an effective metric can be constructed to make it null geodesic [113]. When we take 2M as the measure of distances and set it to unity, the effective metric can be written [105, 110]

$$\begin{aligned} \mathrm {d}s^2=-A(x)\mathrm {d}t^2+B(x)\mathrm {d}x^2+C(x)(\mathrm {d}\theta ^2+\sin ^2{\theta }\mathrm {d}\varphi ^2), \end{aligned}$$
(14)

where the functions are

$$\begin{aligned} A(x)= & {} B(x)^{-1}=1-\frac{1}{x}, \end{aligned}$$
(15)
$$\begin{aligned} C(x)= & {} x^2 W(x), \end{aligned}$$
(16)
$$\begin{aligned} W(x)= & {} W_{\mathrm {PPL}} = \frac{x^3-4\alpha }{x^3+8\alpha } \qquad \mathrm { for } \quad \mathrm { PPL}, \end{aligned}$$
(17)
$$\begin{aligned} W(x)= & {} W_{\mathrm {PPM}} = \frac{x^3+8\alpha }{x^3-4\alpha } \qquad \mathrm { for } \quad \mathrm { PPM}. \end{aligned}$$
(18)

Following the assumption of [110], we also consider that the observer, the source, and the path of the photon are all located in the plane of \(\theta =90^{\circ }\) in the Schwarzschild spacetime, while the observer and the source are very far away from the black hole. It was also found [110] that, in order to ensure a photon always stays outside the event horizon, \(\alpha \) must satisfy the conditions: \(4\alpha <1\) for PPL and \(8\alpha >-1\) for PPM.

3 Time delays between relativistic images

In this section, we will follow the approach proposed in [111] and calculate the time delays between relativistic images of the Weyl tensor coupled photons. For the time component of a null geodesic in the spacetime (14), we have [111]

$$\begin{aligned} \dfrac{\mathrm {d}t}{\mathrm {d}x}=\tilde{P}_1(x,x_0)P_2(x,x_0), \end{aligned}$$
(19)

where the two functions are

$$\begin{aligned} \tilde{P}_1(x,x_0)= & {} \sqrt{\frac{BA_0}{A}},\end{aligned}$$
(20)
$$\begin{aligned} P_2(x,x_0)= & {} \frac{1}{\sqrt{A_0-A\frac{C_0}{C}}}. \end{aligned}$$
(21)

The subscript “0” of a quantity means its value at \(x=x_0\), where \(x_0\) is the closest distance of the photon to the black hole. The time taken by a photon from the source to the observer can be decomposed into three parts [111]

$$\begin{aligned} T = \tilde{T}(x_0) - \int ^{\infty }_{D_{\mathrm {OL}}}\bigg |\frac{\mathrm {d}t}{\mathrm {d}x}\bigg |\mathrm {d}x - \int ^{\infty }_{D_{\mathrm {LS}}}\bigg |\frac{\mathrm {d}t}{\mathrm {d}x}\bigg |\mathrm {d}x, \end{aligned}$$
(22)

where \(D_{\mathrm {OL}}\) and \(D_{\mathrm {LS}}\) are the observer–lens and lens–source distances, and \(\tilde{T}(x_0)\) is defined by [111]

$$\begin{aligned} \tilde{T}(x_0)=\int ^{\infty }_{x_0}\bigg |\dfrac{\mathrm {d}t}{\mathrm {d}x}\bigg |\mathrm {d}x = \int ^{\infty }_{x_0}{2\sqrt{B(x)C(x)A_0}\over {A(x)\sqrt{C_0}\sqrt{{C(x)\over {C_0}}{A_0\over {A(x)}}-1}}}\mathrm {d}x. \end{aligned}$$
(23)

It is assumed that the observer and the source are far from the lens, the time delay between two relativistic images 1 and 2 can be given as [111]

$$\begin{aligned} T_1-T_2= & {} 2\int ^\infty _{x_{0,1}}\left| \dfrac{\mathrm {d}t}{\mathrm {d}x}(x,x_{0,1})\right| \nonumber \\&\times \mathrm {d}x-2\int ^\infty _{x_{0,2}}\left| \dfrac{\mathrm {d}t}{\mathrm {d}x}(x,x_{0,2})\right| \mathrm {d}x, \end{aligned}$$
(24)
$$\begin{aligned}= & {} \tilde{T}(x_{0,1})-\tilde{T}(x_{0,2})+2\int ^{x_{0,2}}_{x_{0,1}}\dfrac{\tilde{P}_1(x,x_{0,1})}{\sqrt{A_{0,1}}}\mathrm {d}x,\nonumber \\ \end{aligned}$$
(25)

where the subscript “, i” (\(i=1,2\)) of a quantity is for the value of the ith relativistic image.

With the technique of SDL [14], the integral of \(\tilde{T}(x_0)\) can be rewritten as [111]

$$\begin{aligned} \tilde{T}(x_{0})=\int ^1_0\tilde{R}(z,x_{0})f(z,x_{0})\mathrm {d}z, \end{aligned}$$
(26)

where the quantity z is defined as

$$\begin{aligned} z=\frac{A-A_0}{1-A_0}, \end{aligned}$$
(27)

and the two functions are

$$\begin{aligned} f(z,x_0)= & {} P_2(x,x_0), \end{aligned}$$
(28)
$$\begin{aligned} \tilde{R}(z,x_{0})= & {} 2\dfrac{1-A_{0}}{A'(x)}\tilde{P}_1(x,x_{0})\left( 1-\dfrac{1}{\sqrt{A_{0}}f(z,x_{0})}\right) . \end{aligned}$$
(29)

The prime means partial derivative against x. In order to find \(\tilde{T}(x_{0})\) in the SDL, we define the radius of the photon sphere \(x_m\) as [6, 7]

$$\begin{aligned} \dfrac{C'(x)}{C(x)}=\dfrac{A'(x)}{A(x)}, \end{aligned}$$
(30)

which leads to

$$\begin{aligned} (x^3+8\alpha )(x^3-4\alpha )(2x-3)\pm 36\alpha x^3(x-1)=0. \end{aligned}$$
(31)

In the last term of the above equation, the plus sign originates from the case of PPL and the minus sign comes from the PPM one. The biggest root of this equation can be taken as \(x_m\), which can be solved numerically. We can obtain \(\tilde{T}(x_{0})\) in the SDL at \(x_0\sim x_m\) and transform the variable \(x_0\) to the impact parameter u, which is given by [6, 114]

$$\begin{aligned} u=\sqrt{\dfrac{C_0}{A_0}} \end{aligned}$$
(32)

and its value at the photon sphere \(x_0=x_m\) is \(u_m\). Finally, we have [111]

$$\begin{aligned} \tilde{T}(u)=-\tilde{a}\ln {\left( \dfrac{u}{u_m}-1\right) }+\tilde{b}+\mathcal {O}(u-u_m), \end{aligned}$$
(33)

where \(\tilde{a}\) and \(\tilde{b}\) are the coefficients. Fortunately, although the exact expressions of these two coefficients are complicated and can be found in [111], they are not directly needed in the following calculation.

If we assume the source, the lens, and the observer are aligned almost in a line and use the approximate relation that [111]

$$\begin{aligned} \int ^{x_{0,2}}_{x_{0,1}}\dfrac{\tilde{P}_1(x,x_{0,1})}{\sqrt{A_{0,1}}}\mathrm {d}x\approx \sqrt{\dfrac{B_m}{A_m}}\ (x_{0,2}-x_{0,1}) \end{aligned}$$
(34)

where the subscript m of a quantity means its value at \(x=x_m\), we have the time delay between n-loop and a m-loop relativistic images [111]

$$\begin{aligned} \Delta T_{n,m} = \Delta T_{n,m}^{\ 0}+\Delta T_{n,m}^{\ 1}, \end{aligned}$$
(35)

where the leading term \(\Delta T_{n,m}^{\ 0}\) and its correction \(\Delta T_{n,m}^{\ 1}\) are

$$\begin{aligned} \Delta T_{n,m}^{\ 0}= & {} 2 \pi (n-m) u_m, \end{aligned}$$
(36)
$$\begin{aligned} \Delta T_{n,m}^{\ 1}= & {} 2\sqrt{\frac{B_m}{A_m}} \sqrt{\dfrac{u_m}{\hat{c}}}\exp \left( {\frac{\bar{b}}{2\bar{a}}}\right) \nonumber \\&\times \left[ \exp \left( {-\frac{m\pi }{\bar{a}}}\right) -\exp \left( {-\frac{n\pi }{\bar{a}}}\right) \right] . \end{aligned}$$
(37)

Here, we used a relation for a spherically symmetric metric, that is, \(\tilde{a} = \bar{a}u_m\) [111]. The quantities \(\bar{a}\), \(\bar{b}\), and \(\hat{c}\) are [14]

$$\begin{aligned} \bar{a}= & {} \frac{R(0,x_m)}{2\sqrt{\beta _m}}, \end{aligned}$$
(38)
$$\begin{aligned} \bar{b}= & {} -\pi +b_R+\bar{a}\ln {2\beta _m\over {A_m}}, \end{aligned}$$
(39)
$$\begin{aligned} \hat{c}= & {} \beta _m\sqrt{\dfrac{A_m}{C_m^3}}\dfrac{{C_m'}{}^2}{2(1-A_m)^2}, \end{aligned}$$
(40)

where

$$\begin{aligned} R(0,x_m)= & {} 2\frac{(1-A_m)\sqrt{B_mA_m}}{A'_m\sqrt{C_m}}, \end{aligned}$$
(41)
$$\begin{aligned} \beta _m= & {} \frac{C_m(1-A_m)^2 (A_m C_m''-C_m A_m'')}{2A_m^2C_m'^2}, \end{aligned}$$
(42)
$$\begin{aligned} b_R= & {} \int ^1_0 \left[ R(z,x_m)f(z,x_m)-\frac{R(0,x_m)}{\sqrt{\beta _mz}}\right] \mathrm {d}z. \end{aligned}$$
(43)

When these quantities are calculated for a given \(\alpha \), the time delays between relativistic images can be worked out.

4 Observables and detectability of polarization direction

In this section, we will take the supermassive black hole Sgr A* with mass \(M_{\bullet }=4.31\times 10^6\) \(M_\odot \) and distance \(D_{\mathrm {OL}}= D_{\bullet }=8.33\) kpc [115] as an example to evaluate the observables of the strong field time delays.

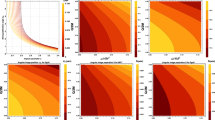
Figure 1 shows the estimated time delays between different relativistic images of the photons coupled to the Weyl tensor in the Schwarzschild spacetime. \(\Delta T_{n,m}\) is represented in units of \(2GM_{\bullet }/c^{3}\approx 42.45\) s. Based on the values of m and n, we consider six cases: (\(n=2\), \(m=1\)), (\(n=3\), \(m=2\)), (\(n=4\), \(m=3\)), (\(n=3\), \(m=1\)), (\(n=4\), \(m=2\)), and (\(n=4\), \(m=1\)). It is clearly shown that the time delays grow with the increment of the difference between n and m and the time delays are almost the same for those with the same value of \(n-m\). The left panel shows the time delays for the case of PPL and the right one is for PPM. It is clear that the \(\Delta T_{n,m}\) responses to the increase of \(\alpha \) are inversely for the cases of PPL and PPM. When \(\alpha =0\), the values of \(\Delta T_{n,m}\) reduce to the ones of the Schwarzschild spacetime.

In order to show the contributions of the correction term \(\Delta T_{n,m}^{\ 1}\) for the whole time delay, we define an indicator as

$$\begin{aligned} \eta _{n,m} \equiv \log _{10}\bigg (\frac{\Delta T_{n,m}^{\ 1}}{\Delta T_{n,m}}\bigg ). \end{aligned}$$
(44)

Figure 2 clearly shows the contributions of \(\Delta T_{n,m}^{\ 1}\) are much smaller than those \(\Delta T_{n,m}^{\ 0}\) by 1–6 orders of magnitude. For a given \(\alpha \) and the same loop difference \(n-m\), \(\eta _{n,m}\) decreases rapidly when n or m increases. \(\eta _{n,m}\) also shows the responses to the increase of \(\alpha \) to be inversely for the cases of PPL (left panel) and PPM (right panel).

Fig. 1
figure 1

Time delays between different relativistic images for Sgr A*. \(\Delta T_{n,m}\) are represented in units of \(2GM_{\bullet }/c^{3}\approx 42.45\) s. The left panel shows the time delays for the case of PPL (\(4\alpha <1\)) and the right one is for PPM (\(8\alpha >-1\))

Full size image

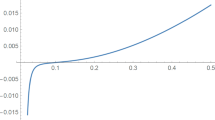
When the first and second relativistic images can be resolved and their angular separation s, brightness difference r, and time delay \(\Delta T_{2,1}\) are measured, the interesting question can be raised whether the directions of polarization PPL and PPM can be detected and determined, which has not been discussed before. The expressions of s and r for these two polarizations can be found in [110], while \(\Delta T_{2,1}\) is given by Eq. (35) in the present work. Here, we assume the uncertainty of the measured s is much smaller than those of the others, because the accuracies of r and \(\Delta T_{2,1}\) depend on how clearly these two images are separated. With different values of the coupling constant \(\alpha _{\mathrm {PPL}}\) and \(\alpha _{\mathrm {PPM}}\), both the PPL and the PPM cases can generate an identical s. In Fig. 3, the green curve shows the value of \(\alpha _{\mathrm {PPL}}\) against \(\alpha _{\mathrm {PPM}}\), and each point \((\alpha _{\mathrm {PPM}}, \alpha _{\mathrm {PPL}})\) on the curve satisfies the relation

$$\begin{aligned} s[W_{\mathrm {PPL}}(\alpha _{\mathrm {PPL}})] = s[W_{\mathrm {PPM}}(\alpha _{\mathrm {PPM}})]. \end{aligned}$$
(45)
Fig. 2
figure 2

The logarithmic contributions of the correction term \(\Delta T_{n,m}^{\ 1}\) for the whole time delay. The left panel shows the contributions for the case of PPL (\(4\alpha <1\)) and the right one is for PPM (\(8\alpha >-1\))

Full size image
Fig. 3
figure 3

The green curve shows \(\alpha _{\mathrm {PPL}}\) against \(\alpha _{\mathrm {PPM}}\), both of which satisfy Eq. (45) and can generate an identical angular separation of the first and second relativistic images. The contrast indicators \(\eta _{r}\) and \(\eta _{\Delta T_{2,1}}\) are, respectively, represented by the blue and red curves, which demonstrate \(\eta _{\Delta T_{2,1}}\) is considerably larger than \(\eta _{r}\)

Full size image

In order to indicate the contrasts of r and \(\Delta T_{2,1}\) given by these two polarization directions, we define the two quantities

$$\begin{aligned}&\eta _r \equiv 2\frac{r_{\mathrm {PPM}}-r_{\mathrm {PPL}}}{r_{\mathrm {PPM}}+r_{\mathrm {PPL}}}, \end{aligned}$$
(46)
$$\begin{aligned}&\eta _{\Delta T_{2,1}} \equiv 2\frac{\Delta T^{\mathrm {PPM}}_{2,1}-\Delta T^{\mathrm {PPL}}_{2,1}}{\Delta T^{\mathrm {PPM}}_{2,1}+\Delta T^{\mathrm {PPL}}_{2,1}}, \end{aligned}$$
(47)

where “PPL”/“PPM” means the value is obtained according to the case of PPL/PPM, and \(\alpha _{\mathrm {PPL}}\) and \(\alpha _{\mathrm {PPM}}\) in the above quantities must satisfy Eq. (45). For the brightness difference r, \(\eta _r\) gives the discrepancy between \(r_{\mathrm {PPL}}\) and \(r_{\mathrm {PPM}}\), which are, respectively, predicted by PPL and PPM, and this discrepancy is normalized by the average value of them. The contrast indicator \(\eta _{\Delta T_{2,1}}\) represents the normalized discrepancy of predicted time delays. Based on the definitions, a larger indicator means two observables associated with it can be more easily distinguished so that the polarization direction can be more clearly determined or ruled out. In Fig. 3, \(\eta _r\) against \(\alpha _{\mathrm {PPM}}\) is shown by the blue curve, and \(\eta _{\Delta T_{2,1}}\) is represented by the red one. At the point of \(\alpha _{\mathrm {PPM}}=0\), both \(\eta _{r}\) and \(\eta _{\Delta T_{2,1}}\) reduce to 0, which is a natural outcome because the coupling of photons to the Weyl tensor vanishes. It is found that \(\eta _{r}\) can reach about 0.1 only when \(\alpha _{\mathrm {PPM}}<-0.1\); and it is almost equal to 0 on the rest and larger part of the domain of \(\alpha _{\mathrm {PPM}}\). In contrast to it, \(\eta _{\Delta T_{2,1}}\) is considerably bigger than \(\eta _{r}\). It can reach about 0.2 when \(\alpha _{\mathrm {PPM}}<-0.1\); and when \(\alpha _{\mathrm {PPM}}>0.15\), it can reach about 0.05, which is larger than \(\eta _{r}\) by a factor of 10. It suggests when the first and second relativistic images are resolved, the measurement of the time delay between them can more effectively improve the detectability of the polarization direction than the measurement of the bright difference does.

5 Conclusions and discussion

In this work, as an extension of the previous work [110], we analyze the strong field time delay for the photons coupled to the Weyl tensor in the Schwarzschild black hole. By making use of the method of SDL [14, 111], we calculate the time delays between relativistic images. We find that these time delays are affected by both the coupling constant \(\alpha \) and the direction of polarization, and they show that the responses to the increase of \(\alpha \) are inversely for the cases of PPL (see left panels of Figs. 1 and 2) and PPM (see right panels of Figs. 1 and 2).

Although it would be very challenging, if the outermost two relativistic images are resolved and their time signals are observed, such a measurement of the time delay can verify the observations of their angular separation and brightness difference. Based on the results of [110] and ours, it is found that the observations of strong field gravitational lensing, including angular separations, brightness differences, and time delays, can possibly detect such a coupling between the photons and the Weyl tensor by comparing the observables with those of the Schwarzschild spacetime. Furthermore, we also find that, after the resolution of the first and second images, the measurement of the time delay can more effectively improve the detectability of the polarization direction than the measurement of bright difference does (see Fig. 3).