1 Introduction

Observational data sets, including the Cosmic Microwave Background (CMB) [1, 2], Supernovae type Ia (SNeIa) [3, 4], Baryonic Acoustic Oscillations (BAO) [5, 6], Observational Hubble Data (OHD) [7, 8], Sloan Digital Sky Survey (SDSS) [9, 10], and Wilkinson Microwave Anisotropy Probe (WMAP) [11, 12], are considered as a criterion for the accuracy of theoretical models. Amongst these constraints, the CMB and SNeIa (because of the abundance of their data sources) attract more attention. It is notable that the SNeIa constraint for high redshift values do not give a good clue to investigate the evolution of the Universe. It is obvious that the results of individual observations give different values for the free parameters of a theoretical model; hence, it is better that, to estimate the best values for the free parameters of the model one considers the whole of the observational data sets, including CMB, SNeIa, BAO, and OHD. This motivated us to study the behavior of the free parameters and their overlaps. Thence, a collective of observations including SNeIa, CMB, BAO, and OHD are considered. Meanwhile the mentioned observational data sets have predicted an ambiguous form of matter which leads to an accelerated phase of present epoch and is well known as dark energy. Based on this ambiguous form of matter, scientists have proposed different proposals up to now. Amongst all of those proposals, the cosmological constant, \(\Lambda \), model attracts the most attention [13, 14]. But this mechanism suffers two well-known drawbacks. The first of them is related to making an estimate of the contribution of quantum fluctuation of the zero point energy, and the second is related to the ratio of \(\Lambda \) and the dark matter energy densities. These problems and also the excellent work by Brans and Dicke [15] motivated scientists to introduce a mechanism in which \(\Lambda \) had a time dependency, namely quintessence [16–18]. Beside the quintessence mechanism, some proposals which have arisen from quantum gravity or string theory are introduced to estimate the cosmological parameters. For instance, one has the tachyon [19, 20], phantom [21–23], quintum [24, 25], k-essence [26, 27] proposals. Also some models which have a risen from quantum field fluctuations or space time fluctuations attract much attention to investigate the dark energy concept. For such models, one can mention Zero Point Quantum Fluctuations (ZPQF) [28–30], Holographic Dark Energy (HDE) [31–36], Agegraphic Dark Energy (ADE), and new-ADE [37–39]. If a scalar field, in the quintessence model, couples to (non-relativistic) matter it induces a fifth force. When the coupling is of order unity, the results of a strongly coupling scalar field is not in good agreement with local gravity tests (for instance in the solar system). Thus a mechanism should exist suppressing the effect of the fifth force; such a mechanism is capable of reconciling strong coupling models with local experiments, as proposed by Khoury and Weltman [40, 41] and also, separately, by Mota and Barrow [42], namely the chameleon-like model. In this mechanism, one cannot choose an arbitrary Lagrangian for matter, \(L_\mathrm{m}\). To avoid a deviation of the geodesic trajectory, the author of [43] has shown that the best choices are \(L_\mathrm{m}=P\) and \(L_\mathrm{m}=-\rho \), where P is the pressure and \(\rho \) is the energy density of matter; for more discussion we refer the reader to [44–46]. Therefore the main motivation of this work is the investigation of the behavior of an interacting scalar field mechanism; based on these calculations and the, SNeIa, CMB, BAO and OHD data sets, the minimum value of \(\chi ^2\) for the effective dark energy equation of state is achieved. The organization of the paper is as follows: The above brief discussions are a review as regards observational and theoretical motivations; they are considered as an introduction. In Sect. 2, the general theoretical discussions arising from a chameleon-like mechanism related to the cosmological parameters, such as the Hubble, deceleration, and coincidence parameters, will be discussed. In Sect. 3, a brief review of the cosmological data sets is presented. In Sect. 4, the observational data sets including SNeIa, CMB, BAO, and OHD are considered, to estimate the minimum value of \(\chi ^2\) related to the free parameters of an ansatz for the effective dark energy equation of state. Finally, Sect. 5, is dedicated to concluding remarks.

2 Conservation and field’s equations in an effective dark energy scenario

In the chameleon-like scalar field scenario, the mass of the scalar field is a function of the local matter density, so that it is sufficiently large in a dense environment. Due to this fact, the equivalence principle (EP) is satisfied in the laboratory [40, 41]. In addition, the Brans–Dicke \(\omega \) parameter for two observational values of \(\gamma \), the post-Newtonian parameter, takes values of order \(10^4\) [47], which satisfies the solar system constraint. The chameleon-like scenario is defined as [43, 44, 48–52]

$$\begin{aligned} S=\int {\mathrm{d}^4 x\frac{1}{2}\sqrt{-g}\left( {R-\partial ^{\mu }\varphi \,\partial _\mu \varphi -2V(\varphi )+2f(\varphi )L}\right) }.\nonumber \\ \end{aligned}$$
(1)

In this equation g is the determinant of the metric, \(V(\varphi )\) is a run away potential and the last term indicates a non-minimal coupling between scalar field and matter sector. It should be noted that L is the Lagrangian density of matter which consists of both dark matter and dark energy sectors as perfect fluid [47–49, 52, 53]. It should be noticed that the background is a spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) Universe, with signature \((+2)\). The variation of the action (1), with respect to (w.r.t.) \(g_{\mu \nu }\) results in the gravitational field equation:

$$\begin{aligned} G_{\mu \nu } = f(\varphi )T_{\mu \nu } + T_{\mu \nu }^{(\varphi )}, \end{aligned}$$
(2)

where the stress-energy density of scalar field is expressed by

$$\begin{aligned} T_{\mu \nu }^{(\varphi )}=\left( {\nabla _\mu \varphi \nabla _\nu \varphi - \frac{1}{2}g_{\mu \nu } (\nabla \varphi )^2 } \right) - g_{\mu \nu } V(\varphi ), \end{aligned}$$
(3)

and

$$\begin{aligned} T_{\mu \nu } = \frac{{ - 2}}{{\sqrt{ - g} }}\frac{{\delta (\sqrt{ - g} L)}}{{\delta g^{\mu \nu } }} \end{aligned}$$
(4)

is the definition of the stress-energy tensor of matter. By considering the 00 and ii components of \(T^{(\varphi )}_{\mu \nu }\), the energy density and pressure could be obtained. After some algebra the conservation equation reads

$$\begin{aligned} \nabla _\mu (G^{\mu \nu } )= \nabla _\mu \left[ f(\varphi )T^{\mu \nu } + T_{(\varphi )}^{\mu \nu } \right] = 0. \end{aligned}$$
(5)

In addition, the variation of the action (1), w.r.t. the scalar field gives the evolution equation,

$$\begin{aligned} \ddot{\varphi }+ 3H\dot{\varphi }= - V(\varphi ) + \frac{{\partial f(\varphi )}}{{\partial \varphi }}L. \end{aligned}$$
(6)

Now, by substituting Eq. (6) into Eq. (5), two conservation equations for scalar field and matter are obtained:

$$\begin{aligned}&\nabla _\mu [T_{(\varphi )}^{\mu 0}] = \dot{f}(\varphi )L, \end{aligned}$$
(7)
$$\begin{aligned}&\nabla _\mu [f(\varphi )T^{\mu 0}] = - \dot{f}(\varphi )L, \end{aligned}$$
(8)

where the overdot denotes derivation w.r.t. ordinary cosmic time, t. As mentioned in the introduction, the Lagrangian of the matter is considered to verify \(L= L_\mathrm{(m)} + L_\mathrm{(de)}\), [52, 54], where the subscript m denotes matter (cold dark matter and baryons) and de refers to dark energy. Then the conservation equations could be rewritten as

$$\begin{aligned}&\nabla _\mu \left[ f(\varphi )T_\mathrm{(m)}^{\mu 0} \right] = - \dot{f}(\varphi )L_\mathrm{(m)}, \end{aligned}$$
(9)
$$\begin{aligned}&\nabla _\mu \left[ f(\varphi )T_\mathrm{(de)}^{\mu 0} \right] = - \dot{f}(\varphi )L_\mathrm{(de)}, \end{aligned}$$
(10)
$$\begin{aligned}&\nabla _\mu \left[ T_{(\varphi )}^{\mu 0} \right] = \dot{f}(\varphi )(L_\mathrm{(m)} + L_\mathrm{(de)} ). \end{aligned}$$
(11)

By combining Eq. (2) and the above equations, it is easy to find

$$\begin{aligned} \nabla _\mu \left[ T_{(\varphi )}^{\mu 0} + f(\varphi )T_\mathrm{(de)}^{\mu 0} \right] = \dot{f}(\varphi )L_\mathrm{(m)}. \end{aligned}$$
(12)

In the next step, by virtue of the definition of \(T_{\mu \nu }^{(\varphi )}\) and Eq. (2), the Einstein tensor is modified as

$$\begin{aligned} G^{\mu \nu } = f(\varphi ) \left[ {T_\mathrm{(m)}^{\mu \nu } + T_\mathrm{(de)}^{\mu \nu } + \frac{1}{{f(\varphi )}}T_{(\varphi )}^{\mu \nu } } \right] . \end{aligned}$$
(13)

Hereafter, we postulate that both scalar field and dark energy behave as a perfect fluid, thence for such a perfect mixture the effective stress-energy tensor is obtained as follows:

$$\begin{aligned} T_\mathrm{(DE)}^{\mu \nu } = T_\mathrm{(de)}^{\mu \nu } + \frac{1}{{f(\varphi )}}T_{(\varphi )}^{\mu \nu }, \end{aligned}$$
(14)

where the subscript DE denotes the effective dark energy. Therefore using Eqs. (7)–(14), the modified Einstein equation and conservation relations are obtained:

$$\begin{aligned}&G^{\mu \nu } = f(\varphi ) \left[ T_\mathrm{(m)}^{\mu \nu } + T_\mathrm{(DE)}^{\mu \nu } \right] ,\end{aligned}$$
(15)
$$\begin{aligned}&\nabla _\mu \left[ f(\varphi )T_\mathrm{(m)}^{\mu 0} \right] = - \dot{f}(\varphi )L_\mathrm{(m)}, \end{aligned}$$
(16)
$$\begin{aligned}&\nabla _\mu \left[ f(\varphi )T_\mathrm{(DE)}^{\mu 0} \right] = \dot{f}(\varphi )L_\mathrm{(m)} . \end{aligned}$$
(17)

It should be noticed that, in the right hand side of the above equations, only \(L_\mathrm{(m)}\) appeared. In fact it could be concluded that the energies for different components of the Universe are not conserved separately. In Refs. [55–57], it has been shown that, for perfect fluids which do not couple directly to the other components of the Universe, there are different Lagrangian densities that are equivalent. Namely, one can find that the two Lagrangian densities \(L_\mathrm{(m)} = P\) and \(L_\mathrm{(m)}=-\rho \) give the same stress-energy tensor and the equation of motions for all components of the system are similar as well. But in an interacting case, in which matter has an interaction with the scalar field, the Lagrangian degeneracy is broken. Based on Ref. [43], the best choice for such models is \(L_\mathrm{(m)} = P\). Using this definition for the Lagrangian of the matter one can obtain

$$\begin{aligned} H^2 = \frac{1}{3}f(\varphi )\left[ \rho _\mathrm{m} + \rho _\mathrm{DE} \right] , \end{aligned}$$
(18)

and also

$$\begin{aligned}&\frac{\mathrm{d}}{{\mathrm{d}t}} \left[ f(\varphi )\rho _\mathrm{m} \right] + 3Hf(\varphi )\rho _\mathrm{m} = 0, \end{aligned}$$
(19)
$$\begin{aligned}&\frac{\mathrm{d}}{{\mathrm{d}t}} \left[ f(\varphi )\rho _\mathrm{DE} \right] + 3Hf(\varphi ) \left[ 1 + \omega _\mathrm{DE} \right] \rho _\mathrm{DE} = 0, \end{aligned}$$
(20)

where \(H=\dot{a}(t)/a(t)\) is the Hubble parameter, a(t) is the scale factor, and \(\omega _\mathrm{DE}\) is the EoS parameter of the effective dark energy and satisfies the EoS equation:

$$\begin{aligned} P_\mathrm{DE} = \omega _\mathrm{DE} \times \rho _\mathrm{DE}. \end{aligned}$$
(21)

To establish an accurate link between theoretical results and observations, one can use the red shift parameter, z, instead of the scale factor; these two cosmological parameters have the relation

$$\begin{aligned} \frac{{a(t_0 )}}{{a(t)}} = 1 + z \, \qquad \dot{z} = - (1 + z)H. \end{aligned}$$
(22)

Thus substituting Eq. (22) into (19) and (20), one finds

$$\begin{aligned}&f(\varphi )\rho _\mathrm{m} = f_0 \times \rho _{\mathrm{m}0} \times (1 + z)^3, \end{aligned}$$
(23)
$$\begin{aligned}&f(\varphi )\rho _\mathrm{DE} = f_0 \times \rho _{\mathrm{DE}0}\times \exp \left[ \int _0^z {3\frac{{1 + \omega _{DE} (\tilde{z})}}{{1 + \tilde{z}}}\mathrm{d}\tilde{z}} \right] ,\nonumber \\ \end{aligned}$$
(24)

where \(\rho _{\mathrm{DE}0}\) and \(\rho _{\mathrm{m}0}\) refer to the energy densities of dark energy and matter at present, respectively.

2.1 Hubble parameter

The dimensionless Hubble parameter and density parameters could be defined as

$$\begin{aligned}&E(z) = \frac{H(z)}{H_0},\end{aligned}$$
(25)
$$\begin{aligned}&{\bar{\Omega }} _{\mathrm{m}0} = \frac{{ \rho _{\mathrm{m}0} }}{{3H_0^2 }}, \end{aligned}$$
(26)
$$\begin{aligned}&{\bar{\Omega }} _{\mathrm{DE}0} = \frac{{ \rho _{\mathrm{DE}0} }}{{3H_0^2 }}. \end{aligned}$$
(27)

The dimensionless density parameters could be rewritten as

$$\begin{aligned}&\Omega _ {\mathrm{m}0} = \frac{{f_0 \times \rho _{\mathrm{m}0} }}{{3H_0^2 }}, \end{aligned}$$
(28)
$$\begin{aligned}&\Omega _ {\mathrm{DE}0} = \frac{{f_0 \times \rho _{\mathrm{DE}0} }}{{3H_0^2 }}. \end{aligned}$$
(29)

Therefore using Eqs. (18) and (25), the dimensionless Hubble parameter is obtained as follows:

$$\begin{aligned}&E^2 (z) = \Omega _{\mathrm{m}0} (1 + z)^3 + \Omega _{\mathrm{DE}0} \exp \left[ {\int _0^z {3\frac{{1 + \omega _\mathrm{DE} (\tilde{z})}}{{1 + \tilde{z}}}d\tilde{z}} } \right] .\nonumber \\ \end{aligned}$$
(30)

2.2 Coincidence parameter

The ratio of dark matter and dark energy is defined as the coincidence parameter:

$$\begin{aligned} r= & {} \frac{{\rho _\mathrm{m} }}{{\rho _\mathrm{DE} }}\nonumber \\ ~= & {} r_0 (1 + z)^3 \exp \left[ - 3\int _0^z {\frac{{1 + \omega _\mathrm{DE} (\tilde{z})}}{{1 + \tilde{z}}}\mathrm{d}\tilde{z}} \right] . \end{aligned}$$
(31)

Also one can obtain

$$\begin{aligned}&\frac{{\mathrm{d}r}}{{\mathrm{d}z}}=\frac{{-3 \omega _\mathrm{DE}(z)}}{{1+z}} r(z). \end{aligned}$$
(32)

Due to the role of this parameter, r, in the investigation of the cosmic evolution, it attracts more attention in observational investigations. In fact one can observe that this importance arises from the relation between the EoS parameter and the evolution of r.

2.3 Deceleration parameter

To investigate the acceleration of the Universe, one can use the deceleration parameter, which is defined by

$$\begin{aligned} q(t) = \frac{{ - 1}}{{a(t)H^2 }}\frac{{\mathrm{d}^2 a(t)}}{{\mathrm{d}t^2 }}. \end{aligned}$$
(33)

The above equation can be rewritten as

$$\begin{aligned} q(z) = - 1 + \frac{3}{2}\left( {\frac{{(1 + \omega _\mathrm{DE} )E^2 - \Omega _{\mathrm{m}0} (1 + z)^3 \omega _\mathrm{DE} }}{{(1 + z)E^2 }}} \right) .\nonumber \\ \end{aligned}$$
(34)

In the present epoch of the Universe evolution, the deceleration parameter is determined by

$$\begin{aligned} q_0 = \frac{1}{2} + \frac{3}{2} \left[ {1 - \Omega _{\mathrm{m}0} }\right] \omega _\mathrm{DE} (0). \end{aligned}$$
(35)

To solve the above equation we introduce an ansatz for the EoS parameter [54, 58]:

$$\begin{aligned} \omega _\mathrm{DE}(z)=-1+\omega _0 + \omega _1 (1+z)^\beta , \end{aligned}$$
(36)

where \(\omega _0\), \(\omega _1\), and \( \beta \) are free parameters of the model, where the minimum value of \(\chi ^2\) for them will be obtained as we address fitting. Also it is notable, if we choose \(\beta =0\), that the model reduces to EoS constant models (for instance \(\Lambda CDM\)) [54]. By substituting (36) in (30), the dimensionless Hubble parameter is obtained as follows:

$$\begin{aligned} E^2 (\{z; \mathrm{{P}}_\mathrm{{i}}\})= & {} \Omega _{\mathrm{m}0}(1+z)^3+ \Omega _{\mathrm{DE}0} (1 + z)^{3\omega _0} \nonumber \\&\times \exp \left[ {3\frac{{\omega _1 }}{\beta }\left( {(1 + z)^\beta - 1} \right) } \right] , \end{aligned}$$
(37)

where

$$\begin{aligned} \{z; \mathrm{{P}}_\mathrm{{i}}\}= & {} \{\Omega _{\mathrm{m}0} ,\omega _0 ,\omega _1 ,\beta \}, \end{aligned}$$
(38)

and \(\{\mathrm{P}_\mathrm{i}\}\) is the set of free parameters which should be determined using the data fitting process. Using Eq. (36), one can rewrite Eqs. (23), (24), and (31), respectively, as

$$\begin{aligned} f(\varphi ) \rho _\mathrm{m}= & {} f_0 \rho _{\mathrm{m}0}\times (1 + z)^3, \end{aligned}$$
(39)
$$\begin{aligned} f(\varphi ) \rho _\mathrm{DE}= & {} f_0 \rho _{\mathrm{DE}0}\times (1 + z)^{3\omega _0 } \nonumber \\&\times \exp \left[ {3\frac{{\omega _1 }}{\beta }\left( {(1 + z)^\beta - 1} \right) } \right] , \end{aligned}$$
(40)

and

$$\begin{aligned} r(z) = r_0 (1 + z)^{ - 3(1 - \omega _0 )} \exp \left[ { - 3\frac{{\omega _1 }}{\beta }\left( {(1 + z)^\beta - 1} \right) } \right] .\nonumber \\ \end{aligned}$$
(41)

3 A brief review as to cosmological observational data sets

In this section, we should emphasize that the analysis is restricted to the background level, and we do not include perturbations. In the following, we want to compare our theoretical results with observations. To this end, we consider four important data sets including SNeIa, CMB, BAO, and OHD. In some papers, it was claimed that OHD, as obtained versus red shift, is comparable with the SNeIa data set, for instance we refer reader to Table 1, Ref. [7] and references therein. This subject motivated us to investigate the effects of this new data set, beside other observations, to improve the theoretical results. As will be discussed, the results of OHD, although not independent of the SNeIa and BAO data sets [7], do not have any dependency on CMB. Also there are two ways to study the CMB and BAO data points; we refer to the full parameter distribution and the Gaussian; in the following the latter will be used.

3.1 Supernovae type Ia

It is clear that supernovae attract more attention in empirical cosmology. Whereas they are very luminous, people interested in them, for instance at closer distances (i.e. lower redshift), could use them to calculate the Hubble parameter, and for farther distances (i.e. higher redshift) they attain an important role in estimating the deceleration parameter q. It is obvious there are uncertainties of a different nature: statistical or random errors and systematic errors. In this work it is remarkable the systematic errors for SNeIa and OHD are neglected. In reality there is always a limit on the statistical accuracy, besides the trivial one that the time for repetitions is limited. The assumption of independence is violated in a very specific way by so-called systematic errors which appear in any realistic experiment. For instance experiments in nuclear and particle physics usually extract the information from a statistical data sample. The precision of the results then is mainly determined by the number N of collected reactions. Besides the corresponding well-defined statistical errors, nearly every measurement is subject to further uncertainties, the systematic errors, typically associated with auxiliary parameters related to the measuring apparatus, or with model assumptions. The result is typically presented in the form

$$\begin{aligned} x = 2.34 \pm 0.06 = 2.34 \pm 0.05(\mathrm{stat}) \pm 0.03(\mathrm{syst}). \end{aligned}$$

The only reason for the separate quotation of the two uncertainties is that the size of the systematic uncertainties is less well known than that of the purely statistical error [60]. By virtue of the likelihood functions, one is able to estimate the minimum value of \(\chi ^2\) for the set of parameters \(\{\mathrm{{p}}_\mathrm{{i}}\}\), as

$$\begin{aligned} {\mathscr {L}}(\{ \mathrm{{p}}_\mathrm{{i}} ,\mu _\mathrm{{0}} \} ) \propto \exp \left[ { - \frac{1}{2}\chi _\mathrm{SNe}^2 (\{ \mathrm{{p}}_\mathrm{{i}} ,\mu _\mathrm{{0}} \} )} \right] , \end{aligned}$$
(42)

where

$$\begin{aligned} \chi _\mathrm{SNe}^2 (\{ \mathrm{{p}}_\mathrm{{i}} ,\mu _\mathrm{{0}} \} )= \sum \limits _{n= 1}^{557} {\frac{{\left[ {\mu _\mathrm{obs} (z_n ) - \mu _\mathrm{th} (z_n;\mathrm {\{p_i , \mu _0\}}) } \right] ^2 }}{{\sigma _n^2 }}}. \end{aligned}$$
(43)

In Eq. (43), \(\mu _\mathrm{obs} (z_n )\) is the observational distance modulus for the nth supernova, \(\sigma _n\) is the variance of the measurement, and \(\mu _\mathrm{th} (z_n )\) is the theoretical distance modulus for the nth supernova, which is defined as

$$\begin{aligned}&\mu _\mathrm{th} (z_n ;\mathrm {\{p_i , \mu _0\}}) = 5\log _{10} \left[ {D_L (z_n ;\mathrm {\{p_i\}})} \right] + \mu _0, \nonumber \\&\mu _0 = 42.38 - 5\log _{10} \left[ h \right] , \\&D_\mathrm{L} (z_n ;{\{\mathrm{p}_\mathrm{i}\}}) = (1 + z)\int _0^z {\frac{{\mathrm{d}{\tilde{z}}}}{{E({\tilde{z}};{ \{\mathrm{p}_\mathrm{i}\}})}}}, \end{aligned}$$

where \(D_\mathrm{L}\) is the luminous distance and \(h\!=\!100~{\mathrm{km}\, \mathrm{s}^{-1}\,\mathrm{Mpc}^{-1}}\). To achieve the best fit of the free parameters, one can marginalize the likelihood function w.r.t. \(\mu _{0}\) [59, 60]. Thence \(\chi _\mathrm{SNe}^2 (\{ \mathrm{{p}}_\mathrm{{i}}\})\) reduces to

$$\begin{aligned} \chi _\mathrm{SNe}^2 (\{ \mathrm{{p}}_\mathrm{{i}}\})=A-\frac{B^2}{C}, \end{aligned}$$
(44)

where A, B, and C are defined as follows:

$$\begin{aligned}&A = \sum \limits _{n = 1}^{557} {\frac{{\left[ {\mu _\mathrm{obs} (z_n ) - \mu _\mathrm{th} (z_n ;\{ \mathrm{{p}}_\mathrm{{i}} ,\mu _\mathrm{{0}} = 0\} )} \right] ^2 }}{{\sigma _n^2 }}} , \end{aligned}$$
(45)
$$\begin{aligned}&B = \sum \limits _{n = 1}^{557} {\frac{{\mu _\mathrm{obs} (z_n ) - \mu _\mathrm{th} (z_n ;\{ \mathrm{{p}}_\mathrm{{i}} ,\mu _{0} = 0\} )}}{{\sigma _n^2 }}} , \end{aligned}$$
(46)
$$\begin{aligned}&C = \sum \limits _{n = 1}^{557} {\frac{1}{{\sigma _n^2 }}}. \end{aligned}$$
(47)

3.2 Cosmic microwave background

According to oscillations appearing in the matter and radiation fields Doppler peaks in the radiation (photon) spectrum are produced. Also it should be noted that the existence of dark energy affects the place of the Doppler peaks in the spectrum diagrams. To determine the shift of these peaks theoretically, the CMB shift parameters are defined as in Refs. [1, 61],

$$\begin{aligned} R_\mathrm{th} (z_\mathrm{rec} ;\{ \mathrm{{p}}_\mathrm{{i}} \} ) = \sqrt{\frac{{\Omega _{\mathrm{m}0} }}{{f_0 }}} \int _0^{z_\mathrm{rec} } {\frac{{\mathrm{d}{\tilde{z}}}}{{E({\tilde{z}};\{ \mathrm{{p}}_\mathrm{{i}} \} )}}}. \end{aligned}$$
(48)

In CMB investigations [62], the \(\chi _\mathrm{CMB}^2\) function versus CMB shift parameter is

$$\begin{aligned} \chi _\mathrm{CMB}^2 (\{ \mathrm{{p}}_\mathrm{{i}} \} ) = \frac{{\left[ {R_\mathrm{obs} - R_\mathrm{th} (z_\mathrm{rec} ;\{ \mathrm{{p}}_\mathrm{{i}} \} )} \right] ^2 }}{{\sigma _R^2 }} \end{aligned}$$
(49)

where \(R_\mathrm{obs} = 1.725\), \(\sigma _R = 0.018\), and \(z_\mathrm{rec} \approx 1091.3\) are observational values of the CMB shift parameter, the uncertainty of R at the \(\sigma _1\) confidence level, and the recombination redshift; see, respectively, Refs. [1, 61].

3.3 Baryonic acoustic oscillations

As in [63] mentioned, because BAO can be considered as a standard length scale in a wide range of redshifts, it is a useful candidate for cosmological models testing. The importance of the BAO mechanism is related to its ability in the estimation of the contents and curvature of the Universe. One can establish a relation between the theoretical BAO parameter, \(A_\mathrm{th}\), and the dimensionless Hubble parameter, Eq. (30), thus:

$$\begin{aligned}&A_\mathrm{th} (z_b ;\{ \mathrm{{p}}_\mathrm{{i}} \} ) \nonumber \\&\quad = \sqrt{\frac{{\Omega _{\mathrm{m}0} }}{{f_0 }}} \left[ {E(z_b ;\{ \mathrm{{p}}_\mathrm{{i}} \} )} \right] ^{ - 1/3} \left[ {\frac{1}{{z_b }}\int _0^{z_{b} } {\frac{{\mathrm{d}{\tilde{z}}} }{{E({\tilde{z}};\{ \mathrm{{p}}_\mathrm{{i}} \} )}}} } \right] ^{2/3},\nonumber \\ \end{aligned}$$
(50)

where \(z_b=0.35\) [5, 6]. Also \(\chi _\mathrm{BAO}^2\) in the investigation of the BAO mechanism is as follows:

$$\begin{aligned} \chi _{\mathrm{{BAO}}}^2 (\{ \mathrm{{p}}_\mathrm{{i}} \} ) = \frac{{\left[ {A_\mathrm{obs} - A_\mathrm{th} (z_\mathrm{rec} ;\{ \mathrm{{p}}_\mathrm{{i}} \} )} \right] ^2 }}{{\sigma _A^2 }}, \end{aligned}$$
(51)

and \(A_\mathrm{{obs}} =0.469(n_s / 0.98)^{-0.35}\) and \(n_s = 0.968\) [6, 59]. It is obvious that the BAO are detected in the clustering of the combined 2dFGRS and SDSS main galaxy samples, and they measure the distance–redshift relation at \(z=0.2\). But we consider BAO in the clustering of the SDSS luminous red galaxies in which measure the distance–redshift relation at \(z=0.35\) [64].

3.4 Observational Hubble data

We suggest that if people want to investigate the accuracy of any theoretical model, it is better, maybe, to consider SNeIa, CMB, BAO, and OHD together. In [7], it was claimed that three different models of the dark energy, i.e. \({\Lambda \mathrm{CDM}}\), \({\varphi \mathrm{CDM}}\), and \(\mathrm{XCDM}\), have been investigated just by considering the H(z) measurement, for more details one can refer Table 1. But one has used \(\bar{H}_0= 68 \pm 2.8\) and \(\bar{H}_0 = 73.8\pm 2.4\), which arose from the SNeIa data [8]. Therefore it is realized that for the comparison between theoretical results and observations only OHD could not be considered. The \(\chi _\mathrm{OHD}^2\) function parameter based on the OHD data set is defined as

$$\begin{aligned} \chi _{\mathrm{{OHD}}}^2 (\{ \mathrm{{p}}_\mathrm{{i}} ,H_{0} \} ) = \sum \limits _{n = 1}^{28} {\frac{{\left[ {H_\mathrm{obs} (z_n ) - H_0 E_\mathrm{th} (z_n ;\{ \mathrm{{p}}_\mathrm{{i}} \} )} \right] ^2 }}{{\sigma _n^2 }}},\nonumber \\ \end{aligned}$$
(52)

after marginalizing w.r.t. \(H_{0}\), to calculate the likelihood, \(\chi _{\mathrm{OHD}}^2\) could be considered, thus:

$$\begin{aligned} \chi _{\mathrm{OHD}}^2 (\{ \mathrm{{p}}_\mathrm{{i}} \} ) = A_H - \frac{{B_H^2 }}{{C_H }}, \end{aligned}$$
(53)

where

$$\begin{aligned} A_H= & {} \sum \limits _{n = 1}^{28} {\frac{{\left[ {H_\mathrm{obs} (z_n )} \right] ^2 }}{{\sigma _n^2 }}}, \end{aligned}$$
(54)
$$\begin{aligned} B_H= & {} \sum \limits _{n = 1}^{28} {\frac{{H_\mathrm{obs} (z_n ) \times E_\mathrm{th} (z_n ;\{ \mathrm{{p}}_\mathrm{{i}} \} )}}{{\sigma _n^2 }}}, \end{aligned}$$
(55)
$$\begin{aligned} C_H= & {} \sum \limits _{n = 1}^{28} {\frac{{\left[ {E_\mathrm{th} (z_n ;\{ \mathrm{{p}}_\mathrm{{i}} \} )} \right] ^2 }}{{\sigma _n^2 }}}. \end{aligned}$$
(56)

In the above equations the subscript obs is for observational quantities and the subscript th is for theoretical ones.

4 Cosmological constraints and data fitting

As mentioned, we have introduced an ansatz by Eq. (36), which consists of three free parameters. Here \(\omega _1 \) indicates the present time value of \(\omega _\mathrm{DE}\). For convenience we can assume \(\omega _\mathrm{{0}}=f_0=1\) and therefore Eq. (36) is reduced to [54, 58]

$$\begin{aligned} \omega _\mathrm{DE}(z)=\omega _1 (1+z)^\beta . \end{aligned}$$
(57)

Also, the mean square of the relative error functions \(\chi ^2\) normally cause the free parameters plane split in two parts. People usually are interested in the regions for which \(\chi ^2 / N \le 1\), where N denotes the amount of observational data. Whereas we use the \(\mathrm{Union}-2\) data set for SNeIa, N for supernovae is \(N_\mathrm{SNe}=557,\) and also for OHD, CMB, and BAO, one has \(N_\mathrm{OHD}=28\), \(N_\mathrm{CMB}=1\), and \(N_\mathrm{BAO}=1\). Since in this work three free parameters appeared, the space of constraints has three dimensions. Thence for clarity, one can map figures on two dimensions (in fact, it is supposed that the free parameters are independent) and their values will be analyzed. The common regions for best fitting of all constraint, play a key role in this study. Based on the above discussions we plot a couple of free parameters in Figs. 1, 2, and 3. In Fig. 1 we investigate the constraints on \(\Omega _{\mathrm{m}0}\) in \(\omega _1 \, \beta \) plate, and also for two constraints SNeIa and OHD minimum points of \(\chi ^2 \) are distinguished. In Fig. 2 using best value of \(\omega _1\), the constraints in \(\Omega _{\mathrm{m}0} \, \beta \) are obtained, in a similar way for best value of \(\beta \), the behavior of constraints in \(\omega _1 \, \Omega _{\mathrm{m}0} \) surface will be shown. Let us, return our attention to Fig. 1 again. For \(\Omega _{\mathrm{m}0}=0.2\), the CMB, BAO and OHD have an overlap region, but they are not in agreement with SNeIa results. Also for a different quantity, the SNeIa and OHD results could be in agreement with together. This different behavior of constraints indicates that if one wants to compare theoretical results with observations, it is better that the greatest set of constraints would be considered. To address overlaps and the effects of individual observations, we plot Figs. 4 and 5. In Fig. 4 the behavior of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) and \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) for \(\Delta \chi _\mathrm{T} ^2 = 3.53, 6.25, 8.02\) are compared. Also in Fig. 5 to investigate degeneracy one can consider \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) and \(\chi _\mathrm{T} ^2 = \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) for \(\Delta \chi _\mathrm{T} ^2 = 0.1, 0.2, 0.3\). These two figures indicate that, although individual OHD data surveying (in comparison with SNeIa, CMB, and BAO) is not so important, it decreases the degeneracy between the free parameters of the model. From Figs. 4 and 5, it is obvious that a collective of four constraints has completely different results in comparison to even three constraints. In the following, by means of observations, we use some custom values which are considered for better estimation of the theoretical parameters of the model. Since all free parameters of the model are independent, the total likelihood function could be introduced as

Fig. 1
figure 1

The contour lines of \(\chi ^2 _\mathrm{SNe} = 557\) (brown), \(\chi ^2 _\mathrm{OHD} = 28.0\) (green), \(\chi ^2 _\mathrm{CMB} = 1.0\) (red), and \(\chi ^2 _\mathrm{BAO} = 1.0\) (blue) of \(\Omega _{\mathrm{m}0}=0.26\) are plotted. Also for the two constraints \(\mathrm{SNeIa}\) and \(\mathrm{OHD}\) the minimum points of \(\chi ^2\) are distinguished. The dashed lines refer to the contour lines which are the greater of the minimum points being only unity

Full size image
Fig. 2
figure 2

The contour lines of \(\chi ^2 _\mathrm{SNe} = 557\) (brown), \(\chi ^2 _\mathrm{OHD} = 28.0\) (green), \(\chi ^2 _\mathrm{CMB} = 1.0\) (red), and \(\chi ^2 _\mathrm{BAO} = 1.0\) (blue) for \(\omega _{1}=-1.1\) are plotted. Also for the two constraints the \(\mathrm{SNeIa}\) and \(\mathrm{OHD}\) minimum point of \(\chi ^2\) are distinguished. The dashed lines refer to the contour lines which are the greater of the minimum points being only unity

Full size image
$$\begin{aligned} {\mathscr {L}}_\mathrm{T} = {\mathscr {L}}_{\mathrm{SNe}} \times {\mathscr {L}}_{\mathrm{OHD}} \times {\mathscr {L}}_{\mathrm{CMB}} \times \mathcal{L}_{\mathrm{BAO}}, \end{aligned}$$
(58)
Fig. 3
figure 3

The contour lines of \(\chi ^2 _\mathrm{SNe} = 557\) (brown), \(\chi ^2 _\mathrm{OHD} = 28.0\) (green), \(\chi ^2 _\mathrm{CMB} = 1.0\) (red), and \(\chi ^2 _\mathrm{BAO} = 1.0\) (blue) for \(\beta =-0.25\) are plotted. Also for the two constraints \(\mathrm{SNeIa}\) and \(\mathrm{OHD}\) the minimum points of \(\chi ^2\) are distinguished. The dashed lines refer to the contour lines which are the greater of the minimum points being only unity

Full size image
Fig. 4
figure 4

In this figure the behavior of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) (dashed contours) and \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) (solid contours) for \(\Delta \chi _\mathrm{T} ^2 = 3.53\;(\hbox {inner loops}), 6.25\;(\hbox {middle loops}), 8.02\;(\hbox {outer loop})\) are compared. The minimum points of these two \(\chi _\mathrm{T} ^2\) functions are distinguished by solid points

Full size image
Fig. 5
figure 5

In this plot we consider \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) (dashed contours) and \(\chi _\mathrm{T} ^2 = \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) (solid contours) for \(\Delta \chi _\mathrm{T} ^2 = 0.1\;(\hbox {inner loops}), 0.2\;(\hbox {middle loops}), 0.3\;(\hbox {outer loop})\) to investigate degeneracy in this work. This figure and Fig. 4 indicate that although the importance of individual OHD data surveying in cosmological investigations (in comparison SNe Ia, CMB and BAO) is not so important, it causes decreasing degeneracy between free parameters of the model. The minimum points of these two \(\chi _\mathrm{T} ^2\) functions are distinguished by solid points

Full size image

therefore the total \(\chi ^2\) function could be obtained:

$$\begin{aligned} \chi _\mathrm{T}^2 = \chi _{\mathrm{SNe}}^2 + \chi _{\mathrm{OHD}}^2 + \chi _{\mathrm{CMB}}^2 + \chi _{\mathrm{BAO}}^2. \end{aligned}$$
(59)

It is considerably significant to attain the maximum amount of the probability and the minimum value of \(\chi ^2\); we should minimize \(\chi _\mathrm{T}^2\). Also it should be noted that in (59) all components have same weight. So the likelihood method is equivalent to the fact that for instance all measurements which lead to CMB are equal to a supernova explosion. We shall return to this problem. Another quantity which could be used for the data fitting process is

$$\begin{aligned} \tilde{\chi }^{2}=\frac{\chi _\mathrm{T}^2}{N_\mathrm{dof}} \end{aligned}$$
(60)

where the subscript dof is an abbreviation of the degree of freedom, and \(N_\mathrm{dof}\) could be defined as the difference between all observational sources and the amount of free parameters. Let us explain it in more detail. Whereas the amounts of all observations is \(557+28+1+1 = 587\), and the number of free parameters is 4, by considering \(H_0\), \(N_\mathrm{dof}\) is equal to 583. Also one knows that the acceptable value for \(\tilde{\chi }^2 \) is 1.05. For convenience, we now define the average relative error functions as follows:

$$\begin{aligned}&\bar{\chi }_{\mathrm{SNe}}^2 = \frac{{\chi _{\mathrm{SNe}}^2 }}{{N_{\mathrm{SNe}} }}, \end{aligned}$$
(61)
$$\begin{aligned}&\bar{\chi }_{\mathrm{OHD}}^2 = \frac{{\chi _{\mathrm{OHD}}^2 }}{{N_{\mathrm{OHD}} }}, \end{aligned}$$
(62)
$$\begin{aligned}&\bar{\chi }_{\mathrm{CMB}}^2 = \frac{{\chi _{\mathrm{CMB}}^2 }}{{N_{\mathrm{CMB}} }}, \end{aligned}$$
(63)
$$\begin{aligned}&\bar{\chi }_{\mathrm{BAO}}^2 = \frac{{\chi _{\mathrm{BAO}}^2 }}{{N_{\mathrm{BAO}} }}. \end{aligned}$$
(64)

Finally we can introduce the \(\chi _\mathrm{m} ^2\) function, which is equal to the maximum of the \(\bar{\chi } ^2\) functions and it could be considered as

$$\begin{aligned}&\chi _\mathrm{{m}}^2 = \mathrm{{max}}\,\mathrm{{of}}\,\left( {\bar{\chi }_{\mathrm{{SNe}}}^2 ,\bar{\chi }_{\mathrm{{OHD}}}^2 ,\bar{\chi }_{\mathrm{{CMB}}}^2 ,\bar{\chi }_{\mathrm{{BAO}}}^2 } \right) . \end{aligned}$$
(65)
Fig. 6
figure 6

In the above diagrams the minimum values of \(\tilde{\chi } ^2\) (blue line) and \(\chi _\mathrm{m} ^2\) (red upper line) versus \(\Omega _{\mathrm{m}0}\), \(\omega _1\), and \(\beta \) parameters have been drawn, respectively

Full size image

In fact, the \(\chi _\mathrm{m} ^2\) function could be considered as a criterion of the accuracy for the models. Now we want to compare the behavior of the \(\chi _\mathrm{m} ^2\) and \(\tilde{\chi } ^2\) functions. Without loss of generality of the model, one can plot the three dimensional shape of \(\chi _\mathrm{m} ^2\) and \(\tilde{\chi } ^2\), versus the free parameters of the model. These diagrams help us to find the best estimation of the free parameters in comparison to the observations; for more clarity one may refer to Fig. 6. In this figure, the first diagram shows the minimum of \(\chi _\mathrm{m} ^2\) and \(\bar{\chi } ^2\) versus \(\Omega _{\mathrm{m}0}\). Also in the two last diagrams of Fig. 6, the minimum points are drawn based on \(\omega _1\) and \(\beta \), respectively. By comparison with the behavior of these relative error functions in Fig. 6 one can realize that there are more points (or neighborhood) in which \(\tilde{\chi } ^2 < 1\), but \(\chi _\mathrm{m} ^2\) exceeds 1.05. In fact this behavior was predictable, because in the definition of \(\tilde{\chi } ^2\), we use the contribution of all observational data set. So, for example the \(\chi _{\mathrm{CMB}}^2\) deviation of the best fitting results could be recompensed by the SNeIa data abundance. We will return to this drawback, after some discussion as regards the likelihood and relative error functions. For illustration, we portrait the different surfaces of three dimensional surfaces, \((\Omega _{{\mathrm{m}0}}, \omega _\mathrm{{1}}, \beta )\), to \((\Omega _{{\mathrm{m}0}}, \beta )\), \((\omega _1 ,\Omega _{{\mathrm{m}0}})\), and \((\omega _1 ,\beta )\), which are presented in Figs. 7, 8,

Fig. 7
figure 7

In diagram a, the image of \(\chi _\mathrm{m} ^2 \le 1\) on the \((\Omega _{\mathrm{m}0}, \beta )\) surface is displayed. In b the minimum point of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) and the shadow of \(\Delta \chi _\mathrm{T} ^2 = 3.53\;(\hbox {inner loop}), 6.25\; (\hbox {middle loop}), 8.02\;(\hbox {outer loop})\) surfaces on the \((\Omega _{\mathrm{m}0}, \beta )\) plate, are plotted. In part c both diagrams a and b are presented to compare the results

Full size image
Fig. 8
figure 8

In diagram a, the image of \(\chi _\mathrm{m} ^2 \le 1\) on the \((\omega _1,\Omega _{\mathrm{m}0})\) surface is displayed. In b the minimum point of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) and the shadow of \(\Delta \chi _\mathrm{T} ^2 = 3.53\; (\hbox {inner loop}), 6.25\;(\hbox {middle loop}), 8.02\;(\hbox {outer loop})\) surfaces on the \((\omega _1,\Omega _{\mathrm{m}0})\) plate, are drawn. In part c both diagrams a and b are considered for comparison

Full size image

and 9. Diagrams B and C are related to \((\chi _\mathrm{T} ^2)_\mathrm{min}\), where the subscript min is for the minimum value of \(\chi _{\mathrm{T}}^2\). It is notable, in a three dimensional space of free parameters, that the confidence levels 68.3, 90, and \(95.4\,\%\) are proportional to the \(\Delta \chi _\mathrm{T} ^2 = 3.53\), \(\Delta \chi _\mathrm{T} ^2 = 6.25\), and \(\Delta \chi _\mathrm{T} ^2 = 8.02\) surfaces, respectively, where \(\Delta \chi _\mathrm{T} ^2 =\chi _\mathrm{T} ^2 - (\chi _\mathrm{T} ^2)_\mathrm{min}\). In diagram b of Figs. 7, 8, and 9 the contour lines of the confidence levels are drawn and in diagram c, both the \(\chi _\mathrm{m} ^2\) surfaces and the contour lines are shown for better comparison. From diagram c it is realized that the confidence level contours exceed the \(\chi _\mathrm{m} ^2\) regions. From this behavior it is concluded that the theoretical prediction of the CMB shift parameter is much greater than its observational value. As mentioned, when the total mean square error function is introduced the weights of all constraints were identical and this causes some problems. As a matter of fact, the results of the likelihood’s parameter, Eq. (59), the effect of the CMB shift parameter in comparison with the abundant SNeIa data set is ignored. For more information, see Table 2 and the definition of \(N_\mathrm{dof}\). To overcome these problems, we redefine \(\chi _\mathrm{T}^2\) by

$$\begin{aligned} \chi _\mathrm{T}^2 = \chi _{\mathrm{SNe}}^2 + \chi _{\mathrm{OHD}}^2 + 3 \, \chi _{\mathrm{CMB}}^2 + 3 \, \chi _{\mathrm{BAO}}^2. \end{aligned}$$
(66)
Fig. 9
figure 9

In diagram a, the image of \(\chi _\mathrm{m} ^2 \le 1\) on the \((\omega _1,\beta )\) surface is displayed. In b the minimum point of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) and the shadow of \(\Delta \chi _\mathrm{T} ^2 = 3.53\;(\hbox {inner loop}), 6.25\; (\hbox {middle loop}), 8.02\;(\hbox {outer loop})\) surfaces on the \((\omega _1,\beta )\) plate, as contour lines, are drawn. In part c both diagrams a and b are compared

Full size image
Table 1 In this table from left to right z, \(H(z) (km\, s^{-1}\, Mpc ^{-1})\), and its uncertainty \(\sigma _{H} (km\, s^{-1}\, Mpc ^{-1})\) in measurement and in related references (by considering the technique which is used) are collected, respectively
Full size table
Table 2 In the table, the quantities related to minimum point of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) are introduced
Full size table
Table 3 This table is related to the minimum point of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{{SNe}} ^2 + \chi _\mathrm{{OHD}} ^2 + 3 \chi _\mathrm{{CMB}} ^2 + 3\chi _\mathrm{{BAO}}^2\)
Full size table
Fig. 10
figure 10

In diagram a, the image of \(\chi _\mathrm{m} ^2 \le 1\) on the \((\Omega _{\mathrm{m}0}, \beta )\) surface is displayed. In b the minimum point of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + 3 \chi _\mathrm{CMB} ^2 + 3 \chi _\mathrm{BAO} ^2\) and the shadow of \(\Delta \chi _\mathrm{T} ^2 = 3.53\;(\hbox {inner loop}), 6.25\;(\hbox {middle loop}), 8.02\;(\hbox {outer loop})\) surfaces on the \((\Omega _{\mathrm{m}0}, \beta )\) surface, as contour lines, are drawn. In part c both diagrams a and b have been presented for comparison

Full size image
Fig. 11
figure 11

In diagram a, the image of \(\chi _\mathrm{m} ^2 \le 1\) on the \((\omega _1,\Omega _{\mathrm{m}0})\) surface is displayed. In b the minimum point of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + 3 \chi _\mathrm{CMB} ^2 + 3 \chi _\mathrm{BAO} ^2\) and the shadow of \(\Delta \chi _\mathrm{T} ^2 = 3.53\;(\hbox {inner loop}), 6.25\;(\hbox {middle loop}), 8.02\;(\hbox {outer loop})\) surfaces on the \((\omega _1,\Omega _{\mathrm{m}0})\) plate, as contour lines, are drawn. In part c both diagrams a and b are presented for comparison

Full size image
Fig. 12
figure 12

In diagram a, the image of \(\chi _\mathrm{m} ^2 \le 1\) on the \((\omega _1,\beta )\) surface is displayed. In b the minimum point of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + 3 \chi _\mathrm{CMB} ^2 + 3 \chi _\mathrm{BAO} ^2\) and the shadow of \(\Delta \chi _\mathrm{T} ^2 = 3.53\; (\hbox {inner loop}), 6.25\;(\hbox {middle loop}), 8.02\;(\hbox {outer loop})\) surfaces on the \((\omega _1,\beta )\) plate, as contour lines, are drawn. In part c the two diagrams a and b are collected for comparison

Full size image
Fig. 13
figure 13

In the above two dimensional likelihood diagrams, the \(68.3\,\%\) confidence level (dotted line), \(90.0\,\%\) confidence level (green dashed line), and \(95.45\,\%\) confidence level (red solid line) after marginalization on the \(\omega _1\), \(\beta \) and \(\Omega _{\mathrm{m}0}\) free parameters are plotted. Note that in this figure we use \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + 3 \chi _\mathrm{CMB} ^2 + 3 \chi _\mathrm{BAO} ^2\) and also the shadow of \(\Delta \chi _\mathrm{T} ^2 = 3.53\;(\hbox {inner loop}), 6.25\;(\hbox {middle loop}), 8.02\; (\hbox {outer loop})\) surfaces

Full size image
Fig. 14
figure 14

In the above diagrams the relative likelihoods are plotted. The 68.3 and \(95.4\,\%\) confidence levels are distinguished as a brown dashed line and a red dot dash line, respectively. It should be noted that in these figures we use \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + 3 \chi _\mathrm{CMB} ^2 + 3 \chi _\mathrm{BAO} ^2\). Also the best fits of the free parameters are \(\beta = -0.24_{-0.23, - 0.44} ^ {+ 0.27, + 0.59}\), \(\omega _1 = -1.04_{-0.08, - 0.16} ^ {+ 0.08, + 0.156}\), and \(\Omega _{\mathrm{m}0} =0.272_{-0.01, - 0.02} ^ {+ 0.01, + 0.02} \)

Full size image

It should be noted that in data fitting and maximization of the probability values the two definitions of \(\chi _\mathrm{T} ^2\), i.e. Eqs. (59) and (66), are not very different. For justifying this claim one can compare Tables 2 and 3, which are related to (59) and (66), respectively. But in figures which are related to confidence levels one can observe that the exceeding of confidence levels is reduced, therefore the re-weight of some constraints can improve the behavior of the model. For more clarification one can refer to Figs. 10, 11, and 12. Now by means of (66), we marginalize the likelihood \(\mathscr {L} (\Omega _{\mathrm{m}0} ,\omega _1 , \beta )\) w.r.t. \(\omega _1\), \(\beta \), and \(\Omega _{\mathrm{m}0}\), respectively. Also the relative probability functions \(\mathscr {L} (\Omega _{\mathrm{m}0}, \beta )\), \(\mathscr {L} (\omega _1, \Omega _{\mathrm{m}0})\), and \(\mathscr {L} (\omega _{1} , \beta )\) in two dimensional confidence levels 68.3, 90, and \(95.4\,\%\) are plotted in Fig. 13. For more investigations, we will draw the one dimensional marginalized likelihood functions \(\mathscr {L}(\Omega _{{\mathrm{m}0}})\) versus \(\Omega _{{\mathrm{m}0}}\), \(\mathscr {L}(\omega _1)\) based on \(\omega _1\) and \(\mathscr {L}(\beta )\) versus \(\beta \) in Fig. 14. Meanwhile in Table 4 one observes the quantities which maximize the marginalized likelihoods using different confidence levels by means of the confidence levels \(\sigma _1 = 68.3\,\%\) and \(\sigma _2 = 95.4\,\%\).

4.1 Typical example

Now we define an effective dark energy as a combination of dark energy \(\rho _\mathrm{de}\) and the scalar field density, \(\rho _\mathrm{DE}=\rho _\mathrm{de}+{\rho _{\varphi }}/{f(\varphi )}\). So, the Friedmann equation is rewritten as

$$\begin{aligned} 3H^2=f(\varphi ) \left( \rho _\mathrm{m} + \rho _\mathrm{DE} \right) . \end{aligned}$$
(67)

A useful parameter in this study is the energy density parameter \(\Omega \). Here \(\Omega _\mathrm{DE}\) and \(\Omega _\mathrm{m}\), respectively, will be taken equal to \(\Omega _\mathrm{DE}=f(\varphi )\rho _\mathrm{DE}/ \rho _\mathrm{c} \) and \(\Omega _\mathrm{m}=f(\varphi ) \rho _\mathrm{m}/ \rho _\mathrm{c}\), in which \(\rho _\mathrm{c}\) is the critical energy density which is defined as \(\rho _\mathrm{c}=3H^2\). As a result, from the Friedmann equation we have \(\Omega _\mathrm{DE}+\Omega _\mathrm{m}=1\). To obtain energy conservation equations for effective dark energy one can obtain the following results:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}{ \left( f(\varphi )\rho _\mathrm{DE}\right) }+3Hf(\varphi )(1+\omega _\mathrm{DE})\rho _\mathrm{DE} = \gamma \rho _\mathrm{m}\dot{f}(\varphi ), \end{aligned}$$
(68)
$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}{\left( f(\varphi )\rho _m\right) }+3Hf(\varphi )(1+\gamma )\rho _\mathrm{m} = -\gamma \rho _\mathrm{m}\dot{f}(\varphi ), \end{aligned}$$
(69)

so that the effective pressure of dark energy is defined as \(p_\mathrm{DE}=p_{\Lambda }+{p_{\varphi }}/{f(\varphi )}\), and one has the effective dark energy equation of state parameter \(\omega _\mathrm{DE}={p_\mathrm{DE}}/{\rho _\mathrm{DE}}\). Also \(\gamma \) is the matter equation of state parameter, which is defined as \(\gamma ={p_\mathrm{m}}/{\rho _m}\). For \(\gamma =\mathrm{constant}\), integrating of Eq. (69) results in the following relation for the cold dark matter energy density:

$$\begin{aligned} \rho _\mathrm{m}=\frac{\rho _\mathrm{em}^0}{a^{3(1+\gamma )}f^{(1+\gamma )}(\varphi )}, \end{aligned}$$
(70)

where \(\rho _\mathrm{em}^0= f_{0}^{(1+\gamma )}(\varphi )\rho _\mathrm{m}^0\). In this step, we suppose that the effective dark energy could be defined as ADE, in other words we assume that

$$\begin{aligned} \rho _\mathrm{DE}\equiv \rho _\mathrm{ADE}=\frac{3n^2}{T^2}, \end{aligned}$$
(71)

where n is a numerical constant and T is the cosmic time, and therefore \(\Omega _\mathrm{DE}\) is obtained: \(\Omega _\mathrm{DE}={f(\varphi )n^2}/{H^2T^2}\). Taking this assumption and using Eq. (68), the equation of state parameter of the effective dark energy could be obtained:

$$\begin{aligned} \omega _\mathrm{DE}=-1 + \frac{2}{3}\frac{1}{n}\sqrt{\frac{\Omega _\mathrm{DE}}{f(\varphi )}} + \frac{\dot{f}(\varphi )}{3Hf(\varphi )}\left( \gamma r - 1 \right) , \end{aligned}$$
(72)

where r is the ratio of cold dark matter and effective dark energy, namely \(r={\rho _m}/{\rho _\mathrm{DE}}={\Omega _\mathrm{m}}/{\Omega _\mathrm{DE}}\). The interaction term in this model generates an extra term for \(\omega _\mathrm{DE}\), which can justify the phantom divide line crossing. By the definition of an ansatz for \(\omega _{e \Lambda }\), one can consider

$$\begin{aligned} \omega _{e \Lambda }+1=\omega _{0}+\omega _{1}(1+z)^{\beta }. \end{aligned}$$
(73)

For fitting the free parameters for ADE in an external scalar field interaction model, we use the 557 Union-2 sample database of SNeIa, and \(\rho _\mathrm{m}= \rho _\mathrm{radiation}+\rho _\mathrm{baryon}+\rho _\mathrm{dark~matter}\). Therefore in this case the Friemann equation is

$$\begin{aligned} 3H^2=f(\varphi ) \left( \rho _\mathrm{m} + \rho _\mathrm{DE} \right) . \end{aligned}$$
(74)

Combining Eqs. (68)–(71), we have

$$\begin{aligned} 3H^2=f(\varphi ) \left( \frac{\rho ^{0}_\mathrm{em}}{a^{3(1+\gamma )}f^{(1+\gamma )}(\varphi )} + \frac{3n^2}{T^2}\right) , \end{aligned}$$
(75)
Table 4 In this table the values which maximize the relative probability functions \(\mathscr {L}(\Omega _\mathrm{{m0}})\), \(\mathscr {L}(\omega _1)\), and \(\mathscr {L}(\beta )\) using the confidence levels \(\sigma _1 = 68.3\,\%\) and \(\sigma _2 = 95.4\,\%\) are calculated. The data sets are includes of SNeIa, CMB, BAO, and OHD in which the weight of \(\chi _\mathrm{CMB}^2\) and \(\chi _\mathrm{BAO}^2\) in the \(\chi _\mathrm{Total}^2\) function is the coefficient 3
Full size table
Fig. 15
figure 15

The observed distance modulus of supernovae (points) and the theoretical predicted distance modulus (red solid line) in the context of ADE model

Full size image
Fig. 16
figure 16

Contour plots for the free parameters \(\omega _{1}\) and \(\beta \), show that the best values for these parameters are \(-1.86<\omega _{1}<-1.62\) and \(-2.27<\beta <-0.73\)

Full size image

where \(\rho ^{0}_\mathrm{em}\) is the effective energy density of matter at the present time. The 557 Union-2 sample database have collected data from red shift parameter of various SNeIa, therefore we rewrite \(E=H/H_0\) versus z as

$$\begin{aligned} E^{2}=\frac{r_{0} (1+z)^{3}+(1+z)^{{3\omega }_{0}} \exp \left\{ 3\frac{\omega _{1}}{\beta }[(1+z)^{\beta }-1] \right\} }{r_0+1}.\nonumber \\ \end{aligned}$$
(76)

To obtain the best fit for the free parameters based on Sect. 3.1 the minimization method leads to

$$\begin{aligned}&\chi ^{2}_{sn_\mathrm{min}}(\omega _0 = 1.1;~ \omega _{1}=-1.65; ~\beta =-2.25),\end{aligned}$$
(77)
$$\begin{aligned}&\chi _\mathrm{min}^2 = A - \frac{{B^2 }}{C}=542.75, \end{aligned}$$
(78)
$$\begin{aligned}&\mu _0 = - \frac{B}{C}= 43.1089, \end{aligned}$$
(79)

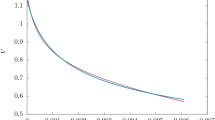
which implies \({\chi ^{2}_\mathrm{sn}}/\mathrm{dof}= \chi ^{2}_{\mathrm{sn}_\mathrm{min}}/\mathrm{dof}= 0.981 (\mathrm{dof} = 553)\). In Fig. 15, we show a comparison between theoretical distance modulus and observed distance modulus of the supernova data. The red solid line indicates the theoretical value of the distance modulus, \(\mu _\mathrm{th}\), for the best value of the free parameters \(\omega _{1}=-1.65\), \(\omega _{0}=1.1\), and \(\beta =-2.25.\)

Fig. 17
figure 17

The plot shows the evolution of effective dark energy parameter, \(\omega _\mathrm{DE}\), versus z, for \(\omega _0=1.1 \), \(\omega _1=-1.68\), and \(\beta =-2.25 \)

Full size image

This shows that the model is clearly consistent with the data since \(\chi ^{2}/\mathrm{dof} = 1\).

Figure 16 shows contour plots for the free parameters \(\omega _{1}\) and \(\beta \); it is shown that the best value for these parameters are \(-1.86<\omega _{1}<-1.62\) and \(-2.27<\beta <-0.73\) in which for the stability condition \(c^2 >0\) we have taken the interface between the green and yellow sector, \(\omega _1=-1.68\).

The evolution of the effective dark energy parameter, \(\omega _\mathrm{DE}\), versus z, for \(\omega _0= 1.1\), \(\omega _1=-1.68\), and \(\beta =-2.25 \) has been shown in Fig. 17. This shows that by increasing z the parameter gets into the phantom phase.

Here \(\omega _{0}\), \(\omega _{1}\), and \(\beta \) are free parameters of the model which are obtained from data fitting. It is clear that if the form of the dark energy density is given, the coupling function, \(f(\varphi )\), could easily be determined. For instance by using Eqs. (68), (69), and (71) one can obtain

$$\begin{aligned} f(\varphi )=f_{0} t^{2} a^{-3\omega _{0}} \exp { \left[ 3\omega _{1}\frac{{(z+1)}^{\beta +2}}{\beta +2} \right] }, \end{aligned}$$
(80)

where \(f_{0}\) is the constant of integration. We have

$$\begin{aligned} \frac{\dot{f}(\varphi )}{f(\varphi )}=3H \left[ \frac{2}{3tH} -\omega _{0}-\omega _1{(1+z)}^{\beta +2} \right] . \end{aligned}$$

A significant result of observational data is the accelerated expansion of the Universe. A good cosmological model should be able to describe this acceleration. A useful quantity to investigate this property of the Universe is the deceleration parameter, which is defined as \(q=-1-{\dot{H}}/{H^2}\). Using Eqs. (67), (68), and (69), one obtains the deceleration parameter given by

$$\begin{aligned} q= & {} -1+\frac{3}{2} \left[ 1-\omega _0-\omega _{1}{(1+z)}^{\beta } \right] \nonumber \\&\times \left( \frac{D_{0}}{1+(1+z)^{3(1-\omega _{0})}(t)\exp [\frac{-3\omega _1 {(1+z)}^{\beta }}{\beta }]} \right) , \end{aligned}$$
(81)

where \(D_{0}\) is the constant of integration. It is clearly seen that for \(\omega _0=1.1,\quad \omega _1=-1.68,\quad \beta =-2.25\), (which we have obtained from data fitting processes) \(q<0\).

5 Conclusion and discussion

Interacting models which contain an external interaction between matter and scalar fields attract more attention. Such mechanisms are capable to suppress the fifth force and also are in good agreement with observations. Using such a powerful mechanism we have found some cosmological parameters referring to the coincidence and deceleration parameters. For instance based on Table 2, and Eqs. (32) and (34) it is clear that r(z) is a decreasing function and q has taken negative values for different values of z. Considering a suitable ansatz for the EoS parameter of effective dark energy, the dimensionless Hubble parameter is obtained. So by means of SNeIa, CMB, BAO, and OHD data sets the minimum value of \(\chi ^2\) for the free parameters of the model are obtained. To estimate the free parameters of an ansatz for the effective dark energy equation of state, the whole of the observational data sets have been considered. For more details one can compare the results of Figs. 4 and 5 with the results of a typical example, see Sect. 4.1. Also for getting a better overlap between the contours with the constraint \(\chi _\mathrm{m}^2\le 1\), the \(\chi _\mathrm{T}^2\) function has been re-weighted. Meanwhile the relative probability functions have been plotted for the marginalized likelihood \(\mathscr {L} (\Omega _{\mathrm{m}0} ,\omega _1 , \beta )\) according to the two dimensional confidence levels 68.3, 90, and \(95.4\,\%\). In addition the values of the free parameters which maximize the marginalized likelihoods using the above confidence levels have been obtained. Based on the above discussions a couple of free parameters have been plotted in Figs. 1, 2, and 3. In Fig. 1, the constraints on \(\Omega _{\mathrm{m}0}\) in the \(\omega _1 \, \beta \) plane have been investigated; and also, for the two constraints the SNeIa and OHD minimum points of \(\chi ^2 \) have been distinguished. In Fig. 2, using the best value of \(\omega _1\), the constraints in the \(\Omega _{\mathrm{m}0} \, \beta \) plane are obtained. In a similar way, for the best value of \(\beta \), the behavior of the constraints in the \(\omega _1 \, \Omega _{\mathrm{m}0}\) plane is shown. Also based on Fig. 1, for \(\Omega _{\mathrm{m}0}=0.2\), the CMB, BAO, and OHD have an overlap region, but they are not in agreement with the SNeIa results; one possible explanation would be incompatibility among the data sets. Also, for different values one can find a region in which SNeIa and OHD are in better agreement against CMB and BAO. This different behavior of the constraints indicates that if one wants to compare theoretical and observational results, it may be better that the greatest set of constraints would be considered. For more investigation of the overlaps and the effects on individual observations, Figs. 4 and 5 have been plotted. In Fig. 4, the behavior of \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) and \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) for \(\Delta \chi _\mathrm{T} ^2 = 3.53, 6.25, 8.02\), have been compared. Also in Fig. 5, we have considered \(\chi _\mathrm{T} ^2 = \chi _\mathrm{SNe} ^2 + \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\) and \(\chi _\mathrm{T} ^2 = \chi _\mathrm{OHD} ^2 + \chi _\mathrm{CMB} ^2 + \chi _\mathrm{BAO} ^2\), for \(\Delta \chi _\mathrm{T} ^2 = 0.1, 0.2, 0.3\), to investigate the degeneracy. These two figures indicate that although individual OHD data surveying in cosmological investigations (in comparison with SNeIa, CMB, and BAO) is not so important it decreases the degeneracy between the free parameters.