Some new Wyman–Leibovitz–Adler type static relativistic charged anisotropic fluid spheres compatible to self-bound stellar modeling

Abstract

In this work some families of relativistic anisotropic charged fluid spheres have been obtained by solving the Einstein–Maxwell field equations with a preferred form of one of the metric potentials, and suitable forms of electric charge distribution and pressure anisotropy functions. The resulting equation of state (EOS) of the matter distribution has been obtained. Physical analysis shows that the relativistic stellar structure for the matter distribution considered in this work may reasonably model an electrically charged compact star whose energy density associated with the electric fields is on the same order of magnitude as the energy density of fluid matter itself (e.g., electrically charged bare strange stars). Furthermore these models permit a simple method of systematically fixing bounds on the maximum possible mass of cold compact electrically charged self-bound stars. It has been demonstrated, numerically, that the maximum compactness and mass increase in the presence of an electric field and anisotropic pressures. Based on the analytic models developed in this present work, the values of some relevant physical quantities have been calculated by assuming the estimated masses and radii of some well-known potential strange star candidates like PSR J1614-2230, PSR J1903+327, Vela X-1, and 4U 1820-30.

1 Introduction

The subject of modeling relativistic compact stellar objects through the analytical solutions of Einstein’s gravitational field equations has a long history and still the interest remains as one of the key issue to the present researchers. Since the work of Schwarzschild [1], Tolman [2] and Oppenheimer and Volkoff [3] the determination of maximum mass of very compact astrophysical objects has been a key issue in relativistic astrophysics. Such findings are important in astrophysics because analytical solutions enable the distribution of matter in the interior of stellar object, under extreme conditions, to be modeled in terms of simple algebraic relations.

The central energy density of compact stellar object could be of the order of $10^{15}$ g cm$^{-3}$, several times higher than the normal nuclear matter density, and due to the absence of reliable information as regards the behavior of matter at such ultra-high density insight into the structure can be obtained by reference to applicable analytic solutions to the equation of relativistic stellar structure [4]. The known analytic solutions of Einstein’s gravitational field equations fall into two classes. The first class that describes “normal” matter neutron stars for which the density vanishes at the surface where the pressure vanishes. The Tolman VII solution with vanishing surface energy density falls into this class and hence is a useful approximation to realistic neutron star models. The class that describes stars for which density is finite, about 2–3 times the normal nuclear matter saturation density [5], at the surface where the pressure vanishes includes Tolman IV solution and the solutions discussed in [6–21]. This type of solutions is a useful approximation to realistic models of “self-bound” strange quark star (strange star for short) [22]. The best-known example of self-bound stars results from the Bodmer–Witten hypothesis also known as the strange quark matter hypothesis asserts that strange quark matter is the ultimate ground state of matter. Still the fundamental significance of this hypothesis remains as a serious possibility in physics and astrophysics [23–27].

An important distinction between quark stars and conventional neutron stars is that the quark stars are self-bound by the strong interaction, gravity just make them massive, whereas neutron stars are bound by gravity. This allows a quark star to rotate faster than would be possible for a neutron star. A quark star can also be bare. The surfaces of a bare strange star and that of normal matter neutron star have striking differences. The very properties of the quark surface, e.g., strong bounding of particles, abrupt density change from $4\times 10^{14}$ g cm$^{-3}$ to $\sim$0 in $\sim$1 fm.

In a very recent past a polytropic quark star model has been suggested [28, 29] in order to establish a general framework in which theoretical quark star models could be tested by observations. The key difference between polytropic quark stars and the polytropic model studied previously for normal (i.e., non-quarkian) stars is that the quark star models with non-vanishing density at the stellar surface may not be avoidable due to the strong interaction between quarks which is relevant to the effect of color confinement. As discussed in [28] the polytropic equations of state are stiffer than the conventional realistic models (e.g., the MIT bag model) for quark matter, and pulsar-like stars calculated with a polytropic equation of state could then have high maximum masses $>$ $2M_\odot$. In this framework of a polytropic model a very low massive quark star can also exist and be still gravitationally stable even if the polytropic index $n>3$.

Apart from the constituents of these types of compact stars, the most fascinating distinction between a strange star and a normal neutron star is the surface electric fields associated with it. Bare strange stars possess ultra-strong electric fields on their surfaces, which, for ordinary strange matter, is around $10^{18}$ and $10^{20}$ V/cm for color superconducting strange matter [30–32]. The influence of energy densities of ultra-high electric fields on the bulk properties of compact stars was explored in [33–38]. It also has been shown that electric fields of this magnitude, generated by charge distributions located near the surfaces of strange quark stars, increase the stellar mass by up to 30 % depending on the strength of the electric field. In contrast to the strange star the surface electric field in the case of neutron star is absent [39]. These features may allow one to observationally distinguish quark stars from neutron stars.

In order to obtain a realistic charged stellar model one can start with an explicit EOS and suitable form of electric charge distribution and then integrating the equation of hydrostatic equilibrium, also known as the charged generalization of Tolman–Oppenheimer–Volkoff (TOV) equation [40], which may be obtained by requiring the conservation of mass-energy, as that determines the global structure of electrically charged stars. The integration starts at the center of the star with a prescribed central pressure and ends where the pressure decreases to zero, indicates the surface of the star. Some recent studies include [41–44]. Such input equations of state do not normally allow for closed-form solutions.

In the second approach one can have insight into such structures by solving the Einstein–Maxwell equations which represent an under-determined system of nonlinear ordinary differential equations of the second order. Due to the high nonlinearity it is difficult to obtain exact solutions to this system. For the special case of a static isotropic perfect fluid, the system of field equations can be reduced to a set of four coupled ordinary differential equations in five unknowns and arrive at exact solutions by making an ad hoc assumption for one of the metric functions or for the energy density. The EOS can then be extracted from the resulting metric. The first exact solutions of field equations, in this approach, known to have astrophysical significance, may have been discovered by Tolman [2]. Out of the different types of exact solutions obtained by Tolman, model V and VI are not considered physically viable, as they correspond to singular solutions (infinite values of the central density and pressure). Except these models, all the other solutions are known as regular solutions (finite and positive pressure and density at the origin). Models IV and VII are found physically viable in the study of compact astrophysical stellar objects. The numerous publications following Tolman’s approach include [29, 45–77]. As might be expected with Tolman’s method, unphysical pressure–density configurations are found more frequently than physical ones.

In recent years, however, several authors followed an alternative approach to present analytical stellar models of electrically neutral/charged compact strange stars within the framework of linear equation of state based on MIT bag model together with a particular choice of metric potentials/mass function [74, 78–85]. Some works also studied the viability of nonlinear EOS based on suitable geometry for the description in the interior 3-spaces of such compact star [11, 86]. This approach leads to physically viable and easily tractable models of superdense stars in equilibrium. Tikekar and Jotania [87, 88], Jotania and Tikekar [89] showed that the ansatz suggested by Tikekar and Thomas [90] has these features and the general three-parameter solution based on it also leads to physically plausible relativistic models of strange stars. Several aspects of physical relevance and the maximum mass of class of compact star models, based on Vaidya–Tikekar ansatz, for the both isotropic and anisotropic pressures have been investigated in [53, 91–93].

Out of the 127 known analytical solutions to Einstein’s equations, compiled in [94], only a few satisfy elementary tests of physical relevance and, hence, are viable in the description of relativistic compact stellar objects. For strange quark stars, the energy density does not vanish at the surface. Known applicable analytic solutions include [4, 5, 22]:

• the Schwarzschild interior solution or the incompressible fluid solution (constant density solution),

• the generalized Tolman IV solution,

• the Matese and Whitman I solution.

In contrast, as far the literature is concerned known to the present authors, the charged analogs of Tolman’s models (V–VI) obtained in [95–101] are not physically viable in the description of compact astrophysical objects as regards the infinite values of the central density and pressure. Though the Schwarzschild constant density solution is physically unrealistic, the charged analogs, obtained in [56, 102–104], and the charged analog of the Matese and Whitman solution, obtained in [105], may be relevant in the description of self-bound electrically charged strange quark stars. Charged analogs of the Tolman IV and VII models [106–108]), as the neutral ones, exhibit the physical features required for the construction of a physically realizable relativistic compact stellar structure. The charged analogs of the Vaidya–Tikekar models have been derived in [109, 110]. Astrophysical consequences of the charged analogs of the Vaidya–Tikekar solutions in modeling a electrically charged compact star have been discussed in [59, 111–114].

It was shown by Bonnor [115, 116] that a spherical body can remain in equilibrium under its own gravitation and electric repulsion if the matter present in the sphere carries a certain modest electric charge density. The problem of the stability of a homogeneous distribution of matter containing a net surface charge was considered by Stettner [117]. Stettner showed that a fluid sphere of uniform density with a modest surface charge is more stable than the same system without charge. The electric charge weakens gravity to the extent of turning it into a repulsive field, as happens in the vicinity of a Reissner–Nordström singularity. Thus the gravitational collapse of spherical matter distribution to a point singularity may be avoided if the matter acquires large amounts of electric charge during an accretion process onto a compact object. The gravitational attraction may then be balanced by electrostatic repulsion due to the same electric charge and by the pressure gradient [40, 118]. Hence the study of the gravitational behavior of compact charged stellar object has raised the possibility of modeling such compact astrophysical objects in terms of simple algebraic relations between the matter pressure and its energy density.

Of course, no astrophysical object is entirely composed of a perfect fluid. The theoretical investigations [119–126] of more realistic stellar models show that the nuclear matter may be locally anisotropic at least in certain very high density ranges $(\rho > 10^{15}$ g cm$^{-3})$, where the nuclear interactions in the stellar matter must be treated relativistically. According to these views, in such massive stellar objects the radial pressure may not be equal to the tangential pressure. Since the pioneering work of Bowers and Liang [127], there has been an extensive literature devoted to the study of anisotropic spherically symmetric static general relativistic configurations (see [75, 76, 79, 82, 97, 128–156] and the references therein).

The principal motivation of this work is to develop some new analytical relativistic stellar models by obtaining closed-form solutions of Einstein–Maxwell field equations following the approach of Durgapal [13], and of Maurya and Gupta [107, 157]. Our analysis depends on several mathematical key assumptions. First, we choose a particular functional form for one of the metric potentials. The form chosen ensures that the metric function is nonsingular, continuous, and well behaved in the interior of the star. On a physical basis this is one of the desirable features for any well-behaved model. Further, we assume particular forms of electric charge distribution and pressure anisotropy. The maximum allowable mass and corresponding values of physical quantities have been determined. The solutions obtained in this work are expected to provide simplified but mathematically easy to analyze charged stellar models with non-zero super-high surface density, which could reasonably model the stellar core of an electrically charged strange quark star by satisfying applicable physical boundary conditions.

The presentation of this work is as follows. The next section, Sect. 2, is devoted to the solution of the Einstein–Maxwell field equations of an anisotropic fluid and derives the pressure and density relation. In Sect. 3 we present the elementary criteria that have to be satisfied by the obtained solution so as to present a realistic stellar model. Section 4 develops the important ratios by matching the obtained metric components with the space-time exterior to the charged object which is described by the unique Reissner–Nordström metric. A physical analysis is presented of the obtained models in Sect. 5. It is demonstrated numerically that we have a maximum compactness, redshift, and mass increase in the presence of an electric field and anisotropic pressures; this is in agreement with some other work [158]. In Sect. 6 some explicit numerical models of relativistic anisotropic stars, of possible astrophysical relevance, are also presented and we also apply our model to some well-known potential strange star candidates to calculate some physical quantities by assuming the estimated masses and predicted radii. Finally, Sect. 7 discusses and concludes the work.

2 Interior solutions of Einstein–Maxwell field equations

2.1 Field equations

In this work we intend to study a static spherically symmetric matter distribution but whose stress tensor may be locally anisotropic and whose interior metric in Schwarzschild coordinates $x^\mu =\left( t,r,\theta ,\varphi \right)$ [2, 3] is given in the following form [127, 128, 131, 138, 149]¹:

$$\begin{aligned} \mathrm{d}s^2=e^{\nu (r)}\mathrm{d}t^2-e^{\lambda (r)}\mathrm{d}r^2-r^2\left( \mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\varphi ^2\right) .\nonumber \\ \end{aligned}$$

(2.1.1)

The functions $\nu$ and $\lambda$ satisfy the Einstein–Maxwell field equations,

$$\begin{aligned} G_\nu ^\mu =R_\nu ^\mu -\frac{1}{2}\delta _\nu ^\mu R=\kappa \left( T_\nu ^\mu +E_\nu ^\mu \right) \end{aligned}$$

(2.1.2)

where $\kappa =8\pi$ is Einstein’s constant. The matter within the star is assumed to be locally anisotropic fluid in nature and consequently $T_\nu ^\mu$ and $E_\nu ^\mu$ are the energy-momentum tensor of fluid distribution and electromagnetic field defined by [131, 159]

$$\begin{aligned} T_\nu ^\mu= & {} \left( P_t+\rho c^2\right) v^\mu v_\nu -P_t\delta ^\mu _\nu +(P_r-P_t)\chi ^\mu \chi _\nu ,\\ E_\nu ^\mu= & {} \frac{1}{4\pi }\left( -F^{\mu m} F_{\nu m}+\frac{1}{4}\delta _\nu ^\mu F^{m n} F_{m n}\right) \end{aligned}$$

where $\rho ,\,P_r,\,P_t,\, v^\mu$, denote the energy density, radial pressure, and tangential pressure of the fluid distribution respectively. $v^\mu$ and $F_{\mu \nu }$ denote the velocity vector and anti-symmetric electromagnetic field strength tensor, defined by

$$\begin{aligned} F_{\mu \nu }=\frac{\partial A_\nu }{\partial x^{\mu }}-\frac{\partial A_\mu }{\partial x^{\nu }}, \end{aligned}$$

(2.1.3)

which satisfies the Maxwell equations,

$$\begin{aligned} F^{\mu \nu }_{;\nu }=\frac{1}{\sqrt{-g}}\frac{\partial }{\partial x^\nu }\left( \sqrt{-g}F^{\mu \nu }\right)= & {} -4\pi j^\mu ,\end{aligned}$$

(2.1.4a)

$$\begin{aligned} F_{\mu \nu ;\lambda }+F_{\nu \lambda ;\mu }+F_{\lambda \mu ;\nu }= & {} 0 \end{aligned}$$

(2.1.4b)

where g is the determinant of quantities $g_{\mu \nu }$ in Eq. (2.1.1), defined by

$$\begin{aligned} g=\left| \begin{array}{cccc} e^\nu &{} 0 &{} 0 &{} 0 \\ 0 &{} -e^\lambda &{} 0 &{} 0 \\ 0 &{} 0 &{} -r^2 &{} 0 \\ 0 &{} 0 &{} 0 &{} -r^2\sin ^2\theta \\ \end{array}\right| =-e^{\nu +\lambda }r^4\sin ^2\theta \end{aligned}$$

and $A_\nu =(\varphi (r),0,0,0)$ is the four-potential and $j^\mu$ is the four-current vector, defined by

$$\begin{aligned} j^\mu =\frac{\rho _{\mathrm {ch}}}{\sqrt{g_{00}}}\frac{\text {d}x^\mu }{\text {d}x^0} \end{aligned}$$

where $\rho _{\mathrm {ch}}$ denotes the proper charge density.

For a static matter distribution the only non-zero component of the four-current is $j^0$. Because of spherical symmetry, the four-current component is only a function of the radial distance, r. The only non-vanishing components of the electromagnetic field tensor are $F^{01}$ and $F^{10}$, related by $F^{01}=-F^{10}$, which describe the radial component of the electric field. From Eq. (2.1.4a) one obtains the following expression for the electric field:

$$\begin{aligned} F^{01}=-e^{-\frac{\nu +\lambda }{2}}\frac{q(r)}{r^2} \end{aligned}$$

where q(r) represents the total charge contained within the sphere of radius r defined by

$$\begin{aligned} q(r)=4\pi \int _0^r{e^{\frac{\lambda }{2}}\rho _{\mathrm {ch}}u^2}\text {d}u. \end{aligned}$$

(2.1.5)

Equation (2.1.5) can be treated as the relativistic version of Gauss’ law.

For the metric (2.1.1), the Einstein–Maxwell field equations may be expressed as the following system of ordinary differential equations [131]:

$$\begin{aligned}&\frac{\nu ^{'}}{r}e^{-\lambda }-\frac{\left( 1-e^{-\lambda }\right) }{r^2} =\kappa P_r-\frac{q^2}{r^4},\end{aligned}$$

(2.1.6)

$$\begin{aligned}&\left( \frac{\nu ^{''}}{2}-\frac{\nu ^{'}\lambda ^{'}}{4}+\frac{\nu ^{'2}}{4}+\frac{\nu ^{'}- \lambda ^{'}}{2r}\right) e^{-\lambda } = \kappa P_t+\frac{q^2}{r^4},\end{aligned}$$

(2.1.7)

$$\begin{aligned}&\frac{\lambda '}{r}e^{-\lambda }+\frac{\left( 1-e^{-\lambda }\right) }{r^2} =\kappa \rho +\frac{q^2}{r^4} \end{aligned}$$

(2.1.8)

where a prime $\left( '\right)$ denotes the r-derivative.

In analogy to the electrically uncharged case, one usually introduces a quantity m(r) by the following expression:

$$\begin{aligned} e^{-\lambda }=1-\frac{2m(r)}{r}+\frac{q^2}{r^2}. \end{aligned}$$

(2.1.9)

If R represents the radius of the fluid distribution then it can be showed that m is constant $m(r=R)=M$ outside the fluid distribution where M is the gravitational mass. Thus the function m(r) represents the gravitational mass of the matter contained in a sphere of radius r. Using Eqs. (2.1.9) and (2.1.6)–(2.1.8), respectively, one can arrive at

$$\begin{aligned}&m(r)=\frac{\kappa }{2}\int \rho r^2 \text {d}r+\frac{q^2}{2r}+\frac{1}{2}\int \frac{q^2}{r^2}\text {d}r,\end{aligned}$$

(2.1.10)

$$\begin{aligned}&\nu '=\frac{\left( \kappa rP_r+\frac{2m}{r^2}-\frac{2q^2}{r^3}\right) }{\left( 1-\frac{2m}{r}+\frac{q^2}{r^2}\right) },\end{aligned}$$

(2.1.11)

$$\begin{aligned}&\frac{\text {d}P_r}{\text {d}r}=-\frac{(P_r+\rho )}{2}\nu '+\frac{q}{4\pi r^4}\frac{\text {d}q}{\text {d}r}+\frac{2(P_t-P_r)}{r}. \nonumber \\ \end{aligned}$$

(2.1.12)

Finally, combining (2.1.11) and (2.1.12), we get

$$\begin{aligned} \frac{\text {d}P_r}{\text {d}r}= & {} -\frac{(P_r+\rho )}{2}\frac{\left( \kappa rP_r+\frac{2m}{r^2}-\frac{2q^2}{r^3}\right) }{\left( 1-\frac{2m}{r}+\frac{q^2}{r^2}\right) }\nonumber \\&+\frac{q}{4\pi r^4}\frac{\text {d}q}{\text {d}r}+\frac{2(P_t-P_r)}{r}, \end{aligned}$$

(2.1.13)

which is the charged generalization of Tolman–Oppenheimer–Volkoff (TOV) equation of a hydrostatic equilibrium for the anisotropic stellar configuration [133]. In Eq. (2.1.13) the additional term, $2(P_t-P_r)/r$, represents the “force” which is due to the anisotropic nature of the fluid. This force is directed outward when $P_t>P_r$ and inward when $P_t<P_r$. The existence of a repulsive force (in the case $P_t>P_r$) allows for the construction of a more compact distribution when using an anisotropic fluid than when using an isotropic fluid.

Instead of solving Eq. (2.1.13), for any prescribed equation of state, we are rather interested in solving Eqs. (2.1.6)–(2.1.8) with the help of the following ansatz [12, 13]:

$$\begin{aligned} e^{\nu }=B_N\left( 1+Cr^2\right) ^N \end{aligned}$$

(2.1.14)

where N is a positive integer and $B_N,\, C>0$ are two constants to be determined by the appropriate physical boundary conditions. Subtracting (2.1.6) from (2.1.7) one obtains the equation of the “pressure anisotropy”,

$$\begin{aligned}&\left( \frac{\nu ^{''}}{2}-\frac{\nu ^{'}\lambda ^{'}}{4}+\frac{\nu ^{'2}}{4}-\frac{\nu ^{'}+\lambda ^{'}}{2r}\right) e^{-\lambda }+\frac{\left( 1-e^{-\lambda }\right) }{r^2}\nonumber \\&\quad =\kappa \Delta +\frac{2q^2}{r^4}. \end{aligned}$$

(2.1.15)

Equation (2.1.15) is a second order ordinary nonlinear differential equation in $\nu$ but first order linear in $\lambda$. An algorithm recently presented by Herrera et al. [149] shows that all static spherically symmetric anisotropic solutions of Einstein’s field equations may be generated from Eq. (2.1.15) by two generating functions $\kappa \Delta$ and $\nu$. In our case we have one additional generating function $2q^2/r^4$.

At this moment it is convenient to introduce the following transformations:

$$\begin{aligned} e^{-\lambda }=Z,\quad x=Cr^2, \end{aligned}$$

(2.1.16)

which transform Eq. (2.1.15) to the following form:

$$\begin{aligned} \frac{\text {d}Z}{\text {d}x}+P(x)Z=Q(x); \end{aligned}$$

(2.1.17)

see Eq. (2.1.17), which is just the charged generalization of Eq. (8) of [149] particularly when the transformations (2.1.16) are imposed. This yields the following solution [160]:

$$\begin{aligned} Z=e^{-\int {P(x)}\text {d}x}\left[ \int {e^{\int {P(x)}\text {d}x}}Q(x)\text {d}x+A_N\right] \end{aligned}$$

(2.1.18)

where

$$\begin{aligned} P(x)= & {} \frac{(N^2-2N-1)x^2-2x-1}{x(1+x)(1+(1+N)x)},\\ Q(x)= & {} \frac{(1+x)}{x(1+(1+N)x)}\left( \frac{2Cq^2}{x}+\Delta x-1\right) , \end{aligned}$$

and $A_N$ is the constant of integration, which may be determined by imposing appropriate physical boundary conditions. Once the metric potential Z is obtained, the other physical variables may be expressed in terms of the generating functions and the equation of state may be extracted, parametrically, from the following equations:

$$\begin{aligned} \frac{\kappa }{C}P_r= & {} \frac{[1+(2N+1)x]}{x(1+x)}Z-\frac{1}{x}+\frac{Cq^2}{x^2},\end{aligned}$$

(2.1.19)

$$\begin{aligned} \frac{\kappa }{C}P_t= & {} \frac{(2N+N^2x)}{(1+x)^2}Z+\frac{[1+(1+N)x]}{(1+x)}\frac{\text {d}Z}{\text {d}x}-\frac{Cq^2}{x^2} ,\nonumber \\\end{aligned}$$

(2.1.20)

$$\begin{aligned} \frac{\kappa }{C}\rho= & {} -2\frac{\text {d}Z}{\text {d}x}-\frac{Z}{x}+\frac{1}{x}-\frac{Cq^2}{x^2}. \end{aligned}$$

(2.1.21)

Table 1 Exact static spherically symmetric perfect fluid solutions of Einstein–Maxwell equations obtained by different charge distributions for isotropic pressure $(\Delta =0)$. The second column shows the models which may be rediscovered from the present model (2.2.1)

2.2 Models of electric charge distribution and pressure anisotropy

The “realistic” charge distribution inside the fluid sphere is not known [161], but it seems intuitively reasonable that due to electrical repulsion the charge distribution should be weighted toward the surface [42]. To model this one can imagine several plausible mathematical forms of $2Cq^2/x^2$, to integrate Eq. (2.1.18). Various authors presented a variety of solutions previously for different suitable choices of the charge distributions with isotropic pressure. Some of the solutions are compiled in Table 1 (also see [162]). In this work we consider the following forms of the electric charge distribution and the pressure anisotropy:

$$\begin{aligned}&\frac{2Cq^2}{x^2}= Kx^{n+1}(1+x)^{1-N} (1+mx)^p(1+(1+N)x)^{\frac{N-1}{N+1}}, \nonumber \\\end{aligned}$$

(2.2.1)

$$\begin{aligned}&\Delta = \delta x(1-2ax)(1+x)^{1-N}(1+(1+N)x)^{\frac{N-1}{N+1}} \nonumber \\ \end{aligned}$$

(2.2.2)

where $K,\,\delta \ge 0$, n is a nonnegative integer, and $m,\,p,\,a$ are any real numbers. It must be emphasized that these hypothetical models of electric charge distribution and pressure anisotropy are chosen, in terms of x, in such a way that these allow us to integrate Eq. (2.1.18) rather than for any particular physical reasons. Moreover, the electric field intensity and anisotropy vanish at the center and remain continuous and bounded in the interior of the star for a wide range of values of the parameters. Thus these choices may be physically reasonable and useful in the study of the gravitational behavior of anisotropic charged stellar objects.

Using Eqs. (2.2.1)–(2.2.2), we get

$$\begin{aligned} Z= & {} F_p(x)+\frac{\delta x^2(1-ax)}{(1+x)^{N-2}[1+(1+N)x]^{\frac{2}{1+N}}}+\frac{1}{(1+x)^{N-2}}\nonumber \\&-\frac{1}{2}G(N)\left( {\begin{array}{c}N-1\\ 2\end{array}}\right) \frac{x}{(1+x)^{N-2}}\nonumber \\&-H(N)\left[ \sum _{i=0}^{N-4}\sum _{j=0}^{i+1}\frac{(-1)^j}{(N+1)^{i+2}}\left( {\begin{array}{c}N-1\\ i+3\end{array}}\right) \left( {\begin{array}{c}i+1\\ j\end{array}}\right) \right. \nonumber \\&\left. \times \frac{x[1+(N+1)x]^{i-j+1}}{\left( i-j+\frac{N+3}{N+1}\right) (1+x)^{N-2}}\right] \nonumber \\&+A_N \frac{x}{(1+x)^{N-2} [1+(1+N)x]^{\frac{2}{1+N}}} \end{aligned}$$

(2.2.3)

where

$$\begin{aligned} F_p(x)=\left\{ \begin{array}{ll} \frac{K}{m^{n+1}}\sum _{i=0}^n\bigg [\frac{(-1)^i}{(n-i+p+1)}\left( {\begin{array}{c}n\\ i\end{array}}\right) \\ \times \frac{x(1+mx)^{n-i+p+1}}{(1+x)^{N-2} [1+(1+N)x]^{\frac{2}{1+N}}}\bigg ] &{} p\ne 0,\\ \frac{K}{n+1}\frac{x^{n+2}}{(1+x)^{N-2} [1+(1+N)x]^{\frac{2}{1+N}}} &{} p=0, \end{array} \right. \end{aligned}$$

$$\begin{aligned} G(N)=\left\{ \begin{array}{l@{\quad }l} 0 &{} N=1,\,2,\\ 1 &{} N\ge 3, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} H(N)=\left\{ \begin{array}{l@{\quad }l} 0 &{} N=1,\,2,\,3,\\ 1 &{} N\ge 4. \end{array} \right. \end{aligned}$$

2.3 Anisotropic charged stellar models

Ishak et al. [175], Lake [176], and recently Maurya and Gupta [107, 157] showed that the ansatz for the metric function (2.1.14) produces an infinite family of analytic solutions of the self-bound type. Five of these were previously known ($N=$ 1, 2, 3, 4, and 5). For example, $N=1$ corresponds to the Tolman IV model, and $N=2,\,3,\,4,\,5$ correspond to Adler [8],² Heintzmann [7],³ and Durgapal models,⁴ respectively. The most relevant case is for $N=2$, for which the speed of sound $\approx 1/\sqrt{3}$ throughout most of the star, similar to the behavior of strange quark matter [180]. The astrophysical significance and the adiabatic stability of the Wyman–Leibovitz–Adler solution $(N=2)$ in modeling neutron stars was first discussed in [181–183].

For $N=2$ the solution of the Einstein–Maxwell system (2.1.6)–(2.1.8), for the model charge distribution and pressure anisotropy considered in Eqs. (2.2.1)–(2.2.2), are then given by the following.

Case I: $p\ne -1$. $n=$ nonnegative integer,

$$\begin{aligned} e^{\nu }= & {} B_2(1+x)^2, \end{aligned}$$

(2.3.1)

$$\begin{aligned} e^{-\lambda }= & {} F_p(x)+\delta \frac{x^2 (1-ax)}{(1+3x)^{2/3}}+1\nonumber \\&+A_2\frac{x}{(1+3x)^{2/3}}, \end{aligned}$$

(2.3.2)

$$\begin{aligned} \frac{2Cq^2}{x^2}= & {} K\frac{x^{n+1}(1+mx)^p (1+3x)^{1/3}}{(1+x)}, \end{aligned}$$

(2.3.3)

$$\begin{aligned} \Delta= & {} \frac{\delta x(1-2ax)(1+3x)^{1/3}}{(1+x)}, \end{aligned}$$

(2.3.4)

$$\begin{aligned} \frac{\kappa }{C}P_r= & {} I_p(x)+\frac{K}{2}\frac{x^{n+1}(1+mx)^p(1+3x)^{1/3}}{(1+x)}\nonumber \\&+\delta \frac{x(1-ax)(1+5x)}{(1+3x)^{2/3}(1+x)}+\frac{4}{(1+x)}\nonumber \\&+A_2\frac{(1+5x)}{(1+3x)^{2/3}(1+x)}, \end{aligned}$$

(2.3.5)

$$\begin{aligned} \frac{\kappa }{C}P_t= & {} \frac{\kappa }{C}P_r+\Delta , \end{aligned}$$

(2.3.6)

$$\begin{aligned} \frac{\kappa }{C}\rho= & {} -J_p(x)-\frac{K}{2}\frac{x^{n+1}(1+mx)^p (1+3x)^{1/3}}{(1+x)}\nonumber \\&-\delta x\frac{(5+(11-7a)x-17ax^2)}{(1+3x)^{5/3}}\nonumber \\&-A_2\frac{(3+5x)}{(1+3x)^{5/3}}. \end{aligned}$$

(2.3.7)

Case II: $p = -1$. $n = 0$,

$$\begin{aligned} e^{\nu }= & {} B_2\left( 1+x\right) ^2, \end{aligned}$$

(2.3.8)

$$\begin{aligned} e^{-\lambda }= & {} \frac{K}{m}\frac{x\ln (1+x)}{(1+3x)^{2/3}}+\delta \frac{x^2 (1-ax)}{(1+3x)^{2/3}}+1\nonumber \\&+A_2\frac{x}{(1+3x)^{2/3}}, \end{aligned}$$

(2.3.9)

$$\begin{aligned} \Delta= & {} \frac{\delta x(1-2ax)(1+3x)^{1/3}}{(1+x)}, \end{aligned}$$

(2.3.10)

$$\begin{aligned} \frac{2Cq^2}{x^2}= & {} K\frac{x(1+3x)^{1/3}}{(1+x)(1+mx)}, \end{aligned}$$

(2.3.11)

$$\begin{aligned} \frac{\kappa }{C}P_r= & {} \frac{K}{m}\frac{\ln (1+mx)(1+5x)}{(1+3x)^{2/3}(1+x)}+\frac{K}{2}\frac{x(1+3x)^{1/3}}{(1+x)(1+mx)}\nonumber \\&+\delta \frac{x(1-ax)(1+5x)}{(1+3x)^{2/3}(1+x)}+\frac{4}{(1+x)}\nonumber \\&+A_2\frac{(1+5x)}{(1+3x)^{2/3}(1+x)}, \end{aligned}$$

(2.3.12)

$$\begin{aligned} \frac{\kappa }{C}P_t= & {} \frac{\kappa }{C}P_r+\Delta , \end{aligned}$$

(2.3.13)

$$\begin{aligned} \frac{\kappa }{C}\rho= & {} -\frac{K}{m}\frac{(3+5x)\ln (1+mx)}{(1+3x)^{\frac{5}{3}}}-\frac{2Kx}{(1+3x)^{\frac{2}{3}}(1+mx)}\nonumber \\&-\frac{K}{2}\frac{x(1+3x)^{1/3}}{(1+x)(1+mx)}\nonumber \\&-\delta x\frac{(5+(11-7a)x-17ax^2)}{(1+3x)^{5/3}}\nonumber \\&-A_2\frac{(3+5x)}{(1+3x)^{5/3}}. \end{aligned}$$

(2.3.14)

Case III: $p = -1$. $n=$ positive integer,

$$\begin{aligned} e^{\nu }= & {} B_2\left( 1+x\right) ^2, \end{aligned}$$

(2.3.15)

$$\begin{aligned} e^{-\lambda }= & {} \frac{K}{m^{n+1}}\sum _{i=0}^{n-1}\left[ \frac{(-1)^i}{(n-i)}\left( {\begin{array}{c}n\\ i\end{array}}\right) \frac{x(1+mx)^{(n-i)}}{(1+3x)^{2/3}}\right] \nonumber \\&+\frac{K}{m}(-1)^n\frac{x\ln (1+mx)}{(1+3x)^{1/3}}+\delta \frac{x^2 (1-ax)}{(1+3x)^{2/3}}\nonumber \\&+1+A_2\frac{x}{(1+3x)^{2/3}}, \end{aligned}$$

(2.3.16)

$$\begin{aligned} \frac{2Cq^2}{x^2}= & {} K\frac{x^{n+1}(1+3x)^{1/3}}{(1+x)(1+mx)}, \end{aligned}$$

(2.3.17)

$$\begin{aligned} \Delta= & {} \frac{\delta x(1-2ax)(1+3x)^{1/3}}{(1+x)}, \end{aligned}$$

(2.3.18)

$$\begin{aligned} \frac{\kappa }{C}P_r= & {} \frac{K}{m^{n+1}}\sum _{i=0}^{n-1}\left[ \frac{(-1)^i}{(n-i)}\left( {\begin{array}{c}n\\ i\end{array}}\right) \frac{(1+mx)^{(n-i)}(1+5x)}{(1+3x)^{2/3}(1+x)}\right] \nonumber \\&+\frac{(-1)^n K}{m^{n+1}}\frac{\ln (1+mx)(1+5x)}{(1+3x)^{2/3}(1+x)}\nonumber \\&+\frac{K}{2}\frac{x^{n+1}(1+3x)^{1/3}}{(1+x)(1+mx)}+\delta \frac{x(1-ax)(1+5x)}{(1+3x)^{2/3}(1+x)}\nonumber \\&+\frac{4}{(1+x)}+A_2\frac{(1+5x)}{(1+3x)^{2/3}(1+x)}, \end{aligned}$$

(2.3.19)

$$\begin{aligned} \frac{\kappa }{C}P_t= & {} \frac{\kappa }{C}P_r+\Delta , \end{aligned}$$

(2.3.20)

$$\begin{aligned} \frac{\kappa }{C}\rho= & {} -\frac{K}{m^{n+1}}\sum _{i=0}^{n-1}\frac{(-1)^i}{(n-i)}\left( {\begin{array}{c}n\\ i\end{array}}\right) (1+mx)^{(n-i-1)}\nonumber \\&\times \frac{\Pi _{m,n,-1,i}(x)}{(1+3x)^{5/3}}- \frac{(-1)^n K}{m^{n+1}}\frac{(3+5x)\ln (1+mx)}{(1+3x)^{5/3}}\nonumber \\&-\frac{(-1)^n K}{m^n}\frac{2x}{(1+mx)(1+3x)^{5/3}}\nonumber \\&-\frac{K}{2}\frac{x^{n+1}(1+3x)^{1/3}}{(1+mx)(1+x)}\nonumber \\&-\delta x\frac{(5+(11-7a)x-17ax^2)}{(1+3x)^{5/3}}-A_2\frac{(3+5x)}{(1+3x)^{5/3}} \end{aligned}$$

(2.3.21)

where

$$\begin{aligned} I_p(x)=\left\{ \begin{array}{l@{\quad }l} \frac{K}{m^{n+1}}\sum _{i=0}^n\bigg [\frac{(-1)^i}{(n-i+p+1)}\left( {\begin{array}{c}n\\ i\end{array}}\right) \\ \times \frac{(1+mx)^{n-i+p+1}(1+5x)}{(1+x)(1+3x)^{2/3}}\bigg ] &{} p\ne 0,\\ \frac{K}{n+1}\frac{x^{n+1}(1+5x)}{(1+x)(1+3x)^{2/3}} &{} p=0, \end{array} \right. \end{aligned}$$

$$\begin{aligned} J_p(x)=\left\{ \begin{array}{l@{\quad }l} \frac{K}{m^{n+1}}\sum _{i=0}^n\bigg [\frac{(-1)^i}{(n-i+p+1)}\left( {\begin{array}{c}n\\ i\end{array}}\right) \\ \times \frac{(1+mx)^{(n-i+p)}\Pi _{m,n,i,p}(x)}{(1+3x)^{5/3}}\bigg ]&{} p\ne 0,\\ \frac{K}{n+1}\frac{x^{n+1}[(2n+5)+(6n+11)x]}{(1+3x)^{5/3}} &{} p=0, \end{array} \right. \end{aligned}$$

$$\begin{aligned} \Pi _{m,n,p,i}(x)= & {} 3+(2mn-2mi+2mp+5m+5)x \\&+(6mn-6mi+6mp+11m)x^2. \end{aligned}$$

In the absence of an electric field $(K=0)$ and pressure anisotropy $(\delta =0)$ Eqs. (2.3.1)–(2.3.21) reduce to the Wyman IIa metric. Hence, the models presented by Eqs. (2.3.1)–(2.3.21) represent the anisotropic charged analogs of the Wyman–Leibovitz–Adler solution. Equations (2.3.5), (2.3.7), (2.3.12), (2.3.14), and (2.3.19), (2.3.21) constitute the equations of state of each case.

3 Elementary criteria for physical acceptability

Due to the high nonlinearity of the Einstein field equations (2.1.2) not many realistic physical solutions are known for the description of static spherically symmetric perfect fluid spheres. Out of 127 solutions only 16 were found to pass elementary tests of physical relevance [94]. A physically acceptable interior solution of the gravitational field equations must comply with certain (not necessarily mutually independent) physical conditions [137, 184–186].

• (a) Regularity conditions:

  • (i) The solution should be free from physical and geometric singularities, i.e., $e^{\nu }>0$ and $e^{\lambda }>0$ in the range $0\le r\le R$.

  • (ii) The radial and tangential pressures and density are nonnegative, $P_r,\,P_t,\,\rho \ge 0$.

  • (iii) Radial pressure $P_r$ should be zero at the boundary $r=R$, i.e., $P_r(r=R)=0$, the energy density and tangential pressure may follow $\rho (r=R)\ge 0$ and $P_t(r=R)\ge 0$.

• (b) Stability conditions:

  • (iv) In order to have an equilibrium configuration the matter must be stable against the collapse of local regions. This requires Le Chatelier’s principle, also known as the local or microscopic stability condition: the radial pressure $P_r$ must be a monotonically non-decreasing function of $\rho$ [129],

    $$\begin{aligned} dP_r/d\rho \ge 0. \end{aligned}$$

• (c) Causality condition:

  • (v) The condition $0\le \sqrt{dP_r/d\rho }\le 1$, $0\le \sqrt{dP_t/d\rho }\le 1$ be the condition that the speed of sound not exceeds that of light.

• (d) Energy conditions:

  • (vi) A physically reasonable energy-momentum tensor has to obey either the

    • strong energy condition (SEC), $\rho -P_r-2P_t\ge 0,\,\rho -P_r\ge 0,\,\rho -P_t\ge 0$ or the

    • dominant energy condition (DEC), $\rho \ge P_r$ and $\rho \ge P_t$.

• (e) Monotone decrease of physical parameters:

  • (vii) Pressure and density, should maximum at the center and monotonically decreasing toward the pressure free interface (i.e., boundary of the fluid sphere). Mathematically,

    $$\begin{aligned} \frac{\text {d}P_r}{\text {d}r}<0,\quad \frac{\text {d}\rho }{\text {d}r}<0,\quad 0<r\le R. \end{aligned}$$

  • (viii) Additionally, the radial velocity of sound may be monotonically decreasing toward the surface. In this context, it is worth mentioning that for different equations of state at ultra-high densities available in the literature [120, 121, 187] it is found that the speed of sound is decreasing outwards from the center of the fluid sphere, i.e.,

    $$\begin{aligned} \frac{\text {d}}{\text {d}r}\left( \frac{\text {d}P_r}{\text {d}\rho }\right) <0 \end{aligned}$$

    for $0\le r\le R$.

  • (ix) The ratio of pressure to density, $P_r/\rho$ and $P_t/\rho$, should be monotonically decreasing with the increase of r, i.e.,

    $$\begin{aligned} \frac{\text {d}}{\text {d}r}\left( \frac{P_r}{\rho }\right) _{r=0}= & {} 0,\quad \frac{\text {d}}{\text {d}r}\left( \frac{P_r}{\rho }\right) _{r=0}<0, \\ \frac{\text {d}}{\text {d}r}\left( \frac{P_t}{\rho }\right) _{r=0}= & {} 0,\quad \frac{\text {d}}{\text {d}r}\left( \frac{P_t}{\rho }\right) _{r=0}<0. \end{aligned}$$

• (f) Matching condition:

  • (x) The interior solution should match continuously with an exterior Reissner–Nordström solution,

    $$\begin{aligned} \text {d}s^2= & {} \left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}\right) \text {d}t^2 -\left( 1-\frac{2M}{r}+\frac{Q^2}{r^2}\right) ^{-1} \\&\times \text {d}r^2-r^2\left( \text {d}\theta ^2+\sin ^2\theta \mathrm{d}\varphi ^2\right) , r\ge R. \end{aligned}$$

    This requires the continuity of $e^{\nu },\, e^{\lambda }$ and q across the boundary $r=R$,

    $$\begin{aligned} e^{\nu (R)}=e^{{-\lambda (R)}}=\left( 1-\frac{2M}{R}+\frac{Q^2}{R^2}\right) \end{aligned}$$

    and $q(R)=Q$, where M and Q represent the total mass and charge inside the fluid sphere, respectively.

  • (g) Charge distribution:

    • (xi) The electric field intensity E, such that $E(0)=0$, is taken to be monotonically increasing, i.e., $\mathrm{d}E/\mathrm{d}r>0$ for $0<r\le R$.

  • (g) Pressure anisotropy:

    • (xii) The pressure anisotropy vanishes at the center, i.e., $\Delta (0)=0$ [127, 188].

  • (h) Allowable mass-to-radius ratio:

    • (xiii) Buchdahl [189] obtained an absolute constraint of the maximally allowable mass-to-radius ratio (M / R) for isotropic fluid spheres of the form $2M/R\le 8/9$ (in the units $c = G = 1$), which states that for a given radius a static isotropic fluid sphere cannot be arbitrarily massive. Böhmer and Harko [190] proved that for a compact object with charge, $Q(<$ $M)$, there is a lower bound for the mass–radius ratio,

      $$\begin{aligned} \frac{3Q^2}{2R^2}\frac{\left( 1+\frac{Q^2}{18R^2}\right) }{\left( 1+\frac{Q^2}{12R^2}\right) }\le \frac{2M}{R}. \end{aligned}$$

      The upper bound of the mass of charged sphere was generalized by Andréasson [191] and one proved that

      $$\begin{aligned} \sqrt{M}\le \frac{\sqrt{R}}{3}+\sqrt{\frac{R}{9}+\frac{Q^2}{3R}}. \end{aligned}$$

4 Physical boundary conditions

4.1 Determination of the arbitrary constant $A_2$

The boundary condition $P_r(R)=0$ can be utilized to specify $A_2$. For Case I:

$$\begin{aligned} A_2= & {} -\frac{I_p(X)(1+3X)^{\frac{2}{3}}(1+X)}{(1+5X)}\\&-\frac{K}{2}\frac{X^{n+1}(1+mX)^p (1+3X)}{(1+5X)}\\&-\delta X(1-aX)-4\frac{(1+3X)^{2/3}}{(1+5X)} \end{aligned}$$

where $X=CR^2$.

4.2 Total charge to radius ratio Q / R

Using $X=CR^2$ in Eq. (2.2.1) we obtain the square of the ratio Q / R,

$$\begin{aligned} \frac{Q^2}{R^2}=\frac{K}{2}\frac{X^{n+2} (1+mX)^p (1+3X)^{1/3}}{(1+X)}. \end{aligned}$$

(4.2.1)

4.3 Total mass-to-radius ratio M / R

By matching the metric coefficients obtained in (2.3.1)–(2.3.2) with the exterior Reissner–Nordström metric at the boundary and with reference to Eq. (4.2.1) one can establish the equation of compactness,

$$\begin{aligned} \frac{2M}{R}=\left( 1-e^{-\lambda (X)}+\frac{Q^2}{R^2}\right) . \end{aligned}$$

(4.3.1)

4.4 Total charge-to-mass ratio Q / M

By Eqs. (4.2.1) and (4.3.1) we obtain the charge-to-mass ratio Q / M,

$$\begin{aligned} \frac{Q}{M}=\frac{2\sqrt{\frac{K}{2}\frac{X^{n+2} (1+mX)^p (1+3X)^{1/3}}{(1+X)}}}{\left( 1-e^{-\lambda (X)}+\frac{Q^2}{R^2}\right) }. \end{aligned}$$

(4.4.1)

4.5 Determination of the constant $B_2$

The constant $B_2$ can be specified by the boundary condition $e^{\nu (R)}=e^{-\lambda (R)}$, which gives

$$\begin{aligned} B_2=(1+X)^{-2}e^{-\lambda (X)}. \end{aligned}$$

(4.5.1)

4.6 Surface redshift

The surface redshift of the charged fluid sphere is given by

$$\begin{aligned} z_s=\sqrt{e^{-\nu (R)}}-1=\frac{(1+X)^{-1}}{\sqrt{B_2}}-1. \end{aligned}$$

5 Construction of physically realistic fluid spheres

5.1 Pressure and density gradients

Differentiating the pressure and density equations (2.3.5)–(2.3.7) with respect to the auxiliary variable x one obtains the pressure and density gradients, respectively, for the model EOS. At this moment the commercial computer algebra system (CAS)⁵ would be useful.

Case I: $p\ne -1,\,n=$ nonnegative integer,

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}P_r}{\text {d}x}= & {} \frac{\text {d}I_p(x)}{\text {d}x}+\frac{K}{2}x^n(1+mx)^{p-1}\frac{\Phi _{m,n,p}(x)}{(1+3x)^{2/3}(1+x)^2}\nonumber \\&+\delta \frac{\Psi _1(x)}{(1+x)^2(1+3x)^{5/3}}-\frac{4}{(1+x)^2}\nonumber \\&+2A_2\frac{(1-5x^2 )}{(1+3x)^{5/3}(1+x)^2}, \end{aligned}$$

(5.1.1)

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}P_t}{\text {d}x}= & {} \frac{\kappa }{C}\frac{\text {d}P_r}{\text {d}x}+\frac{\text {d}\Delta }{\text {d}x}, \end{aligned}$$

(5.1.2)

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}\rho }{\text {d}x}= & {} -\frac{\text {d}J_p(x)}{\text {d}x}-\frac{K}{2}(1+mx)^{p-1}\frac{\Phi _{m,n,p}(x)}{(1+3x)^{2/3}(1+x)^2}\nonumber \\&-\delta \frac{\Psi _2(x)}{(1+3x)^{8/3}}+10A_2\frac{(1+x)}{(1+3x)^{8/3}} \end{aligned}$$

(5.1.3)

where

$$\begin{aligned} \frac{\text {d}I_p(x)}{\text {d}x}=\left\{ \begin{array}{l@{\quad }l} \frac{K}{m^{n+1}}\sum _{i=0}^n\bigg [\frac{(-1)^i}{(n-i+p+1)}\left( {\begin{array}{c}n\\ i\end{array}}\right) \\ \times \frac{(1+mx)^{n-i+p}\Sigma _{m,n,p,i}(x)}{(1+3x)^{5/3}(1+x)^2}\bigg ] &{} p\ne 0,\\ \frac{K}{n+1}\frac{x^{n}\Xi _n(x)}{(1+x)^2(1+3x)^{5/3}} &{} p=0, \end{array} \right. \end{aligned}$$

$$\begin{aligned} \frac{\text {d}J_p(x)}{\text {d}x}=\left\{ \begin{array}{l@{\quad }l} \frac{K}{m^{n+1}}\sum _{i=0}^n\frac{(-1)^i}{(n-i+p+1)}\left( {\begin{array}{c}n\\ i\end{array}}\right) \\ \times \frac{(1+mx)^{n-i+p-1}~\Theta _{m,n,p,i}(x)}{(1+3x)^{8/3}} &{} p\ne 0,\\ \frac{K}{(n+1)}\frac{x^n\Upsilon _n(x)}{(1+3x)^{8/3}} &{} p=0, \end{array} \right. \end{aligned}$$

$$\begin{aligned} \Sigma _{m,n,p,i}(x)= & {} (mn+mp-mi+m+2)\\&+(9mn+9mp+11m-9im)x\\&+(23mn+23mp-23im+23m+10)x^2\\&+(15mn+15mp-15im+5m)x^3,\\ \Phi _{m,n,p}(x)= & {} (n+1)+(mn+mp+m+4n+4)x\\&+(4mn+4mp+4m+3n+1)x^2\\&+(3mn+3mp+m)x^3,\\ \Theta _{m,n,p,i}(x)= & {} (5mn-5im+5mp+5m-10)\\&+(2i^2m^2-4im^2n-4im^2p+2m^2n^2\\&+4m^2np+2m^2p^2-7im^2+7m^2n+7m^2p\\&-22im+5m^2+22mn+22mp+2m\\&-10)x+(12i^2m^2-24im^2n-24im^2p\\&+12m^2n^2+24m^2np+12m^2p^2-34im^2\\&+34m^2n+34m^2p-21im+12m^2+21mn\\&+21mp+m)x^2+(18i^2m^2-36im^2n\\&-36im^2p+18m^2n^2+36m^2np+18m^2p^2\\&-39im^2+39m^2n+39m^2p+11m^2)x^3,\\ \Psi _1(x)= & {} 1+(11-2a)x+(23-20a)x^2\\&+(5-46a)x^3-20ax^4,\\ \Psi _2(x)= & {} 5+(12-14a)x+(11-58a)x^2-68ax^3,\\ \frac{\text {d}\Delta }{\text {d}x}= & {} \delta \frac{(1+(4-4a)x+(1-16a)x^2-8ax^3)}{(1+x)^2(1+3x)^{2/3}},\\ \Xi _n(x)= & {} (n+1)+(9n+11)x+(23n+23)x^2\nonumber \\&+(15n+5)x^3,\\ \Upsilon _n(x)= & {} (2n^2+7n+5)+(12n^2+34n+12)x\nonumber \\&+(18n^2+39n+11)x^2. \end{aligned}$$

The pressure and density gradients for Case II and Case III are reported in Appendix A. See Eqs. (A.1)–(A.3) and (A.4)–(A.6).

5.2 Relativistic adiabatic index and stability

The stability of a fluid sphere, i.e., whether it is Newtonian or relativistic, isotropic or anisotropic, is related to the adiabatic index $\Gamma$ (the ratio of two specific heats). It is well known that the collapsing condition for a Newtonian isotropic sphere is $\Gamma <4/3$ [195]. For an anisotropic general relativistic sphere the adiabatic index is defined by

$$\begin{aligned} \Gamma =\frac{\rho +P_r}{P_r}\frac{\text {d}P_r}{\text {d}\rho }, \end{aligned}$$

(5.2.1)

and the collapsing condition then becomes [196, 197]

$$\begin{aligned} \Gamma <\frac{4}{3}+\left[ \frac{4}{3}\frac{(P_{t0}-P_{r0})}{|P_{r0}^\prime |r}+\frac{1}{2}\kappa \frac{\rho _0P_{r0}}{|P_{r0}^\prime |}r\right] _{\text {max}}, \end{aligned}$$

(5.2.2)

where $P_{r0}$, $P_{t0}$, and $\rho _0$ are the initial radial, tangential, and energy density in static equilibrium satisfying Eq. (2.1.13). The first and last term inside the square brackets, the anisotropic and relativistic corrections, respectively. It is to be noted that the positive anisotropy, $P_t-P_r>0$, increases the unstable range of $\Gamma$ [197, 198].

To study the stability of anisotropic stars under the radial perturbations, Herrera [199] (also see [200]) introduced the concept of “cracking”, breaking of self-gravitating spheres, which results from the appearance of total radial forces of different signs in different regions of the sphere once the equilibrium is perturbed. The occurrence of such a “cracking” may be induced by the local anisotropy of the fluid.

By this concept of cracking Abreu et al. [186] proved that the region of the anisotropic fluid sphere where $-1\le v_{st}^{2}-v_{sr}^{2}\le 0$ is potentially stable, but the region where $0<v_{st}^{2}-v_{sr}^{2}\le 1$ is potentially unstable.

The radial and tangential speeds of sound of the anisotropic sphere developed so far may be obtained from Eqs. (5.1.1)–(5.1.3),

$$\begin{aligned} v_{sr}^{2}= & {} \frac{\text {d}P_r}{\text {d}\rho },\end{aligned}$$

(5.2.3)

$$\begin{aligned} v_{st}^{2}= & {} \frac{\text {d}P_t}{\text {d}\rho }=\frac{\text {d}P_r}{\text {d}\rho }+\frac{\text {d}\Delta }{\text {d}\rho }. \end{aligned}$$

(5.2.4)

To satisfy $-1\le v_{st}^{2}-v_{sr}^{2}\le 0$ throughout the fluid distribution we require $\text {d}\Delta /\text {d}\rho \le 0$. As we have $\text {d}\rho /\text {d}x<0$, we further require that $\text {d}\Delta /\text {d}x\ge 0$, which will be satisfied as long as $\Delta$ is an increasing function of x.

5.3 Specifying the maximum mass and radius

A fluid sphere satisfying conditions (a) and (e) of Sect. 3 will be termed well behaved. For a particular set $(m,n,p,a,\delta )$ the values of $K,\,X$ have been plugged into Eqs. (2.3.5)–(2.3.7) and (5.1.1)–(5.1.3) for which the fluid distribution satisfies the elementary criteria for physical acceptability. Once the compactness M / R and the ratio Q / R of the compact fluid sphere are obtained, the maximum mass can be calculated by using one of the following quantities: (1) radius, (2) central density, (3) surface density, (4) central pressure, or (5) total charge as parameter. In this subsection we describe how to calculate the values of various physical variables. For Case I this can be accomplished by in following way.

5.3.1 For a given radius

• (a) Total mass:

  $$\begin{aligned} M=\frac{R}{2}\left( 1-e^{-\lambda (X)}+\frac{Q^2}{R^2}\right) \end{aligned}$$

  (5.3.1.1)

  where the mass M is in the unit of km.⁶

• (b) Total charge:

  $$\begin{aligned} Q=R\sqrt{\frac{K}{2}\frac{X^2(1+mX)^p(1+3X)^{1/3}}{(1+X)}} \end{aligned}$$

  (5.3.1.2)

  where the charge Q is in the unit of radius.⁷

• (c) Central density:

  $$\begin{aligned} \rho _c=\frac{3X}{\kappa R^2}\left[ \frac{-K}{m(p+1)}-A_2\right] . \end{aligned}$$

  (5.3.1.3)

• (d) Surface density:

  $$\begin{aligned} \rho _s=\frac{X}{\kappa R^2}\Omega (X) \end{aligned}$$

  (5.3.1.4)

  where

  $$\begin{aligned} \Omega (X)= & {} J_p(X)+\frac{K}{2}\frac{X^{n+1}(1+mX)^p (1+3X)^{\frac{1}{3}}}{(1+X)}\\&+\delta X\frac{(5+(11-7a)X-17aX^2)}{(1+3X)^{5/3}}\\&+A_2\frac{(3+5X)}{(1+3X)^{5/3}}. \end{aligned}$$

5.3.2 For a given surface density

$$\begin{aligned} R^2=\frac{X}{\kappa \rho _s}\Omega (X). \end{aligned}$$

(5.3.2.1)

The total mass, total charge, and the central density can be calculated by Eqs. (5.3.1.1)–(5.3.1.3).

5.3.3 For a given central density

The radius of the charged fluid sphere for a prescribed central density can be calculated by the following equation:

$$\begin{aligned} R^2=\frac{3X}{\kappa \rho _c}\left[ \frac{-K}{m(p+1)}-A_2\right] \end{aligned}$$

(5.3.3.1)

where the central energy density $\rho _c$ is given in kg m$^{-3}$ and the radius in m. The total mass, total charge, and the surface density then can be calculated by Eqs. (5.3.1.1), (5.3.1.2), and (5.3.1.4), respectively.

5.3.4 For a given central pressure

The radius of the charged fluid sphere for a prescribed central pressure can be calculated by the following equation:

$$\begin{aligned} R^2=\frac{X}{\kappa P_c}\left[ \frac{K}{m(p+1)}+4+A_2\right] \end{aligned}$$

(5.3.4.1)

where the central pressure $P_c$ is given in N m$^{-2}$.⁸ The total mass, total charge, and the central and surface densities then can be calculated by Eqs. (5.3.1.1)–(5.3.1.4).

5.3.5 For a given electric charge

The radius of the charged fluid sphere for a prescribed total charge can be calculated by

$$\begin{aligned} R=Q/\sqrt{\frac{K}{2}\frac{X^2(1+mX)^p (1+3X)^{1/3}}{(1+X)}} \end{aligned}$$

(5.3.5.1)

where the charge Q is given in km. Then the total mass, total charge, and the central and surface densities can be calculated by Eqs. (5.3.1.1)–(5.3.1.4).

5.4 Physical analysis of the models

For each choice of constant parameters $(K,\,m,\,n,\,p,\,\delta ,\,a)$, the maximum mass of the charged star depends on the corresponding set of maximum values of $X=X_{\mathrm {max}}$ up to which the pressure and density and their gradients satisfy $P_r\ge 0$, $P_t\ge 0$, $\rho \ge 0$, $\text {d}P_r/\text {d}x<0$, $\text {d}\rho /\text {d}x<0$, and the speeds of sound satisfy $0\le \sqrt{\text {d}P_r/\text {d}\rho }\le 1$, $0\le \sqrt{\text {d}P_t/\text {d}\rho }\le 1$ and may be monotonically decreasing with increasing x from center to the boundary.

• Case Ia: Isotropic pressure

  The maximum limit of compactness parameter (2M / R) obtained by Adler [8] set by the causality condition v) for the neutral isotropic fluid sphere is about 0.7. But the neutral model fails to satisfy condition viii). To generate an isotropic charged fluid sphere we set $(m,\,n,\,p,\,\delta ,\,a)=(10^4,\,0,\,0.23,\,0,\,0)$ and $K=0.08$. For this choice the range of values $0<X\le 0.71$ is obtained over which the fluid distribution satisfies the elementary criteria mentioned in Sect. 3. With the decrease of K, X increases. The maximum value of compactness parameter is obtained $(2M/R)_{\mathrm {max}}=0.8066$, using (4.3.1), at $K=0.08,\,X_{\mathrm {max}}=0.71$. Corresponding to $(K,\,X_{\mathrm {max}})$ the total charge-to-radius ratio, and the total charge-to-total mass ratio are found to be $Q/R=0.3641$ and $Q/M=0.9029$ using Eq. (4.2.1). For the particular choice of the stellar surface density $\rho _s = 4.68\times 10^{14}$ g cm$^{-3}$,⁹ as the parameter, the total mass and other physical quantities are calculated by the use of Eqs. (5.3.1.1)–(5.3.1.4) and we found $M_{\mathrm {max}}=2.9057M_\odot$, $R=10.63$ km, $P_c=4.88\times 10^{35}$ dyne cm$^{-2}$, $\rho _c=2.41\times 10^{15}$ g cm$^{-3}$, $Q=4.49\times 10^{20}\,C$, and $z_s=0.7514$. The behaviors of the radial and tangential pressures inside the sphere are presented in Figs. 3 and 4. The figures show that the radial and tangential pressures are nonnegative and monotonically decreasing in nature throughout the fluid distributions. The behavior of the energy density is presented in Fig. 5, which also shows that the energy density is positive and monotonically decreasing inside the fluid distributions. The pressure–density profile for the sphere is plotted, parametrically, in Fig. 6. The pressure and energy density gradients are found to be strictly negative throughout the distribution. The adiabatic speed of sound is found to be less than the speed of light, in the unit $c=1$, and monotonically decreasing in nature.

• Case Ib: Anisotropic pressure

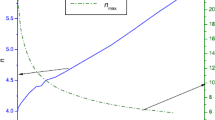
  The mass–radius relation for a sequence of anisotropic charged fluid spheres generated with a particular set of input parameters $m=10^4$, $n=0$, $p=0.23$, $\delta =0.21$, $a=0.75$, $K=0.228$, and $0<X\le 0.65$ with surface density $\rho _s=4.68\times 10^{14}$ g cm$^{-3}$ is in Fig. 1. The behavior of Fig. 1 reproduces that of other quark star models [38]. But a maximum value of $X=X_{\mathrm {max}}$ is found of 0.319 up to which the fluid distribution satisfies the conditions $\text {d}P_t/\text {d}x<0$ and $P_r\ge 0$. Hence, the maximum value of compactness parameter is obtained $(2M/R)_{\mathrm {max}}=0.5978$, at $X_{\mathrm {max}}=0.319$. The charge–radius ratio, and charge–mass ratio are also found to be $Q/R=0.2652$ and $Q/M=0.8874$. The maximum mass is found $M_{\mathrm {max}}=2.1274M_\odot$, with radius $R=10.49$ km, central pressure is $P_c=1.37\times 10^{35}$ dyne cm$^{-2}$, the central energy density is $\rho _c=1.40\times 10^{15}$ g cm$^{-3}$, and the total charge is $Q=3.23\times 10^{20}\,C$, and $z_s=0.4547$. The behavior of pressure anisotropy is demonstrated in Fig. 2. For this particular choice of constant parameters $\Delta$ is found to be maximum at $X=0.319$. The behaviors of radial pressure, tangential pressure, and the energy density inside the sphere are presented in Figs. 3, 4 and 5. The figures show that these matter variables are nonnegative and monotonically decreasing throughout the fluid distributions. The pressure–density profile for this sphere is plotted in Fig. 6. The pressure and energy density gradients are presented in Figs. 7 and 8. From the figure it is clear that the gradients remain strictly negative throughout the distribution. The adiabatic speeds of sound $v_{sr}$ and $v_{st}$ are shown in Fig. 9 from which it is found that the speeds are monotonically decreasing in nature. Figure 10 shows that the condition $-1<v_{st}^2-v_{sr}^2\le 0$ is satisfied throughout the fluid configuration and hence the fluid sphere generated by the particular choice of parameters may be considered potentially stable. The relativistic adiabatic index and the strong energy condition are presented in Figs. 11 and 12. In Tables 2 and 3 we report some values of adjustable parameters and the maximum value of $X=X_{\mathrm {max}}$ up to which the fluid sphere satisfies the elementary criteria stated in Sect. 3, together with $-1<v_{st}^2-v_{sr}^2\le 0$.

  Fig. 1

  

  Mass–radius relation for a sequence of anisotropic charged fluid spheres. The spheres are generated with the input $(m,\,n,\,p,\,\delta ,\,a,\,K)=(10^4,\,0,\,0.23,\,0.21,\,0.75,\,0.228)$, $0<X\le 0.65$ with surface density $\rho _s=4.69\times 10^{14}$ g cm$^{-3}$. The mass has a peak (cross) at $X=0.539$, which corresponds to the point with coordinates (9.16 km, $2.6271M_\odot$) but it is $X=X_{\mathrm {max}}=0.319$ (the solid circle), up to which the sphere satisfies $P_r\ge 0$ and $\mathrm{d}P_t/\mathrm{d}x<0$, which corresponds to (10.49 km, $2.1274M_\odot$)

  Fig. 2

  

  Behavior of pressure anisotropy $\Delta$ for the same charged fluid sphere generated with $(10^4,\,0,\,0.23,\,0.21,\,0.75,\,0.228)$, $X=0.319$

  Fig. 3

  

  Behavior of the radial pressures, $P_r$, in the unit of MeV fm$^{-3}$. The solid (blue) line corresponds to the sphere generated with $(10^4,0,0.23,0,0,0.080)$, $X=0.71$ and the dash-dotted (red) line corresponds to the sphere generated with $(10^4,\,0,\,0.23,\,0.21,\,0.75,\,0.228)$, $X=0.319$

  Fig. 4

  

  Behavior of the tangential pressure, $P_t$, in the unit of MeV fm$^{-3}$. The sphere generated with sphere generated with $(10^4,\,0,\,0.23,\,0.21,\,0.75,\,0.228)$, $X=0.319$

  Fig. 5

  

  Behavior of energy density $\rho$ (MeV fm$^{-3}$) for the same fluid spheres as in Fig. 3

  Fig. 6

  

  Pressure-density profiles, $P_r(\rho )$, for the same fluid spheres as in Fig. 3

  Fig. 7

  

  Behavior of pressure gradients for the same fluid sphere as in Fig. 4. The solid (blue) line corresponds to radial pressure gradient $\kappa \mathrm{d}P_r/C\mathrm{d}x$ and the dash-dotted (red) line corresponds to the tangential pressure gradient $\kappa \mathrm{d}P_t/C\mathrm{d}x$

  Fig. 8

  

  Behavior of energy density gradient $\kappa \text {d}\rho /C\text {d}x$ for the same charged fluid sphere as in Fig. 4

  Fig. 9

  

  Speeds of adiabatic sound for the same fluid sphere as in Fig. 4. The solid (blue) line corresponds to $v_{sr}=\sqrt{\text {d}P_r/\text {d}\rho }$ and the dash-dotted (red) line corresponds to $v_{st}=\sqrt{\text {d}P_t/\text {d}\rho }$

  Fig. 10

  

  The difference $v_{st}^2-v_{sr}^2$. The solid (blue) line corresponds to the same anisotropic charged fluid sphere as in Fig. 4 and the dash-dotted (red) line corresponds to the anisotropic sphere generated by the Case II with the input $(2,\,0,\,-1,\,0.1,\,0.5,\,0.080)$, $X=0.457$

  Fig. 11

  

  Relativistic adiabatic index $\Gamma$ for the same charged fluid sphere as in Fig. 4

  Fig. 12

  

  Strong energy condition for the same charged fluid sphere as in Fig. 4

Through a numerical and a graphical analysis we have demonstrated that the models obtained in Sect. 2.3 satisfy the physical requirements for a wide range of values of $m,\,n,\,p,\,\delta ,\,a$, and K, giving us a possibility for different charge variations and anisotropy within the fluid spheres. The resulting spheres can be utilized to construct physically reasonable compact self-bound charged stellar model such as a charged strange quark star.

Table 2 Some values of parameters $(K,X_{\mathrm {max}})$ for which a well-behaved charge fluid sphere can be generated

Table 3 Maximum mass and the various physical variables of charged fluid spheres for a given surface density

6 An application of the model for some well-known strange star candidates

The analysis of very compact astrophysical objects has been a key issue in relativistic astrophysics for the last few decades. Recent observations show that the estimated mass and radius of several compact objects such as X-ray pulsar Her X-1, X-ray burster 4U 1820-30, millisecond pulsar SAX J 1808.4-3658, X-ray sources 4U 1728-34, PSR 0943+10, and RX J185635-3754 are not compatible with the standard neutron star models [202, 203]. For a recent review on this the readers are referred to [24].

Based on the analytic model developed so far, to get an estimate of the range of various physical parameters of some potential strange star candidates we have calculated the values of the relevant physical quantities, such as the central/surface pressure and density, by using the refined mass and predicted radius of 12 pulsars recently reported in [204]. The values are reported in Table 4.

Table 4 Physical values of energy density and pressure for different strange stars calculated by Case I with $m=10^4,\,n=0$

7 Concluding remarks

In this work we have studied some particular simple families of relativistic charged stellar models obtained by solving Einstein–Maxwell field equations for a static spherically symmetric locally anisotropic fluid distribution. We based our work on three ad hoc assumptions: (1) one of the metric potential, (2) the electric charge distribution, (3) and the pressure anisotropy, the analytical equation of state has been computed from the resulting metric. These families of analytical relativistic stellar models may be considered as anisotropic charged analogs of the Wyman–Leibovitz–Adler solution.

We have shown that the maximum limit of compactness $(2M/R)=0.7$ [8] for the neutral isotropic fluid sphere, by the causality condition, may be changed significantly by the insertion of charge $(K\ne 0)$ without anisotropy $(\delta =0)$. We have also observed that both the isotropic and the anisotropic neutral models fail but charged models exhibit the monotonically decreasing adiabatic sound speeds.

A wide range of values of constant parameters are allowed to specify the maximum mass of charged fluid spheres. At this point we want to make some remark on the particular choice of stellar surface density $\rho _s$. Various authors usually have chosen $\rho _s=2\times 10^{14}$g cm$^{-3}$ to calculate the mass and radius of the charged fluid spheres, which have given rise to the stellar configuration as massive as 4–6$M_\odot$ with much lower central density. Such a massive configuration may not serve as a realistic model for a self-bound star. This choice is, therefore, not a physical one. Modeling a compact (quark) star requires the use of a higher surface density. Certainly, the value of the surface density affects the calculated value of the stellar mass—to see this, we observe that by the method employed in the present work one can obtain an arbitrarily large maximum mass just by inserting a vanishing small surface density (e.g., $0.1-1$ g cm$^{-3}$ to model a thin crust). In our model calculation, the density at the stellar radius was chosen within the range 4–$10\times 10^{14}$g cm$^{-3}$ [205] and drops abruptly to zero, as with all stellar models matching an interior metric to the external Reissner–Nordström form. This sharp drop in density is a reasonable model approximation, since the thickness of the “quark surface” is of order 1 fm, a negligibly small dimension compared to the stellar radius.

In the construction of fluid spheres we assumed a positive anisotropy, $P_t>P_r$, which increases the region of instability, and have shown that the upper bound on the maximum mass decreases in the presence of a positive anisotropy in order to satisfy the condition $-1<v_{st}^2-v_{sr}^2\le 0$ and get the potentially stable sphere. Moreover, for the models the radial speed of sound is obtained $\approx 1/\sqrt{3}$ at the center, and it remains almost the same throughout most of the fluid sphere. This behavior is somewhat like the MIT bag model. An analytical stellar model with such physical features could play a significant role in the description of the internal structure of superdense compact astrophysical objects like electrically charged bare strange quark stars. Nevertheless, it would also be interesting to study the behaviors of strange stars within the framework of a linear equation state, like the MIT bag model, in Wyman–Leibovitz–Adler space-time, which the authors hope to do in the near future.

Appendix A: Pressure and density gradients

We have

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}P_r}{\text {d}x}= & {} K\frac{(1+5x)}{(1+mx)(1+3x)^{2/3}(1+x)}\nonumber \\&+\frac{2K}{m}\frac{\ln (1+mx)(1-5x^2)}{(1+3x)^{5/3}(1+x)^2}\nonumber \\&+\frac{K}{2}\frac{(1+4x+x^2-2mx^3)}{(1+3x)^{2/3}(1+x)^2(1+mx)^2}\nonumber \\&+\delta \frac{\Psi _1(x)}{(1+x)^2(1+3x)^{5/3}}-\frac{4}{(1+x)^2}\nonumber \\&+2A_2\frac{(1-5x^2 )}{(1+3x)^{5/3}(1+x)^2}, \end{aligned}$$

(A.1)

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}P_t}{\text {d}x}= & {} \frac{\kappa }{C}\frac{\text {d}P_r}{\text {d}x}+\frac{\text {d}\Delta }{\text {d}x}, \end{aligned}$$

(A.2)

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}\rho }{\text {d}x}= & {} -K\frac{(3+5x)}{(1+mx)(1+3x)^{5/3}}\nonumber \\&+\frac{10K}{m}\frac{\ln (1+mx)(1+x)}{(1+3x)^{8/3}}\nonumber \\&+2K\frac{(1+x-2mx^2)}{(1+3x)^{5/3}(1+mx)^2}\nonumber \\&-\frac{K}{2}\frac{(1+4x+x^2-2mx^3)}{(1+3x)^{2/3}(1+x)^2(1+mx)^2}\nonumber \\&-\delta \frac{\Psi _2(x)}{(1+3x)^{8/3}}+10A_2\frac{(1+x)}{(1+3x)^{8/3}}, \end{aligned}$$

(A.3)

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}P_r}{\text {d}x}= & {} \frac{K}{m^{n+1}}\sum _{i=0}^{n-1}\bigg [\frac{(-1)^i}{(n-i)}\left( {\begin{array}{c}n\\ i\end{array}}\right) \nonumber \\&\times (1+mx)^{n-i-1}\frac{\Sigma _{m,n,-1,i}(x)}{(1+3x)^{5/3}(1+x)^2}\bigg ]\nonumber \\&\times \frac{(-1)^n K}{m^{n}}\frac{(1+5x)}{(1+mx)(1+3x)^{2/3}(1+x)}\nonumber \\&+\frac{(-1)^n 2K}{m^{n+1}}\frac{\ln (1+mx)(1-5x^2)}{(1+3x)^{5/3}(1+x)^2}\nonumber \\&+\frac{K}{2}x^n\frac{\Phi _{m,n,-1}(x)}{(1+mx)^2(1+3x)^{2/3}(1+x)^2}\nonumber \\&+\delta \frac{\Psi _1(x)}{(1+x)^2(1+3x)^{5/3}}-\frac{4}{(1+x)^2}\nonumber \\&+2A_2\frac{(1-5x^2 )}{(1+3x)^{5/3}(1+x)^2}, \end{aligned}$$

(A.4)

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}P_t}{\text {d}x}= & {} \frac{\kappa }{C}\frac{\text {d}P_r}{\text {d}x}+\frac{\text {d}\Delta }{\text {d}x}, \end{aligned}$$

(A.5)

$$\begin{aligned} \frac{\kappa }{C}\frac{\text {d}\rho }{\text {d}x}= & {} -\frac{K}{m^{n+1}}\sum _{i=0}^{n-1}\frac{(-1)^i}{(n-i)}\left( {\begin{array}{c}n\\ i\end{array}}\right) (1+mx)^{(n-i-2)} \nonumber \\&\times \frac{\Theta _{m,n,i,-1}(x)}{(1+3x)^{8/3}}+\frac{K}{2}(1+mx)^{p-1} \nonumber \\&\times \frac{\Phi _{m,n,-1}(x)}{(1+3x)^{2/3}(1+x)^2}-\delta \frac{\Psi _2(x)}{(1+3x)^{8/3}} \nonumber \\&+10A_2\frac{(1+x)}{(1+3x)^{8/3}} \end{aligned}$$

(A.6)

where $\Sigma _{m,n,p,i}(x)$, $\Phi _{m,n,p}(x)$, $\Theta _{m,n,p,i}(x)$, $\Psi _1(x)$, $\Psi _2(x)$, and $\text {d}\Delta /\text {d}x$ are defined in Sect. 5.1.