1 Introduction

At present, the scientific community dedicated to the study of the universe has deep and intriguing questions unanswered. One of the most fascinating one corresponds to what we know as dark energy (DE) [1–6], a component designed to explain the current acceleration in the expansion of the universe. In its simplest form, this can be described by a perfect fluid with constant energy density, which leads to the useful \(\Lambda \) – cold dark matter (\(\Lambda \)CDM) model, the simplest model that fits a varied set of observational data. However, this model has a high dependence to initial conditions, which makes it unnatural in many ways. For example, the current values for \(\Omega _{\Lambda }\) and \(\Omega _DM\) are of the same order of magnitude, a fact highly improbable, because the dark matter (DM) contribution decreases with \(a^{-3}\), with \(a(t)\) the scale factor; meanwhile the cosmological constant remains constant. This problem in particular is known as the cosmic coincidence problem.

It is for this reason that many of the most sophisticated experiments and instruments have been put in place; the Dark Energy Survey (DES) [7], the Baryon Oscillation Spectroscopic Survey (BOSS) [8], and the upcoming Large Synoptic Survey Telescope (LSST) [9] to mention some, all of them trying to find new insights in the nature of dark energy.

In this context, the most natural way to understand the acceleration of the universe is to assume the existence of a dynamical cosmological constant, or a theoretical model with a dynamical equation of state parameter (\(p{/}\rho =w(z)\)). The source of this dynamical dark energy could be both a new field component filling the universe and a quintessence scalar field [10–16], or it can be produced by modifying gravity [17–23].

In this work, the so-called k-essence model [24, 25] is used, which is a type of dynamical cosmological constant model, but one where the source of its dynamics comes from a non-trivial kinetic term, opposite to the case of a typical quintessence model where the source is a different scalar field potential, and then we put it to the test with current observational data from both type Ia supernovae [26] and the most recently update Hubble parameter measurements [27].

Besides, if we focus, for example, on the dark sector as a whole, it has been proved that the division of this sector into DM and DE is merely conventional, since there exists a degeneracy between the two components, resulting from the fact that gravity only measures the total energy tensor [28] (see also [29–35]). So, by the lack of a well-confirmed detection (nongravitational) of the DM only the overall properties of the dark sector can be inferred from cosmological data, at the background and perturbative level. This result has driven the research to the exploration of alternative models, which consider a single fluid that behaves both as DE and DM, the so-called unified DM models (UDM). So this fluid must drive both the accelerated expansion of the Universe at late times and the formation of structures (see [36] for a review of these models). Of course, a small speed of sound should be an essential characteristic of a viable unified model in order not to impede the structure formation and to have a ISW effect signal compatible with CMB observation [37–42].

In the present work we will consider UDM models derived in the framework of k-essence fields, common in effective field theories arising from string theory and in particular in D-brane models [43–47]. This generalization of the canonical scalar fields models can give rise to new dynamics not possible in quintessence. In the context of cosmology, k-essence was first studied as a model for inflation (k-inflation) [48]. k-Essence models have also addressed the problems of a dynamical DE [49, 50] and the coincidence problem [51, 52]. For example, a particular case is the generalized Chaplygin gas (GCG), which appears as the simplest tachyon field model, introduced in [53], with a constant potential. Moreover, k-fields lead to new Chaplygin gases. Within the models investigated in order to unify DE and DM are the GCG [38, 54–60] and those known as purely kinetic models [39, 61]. The unification of DE, DM, and inflation has been addressed in [62, 63].

Another issue that emerges from the cosmological data is that the exotic behavior of the universal fluid can be characterized by a negative pressure and usually represented by the equation of state \(w= p{/}\rho \), where \(w\) lies very close to \(-1\), most probably being below \(-1\). For example, the last Planck results give \(w = -1.13^{+0.13}_{ -0.10}\) and \(w = -1.090.17\) \((95~\%~CL)\) by using CMB combined with BAO and Union2.1 data [64], respectively, for a constant \(w\) model. In combination with SNLS3 data and \(H_{0}\) measurement, the EoS for this dark component are \(w = -1.13^{+0.13}_{ -0.14}\) and \(w = -1.24^{+0.18}_{-0.19}\) \((2\sigma CL)\), respectively. The possibility of \(w < -1\) is favored at the \(2\sigma \) level. These results are indicating that a phantom behavior of the dark energy component cannot be ruled out from current cosmological data.

As pointed out in [65, 66], dark energy with a constant EoS \(w<-1\) leads to uncommon cosmological scenarios. First of all, there is a violation of the dominant energy condition (DEC), since \(\rho + p <0\). The energy density grows up to infinity in a finite time, which leads to a big rip, characterized by a scale factor blowing up in this finite time. Nevertheless, sudden future singularities are not necessarily produced by fluids violating DEC. Solutions which develop a big rip singularity at a finite time without violating the strong-energy conditions \(\rho >0\) and \(\rho +3p >0\) were found in [67, 68]. Studies of unified dark matter models, which are generalizations of the Chaplygin gas, present an EoS \(w<-1\) but without a big rip type solution in [69].

Another mechanism that allows for a violation of DEC is the existence of dissipation within the cosmic fluids [70, 71]. In the case of isotropic and homogeneous cosmologies, any dissipation process in a FRW cosmology is scalar, and therefore may be modeled as a bulk viscosity within a thermodynamical approach. The bulk viscosity introduces dissipation by only redefining the effective pressure, \(p_\mathrm{eff}\), according to \(p_\mathrm{eff}= p+\Pi = p-3 \zeta H\), where \(\Pi \) is the bulk viscous pressure, \(\zeta \) is the bulk viscosity coefficient and \(H\) is the Hubble parameter, and \(c = 8\pi G= 1\) (as is a common choice). Since the equation of energy balance is \( \dot{\rho }+ 3 H (\rho +p+\Pi )=0\), the violation of DEC, i.e., \(\rho +p+\Pi <0\), implies an increasing energy density of the fluid that fills the universe, for a positive bulk viscosity coefficient. The condition \(\zeta >0\) guarantees a positive entropy production and, in consequence, no violation of the second law of the thermodynamics [72].

Some investigations have considered that the viscous pressure can drive the present acceleration of the Universe, so it can be used to eliminate the dark energy component and to formulate a unified dark matter model with viscous pressure [73–75]. In [76, 77], for example, cosmological models where the only component is a pressureless fluid with a variable and constant bulk viscosity were confronted with the observational data. Nevertheless, the bulk viscosity induces a large time variation of the gravitational potential at late times, which leads to inconsistencies with the integrated Sachs–Wolfe (ISW) effect in such models [78–80]. In order to overcome this problem, Velten and Schwarz [81] proposed a model with a viscous cold dark matter and a cosmological constant, which acts by driving the accelerated expansion of the Universe. Our aim in this work is to investigate UDM models derived in the framework of k-essence fields which can also present dissipative effects.

Usually k-essence is defined as a quintessence, scalar field \(\phi \) with a non-canonical kinetic energy associated with a Lagrangian \(\mathcal {L} = -V(\phi ) F(X)\). In the subsequent calculations, we shall restrict ourselves to the simple k-essence models for which the potential \( V=V_{0}=\) constant. We also assume that \(V_{0}=1\) without any loss of generality. One reason for studying k-essence is that it is possible to construct a particularly interesting class of such models in which the k-essence energy density tracks the radiation energy density during the radiation-dominated era but then evolves toward a constant-density dark energy component during the matter-dominated era. Such a behavior can to a certain degree solve the coincidence problem.

We investigate a dark energy model described by an effective minimally coupled scalar field with a non-canonical kinetic term. If for the moment we neglect the part of the Lagrangian containing ordinary matter, the general action for a k-essence field \(\phi \) minimally coupled to gravity is

$$\begin{aligned} S= S_{G}+S_{\phi }=- \int \mathrm{d}^{4}x \sqrt{-g}\,\left( \frac{R}{2}+ F(\phi ,X)\right) , \end{aligned}$$
(1)

where \(F(\phi ,X)\) is an arbitrary function of \(\phi \) that represents the k-essence action and \(X=\frac{1}{2}\partial _{\mu } \phi \partial ^{\mu } \phi \) is the kinetic term. We now restrict ourselves to the subclass of kinetic k-essence, with an action independent of \(\phi \),

$$\begin{aligned} S_{\phi }= -\int \mathrm{d}^{4}x \sqrt{-g} \,F(X). \end{aligned}$$
(2)

Unless otherwise stated, we consider \(\phi \) to be smooth on the scales of interest so that \(X = \frac{1}{2} \dot{\phi }^2\ge 0\). The energy-momentum tensor of the k-essence is obtained by varying the action (2) with respect to the metric, yielding

$$\begin{aligned} T_{\mu \nu }= F_{X} \partial _{\mu }\phi \partial _{\nu }\phi - g_{\mu \nu }F, \end{aligned}$$
(3)

where the subscript \(X\) denotes differentiation with respect to \(X\). Identifying (3) as the energy-momentum tensor of a perfect fluid, we have the k-essence energy density \(\rho \) and pressure \(p\),

$$\begin{aligned} \rho= & {} F-2XF_{X}, \end{aligned}$$
(4)
$$\begin{aligned} p= & {} -F. \end{aligned}$$
(5)

Throughout this paper, we will assume that the energy density is positive, so that \(F-2 X F_X> 0\). The equation of state for the k-essence fluid can be written as \(p = w_{\phi }\rho =(\gamma _{\phi }-1)\rho \), with \(F>0\),

$$\begin{aligned} w_{\phi }=\gamma _{\phi }-1 = \frac{p}{\rho }= \frac{F}{2XF_{X}-F}. \end{aligned}$$
(6)

2 The k-essence model with dissipation

The Friedman–Lemaître–Robertson–Walker (FLRW) metric for an homogeneous and isotropic flat universe is given by

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{d}t^2+a(t)^2\left[ \mathrm{d}r^2+r^2 \left( \mathrm{d}\theta ^2 + \sin ^2 \theta \, \mathrm{d} \phi ^2\right) \right] , \end{aligned}$$
(7)

where \(a(t)\) is the scale factor and \(t\) represents the cosmic time. In the framework of the first order thermodynamic theory of Eckart [82] the field equations in the presence of bulk viscous stresses yield

$$\begin{aligned}&\left( \frac{\dot{a}}{a}\right) ^2=H^2= \frac{\rho }{3},\end{aligned}$$
(8)
$$\begin{aligned}&\frac{\ddot{a}}{a}=\dot{H}+H^2=-\frac{1}{6} \left( \rho + 3 p_\mathrm{eff} \right) , \end{aligned}$$
(9)

where the effective pressure is given by

$$\begin{aligned} p_\mathrm{eff}=p+\Pi \end{aligned}$$
(10)

and

$$\begin{aligned} \Pi =-3 H \zeta \end{aligned}$$
(11)

is the bulk dissipative pressure; \(\zeta \) is the viscosity. In what follows we will assume a power law dependence for the viscosity in terms of the density,

$$\begin{aligned} \zeta = \zeta _0 \rho ^{\lambda }, \end{aligned}$$
(12)

where \(\zeta _0\) is a positive semi-definite constant with dimension \(M^{1-\lambda }\,L^{3\lambda -1}\,T^{-1}\), and \(\lambda \) may take any value. For example, the most common values are \(\lambda =1{/}2\), i.e., \(\zeta \propto \rho ^{1/2}\) [83–87], and \(\lambda =1\), i.e., \(\zeta \propto \rho \) [88, 89]. These values were chosen because they lead to well-known analytic solutions. Therefore, the conservation equation for the fluid can be written as

$$\begin{aligned} \dot{\rho }+ 3 H (\rho +p+\Pi )=0. \end{aligned}$$
(13)

In this work we consider the following function \(F\) for the k-essence field [53]:

$$\begin{aligned} F(X)=\frac{1}{2\alpha -1}\big [X^{\alpha }-2 \alpha \alpha _0 \sqrt{X}\big ], \end{aligned}$$
(14)

where \(\alpha \) and \(\alpha _0\) are two real constants. This generating function exhibits a transition from a power law phase to a de Sitter stage, inducing a modified Chaplygin gas. The explicit equation of state can be obtained from Eqs. (4) and (5),

$$\begin{aligned} p=(\mathfrak {n}-1)\rho -\mathfrak {n} \,\alpha _0\, \rho ^{\frac{\mathfrak {n}-1}{\mathfrak {n}}}, \end{aligned}$$
(15)

where the parameter \(\mathfrak {n}\) is a function of the constant \(\alpha \), given by

$$\begin{aligned} \mathfrak {n}=\frac{2\alpha }{2\alpha -1}. \end{aligned}$$
(16)

Obviously, the range of this parameter is \(1>\mathfrak {n}>0\), if \(-\infty <\alpha <0\); \(0>\mathfrak {n}>-\infty \), if \(0<\alpha <1/2\), and \(\infty >\mathfrak {n}>1\), if \({1}{/}2<\alpha <\infty \).

Of course, the speed of sound is affected by the viscous pressure, which becomes

$$\begin{aligned} v_\mathrm{ef}^2=\frac{\partial p_\mathrm{ef}}{\partial \rho }= v_{\phi }^2-(\lambda +1{/}2)\frac{\Vert \Pi \Vert }{\rho }, \end{aligned}$$
(17)

where \(v_{\phi }\) is the speed of sound in the purely k-essence background [53], given by

$$\begin{aligned} v_{\phi }^2=(\mathfrak {n}-1)\left( 1-\frac{\alpha _0}{\rho ^{1/\mathfrak {n}}}\right) . \end{aligned}$$
(18)

From Eqs. (8)–(14), together with the EoS (15), we obtain the evolution equation for \(H\) in terms of the redshift,

$$\begin{aligned} -a_0 \frac{{\text {d}} H}{{\text {d}} x}+ a_1 H +a_2 H^{\eta -1}+a_3 H^{\beta -1}=0, \end{aligned}$$
(19)

where \(x=\ln (1+z)\), and the coefficients are given by

$$\begin{aligned} a_0=2,\, a_1=3\mathfrak {n},\, a_{2}=-3^{\frac{\mathfrak {n}-1}{\mathfrak {n}}}\alpha _{0}\mathfrak {n},\, a_{3}=-3^{\lambda +1}\zeta _{0}, \end{aligned}$$
(20)

whereas the exponents read

$$\begin{aligned} \eta =2\left( \frac{\mathfrak {n}-1}{\mathfrak {n}}\right) =\frac{1}{\alpha },\quad \beta =2\lambda +1. \end{aligned}$$
(21)

As a first observation, we note that there are two special values that yield a well-known equation for the case without viscosity [53]: \(\beta =2\) (\(\lambda =1{/}2\)) and \(\beta =\eta \) (\(\lambda =\frac{1-\alpha }{2\alpha }\ne 1{/}2\)). These values lead to a single equation which possesses a generic structure for its quadrature given by

$$\begin{aligned} \frac{{\text {d}}H}{{\text {d}}x}=A_1 H+A_2 H^{\eta -1}\equiv A_1 \left( H+y H^{\eta -1}\right) , \end{aligned}$$
(22)

where \(y\equiv A_2/A_1\), and the new coefficients are given in terms of the above by the following expressions:

$$\begin{aligned}&A_1=\frac{a_1+a_3}{a_0}=\frac{3}{2}(\mathfrak {n}-\sqrt{3}\,\zeta _0), \end{aligned}$$
(23)
$$\begin{aligned}&A_2=\frac{a_2}{a_0}=-\frac{3^{\frac{\mathfrak {n}-1}{\mathfrak {n}}}\alpha _0\,\mathfrak {n}}{2}, \end{aligned}$$
(24)
$$\begin{aligned}&y=\frac{a_2}{a_1+a_3}=\frac{\alpha _0\,\mathfrak {n}}{3^{\frac{1}{\mathfrak {n}}}(\sqrt{3}\zeta _0-\mathfrak {n})}, \end{aligned}$$
(25)

for \(\lambda =1/2\) (the model A), whereas

$$\begin{aligned} A_1= & {} \frac{a_1}{a_0}=\frac{3}{1-2\lambda }, \end{aligned}$$
(26)
$$\begin{aligned} A_2= & {} \frac{a_2+a_3}{a_0}=-\frac{3^{\lambda +\frac{1}{2}}}{2}\left( \frac{2\alpha _0}{1-2\lambda }+\sqrt{3}\zeta _0 \right) , \end{aligned}$$
(27)
$$\begin{aligned} y= & {} \frac{a_2+a_3}{a_1}=\frac{3^{\lambda -\frac{1}{2}}}{2}\, \left( \sqrt{3}\,\zeta _0 (2\lambda -1)-2\,\alpha _0 \right) , \end{aligned}$$
(28)

for \(\lambda \ne 1/2\) (the model B). So, a direct integration of Eq. (22) leads to

$$\begin{aligned} H(z)=H_{0}\, \left[ \frac{(1+z)^{\frac{2 A_1}{\mathfrak {n}}}-A_3}{1-A_3}\right] ^{\frac{\mathfrak {n}}{2}}, \end{aligned}$$
(29)

and therefore the energy density is given by

$$\begin{aligned} \rho (z)=3\,H_{0}^2\, \left[ \frac{(1+z)^{\frac{2 A_1}{\mathfrak {n}}}-A_3}{1-A_3}\right] ^{\mathfrak {n}}, \end{aligned}$$
(30)

where we have defined

$$\begin{aligned} A_3= \frac{\mathcal {R}}{1+\mathcal {R}},\quad \left( \mathcal {R}=\frac{y}{H_{0}^{\frac{2}{\mathfrak {n}}}} \right) . \end{aligned}$$
(31)

We note that the generic expression (30) [or Eq. (29)] has the form found by Chimento [53], and, obviously, this case is entirely recuperated by making \(\zeta _0\rightarrow 0\) and \(\lambda \rightarrow 0\). A second observation is that, in the case \(\lambda \ne 1/2\) and by using Eqs. (21) and (26), the expression (29) takes the form

$$\begin{aligned} H(z)=H_{0}\, \left[ \frac{(1+z)^{3}-A_3}{1-A_3}\right] ^{\frac{\mathfrak {1}}{1-2\lambda }}. \end{aligned}$$
(32)

Finally, there is a future singular value of the redshift, say \(z_s\), for which the Hubble function takes its zero value:

$$\begin{aligned} z_s=A_{3}^{\frac{\mathfrak {n}}{2A_1}}-1. \end{aligned}$$
(33)

We are restricted to the realistic values for the future singularity, so we expect that \(-1<z_s<0\). Thus, this condition imposes the requirement that \(y>0\), which implies that \(\mathfrak {n}<\sqrt{3}\zeta _0\) if \(\lambda =1/2\), and \(\lambda >1/2+\alpha _0/(\sqrt{3}\zeta _0)\) if \(\alpha =(2\lambda +1)^{-1}\). In this context, notice that \(\lambda =1\) (i.e. \(\alpha =1/3\)) leads to the condition \(2\,\alpha _0<\sqrt{3}\,\zeta _0\).

This kind of future singularity corresponds to a novel type, because both the Hubble parameter (29) and the energy density (30) vanish at this redshift.

3 Observational constraints

In this section we use observational data to put some constraints in the free parameters of the models. We use type Ia supernova data, specifically the Union 2 data set [26], and the most recent Hubble parameter \(H(z)\) measurements compiled in [90], consisting of 28 data points ranging in redshift over \(0.015<z<2.3\).

The comoving distance from the observer to redshift \(z\), in a flat universe, is given by

$$\begin{aligned} r(z) = \frac{c}{H_0} \int _0^z \frac{{\text {d}}z'}{E(z')}, \end{aligned}$$
(34)

where \(E(z)=H(z){/}H_0\). The SNIa data give the luminosity distance \(d_L(z)=(1+z)r(z)\). Notice that the procedure we follow differs from those used by Bandyopadhyay et al. [92]. In this work the authors define an intermediate parametrization for the luminosity distance as a function of the two parameters \(\alpha , \beta \), which after the fitting is related to the physical parameters of the model. Here we constrain directly the physical parameters of the model.

We fit the SNIa with the cosmological model by minimizing the \(\chi ^2\) value defined by

$$\begin{aligned} \chi _\mathrm{SNIa}^2=\sum _{i=1}^{557}\frac{[\mu (z_i)-\mu _\mathrm{obs}(z_i)]^2}{\sigma _{\mu i}^2}, \end{aligned}$$
(35)

where \(\mu (z)\equiv 5\log _{10}[d_L(z)/\mathtt Mpc ]+25\) is the theoretical value of the distance modulus, and \(\mu _\mathrm{obs}\) is the corresponding observed one.

From (30) we can write down explicitly

$$\begin{aligned} E(z)=\left[ \frac{(1+z)^{\frac{2 A_1}{\mathfrak {n}}}-A_3}{1-A_3}\right] ^{\frac{\mathfrak {n}}{2}}. \end{aligned}$$
(36)

This form of the solution enables us to test both models at the same time by reinterpreting the constants’ values. The best fit values using both SNIa and \(H(z)\) data lead to a \(\chi ^2_{red}\simeq 0.96\), \(A_1=1.50\,\pm \,0.15\), \(\eta =-0.29\,\pm \,0.19\), and \(A_3=-2.9\,\pm \,0.5\).

For the case \(\lambda =1/2\), the free parameters number three: \(A_1\), the parameter that changes with the model, \(\eta \), which is defined in (21), and \(A_3\), defined in (31). Straightforward calculations lead to \(\mathfrak {n}=0.87\,\pm \,0.07\), \(\zeta _0=-0.075\,\pm \,0.069\), and \(\alpha _0=(2.96\,\pm \,2.6)\times 10^{-4}\). Note that for the case \(\lambda =1/2\), since we have taken \(G=1/8\pi \) and \(c=1\), it is straightforward to see that the parameter \(\zeta _0\) is dimensionless.

Since the exponent in (36) reduces to \(\frac{2 A_1}{\mathfrak {n}}=3\), in the case \(\lambda \ne 1/2\) the free parameters reduce to \(A_3\) and \(\eta \). For this reason, it is not possible to invert the equations completely, because this model is described by three parameters, \(\zeta _0, \alpha _0\), and \(\lambda \). In fact, from the best fit, we can write down directly the value for \(\lambda =-0.65 \pm 0.08\). The other two parameters are tightly related through the relation

$$\begin{aligned} \alpha _0=-\frac{y}{3^{\lambda -1/2}}+2\sqrt{3}(2\lambda -1)\zeta _0. \end{aligned}$$
(37)

Because the best value for parameter \(y\) is large compared with the second term on the right hand side (for reasonable positive values of \(\zeta _0\)), the value for \(\alpha _0\) is largely better constrained than \(\zeta _0\).

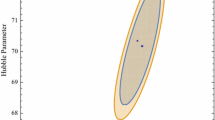
In order to make manifest the quality of the fit of our models, in Fig. 1 we show the theoretical curves of the best fit for each model together with the observational data of \(H(z)\). There we show the 28 data points measurements of the Hubble parameter together with the best theoretical fit. We have to notice that although the lines do not seem to follow the observational points very well, this is because the best fit model was computed using both SNIa data and \(H(z)\) measurements, and the first data set statistically weighs more than the second one, just because of the number of data in each case. We also display in Fig. 2 the confidence level contours for the parameters \(\eta \) and \(A_3\) at one and two \(\sigma \), and in Fig. 3 the confidence contours for the model B parameters.

Fig. 1
figure 1

Using the values of the best fit for each model, here we display the theoretical curve of each model along the observational data for \(H(z)\). The continuous line is model A, and the dashed line describes model B. It should be noted that the values of the best fit were obtained using both measurements of \(H(z)\) and supernovas. We have adopted \(h=0.673\) from the Planck Collaboration [91]

Full size image
Fig. 2
figure 2

Here we display the 68.27 and 95.45 % confidence regions for the parameters \(A_1\), \(A_3\), and \(\eta \) for model A

Full size image
Fig. 3
figure 3

Here we display the 68.27 and 95.45 % confidence regions for the parameters \(A_3\) and \(\eta \) for model B

Full size image

In both cases, because the analysis was performed without imposing external priors on the parameters, we found a preference for nearly zero to negative values for the viscosity constant \(\xi _0\).

Despite the strange results – a negative value for the viscosity constant – after putting in tension our solutions with the data, we have confidence that such an analysis can be done in the first place for any other analytical solution that can be obtained in the future. Of course, we do not expect to find that just our special (analytical) solutions would be the best fit to the data immediately. Cosmology has entered into the era of precision cosmology, and with it, the possibility to rule out effectively a particular cosmological model.

4 Conclusions

We have analyzed the general relations for a model of k-essence generated by the function \(F(X)=\small {\frac{1}{2\alpha -1}}[X^{\alpha }-2 \alpha \alpha _0 \sqrt{X}]\) (proposed by Chimento [53]), when a dissipative pressure \(\Pi \propto \rho ^{\lambda +1/2}\) is included. We found a family of analytical solutions in two special cases: \(\lambda =1/2\) and \(\lambda =(1-\alpha )/2 \alpha \) (with \(\alpha \ne 1/2\)), which come from similar differential equations and possess the same structure as the non-viscous case (compare, for example, Eq. (69) in Ref. [53] with Eq. (30)).

Also, a quick look at Eq. (17) shows that, depending on the value of \(\lambda \), the speed of sound may be greater than (\(\lambda <-1/2\)), equal to (\(\lambda =-1/2\)) or less than (\(\lambda >-1/2\)) the speed of sound without viscosity. Obviously, a well-behaved fluid requires \(\lambda \ge -1/2\), which corresponds to a consistency relation for \(\lambda \).

To let observational data shed light, we confront both analytical solution with measurements of \(H(z)\) and supernovas. The best fit yields the following values for the parameters: \(\chi ^2_{red}\simeq 0.96\), \(A_1=1.50 \pm 0.15\), \(\eta =-0.29\pm 0.19\), and \(A_3=-2.9\pm 0.5\). Therefore, we obtain for the model A \(\mathfrak {n}=0.87\pm 0.07\), \(\zeta _0=-0.075 \pm 0.069\), and \(\alpha _0=(2.96\pm 2.6)\times 10^{-4}\), while for the model B we obtain \(\lambda =-0.65 \pm 0.08\), and the other two parameters are tightly related through Eq. 37. So, both models lead to a controversy as regards the physical meaning (\(\zeta _0<0\) in the model A and \(\lambda <-1/2\) in the model B).

This work can be improved in many ways. On the one hand, we can attempt an alternative way to obtain analytical solutions, a possibility we are already studying using a novel technique proposed to solve complex differential equations [93–98]. In this case, we have the possibility to consider \(\lambda \) a free parameter, enhancing the parameter space to find a best fit with the data.

Certainly a more realistic model would also be interesting to study. In this work we have considered a UDM model assuming nothing but a k-essence field is present. We can add explicitly a dark matter term and/or a radiation component. We are interested in testing if adding these terms would alleviate our concerns about the sign of the viscosity coefficient.