1 Introduction

Observational data on Type-Ia supernovae [1–3] and the CMB [4, 5] has confirmed with sufficient accuracy that nearly 70 percent of energy of the universe is in an exotic form called dark energy, which is responsible for the current acceleration of the universe. The remaining part of the cosmic components consist of nearly 23 to 24 percent of weakly interacting dark matter [6–10] and a few percent forms the luminous matter and radiation. Even with the overwhelming evidence for the existence of these cosmic components the current observational data does not rule out the possible existence of other form of exotic fluid components. One of the examples for such fluids is the dark radiation which can exist in the early or later stage during the evolution of the universe [11].

Recently, considerable attention has been paid to the study of another exotic fluid, the Zel’dovich fluid or stiff fluid, first studied by Zel’dovich [12]. The Zel’dovich fluid is a perfect fluid in which the speed of sound is equal to the speed of light, so that the equation of state becomes \(\omega _z = p_z/\rho _z =1,\) the highest value a fluid can have in consistency with causality. The Zel’dovich fluid or stiff fluid behavior in the cosmological context has been considered by many workers. In dealing with the self-interaction in dark matter the authors in Ref. [13] have shown that the self-interaction field behaves like a stiff fluid. The existence of a Zel’dovich fluid was confirmed in the Horava–Lifshitz gravity-based cosmological models when the so-called detailed balancing conditions [14, 15] were relaxed [16, 17], and the stiff fluid in such a situation had been studied in Refs. [18–20]. The relevance of the existence of the Zel’dovich fluid in the early universe was discussed in Ref. [21]. In certain inhomogeneous cosmological models a stiff fluid appears as an exact nonsingular solution [22, 23]. In the standard evolution of the Friedmann universe the density of the Zel’dovich fluid is found to be decreasing faster than radiation and matter. Consequently its effect on the early universe would be significant. One of the important phenomena that took place in the early universe is the primordial nucleosynthesis which might be influenced by the presence of a stiff fluid. In Ref. [24] the authors have found a limit on the density of the stiff fluid from the constraints on the abundances of the light elements.

In an expanding universe there can be deviations from local thermodynamic equilibrium. Consequently there can arise a bulk viscosity in the cosmic fluid which will restore the equilibrium [25]. This bulk viscosity modifies the effective pressure of the fluid in order to facilitate reestablishment of the equilibrium situation. As soon as the equilibrium is reached the bulk viscous pressure vanishes [25, 26]. In the context of inflation in the early universe it has been shown that an imperfect fluid with bulk viscosity can cause the early accelerated expansion [27]. The later time viscous universe was studied in Ref. [28]. A considerable number of studies by including bulk viscosity in the dark matter setting were carried out by many authors in the context of the late acceleration of the universe [29–31].

Recently considerable interest has been focused on the study of a viscous Zel’dovich fluid in an expanding universe. In Ref. [32] the authors studied the evolution of a viscous Zel’dovich fluid in a flat universe and found that it can have a considerable effect even in the late universe. This work shows that the bulk viscous Zel’dovich fluid can cause the recent acceleration of the universe. To account for the recent acceleration of the universe, various dark energy models with non-exotic components have been studied in the recent literature. One of the actively studied proposals in this regard is bulk viscous dark matter [29, 31]. But there are arguments that this model fails in predicting many properties, including the age of the universe [31]. It is in this context, when there is no consensus on any particular dark energy model, that the authors of Ref. [32] considered the bulk viscous Zel’dovich fluid as a possible candidate for causing the recent acceleration of the universe. In Ref. [33] it was shown that, with a bulk viscous Zel’dovich fluid as cosmic component, the age of the universe also can be predicted reasonably well.

In Ref. [32], it was shown that the non-viscous Zel’dovich fluid density will evolve as \(\rho _z \sim a^{-6},\) in a flat universe with expansion scale factor a. In such a case the Zel’dovich fluid has a notable effect only on the early evolution of universe compared to ordinary dark matter, whose density evolves as \(a^{-3}.\) But the evolution of the bulk viscous Zel’dovich fluid is different from the non-viscous one and it can cause the late acceleration of the universe. The authors of [32] considered this model and proved that a bulk viscous Zel’dovich fluid does produce late acceleration of the universe. However, they did not try to constrain the model with cosmological observational data to arrive at a realistic picture. The question whether the model would successfully allow for a prior radiation dominated phase is also to be considered. In the present work we analyze the evolution of a flat universe with a bulk viscous Zel’dovich fluid and compare the predictions of the model with the latest cosmological data on type Ia supernovae. We evaluate the model parameters including the transport coefficient of bulk viscosity and study the evolution, particularly in the later stage, of the universe.

The paper is organized as follows. In Sect. 2, we consider a flat universe with a bulk viscous Zel’dovich fluid as the only component and derive the Hubble parameter. Then we constrain the model using type Ia supernova data to extract the constant bulk viscous parameter and the present value of the Hubble parameter. We also include the evolution of the equation of state parameter and deceleration in this section. In Sect. 3, we present our analysis of the phase-space structure of the model by including radiation also as a cosmic component to see whether the model naturally allows a prior radiation dominated phase. This is followed by our conclusions in Sect. 4.

2 The bulk viscous Zel’dovich fluid model

In this section we consider a flat universe with a bulk viscous Zel’dovich fluid as the only component. The main feature of the Zel’dovich fluid is that sound velocity in the fluid is equal to that of light. The equation of state [12] is given by

$$\begin{aligned} p_z=\rho _z. \end{aligned}$$
(1)

A similar equation of state was studied with reference to some special case by Masso and Rota [34]. In including the viscosity of the fluid we will follow Eckart’s formulation [35], which deals with viscous dissipative processes occurring in a thermodynamical system when it deviates from local equilibrium. An equivalent formulation was developed by Landau and Lifshitz [37]. However, it was noted that the equilibria in Eckart’s frame are unstable [38] and signals were propagated through the fluid at superluminal velocities [39]. These drawbacks were rectified in a more general formalism by Israel et al. [40, 41], from which Eckart’s theory follows as a first order limit. But many authors are still using Eckart’s theory because of its simplicity. For example, Eckart’s formalism was used in some models on the late acceleration of the universe caused by the bulk viscous dark matter [42–47]. In the mean time Hiscock and Salomonson [48] have shown that Eckart’s formalism can lead to accelerated expansion in the FLRW model. However, later studies have shown that an inflationary solution is possible with the Israel–Stewart formalism also [27]. In the Eckart formalism, the first order deviations from equilibrium can be expressed as an additional non-adiabatic contribution \(\Delta T^{\mu \nu }\) to the energy momentum tensor [35],

$$\begin{aligned} T^{\mu \nu }=\rho u^{\mu } u^{\nu }+p_k h^{\mu \nu }+\Delta T^{\mu \nu }, \end{aligned}$$
(2)

where

$$\begin{aligned} \Delta T^{\mu \nu }= -\zeta u^{\gamma }_{;\gamma } h^{\mu \nu }, \quad h^{\mu \nu }=u^{\mu } u^{\nu } + g^{\mu \nu }, \end{aligned}$$
(3)

with \(\zeta \) the coefficient of viscosity (positive due to the second law of thermodynamics [36]), \(u^{\mu }\) is the four velocity of an observer who measures the energy density and pressure, \(g^{\mu \nu }\) is the metric tensor, and \(u^{\gamma }_{;\gamma }=3H\) for an expansing universe. In the present work we too follow Eckart’s approach. The above results show that the effective pressure of the bulk viscous Zel’dovich fluid can be expressed as

$$\begin{aligned} p_z^{'}=p_z - 3\zeta H \end{aligned}$$
(4)

where \(\zeta \) is the coefficient of viscosity and H is the Hubble parameter.

We consider a flat Friedman universe with FLRW metric given as

$$\begin{aligned} \mathrm{d}s^2=\mathrm{d}t^2 - a^2(t)(\mathrm{d}r^2 + r^2 \mathrm{d}\theta ^2+r^2 \sin ^2\theta \mathrm{d}\phi ^2), \end{aligned}$$
(5)

where t is the cosmic time, a(t) is the scale factor of expansion, \(r,\theta ,\phi \) are the comoving coordinates. This, when combined with the Einstein field equations, gives the dynamical equations

$$\begin{aligned} H^2=\rho /3, \end{aligned}$$
(6)

and the conservation equation

$$\begin{aligned} \dot{\rho } +3H(\rho +p)=0. \end{aligned}$$
(7)

Here we follow the standard convention \(8 \pi G=1\). When these equations are combined with Eq. (4) for the effective pressure, we have

$$\begin{aligned} \mathrm{d}H/\mathrm{d}t+3H^2-\frac{3}{2} \zeta H=0. \end{aligned}$$
(8)

Solving these equations after changing the variable from t to \(x=\log a\) we get

$$\begin{aligned} h=\frac{1}{6} \left( {\bar{\zeta }}+(6-{\bar{\zeta }})a^{-3} \right) , \end{aligned}$$
(9)

where \(h=H/H_0, \,\, H_0\) is the present Hubble parameter and \({\bar{\zeta }}=\zeta /H_0\) is the dimensionless viscous parameter. For \({\bar{\zeta }}=0\) the Hubble parameter becomes \(H \sim H_0 a^{-3}\). The density of the Zel’dovich fluid will then evolve as \(\rho \sim a^{-6}\) and the scale factor will evolve as \(a\sim (H_0 t)^{1/3}\) and hence the universe would be eternally decelerating and the effect of the Zel’dovich fluid will be relevant to the early epoch of the universe [24]. On the other hand, the presence of the viscosity will modify the density in such a way that

$$\begin{aligned} \rho _z = \frac{H_0^2}{12}\left( {\bar{\zeta }}^2 + {\bar{\zeta }} (6-{\bar{\zeta }})a^{-3} + (6-{\bar{\zeta }})^2 a^{-6} \right) . \end{aligned}$$
(10)

In the early universe a term proportional to \(a^{-6}\) would dominate and affect the processes in the early universe like primordial nucleosynthesis [11] etc. But a term proportional to \(a^{-6}\) is drastically decreasing as the universe expands, while the second term, proportional to \(a^{-3},\) is a matter-like term, which in fact guarantees the effect of the bulk viscous Zel’dovich fluid in the later universe. As is obvious from Eq. (4), the viscous term causes a negative pressure, which in turn causes an accelerated phase of expansion in the later stage of the evolution of the universe. In the extreme limit of \(a(t) \rightarrow \infty \) the density behaves as \(\rho _z \rightarrow \frac{H_0^2}{12}{\bar{\zeta }}^2.\) As a result the admissible values of \({\bar{\zeta }}\) are very important in this model, which is to be evaluated by the observational constraints. Since we are interested in the effect of a Zel’dovich fluid in the late evolution of the universe, the bulk viscous coefficient can be determined by contrasting it with supernova data.

2.1 Extraction of the model parameters using Type Ia supernovae data

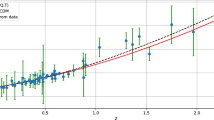
The best fit values of the model parameter \({\bar{\zeta }}\) and the Hubble parameter \(H_{0}\) can be extracted using type Ia supernova observational data. We have used Union data which consists of 307 data points [49] in the redshift range \( 0.01<z<1.6 \). The distance modulus of the supernova at a redshift z is

$$\begin{aligned} \mu _i(z) =(m-M) = 5\log _{10} d_L(z)+25 \end{aligned}$$
(11)

where m is the apparent magnitude, M is the absolute magnitude, and \(d_L(z)\) is the luminosity distance of a supernova in a flat FLRW universe. The expression for the luminosity distance is

$$\begin{aligned} d_L(z, {\bar{\zeta }})=\frac{c(1+z)}{H_0} \int _0^z \frac{dz^{'}}{h(z^{'},{\bar{\zeta }})} \end{aligned}$$
(12)

where \(h(z^{'},{\bar{\zeta }})\) is identical with the normalized Hubble parameter given in Eq. (9). The distance moduli of supernovae at various redshifts are calculated using Eq. (12) and are compared with the corresponding observational data. We then construct the statistical \(\chi ^2\) function

$$\begin{aligned} \chi ^2=\sum _{k=1}^n {\left[ \mu _i-\mu _k \right] ^2 \over \sigma _k^2} \end{aligned}$$
(13)

where \(\mu _i\) is the theoretical value of the distance modulus for a given redshift obtained in the present model, \(\mu _k\) is the observed distance modulus of the kth supernova corresponding to the same redshift as of the theoretical one, \(\sigma _k\) is the variance of the measurement, and n is the number of data points. The best estimates of the parameters \(({\bar{\zeta }}, H_0)\) are obtained by minimizing the \(\chi ^2\) function. The minimum of the \(\chi ^2\) gives measures of the goodness-of-fit of the model apart from giving the best estimates of the model parameters. The confidence regions in Fig. 1 for the parameters \({\bar{\zeta }}\) and \(H_0\) are then constructed for 99.73 and 99.99\(~\%\), respectively, to find the best estimate of the parameters. The values of the parameters are shown in Table 1 and for comparison we have also evaluated the parameters of the \(\Lambda \)CDM model of the universe, which has dark matter and the cosmological constant as the dark energy component. With a dark energy density around \(\Omega _\mathrm{de} \sim 0.7\), the \(\Lambda \)CDM model gives a value of \(\chi ^2/\mathrm{d.o.f} \sim 1.013,\) very close to the value from the present model having bulk viscous Zel’dovich matter as the only component of the universe. The Hubble parameter values are also close to each other. These facts imply that the present model is very much similar to the standard \(\Lambda \)CDM model in predicting the background parameters of the universe. This close agreement on parameter values of the present model with the \(\Lambda \)CDM model gives further hope in pursuing it. With the statistical correction the values of parameters in the present model finally become \({\bar{\zeta }}=5.25\pm 0.14\) and \(H_0=70.20\,\pm \, 0.58.\) In a previous paper [32] we have worked out a single component Zel’dovich fluid model of the universe having dark energy incorporated in terms of linear bulk viscosity, and there we had shown that when \(4< {\bar{\zeta }} <6,\) a transition from deceleration to acceleration took place in the past.

Fig. 1
figure 1

Confidence intervals for the parameters \({\bar{\zeta }}\) and \(H_0.\) The outer curve corresponds to 99.99\(~\%\) probability and the inner one corresponds to 99.73 \(~\%\) probability. The lower dot represents the values of the parameters corresponding to the minimum of the \(\chi ^2\)

Full size image
Table 1 The best estimates of the parameters \({\bar{\zeta }}\) and \(H_0\) evaluated with the supernova type-Ia union data 307 data points
Full size table

2.2 Evolution of cosmic parameters

The behavior of the scale factor in the Zel’dovich fluid dominated universe can be obtained from Eq. (9) as

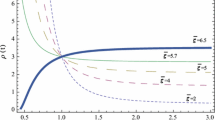
$$\begin{aligned} a(t)= \left( ({\bar{\zeta }} -6)+6e^{\frac{H_0{\bar{\zeta }}}{2}(t-t_0)} \over {\bar{\zeta }}\right) ^{1/3}. \end{aligned}$$
(14)

At sufficiently early time the scale factor can be approximated as \(a(t)\sim (1+3H_0(t-t_0))^{\frac{1}{3}},\) which implies a decelerated phase, while at later times the scale factor behaves as \(a(t)\sim \exp (\frac{{\bar{\zeta }}}{6}H_0(t-t_0))\) showing that the universe shows an accelerated evolution at a later time. Figure 2 shows the evolution of scale factors at various choices of \({\bar{\zeta }}.\) From the figure it is seen that the behavior of the scale factor is different for \({\bar{\zeta }}>6.\) If one finds the expression for the age of the universe it is of the form

$$\begin{aligned} t_0-t_B= \frac{2H_0^{-1}}{{\bar{\zeta }}}\log \left( \frac{6}{6-{\bar{\zeta }}}\right) . \end{aligned}$$
(15)

For \({\bar{\zeta }}>6\) the age is not defined and consequently the universe does not have a big bang. But for the cases \({\bar{\zeta }}<6\) the universe does have a big bang. For the best estimates of the parameter the age of the universe is found to be around 10–12 Gy.

Fig. 2
figure 2

Evolution of scale factor with time. The thick line corresponds to \({\bar{\zeta }} =0.002\), the dashed line corresponds to \({\bar{\zeta }} =5.25\) (best estimate), and the dotted line corresponds to \({\bar{\zeta }}=6.5\)

Full size image

The equation of state of the bulk viscous fluid can be obtained using the standard relation,

(16)

where \(x=\ln a.\) Substituting for h in Eq. (16) using Eq. (9), we have

(17)

Figure 3 shows the variation of the equation of state parameter against the redshift at various choices of \({\bar{\zeta }}.\) In the extreme future (\(z \rightarrow -1\)), \(\omega _z \rightarrow -1\) and it hence corresponds to a de Sitter universe. Otherwise \(\omega _z\) shows a strong dependence on the bulk viscous parameter. For small viscosity, the equation of state parameter remains 1 but reduces to \(-1\) in the distant future. For \({\bar{\zeta }}<6\), like \({\bar{\zeta }}=5.25\), the best estimated value, \(\omega _z\), is positive for \(z>1\). But in the subsequent evolution, it reduces to negative values and finally stabilizes at \(-1\) as \(z \rightarrow -1.\) This means that for \(z<1\) the bulk viscous Zel’dovich fluid mimics the quintessence nature for \({\bar{\zeta }}>6,\). For instance when \({\bar{\zeta }}=6.5\) as in the figure, when \(\omega _z\le -1\) always, it corresponds to a phantom nature.

Fig. 3
figure 3

Evolution of \(\omega _z\) with respect to the scale factor. The thick line corresponds to \({\bar{\zeta }}=0.002\), the dashed line corresponds to \({\bar{\zeta }}=5.25\), and the dotted line corresponds to \({\bar{\zeta }}=6.5\)

Full size image
Fig. 4
figure 4

Evolution of deceleration parameter with respect to redshift. The thick line corresponds to \({\bar{\zeta }}=0.002\), the dashed line corresponds to \({\bar{\zeta }}=5.25\), and the dotted line corresponds to \({\bar{\zeta }}=6.5\)

Full size image

We have also evaluated the deceleration parameter. The basic equation of the deceleration parameter is

$$\begin{aligned} q=-1-\frac{{\dot{H}}}{H^2}. \end{aligned}$$
(18)

Substituting for \(H=H_0h\) from Eq. (9) we have

$$\begin{aligned} q=-1+\frac{3(6-{\bar{\zeta }})}{{\bar{\zeta }} a^3+(6-{\bar{\zeta }})}. \end{aligned}$$
(19)

As seen in Fig. 4, the deceleration parameter q remains \(-1\) for all possible \({\bar{\zeta }}\) in the distant future. For a small value of \({\bar{\zeta }}\) the deceleration remains at 2 until a distant future when it drops to \(-1.\) For the best estimated value of \({\bar{\zeta }}=5.25,\) the switchover from deceleration to acceleration takes place at about \(z=0.52\), which is closely in agreement with the observational constraints. The same will proceed with ever increasing acceleration to an asymptotic value of \(-1\) in a distant future. For values of \({\bar{\zeta }}>6.0,\) such as the one indicated for \({\bar{\zeta }}=6.5\) as in Fig. 4, q is always negative and is increasing as the universe expands, saturating to \(-1\) at \(z \rightarrow -1\) in the future. So the final state of the universe in this model is a de Sitter universe for any positive value \({\bar{\zeta }}.\)

3 Phase-space perspective

A convenient method to understand the global picture of the model is to study the equivalent phase space. A phase-space analysis of the model would indicate whether the model is compatible with a realistic evolution of the universe, i.e. the possible existence of the different stages of the universe like a radiation dominated early phase, and then a matter dominated phase followed by the late accelerating phase. But it is generally difficult to solve the cosmological field equations with more than one cosmic component. For doing the phase-space analysis, one has first to identify the phase-space variables and be able to write down the cosmological equations as a system of autonomous differential equations. The critical points of these autonomous differential equations can then be correlated to the cosmological solutions. The stability of such critical points can be determined by examining the system obtained by linearizing about the critical point. If the critical points were a global attractor, then the trajectories of the autonomous system constructed near a critical point will always be attracted toward it, independent of the initial condition, and it will be stable one.

3.1 Analysis of Zel’dovich fluid in two dimensional phase space

In this section we analyze the phase-space behavior of a flat universe dominated with a bulk viscous Zel’dovich fluid. The behavior of the system in the two dimensional phase space with h and \(\Omega _z\) as the coordinates is examined. The corresponding universe is the one with only a bulk viscous Zel’dovich fluid as the only component. The coupled differential equations are

$$\begin{aligned} {\dot{h}}=H_0\left( \frac{{\bar{\zeta }}}{2}-3h\Omega _z\right) h=P(h,\Omega _z), \end{aligned}$$
(20)
$$\begin{aligned} {\dot{\Omega }}_z=-H_0\left[ \left( 6\left( \Omega _z-1\right) h-{\bar{\zeta }}\right) \Omega _z-{\bar{\zeta }}\right] =Q(h,\Omega _z), \end{aligned}$$
(21)

where \(h=H/H_0\) and \(\Omega _z=\rho _z/3H^2\) and the over-dot refers to a derivative with respect to time. By setting \({\dot{h}}=0\) and \({\dot{\Omega }}_z=0\), we obtain the following three critical points or roots:

$$\begin{aligned} (h_c,\Omega _{zc})=(0,1), \left( \frac{0.87667}{\Omega _z},\Omega _z \right) ,(0.87667,1). \end{aligned}$$
(22)

The first root, (0,1), has a Hubble parameter zero and hence corresponds to a static universe, while the second root depends on the instantaneous value of \(\Omega _z,\) which follows a trajectory as the Zel’dovich fluid density changes, and hence it is not a fixed point. The third root \((h_c,\Omega _{zc})=(0.87667,1)\), having a positive definite value of the Hubble parameter and mass parameter of the Zel’dovich fluid, corresponds to an expanding universe dominated by Zel’dovich fluid. If the system is stable in the neighborhood of a critical point, the linear perturbation in its neighborhood in phase space decays with time. The perturbations around the critical points must satisfy the following matrix equation:

$$\begin{aligned} \begin{bmatrix} {\dot{\epsilon }} \\ {\dot{\eta }} \end{bmatrix} =\begin{bmatrix} \left( \frac{\partial P}{\partial h}\right) _0&\left( \frac{\partial P}{\partial \Omega _z}\right) _0\\ \left( \frac{\partial Q}{\partial h}\right) _0&\left( \frac{\partial Q}{\partial \Omega _z}\right) _0 \end{bmatrix} \begin{bmatrix} \epsilon \\ \eta \end{bmatrix}. \end{aligned}$$
(23)

Here \(\epsilon \) and \(\eta \) are perturbations in h and \(\Omega _z\), respectively, in the neighborhood about a given critical point. The suffix 0 denotes the value evaluated at the critical point, \((h_c,\Omega _{zc}).\) The corresponding Jacobian is

$$\begin{aligned} \begin{bmatrix} \left( \frac{\partial P}{\partial h}\right) _0&\left( \frac{\partial P}{\partial \Omega _z}\right) _0\\ \left( \frac{\partial Q}{\partial h}\right) _0&\left( \frac{\partial Q}{\partial \Omega _z}\right) _0 \end{bmatrix}= H_0 \begin{bmatrix} \left( \frac{{\bar{\zeta }}}{2}-6h\Omega _z\right) \&-3h^2 \\ 6\Omega _z(1-\Omega _z)\&\frac{{\bar{\zeta }}}{2}+3h(1-2\Omega _z) \end{bmatrix}.\nonumber \\ \end{aligned}$$
(24)

If the eigenvalues of the Jacobian matrix are all negative, then the critical point is stable, otherwise the critical point is generally unstable. If the eigenvalues are positive, then the critical point is an unstable node, and if there are both positive and negative eigenvalues, then the critical point is a saddle point.

The eigenvalues corresponding to the first critical point \( (h_c,\Omega _{zc})=(0,1)\) are found to be \(-368.2\) and 184.2. As they are of opposite signs the critical point is a saddle point and hence is unstable. Depending on the initial conditions the nearby trajectories around this point may approach the saddle point, but are repelled by it, finally approaching a possible stable attractor in the future. As in Fig. 5 the trajectories are turning away from the equilibrium point as and when they approach it and finally converge on the critical point shown on the right side of the plot.

The second critical point \((\frac{0.87667}{\Omega _z},\Omega _z)\) is not an isolated point, but varies with \(\Omega _z.\) As per the relationship between h and \(\Omega _z,\) it represents a rectangular hyperbola with the axes \(h=0\) and \(\Omega _z=0\) as asymptotes. The eigenvalues are found to be \((-184.1, \frac{-161.394}{\Omega _z^2}).\) Since both eigenvalues are negative and real, the neighboring trajectories will converge on to the hyperbola and hence the critical point is a stable one. The hyperbola along which the \(\Omega _z\) dependent critical point moves has the coordinate axes \(h=0\) and \(\Omega _z=0\) as the asymptotes, \(h=-\Omega _z\) as the directrix, and (0.9363, 0.9363) as the focus.

Fig. 5
figure 5

Phase-space structure around the critical points. The first critical point (0, 1) is a saddle point. The vector diagram clearly indicates that the trajectories approaching this point are repelled away and are finally converging to the attractor critical point on the right

Full size image

The third critical point is \((h_c,\Omega _{zc})=(0.87667,1).\) It is observed, as in Fig. 5, that this critical point is a global attractor, and physically it corresponds to a flat expanding universe dominated by a bulk viscous Zel’dovich fluid. We linearize Eq. (20), around the third critical point, and formulate the matrix equation similar to Eq. (23). The corresponding eigenvalues are found to be \(-184.2\) and 0.0. The resulting two eigenvalues clearly indicate that the model is stable for all possible initial conditions around this critical point. It appears that the second eigenvalue 0 is suggestive of the absence of any isolated critical point and rather a line segment as a continuous array of critical points. However, a close examination of the vector field plot as in Fig. 6 shows that the field directions are invariably tilted, though slightly, toward a fixed critical point as they approach. However, on low resolution, it seems to be a straight line toward the isolated critical point. This is evident from the continuous plot in the phase-space structure as shown in Fig. 7. So, in reality the isolated critical point exists and the ’0’ eigenvalue leads to a line segment as the best fit close to the critical point. This is clear from the fact that the straight line does not arise from the original procedure of setting \({\dot{h}}=0\) and \({\dot{\Omega }}_z=0\) without the linear approximation and rather results in an isolated point. So, as we said earlier, depending on the initial conditions the trajectories emanating from the surroundings of the saddle critical point are repelled away from it and they finally approach the stable critical point, (0.87667, 1). From the equations of the deceleration parameter (Eq. (18)), it can easily be seen that this critical point corresponds to \(q < 0\) and implies an accelerating phase. This, by and large, implies the stability of the universe dominated by the bulk viscous Zel’dovich fluid, which accelerates the expansion in the later stage.

Fig. 6
figure 6

Vector field plot of the phase space around the third critical point (0, 87667, 1). The vectors encircled show their continuous tilt toward the critical point

Full size image
Fig. 7
figure 7

Plot of phase-space trajectories around the critical point (0, 87667, 1). All trajectories are converging to the critical point and hence it is stable

Full size image

3.2 Analysis of Zel’dovich fluid in the three dimensional phase space

In the realistic case, the universe has a radiation dominated phase followed by a matter dominated phase and a subsequent late accelerated epoch. In order for the present model to imply a realistic evolution of the universe, it predicts a prior radiation dominated phase. Thus, aware of this, we include, besides the Zel’dovich fluid, the conventional radiation also to study the phase-space structure. On including the radiation component also, the first Friedmann equation becomes

$$\begin{aligned} 3H^2=\rho _z+\rho _\gamma , \end{aligned}$$
(25)

where \(\rho _\gamma \) is the radiation density. The conservation equation for the radiation component, by assuming a pressure \(p_\gamma =\rho _\gamma /3\), is

$$\begin{aligned} {\dot{\rho }}_\gamma +4H\rho _\gamma =0. \end{aligned}$$
(26)

The phase-space variables are h, \(\Omega _z\), and \(\Omega _\gamma \) among which the third parameter is \(\Omega _\gamma =\rho _\gamma /3H^2.\) The dynamical equations for these parameters are represented by the coupled differential equations,

$$\begin{aligned} {\dot{h}}= & {} P(h,\Omega _z,\Omega _\gamma )=\left( (3\Omega _z+2\Omega _{\gamma })h-\frac{{\bar{\zeta }}}{2}, \right) h \end{aligned}$$
(27)
$$\begin{aligned} {\dot{\Omega }}_z= & {} Q(h,\Omega _z,\Omega _\gamma )=\left[ 2\left( (3\Omega _z+2\Omega _{\gamma })h-\frac{{\bar{\zeta }} }{2}\right) -6h\right] \Omega _z+{\bar{\zeta }},\nonumber \\ \end{aligned}$$
(28)

and

$$\begin{aligned} {\dot{\Omega }}_{\gamma }=R(h,\Omega _z,\Omega _\gamma )=\left[ 2\left( (3\Omega _z+2\Omega _{\gamma })h-\frac{{\bar{\zeta }} }{2}\right) -2h\right] \Omega _{\gamma }.\nonumber \\ \end{aligned}$$
(29)

The critical points are obtained by setting

$$\begin{aligned} {\dot{h}}=0,\qquad {\dot{\Omega }}_z=0, \qquad {\dot{\Omega }}_{\gamma }=0, \end{aligned}$$
(30)

and they are

$$\begin{aligned} (h_c,\Omega _{zc},\Omega _{{\gamma }c})=\left( \frac{0.87667}{\Omega _{z}}, \Omega _{z},0) ; \, (0,1,0\right) ; \, (1,0.87667,0),\nonumber \\ \end{aligned}$$
(31)

out of which the first critical point is not an isolated one, since in this case h is inversely proportional to the instantaneous value of \(\Omega _z\). The second critical point, (0, 1, 0), has the Hubble parameter \(h=0\), hence corresponds to static universe, and the third one corresponds to an expanding universe dominated by a bulk viscous Zel’dovich fluid. It is to be noted that there is no critical point corresponding to a radiation dominated phase. The stability of the equilibrium points in the case of these three critical points is obtained (this time in the 3D phase-space case), once again by looking at the behavior of phase-space trajectories close to them and generated due to different initial conditions. The coupled differential equations in the linear limit in matrix representation, in the neighborhood of the equilibrium points, are

$$\begin{aligned} \begin{bmatrix} {\dot{\epsilon }} \\ {\dot{\eta }} \\ {\dot{\nu }} \end{bmatrix} =\begin{bmatrix} \left( \frac{\partial P}{\partial h}\right) _0&\left( \frac{\partial P}{\partial \Omega _z}\right) _0&\left( \frac{\partial P}{\partial \Omega _\gamma }\right) _0\\ \left( \frac{\partial Q}{\partial h}\right) _0&\left( \frac{\partial Q}{\partial \Omega _z}\right) _0&\left( \frac{\partial Q}{\partial \Omega _\gamma }\right) _0\\ \left( \frac{\partial R}{\partial h}\right) _0&\left( \frac{\partial R}{\partial \Omega _z}\right) _0&\left( \frac{\partial R}{\partial \Omega _\gamma }\right) _0 \end{bmatrix} \begin{bmatrix} \epsilon \\ \eta \\ \nu \end{bmatrix} \end{aligned}$$
(32)

where \({\dot{\epsilon }}\), \({\dot{\eta }}\), and \({\dot{\nu }}\) are first order perturbation terms of \(P(h,\Omega _z,\Omega _\gamma )={\dot{h}}\), \(Q(h,\Omega _z,\Omega _\gamma )={\dot{\Omega }}_z\), and \(R(h,\Omega _z,\Omega _\gamma )={\dot{\Omega }}_{\gamma }\), respectively, \(\epsilon (t)\), \(\eta (t)\), and \(\nu (t)\) being the first order linear perturbation terms of \(h,\Omega _z\), and \(\Omega _\gamma \), respectively. The square matrix term in Eq. (32) is the Jacobian evaluated at the critical point. We then decouple the differential equations (32) by means of the secular equation and in the process the eigenvalues corresponding to the equilibrium point \((\frac{0.87667}{\Omega _{zc}},\Omega _{zc},0)\) are obtained:

$$\begin{aligned} \begin{array}{ll} \lambda _1 = \frac{0.5}{\Omega _z}\left( -368.2+365.57\Omega _z \right. \\ \left. \quad - \sqrt{135571- 269206\Omega _z+13364\Omega _z^2}\right) , \end{array} \end{aligned}$$
(33)
$$\begin{aligned} \begin{array}{ll} \lambda _2=\frac{0.5}{\Omega _z}\left( -368.2+365.57\Omega _z \right. \\ \left. \quad + \sqrt{135571- 269206\Omega _z+13364\Omega _z^2}\right) , \end{array} \end{aligned}$$
(34)

and

$$\begin{aligned} \lambda _3=\frac{245.466}{\Omega _z}, \end{aligned}$$
(35)

all depending on the instantaneous value of \(\Omega _z.\) The critical point in this case drifts with the variation of \(\Omega _z\) along a rectangular hyperbola on the h–\(\Omega _z\) plane; with the details of the hyperbola the same as in the case of the second critical point in Sect. 3.1. The eigenvalues indicate that the phase-space trajectories, corresponding to various initial conditions, move away from the critical point and hence there is no stable situation. Even when \(\Omega _z=0\) the eigenvalues are such that \(\lambda _1\) is negative, \(\lambda _2=0\), and \(\lambda _3\) positive, and so no stable solution is implied.

Fig. 8
figure 8

Vector field plot of the phase-space structure around the critical point (1, 0.87667, 0)

Full size image

The second critical point (0, 1, 0) has the eigenvalues \(-368.2,\) 368.2, and 184.1, and the third critical point (1, 0.87667, 0) has the eigenvalues \(-403.778, 280.0\), and 167.878. There is one negative eigenvalue and there are two positive eigenvalues for each critical point, which again means there is no stability for the equilibrium points. This means that the phase-space trajectories are not attracted by any of the critical points in the three dimensional case. For example the vector field plot as in Fig. 8 clearly indicates how the phase-space trajectories corresponding to various initial conditions are repelled from, rather than being attracted to the second critical point. So none of the critical points in this case corresponds to a radiation dominated phase and also even the existing critical points are not stable. In fact the third critical point, which corresponds to a Zel’dovich fluid dominated one, is unstable, and it can be concluded that the inclusion of the radiation component may lead to a complete breakdown of the model. The bulk viscous coefficient is taken as a constant in the present study. Since it is a transport coefficient which may depend on the velocity of the fluid component also, such a velocity dependent bulk viscous coefficient may be checked for consistency of a prior radiation dominated phase and this problem we reserve for a future work.

4 Conclusion

In this paper we have considered a flat universe consisting of a bulk viscous Zel’dovich fluid. The viscosity parameter was incorporated as per Eckart’s formalism. We have evaluated the evolution of the Hubble parameter. The model was constrained with SNe Ia data to evaluate the bulk viscous coefficient as \({\bar{\zeta }}=5.25\pm 0.14\) and the present value of Hubble parameter \(H_0=70.20\pm 0.58.\) The behavior of the resulting scale factor shows that the model predicts a late acceleration in the expansion of the universe. Hence the bulk viscous Zel’dovich fluid can mimic the role of the conventional dark energy.

We also studied the model to analyze the stability of the solutions corresponding to various scenarios using the phase-space analysis method. We first analyzed the two dimensional phase-space behavior, where the contribution due to radiation is neglected, and found that there is a past unstable saddle critical point corresponding to a static universe. The phase-space trajectories originating form the vicinity of this saddle like point are repelled away from it and move toward the stable critical point corresponding to an expanding universe dominated by Zel’dovich fluid.

In the second instance we considered a three dimensional phase-space case by incorporating the radiation component too. But obtaining the analytical solution in a two-component universe, especially when one of the fluids is viscous, is practically difficult or impossible, so we have made a suitable phase-space analysis. In this case no critical points are found corresponding to a prior radiation dominated phase; moreover, none of the existing critical points is stable. Hence the present model of the universe with a bulk viscous Zel’dovich fluid, in which the bulk viscosity is characterized by a constant coefficient, first of all, fails to predict a prior radiation dominated phase and, second, the very inclusion of radiation makes the model unstable.