A comprehensive study to the assessment of Arrhenius activation energy and binary chemical reaction in swirling flow

Abstract

Nanotechnology research has a huge impact upon biomedicine and at the forefront of this area are micro and nano devices that use active/controlled motion. In this connection, it is focus to investigate steady three dimensional rotating flow with heat and mass transfer incorporating gyrotactic microorganisms. Buongiorno’s nanofluid formulation is followed for thermophoresis and Brownian motion, porous space, Arrhenius activation energy and binary chemical reaction with some other effects. An enhanced analytical method is applied to solve the nondimensional equations. The non-dimensional parameters effects on the fields of velocity, temperature, nanoparticles concentration and gyrotactic microorganisms concentration are shown graphically. Velocity decreases while temperature and nanoparticles concentration increase with magnetic field strength. Gyrotatic microorganisms motion becomes slow with rotation parameter. Due to rotation, the present problem can be applied in microbial fuel cells, food processing, microbiology, biotechnology and environmental sciences, electric power generating and turbine systems, computer disk drives, mass spectromentries and jet motors.

Introduction

Energy conservation is the voice of the day. All the old methods which restored the energy resources or storage are given up due to the speed of modern life requirements. It is required that to have more energy on account of less expenditures of raw materials which are producer of less byproduct in the form of environmental pollution. In these days scientists and researchers consider nanotechnology as the best option to have all the potentials of present time energy conservations. Nanotechnology rests on nanoparticles made of metallic, non-metallic, carbide or oxide materials having the radius in 100 nm. Choi¹ was the first one who opened the door of nanotechnology by working on nanofluid. Nanofluids have the tonic role when used with microorganisms to provide useful products for life and to eradicate the serious environmental issues. Al-Khaled et al.² studied theoretically the application of bioconvection phenomena in periodically flow of tangent hyperbolic nanofluid over an accelerated moving surface with nonlinear thermal radiation, chemical reaction, thermophoresis and Brownian motion. Khan et al.³ used convective Nield boundary conditions to investigate the rheology of couple stress nanofluid with activation energy, porous media, thermal radiation, gyrotactic microorganisms employing Buongiorno nanofluid model, in addition to, second-order velocity slip (Wu’s slip). Tlili et al.⁴ presented a novel study about the flow, heat and mass transfer as well as motile microorganisms of magnetohydrodynamic Oldroyd-B nanofluid past a stretching cylinder. Alwatban et al.⁵ explained the rheological aspects of Eyring Powell nanofluid past a moving surface where velocity decreases with magnetic force and porous medium while non-Newtonian parameter has opposite effects on velocity. Waqas et al.⁶ worked on numerical side of stretching flow of micropolar nanofluid with microorganisms, activation energy and convective Nield boundary conditions implementing shooting method. Waqas et al.⁷ also organized a project to deliver the explorations on Maxwell viscoelasticity-based micropolar nanofluid with porous media using MATLAB bvp4c package where velocity increases with slip and micro-rotation parameters. Khan et al.⁸ reflected on most gains achieved by including copper nanomaterial in the base fluid. Highest volumes were witnessed in conductivity. Zuhra et al.⁹ estimated the revenue on graphene nanoparticles used for the thermal conductivity. Cloud enhancement rose with the addition of nanopartices. Nanofluid and thermodynamic literature can also exists in the literature with refs. ^{10,11,12,13,14,15,16,17,18,19}.

Rotating flows have applications in formulating the conditions inside the wheel spacing of gas turbines as well as in rotating cavity to model the conditions between compressor disks or co-rotating turbines, thin film fluid flow through a rotating surface, conical diffuser circulative flow, impinging jet disk cooling, shrouded rotation of disks, contra-rotating disks for wheel space in contra-rotating disks of existing engines, gears, bearings, rolling elements, polymer processing, lubrication systems etc. Khan et al.²⁰ provided a sharp entrant into the rapid rotating business which has played catch up with profiles such as flow, heat transfer, chemical reactions and entropy generation. Ahmad et al.²¹ paid attention to the nanofluid whose thermal conductivity jumped on higher quantity as the nanoparticles rise, while a short-covering rally in rotating flow is also added. Hayat et al.²² treated Arrhenius activation energy and binary chemical reaction, irreversibility, heat generation/absorption, viscous dissipation, Brownian motion, thermophoresis in the thermodynamics of Ree-Eyring fluid with nanomaterials in two rotating disks. Li et al.²³ at bioconvection rotating flow opened on a positive note and started to write that exact solutions are obtained analytically for the nonlinear phenomena and the study could provide a theoretical base for comprehending the transportation of unsteady bioconvection. Hayat et al.²⁴ among the key sectors, presented exploration that has rotating linked benefits while flow rate are also remained higher on higher quantity of relevant parameter.

Fluid flows in porous media have numerous applications in environmental sciences and industries like ground water systems, erection of oil reservoirs in insulating systems, geothermal energy systems, heat exchange layouts, nuclear waste disposal, catalytic reactors, flow of water in reservoirs etc. Khan et al.²⁵ shared the index gained for flow and heat transfer at high values of parameters where thermal system shows that as many as parameters were active all of them declined the profile. Rahman et al.²⁶ disclosed that the heating volumes stood high as compared with the turn over of magnetic field parameter quantities. Heat quantifies sharply higher led by suction parameter depreciation in the thermal system while pressure remained also higher for nanoparticles. Khan et al.²⁷ analyzed the Darcy law for porous medium to show the effects on flow and heat transfer of second-grade fluid. Zuhra et al.²⁸ worked on porous medium to investigate the flow of gyrotatic microorganisms and homogeneous-heterogeneous chemical reactions with buoyancy effects. Khan et al.²⁹ reported the role of porous medium in second-grade liquid film flow and heat transfer with entropy generation, chemical reaction and stratification. Palwasha et al.³⁰ discussed porous medium for simultaneous flow and heat transfer in two non-Newtonian nanoliquids with gyrotactic microorganisms and nanoparticles. Khan et al.³¹ presented the porous medium behavior for MHD second-grade nanofluid flow, heat and mass transfer as well as gyrotactic microorganisms in gravity driven problem.

Microorganisms have played a vital role in improving the human beings life, especially, due to the applications on medical side. Without the useful microorganisms, life is impossible to lead. These organisms are too small to see even through a powerful microscope but do big for the environment. Their participation in life is in biofuels, industrial and environmental systems, enzyme biosensors, mass transportations, biotechnology and biological sciences. Researchers have deep interest to work on microorganisms. Khan et al.³² reported a likely surge in nanoparticles and motile organisms transports supporting parametric study. Positive impact of gyrotactic microorganisms fall on the systems denominated by fluid flow. Zuhra et al.³³ presented a study that stands for the thermal system decline due to higher assigned values of energy parameter of slip. Khan et al.³⁴ assembled conclusions on liquid velocity and heating transportation with small organisms as sharp valuation in systems takes place on account of gyrotactic microorganisms. Zuhra et al.³⁵ expected more gains achieved through following the gyrotactic microorganisms for convective instability enhancement possibly facilitating the conduction. Khan et al.³⁶ presented the bioconvection in nanofluid flow in rotating system with entropy generation which shows that gyrotatic microorganisms flow is reduced with increasing the rotation parameter.

Arrhenius activation energy (AAE) is the minimum energy required to start the chemical reaction on which pioneered work is of Arrhenius in 1889. On acquiring the AAE, the particles (atoms, molecules) are ready to take part in chemical reaction. AAE has applications in oil and pharmaceutical industries, MHD, environmental and geothermal systems. More studies and applications of AAE and binary chemical reactions (BCR) are already discussed in the studies with refs. ^{3,4,5,6,11,22}.

To discuss AAE and BCR with bioconvection due to gyrotactic microorganisms in rotating systems of two disks is still require explorations. So, the present study reflects highest gains on including, movements, heating capability, saturation and gyrotactic microorganisms due to Arrhenius activation energy and binary chemical reaction via optimal homotopy analysis method^22,37.

Method

Formulation

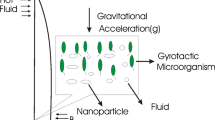
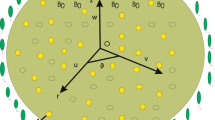
A revolving movement of magnetized, time non-reliant and lack of compressible nanodispersion in three dimensions is under focused in the persistence of porous region, AAE and BCR. A below disc is situated at z equal to zero. Both the discs are at a distance H apart. The speed of below and upper discs are respectively Ω₁ and Ω₂. Similarly their expanding values are respectively a₁ and a₂. Magnetic environment also exists carrying the power B₀ along with the z-side (please consult to Fig. 1).

Figure 1

Geometry of the problem.

For the life of microorganisms, aquas exits as the background dispersion accompanying nanoparticles. The temperatures, tiny particles concentrations and gyrotactic microorganisms are (T₁, T₂), (C₁, C₂) and (N₁, N₂) on the respective disks. The tiny particles saturation on both the disks are obeyed by the actively confined formulation i. e. there exist the tiny particles motion at the walls. Consideration is taken for the tiny particles dispersion that the background dispersion is strong which keeps nothing with the swimming direction as well as movement of the small organisms. The below several profile statements carrying the preservation of grand amount of matter, movement, heating notion, tiny particles saturation, accompanying small organisms are given as in²³

$$\nabla \cdot {\bf{v}}=0,$$

(1)

$${\rho }_{f}({\bf{v}}\cdot \nabla )\nabla \cdot {\bf{v}}=-\nabla p+{\mu }_{f}{\nabla }^{2}{\bf{v}},$$

(2)

$${(\rho c)}_{P}({\bf{v}}\cdot \nabla )T=\alpha {\nabla }^{2}T+\tau \left[\begin{array}{c}{D}_{B}\nabla T\cdot \nabla C+\left(\begin{array}{c}\frac{{D}_{T}}{{T}_{2}}\end{array}\right)\nabla T\cdot \nabla T\end{array}\right],$$

(3)

$$({\bf{v}}\cdot \nabla )C={D}_{B}{\nabla }^{2}C+\left(\begin{array}{c}\frac{{D}_{T}}{{T}_{2}}\end{array}\right){\nabla }^{2}T,$$

(4)

$$\nabla \cdot {\bf{j}}=0,$$

(5)

where v = (u, v, w) manifests the velocity of the nanodispersion, C manifests the tiny particle saturation, ρ_f manifests the tiny dispersion density, P manifests force per unit area, μ_f manifests dynamic viscosity reliant to nanodispersion and small organisms, α manifests heating diffusion of the nanodispersion, $\tau =\frac{{(\rho c)}_{P}}{{(\rho c)}_{f}}$ in which (ρc)_P denotes the heating storage space of tiny particles and (ρc)_f denotes the heating storage space reliant to dispersion. The subscript “f” is used for the base fluid. D_B manifests the nanoparticles random motion diffusivity notation, D_T manifests the heat reliant diffusivity constant, j manifests the microorganisms flux defined as²³

$${\bf{j}}=N{\bf{v}}+N\tilde{v}-{D}_{n}\nabla N,$$

(6)

notice that N manifests the distribution of small organisms, D_n manifests the diffusion of small organisms, $\tilde{v}$ manifests the mean rate of velocity of gyrotactic microorganisms which physical quantity having direction is defined as²³

$$\tilde{v}=\left(\begin{array}{c}\frac{b{W}_{c}}{\Delta C}\end{array}\right)\nabla C,$$

(7)

notice that b manifests the chemotaxis nonvariable and W_c manifests the highest cell traveling motion.

Working on Eqs. (1–5), the velocity, heating, saturation and distribution of small organisms accompanying the effects of magnet environment, porous media, heat source/sink and activation energy with binary chemical reaction are as of a form of^{20,21,22,23,24,25}

$$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0,$$

(8)

$${\rho }_{f}\left(\begin{array}{c}u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{{v}^{2}}{r}\end{array}\right)=-\frac{\partial p}{\partial r}+{\mu }_{f}\left(\begin{array}{c}\frac{1}{r}\frac{\partial u}{\partial r}-\frac{u}{{r}^{2}}+\frac{{\partial }^{2}u}{\partial {r}^{2}}+\frac{{\partial }^{2}u}{\partial {z}^{2}}\end{array}\right)-{\sigma }_{f}{B}_{0}^{2}u-\frac{{\mu }_{f}}{{k}_{0}}u,$$

(9)

$${\rho }_{f}\left(\begin{array}{c}u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}+\frac{uv}{r}\end{array}\right)={\mu }_{f}\left(\begin{array}{c}\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{{r}^{2}}+\frac{{\partial }^{2}v}{\partial {r}^{2}}+\frac{{\partial }^{2}v}{\partial {z}^{2}}\end{array}\right)-{\sigma }_{f}{B}_{0}^{2}v-\frac{{\mu }_{f}}{{k}_{0}}v,$$

(10)

$${\rho }_{f}\left(\begin{array}{c}{\rm{u}}\frac{\partial w}{\partial r}+{\rm{w}}\frac{\partial w}{\partial z}\end{array}\right)=-\frac{\partial p}{\partial z}+{\mu }_{f}\left(\begin{array}{c}\frac{1}{r}\frac{\partial w}{\partial r}+\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{{\partial }^{2}w}{\partial {z}^{2}}\end{array}\right)-\frac{{\mu }_{f}}{{k}_{0}}w,$$

(11)

$$\begin{array}{c}\left(\begin{array}{c}u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}\end{array}\right)=\alpha \left(\begin{array}{c}\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial {r}^{2}}+\frac{{\partial }^{2}T}{\partial {z}^{2}}\end{array}\right)\\ \,+\tau \left[\begin{array}{c}{D}_{B}\left(\begin{array}{c}\frac{\partial T}{\partial r}\frac{\partial C}{\partial r}+\frac{\partial T}{\partial z}\frac{\partial C}{\partial z}\end{array}\right)+\frac{{D}_{T}}{{T}_{2}}{\left(\begin{array}{c}\frac{\partial T}{\partial r}\end{array}\right)}^{2}+{\left(\begin{array}{c}\frac{\partial T}{\partial z}\end{array}\right)}^{2}\end{array}\right]\\ \,+{\sigma }_{f}{B}_{0}^{2}({u}^{2}+{v}^{2})+{Q}_{0}(T-{T}_{2}),\end{array}$$

(12)

$$\begin{array}{c}u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}={D}_{B}\left(\begin{array}{c}\frac{1}{r}\frac{\partial C}{\partial r}+\frac{{\partial }^{2}C}{\partial {r}^{2}}+\frac{{\partial }^{2}C}{\partial {z}^{2}}\end{array}\right)+\frac{{D}_{T}}{{T}_{2}}\left(\begin{array}{c}\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial {r}^{2}}+\frac{{\partial }^{2}T}{\partial {z}^{2}}\end{array}\right)\\ \,-{k}_{r}^{2}(C-{C}_{2}){\left[\begin{array}{c}\frac{T}{{T}_{\infty }}\end{array}\right]}^{m}\exp \left[\begin{array}{c}\frac{-{E}_{a}}{\kappa T}\end{array}\right],\end{array}$$

(13)

$$w\frac{\partial N}{\partial z}+\tilde{w}\frac{\partial N}{\partial z}+N\frac{\partial \tilde{w}}{\partial z}={D}_{n}\frac{{\partial }^{2}N}{\partial {z}^{2}},$$

(14)

upon the extra informations

$$u=r{a}_{1},\,v=r{\Omega }_{1},\,w=0,\,T={T}_{1},\,C={C}_{1},\,N={N}_{1},\,at\,z=0,$$

(15)

$$u=r{a}_{2},\,v=r{\Omega }_{2},\,w=0,\,T={T}_{2},\,C={C}_{2},\,N={N}_{2}\,at\,z=H,$$

(16)

notice that the constituents of velocity are u(r, ϑ, z), v(r, ϑ, z) and w(r, ϑ, z). σ_f is the electrical conductivity of nanofluid, B = (0, 0, B₀) is the magnet environment and k₀ stands for the porosity of space. Q₀ is the heat source/sink coefficient, m is the fitted rate constant such that (−1 < m < 1), E_a is the activation energy in which a is positive dimensional constant, κ = 8.61 × 10⁻⁵ eV/K is the Boltzmann constant and ${k}_{r}^{2}(C-{C}_{2})\,{\left[\begin{array}{c}\frac{T}{{T}_{\infty }}\end{array}\right]}^{m}\exp \frac{-{E}_{a}}{\kappa T}$ is the modified Arrhenius term. $\tilde{w}=\left(\begin{array}{c}\frac{b{W}_{c}}{\varDelta C}\end{array}\right)\frac{\partial C}{\partial z}$ is the velocity component of the vector $\tilde{v}$ in z-side.

Introduced transformations are^23,24,25

$$\begin{array}{c}u=r{\Omega }_{1}f{\prime} (\zeta ),\,v=r{\Omega }_{1}g(\zeta ),\,w=-2H{\Omega }_{1}f(\zeta ),\,\theta (\zeta )=\frac{T-{T}_{2}}{{T}_{1}-{T}_{2}},\,\phi (\zeta )=\frac{C-{C}_{2}}{{C}_{1}-{C}_{2}},\\ h(\zeta )=\frac{N-{N}_{2}}{{N}_{1}-{N}_{2}},\,P={\rho }_{f}{\Omega }_{1}{\nu }_{f}\left(\begin{array}{c}P(\zeta )+\frac{{r}^{2}\varepsilon }{2{H}^{2}}\end{array}\right),\,\zeta =\frac{z}{H},\end{array}$$

(17)

where ${\nu }_{f}=\frac{{\mu }_{f}}{{\rho }_{f}}$ manifests the movement viscousness and $\epsilon$ is the force per unit area representative.

Equation (17) at once justifies the preservation of quantity of matter Eq. (8). Substituting the assignments from Eq. (17) for Eqs. (9–16)

$$f{\prime\prime} {\prime} +\mathrm{Re}\left(\begin{array}{c}2ff{\prime\prime} -f{{\prime} }^{2}+{g}^{2}-Mf{\prime} -\frac{1}{\lambda }f{\prime} \end{array}\right)-\epsilon =0,$$

(18)

$$g{\prime\prime} +\mathrm{Re}\left(\begin{array}{c}2fg{\prime} -Mg{\prime} -\frac{1}{\lambda }g\end{array}\right)=0,$$

(19)

$$P{\prime} =\frac{2}{\lambda }f{\prime} -4\mathrm{Re}ff{\prime} -f{\prime\prime} ,$$

(20)

$$\theta {\prime\prime} +{\Pr }{Re}[\begin{array}{c}2f\theta {\prime} +MEc\,(\begin{array}{c}{(f{\prime} )}^{2}+{g}^{2}\end{array})\end{array}]+Nb\theta {\prime} \phi {\prime} +Nt{(\theta {\prime} )}^{2}+\gamma \theta =0,$$

(21)

$$\phi {\prime\prime} +{Re}\left(\begin{array}{c}2Lef\phi {\prime} +\frac{Nt}{Nb}\theta {\prime} \end{array}\right)+{\gamma }_{1}{({\gamma }_{2}\theta +1)}^{m}\phi \,\exp \,\left(\begin{array}{c}\frac{-E}{{\gamma }_{2}\theta +1}\end{array}\right)=0,$$

(22)

$$h{\prime\prime} +{Re}[\begin{array}{c}2Scfh{\prime} +Pe(h{\prime} \phi {\prime} -h\phi {\prime\prime} )\end{array}]=0,$$

(23)

$$f=0,\,f{\prime} ={k}_{1},\,g=1,\,\theta =1,\,\phi =1,\,h=1,\,P=0\,at\,\zeta =0,$$

(24)

$$f=0,\,f{\prime} ={k}_{2},\,g=\Omega ,\,\theta =0,\,\phi =0,\,h=0\,at\,\zeta =1,$$

(25)

notice that prime (′) represents the differentiability on behalf of ζ. $\Omega =\frac{{\Omega }_{2}}{{\Omega }_{1}}$ is the rotation representative, $\mathrm{Re}=\frac{{\Omega }_{1}{H}^{2}}{{\nu }_{f}}$ manifests the Reynolds quantity, $M=\frac{{\sigma }_{f}{B}_{0}^{2}}{{\rho }_{f}{\Omega }_{1}}$ represents the magnetic field parameter, $\lambda =\frac{{k}_{0}{\Omega }_{1}}{{\nu }_{f}}$ manifests the porosity representative, $\Pr =\frac{{(\rho {c}_{P})}_{f}{\nu }_{f}}{\alpha }$ denotes the Prandtl quantity and $Ec=\frac{{r}^{2}{\Omega }_{1}^{2}}{{c}_{P}({T}_{1}-{T}_{2})}$ is the Eckert quantity, $Le=\frac{{\nu }_{f}}{{D}_{B}}$ represents the Levis representative, $Sc=\frac{{\nu }_{f}}{{D}_{n}}$ represents the Schmidt representative, and $Pe=\frac{b{W}_{c}}{{D}_{n}}$ represents the Peclet representative. The scaled stretching parameters are defined as ${k}_{1}=\frac{{a}_{1}}{{\Omega }_{1}}$, and ${k}_{2}=\frac{{a}_{2}}{{\Omega }_{1}}$. $Nb=\frac{{D}_{B}({C}_{2}-{C}_{1})}{{\nu }_{f}}$ manifests the random movement representative, $Nt=\frac{\tau {D}_{T}({T}_{2}-{T}_{1})}{{\nu }_{f}{T}_{1}}$ represents the thermophoresis representative. $\gamma =\frac{{Q}_{0}}{{\Omega }_{1}{(\rho {c}_{P})}_{f}}$, ${\gamma }_{1}=\frac{{k}_{r}^{2}{H}^{2}}{{\nu }_{f}}$, ${\gamma }_{2}=\frac{{T}_{1}-{T}_{2}}{{T}_{2}}$ and $E=\frac{{E}_{a}}{\kappa {T}_{2}}$ are the heat source/sink, chemical reaction, temperature difference and non-dimensional activation energy parameters respectively.

Upon differentiability of Eq. (18) on behalf of ζ, the equation accomplishes as

$$f{\prime\prime} {\prime\prime} +\mathrm{Re}\left(\begin{array}{c}2ff{\prime\prime} {\prime} +2gg{\prime} -Mf{\prime\prime} -\frac{1}{\lambda }f{\prime\prime} \end{array}\right)=0,$$

(26)

Attaining the solution for Eq. (18) and Eqs. (24–25), the force per unit area representative $\epsilon$ is evaluated like

$$\epsilon =f{\prime\prime} {\prime} (0)-\mathrm{Re}\left[\begin{array}{c}{(f{\prime} (0))}^{2}-{(g(0))}^{2}+Mf{\prime} (0)+\frac{1}{\lambda }f{\prime} (0)\end{array}\right],$$

(27)

Applying inverse process of differentiation on Eq. (20) on behalf of ζ and including the limits as zero to ζ on account of achieving the quantity P as

$$P=-2\left[\begin{array}{c}\mathrm{Re}\left(\begin{array}{c}{(f)}^{2}+\frac{1}{\lambda }{\int }_{0}^{\zeta }\,f\end{array}\right)+(f{\prime} -f{\prime} (0))\end{array}\right],$$

(28)

Computation methodology

Applying optimal homotopy analysis method (OHAM)^22,37, the starting approximations and helping linear quantities exists as

$$\begin{array}{c}{f}_{0}(\zeta )={k}_{1}\zeta -(2{k}_{1}+{k}_{2}){\zeta }^{2}+({k}_{1}+{k}_{2}){\zeta }^{3},\,{g}_{0}(\zeta )=1-\zeta +\Omega \zeta ,\\ \,{\theta }_{0}(\zeta )\,=1-\zeta ,\,{\phi }_{0}(\zeta )=1-\zeta ,\,{h}_{0}(\zeta )=1-\zeta ,\end{array}$$

(29)

$${{\boldsymbol{L}}}_{f}=f{\prime\prime} {\prime\prime} ,\,{{\boldsymbol{L}}}_{g}=g{\prime\prime} ,\,{{\boldsymbol{L}}}_{\theta }=\theta {\prime\prime} ,\,{{\boldsymbol{L}}}_{\phi }=\phi {\prime\prime} ,\,{{\boldsymbol{L}}}_{h}=h{\prime\prime} $$

(30)

characterizing

$$\begin{array}{c}{{\boldsymbol{L}}}_{f}[\begin{array}{c}{C}_{1}+{C}_{2}\zeta +{C}_{3}{\zeta }^{2}+{C}_{4}{\zeta }^{3}\end{array}]=0,\,{{\boldsymbol{L}}}_{g}[\begin{array}{c}{C}_{5}+{C}_{6}\zeta \end{array}]=0,\,{{\boldsymbol{L}}}_{\theta }[\begin{array}{c}{C}_{7}+{C}_{8}\zeta \end{array}]=0,\\ {{\boldsymbol{L}}}_{\phi }[\begin{array}{c}{C}_{9}+{C}_{10}\zeta \end{array}]=0,\,{{\boldsymbol{L}}}_{h}[\begin{array}{c}{C}_{11}+{C}_{12}\zeta \end{array}]=0,\end{array}$$

(31)

evidently C_i(i = 1–12) are known as the randomly chosen quantities.

Outcomes

Outputs are assembled for the simplified statements in Eqs. (19, 21–26) accompanying the assisting informations in Eqs. (24–25) under the usage of MATHEMATICA. The potentialities of linked representatives on the respective profiles are displayed in Figs. (2–38) and Figs. (39–47). Physical sketch of the problem is presented in Fig. 1.

Figure 2

Axisymmetric movement graph with exceeding values of Re.

Figure 3

Axisymmetric movement graph with exceeding values of k₁.

Figure 4

Axisymmetric movement graph with exceeding values of k₂.

Figure 5

Axisymmetric movement graph with exceeding values of Ω.

Figure 6

Axisymmetric movement graph with exceeding values of λ.

Figure 7

Axisymmetric movement graph with exceeding values of Re.

Figure 8

Axisymmetric movement graph with exceeding values of k₁.

Figure 9

Axisymmetric movement graph with exceeding values of k₂.

Figure 10

Axisymmetric movement graph with exceeding values of Ω.

Figure 11

Axisymmetric movement graph with exceeding values of M.

Figure 12

Axisymmetric movement graph with exceeding values of λ.

Figure 13

Axisymmetric movement graph with exceeding values of Re.

Figure 14

Axisymmetric movement graph with exceeding values of k₁.

Figure 15

Axisymmetric movement graph with exceeding values of k₂.

Figure 16

Axisymmetric movement graph with exceeding values of Ω.

Figure 17

Axisymmetric movement graph with exceeding values of M.

Figure 18

Temperature graph with exceeding values of Re.

Figure 19

Temperature graph with exceeding values of Nb.

Figure 20

Temperature graph with exceeding values of k₁.

Figure 21

Temperature graph with exceeding values of k₂.

Figure 22

Temperature graph with exceeding values of Ω.

Figure 23

Temperature graph with exceeding values of Ec.

Figure 24

Temperature graph with exceeding values of Pr.

Figure 25

Temperature graph with exceeding values of M.

Figure 26

Temperature graph with exceeding values of γ.

Figure 27

Concentration graph with exceeding values of Re.

Figure 28

Concentration graph with exceeding values of Le.

Figure 29

Concentration graph with exceeding values of Nt.

Figure 30

Concentration graph with exceeding values of Nb.

Figure 31

Concentration graph with exceeding values of k₁.

Figure 32

Concentration graph with exceeding values of k₂.

Figure 33

Concentration graph with exceeding values of Ω.

Figure 34

Concentration graph with exceeding values of Ec.

Figure 35

Concentration graph with exceeding values of Pr.

Figure 36

Concentration graph with exceeding values of M.

Figure 37

Concentration graph with exceeding values of E.

Figure 38

Concentration graph with exceeding values of γ₁.

Figure 39

Motile microorganisms concentration graph with exceeding values of Re.

Figure 40

Motile microorganisms concentration graph with exceeding values of Nb.

Figure 41

Motile microorganisms concentration graph with exceeding values of Le.

Figure 42

Motile microorganisms concentration graph with exceeding values of Nt.

Figure 43

Motile microorganisms concentration graph with exceeding values of Pe.

Figure 44

Motile microorganisms concentration graph with exceeding values of k₁.

Figure 45

Motile microorganisms concentration graph with exceeding values of k₂.

Figure 46

Motile microorganisms concentration graph with exceeding values of Ω.

Figure 47

Motile microorganisms concentration graph with exceeding values of Sc.

Axial velocity profile

Figure 2 shows that velocity distribution f(ζ) has an increasing behavior for larger values of Reynolds number Re. Higher quantities of Re indicate the increment in flow rate. Figure 3 shows that the axial movement f(ζ) increases due to k₁ while the opposite trend for velocity f(ζ) is observed in Fig. 4 for increasing the k₂ since in this way stretching for the flow is decreased, consequently, the boundary layer thickness is made low. Figure 5 exhibits all the assigned values of Ω and axial velocity f(ζ) which shows the successful completion of their effects. Physically, the velocity is partially shifted on account of swirling. Figure 6 shows that on establishing porous medium to the fluid flow, the velocity f(ζ) is decreased. The fact is that the presence of porous medium with gradually increasing values increase the resistance in flow of fluid which boosts friction close to the wall, therefore, the velocity is diminished and the boundary layer is made thin. For λ = 0, the system becomes when the fluid does not saturate the porous space.

Radial velocity profile

Figure 7 displays that the velocity component f’(ζ) decreases owing to strong impacts of Reynolds number Re. Figure 8 demonstrates that f’(ζ) reliant to radial direction declines for numerous values of stretching parameter k₁. Physically, an enhancement in k₁ depicts that the radial component of velocity field is less dominant in the present rotating flow. The effect of stretching parameter k₂ on f’(ζ) is shown in Fig. 9. It provides that velocity distribution is smaller with an increment in k₂. It is felt that radially motion f’(ζ) accelerates with rotation quantity Ω in Fig. 10 which offers the significance recognition of the present work. Figure 11 shows that magnetic field parameter M is associated with low level of velocity. Lorentz forces are produced due to the existence of magnetic field which ultimately resist the flow. When M = 0, the study becomes of hydrodynamic nature. Figure 12 is related to the porous medium parameter λ and the radial velocity f’(ζ). The flow is concerned to the dual nature. For 0.0 ≤ ζ ≤ 0.5, the velocity f’(ζ) is decreased but when the ζ crosses the value of 0.50, the flow is of increasing behavior.

Tangential velocity profile

Figure 13 is showing the effect of Reynolds number Re on tangential velocity g(ζ). It is perceived that for improving values of Re, the graph shows a decreasing behavior. In Fig. 14, tangential velocity g(ζ) is decreased with increasing the stretching parameter k₁. Figure 15 witnesses that the tangential velocity g(ζ) shifts to the effective decreasing results with the stretching parameter k₂. A decay of the momentum boundary layer is observed. Figure 16 points out that the rotation parameter Ω increases the tangential velocity g(ζ). Figure 17 projects that for the digital values 0.90, 2.90, 4.90, and 6.90 of M, the magnetic field is taking over the control to reduce the tangential velocity.

Temperature profile

Figure 18 shows the maximization of temperature θ(ζ) and Reynolds number Re. This improvement in heat transfer is physically attributed as increasing values of Re result in enhancement of thickness of the fluid which surges the temperature. Brownian motion parameter Nb and temperature θ(ζ) in Fig. 19 show that upon increasing Nb, the improvement is made in heat transfer. In Brownian motion, the particles kinetic energy increases due to the collision hence temperature is made high. In Fig. 20, the temperature θ(ζ) shows high values due to its ability to get the values of the stretching parameter k₁. Figure 21 is shown for the respective choices of stretching parameter k₂ and for temperature θ(ζ). It is just needed to fill the gape through values of k₂ and increase the temperature. The rotation parameter Ω generates extra heating to the system in Fig. 22. Temperature θ(ζ) is increased just on increasing the parameter Ω. The greater values of Ec are used to access the enhanced temperature θ(ζ) in Fig. 23. The agent Ec assigns the values to a concerned system. It is seen that temperature increases against the quantities of Ec. It is a fact that Eckert number is a ratio of enthalpy difference and kinetic energy. That’s why temperature increases for the greater values of Ec. The system gets the parameter Pr feeding the designated values 0.80, 3.80, 6.80 and 9.80 during swirling to enhance the temperature shown through Fig. 24. The temperature θ(ζ) is changed to highest level after the high status of magnetic field parameter M as shown in Fig. 25. Due to the application of magnetic field, the Lorentz forces result in the good movement of molecular movement of nanoparticles, increasing θ(ζ). Figure 26 shows the effect of heat generation/absorption parameter γ on temperature θ(ζ) which shows that temperature increases with increasing values of γ. Note that the γ values greater than zero represents the heat generation and γ values less than zero shows the heat absorption parameter.

Nanoparticles concentration

It is observed that nanoparticles concentration ϕ(ζ) is decreasing with the increasing values of Reynolds number Re in Fig. 27. ϕ(ζ) is decreased when the Lewis number Le is enhanced for the positive values as demonstrated in Fig. 28. The reason is that the given values decrease the diffusion of concentration. Figure 29 shows that the thermophoresis parameter Nt decreases the nanoparticles concentration ϕ(ζ). In Fig. 30, Brownian motion parameter Nb enhances the nanoparticle concentration ϕ(ζ). Physically, higher values of Nb retain the small amount of viscous force and larger coefficient of Brownian diffusion so the temperature enhances which improves the concentration. The stretching parameter k₁ reduces the concentration ϕ(ζ) by data 0.70, 3.70, 6.70, and 9.70 as demonstrated in Fig. 31. Another stretching parameter k₂ provides the results in Fig. 32 in which the concentration ϕ(ζ) is changed to the high level. The rotation parameter Ω is used to see the changes made in the concentration ϕ(ζ) through Fig. 33. Concentration is made weak through rotation. Eckert number Ec provides the enhanced saturation of nanoparticles as shown through Fig. 34. Figure 35 shows that concentration ϕ(ζ) is promoted to high stage due to the parameter Pr. The magnetic field parameter M also helps to strengthen the enhancement of nanoparticles saturation shown through Fig. 36. Figure 37 depicts that nanoparticles concentration enhances with the non-dimensional activation energy parameter E. Equation (22) shows the strong coupling of the nanoparticle concentration ϕ with ${\gamma }_{1}{({\gamma }_{2}\theta +\mathrm{1)}}^{m}$ and $exp\left(\begin{array}{c}\frac{-E}{{\gamma }_{2}\theta +1}\end{array}\right)$. So if the activation energy rises, the nanoparticles concentration is easily enhanced. Physically, it is due to the fact that due to activation energy, the system gets an extra energy which enhances the chemical reaction and hence the concentration. Figure 38 reveals that the nanoparticles concentration is enhanced with the greater values of chemical reaction parameter γ₁.

Motile microorganisms concentration

Figure 39 depicts that gyrotactic microorganisms flow is high under the excessive values of Re. Figure 40 is about the parameter Nb and motile microorganisms concentration h(ζ). Physically, Brownian motion has effect on the random movement of the nanoparticles. So in the presence of gyrotactic microorganisms, the parameter Nb has the leading role in decreasing h(ζ). In Fig. 41, the Lewis number Le corresponds to the higher motile microorganisms concentration h(ζ). Figure 42 represents that motile microorganisms concentration h(ζ) for the larger values of thermophoresis parameter Nt. An enhancement in Nt provides the substantial thermophoretic force on account of which nanoparticles transfer to lower energy state level thereby microorganisms concentration becomes high. Motile microorganisms concentration h(ζ) reach to the peak point for the prescribed values of Peclet number Pe in Fig. 43. The inspection of the performance of Pe with respect to (h(ζ)) is easily confirmed from Eq. (23). It is witnessed that as Pe is attempting to resume positive values, event causes h(ζ) to high position. In Fig. 44, as the stretching parameter k₁ begins to 0.70 until 3.70, motile microorganisms concentration h(ζ) drops down while in Fig. 45, motile microorganisms concentration h(ζ) is associated to the high values of stretching parameter k₂ which has positively influenced the h(ζ). The rotation parameter Ω shows a weaker diffusivity of microorganisms in Fig. 46. Figure 47 visualized the decreasing phenomena of motile microorganisms concentration h(ζ) due to the variation in Schmidt number Sc. Probably, the abundance of Sc, the concentration h(ζ) stops to nurturing.

Conclusions

Analytical analysis is addressed to the Buongiorno’s nanofluid model for stretchable rotating disks with gyrotactic microorganisms flow, porous medium, Brownian motion and thermophoresis, heat source/sink, Arrhenius activation energy and binary chemical reaction. Optimal homotopy analysis method (OHAM) is applied for the solution which is shown through graphs for the interesting effects of all the embedded parameters. Possible future work is to investigate the non-Newtonian and hybrid nanofluids for rotating systems under different boundary conditions.