1 Introduction

There is a need for new approaches measuring inter-rater agreement in ordinal settings because the measures typically used are not unproblematic (e.g., [23]) and there has been no method especially designed for ranking settings developed yet. This article introduces a new approach using the probability of consistencies in a setting where n independent raters rank k items. Rankings are ratings in an ordinal setting, assigned to items without replacement. They are often used in psychometric procedures like standard settings or assessment centers in order to figure out whether raters agree on the difficulties of items or ability of applicants. In addition to the best scoring items or applicants, also inter-rater agreement is of concern. In an assessment center, it is important both to know which candidate was evaluated best and whether raters agreed or not. It might be the case that an applicant is not obtaining the best score because he or she was poorly evaluated by one rater only. For instance, at the University of Applied Sciences Wiener Neustadt amongst other criteria like psychological tests and questionnaires an assessment center is part of the selection process of bachelor applicants. There are assessment centers for specific conditions (e.g., self-presentation). Afterward, the mean ratings are used as one criterion to decide whether applicants are rejected or admitted. Rankings were additionally included as indifferent ratings (no decision between candidates) were shown to be problematic. Rankings can be used to evaluate whether assessors are able to rank applicants and to investigate to which extent rankings are consistent among the raters.

To evaluate whether raters agree or disagree on the performance of an applicant inter-rater reliability measures are used. Measures evaluating inter-rater agreement in a classic rating setting exist, but they are highly discussed (e.g., [10]; [25]) and problematic in ranking settings. Cohen’s kappa and Fleiss’ kappa are, for instance, known for penalizing raters in specific settings, are highly dependent on the marginals and should not be used in ranking settings. Furthermore, even though rater agreement is often of interest, there are no suiting measures that can deal with a ranking setting. This article tries to fill this gap introducing a new measure using the so-called sum of pairwise absolute row differences (PARDs). The sum of PARDs is a directly interpretable measure (p value equivalent) and is not biased in ranking settings, so its use is highly recommended. In addition, unlike already existing measures, as shown in the results section, the new measure is as appropriate in small settings as it is in bigger settings, since it is taking into account both the number of raters and the number of items to be ranked. Another advantage of the presented approach is that it is possible to compare the result within and between settings. The overall research question of this paper is to which extent the PARDs approach is a suitable measure to describe inter-rater agreement in a ranking setting. The first simulation studies compare the PARDs measure to already existing measures, and the second simulation study deals with the question how many matrices are necessary.

This paper starts providing a literature review on existing measures and their usability in ranking settings and continues introducing the sum of PARDs-approach. Both the theoretical derivation and the computational implementation are discussed. To complete the article results of a simulation study comparing the existing measures with the results retrieved from the PARDs approach and another simulation study showing the comparison of matrices of different sizes. Conclusions and suggestions for future research are given at the end of this article.

2 Literature Review

2.1 Existing Measures

Many measures exist aiming to assess inter-rater reliability. A main distinction can be made between agreement measures (e.g., kappa, Tau approaches) and correlational approaches (e.g., Pearson correlation coefficient, Spearman correlation coefficient, intra-class correlation). In this section, the main ideas of this approaches are discussed and their suitability in ranking problems is analyzed.

2.1.1 Kappa-like Approaches

Although the idea of kappa-like approaches was discussed earlier, Cohen [5] first suggested the Cohen’s kappa coefficient (\(\kappa\)) in 1960 as an agreement measure among two raters rating nominal categories. Cohen’s kappa \(\kappa\) is calculated by the famous formula

$$\begin{aligned} \kappa =\frac{p_0-p_e}{1-p_e} \end{aligned}.$$
(2.1)

The two values used in order to calculate \(\kappa\) are \(p_0\) and \(p_e\): The first one is the relative observed agreement among raters, and the latter one is the hypothetical probability of chance agreement. \(p_e\) is calculated using the observed data to calculate the probabilities of each rater randomly choosing each category. The value of \(\kappa\) is 1 when perfect agreement between two raters occurs, and 0 in case the agreement is equal to the expected agreement under independence assumption. It is negative when agreement is less than expected by chance.

Scott’s pi is very similar to Cohen’s kappa and was introduced by Scott in 1955 [22]. The difference between the two approaches is that the expected agreement is calculated in a different way. Scott’s pi uses the assumption that raters are having the same distribution of responses. Although Fleiss introduced a multiple-rater agreement coefficient as a generalized kappa coefficient in 1971, it in fact generalizes Scott’s pi coefficient [13]. Fleiss’ kappa was developed by Fleiss and Kappa in 1973 [9], and in its general form, it is used for analyzing agreement between more than two raters rating nominal categories. In addition to the fact that kappa-like measures are based on questionable marginal homogeneity assumptions [15] and they are highly dependent on marginal distributions [27], these measures do not take into account the ordinal scale in ranking settings. Therefore, they are not suited to be used in this framework. Although Landis and Koch in 1977 [18] describe kappas lower than zero as poor agreement, 0.01–0.20 as slight agreement, 0.21–0.40 as fair agreement 0.41–0.60 as moderate agreement, 0.61–0.80 as substantial agreement and 0.81–1.00 as almost perfect agreement, there does not exist consensus about how large the value should be in practice.

Fleiss’ kappa can also be applied to ordinal data in case weights are introduced and used to take into account greater and smaller deviations of the raters from each other. The original idea of a weighted kappa approach is based on ordinal settings, where larger distances between raters have to be penalized [6]. The most commonly used weights for this approach are linear and quadratic [24]. However, both are criticized on their arbitrary forms and it can be shown that, under specific conditions, the linear weighted kappa is equivalent to a product moment correlation [6]. In case of the quadratic weight, it holds that it is equivalent to a intra-class correlation [21]. This means those measures do not differ from later described approaches. There also exists a kappa coefficient for cardinal scales that is asymptotically equivalent to the intra-class correlation (ICC) estimated from a two-way random effects ANOVA as discussed by Fleiss and Kappa in 1973 [9]. In some cases, Fleiss’ kappa may return low values, even when agreement is actually high. That is why attempts have also been made to correct for that [8].

2.1.2 Correlational Approaches

Correlational approaches are commonly used in any setting where the linear association between multiple outcomes is of interest. Well-known measures are the Pearson correlation coefficient which directly compares the directions of two variables, while the Spearman correlation coefficient, on the other hand, provides information about similar and dissimilar ranks. Third, the intra-class correlation (ICC) is a special case of a correlation used in settings, where measurements are organized in groups. Therefore, these approaches might be predetermined to be used in ranking settings. According to the correlational approaches and the ICC approach, there are some interpretation rules suggested: Cicchetti [4] suggests the following guidelines for interpretation for kappa and ICC measures: Less than 0.40 is considered poor. Values between 0.40 and 0.59 can be considered as fair, values between 0.60 and 0.74 as good and values between 0.75 and 1.00 as excellent. Koo and Li [17] suggest slightly different values: They consider below 0.50 as poor, between 0.50 and 0.75 as moderate, between 0.75 and 0.90 as good and above 0.90 as excellent. For interpreting correlations, the suggestions of Cohen [7] are usually used. Another approach often used is Kendall’s Tau [16]. It is a nonparametric approach measuring ordinal associations between two measured quantities, calculated by

$$\begin{aligned} \tau _{c}=\frac{2\times (n_\mathrm{c}-n_\mathrm{d})}{n^{2}\times \frac{m-1}{m}} \end{aligned}$$
(2.2)

where \(n_\mathrm{c}\) is the number of concordant pairs, \(n_\mathrm{d}\) is the number of discordant pairs, r is the number of rows, c is the number of columns and \(m= \mathrm{min} (r,c)\). Compared to the kappa-like approaches, it directly assumes an ordinal setting, in which a high coefficient represents a similar rank between variables and a low coefficient a dissimilar rank. However, considering its definition it is only useful in a setting with two variables which is a serious limitation for larger ranking settings.

In fact, practitioners use this type of approaches in combination with kappa-like approaches in standard settings and psychometric studies to determine inter-rater agreement (e.g., [3]; [20]). Theoretical research on the other hand doubts the applicability of these approaches for several reasons: First, a correlation does only provide information about similar directions across items [10] which is a serious restriction in the case of rankings. Moreover, neither of the correlational approaches does correct for chance agreement [11] which is a serious issue in inter-rater settings. Therefore, in most of the practical implications correlations are not used as the only measure of inter-rater agreement. The approaches provided in the literature show problems with the measures currently used in ranking settings and confirm that a new approach is necessary. In general, it is to point out that there is a lack of inter-rater reliability measures accounting for the closeness of ratings and at the same time correcting for chance agreement. Although there are some strengths of the correlational approaches, they are not taking into account chance agreement. This is the gap this article tries to fill by discussing a new approach to calculate inter-rater agreement in ranking settings.

3 Methodological Approach

In this chapter, we will introduce a new method specifically designed to fit any ranking setting where n independent raters (assessors) decide on k options while accounting for the issues discussed in the literature review. First, we describe the suggested method from a theoretical perspective. The new approach using the probability of consistencies in a setting where n independent raters rank k items was first presented at the Psychometric Computing Conference 2019 in Prague [2], while further developments were discussed at the Simulation and Statistic Conference in Salzburg [1]. The discrete theoretical probability distribution of the sum of the pairwise absolute row differences (PARDs) assuming n raters randomly ranking k items is used to evaluate inter-rater agreement of empirically retrieved rating results. This is done by calculating the sum of PARDs in an empirically obtained \(n\times k\) matrix together with the theoretically expected distribution of the sum of PARDs assuming raters randomly ranking items. In particular, a p value equivalent in a discrete setting is found to evaluate inter-rater agreement of the empirically retrieved rating results.

The first part of this section describes this method in detail. Afterward, a first part of a simulation study will show the performance of the method compared to other well-known inter-rater agreement measures offered in the literature and a second part of a simulation study will show how accurate simulation approaches are in case of different sizes of matrices.

3.1 Sum of Pairwise Absolute Row Differences (PARDS)—A Measure for Inter-Rater Agreement

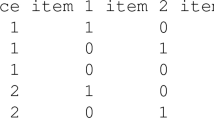
Consider the following typical ranking problem: As mentioned earlier, at the University of Applied Sciences Wiener Neustadt an assessment center is part of the selection process of bachelor applicants. For instance, \(n=3\) independent raters are rating and ranking the performance of \(k=3\) applicants in a specific condition (e.g., self-presentation). Afterward, the mean ratings are used as one criterion to decide whether applicants are rejected or admitted. Rankings were additionally included as indifferent ratings (no decision between candidates) were shown to be problematic. Rankings can be used to evaluate whether assessors are able to rank applicants and to investigate to which extent rankings are consistent among the raters. But how can meaningful criteria for inter-rater agreement be assessed in case of the assessment center rankings? A ranking example is presented in Table 1.

Table 1 Example 3 × 3 setting
Full size table

In the PARDs approach, the pairwise absolute row differences are first calculated as shown in Table 2. The absolute value of these differences is used as both positive and negative differences may occur.

Table 2 PARDs 3 × 3 setting
Full size table

Afterward, the sum of all entries in the matrix (sum = 4) is calculated, and therefore, all pairwise row differences are taken into account. This is done to find an overall agreement measure for the whole matrix. In order to determine how probable this or a more extreme result (this or a smaller sum of PARDs) is, compared to a setting in which numbers are assigned randomly and without repetition, the discrete probability distribution function of this sum in a given setting is needed. More generally, consider a ranking setting with n independent raters and k options. A row difference accounts for the differences between each individual rater. If all raters agree on the ranking, this difference will be zero for all columns. Therefore, in a setting in which all raters are ranking the items in the same way, the sum of PARDs will be zero. If a difference exists in the rankings, it increases with the dissimilarity in the rankings. This means a larger disagreement leads to a larger difference. Agreement on the other hand is given, if the sum of PARDs reveals a small value. Now the question arises how the size of the sum of PARDs can be judged. We suggest to determine or estimate the probability of the empirically calculated sum of PARDs or a smaller sum of PARDs.

If k numbers are assigned to k places without replacement, there are in general k! ways to arrange them. This means there are k! different options to construct one row of the matrix. Furthermore, in a \(n \times k\) setting the number of possible matrices is \(k!^{n}\). With this information, it is possible to determine the total of a sum of PARDs of zero. Since a sum of PARDs of zero would mean that the rankings are the same and therefore the rows must be the same, there are k! ways of obtaining such a so-called zero difference. Therefore, the probability of a zero difference is given by: \(P(d_{0})=\frac{k!}{k!^{n}}\). The zero difference represents a benchmark for the whole process as it refers to a setting where all raters agree on all ranking decisions (total agreement). This has to be taken into perspective with other outcomes, in particular the sum of PARDs, possible in a specific setting. Some laws for specific settings can be derived, like the maximum number of differences per column is given by \(\mathrm{Diff}_\mathrm{col}=(n-1)+(n-2)+...(n-(n-1))\). Finding a general formula to obtain the sum of PARDs and their probabilities is only possible for certain, small settings. In order to estimate the probability of a certain sum of PARDs, another approach is to find all possible matrices, calculate their sum of PARDs and determine their frequencies. Simulation is necessary for bigger matrices, and both approaches were implemented using R [19] and the R-package gtools [26]. Back to the example mentioned above with \(n=3\) raters ranking \(k=3\) items, all possible matrices can be created and the discrete probability function can be determined as presented in Fig. 1.

Fig. 1
figure 1

Discrete probability function \(3 \times 3\)

Full size image
Fig. 2
figure 2

Discrete distribution function \(3 \times 3\)

Full size image

The cumulative probability shown in Fig. 2 can be used as a measure for inter-rater agreement and is directly interpretable. In the displayed example, the inter-rater reliability is approximately 0.19, meaning that in a random setting a sum of PARDs of 4 or lower results in approximately 19 percent of the cases. The approach allows for probabilities of matrices and their sums of PARDs to be calculated. Instead of a rather uninformative comparison, it is possible to directly calculate and compare probabilities of a specific outcome to all other possible outcomes in a setting. This leads to a single cumulative probability for each empirical setting, corresponding to the single scores used in the other inter-rater agreement measures. Because this measure is a cumulative probability, it is directly interpretable, and therefore, it is more informative than other measures. For small settings, it is possible to generate all matrices and calculate their relative frequencies used as probability estimates. As mentioned earlier, for bigger settings (e.g., \(5 \times 4\) settings) it is necessary to simulate matrices and to estimate their cumulative probability functions, because the number of possibilities increases k factorial to the power of n. For instance, creating all possible matrices of a \(5 \times 4\) takes approximately 7 minutes. The creation of all matrices in a \(4 \times 5\) is not possible given the system information provided in Sect. 4.1.

A simulation approach is often used if it is not intended or feasible to fit a specific model with real data. Instead of finding an exact solution for one realization, a simulation is capable of considering many outcomes and data variations. This is especially useful if the number of observed possibilities is too large as in the case of the PARDs approach. It is easy to see that for increasing n and k a computation of all sum of PARDs and corresponding probabilities is not feasible and not even necessary (as shown later in this study). Furthermore, the aim of this approach lies in a determination of a p value equivalent and comparable measure within and between settings, not in an exact determination of the probability for each sum of PARDs. More specific, the process enables a comparison between a single realization (the empirically observed inter-rater agreement matrix and its corresponding sum of PARDs) and the total amount of possible deviations in the same setting. The first is deterministic if the rating is over, and the second is also deterministic at all times in a specific setting. For the comparison, it is enough to know where the empirically observed realization lies in the distribution function and how much distribution mass is in the lower tail form this point. This is how the simulation approach of the sum of PARDs works: Instead of computing every possible difference matrix to obtain the distribution function, only a fixed value of matrices (e.g., \(10^6\)) is computed based on the combinatorial logic of this process and the resulting relative frequencies are calculated and used as an estimate for the probabilities of the sum of PARDs. Using such a simulation approach, one has to determine how to deal with the small and therefore unlikely sum of PARDs. If they are not treated at all, they are systematically under represented, resulting in overestimating the cumulative probabilities of the sum of PARDs. This would be especially problematic because they are in particular of interest, since the aim of this measure is to represent inter-rater agreement. That is why we suggest to make use of the probabilities and values known (like the probability of the zero difference) and to fit a continuous logistic growth curve model in order to correct for the under-representation of the small differences using the R-package nls2 [12]. The fitting of a logistic growth curve model is demonstrated using a \(5 \times 10\) (Fig. 3).

Fig. 3
figure 3

Logistic growth curve model \(5 \times 10\)

Full size image

3.2 Simulation Studies

Since a new measure is defined in this article, first attempts should be made to investigate how well the sum of PARDs approach works, for both settings in which exact calculation of the probabilities is possible and for those in which simulation is necessary. Therefore, the first goal of this study is to compare it with already existing, well-known measures like the Fleiss weighted linear kappa, the intra-class correlation, the Pearson and the Kendall correlation. This is the first small simulation study of this paper. For this simulation study, 1000 times 1 million matrices in a \(5 \times 10\) setting were simulated and small, medium sized and a large sum of PARDs were compared to the other mentioned measures. Small was considered to have a cumulative probability lower than 0.05, medium around 0.5 and large higher than 0.9.

The second simulation study aims to investigate how accurate different numbers of simulated matrices are compared to each other. Or in other words: How many matrices are needed for a sufficient result? This was tested using the following matrices sizes: \(3 \times 5\), \(3 \times 6\) and \(3 \times 7\). The reason is that for these rather small matrices it is possible to compare the retrieved estimates to the calculated values. Furthermore, this study and the mentioned settings were in line with a real application case at the University of Applied Sciences Wiener Neustadt where the application of the sum of PARDs was used and the results of the simulation studies were important. In each case, first the number of all possible matrices was created (N). Afterward, the numbers of to be simulated matrices were determined: The first simulation used \(10 \times N\), the second simulation used \(N-matrices\), the third \(0.1 \times N\), the fourth \(0.01 \times N\), the fifth \(0.001 \times N\) and the sixth \(0.0001 \times N\). In case the simulation ended up with less than 15 matrices, the results were not used. For each scenario, 1000 samples of the targeted size were randomly sampled and their sum of PARDs and corresponding probabilities were estimated by fitting a logistic growth curve model using the R-package nls2 [12].

4 Results

4.1 Calculation Times and Systems Used

In order to provide an overview of the calculation times for various settings, the calculation times are reported underneath (Tables 3, 4 and  5) using the following system: Windows 10 Education 64-Bit (10.0, Build 18362); CPU: Intel Core i7-8565U, 1.80 GHz(8 CPUs), 2.0 GHz; RAM: 16348 MB; Graphics: Intel UHD Graphics 620 8256 MB capacity, 128MB VRAM. \(1000 \times 10^6\) matrices were simulated and reported in seconds.

Table 3 Setting \(2 \times i\)
Full size table
Table 4 Setting \(3 \times i\)
Full size table
Table 5 Setting \(4 \times i\)
Full size table

4.2 Simulation Study I

1000 times 1 000 000 matrices were simulated. A small (lower than cumulative probability of .05), a medium-sized (around .50) and a large effect according to the PARDs approach were compared (higher than .90). In particular, the chosen sum of PARDs values was 220, 332 and 380. For each sum of PARDs, the corresponding matrices were selected and the other measures were calculated. Provided in the table underneath are the empirically retrieved mean values and the standard deviations of the simulated samples (Table 6).

Table 6 Comparison \(5 \times 10\)
Full size table

A high agreement (low sum of PARDs) corresponds to a fair agreement according to Fleiss’ weighted linear kappa [18]. Also the ICC and the Pearson and Kendall correlation coefficient suggest a fair or moderate agreement. For both the medium and the large-sized effects, no agreement regarding the other measures can be found. To summarize the results of this simulation study it can be stated that the interpretations of the effect sizes are comparable.

4.3 Simulation Study II

Underneath the distribution functions of the different scenarios are displayed in Figs. 4,5 and 6. It can be seen that in case of small samples the smallest differences are not included in the simulated sum of PARDs (e.g., 0, 4,...). In the simulated scenarios, the estimated probabilities in smaller samples are higher than in larger samples. This means in the respective scenarios the probabilities are overestimated in case of too small samples, but it can also be seen that the logistic growth curve model is hardly influenced by the changes in the sample sizes. There seems to be a slightly increasing variability with decreasing sample size.

Fig. 4
figure 4

Fitted logistic growth curve models \(3 \times 5\)

Full size image
Fig. 5
figure 5

Fitted logistic growth curve models \(3 \times 6\)

Full size image
Fig. 6
figure 6

Fitted logistic growth curve models \(3 \times 7\)

Full size image

5 Discussion and Conclusion

The aim of this work is to introduce the sum of PARDs measure as a measure displaying inter-rater agreement in ranking settings. There is a need for a measure like this because the existing measures mentioned in the literature review all have shortcomings, especially if they are used in ranking settings. The sum of PARDs measure has the advantage that it was developed especially for ranking settings. The PARDs measure can be seen as an effective way to represent all the complex information of the ranking process in a single value without using any irrelevant information. It has to be noted that the PARDs measure was originally developed for ranking settings. Future research will also deal with the extension of the approach. Another advantage is that it can also be compared across different settings, since it is using cumulative probabilities of discrete (or estimated continuous) distribution functions.

A small, first simulation study showed that there is the same tendency across the compared measures. A large \(5 \times 10\) matrix was used in the first simulation study. In this setting, a high inter-rater agreement according to the sum of PARDs approach corresponded to a fair agreement according to the other measures. The second simulation study aimed to investigate how many matrices are necessary for a valid result. It can be seen that in the scenario of \(3 \times 5\), \(3 \times 6\) and \(3 \times 7\) matrices the estimates were quite robust, especially in case the logistic growth curve model is used and even for the smallest sample sizes. In future research, the question has to be answered whether this is because the PARDs approach using the simulated matrices is systematically overestimating the inter-rater agreement or because the other measures are systematically underestimating the inter-rater agreement in the ranking setting. This method can, for instance, be used to identify assessors who tend to rank applicants differently in assessment centers or wherever items are ranked and agreement needs to be investigated.

The aim of this article is to present first considerations of the sum of PARDs approach and first results of simulation studies. It is not the aim to provide a mathematical proof of statistical properties of the measure, and the article is not claiming that this measure is already sufficiently tested using larger simulation studies. This was not the scope of this paper anymore and is planned to be investigated in the future. Also, a general rule how many matrices are necessary in larger settings has to be found. In addition, techniques on how to deal with missing values are planned to be considered and the method will be implemented in a R-package. Meaningful cutoff criteria are not suggested because a directly interpretable measure is provided and the researcher can therefore decide on his or her own about the required effect size in a given setting. One disadvantage of this approach is of course the necessary computation power in case of bigger settings, but because computational power will get better in the future it can be seen as only a current limitation (e.g., Kambatla, Kollias, Kumar and Grama in 2014 [14]). Furthermore, it will not be necessary for practitioners to create or simulate the matrices by themselves, and the theoretical (simulated) probability functions will be included in the planned R-package.

Since it is a measure developed for ranking settings and usually practitioners usually rank a small number of items, its application cases are typically smaller sized matrices. The reason for this is that it is difficult for human raters to be accurate if a too large number of options are presented which have to be ranked according to some criterion. In particular in small settings, the suggested sum of PARDs measure is computed fast and it seems to be promising, because it is using each and every data point and it is directly interpretable because it is a cumulative relative frequency used as an estimate for the cumulative probability. The sum of PARDs approach is the only inter-rater agreement measure represented by a probability.