1 Introduction

In the conference paper [1] we conjectured the possibility of applying our regular decomposition algorithm [2] to very large graphs, for which the full adjacency information is not possible to process, using a sampling approach. In this paper we develop the corresponding theory. Using martingale techniques, we prove claims of the preceding paper and give precise conditions under which they are true. This method allows to abandon the customary assumption that the graph be generated by a SBM.

The so-called Big Data is a hot topic in science and applications. Revealing and understanding various relations embedded in such large data sets is of special interest. In mathematical terms, such relations form a huge graph. The size of the graph may be so big that sampling of subgraphs is the only practically feasible operation. Furthermore, part of the information may be inaccessible, faulty or missing. Our method suggests a way to overcome such hurdles in the case of dense data.

One example is the case of semantic relations between words in large corpora of natural language data. Relations can also exist between various data sets, forming large higher-order tensors, thus requiring integration of various data sets. In such a scenario, algorithms based on stochastic block models (SBMs, also known as generalized random graphs [3]; for a review see, e.g., [4]) and their extensions are very attractive solutions, instead of simple clustering like k-means.

A strong result, less known among practitioners, is Szemerédi’s regularity lemma (SRL) [5]. SRL in a way supports a SBM-based approach to large data analysis, because it proves the existence of a SBM-like structure for any large graph, and has generalizations to similar objects like hypergraphs. SRL has been a rich source in pure mathematics—it appears as a key element of important results in many fields. We think that in more practical research it is also good to be aware of the broad context of SRL as a guiding principle and a source of inspiration. To emphasize this point, we call this kind of approach to SBM and a concrete way to fit data to it regular decomposition (RD).

Traditionally, SBM has been used for the so-called community detection in networks, like partitioning a network into blocks that are internally well connected and almost isolated from each other. From the point of view of SRL, this is too restrictive. According to SRL, the relations between the groups are more informative than those inside the groups, traditionally emphasized in community detection. Regular decomposition takes both aspects into account on equal footage. In [6] a more general scope of spectral clustering is introduced: the discrepancy-based spectral clustering that favors regular structures.

The methodology of RD has been developed in our previous works, first introduced in [7] and later refined and extended in [1, 2, 8,9,10]. In [2] we used Rissanen’s minimum description length principle (MDL) [11] in RD. In [10] we extend RD to the case of large and sparse graphs using graph distance matrix as a basis.

In the current paper, we restrict ourselves to the case of very large and dense simple graphs. Other cases like rectangular matrices with real entries can be probably treated in very similar manner using the approach described in [2]. We aim to show that large-scale block structures of such graphs can be learned from bounded size, usually quite small, samples. The block structure found from a sample can then be extended to the rest of the graph in just a linear time w.r.t. n, the number of nodes.

The block label of a given node can be found independently of all other nodes, provided a good enough sample was used. This allows parallel computations in RD algorithm. The labeling of a node requires only the information on links from that node to the nodes of the fixed sample. As a result, the labeling can be done independently in many processing cores sharing the same graph and the sample.

The revealed structure is useful for many applications like those that involve counting numbers of small subgraphs or finding motifs. It also helps in finding a comprehensive overall understanding of graphs when the graph size is far too large for complete mapping and visualization. We also introduce a new version of the RD algorithm for simple graphs that tolerates missing data and noise.

2 Related Work

Our theoretical description is partly overlapping with SBM literature using the apparatus of statistical physics, see, e.g., extensive works by T.P. Peixoto. In particular, the use of MDL to find the number of blocks has been studied earlier by Peixoto [12]. We think that such multitude of approaches is only beneficial since it brings in results and ideas of different fields and is understandable by a wider community of researchers.

Recently, impressive progress has been achieved in the theory of nonparametric statistical estimation of large and sparse graphs [13, 14]. Under certain conditions, latent models like the SBM can be found from samples of links, linear in number of nodes sizes. Our work could be seen as a special case when the target is to find a block structure from a large graph using a specific algorithm. We show that in the dense case, the sample size is just a finite constant, instead of a linear function of the number of nodes, needed in the sparse case. Moreover, the algorithm in [14] is much more complicated than ours and may be difficult to use in practice. In a recent mostly experimental work [10], we attempted to use regular decomposition in a sparse graph case using graph distance as similarity measure between nodes.

A clustering method that can find the clusters from large enough samples is called consistent. As stated in [15], there are quite few results in proving consistency of clustering methods. The consistency of classical k-means clustering was proven by Pollard [16].

von Luxburg et al. [15] proved consistency of spectral clustering in a special case. It was shown that under some mild conditions, the spectral clustering of sampled similarity matrix of data with two clusters will converge to the spectral clustering of the limit corresponding to the infinite data. In this respect the so-called normalized approach that uses normalized Laplacian (see Sect. 6.2) was found preferable. Spectral clustering can be seen as an alternative to regular decomposition, since it can reveal similar block structures in adjacency—or similarity matrices [17].

3 Regular Decomposition of Graphs and Matrices

Regular decomposition finds a structure that mimics the regular partitions promised by SRL. SRL says, roughly speaking, that the nodes of any large enough graph can be partitioned into a bounded number, k, of equally sized ‘clusters,’ and one small exceptional set, in such a way that links between most pairs of clusters look like those in a random bipartite graphs with independent links and with the link probability that equals to the link density. SRL is significant for large and dense graphs. However, similar results hold also to many other cases and structures, see the references in [18].

In RD, we simply replace the random-like bipartite graphs of SRL by a set of truly random bipartite graphs and use it as a modeling space in the MDL theory. We disregard the requirement of having blocks of equal sizes and also model the internal links of regular clusters by a random graph. The next step is to find an optimal model that explains the graph in a most economic way using MDL [2].

In the case of a matrix with nonnegative entries, we replace random graph models with a kind of bipartite Poissonian block models: A matrix element \(a_{i,j}\) between row i and column j is thought to correspond to a random multi-link between nodes i and j, with the number of links distributed as a Poisson random variable with mean \(a_{i,j}\) (see [9]). The bipartition is formed by the sets of rows and columns, respectively. Then the resulting RD is very similar to the RD of binary graphs. This approach allows also the analysis of several interrelated data sets and corresponding graphs, for instance, using corresponding tensor models. In all cases, the RD algorithm is very compact, containing just few lines of code in high-level languages like Python, and uses standard matrix-algebraic operations.

In RD, the unlossy code that describes a simple graph \(G=(V,E)\) with respect to a partition \(\xi =\{A_1,\ldots ,A_k\}\) of V has a length at most (and, for large graphs, typically close to)

$$\begin{aligned} L(G|\xi )&= L_1(G|\xi )+L_2(G|\xi )+L_3(G|\xi )\nonumber \\&\quad \quad +\,L_4(G|\xi )+L_5(G|\xi ),\nonumber \\ L_1(G|\xi )&= \sum _{i=1}^kl^*(|A_i|),\nonumber \\ L_2(G|\xi )&= \sum _{i=1}^kl^*\left( {|A_i|}\atopwithdelims (){2}d(A_i)\right) \nonumber \\&\quad \quad +\,\sum _{i<j}l^*\left( |A_i||A_j|d(A_i,A_j)\right) ,\nonumber \\ L_3(G|\xi )&= |V|H(\xi ),\nonumber \\ L_4(G|\xi )&= \sum _{i=1}^{k} {|A_i|\atopwithdelims ()2} H(d(A_i)),\nonumber \\ L_5(G|\xi )&= \sum _{i<j}|A_i||A_j|H(d(A_i,A_j)), \end{aligned}$$
(1)

where \(l^*(m):=\log (m)+\log \log (m)+\cdots\) is the coding length of an integer m and

$$\begin{aligned} H(p)=-p\log p -(1-p)\log (1-p) \end{aligned}$$

is the entropy of the Bernoulli(p) distribution. A corresponding representation exists also for the coding length of a matrix, interpreted as an average of a Poissonian block model (see details in [2]).

Figure 1 shows a typical RD analysis result of a symmetric real matrix. The regular groups are obtained by permuting the rows (and accordingly the columns) of the left-hand side symmetric matrix and are presented on the right-hand side panel as homogeneous quadratic or rectangular blocks. For a non-symmetric rectangular matrix, the visual effect of RD is similar to chessboard.

Fig. 1
figure 1

Left: the similarity matrix between 4088 sentences from Charles Darwin’s Origin of Species. Right: the same matrix with sentences reordered in 20 regular groups revealing a characteristic chessboard structure

Full size image

3.1 Matrix Formulation of the RD Algorithm for Graphs

Definition 1

For a given graph G with n nodes, adjacency matrix A and a partition matrix \(R\in {{{\mathcal {R}}}}_k\), we denote:

$$\begin{aligned} P_1(R):= R^TAR, \end{aligned}$$

where \(\cdot ^T\) stands for matrix transpose. R is by definition a binary \(n\times k\) matrix with rows that are indicators for regular group membership of the corresponding nodes. For instance, if the row i of R is (0, 1, 0, 0), this means that node i belongs to the regular group number 2.

The block sizes are the column sums of R and are denoted

$$\begin{aligned} n_\alpha :=(R^TR)_{\alpha ,\alpha },\quad 1\le \alpha \le k. \end{aligned}$$

The number of links within each block and between block pairs \((\alpha , \beta )\) is uniquely defined by \(P_1(R)\) and denoted as

$$\begin{aligned} e_{\alpha ,\beta }(R)= \left( 1-\frac{1}{2}\delta _{\alpha ,\beta }\right) (P_1(R))_{\alpha ,\beta }. \end{aligned}$$

Finally, we define the \(k\times k\) link density matrix P:

$$\begin{aligned} (P(R))_{\alpha ,\alpha }:= \,&{} \, 1_{\{n_\alpha >1\}}\frac{e_{\alpha ,\beta }(R)}{{n_\alpha \atopwithdelims ()2}},\\ (P(R))_{\alpha ,\beta }:=\, & {}\, \frac{e_{\alpha ,\beta }(R)}{n_\alpha n_\beta },\ \alpha \not =\beta ,\\ \alpha ,\beta\in \,& {} \{1,2,\ldots ,k\} \end{aligned}$$

By (1), the length of the code \(l_k\) that uniquely describes the graph G(A) corresponding to A, using the model (R, P), \(R\in {{{\mathcal {R}}}}\), can be computed as follows:

Definition 2

$$\begin{aligned} l_k(G(A)\mid R):= & {} \sum _{1\le i< j\le k}n_in_j H((P(R))_{i,j})\\&+\,\sum _{1\le i\le k}{n_i\atopwithdelims ()2}H((P(R))_{i,i})\\&+\, l_k(R), \end{aligned}$$

where

$$\begin{aligned} l_k(R)= \sum _{1\le i\le k}n_iH(n_i/n)+ \sum _{1\le i\le j\le k}l^*(e_{i,j}(R)) \end{aligned}$$

presents the length of a code describing the model (the partition and the link densities).

The two-part MDL program of finding the optimal model, denoted as \(R_{k^*}\), can now be written as:

$$\begin{aligned} (k^*,R_{k^*}) :=\arg \, \min _{1\le k\le n}\min _{R\in {{{\mathcal {R}}}}_k }l_k (G(A)\mid R\in {{{\mathcal {R}}}}_k) \end{aligned}$$
(2)

To solve this program approximately, we use the following greedy algorithm.

Algorithm 1

Greedy Two-part MDL

Input: \(G=G(A)\) is a simple graph of size n.

Output: \((k^*,R_{k^*}\in {{{\mathcal {R}}}}_{k^*}), k^*\in \{1,2,\ldots ,n\}\), such that the two-part code for G is approximately equal to the shortest possible for all possible block models with number of blocks in the range from 1 to n.

Start: \(k=1\), \(l^*=\infty\), \(R\in {{{\mathcal {R}}}}_1=\left\{ \mathbf{{1}}\right\}\), \(k^*=1\), where \(\mathbf {1}\) is the \(n\times 1\) matrix with all elements equal to 1.

1. Find

$$\begin{aligned} {\hat{R}}_k(G):=\arg \, \min _{R\in {{{\mathcal {R}}}}_{k}} l_k (G\mid R) \end{aligned}$$

using subroutine ARGMAX k (Algorithm 2).

2. Compute \(l_k(G)= \lceil l_k(G\mid {\hat{R}}(G))\rceil +l_k ({\hat{R}}(G))\)

3. If \(l_k(G)< l^*\) then \(l^*=l_k(G)\), \(R_{k^*}={\hat{R}}_k(G)\) , \(k^*=k\)

4. \(k=k+1\)

5. If \(k>n\), Print \((R_{k^*},k^*)\) and STOP the program.

6. GoTo 1.

Definition 3

A mapping \(\varPhi :{{{\mathcal {R}}}}_k\rightarrow {{{\mathcal {R}}}}_k\) is defined as follows. First, define the following matrices element-wise:

$$\begin{aligned}&(LogP(R))_{\alpha ,\beta }:=\log (P(R)_{\alpha ,\beta })\\&(Log[1-P(R)])_{\alpha ,\beta }:=\log [1-P(R)_{\alpha ,\beta }],\\&(1-A)_{\alpha ,\beta }:=1-A_{\alpha ,\beta },\\&L(R):=-AR(LogP(R))^T-(1-A) R Log[1-P(R)], \end{aligned}$$

where we set \(\log 0:=0\) since it appears only in the combination \(0\log 0=0\) in matrix L, \(\alpha ,\beta \in \{1,2,\ldots ,k\}\),

$$\begin{aligned} \beta (i,R):= \inf \{\beta :\beta =\arg \min _{1\le \alpha \le k}(L(R))_{i,\alpha }\}, 1\le i\le n, \end{aligned}$$

and finally define the matrix function \(\varPhi (\cdot )\) element-wise on argument R:

$$\begin{aligned} \varPhi (R)_{i,\alpha }= \delta _{\alpha ,\beta (i,R)}, i\in \{1,2,\ldots ,n\}. \end{aligned}$$

The mapping \(\varPhi (R)\) defines a greedy optimization of partition R, where each node is replaced to a new block independently of all other placements, hence the term ‘greedy algorithm.’

Algorithm 2

ARGMAX k

Algorithm for finding regular decomposition for fixed k.

Input: A: the adjacency matrix of a graph (an \(n\times n\) symmetric binary matrix with zero trace); N: an integer (the number of iterations in the search of a global optimum); k: a positive integer \(\le n\).

Start: \(m=1\).

1. \(i:=0\); generate a uniformly random element \(R^i\in {\mathcal {R}}_k\).

2. If any of the column sums of \(R^i\) is zero, GoTo 1, if not, then compute:

$$\begin{aligned} R^{i+1}:=\varPhi (R^i). \end{aligned}$$

3. If \(R^{i+1}\ne R^i\), set \(i:=i+1\) and GoTo 2,

4. \(R(m):=R^i\); \(m=m+1\);

\(l(m):= \sum _{i=1}^n \min _{1\le \alpha \le k}(L(R(m)))_{i,\alpha }\).

5. If \(m<N\), GoTo 1.

6. \(M:=\{m: l(m)\le l(i),i=1,2,\ldots ,N\}\); \(m^*:=\inf M\).

Output Solution: \(R(m^*)\).

In ARGMAX k the outer loop 1–5 runs several (N) optimization rounds finding each time a local optimum, and finally, the best local optimum is the output of Algorithm 2. At each optimization round, the inner loop 2–3 improves the initial random partition until a fixed point is reached and no further improvements of the partition are possible. This fixed point is an indication that a local optimum is found.

For very large graphs, the program may not be solvable in the sense that it is not possible and reasonable to go through all possible values of \(k\in \{1,2,\ldots , n\}\). One option is to limit the range of k. In case that no minimum is found, then use as an optimal choice the model found for the largest k within this range. Another option is to find the first minimum with smallest k and stop. When the graph is extremely large, it makes sense to use only a randomly sampled subgraph as an input—indeed, when \(k^*<<n\), a large-scale structure can be estimated from a sample as we shall show.

3.2 Regular Decomposition with Missing Link Information

Now assume that part of the link information is lost. We only consider the simplest case when the link information is lost uniformly randomly over all node pairs. We also exclude the possibility of a sparse representation of graphs, when only those node pairs that have links are listed, since this would lead to unsolvable ambiguity in our setting; indeed, if some node pair is not in the list, it could mean one of two cases: There is no link, or the link information is lost.

We formulate how the matrices used in the previous section are modified. The RD algorithms themselves are unaltered.

Denote by A the adjacency matrix with missing link values replaced by \(-1\)’s. A is symmetric, and we also assume that we know its true dimension (the number of nodes). We put \(-1\) on the diagonal of A, just for the convenience of further formulas. Define

$$\begin{aligned} D:=\frac{A+|A|}{2}, \end{aligned}$$

where the absolute value of a matrix is defined element-wise. Thus, D has the same elements as A, except that the entries equal to \(-1\) are replaced by 0’s. Next define a ‘mask matrix’

$$\begin{aligned} B:=\frac{A-|A|}{2}+1, \end{aligned}$$

where \(+1\) means element-wise addition of 1 to all elements of the matrix. That is, \(b_{i,j}=0\) if and only if \(a_{i,j}=-1\), and \(b_{i,j}=1\) otherwise. In other words, B is the indicator of known link data in A. The matrix \(P_1\) is now:

$$\begin{aligned} P_1(R):=R^TDR. \end{aligned}$$

The number of observed links in a block indexed by \((\alpha ,\beta )\) is

$$\begin{aligned} e_{\alpha ,\beta }= \left( 1-\frac{1}{2}\delta _{\alpha ,\beta }\right) (P_1(R))_{\alpha ,\beta }. \end{aligned}$$

We also need the following matrix, whose elements present the number of node pairs in block \((\alpha ,\beta )\) that contain link data:

$$\begin{aligned} (N)_{\alpha ,\beta }= n_{\alpha ,\beta }&:= \left( 1-\frac{1}{2}\delta _{\alpha ,\beta }\right) \sum \nolimits _{i,j}r_{i,\alpha }r_{j,\beta }b_{i,j}\\&=\left( 1-\frac{1}{2}\delta _{\alpha ,\beta }\right) (R^TBR)_{\alpha ,\beta }. \end{aligned}$$

The P-matrix is defined as the link densities in the observed data:

$$\begin{aligned} (P(R))_{\alpha , \beta }:=1_{\{n_{\alpha ,\beta }>0\}}\frac{e_{\alpha ,\beta }}{n_{\alpha ,\beta }}. \end{aligned}$$

As stated above, we assume that the matrix elements of P are close to the corresponding actual link densities in the case that we would have complete link data. This also assumes that the graph and the blocks must have large size.

The cost function in Definition 2 remains unaltered. Now the P-matrix elements are only estimates based on observed data and not the exact ones. The block sizes are the true ones that are known since we assume that we know the actual number of nodes in the graph. The interpretation is that the contributions of missing data entries in a block are replaced by the average contribution found from the observed data of that block. It should be noted that similar scaling must be done in the RD algorithms that find the optimum of the cost function. For example, A should be replaced with D, and summing over elements of D should be rescaled so that the contribution is proportional to the true size of the corresponding block.

4 Sparse Sampling Scheme Formulation

Assume that a large graph has a ‘regular structure’ that minimizes the regular decomposition MDL program with k regular groups, \(\xi :=\{V_1,V_2,\ldots , V_k\}\) having sizes \(n_1,n_2,\ldots , n_k\) and irreducible link density matrix with elements \(0<d_{i,j}<1\). The number of nodes in G is denoted as N, and it is assumed that the relative sizes \(r_i:=n_i/N\) of the groups are such that \(k r_i \ge c\), where c is a positive constant and not too small, say, \(c=1/10\). This condition means that none of the regular groups is very small. Such small groups would be ‘artifacts’ and are excluded by MDL criteria or by the practical RD algorithm that refuses forming too small groups. Here the aim of this condition is that when we make a uniformly random sample of n nodes, then all numbers \(r_in\), the expected number of sample nodes from each group, are big enough. On the other hand, this condition could probably be relaxed so that even small groups could be allowed. Their role in the classification problem we formulate is not decisive since the big groups are normally most decisive in this respect. However, we use this limitation in the sequel, for simplicity.

The optimal regular structure is, in particular, such that it is not possible to move even a single node from one group into another without some positive penalty in the following cost function (the log-likelihood part of it), the cost of placing a node v into group j

$$\begin{aligned} L_j(v):=\sum _{1\le i\le k}(-e_i(v)\log d_{i,j}-(n_i-e_i(v))\log (1-d_{i,j})), \end{aligned}$$

where \(e_i(v)\) is the number of links between node v and nodes in group i. This means that the cost of changing a group membership is positive for all nodes:

$$\begin{aligned} v\in V_j \rightarrow L_s(v)-L_j(v)>0,\quad \forall s\ne j, \end{aligned}$$

where \(V_j\in \xi\) is a regular group. The minimal penalty is denoted by \(\delta\):

$$\begin{aligned} \delta = \min _{v\in V_j, s\in V_s, s\ne j} (L_s(v)-L_j(v))>0. \end{aligned}$$

Here we need a condition that \(\delta\) is large. We require that the graph G and its optimal regular decomposition has the property:

$$\begin{aligned} \delta = cN,\quad c>0. \end{aligned}$$

This condition has similar motivation as the one for group sizes. We assume that N is very large; if \(\delta\) is not comparable with N, then in a reasonable sample the corresponding difference becomes hopelessly small. We see in the sequel that the expected value of such a difference is large and it seems reasonable to place this condition. Also in the case of a SBM as the generator of G we would get such a condition on \(\delta\) with exponential probability. We could relax this condition by assuming that it holds for most of the nodes v. For simplicity we use this condition as it is.

Consider making a uniformly random sample of n nodes of G, and retrieve the corresponding induced subgraph \(G_n\). The claim is that if n is sufficiently large, then \(G_n\) has a regular structure that has almost the same densities and relative sizes of the groups and correct membership in regular groups. Further, if \(G_n\) is used as a classifier, the misclassification probability is small, provided the regular structure of \(G_n\) has large enough groups to allow good approximation of the parameters of the regular structure of \(G_n\). Compare this claim with Lemma 2.3 from [18]:

Lemma 1

(Fox et al. [18]) Let X and Y be vertex subsets of a graph G. Let \(X' \subseteq X\) and \(Y'\subseteq Y\) be picked uniformly at random with \(|X'|=|Y'|=k\). Then

$$\begin{aligned} {\mathbf {P}}(|d(X' -Y')-d(X,Y)|<\delta )\ge 1-2e^{-\delta ^2k/4}. \end{aligned}$$

The proof is based on Azuma’s equality for the edge exposure martingale. In our case we use a similar idea for the proofs.

5 Sampled Cost Function Estimation

First we show that in expectation the sampled cost function resolves well the correct optimum. Next, we study a harder problem of estimating the probability of a deviation of the randomly sampled cost function from its expected value. Finally, it is shown that with exponential probability, in n, the sampled cost function is able to resolve the correct block structure.

5.1 Expectation of the Sampled Cost Function

The cost function of a node \(v\in V_i\) is just the length of the code (say, in number of bits) that describes the links of that node in G using the regular structure as the link probability distribution function. Select a node v uniformly at random. Then the cost function is a random variable. If \(v\in V_i\), the cost function of placing \(v \in V_\alpha\) has the value

$$\begin{aligned} L_{i,\alpha }(v):= & {} \sum _{j\in \{1,2,\ldots ,k\}} \left( -e_j(v)\log d_{j,\alpha }\right. \\&\left. -(n_j-e_j(v) )\log (1-d_{j,\alpha })\right) , \end{aligned}$$

where \(e_j(v), (j=1,2,\ldots ,k)\) are random variables, the other parameters being constants. The expectation of \(e_j(v)\), conditionally that \(v\in V_i\), is

$$\begin{aligned} {{\mathbf {E}}}(e_j(v)|v\in V_i)=n_j d_{i,j}, \end{aligned}$$

which follows from the definition of \(d_{i,j}\) as an arithmetic average of the fraction of node pairs that have links between regular groups i and j, or inside a regular group i if \(i=j\). As a result:

$$\begin{aligned} C_{i,\alpha }:=\, &{{\mathbf {E}}}(L_{i,\alpha }|v\in V_i)\\=\,& n_j \sum _{j\in \{1,2,\ldots ,k\}} \left( -d_{i,j}\log d_{j,\alpha }\right. \\&\quad \left. -(1-d_{i,j})\log (1-d_{j,\alpha })\right) . \end{aligned}$$

Proposition 3

Requiring that all groups are large and that for all pairs \((i,\alpha ), i\ne \alpha\), there is at least one index j with \(d_{i,j}\ne d_{j,\alpha }\), we have:

$$\begin{aligned} \min _{\{i,\alpha : \alpha \ne i, i,\alpha \in \{1,2,\ldots , k\}\}}(C_{i,\alpha }-C_{i,i})= c N, \quad c>0, \end{aligned}$$

where c is a constant.

Proof

It is easy to check that in the above formula for \(C_{i,\alpha }\), all terms in the sum, \(-d_{i,j}\log d_{j,\alpha }-(1-d_{i,j})\log (1-d_{j,\alpha })\), are nonnegative and each of them has an absolute minimum on argument \(d_{j,\alpha }\) when the corresponding densities are equal, \(d_{i,j}=d_{j,\alpha }\). Therefore, in \(C_{i,\alpha }-C_{i,i}\) the coefficients of \(n_j\), \(-d_{i,j}\log d_{j,\alpha }-(1-d_{i,j})\log (1-d_{j,\alpha })-(-d_{i,j}\log d_{i,j}-(1-d_{i,j})\log (1-d_{i,j}))\), are nonnegative for all j, and, according to the condition, at least one of them is strictly positive, because the corresponding densities are not equal. Since all \(n_j\) are proportional to N, the claim follows.\(\square\)

In general setting, the difference \(L_{i,\alpha }(v)- L_{i,i}(v)\) is not necessarily as large as the expected value for all nodes v. The only thing that can be guaranteed is that the value is positive (definition of an optimum). In the case of a true stochastic block model as a generator of the graph G, almost all differences \(L_{i,\alpha }(v)- L_{i,i}(v)\) are of the order of the expectation (positive and linear in N). Sub-linear terms could be called ‘outliers,’ since there is not much difference in terms of cost, in whichever group we place the corresponding nodes.

We now simply postulate that there are no outliers corresponding to the optimal regular structure we are dealing with. This means that

$$\begin{aligned} \forall v\in V: L_{i,\alpha }(v)- L_{i,i}(v) \ge \delta = cN, c>0. \end{aligned}$$

Consider a uniformly random sample of n nodes from V, denoted as \({\hat{V}}\subset V\). Denote by \({\hat{\xi }}\) (we shall use systematically ‘hat,’ \(\hat{}\), over a symbol of a variable to denote a corresponding sampled value) the partition of \(V_n\) that is a subpartition of \(\xi\), meaning that two nodes are in the same part of \({\hat{\xi }}\) if and only if they are in the same part of \(\xi\). Assume that all parts of \({\hat{\xi }}\) are ‘large,’ meaning that their relative sizes are close to those in \(\xi\). The probability of this condition can be made close to one, taking n large enough. This probability will be estimated later on, see Proposition 9. Take a uniformly random node \(v\in V\). Consider the following classifier based on \({\hat{\xi }}:\)

$$\begin{aligned} v\rightarrow \,& {} V_{\alpha *},\nonumber \\ \alpha ^*= & {} \arg \min _{\alpha \in \{1,2,\ldots ,k\}}{\hat{L}}_{i,\alpha }(v),\nonumber \\ {\hat{L}}_{i,\alpha }(v):= & {} \sum _{j\in \{1,2,\ldots ,k\}} \left( -{\hat{e}}_j(v)\log d_{j,\alpha }\right. \nonumber \\&\left. -({\hat{n}}_j-{\hat{e}}_j(v) )\log (1-d_{j,\alpha })\right) , \end{aligned}$$
(3)

where \({\hat{e}}_j(v)\) is the number of links joining group j of \({\hat{\xi }}\) and node v. The sizes of regulars groups in \({\hat{\xi }}\) are denoted as \({\hat{n}}_i\), and the groups of \({\hat{\xi }}\) are denoted as \({\hat{V}}_i\) for every \(i=1,2,\ldots ,k\), using same indexing as in \(\xi\). Note that here we use the link densities between the regular groups of the large graph. Later, we shall show that the link densities in \({\hat{\xi }}\) are close enough with a probability close to 1. This is another claim that needs to be justified (see Sect. 5.3).

Obviously, \({\hat{e}}_j\) is a random variable with a hypergeometric distribution. If we call ‘success’ a case when a sampled node from \({\hat{V}}_j\) has a link to node v, then there are \(e_j(v)\) favorable outcomes out of \(n_i\) possible choices. According to a well-known result, conditionally on sample size, \({\hat{n}}_j\), the expectation is

$$\begin{aligned} {\mathbf {E}}({\hat{e}}_j(v)|{\hat{n}}_j)= e_j(v) \frac{{\hat{n}}_j}{N}. \end{aligned}$$

Since \({\hat{n}}_i, i=1,2,\ldots , k\), are distributed according to a multivariate hypergeometric distribution, we get easily

$$\begin{aligned} {\mathbf {E}} {\hat{n}}_j=r_j n, \end{aligned}$$

and we have

$$\begin{aligned} {\mathbf {E}}{\hat{e}}_j(v)= \frac{e_j(v)}{n_j} r_j n= e_j(v) \frac{n}{N}. \end{aligned}$$

We have shown the following:

Proposition 4

$$\begin{aligned} {\mathbf {E}}{\hat{L}}_{i,\alpha }(v)=\frac{n}{N}L_{i,\alpha }(v). \end{aligned}$$

In other words, the expectation of a sampled cost function is just a rescaled version of the cost function for the whole graph. Using this result, we see:

$$\begin{aligned}&\forall v\in V_i,\, \alpha \ne i:\\&{\mathbf {E}} ({\hat{L}}_{i,\alpha }(v)-{\hat{L}}_{i,i}(v))= \frac{n}{N}(L_{i,\alpha }(v)-L_{i,i}(v))\\&\quad\quad \quad \ge \frac{n}{N} c N=cn,\quad c>0. \end{aligned}$$

5.2 Deviations of the Sampled Block Sizes from the Expected Values

Assume that all link densities fulfill \(0<d_{i,j}<1\). Excluding cases with zero or one densities are not limitations, since in both cases the sampled structures are deterministic (for density 1, all sampled pairs have links, and in the other case, no pairs have links).

When \(v\in V_i\), we can write

$$\begin{aligned} {\hat{L}}_{i,\alpha }(v)=\sum _{1\le j \le k}(a_{j,\alpha }{\hat{e}}_j(v) +b_{j,\alpha }({\hat{n}}_{j,\alpha }-{\hat{e}}_{j,\alpha })), \end{aligned}$$

where

$$\begin{aligned} a_{j,\alpha }:= -\log d_{j,\alpha },\quad b_{j,\alpha }:=-\log (1-d_{j,\alpha }) \end{aligned}$$

are all positive constants. Denote a normalized version as

$$\begin{aligned} {\hat{Y}}_{i,\alpha }(v):=\frac{ {\hat{L}}_{i,\alpha }(v)}{c_\alpha }, \end{aligned}$$

where

$$\begin{aligned} c_\alpha :=\max _{1\le j \le k} |a_{j,\alpha }-b_{j,\alpha }|. \end{aligned}$$

This normalization guarantees that if one of the arguments of \({\hat{L}}_{i,\alpha }(v)\), \({\hat{e}}_j\), changes by an amount \(\epsilon\) with \(|\epsilon |\le 1\), then the absolute value of the difference is upper-bounded by 1:

$$\begin{aligned} |\varDelta {\hat{Y}}_{i,\alpha }|= \frac{|\epsilon (a_{j,\alpha }-b_{j, \alpha })|}{c_\alpha }\le |\epsilon |\le 1. \end{aligned}$$

Define the following random process with discrete time \(t\in \{0,1,2,\ldots ,n\}\). Choose \({\hat{n}}_j\) nodes uniformly at random from \(V_j\), without replacement. Denote the sampled nodes in order they were drawn: \((v_j(1),\ldots ,v_j({\hat{n}}_j)))={\hat{V}}_j\) and similarly for all \(1\le j\le k\). Then choose \(v\in V_i\) uniformly at random from the remaining nodes. Correspondingly, define the random variables \(x_j(1),\ldots , x_j({\hat{n}}_j)\), so that \(x_j(i)=1\) if \((v_j(i),v)\) is a link in G and otherwise \(x_j(i)=0\).

Obviously, we have the following conditional probabilities:

$$\begin{aligned}{\mathbf {P}}(x_j(t)=&1|x_j(t-1),x_j(t-2),\ldots ,x_j(1))\\& =\frac{e_j(v)-\sum _{1\le s\le t-1}x_j(s)}{n_j-(t-1)}. \end{aligned}$$

Define the following vertex exposure process, corresponding to \(x_j(t)\):

$$\begin{aligned} E_j(0;\,v)={\mathbf {E}}{\hat{e}}_j(v)={\hat{n}}_j\frac{e_j(v)}{n_j}, \end{aligned}$$

\(E_j(t;\,v)\) is the expectation of \({\hat{e}}_j\) after \(x_j(1),\ldots ,x_j(t)\) are known, and the contribution of unexposed variables \(x_j(t+1),\ldots , x_j({\hat{n}}_j)\) is replaced by the expected value. Using the formulas for hypergeometric expectations, we get the following:

$$\begin{aligned} E_j(t;\,v)= \sum _{1\le s\le t}x_j(s)+ \frac{({\hat{n}}_j-t)(e_j(v)- \sum _{1\le s\le t}x_j(s))}{n_j-t}. \end{aligned}$$

Proposition 5

\(E_j(\cdot )\) is a martingale.

Proof

We need to show that

$$\begin{aligned} {\mathbf {E}}(E_j(t;\,v)|E_j(t-1;\,v),\ldots E_j(0,v))= E_j(t-1;\,v). \end{aligned}$$

It is well known that such an exposure process is always a martingale. However, we check this condition as a ‘sanity check’ of our construction.

$$\begin{aligned}&{\mathbf {E}}(E_j(t;\,v)|E_j(t-1;\,v),\ldots E_j(0;\,v))\\&\quad ={\mathbf {E}}(x_j(t)|x_j(t-1),\ldots , x_j(1))+\sum _{1\le s\le t-1}x_j(s)\\&\qquad +\, ({\hat{n}}_j-t)\{e_j(v)- \sum _{1\le s\le t-1}x_j(s)\\&\qquad -\,{\mathbf {E}}(x_j(t)|x_j(t-1),\ldots , x_j(1)))\}/(n_j-t). \end{aligned}$$

Note that

$$\begin{aligned}&{\mathbf {E}}(x_j(t)|x_j(t-1),\ldots , x_j(1))\\&\quad ={\mathbf {P}}(x_j(t)=1|x_j(t-1),x_j(t-2),\ldots ,x_j(1))\\&\quad =\frac{e_j(v)-\sum _{1\le s\le t-1}x_j(s)}{n_j-(t-1)}. \end{aligned}$$

Denote \(x={\hat{n}}_j, s_m=\sum _{s=1}^mx_j(s), e_j(v)=e\) and \(n_j=n\). In these terms, we can write

$$\begin{aligned}&E_j(t)=s_t+\frac{(x-t)(e-s_t)}{n-t},\\&{\mathbf {E}}(x_j(t)|x_j(t-1),\ldots , x_j(1))=\frac{e-s_{t-1}}{n-(t-1)}. \end{aligned}$$

Now,

$$\begin{aligned}&{\mathbf {E}}(E_j(t;\,v)|E_j(t-1;\,v),\ldots E_j(0;\,v))\\&\quad =s_{t-1}+ \frac{e-s_{t-1}}{n-(t-1)}+ \frac{(x-t)\left(e- s_{t-1}-\frac{e-s_{t-1}}{n-(t-1)})\right)}{n-t}\\&\quad =E_j(t-1;\,v)-\frac{(x-(t-1))(e-s_{t-1})}{n-(t-1)}+ \frac{e-s_{t-1}}{n-(t-1)}\\&\qquad +\frac{(x-t)\left(e- s_{t-1}-\frac{e-s_{t-1}}{n-(t-1)})\right)}{n-t}\\&\quad =E_j(t-1;\,v)- \frac{(x-t))(e-s_{t-1})}{n-(t-1)}\\&\qquad +\frac{(x-t)\left(e- s_{t-1}-\frac{e-s_{t-1}}{n-(t-1)})\right)}{n-t}\\&\quad =E_j(t-1;\,v)+(x-t)(e-s_{t-1})\left( \frac{1}{n-t}-\frac{1}{n-(t-1)}\right) \\&\qquad -\frac{(x-t)(e-s_{t-1})}{(n-t)(n-(t-1))}\\&\quad =E_j(t-1;\,v)+\frac{(x-t)(e-s_{t-1})}{(n-t)(n-(t-1))}\\&\qquad -\frac{(x-t)(e-s_{t-1})}{(n-t)(n-(t-1))}\\&\quad =E_j(t-1;\,v). \end{aligned}$$

\(\square\)

Let us construct the random process

$$\begin{aligned} X_{i,\alpha }(t;\,v),\quad v\in V, \end{aligned}$$

where t is discrete time from 0 to n. First, define the following ramp functions for each \(1\le i\le k\):

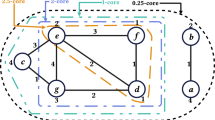
$$\begin{aligned} \theta _i(t):= \,& {} \theta \left( t-\sum _{j=1}^i{\hat{n}}_j\right) \left( \left( t-\sum _{j=1}^i{\hat{n}}_j\right) \right. \\&\times \,\theta \left( \sum _{j=1}^{i+1}{\hat{n}}_j-t) +{\hat{n}}_i\theta \left( t-\sum _{j=1}^{i+1}{\hat{n}}_j\right) \right) , \end{aligned}$$

where \(\theta (\cdot )\) is the Heaviside step function, with agreement \(\theta (0)=0\), \({\hat{n}}_{k+1}=0\) and \(t\in \{0,1,\ldots ,\sum _{j=1}^k{\hat{n}}_j\}\) (Fig. 2).

Fig. 2
figure 2

Schematic graphics of \(\theta _i(t)\); it ramps from zero to \({\hat{n}}_i\) within some time interval \([t(i),t(i+1)]\), with step size equal to 1, and outside the interval, remains constant. This interval corresponds to the one of span of process \(E_i(\cdot )\)

Full size image

By definition,

$$\begin{aligned} X_{i,\alpha }(t;\,v):= & {} \frac{1}{c_\alpha }\sum _{j=1}^k \left( -E_j(\theta _j(t);\,v)\log {d_{j,\alpha }}\right. \\&\quad \left. -\,({\hat{n}}_j-E_j(\theta _j(t);\,v))\log (1-d_{j,\alpha })\right) , \end{aligned}$$

where we refer to the previous definitions of \(E_j(\cdot ), v\) and \(\theta _j(\cdot )\) and \(t=0,1,\ldots , n\).

Proposition 6

\(X_{i,\alpha }(\cdot ;\,v)\) is a martingale and

$$\begin{aligned} |X_{i,\alpha }(t;\,v)-X_{i,\alpha }(t-1;\,v)|\le 1, \forall t: 1\le t\le n. \end{aligned}$$

Proof

At each discrete time, only one of the subprocesses \(E_j(\cdot )\) is ‘active.’ By this, we mean that for any moment of time t only one subprocess \(E_j(\cdot )\) is progressing, the others are either in the final state when all links to v are revealed, or are completely un-revealed, and the corresponding value equals the expectation. Therefore, Proposition 5 is sufficient to show the conditional expectation property. The normalization coefficient \(c_\alpha\) guarantees the upper bound for the absolute values of step-wise changes of the process. \(\square\)

As a result, we get the following:

Proposition 7

For all \(\alpha , i\in \{1,2,\ldots , k\}\):

$$\begin{aligned} {\mathbf {P}}|(X_{i,\alpha }(n;\,v)-{\mathbf {E}}X_{i,\alpha }(n;\,v)|\le t)\ge 1-2e^{-\frac{t^2}{2n}}. \end{aligned}$$

Proof

Use the standard Azuma’s inequality (e.g., Theorem 2.25 in [19]). The inequality is true for all indices \(\alpha\) and i since there is only one link exposure process, and for any of them the inequality is true with right-hand side that is independent of those indices. \(\square\)

Next, define the following vector process. It corresponds to uniformly random sampling of n nodes from V. Its components correspond to the numbers of nodes in the classes of \({\hat{\xi }}\). It has \(n+1\) time steps and starts from all components equal to zero, and at \(t=1\), the value of ith component is \({\mathbf {E}}{\hat{n}}_i=n n_i/N\). After that the first node and its class in \(\xi\), let it be i, are revealed, and the corresponding component is changed to the expected value of \({\hat{n}}_i\) conditionally to this information. And so on, until the process ends with all components having their final values, like \({\hat{n}}_i\). By normalizing this process with the coefficient \(13\sqrt{k}\) such a process is denoted as \({\mathbf {N}}(t)\).

Proposition 8

Assume that the graph size N is large enough and the sample size is small with \(n\le \sqrt{n}_i\), \(\forall i\). Then \({\mathbf {N}}(\cdot )\) is a vector martingale with maximal increment of its Euclidean norm equal to 1.

Proof

The martingale property follows from the general character of the process as an exposure (see Proposition 5). It remains to check the step bound. Let \(x_i(t)\) denote the increase in the number of nodes in class i at time step t. Then \(x_i(t)\) equals 1 if the tth node happens to belong to class i and equals zero otherwise. Using the obvious multivariate hypergeometric distribution we see that the non-normalized \(i\hbox {th}\) component of the process at time t is

$$\begin{aligned} X_i(t)=\sum _{s=1}^tx_i(t)+ \frac{(n-t)\left(n_i-\sum _{s=1}^t\right)}{N-t}. \end{aligned}$$

Using the short-hand notations \(x=n_i\), \(s_t=\sum _{s=1}^tx_i(t)\), we write:

$$\begin{aligned}&|X_i(t)-X_i(t-1)|\\&\quad =\Big |s_t-s_{t-1}+ \frac{(n-t)(x-s_t)}{N-t}- \frac{(n-t+1)(x-s_{t-1})}{N-t+1}\Big |\\&\quad =\Big |s_t-s_{t-1}\\&\qquad + \frac{(1+N-t)(s_{t-1}+(t-n)(s_t-s_{t-1})-x))}{(N-t)(N-t+1)}\Big |. \end{aligned}$$

We see that the dominating term (largest in absolute value) in the nominator is \(-xN=-n_iN\), since we assume a large graph and much smaller sample size, and we can assume that the whole numerator is negative; thus, the upper bound of the absolute value of the numerator can be obtained by making the rest of terms as small as possible:

$$\begin{aligned}&|(1+N-t)(s_{t-1}+(t-n)(s_t-s_{t-1})-x))|\\&\quad =|-xN\\&\qquad +(1+N-t)\left( s_{t-1}+(t-n)(s_t-s_{t-1})\right) -x(1-t)|\\&\quad \le |-xN+(N+1)(-n)-x|\\&\quad \le xN+(N+1)n+x\le 3xN, \end{aligned}$$

where we used also \(s_t-s_{t-1}\le 1\), \(0 \le t\le n\), and in the final upper bound we assume that n is much smaller than \(n_i\) or N. As a result we get:

$$\begin{aligned} |X_i(t)-X_i(t-1)|\le 1+ \frac{3n_iN}{(N-n)^2}. \end{aligned}$$

Assuming that \(n\le N/2\), we have

$$\begin{aligned} |X_i(t)-X_i(t-1)|\le 1+ \frac{12 n_i N}{N^2}\le 13. \end{aligned}$$

Finally, for the Euclidean norm we get:

$$\begin{aligned} || {\mathbf {X}}(t)-{\mathbf {X}}(t-1)||^2=\sum _{i=1}^k( X_i(t)-X_i(t-1))^2\le k 13^2. \end{aligned}$$

Thus, by defining \({\mathbf {N}}(t)=\frac{{\mathbf {X}}(t)}{13\sqrt{k}}\), we obtain

$$\begin{aligned} || {\mathbf {N}}(t)-{\mathbf {N}}(t-1)||\le 1. \end{aligned}$$

\(\square\)

Using the Azuma inequality for a vector-valued martingale, given in [20], we get:

Proposition 9

Under the same conditions as in Proposition 8, we have:

$$\begin{aligned} {\mathbf {P}}\left( \max _{1\le i\le k}|{\hat{n}}_i-r_i n|\le 13\sqrt{k} (n^{3/4}+1)\right) \ge 1-2e^{1-\sqrt{n}/2}. \end{aligned}$$

Proof

We just check the conditions of the theorem in [20] that are all fulfilled after centering the \({\mathbf {N}}(\cdot )\) to expected value at time \(t=n\). The theorem then states:

$$\begin{aligned} {\mathbf {P}}(||{\mathbf {N}}(n)-{\mathbf {E}}{\mathbf {N}}(n)||\ge a)< 2e^{1-(a-1)^2/2n}. \end{aligned}$$

This is equivalent to

$$\begin{aligned} {\mathbf {P}}(||{\mathbf {X}}(n)-{\mathbf {E}}{\mathbf {X}}(n)||\ge 13 a \sqrt{k} )<2e^{1-(a-1)^2/2n}. \end{aligned}$$

The expectations of components are \({\mathbf {E}}X_i(n)={\mathbf {E}}{\hat{n}}_i=r_in\). Since \(||{\mathbf {X}}(n)-{\mathbf {E}}{\mathbf {X}}(n)||\ge \max _{1\le i\le k}|{\hat{n}}_i-r_i n|\), we get the claimed inequality by choosing \(a= 1+n^{3/4}\). \(\square\)

5.3 Deviations of Sampled Link Densities from Their Expectations

Finally, we estimate the deviations of link densities between sampled groups, \({\hat{d}}_{i,j}\), from their expected values \(d_{i,j}\), conditionally on sampled group sizes \({\hat{n}}_i\). We simply reuse Theorem 2.2. from [18].

Proposition 10

Provided \(r_in/2\le {\hat{n}}_i\le 2 r_i n\), we have:

$${\mathbf {P}}\left\{ \max _{1\le i\le j}|{\hat{d}}_{i,j}-d_{i,j}|\le \right. \left. \frac{1}{\root 4 \of {n}}\right\} \ge 1- k(k-1)\exp (-\sqrt{n} a),$$

where

$$\begin{aligned} a= \min _{i\ne j} \{(r_ir_j)^2/(32 (r_i+r_j)^3), (r_i-1/n)^2/ r_i^3\}. \end{aligned}$$

Proof

Use Theorem 2.2 of [18] and reasoning therein for a given pair (i, j) and the conditions on sizes \(r_in/2\le {\hat{n}}_i\le 2 r_i n\), and finally the union bound to estimate that all densities are within the range. The coefficient a corresponds to the weakest exponent. \(\square\)

5.4 Probability of Deviation of Sampled Cost Function from the Expectation

Using the results of previous sections we can formulate and prove the main result:

Theorem 1

Provided \(n\ge m\), \(m=f ^4\), then uniformly random sampling of n nodes and grouping of these nodes as in \(\xi\) has the property: If \(v\in V\) is a random node from \(V_i\), outside the sample, then for all \(\alpha \ne i\):

$$\begin{aligned} {\mathbf {P}}({\hat{L}}_{i,\alpha }(v;\,{\hat{D}})-{\hat{L}}_{i,i}(v;\,{\hat{D}})>0) \ge 1-g\exp (-\phi \sqrt{n}), \end{aligned}$$

where

$$\begin{aligned}&{\hat{L}}_{i,s}(v;\,{\hat{D}}) :=\sum _{j\in \{1,2,\ldots ,k\}} (-{\hat{e}}_j(v)\log {\hat{d}}_{j,s}\\&\quad -({\hat{n}}_j-{\hat{e}}_j(v) )\log (1-{\hat{d}}_{j,s})),\\ \phi&= \min (a,1/2),\\g&=2+k(k+1),\\a&=\min _{i\ne j}\left( (r_ir_j)^2/(32 (r_i+r_j)^3), (r_i-1/n)^2/ r_i^3\right) ,\\d_1&=\min (d_{i,j}),\\ d_2&=1-\min (1-d_{i,j})\\&d_m=\left\{ \begin{array}{ll} d_1,\ \text{ if }\ \min (d_1,1-d_2)=d_1,\\ d_2,\ \text{ if }\ \min (d_1,1-d_2)=1-d_2, \end{array} \right. \\B&=14k^{3/2} \log \left( \frac{1}{d_1(1-d_2)}\right) , \\ m_{1,2}&= \max \left( \frac{1}{d_1^2},\frac{1}{(1-d_2)^2}\right) \\f_1&= \frac{2}{c}\left( B+|\log (1-d_m)/d_m)|\right. \\ &\quad \left. +\frac{k}{d_1(1-d_2)}+2km_{1,2}\right) ,\\f_2&= 1/\min (d_1/2,(1-d_2)/2),\\f&=\max (f_1,f_2), \end{aligned}$$

and where \({\hat{d}}_{i,j}\) are the (random) link densities between sampled group pairs \(({\hat{V}}_i,{\hat{V}}_j)\) or inside a single sampled group.

The meaning of Theorem 1 is that if we build a classifier based on observed random sample of n nodes and its regular structure, then the rest of nodes can be classified correctly with probability that is exponentially close to one.

Proof

To avoid extensively lengthy writing we use a short-hand notation with probabilistic bounds. For instance, instead of

$$\begin{aligned}&{\mathbf {P}}\left\{ \max _{1\le i\le j}|{\hat{d}}_{i,j}-d_{i,j}|\le \frac{1}{\root 4 \of {n}}\right\} \\&\quad \ge 1- k(k-1)\exp (-\sqrt{n} a), \end{aligned}$$

we write \({\hat{d}}_{i,j}=d_{i,j}+ \frac{c_{i,j}}{\root 4 \of {n}}, |c_{i,j}|\le 1\). In the final step we return to the corresponding probabilistic bounds. First, we want to show that

$$\begin{aligned} {\hat{L}}_{i,s}(v;\,{\hat{D}})= & {} {\hat{L}}_{i,s}(v)+ \frac{f_{i,s}k}{d_1(1-d_2)}n^{3/4}\\&+\,2\sqrt{n} k g_{i,s}m_{1,2},\\ |f_{i,s}|\le & {} 1,\quad |g_{i,s}|\le 1, \end{aligned}$$

provided that

$$\begin{aligned} \frac{1}{\root 4 \of {n}}\le \min (d_1/2,(1-d_2)/2). \end{aligned}$$

We use the Taylor expansion of logarithm function truncated at the linear term and Taylor’s remainder theorem for estimating the error:

$$\begin{aligned}&{\hat{L}}_{i,s}(v;\,{\hat{D}})\\&\quad:= \sum _{j\in \{1,2,\ldots ,k\}} \left(-{\hat{e}}_j(v)\log {\hat{d}}_{j,s}-({\hat{n}}_j-{\hat{e}}_j(v) )\log (1-{\hat{d}}_{j,s})\right)\\&\quad ={\hat{L}}_{i,s}+ \sum _{j\in \{1,2,\ldots ,k\}} \left[ \frac{-{\hat{e}}_j(v)}{d_{j,s}} +\frac{({\hat{n}}_j-{\hat{e}}_j(v) )}{1-d_{j,s}}\right] \frac{c_{i,s}}{\root 4 \of {n}}+R_2, \end{aligned}$$

where \(R_2\) is the remainder. First, the bound of the absolute value of the second term is:

$$\begin{aligned}&\Big | \sum _{j\in \{1,2,\ldots ,k\}} \left\{ \frac{-{\hat{e}}_j(v)}{d_{j,s}} +\frac{({\hat{n}}_j-{\hat{e}}_j(v) )}{1-d_{j,s}} \right\} \frac{c_{i,s}}{\root 4 \of {n}} \Big |\\&\quad \le \sum _{j\in \{1,2,\ldots ,k\}} \left( \frac{|{\hat{n}}_{j,s}d_{j,s}-{\hat{e}}_j(v)0|}{d_{j,s}(1-d_{j,s})}\right) \frac{|c_{i,s}|}{\root 4 \of {n}}\\&\quad \le \sum _{j\in \{1,2,\ldots ,k\}} \left( \frac{n}{d_{j,s}(1-d_{j,s})}\right) \frac{1}{\root 4 \of {n}}\\&\quad \le \frac{k}{d_1(1-d_2)}n^{3/4}, \end{aligned}$$

where we used the facts that \({\hat{n}}_{j,s}\le n\) and \({\hat{e}}_j(v)\le n\). As a result, we get the second term in the Taylor expansion of \({\hat{L}}_{i,s}(v;\,{\hat{D}})\). Next, we estimate the absolute value of \(R_2\). Obviously, \(R_2\) is a sum of remainders corresponding to each term of the sum of \({\hat{L}}_{i,s}(v;\,{\hat{D}})\). For each term we use the proposition according to which \(f(a+\delta )=f(a)+f'(a)\delta + r_2(x)\), where \(|r_2(x)|\le M \delta ^2/2\), where \(M=\sup _{x\in (a-|\delta |,a+|\delta |)}|f''(x)|\). In our case we have terms like

$$\begin{aligned}&\frac{1}{2}\sup _{d_{j,s}-1/\root 4 \of {n}\le x\le d_{j,s}+1/\root 4 \of {n}}\left| \frac{{\hat{e}}_j(v)}{x^2} +\frac{{\hat{n}}_j-{\hat{e}}_j}{(1-x)^2}\right| \frac{|c_{j,s}|^2}{\sqrt{n}}\\&\quad \le \frac{1}{2} \left\{ \frac{n}{(d_{j,s}-1/\root 4 \of {n})^2} + \frac{n}{(1-d_{j,s}-1/\root 4 \of {n})^2}\right\} \frac{|c_{j,s}|^2}{\sqrt{n}}\\&\quad \le \frac{1}{2} \left\{ \frac{1}{(d_{1}-1/\root 4 \of {n})^2}+\frac{1}{(1-d_{2}-1/\root 4 \of {n})^2}\right\} \sqrt{n}\\&\quad \le 2\sqrt{n} \max \left( \frac{1}{d_1^2},\frac{1}{(1-d_2)^2}\right) , \end{aligned}$$

where we used the condition \(\frac{1}{\root 4 \of {n}}\le \min (d_1/2,(1-d_2)/2)\). Using this uniform bound for all terms, we obtain the third term in the expansion.

Next, we need to analyze the first term \({\hat{L}}_{i,s}(v)\), the cost function with the right densities, using Propositions 5 and 7. From Proposition 5 it follows that

$$\begin{aligned} {\hat{L}}_{i,s}(v)= {\mathbf {E}}{\hat{L}}_{i,s}(v)+ c_sz_{i,s}n^{3/4}, \quad |z_{i,s}|\le 1, \end{aligned}$$

where the expectation, conditioned on the sizes of sampled groups \({\hat{n}}_j\), is

$$\begin{aligned}&{\mathbf {E}}{\hat{L}}_{i,s}(v)\\&\quad =\sum _{j=1}^k \left[ -\frac{e_j(v) {\hat{n}}_j}{n_j}\log d_{j,s}-\left[ {\hat{n}}_j - \frac{e_j(v) {\hat{n}}_j}{n_j} \right] \log (1-d_{j,s}) \right] . \end{aligned}$$

Using Proposition 7, we get

$$\begin{aligned} {\hat{n}}_j=r_jn+14\sqrt{k}s_jn^{3/4},\quad |s_j|\le 1. \end{aligned}$$

Substituting this, and noting the fact \(n_j=r_jN\), we have

$$\begin{aligned}&{\mathbf {E}}{\hat{L}}_{i,s}(v)\\&\quad= \sum _{j=1}^k \left\{ -\frac{e_j(v) r_jn}{r_jN}\log d_{j,s} \right. \\&\quad \left. -\,\left( r_jn-\frac{e_j(v) r_jn}{r_jN}\right) \log (1-d_{j,s})\right\} \\&\quad + \,14\sqrt{k}n^{3/4}\sum _{j=1}^ks_j\left\{ -\frac{e_j(v) }{n_j}\log d_{j,s}\right. \\&\quad \left. -\,\left( 1-\frac{e_j(v) }{n_j}\right) \log (1-d_{j,s})\right\} . \end{aligned}$$

The first term is

$$\begin{aligned}&\frac{n}{N}\sum _{j=1}^k\left( -e_j(v) \log d_{j,s}-(n_j-e_j(v))\log (1-d_{j,s})\right) \\&\quad =\frac{n}{N}L_{i,s}(v), \end{aligned}$$

and the second term has an absolute bound:

$$\begin{aligned}&14\sqrt{k}n^{3/4}\left| \sum _{j=1}^ks_j\left\{ -\frac{e_j(v) }{n_j}\log d_{j,s}\right. \right. \\&\quad \left. \left. -\left( 1-\frac{e_j(v) }{n_j}\right) \log (1-d_{j,s})\right\} \right| \\&\qquad \le 14\sqrt{k}n^{3/4}\sum _{j=1}^k(-\log d_{j,s}-\log (1-d_{j,s}))\\&\qquad \le 14 \sqrt{k} kn^{3/4} \log \left( \frac{1}{d_1(1-d_2)}\right) , \end{aligned}$$

where we used the fact that \(0\le e_j(v)/n_j\le 1\). As a result we have:

$$\begin{aligned} {\mathbf {E}}{\hat{L}}_{i,s}(v)= \frac{n}{N}L_{i,s}(v)+ B b_{i,s} n^{3/4}, \end{aligned}$$

with \(|b|\le 1\) and B as in the claim of the theorem. Combining these estimates, we have

$$\begin{aligned} {\hat{L}}_{i,s}(v)= \frac{n}{N}L_{i,s}(v)+ (B b_{i,s}+ c_sz_{i,s}) n^{3/4}. \end{aligned}$$

Gathering all pieces, we get finally:

$$\begin{aligned} {\hat{L}}_{i,s}(v;\,{\hat{D}})= \frac{n}{N}L_{i,s}(v)+ u_{i,s} n^{3/4} \end{aligned}$$

with

$$\begin{aligned} u_{i,s}=B b_{i,s}+ c_sz_{i,s}+ \frac{f_{i,s}k}{d_1(1-d_2)} +\frac{2 k g_{i,s}m_{1,2}}{\root 4 \of {n}}. \end{aligned}$$

Thus,

$$\begin{aligned}&{\hat{L}}_{i,s}(v;\,{\hat{D}})-{\hat{L}}_{i,i}(v;\,{\hat{D}})\\&\quad =\frac{n}{N}\left( L_{i,s}(v)-L_{i,i}(v)\right) +(u_{i,s} -u_{i,i})n^{3/4}, \end{aligned}$$

since by condition

$$\begin{aligned} \frac{n}{N}\left( L_{i,s}(v)-L_{i,i}(v)\right) \ge cn, \end{aligned}$$

a sufficient condition for \({\hat{L}}_{i,s}(v;\,{\hat{D}})-{\hat{L}}_{i,i}(v;\,{\hat{D}})>0\) is that \(cn>|u_{i,s}-u_{i,i}|n^{3/4}\). Since \(|u_{i,s}-u_{i,i}|/c\) is bounded by a constant \(f_1\), this condition is achievable with sufficiently large n. It can be seen that we can choose \(f_1\) as in the claim of the theorem. We had another condition \(\frac{1}{\root 4 \of {n}}\le \min (d_1/2,(1-d_2)/2)\), or \(\root 4 \of {n}\ge 1/ \min (d_1/2,(1-d_2)/2) :=f_2\).

As a result, if \(f=\max (f_1,f_2)\), then \(n\ge f^4\) implies \({\hat{L}}_{i,s}(v;\,{\hat{D}})-{\hat{L}}_{i,i}(v;\,{\hat{D}})>0\), with a probability that we estimate now. We use a simple union bound. Let \(A_1,A_2,\ldots\) denote some events that correspond to the violation of one of the conditions in our proof. Then the event that at least one of them happens is given by the union of these events. The probability of this event always fulfills \({\mathbf {P}}(\cup _i A_i)\le \sum _i{\mathbf {P}}(A_i)\). Thus, the probability that none of the conditions is violated is not less than \(1-\sum _i{\mathbf {P}}(A_i)\). All \({\mathbf {P}}(A_i)\) are exponentially small in n, and so is their sum, with an exponent that has the smallest positive constant. The result of this count is given in the formulation of the theorem. \(\square\)

6 Simulations for Large-Graph Analysis Based on Sampling

6.1 Regular Decomposition

We illustrate the suggested sampling scheme and its application to analyze very large graphs. The results are illustrated in Figs. 3, 4, 5, 6, 7 and 8.

Fig. 3
figure 3

Adjacency matrix of a random graph with \(k=10\), and equal size blocks and 1000 nodes

Full size image
Fig. 4
figure 4

Adjacency matrix of a random graph with \(k=10\), and equal size blocks, generated from the same model as in previous picture but with only 200 nodes

Full size image
Fig. 5
figure 5

Classification success percentile as a function of n using several repetitions of experiments and 1000 classification instances for each. Already a sample with 200 nodes generates a model with almost a perfect classifier

Full size image
Fig. 6
figure 6

A sample graph with 50 nodes that is insufficient to create a successful classifier—the result is similar to completely random classification

Full size image
Fig. 7
figure 7

200-node sample, from the same model as above, that generates almost a perfect classifier—no errors detected in experiments

Full size image
Fig. 8
figure 8

A scheme of RD for a huge graph shown at the top; in reality, we assume a much larger graph than what is shown in the picture. First, a moderate size sample of \(n_0\) nodes and induced subgraph is formed. RD is applied to this small graph; groups \({\hat{\xi }}_{n_0}\) and matrix \({\hat{P}}\) are found, shown as the graph in the middle. Then, sequentially, any node v from the big graph can be classified to a regular group using just counts of links of this chosen node to regular groups of the sample graph. This classification requires a constant number of computations, upper-bounded by \(k^2 n_0\), with elementary functions. As a result, nodes of the whole graph can be classified in just linear time with respect to number of nodes. After the classification is done (shown in the ring shape structure at the right side) the RD of the large graph is done simply by retrieving link information. The result is shown in the lower graph

Full size image

Assume that a large graph is generated from a SBM. Denote the blocks by

$$\begin{aligned} V_1,V_2,\ldots , V_k \end{aligned}$$

and the link probability matrix by P, that is, a \(k\times k\) symmetric matrix with entries in (0, 1). We also assume that no two rows are identical, to avoid a redundant structure. Then we generate links between blocks and within blocks using P as independent link probabilities. The size of the graph G is assumed large and denoted by N.

Now take a uniform random sample of size n of the nodes. Denote the graph induced by sampling as \(G_n\). The relative sizes of blocks are denoted as \(r_i:=\frac{|V_i|}{N}\). The probability of sampling a node from block i is \(r_i\). We want to test whether the block structure of G can be reconstructed from a small sample, the size of which does not depend on N and with time complexity \(\varTheta (N)\). We believe that the answer is positive.

For simplicity, assume that we know the block structure of \(G_n\) by having run an ideally working RD algorithm. This is not too far from reality, although some of the nodes may in reality be misclassified. However, there is not a big difference, if most of the nodes are correctly classified and n is not very small. The real graphs, however, are not generated from any SBMs, and this is a more serious drawback. In the latter case we would like to show that it is not necessary to run RD on G; rather, it is sufficient to run RD on \(G_n\) and just classify the rest of the nodes based on that structure.

In \(G_n\), we denote the blocks as \({\hat{V}}_1,{\hat{V}}_2,\ldots , {\hat{V}}_k\), and the empirical link densities between these blocks as \({\hat{d}}_{i,j}\). The relative sizes of the blocks as well as the link densities deviate in \(G_n\) from their counterparts in G. Now assume that we take a node \(i\in V_\beta\) outside \(G_n\) together with its links to \(G_n\). What is the probability that the RD classifier places this node into \({\hat{V}}_\beta\)?

Denote by \(e_\alpha (v)\) the number of links from v to \({\hat{V}}_\alpha\), \(n_\alpha :=|{\hat{V}}_\alpha |\). The RD classifier based on \(G_n\) is the following program:

$$\begin{aligned} &C_\alpha (v|{\hat{\xi }},{\hat{d}},k):= {} \sum _{j=1}^k\left[ -e_j(v)\log {\hat{d}}_{j,\alpha }\right. \\&\quad \left. -\,(n_j-e_j(v))\log (1-{\hat{d}}_{j,\alpha })\right] ,\\ &\alpha ^*= {} \arg \, \min _\alpha (C_\alpha (v|{\hat{\xi }},{\hat{d}},k)), \end{aligned}$$

where \({\hat{\xi }}=\left\{ {{\hat{V}}_1,{\hat{V}}_2,\ldots , {\hat{V}}_k}\right\}\) and \({\hat{d}}\) stands for the \(k\times k\) matrix with matrix elements \({\hat{d}}_{i,j}\). To compute the optimal block for node i we need to compute and check a list of k numbers as well as compute the densities \(e_\alpha (i)\). The computation time is upper-bounded by \(\varTheta (k n)\). For a size n that is independent on N, the computation takes only a constant time. By this, we mean that it is enough to have some constant n regardless of how large the graph is. Such an n depends on the relative sizes of blocks and on k. This is because it is obviously necessary to have enough samples from each block to be able to obtain good estimates of link densities, and if some blocks are very small, more samples are needed.

We made experiments with \(k=10\) and with equal relative sizes of blocks. The P-matrix elements were i.i.d. \(\hbox {Uniform}(0,1)\) r.v.’s. In this case, already \(n>200\) is such that no classification error was found in a long series of experiments with repetitions of random samples and classification instances. Of course, errors are always possible, but they become insignificant already when each block has about 20 members. A similar situation is met with non-equal block sizes, but then the small blocks dictate the required n. When the smallest block has more than a couple of dozen nodes, the errors become unnoticeable in experiments.

We conjecture that if such a block structure or close to it exists for a large graph, it can be found out using only a very small subgraph and a small number of links per node in order to place every node into right blocks with only very few errors. This would give a coarse view on the large graph useful for getting an overall idea of link distribution without actually retrieving any link information besides labeling of its nodes. For instance, if we have a large node set, then the obtained labeling of nodes and the revealed block densities would allow computation of, say, the number of triangles or other small subgraphs, or the link density inside a set. It would be possible to use this scheme in the case of a dynamical graph, to label new nodes and monitor the evolution of its large-scale structure.

We can also adapt our RD method to the case of multilayer networks and tensors, etc. A similar sampling scheme would also be desirable and probably doable. On the other hand, large sparse networks need principally new solutions and development of a kind of sparse version of RD. These are major directions of our future work.

6.2 Spectral Clustering and Comparison with RD

For comparison, we repeated the experiments of the previous section using a spectral clustering method (see, e.g., [21]), to find a block structure in the sample. For more about the rigorous theory of spectral clustering and its variants, see [17].

The purpose is to compare the performance of spectral clustering with RD. The quality of spectral block structure was then evaluated similarly as in previous RD case, by counting the success rate of classification of additional 1000 nodes of the graph, and using the same classifier as in previous section. We also checked the accuracy of spectral clustering versus RD.

Spectral clustering is a highly popular way of obtaining community and other stochastic block model structures in data. It combines spectral analysis of most significant eigenvectors associated with the graph with k-means clustering. For definiteness, we describe the steps of this method as follows. Let \(W_{i,j}\) be the adjacency matrix of a simple graph with n nodes. Define a diagonal matrix D with elements

$$\begin{aligned} D_{i,i}=\sum _{1\le j\le n}W_{i,j} \end{aligned}$$

and the normalized adjacency matrix \(W_D\) as

$$\begin{aligned} W_D= D^{-\frac{1}{2}}WD^{-\frac{1}{2}}. \end{aligned}$$

\(W_D\) is related to the normalized graph Laplacian as \(L=I-W_D.\) (Note that in [21] \(W_D\) is denoted as L.) Denote k eigenvectors of \(W_D\) corresponding to k largest by absolute value eigenvalues as \(X_1,\ldots X_k\). Form a matrix X, where the columns are \(X_1,\ldots X_k\). As a result, X is an \(n\times k\) matrix. Each row of X is treated as vector in k-dimensional Euclidean space. Next, run the k-means algorithm on these n vectors and cluster them into k clusters. The clustering of nodes is taken to be identical to the k-means clustering of rows of X.

In our case, it turned out that if we take \(k=10\) in the matrix X and \(k=10\) in k-means algorithm, the result was very poor and the blocks were not found. Based on numerical experiments we choose \(k=5\) for X and \(k=10\) in k-means, in order to have best results for finding the \(10\times 10\) block structure of W. In this way the method was able to find the blocks with reasonable accuracy.

The spectral method performed somewhat worse than RD, as can be seen in Fig. 9. It needed a sample size of about 1000 nodes to have a low average error rate, instead of 200 that was enough for RD. Moreover, even for \(n=1000\), some random cases resulted in very poor performance, corresponding to a completely unsuccessful classifier. When n is around thousand and making 100 repetitions, we observed that almost all cases were error-free, but in a couple of cases the success rate was only around 10%, meaning a completely random classification. The blocks in our experiments did not have fixed sizes, only their expected sizes were fixed and equal. In a series of experiments, the link probability matrix was kept constant. Maybe these random variations of block sizes can explain such an instability. If n is not large enough, these variations can be very big. One cluster can become very small just by fluctuations caused by sampling. Such small clusters can be seen as outliers, since the nodes in such groups are very few and different from all others. It is well known that spectral clustering suffers from such outliers that should be removed from data before clustering. RD does not suffer from this feature, and we did not observe sensitivity of clustering to random fluctuations of the cluster sizes.

In the theory of spectral clustering there are usually balancing conditions on the way how the sizes of clusters grow as \(n\rightarrow \infty\) [17]. For instance, the block sizes \(n_1,\ldots ,n_k\) are such that \(\exists c: \quad 0<c\le 1/k\) s.t. \(\sum _i n_i \rightarrow \infty\) and \(n_i/n\ge c\) as \(n\rightarrow \infty\). Such conditions are needed to prove consistency properties of spectral clustering methods [15, 17].

Results  are demonstrated in Figs. 10, 11 and 12. Here we pick up one particular sample where spectral clustering produced a poor model with high rate of errors in classification. It was found that the block structure was only partially found using this method. Applying RD to the same sample produced a perfectly correct clustering. We also checked all cases where the spectral clustering produced a poor classification model. We found that in these cases the smallest and largest blocks of the sampled graph deviated a lot from their expectation, while in the case that the model was successful the sizes were systematically closer to the expectation, see Fig. 12.

Fig. 9
figure 9

Spectral method for finding block structure. Classification success percentile as a function of n using several repetitions (100) of experiments and 1000 classification instances for each

Full size image
Fig. 10
figure 10

Left: the true block structure. Right: the block structure found with spectral clustering. There are some large differences to be seen. In this case classifier based on the structure at right completely fails. In comparision, the RD method finds the correct structure without a single error

Full size image
Fig. 11
figure 11

Errors of spectral clustering in case when the corresponding classifier has high error rate, for a fixed sample graph with \(n=400\). The points correspond to nodes. Nodes exactly at diagonal are correctly clustered, and those off the diagonal are in wrong clusters. In case of applying RD to the same graph the nodes are 100% correctly clustered

Full size image
Fig. 12
figure 12

Minimal and maximal block sizes in various experiments. These variations are result of choosing cluster assignment of each node uniformly at random and independently of all other nodes. Each horizontally aligned point pair corresponds to values in a single experiment, where the horizontal coordinate is the value itself. Blue points are from instances that resulted in high, more than 30 %, error rate in subsequent classification of nodes. The orange points correspond to cases when this error rate was less than 1%. Average block size is 50, following from parameters \(n=500\) and \(k=10\). This plot suggests high correlation between error rate and large deviations in block sizes. In case of blue points, the values are roughly twice larger or smaller than the average and in case of orange points the difference is much smaller

Full size image

We conclude that RD is more preferable and stable for finding a block structure of a sample graph. RD is capable of finding blocks in the case of poor balancing of block sizes. This can happen when sampling a large graph even though the blocks are balanced yet, say, the biggest block is twice the smallest. In the sample this can result in a fatal error for spectral clustering, when one sampled block, by chance, has only few representatives. RD seems to be more robust against such small samples of blocks and thus requires smaller sample sizes than spectral clustering.

7 Conclusions and Future Work

Our future work will be dedicated to the case of sparse graphs, which is the most important in Big Data. One idea we are currently studying is to use the matrix of hop-count distances between nodes instead of a sparse adjacency matrix [10].

For large dense graphs, testable graph parameters are nonparametric statistics that can be consistently estimated by appropriate sampling, introduced by László Lovász and coauthors, see also [17]. We plan to show that the MDL statistics and the multiway discrepancies of [6] are testable, possibly with appropriate normalizations. If so, they can be concluded from a smaller part of the graph that has advantages with regard to the computational complexity of our algorithms.