Security-constrained model for integrated power and natural-gas system

Abstract

One of the main factors impacting the reliability of energy systems nowadays is the growing interdependence between electricity and gas networks due to the increase in the installation of gas-fired units. Security-constrained unit commitment (SCUC) models are used to economically schedule generating units without compromising the system reliability. This paper proposes a novel SCUC formulation that includes dynamic gas constraints, such as the line pack, and transmission contingencies in power and gas networks for studying the integrated system reliability. A Benders’ decomposition with linear programming techniques is developed to be able to study large systems. By including dynamic gas constraints into the SCUC, the proposed model accounts for the flexibility and reliability that power systems require from gas systems in the short term. Case studies of different size and complexity are employed to illustrate how the reliability of one system is affected by the reliability of the other. These experiments show how both systems operate in a secure way (by including contingencies) increases operating costs by approximately 9% and also show how these costs can vary by 24% depending on the line pack scheduling.

1 Introduction

Since the turn of the century, a large number of gas-fired generators have been installed because of their low emissions, low capital investment costs, low gas prices, operation flexibility, fast response, and high efficiency. The increment of these units results in a growing dependence on natural gas as a primary fuel for electricity generation and a higher level of integration between power and gas systems [1]. Because there are financial and physical relations that may affect the operation of one system as a function of the behavior of the other, a planning and operation involving electricity and natural gas is necessary to coordinate energy production and fuel delivery. A more realistic and coordinated operation of power and gas systems is critical to ensure a reliable, secure and economic joint performance. These situations are posing systemic challenges to the reliable operation of the interconnected grid [2].

1.1 Short-term reliability of integrated system

The reliability of an integrated energy system can be understood as its capability of satisfying two functions: adequacy and security [3]. Adequacy is the ability of the system to supply energy to any consumer at all times, taking into account scheduled and credible unscheduled outages of system components. Security is the ability of the system to withstand such disturbances. Given the growing interdependence between power and gas networks, real events have demonstrated that the reliability of one system depends not only on its components but also on the reliability of the other system. For some power system operators, the most critical contingency is not associated with a transmission line or a transformer but with a pipeline [4]. On the one hand, with more power plants being supplied by natural gas, the power system operation is facing higher risks because of gas outages, gas supply limitations, or pressure losses. These events can force multiple units to go offline. On the other hand, the operation of gas systems is facing higher volatile demands given that flexible gas-fired generators are being utilized to back up intermittent renewable generation. However, the flexibility offered by gas-fired units can only be fully exploited if the gas supply is sufficiently flexible and reliable [5].

Similarly to power networks, gas infrastructures are also vulnerable to outages. Disruptions of gas supply can happen due to e.g. extreme weather conditions, maintenance routines, cyber-attacks, or geopolitical issues [1, 4, 6–8]. Although such disruptions are not so frequent, they must be studied because of its great impact on the system operation. When congestions appear in the gas grid, the gas supplied to produce electricity is one of the first candidates to be curtailed because gas transportation companies and generation utilities trade the fuel according to interruptible contracts [9]. In addition, there is a lack of regulatory mechanisms to promote the scheduling of sufficient operating reserves that ensure the security of the embedded system [7]. As a result, contingency-analysis programs and security-constrained unit commitment models are required to guarantee the reliability of both systems in the short term.

Several works have been developed to demonstrate the need of integrating the operation of power and gas networks. A literature review is presented in [10]. Regarding reliability analysis considering contingencies in both networks, few studies can be found in the literature. References [11, 12] propose stochastic models with random outages of system components to evaluate the security in the mid- and short-term respectively. Otherwise, [13, 14] show security-constrained unit commitment (SCUC) models that account for the reliability of the integrated system by adding pre- and post-contingency transmission constraints to the unit commitment (UC) problem. Reference [13] proposes a Benders’ decomposition to perform contingencies in both power and gas networks, and [14] uses linear sensitivity factors. Nonetheless, all these models represent the gas system in steady state, neglecting the gas travel velocity and compressibility. This representation could lead to non-realistic or infeasible results when accounting for the continuity of supply [9, 15].

1.2 Integrated power and dynamic gas networks

Gas systems own slower dynamics than electric systems and require longer stabilization times to respond to swings in loads and disruptions. Gas flows travel at a much lower velocity than electricity, and the gas can be stored in pipelines to be used in the short term. The consideration of these attributes is imperative to provide the grade of flexibility and reliability that power systems demand from gas systems nowadays.

To the best of the authors’ knowledge, only [9, 15–17] have proposed integrated models considering the gas dynamics. These works basically differ from each other in the way to deal with the nonlinear and non-convex gas flow equation. While [9] uses the Newton–Raphson method, [15] implements piecewise linear approximations, and [16, 17] includes successive linear programming (SLP) techniques. Nevertheless, none of these proposals model gas network contingencies in the optimization process. The modeling of gas network contingencies into the SCUC is not a trivial task because it results in a nonlinear, non-convex, and large-scale problem difficult to solve.

1.3 Contribution

In light of the challenges, developments, and difficulties mentioned above, additional efforts are required to perform better combined reliability studies of power and gas networks. References [14, 15] propose a step forward based on the previous work presented. Reference [14] develops a SCUC capable of evaluating the integrated system security using a steady-state approach, [15] addresses the integration of energy systems in normal conditions (without contingencies) considering the gas dynamic. This paper models the integrated system security by taking into account the gas travel velocity and line pack. Specifically, the contributions of this paper are:

• 1) The formulation of an optimization problem that integrates power and natural gas operation including the gas dynamics and network contingencies of both systems into the decision process. This formulation accounts for an accurate representation of the energy adequacy because it includes the gas dynamic. In addition, this proposal procures for the system security because it models contingencies of components in both power and gas networks.

• 2) The development of a methodology based on Benders’ decomposition able to solve real integrated systems. The master problem solves the SCUC without gas constraints, and subproblems deal with the gas network and its contingencies using the SLP projection method to linearize gas constraints.

The proposed model is intended to be used by system operators, energy companies, planners, and regulators interested in studying the short-term reliability of integrated power and gas networks.

2 Problem formulation

The integrated power and gas model with security constraints presented below seeks to schedule the energy production (power and gas) economically while meeting simultaneously network constraints for pre- and post-contingency conditions. Assuming that vectors $\varvec{x}$ and $\varvec{v}$ represent power and gas variables in pre-contingency respectively, $\varvec{y}$ and $\varvec{z}$ represent power and gas variables in post-contingency respectively, $\varvec{c}_\mathrm {p}^\mathrm {T}/\varvec{c}_\mathrm {g}^\mathrm {T}$ are power/gas production costs in pre-contingency, $\varvec{c}_\mathrm {dp}^\mathrm {T}/\varvec{c}_\mathrm {dg}^\mathrm {T}$ are penalties for power/gas deviations in post-contingency, $\varvec{A}, \varvec{E}, \varvec{H}, \varvec{K}, \varvec{b}$ are the constraint coefficient matrix and vectors, the proposed formulation can be generically written as:

$$\begin{aligned} \text {min}\quad&\varvec{c}_\mathrm {p}^\mathrm {T}\varvec{x} +\varvec{c}_\mathrm {dp}^\mathrm {T}\varvec{y} +\varvec{c}_\mathrm {g}^\mathrm {T}\varvec{v} + \varvec{c}_\mathrm {dg}^\mathrm {T}\varvec{z} \end{aligned}$$

(1)

$$\begin{aligned} \text {s.t}\quad&\varvec{A}_1\varvec{x} \ge \varvec{b}_1 \end{aligned}$$

(2)

$$\begin{aligned} \qquad&\varvec{A}_2\varvec{x} +\varvec{E}_2\varvec{y} \ge \varvec{b}_2 \end{aligned}$$

(3)

$$\begin{aligned} \qquad&\varvec{A}_3\varvec{x} +\varvec{H}_3\varvec{v} \ge \varvec{b}_3 \end{aligned}$$

(4)

$$\begin{aligned} \qquad&\varvec{A}_4\varvec{x} +\varvec{H}_4\varvec{v} +\varvec{K}_4\varvec{z} \ge \varvec{b}_4 \end{aligned}$$

(5)

Each of these equations is discussed below.

2.1 Objective function

From the point of view of a system operator, regulator, planner, or vertically integrated utility interested in optimizing the whole system, the objective function (1) minimizes costs associated with energy supply, storage, contractual obligations, load shedding, and deviations in post-contingency to guarantee feasibility. The terms $\varvec{c}_\mathrm {p}^\mathrm {T}\varvec{x}+\varvec{c}_\mathrm {dp}^\mathrm {T}\varvec{y}$ correspond to the traditional SCUC formulation that is presented in detail in [3, 18] or [19]; $\varvec{c}_\mathrm {p}^\mathrm {T}\varvec{x}$ represents power production, startup, shutdown, and non-served power costs in pre-contingency; $\varvec{c}_\mathrm {dp}^\mathrm {T}\varvec{y}$ represents penalties of power flow deviations in post-contingency. Similarly, $\varvec{c}_\mathrm {g}^\mathrm {T}\varvec{v}$ and $\varvec{c}_\mathrm {dg}^\mathrm {T}\varvec{z}$ correspond to gas operating costs in pre- and post-contingency respectively: $\varvec{c}_\mathrm {g}^\mathrm {T}\varvec{v}$ represents gas production costs, compression costs, storage costs, and load shedding penalizations (6); and $\varvec{c}_\mathrm {dg}^\mathrm {T}\varvec{z}$ represents penalizations for over and under pressures, load shedding, and gas production deviations with respect to the gas production when the pipeline l fails (7). Load shedding and penalizations are included in the formulation to guarantee feasibility.

$$\begin{aligned}&\varvec{c}_\mathrm {g}^\mathrm {T}\varvec{v}=\sum _{t\in T}\left\{ \sum _{w\in W}C_{w}^{W}g_{w,t}+\sum _{(io)\in CM}C{}_{io}^{C}(p_{o,t}-p_{i,t})\right. \nonumber \\&\left. \qquad \qquad \quad \;+\sum _{s\in S}C_{s}^{S}q_{s,t}^{out}+\sum _{i\in I}C{}_{i}^{I}ng{}_{i,t}\right\} \end{aligned}$$

(6)

$$\begin{aligned}&\varvec{c}_\mathrm {dg}^\mathrm {T}\varvec{z}=\sum _{t\in T}\sum _{l\in L}\left\{ \sum _{i\in I}\left[ C_{i,l}^{DG}(\triangle p_{i,t,l}+\nabla p_{i,t,l})+C_{i,l}^{I}ng_{i,t,l}\right] \right. \nonumber \\&\left. \qquad \qquad \qquad \quad +\sum _{w\in W}C_{w,l}^{DW}(\triangle g_{w,t,l}+\nabla g_{w,t,l})\right\} \end{aligned}$$

(7)

where indices $t\in T$ are hourly periods running from 1 to T hours; $w\in W$ are gas wells; $(io)\in CM$ are compressors going from i to o; $s\in S$ are gas storage facilities; $i,o\in I$ are gas nodes; $l\in L$ are pipeline contingencies, from 0 (no contingencies) to L; $C_w^W/C_{s}^{S}$ are gas production/storage costs ($/(Sm$^{3}$)); $C_{io}^{C}$ is compression costs ($/bar); $C_{i}^{I}$ is non-served gas costs ($/(Sm$^{3}$)); $C_{i}^{DG}$ is penalization of over and under pressures ($/bar); $C_{w}^{DW}$ is penalization of production deviations ($/(Sm$^{3}$)); $g_{w}$ is gas production (Sm$^{3}$/s); $p_{i}$ and $p_{o}$ are nodal pressure (bar); $q_{s}^{out}$ is outflows of a storage (Sm$^{3}$/s); $ng_{i}$ is non-served gas (Sm$^{3}$/s); $\triangle p_{i}/\nabla p_{i}$ are over/under pressures (bar); $\triangle g_{w}/\nabla g_{w}$ are over/under deviations of gas production (Sm$^{3}$/s).

2.2 Security-constrained unit commitment

Equations (2) and (3) represent the SCUC problem, which schedules generating units economically while meeting network constraints for pre- and post-contingency conditions. The general equation $\varvec{A}_1\varvec{x}\ge \varvec{b}_1$ represents the power pre-contingency state, and the equation $\varvec{A}_2\varvec{x}+\varvec{E}_2\varvec{y}\ge \varvec{b}_2$ corresponds to the post-contingency. Prevailing constraints of a SCUC model based on DC power flows are: the power system balance, spinning reserve requirements, generating capacity limits, ramp rates, logic constraints, minimum up/down times, startup and shutdown trajectories, and power flows for pre- and post-contingency states. Since this problem has been widely studied, the reader is referred to [3] and [18–21] for detailed formulations.

2.3 Security-constrained gas dispatch

Analogously to power systems, network and security constraints can also be incorporated in the modeling of gas systems to study their reliability. This section presents a simplified and tractable dynamic gas network formulation with pre- and post-contingency constraints (4) and (5) respectively. Initially, nodal balance (8) and flow constraint (9) in pre- ($l=0$) and post-contingency ($l\ge 1$) correspond to

$$\begin{aligned}&\sum _{o\in n(i)} \left( q_{io,t,l}^{out}-q_{io,t,l}^{in}\right) +\sum _{s\in i}\left( q_{s,t}^{out}-q_{s,t}^{in}\right) - \sum _{u\in nc(i)} \phi _{u}e_{u,t}\nonumber \\&\quad +ng_{i,t,l}+\sum _{w\in i} \left( g_{w,t}+\triangle g_{w,t,l}- \nabla g_{w,t,l}\right) =D_{i,t}^{G}\,\\&\qquad \forall i,t,l=0,1,\cdots ,L \end{aligned}$$

(8)

$$\begin{aligned}&q_{io,t,l}\left| q_{io,t,l}\right| =\dot{K}{}_{io}\left( p_{i,t,l}^{2}-p_{o,t,l}^{2}\right) \nonumber \\&\qquad \forall (io)\in PL \quad t,l=0,1,\cdots ,L \end{aligned}$$

(9)

where $\dot{K}_{io}=\left( \frac{\pi }{4}\right) ^{2}\frac{D_{io}^{5}}{L_{enio}F_{io}RT_pZ\rho _{0}^{2}}$; $q_{io,t,l}=\frac{q_{io,t,l}^{out}+q_{io,t,l}^{in}}{2}$; $(io)\in PL$ are the set of pipelines going from node i to o; $o\in n(i)$ are nodes/generators connected to i; $u\in nc(i)$ are gas-fired units; $D_{i}^{G}$ is gas loads (Sm$^{3}$/s); $D_{io}/L_{enio}$ are pipeline diameter/length (m); $F_{io}$ is pipeline friction coefficient; R is gas constant (m$^{3}$bar/(kgK)); $T_p$ is gas temperature (T); Z is gas compressibility; $\rho _{0}$ is gas density in standard conditions (kg/m$^{3}$); $\phi _{u}$ is power conversion factor (Sm$^{3}$/MWh); $q_{io}^{in}$ is the flow of a pipe in the inlet node i (Sm$^{3}$/s); $q_{io}^{out}$ is the flow of a pipe in the outlet node o (Sm$^{3}$/s); $q_{s}^{in}$ is inflows of a storage (Sm$^{3}$/s); $e_{u}$ is power production of gas-fired units (MWh); $q_{io}$ is average gas flows (Sm$^{3}$/s).

Equation (9) is known as the general flow equation that besides being nonlinear is non-convex. Production deviations in post-contingency are bounded by the maximum ($\overline{G}_{w}$) and minimum ($\underline{G}_{w}$) production bounds (10) defined either by technical or contractual limitations.

$$\begin{aligned}&\underline{G}_{w,t}\le g_{w,t}-\nabla g_{w,t,l}+\triangle g_{w,t,l}\le \overline{G}_{w,t} \nonumber \\&\quad \forall w,t,l=1,2,\cdots ,L \end{aligned}$$

(10)

In addition to these constraints, the gas dynamics involves also the consideration of gas compressibility. The inflow on a pipe can be different from the outflow and such difference (the amount of gas mass stored in the pipe) is known as line pack. The line pack is a function of the pipes’ characteristics and the average pressure (11), and complies with the mass conservation equation (12) in pre- and post-contingency.

$$\begin{aligned} m_{io,t,l}\,=\, & {} \ddot{K}{}_{io}p_{io,t,l}\quad \forall (io)\in PL \quad t,l=0,1,\cdots ,L \end{aligned}$$

(11)

$$\begin{aligned} m_{io,t,l}\,=\, & {} m_{io,t-1,l}+q_{io,t,l}^{in}-q_{io,t,l}^{out}\nonumber \\&\quad \forall (io)\in PL \quad t,l=0,1,\cdots ,L \end{aligned}$$

(12)

where $\ddot{K}_{io}=\frac{\pi }{4}\frac{L_{enio}D_{io}^{2}}{RT_pZ\rho _{0}}$; $p_{io,t,l}=\frac{p_{i,t,l}+p_{o,t,l}}{2}$; $m_{io}$ is the gas mass (line pack) (Sm$^{3}$); $p_{io}$ is the average pressure of the pipeline (bar). Equations (9), (11) and (12) implicitly represent how gas pressure and velocity affect the mass flow. The gas stored in storage facilities (such as tanks or aquifers) is also calculated analogously to the mass conservation equation (12). On the other hand, pressure deviations in post-contingency are constrained by maximum ($\overline{P}_{i}$) and minimum ($\underline{P}_{i}$) limits (13) according to technical characteristics, contracted quantities or security reasons.

$$\begin{aligned} \underline{P}_{i}-\nabla p_{i,t,l}\le p_{i,t,l}\le \overline{P}_{i}+\triangle p_{i,t,l}\quad \forall i,t,l=0,1,\cdots ,L \end{aligned}$$

(13)

And for compressors, (14) is used to bound how much the gas can be compressed in a node according to the compression factor $\varGamma _{io}$.

$$\begin{aligned} p_{o,t,l}\le \varGamma _{io}p_{i,t,l}\quad \forall (io)\in CM \quad t,l=0,1,\cdots ,L \end{aligned}$$

(14)

To be able to obtain a tractable optimization model, this formulation assumes isothermal flows and horizontal pipelines, it neglects the inertia and kinetic energy due to their small contribution to the solution, it utilizes a constant compressibility factor Z, and it ignores the fuel consumed by compressors. Additionally, notice that the nodal balance equation (8) is the only constraint coupling power ($\varvec{x}$) and gas variables ($\varvec{v}$) and ($\varvec{z}$) in pre- and post-contingency by including the gas consumed by gas units according to the conversion factor ($\phi _{u}e_{u,t}$). As a result, the general equations (4) and (5) take the form of $\varvec{H}_3\varvec{v}\ge \varvec{b}_3$ and $\varvec{H}_4\varvec{v}+\varvec{K}_4\varvec{z}\ge \varvec{b}_4$ respectively for the remaining constraints.

The reader could refer to [15] for further details about this model’s assumptions and the derivation of (9) and (12).

3 Solution methodology

3.1 Solution of integrated system

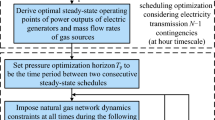
The integrated power and gas formulation with security constraints (1)–(5) presented in Section 2 is a nonlinear, non-convex, large-scale, and NP-hard problem that is considered difficult to solve. Given that this problem is composed by subproblems with different natures, and the resulting formulation has an L-shape of the constraint matrix, it is possible to apply the Benders’ decomposition technique to be able to solve large systems with a significant number of contingencies. The idea is to break up the problem into separate smaller subproblems that are easier to solve and then re-integrate them to get an overall solution [22], as shown in Fig. 1. In Fig. 1 $\varepsilon$ is the tolerance value; j is the iteration number.

Fig. 1

Process of Benders’ decomposition for solving the integrated system

3.1.1 Solving master problem

The master problem (15)–(18) aims to solve the SCUC problem taking into account information from the gas network operation. Firstly, the network constrained unit commitment (NCUC) problem is calculated. In the first iteration, the NCUC schedules generating units economically, taking into account power network constraints in pre-contingency (16). Then, dispatch and commitment decisions are employed to perform the security analysis for $n-1$ contingencies. If any network violation is found, security constraints (17) are incorporated into the NCUC problem. This algorithm iterates via linear sensitivity factors until no further violations occur (as detailed in [23]). When the SCUC finishes, the output of gas-fired units ($\hat{\varvec{x}}\in \varvec{x}$) are submitted to the subproblem in order to perform the gas dispatch and security evaluation for $l-1$ pipeline contingencies.The recourse function $\mathbf {\beta (\varvec{x})}$ is an approximation of the optimal value of subproblems as a function of the masters’ decision variables. Optimality Benders’ cuts (18) are added to the master problem in each iteration j in order to adjust the output of gas-fired units according to the impact they have on the gas system operation. $\mu$ and $\lambda$ are dual variables from subproblems described next.

$$\begin{aligned} \text {min}\quad&\varvec{c}_\mathrm {p}^\mathrm {T}\varvec{x} +\varvec{c}_\mathrm {dp}^\mathrm {T}\varvec{y} +\beta (\varvec{x}) \end{aligned}$$

(15)

$$\begin{aligned} \text {s.t}\quad&\varvec{A}_1\varvec{x} \ge \varvec{b}_1 \end{aligned}$$

(16)

$$\begin{aligned} \qquad&\varvec{A}_2\varvec{x} +\varvec{E}_2\varvec{y} \ge \varvec{b}_2 \end{aligned}$$

(17)

$$\begin{aligned} \qquad&\beta (\varvec{x}) \ge \omega ^{j} (\hat{\varvec{x}}^{j})+ \left( \mu ^j\varvec{A}_3 + \lambda ^j\varvec{A}_4\right) (\hat{\varvec{x}}^{j}-\varvec{x}) \end{aligned}$$

(18)

where $\omega ^{j}$ is described as (19).

3.1.2 Solving subproblems

Taking into account the production of gas-fired units ($\hat{\varvec{x}}^{j}$) calculated by the master problem in the iteration j, subproblems (19)–(21) calculate the gas network optimization with security constraints. This problem optimizes gas production, storage, and compression taking into account gas network constraints in pre- (20) and post-contingency (21).

$$\begin{aligned} \text {min}\quad&\omega ^{j}(\hat{\varvec{x}}^{j})= \varvec{c}_\mathrm {g}^\mathrm {T}\varvec{v} +\varvec{c}_\mathrm {dg}^\mathrm {T}\varvec{z} \end{aligned}$$

(19)

$$\begin{aligned} \text {s.t}\quad&\varvec{H}_3\varvec{v} \ge \varvec{b}_3-\varvec{A}_3\hat{\varvec{x}}^{j} \end{aligned}$$

(20)

$$\begin{aligned}&\qquad\varvec{H}_4\varvec{v} + \varvec{K}_4\varvec{z} \ge \varvec{b}_4-\varvec{A}_4\hat{\varvec{x}}^{j} \end{aligned}$$

(21)

The dual variables from (20) are denoted as $\mu$, and from (21) as $\lambda$. The coupling constraints from which $\mu$ and $\lambda$ are calculated correspond to the nodal balances (8) in pre- ($l=0$) and post-contingency ($l\ge 1$) respectively. Once the gas network optimization with security constraints is solved, Benders’ cuts (18) are added to the master problem.

The nonlinear and non-convex gas flow equation (9) is linearized using a SLP approach called projection method. It is described in detail in Section 3.2.

3.1.3 Stopping criteria

The algorithm iterates if the master problem changes its solution, until the maximum number of iterations (22) is reached, or until optimality criteria is reached (objective functions of master and subproblems are close enough).

$$\begin{aligned} \frac{\left| \varvec{c}_\mathrm {g}^\mathrm {T}\hat{\varvec{v}}^j+\varvec{c}_\mathrm {dg}^\mathrm {T}\hat{\varvec{z}}^j-\beta (\varvec{x})\right| }{\left| \varvec{c}_\mathrm {p}^\mathrm {T}\hat{\varvec{x}}^j+\varvec{c}_\mathrm {dp}^\mathrm {T}\hat{\varvec{y}}^j+\varvec{c}_\mathrm {g}^\mathrm {T}\hat{\varvec{v}}^j+ \varvec{c}_\mathrm {dg}^\mathrm {T}\hat{\varvec{z}}^j\right| }\le \varepsilon \end{aligned}$$

(22)

3.2 Linearization of gas flow equation

The projection method from [24] is adapted to linearly approximate the general flow equation (9). This method has been selected because its flexibility, efficiency, simplicity, and its success for solving real systems. The projection method is flexible because it progressively adapts the linear approximation to any possible solution. Contrary to the iterative approximation from [25], the projection method always consider the whole feasible region of the function. Furthermore, this is an efficient method because it does not require initial iterations to avoid bad starting points, such as the Newton–Raphson. Finally, it is simple to implement and does not add extra variables to the formulation. The idea of the projection method is to approximate the flow equation iteratively through planes, as shown in Fig. 2 and following this algorithm:

Fig. 2

Linear approximation of the gas flow equation

• Step 1: Approximate the nonlinear equation through a plane coinciding with the maximum flow and the origin. The origin is chosen because it represents the point of symmetry for the plane.

• Step 2: Project the solution to the curve in each coordinate and measure the relative error of each variable. If all errors are below certain tolerances, the process is finished, otherwise go to step 3. Projected solutions are computed by replacing obtained solutions for each pair of variables in the general flow equation (9).

• Step 3: Define a new plane in the neighborhood of the solution and the curve, execute the optimization problem, and return to step 2. The new plane is defined as the tangent to the curve, according to the Taylor series expansion around the point coinciding with the obtained flow and one of the end nodal pressures. The first order Taylor series expansion of (9) is derived in detail in [26].

3.3 Additional considerations

Similarly to the other linearization algorithms proposed in the literature, the projection method does not guarantee global convergence either. One alternative to aid convergence is the addition of heuristics into the iterative algorithm. Variable bounds are progressively included in the iterations to narrow the feasible region. These bounds are always set according to the value of the flow obtained in the previous iteration to reduce the chance of finding infeasible solutions. Moreover, pipelines with small pressure differences ($\left| p_{i,t}-p_{o,t}\right| \le \varepsilon$) are approximated by a plane with a large and constant inclination to avoid numerical instability. More sophisticated methods for the aiding of convergence in SLP algorithms can be found e.g. in [27, 28] that prove global convergence in filter-type methods.

Additionally, the Benders’ cuts presented in Section 3 are generated from the solution of a successive approximation of the nonlinear gas flow equation (9). Theoretically, this may make the subproblems non-convex depending on the linearization error. Some possibilities that could be explored further to try to guarantee global optimality from a Benders’ decomposition with non-convex subproblems are:

• 1) The addition of selectivity into the Benders’ cuts in order to activate them only in the vicinity of the solution from which they were created. This alternative could add a high computational burden if binaries are used for the selectivity.

• 2) Convexify the subproblems by using Lagrangian relaxation, as proposed by [29], thus gas flow equations can be piecewise linearized as shown in [15]. The obtained solution of subproblems would be feasible for the relaxed problem, but it could be integer infeasible. As a result, the quality of this method depends also on the quality of the convexification.

4 Case studies

Two case studies are presented below to illustrate that the proposed model is able to evaluate the adequacy and security of an integrated system. The first case study shows a small system that is useful to discuss and clarify the basic concepts of the proposed model. The second case study includes a larger system that illustrates the relevance of contingencies in the system operation. Both case studies consist of a unit commitment of 24 hours. The projection method employed for solving the gas system ensures a maximum relative error of 1% in all variables and does not include any heuristic (it converges without additional bounds). All experiments were carried out using CPLEX 12.6.1 on an Intel Core i5 3.2-GHz personal computer with 16 GB of RAM memory. All data are available online at https://goo.gl/jbX17B.

4.1 Study results of Case 1

The 3-bus power system and 7-node natural gas network are integrated as shown in Fig. 3a, which is used as Case 1 for study. The power system corresponds to the classical network presented in [3] to illustrate the SCUC problem. The gas system is taken from [13] that uses it to simulate pipeline contingencies in steady state. These systems are coupled by gas-fired units U2 and U3 that consume gas from nodes 4 and 7 respectively under interruptible contracts. The SCUC is evaluated in the power system by considering that all lines can fail individually. In the gas system, the pipeline 3–6 is the only element included in the set of contingencies.

Two different experiments are conducted to evaluate security, adequacy and economy of the integrated system operation and to show how operators can use the line pack to mitigate contingencies and procure for the system reliability. Example 1 (Exp1) assumes a high initial line pack of 19.84 MSm³, and Example 2 (Exp2) starts the operation with a low initial line pack of 16.57 MSm³.

4.1.1 Security analysis

Figure 3 presents the following obtained results for the period 2 of both experiments: generation output (GW), power flows (GWh with arrows), power demands (GWh), gas production (MSm$^{3}$), gas in- and output flows (MSm$^{3}$h with arrows), gas demands (MSm$^{3}$h), and nodal pressures (bar underlined).

The obtained results for Exp1, depicted in Fig. 3a and Fig. 3b, show how decisions for the pre-contingency take into account what happens when elements fail.

• 1) The production of unit U2 was required to avoid overloads when the line 1–2 fails. With this production, the outage of line 1–2 leads the other lines to reach their maximum transport capacity of 0.05 GW, as shown in Fig. 3b. Notice that the compressor in post-contingency compressed more gas than in pre-contingency in order to increase the injected gas in pipeline 3–4 and to be able to deliver the required quantity of gas in node 4 by U2.

• 2) All the gas in node 7 demanded from U3 was fed with line packed gas (the well W2 was not producing). These situations demonstrate how with an adequate planning, the line pack is an important tool to support contingencies or varying loads.

• 3) For this experiment, both pre- and post-contingency cases were operated with adequate levels of security and adequacy.

Fig. 3

Pre- and post-contingency when line 1–2 and pipeline 3–6 fail for t = 2

Table 1 Obtained results for all experiments

A different operation was obtained when the initial line pack level was low in the case Exp2, which is depicted in Fig. 3c and Fig. 3d. It can be observed that:

• 1) The generation in U2 was not as high as the generation obtained for case Exp1 because the gas system was unable to deliver the required fuel in node 4.

• 2) Although both gas wells were producing at their maximum capacity and the storage injected gas at its maximum withdrawal limit, the pressure at node 4 reached its minimum level of 50 bar (see Fig.3c).

• 3) In pre-contingency, all network elements are operated between their secure levels.

• 4) In post-contingency, two situations arise that compromise the system security. Firstly, with a production of 0.034 GW in U2, the line 2–3 (with a flow of 0.088 GWh) was overloaded by 0.038 GW. Secondly, due to low line pack levels, a deviation of 0.04 MSm³ resulted for the production of well W1. Pipelines 1–2 and 3–4 were not able to store all the gas if the well W2 maintained its original production of 1 MSm³ when the pipeline 3–6 failed.

4.1.2 Adequacy analysis

A general overview of Exp1 and Exp2 for all periods is presented in Table 1. This table shows for the gas system the total production (Prod.), production deviations in post-contingency (Prod.Dev.), gas stored (Stor.), and line pack levels in pre-contingency (LP-pre.). For the power system, the total production (Prod.) and flow deviations in post-contingency (Flow.Dev.) are presented.

Clearly, Exp1 produced less gas, spent less stored gas, and kept more line packed gas because it was able to use the line pack to support all contingencies and feed the load. The differences obtained for the gas system operation are explained by using Fig. 4. It depicts obtained results of total production, storage, and line pack to show the impact of contingencies and line pack policies on the system operation. It can be seen that if the gas system starts with a low line pack level, the production must provide the gas required to feed the load and increase the system line pack to be able to feed the peaks. Fig. 4 shows how Exp2 took almost 4 hours to reach the adequate level of line pack, time in which the storage and wells were highly utilized.

Fig. 4

Gas production, storage, and line pack in pre-contingency

4.1.3 Economic analysis

Differences between system operating costs are given in Table 2. In pre-contingency, the power and gas systems in Exp1 are 4% and 12% cheaper than Exp2 respectively because the gas network is able to feed the demand using the line pack during the first hour of the day. In post-contingency, the power and gas systems in Exp1 are 35% and 4% cheaper than Exp2 respectively because of deviations of gas production and higher overloads in power flows caused by low line pack levels of Exp2.

The solution of these experiments required, on average, 18 Benders’ iterations, and 5 iterations to solve the SLP algorithm in gas subproblems. Both case studies were solved in 22.75 seconds on average.

In summary, the obtained results show that if the gas system starts its operation with a low line pack level, the production from wells and storages must provide the gas required to feed the load and increase the system line pack in the following hours to be able to feed the peak demand. High initial line pack levels allow system operators to reduce operating costs, especially during the first hours of the day. Without considering the line pack, the energy adequacy can be underestimated and a more expensive operation would result.

Table 2 System operating costs for all experiments

4.2 Study results of Case 2

The interconnected system presented in [14] and shown in Fig. 5, composed by the IEEE 24-bus power system and a modified version of the Belgian high-calorific 20-node gas network, which is used as Case 2 for study, is employed to validate the proposed model and method. The set of credible contingencies is composed by pipelines 4–8, 12–13, 8–11 and all transmission lines. Gas-fired units U1, U4, and U5 consume gas from nodes 5, 14, and 15 respectively. In this case study, two experiments are performed in order to evaluate the effect on the system operation including outages in the transmission network: Example 3 (Exp3) that estimates the system operation under normal conditions (without contingencies), and Example 4 (Exp4) that includes the evaluation of transmission contingencies in both power and gas grids.

Fig. 5

IEEE 24-bus power system and Belgian 20-node gas network

The difference of the dispatch solution for each experiment is presented in Table 3. Units are upwardly organized in merit order (the cheapest at the bottom). The sign “+” means positive differences and “–” negative ones. The units with a total difference of zero are not presented in the table. The optimal solution for the case without contingencies (Exp3) was to replace production of U1 and U4 by production of U2, U3 and U6 almost all the time to reduce the gas consumption. When contingencies are evaluated, the case Exp4 required an increase in production of U5 during hours 9–24 in order to support the outage of line 3–24. The output of U1 was curtailed during the whole day to avoid overloads of transmission lines 1–2, 1–3 and 1–5 when different contingencies occur. Similarly, the production of U4 must be reduced by the outage of line 12–13. For this case study, only the line 8–9 is overloaded by 0.01 GW when the line 8–10 failed in hour 3. All other contingencies were securely supported.

Table 3 Dispatch differences between Exp3 and Exp4

With respect to the gas system, all pipeline outages were also supported without harming the system security. Differences between Exp3 and Exp4 are relevant in production decisions, as shown in Table 1. For these experiments, the impact on power network contingencies is the reduction of the gas consumption. Without contingencies, the total production of gas-fired units is higher, the gas taken out from storages is lower and there is more line pack in the system. The most impactful contingency was pipe 4–8 during hours 8–24, resulting in node 16 reaching the lowest bound of 50 bar.

A higher dispatch of expensive units U2, U3, and U6 increased the operating cost of Exp4 in a 12% increase with respect to Exp3, as presented in Table 2. The cost of the gas system was also higher in Exp4 (6%) due to a significant use of compressors and the stored gas in tanks. In post-contingency, only deviations in the flow of the line 8–9 were penalized, the remaining of transmission elements of both networks were safely operated. The consideration of contingencies increased the total system operation cost in a 9%. The solution of contingencies (Exp4) took 48.955 seconds, 5 Benders’ iterations, and a maximum of 9 SLP iterations in gas subproblems. In summary, although the proposed model increases computing time in comparison to actual SCUC models, it estimates more accurately operating costs and guarantees feasible and optimal results when contingencies appear.

5 Conclusion

This paper presents a SCUC with dynamic gas constraints, such as the line pack, that can be employed to study the integrated system reliability by including contingencies of power and gas transmission networks in the optimization. Contingencies are evaluated by using the Benders’ decomposition method that is able to cope with large integrated systems and significant number of contingencies. Case studies demonstrate how this proposal not only takes into account the system security but also allows the estimation of the energy adequacy because it includes the gas dynamics (line pack). Models and methods presented herein can be used to operate the integrated system defensively, preventing cascading events, and ensuring the continuity of supply, since, as shown previously, the reliability of one system depends not only on its own components but also on the reliability of the other system.

Future work could be conducted in order to derive a method that guarantees global optimality by introducing e.g. selection into the Benders’ cuts or by convexifying the subproblems, as discussed in Section 3.3. In addition, the stochasticity associated with, e.g. demand, contingencies or the production of renewables should be included in the decision process to analyze the impact of such uncertainties on the operation of the system.