Reliability evaluation of integrated electricity–gas system utilizing network equivalent and integrated optimal power flow techniques

Abstract

The wide utilization of gas-fired generation and the rapid development of power-to-gas technologies have led to the intensified integration of electricity and gas systems. The random failures of components in either electricity or gas system may have a considerable impact on the reliabilities of both systems. Therefore, it is necessary to evaluate the reliabilities of electricity and gas systems considering their integration. In this paper, a novel reliability evaluation method for integrated electricity–gas systems (IEGSs) is proposed. First, reliability network equivalents are utilized to represent reliability models of gas-fired generating units, gas sources (GSs), power-to-gas facilities, and other conventional generating units in IEGS. A contingency management schema is then developed considering the coupling between electricity and gas systems based on an optimal power flow technique. Finally, the time-sequential Monte Carlo simulation approach is used to model the chronological characteristics of the corresponding reliability network equivalents. The proposed method is capable to evaluate customers’ reliabilities in IEGS, which is illustrated on an integrated IEEE Reliability Test System and Belgium gas transmission system.

1 Introduction

As a highly efficient and sustainable source of energy, natural gas has become an appealing fossil fuel for electricity generation in various countries. In the United States, gas consumption from electricity systems increased from 27% in 2005 to 39% in 2016 [1]. Even in China, which has relatively high natural gas prices, the electricity generation from gas-fired generating units (GFUs) showed a sharp year-on-year growth of 12.81% in 2016 [2]. In addition, a new developed technology, power-to-gas (PTG), links electricity and gas systems by converting surplus electricity into gas that is compatible with existing gas infrastructures [3]. The wide deployments of GFUs and PTGs tend to intensify the interaction between these formerly isolated energy systems, and the concept of the integrated electricity–gas system (IEGS) has been developed accordingly.

In IEGS, securing the balance between supply and demand continuously in terms of both electricity and gas and maintaining their reliabilities are vital but challenging tasks [4]. Intensified energy interaction between the electricity and gas systems driven by GFUs and PTGs has led to new contingency scenarios such as failures triggered in gas systems that propagate to electricity systems [5]. On August 15, 2017, in Taiwan, China, two gas supply pipe valves were closed and the liquefied natural gas supply was stopped for 2 min owing to human error, causing a 4-GW electricity supply disruption [6]. An insufficient electricity supply might also influence the functioning of gas systems, as the gas injections from PTGs are correlated to their electricity consumptions [7]. Consequently, it is of great significance and requires additional effort to incorporate the interdependency between electricity and gas systems into the reliability evaluation of IEGS.

Reliability evaluations of both electricity systems [8] and gas systems [9, 10] have been well studied. However, the integration of electricity and gas systems brings additional complexities and new challenges to the reliability evaluation of IEGS. Firstly, random failures of components in either electricity or gas system, such as GFUs or PTGs, affect the other system [11]. The majority of previous studies focused on assessing the electricity reliability indices in the IEGS planning or unit commitment, while the reliability of the gas system was usually ignored [12, 13]. Moreover, the electricity and gas power flows were usually calculated or optimized separately in the reliability evaluation of IEGS [14, 15]. Since GFUs and PTGs have made it possible for bidirectional energy exchange between electricity and gas systems, the reliability of IEGS can be improved if the operation of IEGS is co-optimized in terms of both electricity and gas flows as compared with the separate operation in either system [4]. Therefore, the integrated electricity and gas optimal power flow (IOPF) must be conducted in the reliability evaluation of IEGS.

In addition, reliability usually contradicts the economics during the operation of IEGS [16]. Hence, it is important to consider the economic loss caused by insufficient electricity and gas supply in the reliability evaluation of IEGS. In previous research, economic loss was usually characterized by the value of lost load (VOLL) or customer damage functions [17]. However, when simultaneously considering the available electricity and gas infrastructures for customers, the economic loss from an interruption of electricity loads may be reduced by the substitution of gas [18]. Therefore, the economic evaluation of electricity load interruptions should be extended to suit IEGS.

This paper proposes a reliability evaluation method for IEGS considering the mutual impact and the co-optimized operation of electricity and gas systems. First, the reliability network equivalent (RNE) is introduced to represent the reliability models of components in IEGS including GFUs, conventional fossil generating units (CFUs), gas sources (GSs), and PTGs. The main principle of RNE is to use an equivalent element to replace a portion of the entire system, and therefore decompose a large system into a series of simpler subsystems [19]. Compared to the conventional method based on the forced outage rate, RNE provides a flexible tool to represent the multi-state reliability model of the combination of components in IEGS. Moreover, RNE has been validated as efficient for reducing the number of system states and decreasing the computational effort in the reliability evaluation of composite electricity systems [20]. The time-sequential Monte Carlo simulation (TSMCS) is adopted to model the chronological characteristics of corresponding RNEs [20]. A contingency management schema is proposed considering the coupling between electricity and gas systems using the proposed IOPF technique. The reliability indices are further specified to the nodal scale in order to reflect the differences of reliabilities among buses and to provide useful information for the reliability management of nodal customers in IEGS.

2 Framework of IEGS

IEGS transports electricity and gas from energy supplies to consumers in different locations. In the IEGS studied in this paper, the electricity supply components include GFUs and CFUs, and the gas supply components include gas sources (GSs) and PTGs. The framework of the studied IEGS is illustrated in Fig. 1. GFUs are directly connected to the gas transmission system owing to the high pressure requirement of gas [21].

Fig. 1

Framework of studied IEGS

As the fossil fuel of GFUs, gas is regarded as the load of the gas system and is limited by the operating condition of the gas system. Similarly, PTGs are installed at critical buses as a kind of complementary measure to secure the gas supply, and they are regarded as electricity loads in the electricity system. In the proposed framework, GFUs and PTGs are the key components to realize bidirectional energy exchange between the electricity and gas systems.

At some joint buses, both electricity and gas supply infrastructures are available for customers. For some special electricity loads, electricity is the dominating energy sector in most cases. However, if the electricity supply is insufficient, these loads can also be satisfied by an alternative gas. For instance, the requirement for a constant temperature on industrial production lines can be fulfilled by either electrical or gas-fired boilers. This part of the load is defined as the flexible load in this paper. Accordingly, conventional electricity loads and gas loads in the studied IEGS can only be supplied by their corresponding energy sectors.

3 Reliability network equivalents for IEGS

3.1 Reliability network equivalents for GFUs

GFUs present both controllability and stochastics on the operation horizon. Controllability indicates that the electricity generation of GFUs is limited by their electricity capacities. The stochastics lie in the dispatchable electricity capacities of GFUs as determined by random failures and corresponding repairs. The reliability model for a single GFU can be represented as a multi-state model where the available electricity capacity can derate completely or partially. In [22], a practical gas-fueled cogeneration power plant with a normal electricity capacity of 6.6 MW is represented as a six-state reliability model. Multi-state representation provides a more accurate and flexible tool in the availability evaluation of GFU capacity.

Generally, for a GFU $j$ at bus $i$ with $NH_{j}^{gfu}$ states ($NH_{j}^{gfu} \ge 2$), the stochastic electricity capacity of GFU $j$ can be denoted as $EC_{j}^{gfu} (t) \in \{ EC_{j}^{gfu,1} , \ldots ,EC_{j}^{{gfu,h_{j}^{gfu} }} , \ldots ,EC_{j}^{{gfu,NH_{j}^{gfu} }} \}$. Here, the electricity capacity for state $h_{j}^{gfu}$ is $EC_{j}^{{gfu,h_{j}^{gfu} }}$.

The power output of a GFU is also subject to the adequacy of the gas supply, which may be influenced by random failures in the gas system. The following equation evaluates the power output $P_{j}^{e,gfu} (t)$ of GFU $j$ at time $t$ corresponding to its gas injection $P_{j}^{g,gfu} (t)$ [23]:

$$P_{j}^{g,gfu} (t) = (a_{j} P_{j}^{e,gfu} (t)_{{}}^{2} + b_{j} P_{j}^{e,gfu} (t) + c_{j} )/H_{g}^{{}}$$

(1)

where $a_{j}^{{}}$, $b_{j}^{{}}$ and $c_{j}^{{}}$ are the coefficients of the heat rate for GFU $j$; and $H_{g}^{{}}$ is the high heat value of natural gas [23]. The solution of (1) can be written as:

$$P_{j}^{e,gfu} (t) = \left( { - b_{j}^{{}} + \sqrt {b_{j}^{2} - 4a_{j}^{{}} (c_{j}^{{}} - H_{g}^{{}} P_{j}^{g,gfu} (t))} } \right)/\left( {2a_{j}^{{}} } \right)$$

(2)

Therefore, the dispatchable electricity capacity of GFU $j$ for state $h_{j}^{gfu}$ can be evaluated as:

$$DEC_{j}^{gfu} = \hbox{min} \left\{ {EC_{j}^{{gfu,h_{j}^{gfu} }} ,\left( { - b_{j}^{{}} + \sqrt {b_{j}^{2} - 4a_{j}^{{}} (c_{j}^{{}} - H_{g}^{{}} \overline{{P_{j}^{g,gfu} }} )} } \right)/\left( {2a_{j}^{{}} } \right)} \right\}$$

(3)

where $\bar{P}_{j}^{g,gfu}$ is the upper boundary of the gas injection for GFU $j$ as determined by the operation of the gas system.

The $NG_{i}^{gfu}$ GFUs at bus $i$ can be aggregated into an equivalent GFU (EGFU) and represented as a multi-state model. The electricity capacity of the EGFU is a random variable at time $t$ taking values from $\{ AEC_{i}^{Egfu,1} , \ldots ,AEC_{i}^{{Egfu,h_{i}^{Egfu} }} , \ldots ,AEC_{i}^{{Egfu,NH_{i}^{Egfu} }} \}$ in ascending order. The electricity capacity for state $h_{i}^{Egfu}$ can be calculated as:

$$AEC_{i}^{{Egfu,h_{i}^{Egfu} }} = \sum\limits_{j = 1}^{{NG_{i}^{gfu} }} {DEC_{j}^{{gfu,h_{j}^{gfu} }} }$$

(4)

It should be noted that$NH_{i}^{Egfu} \le \prod\limits_{j = 1}^{{NG_{i}^{gfu} }} {NH_{j}^{gfu} }$. The transitions between different states of the EGFU are represented as multi-state Markov models [20]. The transition rate between states $p$ and $q$ for GFU $j$ and the EGFU are denoted as $\lambda_{p,q}^{{gfu_{j}^{{}} }}$ and $\lambda_{p,q}^{Egfu}$, respectively. The multi-state representation from a single GFU to the EGFU using the RNE is illustrated in Fig. 2.

Fig. 2

Multi-state representation of EGFU using RNE

The following TSMCS procedures are utilized to determine the chronological characteristics of an EGFU:

Step 1: Determine the initial state of the EGFU, $h$, according to its steady-state probability [20]. Calculate the corresponding dispatchable electricity capacity $AEC_{i}^{Egfu,h}$ according to (1)–(4).

Step 2: Generate a random number $U$ following uniform distribution $(0,1)$, and convert it to the duration of the EGFU in current state $T_{{}}^{h}$ following the corresponding exponential distribution $\sum\limits_{h' = 1,h' \ne h}^{{NH_{i}^{Egfu} }} {\lambda_{h,h'}^{Egfu} } \cdot \exp \left[ {\left( {\sum\limits_{h' = 1,h' \ne h}^{{NH_{i}^{Egfu} }} {\lambda_{h,h'}^{Egfu} } } \right)t} \right]$ [24].

Step 3: Determine the next state of the EGFU. The probability of entering each state $h'$ ($h \ne h'$) can be calculated as:

$$\hbox{Pr}_{h,h'}^{Egfu} = {{\lambda_{h,h'}^{Egfu} } \mathord{\left/ {\vphantom {{\lambda_{h,h'}^{Egfu} } {\left( {\sum\limits_{h' = 1,h' \ne h}^{{NH_{i}^{Egfu} }} {\lambda_{h,h'}^{Egfu} } } \right)}}} \right. \kern-0pt} {\left( {\sum\limits_{h' = 1,h' \ne h}^{{NH_{i}^{Egfu} }} {\lambda_{h,h'}^{Egfu} } } \right)}}$$

(5)

where $\sum\limits_{h' = 1,h' \ne h}^{{NH_{i}^{Egfu} }} {\Pr_{h,h'}^{Egfu} } = 1$. The next state of the EGFU is determined by the state transition sampling technique [24].

Step 4: Evaluate the corresponding dispatchable electricity capacity $AEC_{i}^{Egfu,h'}$ and the duration of state $T^{h'}$ as in Steps 2 and 3.

Step 5: Repeat Steps 2, 3 and 4 until the total duration of the studied period is reached.

3.2 Reliability network equivalents for CFUs

The stochastic characteristics of CFUs are represented as a binary-state model where the state of CFU $j$, $h_{j}^{cfu}$, takes random values from set $\{ 0,1\}$. $h_{j}^{cfu} = 0$ and $h_{j}^{cfu} = 1$ represent the complete failure state and well-functioning state, respectively. The corresponding electricity capacities are 0 and $EC_{j}^{cfu,1}$, respectively [25].

Different from GFUs, the fossil fuels of CFUs are regarded to be sufficient, and the power generation is constrained only by its electricity capacity subject to random failures. Therefore, the dispatchable electricity capacity of CFU $j$, $DEC_{j}^{cfu}$, can be evaluated as:

$$DEC_{j}^{cfu} = \left\{ {\begin{array}{*{20}l} {EC_{j}^{cfu,1} } \hfill & {\quad h_{j}^{cfu} = 1} \hfill \\ 0 \hfill & {\quad h_{j}^{cfu} = 0} \hfill \\ \end{array} } \right.$$

(6)

The $NG_{i}^{cfu}$ CFUs at bus $i$ can also be aggregated into an equivalent CFU (ECFU) and represented as a multi-state model. The electricity capacity for an ECFU at time $t$ varies in$\{ AEC_{i}^{cfu,1} , \ldots ,AEC_{i}^{{cfu,h_{i}^{Etfu} }} , \ldots ,AEC_{i}^{{cfu,NH_{i}^{Etfu} }} \}$. The electricity capacity of ECFU in state $h_{i}^{Ecfu}$ can be calculated as:

$$AEC_{i}^{{Ecfu,h_{i}^{Ecfu} }} = \sum\limits_{j = 1}^{{NG_{i}^{cfu} }} {h_{j}^{cfu} EC_{j}^{cfu,1} }$$

(7)

The chronological characteristics of ECFUs are determined by utilizing TSMCS procedures similar to those described in Section 3.1.

3.3 Reliability network equivalents for gas sources

GSs can be controlled within their gas capacities during IEGS operation. The GSs at a gas bus usually consist of several gas wells or gas storage facilities, and each is represented as a binary-state model. The state of GS j,$h_{j}^{gs}$, takes random values from set {0,1}. $h_{j}^{gs} = 0$ and $h_{j}^{gs} = 1$ represent the complete failure and well-functioning states where the gas capacities are 0 and $GC_{j}^{gs,1}$, respectively.

Similarly, the $NG_{i}^{gs}$ GSs at bus $i$ can be aggregated into equivalent GSs (EGSs) and represented as a multi-state model. The gas capacity of the EGS at time $t$ is a random value that varies in$\{ AGC_{i}^{Egs,1} , \ldots ,AGC_{i}^{{Egs,h_{i}^{Egs} }} , \ldots ,AGC_{i}^{{Egs,NH_{i}^{Egs} }} \}$. The dispatchable gas capacity of an EGS in state $h_{i}^{Egs}$ can be calculated as:

$$AGC_{i}^{{Egs,h_{i}^{Egs} }} = \sum\limits_{j = 1}^{{NG_{i}^{gs} }} {h_{j}^{gs} GC_{j}^{gs,1} }$$

(8)

The chronological characteristics of EGSs are also determined by utilizing TSMCS procedures similar to those described in Section 3.1.

3.4 Reliability network equivalents for power-to-gas facilities

PTG modules in a real PTG facility usually operate in parallel [26]. Hence, when one electricity supply path fails, the corresponding PTG module fails, but the entire PTG facility may only suffer a derating. We assume that the modules are the same to homogenize the heterogenic reliability characteristics and simplify the gas capacity calculation. Thus, $\forall j,GC_{j}^{ptg} = GC_{{}}^{ptg}$. All of the PTG modules can be represented by the same binary-state model. The state of PTG module $j$, $h_{j}^{ptg}$, takes random values from set $\{ 0,1\}$, and the gas capacity of PTG $j$ at time $t$ satisfies $GC_{j}^{ptg} (t) \in \{ 0,EC_{{}}^{ptg,1} \}$.

The gas production of a PTG is dependent on the adequacy of the electricity supply at the corresponding bus, which may be influenced by random failures in the electricity system. The following equation evaluates the gas production $P_{j}^{g,ptg} (t)$ of PTG $j$ at time $t$ corresponding to its electricity consumption $P_{j}^{e,ptg} (t)$ [27]:

$$P_{j}^{g,ptg} (t) = P_{j}^{e,ptg} (t)/(\eta_{{}}^{ptg} H_{g} )$$

(9)

where $\eta_{{}}^{ptg}$ is the efficiency of the energy conversion.

Therefore, the dispatchable gas capacity provided by PTG $j$ in state $h_{j}^{ptg}$ can be evaluated as:

$$DGC_{{}}^{ptg} = \hbox{min} \left\{ {GC_{{}}^{ptg} ,\overline{P}_{{}}^{e,ptg} /(\eta_{{}}^{ptg} H_{g} )} \right\}$$

(10)

where $\bar{P}_{{}}^{e,ptg}$ is the upper boundary of the electricity supply for the PTG as determined by the electricity system state.

A PTG facility (EPTG) at bus $i$ may have $NG_{i}^{ptg}$ PTG modules, and its equivalent can be represented by a multi-state model. The gas capacity of the EPTG varies in $\{ AGC_{i}^{ptg,1} , \ldots ,AGC_{i}^{{ptg,h_{i}^{Eptg} }} , \ldots ,AGC_{i}^{{ptg,NH_{i}^{Eptg} }} \}$. The dispatchable gas capacity of the EPTG in state $h_{i}^{Eptg}$ can be evaluated as:

$$AGC_{i}^{{Eptg,h_{i}^{Eptg} }} = DGC_{{}}^{ptg} \cdot \sum\limits_{j = 1}^{{NG_{i}^{ptg} }} {h_{j}^{ptg} }$$

(11)

where $h_{j}^{ptg}$ is the state of PTG $j$.

The chronological characteristics of EPTGs are also determined by utilizing TSMCS procedures similar to those described in Section 3.1.

4 Contingency management schema for IEGS considering the interruption cost of customers

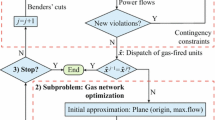
If the electricity or gas supply suffers from an inadequacy in a contingency state, the electricity and gas injections from EGFUs, ECFUs, EGSs, and EPTGs will be redispatched and the electricity and gas loads may be curtailed to maintain the balance of the IEGS. To determine the energy injections and possible load curtailments, a contingency management schema is proposed as shown in Fig. 3. As can be seen, the operation of IEGS is optimized based on IOPF, where the dispatchable electricity and gas capacities of the EGFUs, ECFUs, EGSs, and EPTGs and the transmission constraints and coupling of the electricity and gas systems are included.

Fig. 3

Contingency management schema for IEGS

The objective of contingency management is to minimize the system operation cost and maximize customer reliability. In this paper, customer reliability requirements are implicitly represented by using customer interruption costs (ICs). However, owing to the integration of electricity and gas infrastructures at some buses, ICs should be evaluated quantitatively by considering flexible loads with selectivity between different energy sectors.

4.1 ICs considering energy substitution

An IEGS bus usually involves different customers including industry, residential, and commercial, etc. The electricity load $P_{d,i}^{e}$ and gas load $P_{d,i}^{g}$ at bus $i$ are summated by the loads of involved customers, and the electricity load of customer $j$ includes the flexible load $P_{d,i,j}^{fl}$ and conventional electricity load $P_{d,i,j}^{el}$:

$$\left[ {\begin{array}{*{20}c} {P_{d,i}^{e} } & {P_{d,i}^{g} } \\ \end{array} } \right]^{\text{T}} = \left[ {\begin{array}{*{20}c} {\sum\limits_{{j \in \varXi_{i} }} {P_{d,i,j}^{e} } } & {\sum\limits_{{j \in \varXi_{i} }} {P_{d,i,j}^{g} } } \\ \end{array} } \right]^{\text{T}}$$

(12)

$$P_{d,i,j}^{e} = \sum\limits_{{j \in \varXi_{i} }}^{{}} {(P_{d,i,j}^{el} + P_{d,i,j}^{fl} )}$$

(13)

where $\varXi_{i}^{{}}$ is the set of customers at bus $i$. IC describes the willingness of a customer to pay to avoid load curtailment. This is associated with the interruption duration and the customer type [17]. The electricity IC for customer $j$ at bus $i$ is denoted as $IC_{i,j}^{e} (T)$. Interruptions of the flexible load $IC_{i,j}^{{{\prime }e}} (T)$ with a duration of less than a certain time threshold $\chi$ cannot be noticed by customers, as described in (14) and (15) [28]:

$$\left[ {\begin{array}{*{20}c}{IC_{i,j}^{el} (T_{{}}^{h} )} & {IC_{i,j}^{fl}} (T_{{}}^{h} ) \\ \end{array}} \right]^{\text{T}} { = }\left[ {\begin{array}{*{20}c} {\alpha_{i,j}^{el}} & {\alpha_{i,j}^{fl}} \\ \end{array}} \right]^{\text{T}} \cdot IC_{i,j}^{e} (T_{{}}^{h} )$$

(14)

$$IC_{i,j}^{{{\prime }e}} (T_{{}}^{h} ) = \left\{ {\begin{array}{*{20}l} {IC_{i,j}^{el} (T_{{}}^{h} )} \hfill & {\quad 0 < T_{{}}^{h} \le \chi } \hfill \\ {IC_{i,j}^{e} (T_{{}}^{h} )} \hfill & {\quad T_{{}}^{h} > \chi } \hfill \\ \end{array} } \right.$$

(15)

where $T_{{}}^{h}$ is the interruption duration for IEGS at state $h$; $\alpha_{i,j}^{el}$ and $\alpha_{i,j}^{fl}$ are the ICs of conventional and flexible electricity loads, respectively; and IC^el_{i, j} and IC^fl_{i, j} are the ICs of conventional and flexible electricity loads, respectively.

The IC of gas load $IC_{i,j}^{g}$ can be estimated by the following heat value model:

$$IC_{i,j}^{g} (T_{{}}^{h} ) = IC_{i,j}^{e} (T_{{}}^{h} ) \cdot H_{g} \eta_{i,j}^{e} /\eta_{i,j}^{g}$$

(16)

where $\eta_{i,j}^{e}$ and $\eta_{i,j}^{g}$ are the efficiencies of utilizing electricity and gas for the same task, respectively. The nodal ICs for the electricity and gas loads at bus $i$ are calculated as weighted averages of the ICs of the corresponding customers:

$$\left[ {\begin{array}{*{20}c} {IC_{i}^{e} (T_{{}}^{h} )} & {IC_{i}^{g} (T_{{}}^{h} )} \\ \end{array} } \right]^{\text{T}} = \left[ {\begin{array}{*{20}c} {\sum\limits_{{j \in \varXi_{i} }}^{{}} {\gamma_{i,j}^{e} \cdot IC_{i,j}^{{{\prime }e}} (T_{{}}^{h} )} } & {\sum\limits_{{j \in \varXi_{i} }}^{{}} {\gamma_{i,j}^{g} \cdot IC_{i,j}^{g} (T_{{}}^{h} )} } \\ \end{array} } \right]^{\text{T}}$$

(17)

where $\left[ {\begin{array}{*{20}c} {\gamma_{i,j}^{e} } & {\gamma_{i,j}^{g} } \\ \end{array} } \right]_{{}}^{\text{T}} = \left[ {\begin{array}{*{20}c} {P_{d,i,j}^{e} /P_{d,i}^{e} } & {P_{d,i,j}^{g} /P_{d,i}^{g} } \\ \end{array} } \right]_{{}}^{\text{T}}$.

4.2 IOPF-based contingency management schema for IEGS

In the IEGS studied in this paper, both electricity and gas systems are regulated by a single independent system operator (ISO). The goal of the ISO in contingency management is to minimize the total system cost, including the gas purchasing cost of EGSs, the electricity generation cost of ECFUs, and the ICs of electricity and gas loads. Several assumptions are made to simplify this problem: 1) in each system state, contingency management is conducted independently, which indicates that the interruption costs for different system states are also calculated independently; 2) both electricity and gas systems can be stabilized soon after the change in the system state.

Based on these, the objective function can be decoupled at each system state $h$ as formulated in (18). The solutions for contingency management in every independent system state are also guaranteed to be the optimum solutions over the entire operation horizon. The corresponding curtailments of electricity and gas loads with the minimum total system cost are utilized to calculate the reliability indices of the customers and the entire system.

$$\begin{aligned} \hbox{min} \;F_{h}^{{}} & = \left( {\sum\limits_{i = 1}^{{NB^{e} }} {GC_{i}^{{}} (P_{i}^{e} ,Q_{i}^{e} )} + \sum\limits_{i = 1}^{{NB_{{}}^{g} }} {\rho_{s,i}^{g} P_{i}^{g} } } \right. \\ & \quad \left. { + \sum\limits_{i = 1}^{{NB^{e} }} {LC_{i}^{e} \cdot IC_{i}^{e} (T_{{}}^{h} )} + \sum\limits_{i = 1}^{{NB^{g} }} {LC_{i}^{g} \cdot IC_{i}^{g} (T_{{}}^{h} )} } \right) \\ \end{aligned}$$

(18)

where $NB_{{}}^{e}$ and $NB_{{}}^{g}$ are the numbers of electricity and gas buses, respectively; $\rho_{s,i}^{g}$ and $P_{i}^{g}$ are the gas price and gas supply at bus $i$, respectively;$GC_{i}^{{}}$ is the electricity generation cost for CFUs at bus $i$. This is usually fitted as a polynomial function or a piecewise linear function associated with CFUs’ active and reactive power generations, $P_{i}^{e}$ and $Q_{i}^{e}$ [23].

The control variables at bus $i$ are listed as vector $X_{i}^{{}}$ in (19), including the electricity generations of EGFUs, ECFUs, the gas supplies of EGSs and EPTGs, the electricity consumptions of EPTGs $P_{i}^{e,Eptg}$, the gas consumptions of EGFUs $P_{i}^{g,Egfu}$ and the electricity and gas load curtailments at different buses. Their upper and lower boundaries are denoted as ${\overline{X}}_{i}$ and ${\underline{X}}_{i}$ , respectively. Equations (19)–(27) are the constraints for the IOPF in contingency state $h$. The control variables should follow the constraints shown in (20). In particular, the upper boundaries of $P_{i}^{e}$, $Q_{i}^{e}$, and $P_{i}^{g}$ are determined by the capacities of EGFUs $AEC_{i}^{Egfu,h}$, ECFUs $AEC_{i}^{Ecfu,h}$, EGSs $AGC_{i}^{Egs,h}$, and EPTGs $AGC_{i}^{Eptg,h}$ as described in Section 3.

$$X_{i}^{{}} = [\begin{array}{*{20}c} {P_{i}^{e} } & {Q_{i}^{e} } & {P_{i}^{g} } & {P_{i}^{e,Eptg} } & {P_{i}^{g,Egfu} } & {LC_{i}^{e} } & {LC_{i}^{g} } \\ \end{array} ]$$

(19)

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X}_{i} \le X_{i}^{{}} \le \bar{X}_{i}$$

(20)

$$P_{i,}^{e} + jQ_{i}^{e} - P_{d,i}^{e} - jQ_{d,i}^{e} - P_{i}^{e,Eptg} - LC_{i}^{e} - \sum\limits_{{j \in \varPsi_{i}^{e} }}^{{}} {f_{ij}^{e} } = 0$$

(21)

$$P_{s,i}^{g} - P_{d,i}^{g} - P_{i}^{g,Egfu} - \sum\limits_{{j \in \varPsi_{i}^{g} }}^{{}} {f_{ij}^{g} } = 0$$

(22)

$$f_{ij}^{e} = V_{i} V_{j} [(G_{ij} \cos \theta_{ij} + B_{ij} \sin \theta_{ij} ) +\text{ j}(G_{ij} \sin \theta_{ij} - B_{ij} \cos \theta_{ij} )]$$

(23)

$$f_{ij}^{g} = K_{ij} S_{ij} \sqrt {\left| {\pi_{i}^{2} - \pi_{j}^{2} } \right|}$$

(24)

$$S_{ij} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad \pi_{i} \ge \pi_{j} } \hfill \\ { - 1} \hfill & {\quad \pi_{i} < \pi_{j} } \hfill \\ \end{array} } \right.$$

(25)

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}_{ij}^{e} \le f_{ij}^{e} \le \bar{f}_{ij}^{e}$$

(26)

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}_{ij}^{g} \le f_{ij}^{g} \le \bar{f}_{ij}^{g}$$

(27)

Equations (21) and (22) are the power balance constraints for the electricity and gas buses, respectively, where the influences of EGFUs, EPTGs, and load curtailments are incorporated. $f_{ij}^{e}$, and $f_{ij}^{g}$, respectively, are the electricity and gas flows from bus $i$ to $j$. ${\overline{f}}_{ij}^{e}$, ${\underline{f}}_{ij}^{e}$ and ${\overline{f}}_{ij}^{g}$, ${\underline{f}}_{ij}^{g}$ are the upper and lower boundaries of corresponding electricity and gas flows. The electricity flow is calculated using the AC model in (23). $V_{i}^{{}}$ and $\theta_{ij}^{{}}$ are the amplitude and phase angle, respectively. $G_{ij}^{{}}$ and $B_{ij}^{{}}$ are the conductivity and susceptance of the electricity branch from bus $i$ to $j$, respectively. $\varPsi_{i}^{e}$ and $\varPsi_{i}^{g}$ are the sets of electricity branches and gas pipelines connected to bus $i$, respectively. Equation (24) is the Weymouth equation, which has been widely used for the calculation of industrial gas flow [29]. $\pi_{i}$ and $\pi_{j}$ are the natural gas pressures. $K_{ij}^{{}}$ and $S_{ij}^{{}}$ are the parameters of the gas pipeline and the value of the Dirichlet function, respectively. Equations (26) and (27) are the constraints for the electricity and gas flows, respectively.

5 TSMCS procedures and reliability evaluation

The expected energy not supplied (EENS) is widely used for the reliability evaluation of electricity systems. To accommodate the two energy sectors in IEGS, a new reliability index, expected gas not supplied (EGNS), is introduced. EENS and EGNS are calculated as (28) and (29), respectively.

$$EENS_{i}^{{}} = \left( {\sum\limits_{{i_{s} = 1}}^{NS} {\left( {\sum\limits_{k = 1}^{NK} {T_{k} LC_{i,k}^{e} } /\sum\limits_{k = 1}^{NK} {T_{k} } } \right)} } \right)/NS$$

(28)

$$EGNS_{i}^{{}} = \left( {\sum\limits_{{i_{s} = 1}}^{NS} {\left( {\sum\limits_{k = 1}^{NK} {T_{k} LC_{i,k}^{g} } /\sum\limits_{k = 1}^{NK} {T_{k} } } \right)} } \right)/NS$$

(29)

where $NK$ and $NS$ are the number of system states in one studied period and the time of simulation, respectively.

The stopping criterion for the reliability evaluation is the coefficient of variation of EENS, which is calculated by

$$\zeta = STD(EENS)/E(EENS)$$

(30)

where $STD(EENS)$ and $E(EENS)$ are the standard deviation and expectation of EENS, respectively.

The TSMCS procedure for evaluating reliability indices consists of the following steps:

Step 1: Generate the state sequences of EGFUs, ECFUs, EGSs, and EPTGs at each bus by utilizing the approach described in Section 3. From the sampled sequences, determine the states $h_{i}^{Egfu}$, $h_{i}^{Ecfu}$, $h_{i}^{Egs}$, and $h_{i}^{Eptg}$ of the EGFUs, ECFUs, EGSs, and EPTGs; the corresponding electricity capacities $AEC_{i}^{Egfu}$ and $AEC_{i}^{Ecfu}$ and the gas capacities $AGC_{i}^{Egs}$ and $AGC_{i}^{Eptg}$.

Step 2: Utilize the IOPF model developed in Section 4 to evaluate the electricity and gas load curtailments of different buses.

Step 3: Calculate the reliability indices EENS and EGNS according to (28) and (29).

Step 4: Calculate the stopping criteria according to (30). Go to Step 1 if the confidence intervals are not satisfied. Otherwise, output the final reliability indices as calculated in Step 3.

The computation complexity of the reliability evaluation technique of IEGS proposed in this paper involves two aspects: the massive system states combined by the components’ states, and the calculation of IOPF. First, suppose the numbers of the states for GFUs are all $NH_{{}}^{gfu}$. The reliabilities of the CFUs, PTGs, and GSs are represented as binary-state models. Therefore, the computation complexity of the system state combined by the components’ states is $O(2_{{}}^{{NG_{{}}^{cfu} + NG_{{}}^{ptg} + NG_{{}}^{gs} }} (NH_{{}}^{gfu} )_{{}}^{{NG_{{}}^{gfu} }} )$, where $NG_{{}}^{gfu}$, $NG_{{}}^{cfu}$, $NG_{{}}^{gs}$, and $NG_{{}}^{ptg}$ are the numbers of GFUs, CFUs, GSs, and PTGs, respectively.

However, in the practical reliability evaluation, the number of system states can be reduced by utilizing a like-terms collection technique during the RNE technique. For example, multiple GFUs with the same electricity capacity can coexist at the same bus. Therefore, many identical electricity capacities of EGFU $AEC_{i}^{Egfu}$ can be produced with the aggregation of GFUs, and the number of states of the EGFU can be reduced.

Secondly, by aggregating components to their corresponding equivalents using the RNE, the number of decision variables is significantly reduced. Suppose the numbers of EGFUs, ECFUs, EGSs, and EPTGs in IEGS are all at their maximum values $NB$, where $NB$ represents the number of bus. With the given numbers of variables, the computation complexity for solving IOPF using the interior-point method is $O( 4^{3.5} \cdot NB^{3.5} )$ [30]. Therefore, the computational complexity of the proposed reliability evaluation method is $O\left( {NB_{{}}^{ 3. 5} \cdot 2_{{}}^{{NG_{{}}^{cfu} + NG_{{}}^{ptg} + NG_{{}}^{gs} { + 7}}} \cdot (NH_{{}}^{gfu} )_{{}}^{{NG_{{}}^{gfu} }} } \right)$.

The proposed method in this paper can be adopted for short-term studies such as day-ahead studies. The evaluation results can provide a prevision for the ISO to devise load curtailments against the contingency system states, and an advanced warning for customers to prearrange their energy-related tasks and avoid unexpected interruptions [31].

6 Case study

To illustrate the reliability evaluation method proposed in this paper, a test IEGS system is developed based on the IEEE RTS [25] and the Belgium natural gas transmission system [32], as shown in Fig. 4. The following modifications are made: ① the electricity and gas systems are topologically connected by flexible loads, GFUs, and PTGs according to Fig. 4; ② three PTGs with a gas capacity of 0.5 Mm³/day are installed at gas buses (GBs) 7, 10, and 16, respectively; ③ the original oil steam-generating units with electricity generation capacities of 12, 20, and 100 MW at electricity buses (EBs) 15, 13, 14, and 2 are replaced with GFUs with the same capacities, and the coefficients of the heat rate for the GFUs are set according to [23]; and ④ the customer allocations at the buses are set according to [33]. The gas prices of the GSs are set according to [23], and the load in the electricity system is set to its peak value of 2850 MW.

Fig. 4

Diagram for integrated IEEE RTS and Belgium natural gas transmission system

The simulations are conducted on a 3.4 GHz Dell desktop. The approximate compution time is 0.2 s for an IOPF and 15 min for the entire reliability evaluation procedure. Simulations are performed on the following three specific cases to verify the proposed reliability evaluation method.

6.1 Case 1: reliability impacts of random failures of GSs

In Case 1, the impacts of random failures of GSs on the reliability of IEGS are evaluated. Three scenarios are considered in this case: scenario A is the basic case where the state transition rates of the GSs are set to the same values as the CFUs in the electricity system. In scenario B, the failure rates of the GSs are set to zero. In scenario C, the failure rates are set to 10 times of the values in scenario A. The flexible loads of the customers are not considered in Case 1.

For scenario A, two representative system states A1 and A2 with compound failures of CFUs and GSs are illustrated in Table 1, showing different causes of EENS or EGNS spikes.

Table 1 Representative component failures

In system state A1, the derating of the 255 MW electricity supply and 1.8 Mm³/day gas supply are triggered by component failures. The balance in the gas system is still maintained without curtailment, while electricity load curtailments at EB 2 and EB 7 occur, and the EENS is relatively high.

System state A2 is a typical illustration of failures propagating from the gas system to the electricity system. The derating of the GS at GB 1 reaches 8.695 Mm³/day. All of the GSs in IEGS are at their maximum dispatchable gas capacities except the GS at GB 8. Although the entire gas supply in IEGS still exceeds the gas load, the gas pressures at GB 8 and GB 16 are 66.2 and 50 bar, respectively, reaching their upper and lower bounds. Thus, the redundant gas supply at GB 8 cannot be transported to GBs 3, 6, 15, and 16, and their corresponding gas loads are curtailed. Gas shortages also occur at buses with GFUs. Therefore, some electricity loads have been curtailed.

The EENS and EGNS in IEGS at different buses in the three scenarios are shown in Figs. 5 and 6, respectively. It can be concluded that random failures in the gas system have a great impact on the reliability of IEGS. With the growth in the failure rates of the GSs, the EENS in the electricity system and EGNS in the gas system both increase sharply. For example, the EENS at EB 14 increases dramatically from 4.58 MW in scenario A to 19.81 MW in scenario C.

Fig. 5

Nodal EENS of IEGS with different failure rates of GSs

Fig. 6

Nodal EGNS of IEGS with different failure rates of GSs

It is worth noting that different buses present different increasing levels of reliability indices for scenarios A to C. For example, the EENSs at EBs 14 and 15 increase by 332% and 233%, respectively. This is because the electricity load at EB 14 is directly supplied by GFUs, which is severely influenced by an insufficient gas supply. By contrast, the electricity load at EB 15 is mostly supplied by CFUs at adjacent EBs and suffers less from insufficient gas.

Actually, scenario A represents the reliability evaluation of the electricity systems that ignores the insufficient gas supply for GFUs, and scenario B represents the reliability evaluation that considers random failures in gas systems. Comparing scenarios A and B, it can be concluded that these two reliability evaluation methods lead to distinguished results. The evaluation result is worse when the influence of the gas system is considered, but it is more credible and practical in realistic applications.

Moreover, the various reliability indices at different buses in Figs. 5 and 6 indicate the topological weakness of the studied IEGS. EB 14 is the weakest bus in the electricity system with the EENSs of 4.58, 1.67, and 19.81 MW in scenario A, B, and C, respectively, while EB 19 has the lowest EENS. This is mainly because EB 19 is close to electricity generators and has customers with relatively high ICs. In the contingency management schema proposed in this paper, EB 19 is given priority to avoid load curtailment. In the gas system, the EGNS at GB 15 is the highest among all of the GBs, with values of 0.13, 0, and 0.88 Mm³/day for scenario A, B, and C, respectively.

By contrast, the ENGSs at GBs 7, 10, 12, 19, and 20 are close to zero. This can be explained as follows. The gas loads at GB 15 and GB 16 add up to 33.69 Mm³/day, taking 50.85% of the total gas load. In addition, GB 15 and GB 16 are the terminals of a gas transmission and are indirectly connected to two GSs with a total gas capacity of 3.24 Mm³/day. Therefore, the gas loads at GB 15 and GB 16 are easily to curtail. Owing to the redundant capacity of the gas pipeline between GB 15 and GB 16, the gas load curtailments are allocated based on the ICs. With different proportions of customer types, the nodal IC at GB 15 is lower than that of GB 16, and thus it is assigned a higher gas load curtailment.

To validate the efficiency of the proposed reliability evaluation method, it is compared with the TSMCS without utilizing RNE. The computation time of both methods is presented and compared for all three scenarios in Table 2. The average computation time decreases by 19.18% with the implementation of RNE.

Table 2 Comparison of computation time for different methods

6.2 Case 2: reliability impacts of GFUs and PTGs

In case 2, the impacts of different capacities of energy conversion components including GFUs and PTGs on the reliability of IEGS are analyzed. Four specific scenarios are designed with 0%, 25%, 50%, and 100% of the preset capacities of the GFUs and PTGs. These are denoted as scenario A, B, C, and D, respectively. The failure rates of the GSs are set to the same values as in scenario A of case 1. Flexible loads are not considered in Case 2.

A comparison between Scenario A and D is presented in Figs. 7 and 8, respectively. It can be seen that adequate capacities of GFUs and PTGs at critical buses improve the nodal reliabilities of the corresponding and adjacent buses. For example, compared with scenario A, the expected utilization rate of the GFU at EB 7 is 88.75% in scenario D, and its EENS decreases from 21.26 to 5.31 MW. The EENS at adjacent EB 3 also decreases from 6.59 to 2.40 MW.

Fig. 7

Impacts of different capacities of GFUs and PTGs on nodal EENS

Fig. 8

Impacts of different capacities of GFUs and PTGs on nodal EGNS

The reliability impacts on the gas system are similar. GB 15 is the weakest bus, as indicated by the previous Case 1. The increasing capacity of the PTGs at GB 16 covers the gas shortages at GB 15 and GB 16. Thus, the EGNS at GB 15 decreases from 1.17 to 0.13 Mm³/day, and the EGNS at GB 16 also drops significantly by 98.79%.

Table 3 lists the cost decomposition and reliability indices at representative buses in the four scenarios. It can be observed that larger capacities of GFUs and PTGs help to reduce the system cost and improve the reliabilities at critical buses. Moreover, the decrease in the system cost is mainly owing to the reduction of the ICs of the electricity and gas loads. This indicates that even with the same capacities of GSs and CFUs as the sources of energies, the load curtailments and enormous ICs can decrease when there is a more interactive energy exchange between the electricity and gas systems though larger capacities of the GFUs and PTGs.

Table 3 Reliability and cost of IEGS with different capacities of GFUs and PTGs

In particular, the adoption of the PTG provides a new perspective for increasing the reliability of IEGS. Four scenarios are built to evaluate the reliability of IEGS with 0%, 50%, 100%, and 200% of the preset capacities of the PTGs. These are denoted scenario E, F, G, and H, respectively. The capacities of the GFUs and the failure rates of the GSs are set to the same values as in scenario A of Case 1. Flexible loads are not considered.

The reliability indices of IEGS in terms of electricity and gas systems with different PTG capacities are presented in Figs. 9 and 10, respectively. It can be observed that the EENS in the electricity system generally increases with the increase in the PTG capacities. However, since the large capacities of the PTGs provide more opportunities for bidirectional energy exchanges between the electricity and gas systems among the locations, it is worth noting that the nodal EENSs do not increase consistently. In other words, the increase of nodal EENSs at some EBs are not monotonic as the capacities of the PTGs increase. By contrast, the nodal EGNSs at all GBs decrease with increasing capacities of the PTGs.

Fig. 9

Nodal EENS of IEGS with different capabilities of PTGs

Fig. 10

Nodal EGNS of IEGS with different capabilities of PTGs

6.3 Case 3: Reliability impacts of flexible loads

In Case 3, the characteristics of flexible loads, including their proportions in the total electricity load and the time thresholds $\chi$, are considered. Five scenarios are given, and the characteristics of their flexible loads are listed in Table 4. The capacities of the GFUs and PTGs in all scenarios are set to the same values as scenario A of Case 1. The different ICs and reliability indices are presented in Table 3.

Table 4 Reliability and cost of IEGS with different characteristics of flexible loads

Comparing scenario A, B, and C, it can be observed that when the proportion of the flexible load increases, the ICs of the electricity and gas loads decrease, and the reliability of IEGS improves. For scenario C, D, and E, it can be seen that an increase in the time threshold leads to a decrease in the ICs of the electricity and gas loads. However, the trends of EENS and EGNS of IEGS are not monotonic, which can be explained as follows. With an increase in the time threshold, the ICs of the electricity loads are lower because of the lower ICs of the flexible loads in the contingency states of IEGS with durations less than the given time threshold. Therefore, load curtailments are more likely to be adopted than the increase of the electricity or gas supply.

7 Conclusion

The utilization of GFUs and the development of PTGs have intensified the interaction between electricity and gas systems, and it brings new challenges to the reliability evaluation of IEGS. This paper propose a reliability evaluation method for IEGS considering the interaction between electricity and gas systems. RNEs are utilized to represent reliability models of GFUs, CFUs, GSs, and PTGs in IEGS. A contingency management schema is developed considering the coupling between electricity and gas systems based on the IOPF technique. The TSMCS is used to simulate the chronological characteristics of corresponding RNEs and obtain the reliability indices.

The reliabilities of IEGS at different buses are evaluated in multiple cases. The results demonstrate that random failures in the gas system, the capacities of energy conversion components including GFUs and PTGs, and the characteristics of flexible loads greatly affect the reliability of IEGS. The proposed reliability evaluation method provides a feasible tool for the reliability management of both ISO and nodal customers in IEGS.