Dynamical and transport properties in plasmas including three-particle spatial correlations

Abstract

In this work, we study the two and triplet static correlation functions in plasma when the ions interact via the Debye screened potential and via the Deutsch screened potential. The latter takes into consideration the possible quantum effects at short distances. The ratio of the mean distance between two ions and the thermal De Broglie wavelength $r_{i}/\lambda_{\mathrm{T}}$ gives the measure of these effects. Our investigation is developed in the conditions of weak coupling parameter ($\varGamma <1$). The pair and the triplet correlation functions are calculated numerically and compared to the correlation functions due to the Kirkwood superposition approximation (KSA). Some applications to the ion velocity auto-correlation function D(t) and the electric field auto-correlation function C(t) at an ion (assumed to be an impurity) and the diffusion coefficient D are calculated for the two kinds of potentials in different plasma conditions. The comparison with other results found in the literature shows a well satisfactory agreement, for the static as well as the dynamic properties.

Introduction

The equilibrium properties of a plasma considered as a liquid of charged particles (in the hydrodynamical description) are fully described by a set of probability density functions $g({\mathbf{r}}_{1},\ldots ,{\mathbf{r}}_{n})$ of location of particles at points ${\mathbf{r}}_{1},\ldots ,{\mathbf{r}}_{n}$, when the total potential energy of a liquid is given by a sum of isotropic pair potentials [1], and the physical properties (pressure, energy density, etc.) [2] are defined by the pair correlation function $g({\mathbf{r}}_{1}, {\mathbf{r}}_{2})$. However, even in the approximation of pair interaction, higher order correlation functions are of interest. Information on the triplet correlation function $g({\mathbf{r}}_{1},{\mathbf{r}}_{2},{\mathbf{r}}_{3})$ is of importance in calculating the properties of the medium (entropy, thermal expansion coefficients, etc.) [3]. Explicit knowledge of triplet correlations is also required in perturbation theories for static fluid properties [4] and in the theories of transport properties [5]. The triple distribution function can be computed either via computer simulation methods like (the Monte Carlo method, molecular dynamics method) [6–8], or via the theoretical methods [9]. It can also be determined experimentally [3, 4, 10].

In this paper the obtained results are based on theoretical studies of the structure functions and the transfer phenomena in the plasmas in terms of two-particle and three-particle correlation. We have theoretically obtained three-particle correlation functions and analyzed them and compared with the superposition approximation [11]. Overall in this paper we use two kinds of screened potentials: the screened Debye potential $V(r)=q\exp (-r/\lambda_{\mathrm{D}})/r$ and the screened Deutsch potential $V^{\mathrm{{SD}}}(r)=q\exp (-r/\lambda_{\mathrm{D}})(1-\exp (-r/\lambda_{\mathrm{T}}))/r$ [12], where r is the interparticle spacing, $\lambda_{\mathrm{D}}$ is the screening Debye length, $\lambda_{\mathrm{T}}$ the thermal Broglie wave length and q is the ion charge. $\varGamma =q^{2}/k_{\mathrm{B}}\text{Tr}_{i}$ is the coupling parameter, where $r_{i}=(3/4\pi \rho )^{1/3}$ is the mean interparticle spacing, $\rho$ the particles density whereas $k_{\mathrm{B}}$ is the Boltzmann constant and T is the equilibrium temperature of the system. Our paper is organized as follows: in the next section, we present some theoretical implementations describing the pair correlation functions, following which the theoretical derivation of the three correlation functions for different plasma conditions for both kinds of potential is presented. In the subsequent section, we present some applications of the static structure functions on the calculation of the dynamical properties as the time auto-correlation functions of the ions velocity and of the electrical micro-field on an ion (considered as an impurity), and the related transport quantities. The results with discussion are reported before the concluding section. The final section contains conclusion with some perspectives.

Static pair correlation functions

To define the pair correlation functions g(r) that represents a static structure function, we introduce the probability of a configuration of N particles in a volume V in equilibrium with a thermal bath at temperature T,

$$\begin{aligned} g(r_{1},r_{2})=V^{2}\left( 1-\frac{1}{N}\right) \frac{\int \exp (-\beta V_{N}(r^{N})){\mathrm{d}}{\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N}}{Z_{N}} \end{aligned}$$

(1)

For the case where $N\rightarrow \infty$ such as $N/V=\rho$ is finite (thermodynamical limit):

$$\begin{aligned} g(r_{1},r_{2})=V^{2}\frac{\int \exp (-\beta V_{N}(r^{N})){\mathrm{d}}{\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N}}{Z_{N}} \end{aligned}$$

(2)

where $\beta =1/k_{\mathrm{B}}T$, $Z_{N}$ and $V_{N}(r^{N})$ are the configuration integral and the total potential energy, respectively, given by

$$\begin{aligned} Z_{N}=\int \exp (-\beta V_{N}(r^{N})){\mathrm{d}}{\mathbf{r}}_{1}\ldots {\mathrm{d}}{\mathbf{r}}_{N} \end{aligned}$$

(3)

$$\begin{aligned} V_{N}(r^{N})=\sum \limits_{1\le i\langle j\le N}v(r_{ij}) \end{aligned}$$

(4)

where $v(r_{ij})$ is the binary interaction between the ith and jth ions. By substituting (4) in (2), we find

$$\begin{aligned} g(r_{1},r_{2})=V^{2}\frac{\int \exp \left( -\beta \sum \nolimits_{1\le i< j\le N}v(r_{ij})\right) {\mathrm{d}}{\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N}}{Z_{N}} \end{aligned}$$

(5)

When we extract away the first term $v(r_{12})$ from the sum present at the exponential, because it is not concerned by the integration, we find

$$\begin{aligned} g(r_{1},r_{2})= & {} \frac{V^{2}}{Z_{N}}\exp (-\beta v(r_{12}))\int \exp \left( -\beta \sum \limits_{_{i\ge 1,j\ge 3(i\langle j)}}v(r_{ij})\right) {\mathrm{d}} {\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N} \end{aligned}$$

(6)

$$\begin{aligned}= & {} \frac{V^{2}}{Z_{N}}\exp (-\beta v(r_{12}))\int \prod \limits_{_{i\ge 1,j\ge 3(i\langle j)}}\exp (-\beta v(r_{ij})){\mathrm{d}}{\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N} \end{aligned}$$

(7)

then, the pair correlation function becomes

$$\begin{aligned} g(r_{1},r_{2})=\frac{V^{2}}{Z_{N}}\exp (-\beta v(r_{12}))\int \prod \limits_{_{i\ge 1,j\ge 3(i< j)}}(1+f_{ij}){\mathrm{d}}{\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N} \end{aligned}$$

(8)

where

$$\begin{aligned} f_{ij}=\exp (-\beta v(r_{ij}))-1. \end{aligned}$$

(9)

As we have the product expansion

$$\begin{aligned} \prod_{ij}(1+f_{ij})= & {} 1+\sum \limits_{i<j} f_{ij}+\sum \limits_{i< j,k< l}f_{ij}f_{kl}+\cdots \end{aligned}$$

(10)

$$\begin{aligned}\approx & {} 1+\sum \limits_{i\prec j}f_{ij}+\sum \limits_{i< j,k< l}f_{ij}f_{kl} \end{aligned}$$

(11)

we can develop the pair correlation as the following

$$\begin{aligned} g(r_{1},r_{2})= & {} \frac{V^{2}}{Z_{N}}\exp (-\beta v(r_{12})) \\ &\times \int \left( 1+\sum \limits_{i\ge 1,j\ge 3(i<j)}f_{ij}+\sum \limits_{i\ge 1,j\ge 3(i<j),k\ge 1,l\ge 4(k<l)}f_{ij}f_{kl}\right) {\mathrm{d}}{\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N} \end{aligned}$$

(12)

The integrals in Eq. (12) can be formally written as

$$\begin{aligned} \int {\mathrm{d}}{\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N}=V^{N-2} \end{aligned}$$

(13)

$$\begin{aligned} \int \sum \limits_{i\ge 1,j\ge 3(i<j)}f_{ij}{\mathrm{d}}{\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N}=V^{N-2}\left( \rho \frac{N}{2}\beta_{1}\right) \end{aligned}$$

(14)

$$\begin{aligned} \int \sum \limits_{i\ge 1,j\ge 3(i<j),k\ge 1,l\ge 4(k<l)}f_{ij}f_{kl}{\mathrm{d}} {\mathbf{r}}_{3}\ldots {\mathrm{d}}{\mathbf{r}}_{N}=V^{N-2}\left( \frac{N^{2}}{8}\rho^{2}\beta_{1}^{2}+\rho b(r_{1},r_{2})\right) \end{aligned}$$

(15)

where $\rho$ is the ion density and

$$\begin{aligned} \beta_{1}=\int (\exp (-\beta v(r))-1){\mathrm{d}}{\mathbf{r}}=\int f(r){\mathrm{d}}{\mathbf{r}} \end{aligned}$$

(16)

$$\begin{aligned} b(r_{1},r_{2})=\int f_{13}f_{23}{\mathrm{d}}{\mathbf{r}}_{3}=\frac{1}{(2\pi )^{3}r_{12}}\int k{\mathrm{d}}\mathbf{k }\vert f(k)\vert^{2}\sin (kr_{12}) \end{aligned}$$

(17)

where f(k) is the Fourier transform of f(r)

$$\begin{aligned} f(k)=\int f(r)\exp (i\mathbf{k }.{\mathbf{r}}){\mathrm{d}}{\mathbf{r}} \end{aligned}$$

(18)

When we replace formula (13)–(15) in Eq. (12), we obtain $g(r_{1},r_{2})$ by the following result

$$\begin{aligned} g(r_{1},r_{2})=\frac{\exp (-\beta v(r_{12}))V^{N}}{Z_{N}}\left( 1+\rho b(r_{1},r_{2})+\frac{N}{2}\rho \beta_{1}+\frac{N^{2}}{8}\rho^{2}\beta_{1}^{2}\right) \end{aligned}$$

(19)

Using the condition of the weakness coupling ($1\gg \frac{\rho \beta_{1}}{2}$), we estimate in the same manner the partition function $Z_{N}$ which appears in (19):

$$\begin{aligned} Z_{N}=V^{N}\left( 1+\rho \beta_{1}\frac{N}{2}+\frac{N^{2}}{8}\beta_{1}^{2}\rho^{2}\right) =V^{N}\left( 1+\frac{\rho \beta_{1}}{2}\right)^{N}\simeq V^{N} \end{aligned}$$

(20)

When we drop the last two terms in (19), we can write the pair correlation function $g(r_{1},r_{2})$ as

$$\begin{aligned} g(r_{1},r_{2})=\exp (-\beta v(r_{12}))(1+\rho b(r_{1},r_{2})) \end{aligned}$$

(21)

If the interparticle interaction is spherically symmetric and if the system is treated as an isotropic fluid, then $g(r_{1},r_{2})$ depends only on the distance $r_{12}=\vert {\mathbf{r}}_{1}-{\mathbf{r}}_{2}\vert$ between ions 1 and 2. We adopt the notation $g(r)=g(r_{12})$ and define the radial distribution function g(r) as

$$\begin{aligned} g(r)=\exp (-\beta v(r))(1+\rho b(r)) \end{aligned}$$

(22)

The last formula gives a correction to the commonly known formula $g(r)=\exp (-\beta v(r))$ (Boltzmann factor formula), usually used by many authors for representing an acceptable approximation of the radial distribution function.

Fig. 1

Pair correlation function g(r) calculated by our model for different coupling parameters $\varGamma =0.1, 0.5, 1.$ and different effect quantum parameters $r_{i}/\lambda_{\mathrm{T}}$ and for two interaction potentials (Debye and Deutsch)

Three correlation functions

In the canonical ensemble in which particles interact by a pair potential v(r), the triplet correlation function is defined as [1]

$$\begin{aligned} g^{(3)}({\mathbf{r}}_{1},{\mathbf{r}}_{2},{\mathbf{r}}_{3})=V^{3}\frac{\int \exp (-\beta V_{N}(r^{N})){\mathrm{d}}{\mathbf{r}}_{4}\ldots {\mathrm{d}}{\mathbf{r}}_{N}}{Z_{N}} \end{aligned}$$

(23)

where ${\mathbf{r}}_{i}$ is the position vector of the ith particle. The function $g^{(3)}({\mathbf{r}}_{1},{\mathbf{r}}_{2},{\mathbf{r}}_{3})$ defines the probability of simultaneous detection of three particles in the vicinity of points ${\mathbf{r}}_{1}$, ${\mathbf{r}}_{2},$ ${\mathbf{r}}_{3}$. Unlike the binary function g(r), the $g^{(3)}({\mathbf{r}}_{1},{\mathbf{r}}_{2},{\mathbf{r}}_{3})$ depends on three space coordinates and, accordingly, enables one to obtain an additional information about the structure of particles. the Kirkwood superposition approximation (KSA) [11] is most frequently employed to approximate the three-particle correlation function

$$\begin{aligned} g^{(3)}({\mathbf{r}}_{1},{\mathbf{r}}_{2},{\mathbf{r}}_{3})\simeq g_{\mathrm{{SA}}}^{(3)}({\mathbf{r}}_{1},{\mathbf{r}}_{2},{\mathbf{r}}_{3})=g({\mathbf{r}}_{1}, {\mathbf{r}}_{2})g({\mathbf{r}}_{2},{\mathbf{r}}_{3}) g({\mathbf{r}}_{1},{\mathbf{r}}_{3}) \end{aligned}$$

(24)

We calculate the function $g({\mathbf{r}}_{1},{\mathbf{r}}_{2},{\mathbf{r}}_{3})$ in the same way for computing g(r) (see Eq. (21)), and we have acquired the result

$$\begin{aligned} g^{(3)}({\mathbf{r}}_{1},{\mathbf{r}}_{2},{\mathbf{r}}_{3})=\mathrm{e}^{-\beta (v(r_{12})+v(r_{23})+v(r_{13}))}(1+\rho (b_{1}(r_{12})+b_{2}(r_{23})+b_{3}(r_{13})) \end{aligned}$$

(25)

where

$$\begin{aligned} b_{1}(r_{12})=\int f_{14}f_{24}{\mathrm{d}}{\mathbf{r}}_{4}=\frac{1}{\left( 2\pi \right)^{3}r_{12}}\int k\left| f(k)\right|^{2}\sin (kr_{12}){\mathrm{d}}{} \mathbf k \end{aligned}$$

(26)

$$\begin{aligned} b_{2}(r_{23})=\int f_{24}f_{34}{\mathrm{d}}{\mathbf{r}}_{4}=\frac{1}{(2\pi )^{3}r_{23}}\int k\vert f(k)\vert^{2}\sin (kr_{23}){\mathrm{d}}{} \mathbf k \end{aligned}$$

(27)

$$\begin{aligned} b_{3}(r_{13})=\int f_{14}f_{34}{\mathrm{d}}{\mathbf{r}}_{4}=\frac{1}{(2\pi )^{3}r_{13}}\int k\vert f(k)\vert^{2}\sin (kr_{13}){\mathrm{d}}{} \mathbf k \end{aligned}$$

(28)

and

$$\begin{aligned} f(k)=\frac{1}{k}\int rf(r)\sin (kr){\mathrm{d}}{\mathbf{r}} \end{aligned}$$

(29)

Fig. 2

Comparison between triplet correlation function $g^{(3)}(r,r,r)^{1/3}$ and the triplet correlation function in the Kirkwood superposition approximation for: Debye potential ($\varGamma =0.1)$ at the left, Deutsch potential for different $r_{i}/\lambda_{\mathrm{T}}$ at the right

Numerical calculations of the function b [formula (17)], b1, b2 and b3 [formula (26)–(28)], for both kinds of potentials, allow us to compute the static structure functions as shown in Figs. 1 and 2. Now, we are able to apply the above results to compute the dynamic properties and the transport coefficients.

Application to dynamic and transport properties

By following the theory presented in [13], we have obtained the velocity and the micro-field auto-correlation functions D(t) and C(t) as the sum of three exponentials

$$\begin{aligned} D(t)=\sum D_{i}\mathrm{e}^{Z_{i}t},\quad C(t)=\sum C_{i}\mathrm{e}^{Z_{i}t} \end{aligned}$$

(30)

where the coefficients $D_{i}$ and $C_{i}$ are given by

$$\begin{aligned} D_{i}=-(\omega_{0}/Z_{i})C_{i} \end{aligned}$$

(31)

and

$$\begin{aligned} C_{1}=\left( \varLambda +Z_{1}\right) Z_{1}\left( Z_{3}-Z_{2}\right) /\Delta \end{aligned}$$

(32)

$$\begin{aligned} C_{2}=\left( \varLambda +Z_{2}\right) Z_{2}\left( Z_{1}-Z_{3}\right) /\Delta \end{aligned}$$

(33)

$$\begin{aligned} C_{3}=\left( \varLambda +Z_{3}\right) Z_{3}\left( Z_{2}-Z_{1}\right) /\Delta \end{aligned}$$

(34)

$$\begin{aligned} \Delta =\left( Z_{1}-Z_{2}\right) \left( Z_{2}-Z_{3}\right) \left( Z_{3}-Z_{2}\right) \end{aligned}$$

(35)

and the $\left\{ Z_{i}\right\}$ are solutions to the cubic equations (relative to Debye and Deutsch potentials respectively)

$$\begin{aligned} Z^{3}+\varLambda_{\mathrm{{Debye}}} Z^{2}+\omega_{1}^{2}Z+\varLambda_{\mathrm{{Debye}}} \omega_{0}^{2}=0 \\ Z^{3}+\varLambda_{\mathrm{{Deutsch}}} Z^{2}+\varOmega_{1}^{2}Z+\varLambda_{\mathrm{{Deutsch}}} \varOmega_{0}^{2}=0 \end{aligned}$$

(36)

The analysis made up to this point applies for arbitrary interaction potentials and plasma composition. To illustrate the physical content of our investigation, we consider the special case of a OCP one-component plasma with an impurity ion of the same mass and the same charge (m, q) for one component of the plasma ions. Before starting the evaluation of the three necessary parameters to solve the above cubic equation, remember the well-known useful Green–Kubo relation that gives the self-diffusion coefficient D from the velocity auto-correlation function D(t)

$$\begin{aligned} D=\frac{1}{m\beta }\int_{0}^{\infty } D(t){\mathrm{d}}t \end{aligned}$$

(37)

Determination of parameters

To calculate the auto-correlation functions D(t) and C(t) we need to know the three $Z_{i}$ roots which are connected to parameters $\omega_{0}$, $\omega_{1}$, $\varLambda$ which in turn must be calculated.

We attack now to determine all the parameters necessary in the description of the dynamics. These parameters allow us, first, to solve the cubic algebraic equation (36).

Evaluation of $\omega_{0}, \varOmega_{0}$

Consider first $\omega_{0}$ defined in [14]

$$\begin{aligned} \omega_{0}^{2}=(\beta q^{2}/3m)\langle E^{2}\rangle =-( \beta q/3m)\langle \mathbf{E }\cdot \nabla v(r)\rangle \end{aligned}$$

(38)

where v(r) is the potential of the interaction between the impurity ion and the surrounding plasma. This expression (38) can be rewritten, after making a part integral

$$\begin{aligned} \omega_{0}^{2}=-(q/3m)\langle \nabla \cdot \mathbf{E }\rangle \end{aligned}$$

(39)

It is noted here that the background does not contribute to $\omega_{0}^{2}$

$$\begin{aligned} \nabla_{0}\cdot \mathbf{E }_{b}=0 \end{aligned}$$

(40)

Then (38) leads to the two results

$$\begin{aligned} \omega_{0}^{2}=-\frac{1}{3}(nq/m) \int {\mathrm{d}}{\mathbf{r}}\nabla . \mathbf{e }({\mathbf{r}})g(r) \end{aligned}$$

(41)

where g(r) is the pair correlation functions for the probability to find a plasma ion of species a at a distance r from the impurity ion of mass m and charge q, n is the density of the plasma, and

$$\begin{aligned} \nabla \cdot e({\mathbf{r}})=-\Delta v(r)=-\left( \frac{\partial^{2}}{\partial r^{2}}+\frac{2}{r}\frac{\partial }{\partial r}\right) v(r) \end{aligned}$$

(42)

Here v(r) must be either the screened Debye potential or the screened Deutsch potential.

Debye potential case

$$\begin{aligned} \omega_{0}^{2}=\frac{1}{3}\omega_{p}^{2}\int \limits_{0}^{\infty }{\mathrm{d}}rrk_{\mathrm{D}}^{2}\mathrm{e}^{-k_{\mathrm{D}}r}g(r),\quad \omega_{p}^{2}=4\pi \rho q^{2}/m \end{aligned}$$

(43)

Deutsch potential case

$$\begin{aligned} \varOmega_{0}^{2}=\frac{1}{3}\left( \frac{mq}{m_{0}q}\right) \omega_{p}^{2}\int \limits_{0}^{\infty }{\mathrm{d}}rr(k_{\mathrm{D}}^{2}\mathrm{e}^{-k_{\mathrm{D}}r}-(k_{\mathrm{D}}+k_{\mathrm{T}})^{2}\mathrm{e}^{-(k_{\mathrm{D}}+k_{\mathrm{T}})r})g(r) \end{aligned}$$

(44)

Evaluation of $\omega_{1}, \varOmega_{1}$

$$\begin{aligned} \omega_{1}^{2}= & {} (q^{2}/3m\omega_{0}^{2})(nm/\mu )\int {\mathrm{d}} {\mathbf{r}}[\partial e_{\alpha }({\mathbf{r}})/\partial r_{j}]^{2}g(r) \end{aligned}$$

(45)

$$\begin{aligned}&+\,(9\omega_{0}^{2})^{-1}\left\{ (nq/m)\int {\mathrm{d}}{\mathbf{r}} \nabla \cdot \mathbf{e }_{\alpha }({\mathbf{r}})g_{\alpha }(r)\right\}^{2} \end{aligned}$$

(46)

$$\begin{aligned}&+\,(q^{2}/3m\omega_{0}^{2})\sum \limits_{\sigma }( n^{2})\int {\mathrm{d}}{\mathbf{r}} {\mathrm{d}}{\mathbf{r}}^{{\prime }}[ \partial e({\mathbf{r}})/\partial r_{j}^{{\prime }}] [ \partial e({\mathbf{r}})/\partial r]\end{aligned}$$

(47)

$$\begin{aligned}&\times \, \{g^{(3)}({\mathbf{r}},{\mathbf{r}}^{{\prime }}) -g(r)g(r^{{\prime }})\} \end{aligned}$$

(48)

where $\mu =m/2$ is the reduced mass. The second term of the last formula can be simplified to give the form

$$\begin{aligned} \omega_{1}^{2}&= \omega_{0}^{2}+(q^{2}/3m\omega_{0}^{2}) (nm/\mu )\int {\mathrm{d}}{\mathbf{r}}[\partial e({\mathbf{r}})/\partial r_{j}]^{2}g(r) \end{aligned}$$

(49)

$$\begin{aligned}&+\,(q^{2}/3m\omega_{0}^{2})(n^{2}) \int {\mathrm{d}}{\mathbf{r}} {\mathrm{d}}{\mathbf{r}}^{{\prime }}[\partial e({\mathbf{r}})/\partial r_{j}^{{\prime }}][\partial e({\mathbf{r}})/\partial r] \end{aligned}$$

(50)

$$\begin{aligned}&\times \, \{g^{(3)}({\mathbf{r}},{\mathbf{r}}^{{\prime }}) -g(r)g(r^{{\prime }})\} \end{aligned}$$

(51)

To be able to make the last integrals, we need two and three correlation functions (static structure functions) $g^{2}, g^{3}$ that are given in “Static pair correlation functions” and “Three correlation functions”.

Debye potential case

$$\begin{aligned} \omega_{1}^{2}=\omega_{0}^{2}(1+(m/\mu I_{0}^{2}) I_{1}+(3/I_{0}^{2})I_{2}) \end{aligned}$$

(52)

where

$$\begin{aligned} I_{0}=\int \limits_{0}^{\infty }{\mathrm{d}}rrk_{\mathrm{D}}^{2}e^{-k_{\mathrm{D}}r}g(r) \end{aligned}$$

(53)

and

$$\begin{aligned} I_{1}=\int \limits_{0}^{\infty }{\mathrm{d}}rr^{-4}\mathrm{e}^{-2k_{\mathrm{D}}r}[6+12k_{\mathrm{D}}r+10(k_{\mathrm{D}}r)^{2}+4(k_{\mathrm{D}}r)^{3}+(k_{\mathrm{D}}r)^{4}] g(r) \end{aligned}$$

(54)

$$\begin{aligned} I_{2}=\int \limits_{0}^{\infty }{\mathrm{d}}r{\mathrm{d}}r^{{\prime }}rr^{{\prime }}k_{\mathrm{D}}^{4}\mathrm{e}^{-k_{\mathrm{D}}r}\mathrm{e}^{-k_{\mathrm{D}}r^{{\prime }}}\{g^{(3)}({\mathbf{r}},{\mathbf{r}}^{{\prime }}) -g(r)g(r^{{\prime }})\} \end{aligned}$$

(55)

Deutsch potential case

$$\begin{aligned} \varOmega_{1}^{2}=\varOmega_{0}^{2}(1+(m/\mu I_{0}^{{\prime }2}) I_{1}^{{\prime }}+(3/I_{0}^{{\prime }2})I_{2}^{{\prime }}) \end{aligned}$$

(56)

where

$$\begin{aligned} I_{0}^{{\prime }}=\int \limits_{0}^{\infty }{\mathrm{d}}rr(k_{\mathrm{D}}^{2}\mathrm{e}^{-k_{\mathrm{D}}r}-(k_{\mathrm{D}}+k_{\mathrm{T}})^{2}\mathrm{e}^{-(k_{\mathrm{D}}+k_{\mathrm{T}})r})g(r) \end{aligned}$$

(57)

$$\begin{aligned} I_{1}^{{\prime }}=\int \limits_{0}^{\infty }{\mathrm{d}}rr^{-4}\mathrm{e}^{-2k_{\mathrm{D}}r}[A-2\mathrm{e}^{-k_{\mathrm{T}}r}B+\mathrm{e}^{-2k_{\mathrm{T}}r}C]g(r) \end{aligned}$$

(58)

and

$$\begin{aligned} I_{2}^{{\prime }}= & {} \int \limits_{0}^{\infty }{\mathrm{d}}r{\mathrm{d}}r^{{\prime }}rr^{{\prime }} (k_{\mathrm{D}}^{2}\mathrm{e}^{-k_{\mathrm{D}}r}-k_{\mathrm{{DT}}}^{2} \mathrm{e}^{-k_{\mathrm{{DT}}}r})(k_{\mathrm{D}}^{2}\mathrm{e}^{-k_{\mathrm{D}} r^{{\prime }}}-k_{\mathrm{{DT}}}^{2}\mathrm{e}^{-k_{\mathrm{{DT}}}r^{{\prime }}}) \\ &\times \{g^{(3)}({\mathbf{r}},{\mathbf{r}}^{{\prime }})-g(r) g(r^{{\prime }})\} \end{aligned}$$

(59)

where

$$\begin{aligned} A&= (k_{\mathrm{D}}r)^{4}+4(k_{\mathrm{D}}r)^{3}+10(k_{\mathrm{D}}r)^{2}+12k_{\mathrm{D}}r+6 \end{aligned}$$

(60)

$$\begin{aligned} B&= (k_{\mathrm{D}}k_{\mathrm{{DT}}})^{2}r^{4}+2(k_{\mathrm{D}} k_{\mathrm{{DT}}}^{2}+k_{\mathrm{D}}^{2}k_{\mathrm{{DT}}})r^{3} +2(3k_{\mathrm{D}}k_{\mathrm{{DT}}}+k_{\mathrm{D}}^{2}+k_{\mathrm{{DT}}}^{2})r^{2} \\ &+\,6(k_{\mathrm{D}}+k_{\mathrm{{DT}}})r+6 \end{aligned}$$

(61)

$$\begin{aligned} C&= (k_{\mathrm{{DT}}}r)^{4}+4(k_{\mathrm{{DT}}}r)^{3}+10(k_{\mathrm{{DT}}}r)^{2} +12k_{\mathrm{{DT}}}r+6 \end{aligned}$$

(62)

$$\begin{aligned} k_{\mathrm{{DT}}}&= k_{\mathrm{D}}+k_{\mathrm{T}} \end{aligned}$$

(63)

It is understood that the integration variables and screening length $k_{\mathrm{D}}^{-1},k_{\mathrm{T}}^{-1}$ are in units of the ion sphere radius, $r_{i}=(3/4\pi \rho )^{1/3}$.

Evaluation of $\varLambda_{\mathrm{{Debye}}}, \varLambda_{\mathrm{{Deutsch}}}$

We use the following expression [13]

$$\begin{aligned} \varLambda_{\mathrm{{Debye}}} =(( m/\mu ) I_{1}+3I_{2})/(I_{0}^{2}m\beta D) \end{aligned}$$

(64)

and the same formula for Deutsch case using $I'_{0,1,2}$ defined above (56)–(59). At this stage, we need the self coefficient diffusion D. To proceed, we calculate D with self-consistent method: we give at first an initial value to D, and compute $\varLambda$ with respect the last formula. Then we have the three coefficients of the cubic equation ($\omega_{0}$, $\omega_{1}$ and $\varLambda$). We are able to solve this equation and then to have the velocity auto-correlation function D(t). Using the Eq. (37), we get the self-diffusion coefficient D. Using the obtained value of D in the equation to have a new value of $\varLambda$, and by solving the cubic equation, we get the velocity auto-correlation function D(t). Integrated, the latter gives a new self-diffusion coefficient D. This procedure must be repeated till we get the convergence.

Table 1 $\varGamma$ Dependence of the diffusion coefficients $D^{*}$ is given in units of $\omega_{p}r_{i}^{2}$

Table 2 $\varGamma$ dependence of $\omega_{0}$, $\omega_{1}$ , are given in units of ion plasma frequency $\omega_{p}$

Fig. 3

Time dependence of the electric field correlation function for different coupling parameters $\varGamma =0.1, 0.5, 1.$ and for different $r_{i}/\lambda_{\mathrm{T}}$ and different potentials. The time t is given in units of $\omega_{p}^{-1}$

Fig. 4

Time dependence of the velocity auto-correlation function for coupling parameters $\varGamma =0.1, 0.5, 1.$ and for different $r_{i}/\lambda_{\mathrm{T}}$ and different potentials. The time t is given in units of $\omega_{p}^{-1}$

Results and discussions

We have presented a model for the pair correlation function and the triplet correlation function given by the Eqs. (22) and (25) for different coupling parameters $\varGamma$, using the screened Debye potential and the screened Deutsch potential

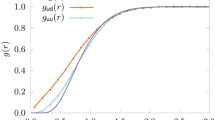
In Fig. 1 we have presented and compared the pair correlation function g(r) calculated by our model for different coupling parameters $\varGamma$ and different ratios $r_{i}/\lambda_{\mathrm{T}}$ for the two potentials. We note, in the case of the Debye potential, that the curve starts from zero: when the distance r (between two ions) goes to zero; g(r) goes to zero too. Whereas when the distance goes to infinity, the pair correlation function g(r) goes to one. For the screened Deutsch potential, we note that the curve not start from zero (contrary to Debye case). This means that the correlation between the ions is more significant in the weak range of the ratio $r_{i}/\lambda_{\mathrm{T}}$. This indicates that, in this range, the probability of interaction between two ions is more important. Readibly, this phenomenon is due to the quantum effects.

Figure 2 shows the triplet correlation function in the equilateral triangle geometry for the coupling parameter $\varGamma =0.1$ for the two potentials. To allow a comparison, we have taken the cubic root $\root 3 \of {g^{(3)}(r,r,r)}$ and the cubic root of the triplet correlation function in the Kirkwood superposition approximation $\root 3 \of {g_{\mathrm{{SA}}}^{(3)}(r,r,r)}=g^{(2)}(r)$ [11]. We have obtained a very good agreement as it is shown in Fig. 2.

To calculate the time auto-correlation functions D(t) and C(t) we need to know the frequencies $Z_{i}$ (roots of the algebraic cubic equations (36)) and the coefficients $C_{i}$ (or $D_{i}$, respectively). They are expressed by three parameters—the diffusion constant D, and the frequencies $\omega_{0}$, $\omega_{1}$ for the screened Debye potential and $\varOmega_{0}$, $\varOmega_{1}$ for the screened Deutsch potential. The frequencies $\omega_{0}$, $\varOmega_{0}$ are functions of the pair correlation function $g^{2}$, whereas the frequencies $\omega_{1}$, $\varOmega_{1}$ are functions of the triplet correlation function $g^{3}$. To calculate the frequencies $\omega_{1}$ and $\varOmega_{1}$ we need the knowledge of the triplet correlation functions.Table 1 shows the values of the diffusion coefficients ($D_{\mathrm{{Debye}}}^{*}$ and $D_{\mathrm{{Deutsch}}}^{*}$) (given in units of $\omega_{p}r_{i}^{2}$), for different values of the coupling parameter $\varGamma$ and different values of the ratio $r_{i}/\lambda_{\mathrm{T}}$. We have compared $D_{\mathrm{{Debye}}}^{*}$ and $D_{\mathrm{{Deutsch}}}^{*}$ with the diffusion coefficient computed by the simulation technique earlier by (M. A. Berkovsky) [14]. We note a good agreement between Debye case and M. A. Berkovsky simulation. So, there is a difference with the Deutsch potential case. We also note that the coefficient $D_{\mathrm{{Deutsch}}}^{*}$ increases when $r_{i}/\lambda_{\mathrm{T}}$ decreases in each coupling category because it is related to the temperature contrary to the case of Debye potential.

Table 2 shows the $\varGamma$ dependence of $\omega_{0}$, $\varOmega_{0}$, $\omega_{1}$ and $\varOmega_{1}$ (in units of the OCP plasma frequency $\omega_{p}$) and $\varLambda$. We show that the results for the case of the Debye potential are different from those obtained in the case of the screened Deutsch potential. The comparison was made for different values of the coupling parameter $\varGamma$ and for different values of the ratio $r_{i}/\lambda_{\mathrm{T}}$.

Figure 3 shows the time auto-correlation function of the electric micro-field C(t) for different coupling parameter $\varGamma$ and different values of the ration $r_{i}/\lambda_{\mathrm{T}}$. We notice that the time auto-correlation function of the electric micro-field C(t) increases when the ratio $r_{i}/\lambda_{\mathrm{T}}$ decreases. Furthermore, we note that C(t) decreases up to zero in small time. This indicates that the ratio $r_{i}/\lambda_{\mathrm{T}}$ is small when the correlation between the ions is very strong. Figure 4 shows the velocity auto-correlation function D(t) for different coupling parameters $\varGamma$ and different ratios $r_{i}/\lambda_{\mathrm{T}}$. As it is clear, D(t) increases when the ratio $r_{i}/\lambda_{\mathrm{T}}$ decreases. Here we note that the time auto-correlation function of the velocity D(t) decreases up to zero in a long time. This indicates that the ratio $r_{i}/\lambda_{\mathrm{T}}$ is small when the correlation between the ions is very strong. Therefore, the diffusion coefficient increases when the time auto-correlation function of the velocity D(t) is larger, because the diffusion coefficient D is equal to the integral of D(t) [see Green–Kubo formula (37)].

Conclusion and perspectives

In this work, we have presented a model for the pair and the triplet correlation function theoretically of a one-component plasma at for weak and intermediate coupling $\varGamma \le 1$ and for $r_{i}/\lambda_{\mathrm{T}}\le 1$. This is done using the screened Debye potential and the screened Deutsch potential. We have found that the pair correlation function $g^{2}(r)$, for both potentials, are rather close, but start to deviate from each other when the coupling parameter $\varGamma$ increases with a decreasing $r_{i}/\lambda_{\mathrm{T}}$. Nevertheless, the use of the Deutsch potential is preferable because it considers in more realistic physics the short distance collisions, i.e. the collisions occurring at distances smaller than the De Broglie wavelength. In other hand, we have computed the dynamical properties: the time auto-correlation function of the velocity D(t) and the time auto-correlation function of the electric micro-field C(t). We have noticed, when the ratio $r_{i}/\lambda_{\mathrm{T}}$ is small the correlation between the ions is very strong. Therefore, the velocity auto-correlation function D(t) and the electric field auto-correlation function C(t) are large for a weak value of $r_{i}/\lambda_{\mathrm{T}}$. As a consequence, the self-diffusion coefficient D is more important for the strongly coupled plasmas.