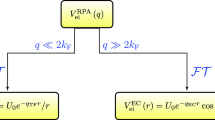
Abstract
As is well known, for plasmas of high density and modest temperature, the classical kinetic theory needs to be extended. Such extensions can be based on the Schrödinger Hamiltonian, applying a Wigner transform of the density matrix, in which case the Vlasov equation is replaced by the celebrated Wigner–Moyal equation. Extending the treatment to more complicated models, we investigate aspects such as spin dynamics (based on the Pauli Hamiltonian), exchange effects (using the Hartree–Fock approximation), Landau quantization, and quantum relativistic theory. In the relativistic theory, we first study cases where the field strength is well-beyond Schwinger critical field. Both weakly relativistic theory (gamma factors close to unity) and strongly relativistic theory are investigated, using assumptions that allow for a separation of electron and positron states. Finally, we study the so-called Dirac–Heisenberg–Wigner (DHW) formalism, which is a fully quantum relativistic theory, allowing for field strengths of the order of the Schwinger critical field or even larger. As a result, the quantum kinetic theory is extended to cover phenomena such as Zitterbewegung and electron–positron pair creation. While the focus of this review is on the quantum kinetic models, we illustrate the theories with various applications throughout the manuscript.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Historically, the vast majority of plasma physics has been limited to classical (nonquantum) phenomena. With important applications, such as magnetically confined fusion plasmas and space plasmas, where the density is modest and the temperature is high, the focus of plasma physics on classical models has been natural. However, in recent times, much work (see, e.g., Refs. Manfredi et al. 2019; Shukla and Eliasson 2011; Melrose 2020; Shukla and Eliasson 2010; Vladimirov and Tyshetskiy 2011, and references therein) has been devoted to the regime of high density and a low or modest temperature, allowing for quantum mechanical phenomena to influence the dynamics. We will come back to which concrete systems that can be of interest in such a context.
Out of the possible quantum effects, maybe the most basic one is particle dispersion (see, e.g., Haas 2011; Crouseilles and Manfredi 2014; Haas and Shukla 2008; Haas et al. 2008). This spread out in the wave function is captured already in the Schrödinger equation, but arguably this is one of the most important quantum mechanical mechanisms. Another basic, and important, phenomenon is the degeneracy effect (Manfredi et al. 2019; Shukla and Eliasson 2011; Melrose 2020; Shukla and Eliasson 2010; Vladimirov and Tyshetskiy 2011; Tyshetskiy et al. 2014, 2013), entering when the density becomes high enough to make the Fermi temperature significant in relation to the thermodynamic temperature. A related phenomenon, also dependent on the antisymmetry of the many-body wave-function of electrons, but considerably more complicated to model mathematically, is the exchange interaction (Crouseilles et al. 2008; Haas 2021; Andreev 2014; Zamanian et al. 2013, 2015; Ekman et al. 2015; Brodin et al. 2019), whose importance probably has been undervalued in the recent plasma research literature. Upgrading from the Schrödinger Hamiltonian to the Pauli Hamiltonian, the spin dynamics enter the picture (Hurst et al. 2014; Brodin et al. 2008; Zamanian et al. 2010; Andreev 2016, 2018; Andreev and Kuzmenkov 2017; Andreev 2017), with physics such as the magnetic dipole force, spin precession, and (spin) magnetization currents. Extending the models to cover the weakly relativistic regime (Asenjo et al. 2012; Hurst et al. 2017; Ekman et al. 2021), spin–orbit interaction, Thomas precession, and a spin-dependent polarization current are new features of the theory. Finally, in the regime of strong fields (Ekman et al. 2017, 2019) and fully relativistic theory (Bialynicki-Birula et al. 1991), phenomena such as strong Landau quantization (Al-Naseri et al. 2020), and electron–positron pair creation (Bialynicki-Birula et al. 1991; Al-Naseri et al. 2021; Hebenstreit et al. 2011; Sheng et al. 2019; Aleksandrov and Kohlfurst 2020; Mendonça 2021) come into play.
Before proceeding to the more theoretical aspects, we should get an idea what concrete systems that are of interest. One such answer is explored in some detail in the recent review by Manfredi et al. (2019), where metallic nano-objects are in focus. As described in that work, the properties of metallic particles ranging in size from a few to several hundred nanometer can be well modeled with quantum kinetic theory. Importantly, the nano-particles are of interest for applications in nano-photonics and other technological applications.
Furthermore, by identifying the quantum regime in a density temperature diagram, as done, e.g., by Bonitz (2016), Asenjo et al. (2012) a reasonably complete picture of quantum plasmas can be presented. Besides the solid-state regime, that might be of most technological interest (including applications to, e.g., spintronics (Wolf et al. 2001), plasmonics (Atwater 2007), nanotubes (Moradi 2008), quantum wells (Manfredi and Hervieux 2007), and quantum dots (Liu 2018)), quantum plasmas can be found in rather diverse contexts, including dense astrophysical objects (Chabrier et al. 2002; Uzdensky and Rightley 2014) (white dwarf stars, neutron stars), warm dense matter, laboratory plasmas (Glenzer and Redmer 2009), and plasmas in the early universe (Thomas et al. 2020). While a temperature density diagram of the background gives important information, we also note that quantum behavior can be induced directly by the electromagnetic fields. For example, strong laser fields may potentially induce quantum phenomena such as spin polarization, as explored in Del Sorbo et al. (2017), Sorbo et al. (2018), Li et al. (2019). Moreover, in an astrophysical context, strong magnetic fields from pulsars and/or magnetars (Harding and Lai 2006) may lead to very pronounced Landau quantization. Finally, as we will discuss in section VI, a sufficiently strong electrostatic field leads to Schwinger pair production of electrons and positrons (Bialynicki-Birula et al. 1991; Al-Naseri et al. 2021; Hebenstreit et al. 2011; Sheng et al. 2019; Aleksandrov and Kohlfurst 2020). Thus, when intense electromagnetic fields are involved, there are several ways quantum phenomena can enter the picture, even when the parameters of density and temperature correspond to the classical regime.
The paper is organized as follows: In Sect. 2, we study foundations of quantum kinetic theory, in particular the density matrix, the von Neumann equation, and the Wigner transform (Wigner 1932). To focus on the fundamentals, for much of the section, we avoid the complications of spin and electromagnetic fields, and base the treatment on the simplest form of the Schrödinger equation. The theory is illustrated with examples from linear theory. In Sect. 3, the treatment is extended to cover many-particle physics (in the quantum mechanical sense). In particular, the quantum mechanical version of the BBGKY-hierarchy is used to study exchange interaction, with a particular focus on electrostatic linearized theory. Exchange corrected dispersion relations are computed, for Langmuir waves and ion-acoustic waves, in the degenerate and nondegenerate regime. In Sect. 4, we allow for electromagnetic fields and spin dynamics. For that purpose, the Schrödinger Hamiltonian is replaced with the Pauli Hamiltonian. Two equivalent but different versions of quantum kinetic theory are presented. The linear theory of the model is solved in the long-scale limit for the case of a homogeneous magnetized plasma, generalizing previous results to include an an-isotropic background distribution. Next, in Sect. 5, a multitude of different problems are discussed that is not covered by the previous theories. This includes quantum kinetic conservation laws, relativistic Landau quantization, and aspects of nonlinear spin dynamics, focusing on the ponderomotive force. In Sect. 6, we study the fully quantum relativistic case, using the Dirac–Heisenberg–Wigner (DHW) formalism, originally derived by Bialynicki-Birula et al. (1991). The equations are used to study electrostatic fields, and some deviations from simpler theories are pointed out. Moreover, we show how to relate the DHW formalism to limiting cases studied in the previous sections. Finally, the paper ends with concluding remarks in Sect. 7.
2 The gauge-invariant Wigner theory
The aim of this section is to give a brief introduction to how the Wigner functions can be used to describe quantum effects in plasmas. To this, we start with a review of the density matrix and some of its properties. After that, we go on to define the Wigner transformation, which is a transformation that brings the evolution equation in a form similar to classical kinetic theory. We comment on the interpretation of the Wigner function and some of the key properties. Finally, we consider a system in an electromagnetic field and give a description of the gauge-invariant Wigner function and the corresponding evolution equation.
2.1 The density matrix
To describe an N-particle system, where the initial state is known, we can use a many-particle wave function \(\psi = \psi ({\mathbf {r}}_{1}, \ldots {\mathbf {r}}_N, t)\). Here, \({\mathbf {r}}_i\) is the position for the i:th particle and \(|\psi ({\mathbf {r}}_1, \ldots {\mathbf {r}}_N), t |^2 d^3r_1 \ldots d^3r_N\), is the probability of simultaneously measuring the particles at respective positions in the volume \(d^3r_i\) around \({\mathbf {r}}_i\). Assuming that the particles have mass m and are moving in a potential \(V = V({\mathbf {r}}_1, \ldots {\mathbf {r}}_{N})\), the evolution follows the Schrödinger equation:
supplemented by the initial state of the system
The exact state of a multi-particle system cannot be known in general; instead, the best we can hope for is the knowledge of a statistical distribution of states. To handle this situation, it is then necessary to use the so-called density matrix. It is defined as
where \(p_i\) is the probability of finding the system in state \(\psi _i\), and the sum is over all states that the system can be in. From normalization, we require that
which can be interpreted that the total probability of finding the system in one of the states \(\psi _i\) is unity. E.g., in the case where the system is in thermal equilibrium with temperature T, the density matrix is
where
is the partition function, and the sum is over all eigenstates \(\psi _{E_i}\) to the Hamiltonian, \({\hat{H}} \psi _{E_i} = E_i \psi _{E_i}\).
From the definition above together with the Schrödinger equation (and its complex conjugate), we can derive the evolution equation for the density matrix
This is called the von Neumann equation, or alternatively, the quantum Liouville equation (see, e.g., Ref. Bonitz 2016). The density matrix describes the system completely, and we can use it to calculate, e.g., the probability of finding the particles at respective positions \({\mathbf {r}}_1, \ldots {\mathbf {r}}_N\) as the diagonal elements
One thing to note about the density matrix is that it changes under a gauge transformation. E.g., in case of a single-particle interacting with an electromagnetic field described by the potentials \(\phi\), \({\mathbf {A}}\), a gauge transformation
the density matrix transforms as
where q is the charge of the particle, see, e.g., (Sakurai and Napolitano 2017). In the N-particle case, the density matrix obtains a phase-factor \(\exp \left( i q \Lambda ({\mathbf {r}}_i ,t ) /\hbar \right)\) for each \({\mathbf {r}}_i\), and a factor \(\exp \left( -iq \Lambda ({\mathbf {r}}'_i ,t) / \hbar \right)\) for each \({\mathbf {r}}_i'\).
The density matrix encodes all the information about the system. However, the evolution equation (7) involves a huge number of variables, six for each particle, so it is not directly applicable when considering plasmas. In Appendix A, we derive the mean-field approximation, which is a common approximation used when modeling plasmas. We here state the most important conclusions. In the mean-field approximation, density matrix only depends on two variables
where the diagonal elements yields the density of particles at a given position in space
with the normalization
where N is the total number of particles. The mean-field Hamiltonian formally looks like it is describing a one-particle system, but is modified in that the fields are the self-consistent fields created by all the particles. For example, for an electrostatic plasma, we have
where \(\phi\) is the self-consistent field, which is relate to the particle density via Poisson’s equation
Here, we have added a neutralizing and homogeneous charge density \(- q n_0\). The mean-field approximation is usually applicable in cases where particle correlations can be neglected. E.g., in cases where particle–particle collisions can be neglected. By including further terms in the BBGKY-hierarchy, it is possible to include particle collisions, see e.g., Ref. (Bonitz 2016) In the discussion above, we have also neglected any reference to the particle statistics. Since we are dealing with fermions, one should really take into account the antisymmetry of the wave function. In Sect. 3, we generalize the mean-field approximation to account for this. The resulting approximation is usually called the Hartree–Fock approximation.
2.2 The Wigner transformation
A key tool when deriving quantum kinetic equations from the Schrödinger or Pauli Hamiltonian is the Wigner transform, introduced by Eugene Wigner in his famous paper from 1932 (Wigner 1932). Using this transform on the density matrix, a kinetic evolution generalizing the classical Vlasov equation can be derived. This connection with classical theory is helpful for guiding the physical intuition, and the transformed quantities are typically more attractive for practical calculations. Wigner’s original approach has been further developed by others, in particular Moyal (1949), and the Wigner equation is sometimes also referred to as the Wigner–Moyal equation.
The Wigner transform of the density matrix is defined by
We can see that e.g.
gives the local density of particles, and similarly
is the momentum distribution of the particles. However, in contrast to the Vlasov distribution, the Wigner distribution can be negative in certain regions. This is attributed to the Heisenberg uncertainty principle, and we should hence be careful in interpreting the Wigner function \(W({\mathbf {r}}, {\mathbf {p}}, t)\) as a classical phase-space distribution. Irrespective of that, the Wigner function can still be used to calculate macroscopic properties of the system, such as, e.g., the charge and current densities.
If the system is described by the Hamiltonian, (15), we can derive the evolution equation for W using the Schrödinger equation as follows: The evolution equation for the density matrix is given by
Using the variable change
the equation is cast into
We now want to take the Fourier transformation of this and re-identify the Wigner function in each term. To do this, we can use the following trick:
where \(f({\mathbf {r}}, i \hbar \nabla _{\mathbf {p}})\) is defined by its Taylor expansion. Here, the arrow over \(\overleftarrow{\nabla }_{\mathbf {p}}\) indicates that the operator should act to the left on the exponential function only. For the term containing \(\nabla _{\mathbf {z}}\), we make a partial integration. Doing this, we finally get the equation
In the mean-field approximation, the equation above describes a system of particles interacting via the electric potential created by all the particles via
where we have assumed that there is a homogeneous, neutralizing background of particles with charge density \(-qn_0\) (note that \(q = -e < 0\) for electrons with our conventions). These two equations together with the appropriate initial conditions yield the dynamics of the system.
The Wigner distribution W function can be used to calculate any expectation value in a similar way to how this is done in classical kinetic theory. For example, we have
For a general operator \({\hat{O}} = O(\hat{{\mathbf {r}}}, \hat{{\mathbf {p}}})\), depending on both the position and momentum variables, we must first put all the position and momentum operators in completely symmetric form using the commutation relations, and then replace all operators with the corresponding phase-space variables. For example, to calculate the expectation value of the operator \({\hat{O}} = {\hat{x}} {\hat{p}}_x\), we first write
Therefore, the phase-space function corresponding to \({\hat{O}} = {\hat{x}}{\hat{p}}_x\) is \(O(x, p_x) = x p_x + i \hbar\). Note that this particular operator is not a physical observable, since it is not Hermitian; we only chose it to illustrate the procedure. It also works in the other direction. Therefore, to find out which quantum mechanical operator corresponds to the phase-space function \(O(x,p_x) = x p_x\), we first write the function in symmetric form and then replace the variables with their corresponding operators
This correspondence between operators and phase-space functions is called Weyl ordering, see e.g. (Zachos et al. 2005).
As an example of the usefulness of Eq. (24), consider linear waves where the distribution function can be written
where \(W_0 ({\mathbf {p}})\) is a spatially homogeneous equilibrium, e.g., a Maxwell–Boltzmann distribution. Similarly, we write the potential as
Linearising the evolution equations above and solving for \(\phi _1\), we get the dispersion relation
where the last equation is obtained by a change of variables. In the limit \(\hbar \rightarrow 0\), this reduces to the classical Vlasov dispersion relation. This dispersion relation has been investigated in detail in Ref. (Eliasson and Shukla 2009). There, it is shown that for a fully degenerate background distribution (\(T = 0\)), the wave particle damping disappears in the Vlasov limit, since the phase-velocity \(\omega / k\) always exceeds the Fermi velocity. Furthermore, the critical wave number \(k_c\), at which the Landau damping sets in, was computed.
Returning to the general case, Eq. (24), it is straightforward to show that this equation reduces to the classical Vlasov equation for long macroscopic scale lengths. In particular, if the potential varies on a scale length L, i.e., \(\nabla \phi \sim \phi / L\), and the characteristic velocity of the system is v, \(\nabla _p W \sim W / m v\), then in the limit
we may keep the first nonvanishing terms in a Taylor expansion of the potential in Eq. (24). We then get
i.e., the Vlasov equation, where \({\mathbf {E}} = - \nabla _{\mathbf {r}} \phi\). By keeping further terms in the expansion, we may use this method to derive quantum corrections to an arbitrary order, see, e.g., Ref. (Manfredi 2005).
2.3 The gauge-invariant Wigner function
The Hamiltonian describing a charged particle of mass m and charge q (\(q = -e\) for electrons) interacting with a magnetic field is given by
where \(\phi\) and \({\mathbf {A}}\) are the (mean-field) electromagnetic potentials. Note that, here, \(\hat{{\mathbf {p}}} = - i \hbar \nabla _{\mathbf {r}}\) is the canonical momentum operator, and it is related to the velocity via the vector potential in the usual way. Here, we take \(\phi\) and \({\mathbf {A}}\) to be the mean-field potentials created by all the particles. The density matrix \(\rho ({\mathbf {r}}, {\mathbf {r}}', t)\) describing the state of the system is then the reduced density matrix; see Appendix A for a detailed discussion.
Under a gauge transformation, the density matrix changes according to Eq. (11). Due to this, the Wigner function W defined in Eq. (17) will not be gauge-invariant. Furthermore, the momentum variable, \({\mathbf {p}}\) will be related to the velocity in a gauge-dependent way. To get something that is more attractive to work with, we will use a modified version of the Wigner transformation, first constructed by Stratonovic (1970). The definition is
An important aspect of this transformation is that the momentum variable \({\mathbf {p}}\), is the kinetic momentum related to the velocity via \({\mathbf {p}} = m {\mathbf {v}}\). This can be seen by calculating the momentum density
where \(\left\{ \cdot , \cdot \right\}\) denotes the anticommutator. The right-hand side can be identified as the (kinetic) momentum density. The evolution equation for the reduced density matrix can be derived in a similar fashion to how Eq. (20) was obtained. We can then obtain the evolution equation for the gauge invariant Wigner function as in the previous subsection. The result is Serimaa et al. (1986)
where
We note that, since the equation is completely expressed in terms of the electric and magnetic field, it is manifestly gauge-invariant. Also, since the momentum variable involved is the kinetic momentum, we may make the trivial variable change \({\mathbf {p}} = m {\mathbf {v}}\) and express the Wigner function as \(W = W ({\mathbf {r}}, {\mathbf {v}}, t)\). In the classical limit, i.e., when Eq. (32) applies, this reduces to the Vlasov equation. By Taylor-expanding the functions \(\Delta {\mathbf {p}}, \tilde{{\mathbf {E}}}\), and \(\tilde{{\mathbf {B}}}\), it is possible to obtain approximations to arbitrary order in \(\hbar\).
The models we have explored in this section are of importance in their own right, and have been used, for example, to consider quantum dispersive effects, see, e.g., Refs. (Shukla and Eliasson 2011; Vladimirov and Tyshetskiy 2011) and references therein. However, in what follows, we will continue with more elaborate models including additional physical phenomena, such as exchange effects, spin, and relativistic effects.
3 Exchange effects
Exchange interaction in plasmas follows from electrons being fermions, with a totally antisymmetric wave-function. Since a full many-body wave-function is too difficult to study without approximations, the first step is usually to introduce Slater determinants to construct an antisymmetric many-body wave-function from the single-particle ones. This is done as follows:
where \(\psi _1\), \(\psi _2\),...\(\psi _n\) denote different single-particle wave-functions. However, this construction in itself will not be sufficient to cover exchange effects. Instead, one must go beyond the simplest mean-field description. Covering exchange effects is usually referred to as the Hartee–Fock approximation (MacDonald and Bryant 1987), in contrast to the Hartree approximation, where exchange effects are ignored.
The relative importance of exchange effects in plasmas is proportional to the parameter \(H^2=(\hbar \omega _p/E_k)^2\) (Crouseilles et al. 2008; Haas 2021; Zamanian et al. 2013, 2015; Ekman et al. 2015; Brodin et al. 2019), where the characteristic kinetic energy \(E_\mathrm{k}\) is given by \(E_\mathrm{k}=k_\mathrm{B} T_\mathrm{F}\) for a degenerate plasma (with \(T_\mathrm{F}>T\)) and by \(E_\mathrm{k}=k_\mathrm{B} T\) for the nondegenerate case (with \(T>T_\mathrm{F}\)). The above suggests that exchange effects are as important as the more basic particle dispersive effects, described by the Wigner–Moyal equation of the previous section. If so, the common approach of including particle dispersive effects through the Wigner equation, but simultaneously neglecting exchange effects would be highly questionable. Fortunately, while the relative importance scales with temperature and density as given by the H-parameter, the overall importance is also proportional to another dimensionless constant that often is much smaller than unity, see, e.g., Ref. (Brodin et al. 2019) for a more detailed discussion. Hence, the use of the Wigner equation from the preceding section, neglecting exchange effects, can still be a good approximation. What complicates the picture is that the importance of exchange effects is not just dependent on the background plasma parameters (temperature and density), but also of the specific problem under study. Below, we will illustrate this by considering simple examples of high-frequency Langmuir waves and low-frequency ion-acoustic waves.
3.1 General electrostatic theory
Since the theory becomes more complicated for the electromagnetic case, we here present a general quantum kinetic approach to exchange effects in the electrostatic limit. The full electromagnetic case will be discussed briefly in the end of Sect. 3.4.
Our treatment will follow Ref. (Zamanian et al. 2013), but leaving out some of the technical details. We here consider a completely ionized electron-ion plasma with the particles interacting through a mean-field scalar potential. Quantum effects for the ions will be completely neglected as will effects due to the self-energy and particle correlations (Bonitz 2016). The state of the N-electrons is described by the density operator \({\hat{\rho }}_{1\ldots N}\) (see, for example, Ref. (Bonitz 2016)), and the dynamics is given by the von Neumann equation with the Hamiltonian
The last term accounts for the interaction with the electric potential created by the ions. In Appendix A, we derive the mean-field approximation, in the case where we can neglect exchange effects. Here, we generalize that method to take into account the antisymmetry of the wave function for the electrons. We introduce the reduced density operators according to
where \(\mathrm {Tr}_{s+1\ldots N}\) denotes the trace over particles \(s+1\) to N (i.e., integrating over the position degree of freedom and summing over the spins), and \({\hat{\Lambda }}_{1\ldots s}\) is the antisymmetrization operator that takes an s-particle state and makes it completely antisymmetric (Boercker and Dufty 1979). We will only need to know that \(\hat{ \Lambda }_{12}=1-{\hat{P}}_{12}\) where \({\hat{P}}_{12}\) interchanges particle 1 and 2, i.e. \({\hat{P}}_{12}\psi ({\mathbf {r}}_{1},{\mathbf {r}}_{2})=\psi ({\mathbf {r}}_{2},{\mathbf {r}}_{1})\) (see, e.g., Ref. (Bonitz 2016) for further details). The evolution for the one-particle density operator is given by
where \({\hat{h}}_{1}=\hat{{\mathbf {p}}}^{2}/(2m_{e})\) and \({\hat{V}}_{12} = V(\hat{{\mathbf {r}}}_{1} - \hat{{\mathbf {r}}}_{2}) = e^{2}/(4\pi \epsilon _{0} |\hat{{\mathbf {r}}}_{1} - \hat{{\mathbf {r}}}_{2} |)\) and \({\hat{\rho }}_{12}\) is the two-particle density operator. The effects of two-particle correlations \({\hat{g}}_{12}\) can be separated out of the two-particle density operator by writing it in the form
see, e.g., Ref. (Wang and Cassing 1985). We are interested in the collisionless limit where a mean-field approximation will suffice. This approximation is obtained by neglecting the correlation \({\hat{g}}_{12}\) (Wang and Cassing 1985). Utilizing this in Eq. (41), we obtain
where \({\bar{V}}_{1}=\mathrm {Tr}_{2}{\hat{V}}_{12}{\hat{\rho }}_{2}{\hat{\Lambda }} _{12}\) is the Hartree–Fock potential operator. This is a closed system for the one-particle density operator.
To obtain a connection to the classical kinetic theory, we use the Wigner representation (Wigner 1932) of this equation. Using the complete set of states \(|{\mathbf {x}}, \alpha \rangle\), where \({\mathbf {x}}\) is the position and \(\alpha = 1,2\) is the spin along the axis of quantization, this representation is obtained as
where \(\rho ({\mathbf {r}}, \alpha {;} {\mathbf {r}}', \beta ) = \langle {\mathbf {r}}, \alpha |{{\hat{\rho }}}_1 |{\mathbf {r}}', \beta \rangle\) is the density matrix. This is a slight generalization of Eq. (17), where we trivially include the spin variables. Note, however, that the resulting Wigner function depends on the two spin variables and is hence a 2-by-2 matrix. Writing Eq. (43) first in the position representation and Wigner transforming the result (using, e.g., the method outlined in Sect. 2.2), we obtain
where
is the total (mean-field and the ionic field) potential and
is the Coulomb potential. The left-hand side of Eq. (45) represents the electrostatic limit of the Wigner–Moyal equation, but keeping the spin dependence (as encoded in \((\alpha , \beta )\)), while the right-hand side is the correction due to exchange effects. This term is nonlocal in phase space and nonlinear in the distribution function.
Two steps of our general treatment remain, taking the long-scale limit and averaging over the spin states \((\alpha , \beta )\). The first step is straightforward, just expanding the equations in \(\hbar \nabla _r \nabla _p\). The second step takes a little more work, but can be done with the help of the spin transform. The spin transform will be discussed in detail in the next section (Section IV), and the details regarding the procedure for our specific case can be found in Ref. (Zamanian et al. 2013). Thus, we will omit these details here, and proceed directly to the end result, the spin averaged evolution equation (assuming all spin directions equally probable) in the long-scale limit (\(\hbar \nabla _x\nabla _p \ll 1\)). The evolution equation then reads
where \(\partial _r^i \equiv \partial /\partial r_i\) and analogously for \(\partial _p^i\), and an arrow above an operator indicates in which direction it acts. We have also used the summation convention, so that a sum over indices occurring twice in a term is understood.
3.2 High-frequency Langmuir waves
Equation (48) is derived using a perturbative approach where exchange effects are considered to be small. Thus, there is little reason trying to solve Poisson’s equation together with (48) exactly. Instead, we first solve Eq. (48) dropping the right hand side altogether (i.e., we solve the Vlasov equation), and then substitute these solutions into the right-hand side, to evaluate the exchange correction to first order. Even this simplified treatment might be rather difficult, unless the zero-order Vlasov solution is fairly simple. To focus on a case that can be treated analytically to a large degree, we now consider the case of linear Langmuir waves in a homogeneous plasma. The general procedure is as follows:
-
1.
Pick a background distribution function (e.g., a Maxell-Boltzmann or a Fermi-Dirac distribution), linearize the left-hand side Vlasov equation, make a plane wave ansatz, and compute the perturbed distribution function.
-
2.
Linearize the right-hand side exchange term (keep terms where one factor is the linear perturbation, and the other is the background), substitute the distribution functions from the previous step and compute the integrals, and find the exchange correction to the perturbed distribution function.
-
3.
Make a final momentum integration to find the exchange contribution to the charge density, and use this in Poisson’s equation to find the exchange correction to the susceptibility.
Treating the ions as immobile, considering a Maxwell–Boltzmann background distribution for the electrons, and performing the steps outlined above, Ref. (Zamanian et al. 2015) was able to derive the following result:
Here, \(\chi _{\mathrm {cl}}\) is the classical electron susceptibility, given by \(\chi _{\mathrm {cl}}=(e^{2}/\varepsilon _{0}m)\int f_{0}d^{3}v/\left( \omega -kv_{z}\right) ^{2}\), and \(\chi _{\mathrm {exc}}\) is the exchange correction to the susceptibility, given by
where the velocity integrations (normalized against the thermal velocity) covers all of velocity space. In general, the last integrals to find \(\chi _{\mathrm {exc}}\) must be solved numerically. However, the case of most interest is when \(kv_{T}/\omega \ll 1\), such that the Landau damping is weak, in which case we can expand the integrals in powers of \(kv_{T}/\omega\). To leading order in \(kv_{T}/\omega\) , neglecting the pole contribution associated with Landau damping altogether, Eq. (49) reduces to
After correcting a slight numerical error in Eq. (49) of Ref. (Von Roos and Zmuidzinas 1961), we note that the result there is exactly a factor two larger than our result above. The difference is due to that Ref. (Von Roos and Zmuidzinas 1961) does not take into the spin part of the wave-function. We note that it is the full many-body wave-function that should be antisymmetric with respect to particle interchange, not just the spatial part. Ignoring this over-estimates the exchange correction by a factor of two. When noting the negative sign of the exchange term in Eq. (51), it is worth recalling the use of a perturbative treatment in the derivation, which means that the exchange contribution must be a correction. Thus, the second term of the right-hand side cannot change sign. If it did, the Langmuir waves would be unstable, which of course is not physical for a background state in thermodynamic equilibrium. In this context, it is also worth noting that the contribution from electron correlation tends to be of comparable magnitude for Langmuir waves (Crouseilles et al. 2008).
While the scaling with temperature and density is the same as for many other quantum phenomena (proportional to \(H^{2}=\hbar ^{2}\omega _{p}^{2}/m^{2}v_{T}^{4}\)) , we note that the overall factor also contains the small dimensionless number 1/90 which appears for geometrical reasons. Due to this small number, it makes sense to ignore exchange effects at the same time as other quantum effects are kept. However, as we will see below, there is no general principle guaranteeing the relative smallness of exchange effects. Thus, whether or not exchange effects can be ignored for other specific problems, as compared to particle dispersive effects, has to be determined on a case-by-case basis. Moreover, we note that the case of degenerate electrons requires different integrals to be solved. We omit this case here, but point out that the exchange contribution to the Langmuir wave dispersion relation with a fully degenerate Fermi-Dirac background distribution can be found in Ref (Ekman et al. 2015).
Before ending this subsection, we point out that although the scaling is not exactly the same, nevertheless, electron correlations often are significant at the same time as exchange effects. A way to cover both strong coupling effects (electron correlations) and exchange effects beyond the mean-field level is the path integral quantum Monte Carlo approach (Dornheim et al. 2018; Hamann et al. 2020; Zhang et al. 2016). In particular, results for the dynamic structure factor, closely related to the Langmuir susceptibility, have been presented in Refs (Dornheim et al. 2018; Hamann et al. 2020).
3.3 Low-frequency ion-acoustic waves
The general procedure numbered 1–3 of the previous subsection still applies for ion-acoustic waves. However, the concrete integrals that need to be solved depend on whether the electrons are degenerate or nondegenerate (assuming we limit ourselves to a thermodynamic background distribution). Also, the integration will be simplified in the quasi-neutral regime, that applies for frequencies \(\omega \ll \omega _{pi}\). An additional thing to consider is the Landau damping, that often can be neglected for Langmuir waves, but generally tends to be significant for ion-acoustic waves. Thus, we must use the Landau contours when evaluating the integrals, and keep track of both the real and imaginary parts. The case of cold classical ions and a Maxwell–Boltzmann distribution for electrons was considered by Ref. (Zamanian et al. 2013), and the dispersion relation in the quasi-neutral limit was found to be
where \(c_{s}=\left( m_{e}/m_{i}\right) ^{1/2}v_{Te}\) is the classical ion-acoustic velocity and we have introduced the classical electron Landau damping, \(\gamma _{\text {cl}} = k c_s \sqrt{\pi /8} \sqrt{m_e/m_i}\), in the cold ion limit (Boyd and Sanderson 2003). The coefficients of the real and imaginary quantum terms (0.8 and 3, respectively) are only approximate, as the final step involves a numerical integration. An important result from this calculation is that the exchange corrections now are proportional to a factor of the order unity times the quantum parameter \(H^2\), in contrast to the previous case of Langmuir waves. As a consequence, when studying short-scale dynamics, it is not a good approximation to keep the particle dispersive terms through the Wigner–Moyal equation, and simultaneously drop the exchange contribution.
Next, we turn our attention to the same case as above, but with degenerate electrons. In the quasi-neutral limit, the dispersion relation can then be computed as (see, e.g., Ref. (Ekman et al. 2015) for details]
where \(\alpha =\sqrt{m_e/3m_i}\). Apparently, the relative magnitude of the exchange terms is even larger than for the nondegenerate case, and, accordingly, independently of the background distribution, the omission of exchange terms in the quantum regime cannot be justified for ion-acoustic waves.
3.4 Exchange effects: final discussion

Reproduced from Ref. (Zamanian et al. 2015), with the permission of AIP Publishing
Exchange contribution to the susceptibility, kinetic (solid) and hydrodynamic (dashed), for Langmuir modes. a Full range of \(\omega /kv_F\). b Detail of the high-frequency regime, showing different limits for I (the normalized kinetic exchange contribution) and \(I^h\) (the normalized hydrodynamic exchange contribution).

Reproduced from Ref. (Zamanian et al. 2015), with the permission of AIP Publishing
The exchange contribution to the susceptibility, kinetic (solid) and hydrodynamic (dashed), for ion-acoustic modes. Note that, in the kinetic case, there is also an imaginary part (dotted). The irregularities in the real part of \(I(\omega /kv_F)\) are due to the numerical resolution.
As illustrated above, due to the nontrivial momentum integrals, a first principal kinetic treatment of exchange effects is complicated. Going beyond the simplest cases, like the ones studied above, would require a major numerical effort. Even so, only perturbative treatments where exchange effects are small would be possible. However, the topic is an important one, as exchange effects are not generally small compared to other quantum effects. A tentative conclusion, suggested by the above findings, would be that the exchange contribution might be limited (to the extent that it could be negligible) for high-frequency phenomena, but not for low-frequency phenomena. However, more studies need to be done to put such a conclusion on a firm ground.
An important generalization of the above treatment is to cover also electromagnetic phenomena. Some key steps toward that goal were taken in Ref. (Zamanian et al. 2015), although no concrete examples were worked out. An important issue to address in this case is the gauge invariance, as the exchange integrals tend to be dependent on the electromagnetic potentials, rather than the electromagnetic fields.
In light of the challenging nature of the kinetic exchange contribution, it would be valuable to have less complex models, allowing for computational progress also beyond the perturbative regime. A quantum hydrodynamical model fulfilling this criterion has been put forward by Ref. (Crouseilles et al. 2008). In addition to exchange effects, this model also covers the effect of electron correlations. Importantly, the hydrodynamical model is easy to use for practical calculation, as the exchange and correlation terms do not add much extra difficulty compared to pressure and particle dispersive terms. However, a drawback is that the model is based on time-independent density functional theory (DFT), and hence, the applicability to dynamical phenomena is uncertain at best. A comparison of the hydrodynamical and kinetic models, to some extent covering regimes not presented above, has been made in Ref. (Brodin et al. 2019), and the numerical comparisons are shown in Figs. 1 and 2, borrowed with permission from the original source. The overall conclusion is that there is a reasonable agreement between the hydrodynamic and the kinetic models in the long wavelength high-frequency regime, but otherwise, this particular hydrodynamical model tends to largely underestimate the importance of exchange effects. Note, however, that several improved quantum hydrodynamical models have been put forward in the recent literature; see, e.g., Refs. (Moldabekov et al. 2018; Bonitz et al. 2019; Manfredi et al. 2021).
In this context, let us also point out that for solid-state plasmas in particular, a large number of functionals in DFT have been presented including exchange and correlation effects. After the early foundation of DFT was laid (Kohn and Sham 1965), much progress has been made with results going beyond the local density approximation (LDA), where it is assumed that the exchange and correlation energy at a certain position depends only on the electron number density at the same point. Thus, nowadays, DFT comes in many flavors, e.g., accounting for the different density of the two spin states (local spin density approximation, LSDA), also using functionals that depend on the current density and not just the number density (current density functional theory), including effects of the local electron density gradient (referred to as the generalized-gradient approximations, GGA), and accounting for a time-dependence (applying time-dependent density functional theory TDDFT rather than just DFT). In particular, open-source software projects such as "quantum espresso" (Giannozzi et al. 2009) have been instrumental for spreading the use of DFT methods in the field of materials physics. For an overview of density functional theory in solid-state plasmas, see, e.g., Ref. (Hasnip et al. 2014).
4 The Pauli Hamiltonian and Spin dynamics
Next, we will generalize the treatment based on the Schrödinger equation to include the spin dynamics. In principle, the formalism is similar to that of Sect. 2. In particular, the higher order terms in the BBGKY-hierarchy (Bogolyubov 1946) are dropped, and thus, the evolution equation will be derived from the single-particle density matrix, using the von Neumann equation, followed by a Wigner transform. Nevertheless, there is an important difference compared to the previous case, as the density matrix now depends on the spin state. As a result, the single component in the Scrödinger case is replaced by a two by two matrix, where the different components represent different spin states. The changes needed to obtain the kinetic evolution equation are outlined in subsection A, and two different but equivalent systems are presented. Then, in subsection B, we use the model to derive the linear conductivity tensor in a magnetized plasma, generalizing previous results to cover the case of an an-isotropic background distribution.
4.1 Derivation of evolution equations
Including the spin dynamics, in the lowest (nonrelativisitic) approximation, we replace the Schrödinger Hamiltonian of Sect. 2 with the Pauli Hamiltonian
where \(\varvec{\sigma }\) here denotes a vector with the \(2\times 2\) Pauli matrices as components. Following Ref. Zamanian et al. (2010), we are able to construct a gauge-invariant scalar kinetic theory using a density matrix description for a spin-1/2 particle.
The basis states are \(|{\mathbf {x}},\alpha \rangle = |{\mathbf {x}}\rangle \otimes |\alpha \rangle\), where \(|{\mathbf {x}} \rangle\) is a state with position \({\mathbf {x}}\) and \(|\alpha \rangle\) is the state with spin-up \(\alpha = 1\) or spin-down \(\alpha =2\). As a starting point for the derivation, we use the spinor state \(\psi \left( {\mathbf {x}},\alpha ,t \right) = \langle {\mathbf {x}} ,\alpha \vert \psi \rangle\) which fulfill the dynamical equation \(i\hbar \partial _{t} \psi \left( {\mathbf {x}},\alpha ,t\right) = {\hat{H}}\psi \left( {\mathbf {x}},\alpha ,t\right)\), with the Hamiltonian (54). The density matrix is now given by
where, as before, \(p_{i}\) is the probability to have a state \({\psi }_{i}\), but we have the additional dependence on spin state. Similarly as before, the von Neumann equation applies, i.e., the evolution equation for the density matrix is
Once the density matrix has been defined, we can define the Wigner–Stratonovich transform (Stratonovic 1970) as
where the phase
is used to ensure gauge invariance of the resulting distribution function. This is the same transformation as in Eq. (35) with the modification that it must to be taken separately for each component of the 2-by-2 density matrix.
In principle, Eq. (56) together with Eq. (57) gives us a kinetic evolution equation, and we could be content with this. However, the individual components of \(W_{\alpha \beta }\) have no clear physical interpretation, and it is desirable to construct functions that can be understood more intuitively. Two ways to do this have been presented in the literature, that we will describe below.
The first way is to make a spin transform [or Q-transform, as it has also been called (Scully and Wódkiewicz 1994)], which creates a single scalar function f from the Wigner matrix \(W_{\alpha \beta }\). The attractive feature here is that the charge and current sources in Maxwell’s equation can be calculated from a single scalar function f, which plays a role much like the distribution function of classical physics. However, there is a price to pay, since the transform extends the classical phase space to include an extra independent variable, namely the spin. Thus, our scalar function has the functional dependence \(f=f({\mathbf {r}},{\mathbf {p}},{\mathbf {s}},t)\).
Following this approach, thoroughly discussed in Ref. Zamanian et al. (2010), we here define a scalar distribution function \(f({\mathbf {r}},{\mathbf {p}},{\mathbf {s}},t)\) in the extended phase space as:
where W is the 2-by-2 matrix with entries \(W_{\alpha \beta }\), \({\mathbf {s}}\) is a vector of unit length, and \(\mathrm {tr}\) denotes the trace over the spin indices. The spin variable can be expressed in terms of spherical coordinates \({\mathbf {s}} = (\cos \varphi _s \sin \theta _s, \sin \varphi _s \sin \theta _s, \cos \theta _s)\). Integrating over momentum
we find that the reduced distribution function \(f({\mathbf {r}}, {\mathbf {s}}, t)\) gives the probability to find the particle at position \({\mathbf {x}}\) with spin-up in the direction of \({\mathbf {s}}\). Similarly, defining
we find that \(f({\mathbf {p}},{\mathbf {s}},t)\) gives the probability to find the particle with momentum \({\mathbf {p}}\) with spin-up in the direction of \({\mathbf {s}}\). Moreover, we note that the expectation value for the spin polarization density is now given by
where we stress the need for the factor 3. Here, the measure of integration for the spin is \(d^2s = \sin \varphi _s d\theta _s d\phi _s\). This follows from the form of the transformation (59) and is needed to compensate for the quantum mechanical smearing of the distribution function in spin space. Equations (56), (57), and (59) determine the evolution equation for \(f({\mathbf {r}},{\mathbf {p}},{\mathbf {s}},t)\). We refer to Ref. Zamanian et al. (2010) for a more thorough description of the technical details, and move on to the final result for the evolution equation. Note that in the Pauli limit that is studied here, the momentum–velocity relation is simply \(\mathbf{p} = m\mathbf{v}\), in which case the variable change \(f({\mathbf {r}},{\mathbf {p}},{\mathbf {s}},t)\rightarrow f({\mathbf {r}},{\mathbf {v}},{\mathbf {s}},t)\) is trivial. Using the velocity as an independent variable, the equation can be written as
where, as in Eq. (37), we have defined
In the long-scale limit, for spatial variations much longer than the characteristic de Broglie length, the local approximations \(\tilde{{\mathbf {E}}}\approx {{\mathbf {E}}}\), etc, apply, and the term \(\propto \Delta \tilde{{\mathbf {v}}}\) can be dropped altogether. As a result, the equation accounting for spin dynamics, but dropping short-scale physics, is given by
Together with Maxwell’s equations, Eq. (63) [or Eq. (68) in the long-scale limit)] provides a closed description for the spin dynamics, where the electron charge density is given by
and the current density is given by
Here, the two-dimensional spin integration is made over the Bloch sphere (naturally represented in spherical spin coordinates), and \({{\hat{s}}}\) is the spin unit vector. As done above, the current density is naturally divided into its free contribution \({\mathbf {J}}_{f}\) and the contribution \({\mathbf {J}}_{M}\) due to the spin magnetization. The physics of the evolution equation can be understood as follows. The basic effect of short-scale particle dispersion is captured in the nonlocal variables defined in Eqs. (64)–(67), and the same physics is present already without the spin effects of the Pauli Hamiltonian, as described already in Sect. 2. The effects due to the spin that are genuinely new all survive in the long-scale limit, as seen in Eq. (68). The first terms of the equation are familiar from classical physics, and then, we have the effects of the magnetic dipole force, and the last term is the spin precession. To a large degree, Eq. (68) agrees with a semiclassical kinetic theory (Brodin et al. 2008). The main difference is that the magnetic dipole force has a slightly more complicated dependence \(\propto \nabla _{\mathbf {r}} [ (\hat{{\mathbf {s}}} + \nabla _{\hat{{\mathbf {s}}}} ) \cdot {\mathbf {B}} ] \cdot \nabla _{\mathbf {v}} f\) rather than the simpler semiclassical expression \(\propto \nabla _{\mathbf {r}} [ (\hat{{\mathbf {s}}}) \cdot {\mathbf {B}} ] \cdot \nabla _{\mathbf {v}} f\). The reason for this difference is discussed in Ref. Zamanian et al. (2010).
In the next subsection, we will demonstrate how to handle the extra spin dependence in practical calculations. However, it is not necessary to use the Q-transform and introduce spin as an extra independent variable. Instead, we can proceed as Ref. Hurst et al. (2014) and split the Wigner matrix \(W_{ab}\) into a vector part and a scalar part.
Specifically, we can split the Wigner matrix W (with entries \(W_{\alpha \beta }\)) into the scalar, defined as
and the vector \({\mathbf {f}}\) defined as
With these definitions, the Wigner matrix can be reconstructed as
where the Pauli spin matrices building up the vector \(\varvec{\sigma }\) has been complemented with the unit matrix \(\sigma _{0}.\) With the aid of (71)–(73), the equation for the Wigner matrix can be rewritten in terms of \(f_{0}\) and \({\mathbf {f}}\), with the result
and
where the definitions for \(\tilde{{\mathbf {E}}}\), \(\Delta \tilde{{\mathbf {v}}}\), and \(\tilde{{\mathbf {B}}}\) are the same as in (64)–(66). As expected, Eqs. (74) and (75) are completely equivalent to (63). The scalar function \(f_{0}\) captures the phase-space density, that is, the charge density is computed as
whereas the vector \({\mathbf {f}}\) gives the spin density (which in the approximation of the Pauli Hamiltonian used here coincides with the magnetization). Thus, the magnetization current is given by
and the full current density to be used in Ampere’s law, therefore, is
Note that in the long-scale limit, the approximations \(\tilde{{\mathbf {E}}} \rightarrow {\mathbf {E}}\), etc., apply, in which case the long-scale version of (74) and (75) agrees with Eq. (68)). Equations (74) and (75) have been used by Ref. Hurst et al. (2014) to derive fluid equation, with the aid of moment expansions. For more applications of Eqs. (74) and (75), see, e.g., Refs. Manfredi et al. (2019); Manfredi and Hurst (2015).
After presenting two different (but equivalent) systems derived from the Wigner matrix, one can ask what has been gained. After all, all the physics is already contained in the equations for \(W_{ab}\). However, the coupled equations for the components of \(W_{ab}\) do not provide much help of guiding the physical intuition. The individual components do not carry physical meaning themselves, only the complete object does. By contrast, the scalar object \(f({\mathbf {r}},{\mathbf {v}},{\mathbf {s}},t)\) can be applied much like a classical distribution function, but in an extended phase space. Similarly, \(f_{0}\) can be viewed much like a classical distribution function, but in this case averaged over the spin state, whereas the spin properties are captured in the vector \({\mathbf {f}}\). As a consequence, the quantities of the two theories can be related by the relations \(f_{0}( {\mathbf {r}},{\mathbf {v}},t)= \int d^{2}s\, f({\mathbf {r}},{\mathbf {v}},\hat{{\mathbf {s}}},t)\) and \({\mathbf {f}}({\mathbf {r}}, {\mathbf {v}}, t) = \int d^{2}s\, {\mathbf {s}}f({\mathbf {r}},{\mathbf {v}},\hat{{\mathbf {s}}},t)\).
Each of the two formulations has its own advantages. First, the latter formulation [Eqs. (74) and (75)] gives somewhat shorter equations. There is no explicit spin-precession term, and the magnetic dipole force is now a bit simpler [one does not need the operator \((\hat{{\mathbf {s}}} + \nabla _{\hat{{\mathbf {s}}}})\)]. As a result, these equations constitute a rather direct extension of the Vlasov equation. More importantly, not having the extra independent variable \(\hat{{\mathbf {s}}}\) makes the latter equations more suitable for a direct numerical approach. On the other hand, Eq. (63) is attractive when aiming for analytical solutions. Since only a scalar function is involved, and the structures of the extra terms are similar to the classical ones, most analytical approaches developed for the Vlasov equation can be adopted directly, with the simple addition of an extra integration over spin space. Moreover, in the case of the long-scale version, Eq. (68), replacing the magnetic dipole force with its semiclassical correspondence, allows the equation to be written in a form consistent with classical PIC-schemes (see Ref. Crouseilles et al. 2021), in which case an efficient and attractive numerical scheme is possible.
4.2 The linear conductivity tensor
We will here limit ourselves to the case of long spatial scale length (much longer than the characteristic de Broglie length), in which case the local approximations \({\tilde{\mathbf {E}}\rightarrow E}\), \({\tilde{\mathbf {B}} \rightarrow B}\), etc., apply. Thus, the evolution equation for \(f(\mathbf { r,v,}\hat{{\mathbf {s}}},t)\) is given by Eq. (68), and the current density to be used in Ampere’s law is given by (70).
In this section, we only consider the electron contribution to the current density, as the classical ion-contribution can be found in the textbook literature, see, e.g., Ref. (Swanson 2003) found. Below, we will derive the linear conductivity tensor \(\sigma _{ij}\) in a homogeneous magnetized plasma, defined as \(J_{i}=\sigma _{ij}E_{j}\), for such a system, where \(\sigma _{ij}\) contains both the free and magnetization current densities. With the conductivity tensor known, it is straightforward to find the dispersion relations for arbitrary wave modes.
We start by linearizing the kinetic Eq. (68) according to \(f=f_{0}+f_{1}\) and \({\mathbf {B}}={\mathbf {B}}_{0}+{\mathbf {B}}_{1}\), where the subscript 0 denotes an unperturbed quantity and the subscript 1 denotes a perturbation, and we take \({\mathbf {B}}_{0}=B_{0}\hat{{\mathbf {z}}}\). Before proceeding, let us point out a few quantum effects that may be contained already in the unperturbed distribution function:
-
1.
Fermi-Dirac statistics This effect is well known. For \(\hbar ^{2}n_{0}^{2/3}/m_{e}k_{B}T\) much larger than unity, we will have almost complete degeneracy, whereas if the parameter is much smaller than unity, the thermodynamic background distribution can be approximated by a Maxwellian.
-
2.
Landau quantization The quantization of perpendicular energy states becomes important in the regime of very strong magnetic fields, or very low temperatures, when \(\hbar \left| \omega _{ce}\right| /k_{B}T\rightarrow 1\), where \(k_{B}\) is Boltzmann’s constant and \(\omega _{ce}=-eB_{0}/m_e\) is the electron cyclotron frequency.
-
3.
Spin splitting: The two spin states, up- and down relative to the magnetic field, have different probability distributions in spin space. As a result, the general time-independent distribution function can be written as \(f_{0}=f_{0+}+f_{0-}\) with \(f_{0\pm }=(1/4\pi )F_{0\pm }(\mathbf {v })(1\pm \cos \theta _{s})\), where for a time-independent distribution function, \(F_{0\pm }\) can be arbitrary functions of \((v_{\perp },v_{z})\), and \(F_{0\pm }\) is normalized, such that \(\int d^{3}v\, F_{0\pm } = n_{0\pm }\) with \(n_{0\pm }\) being the number densities of the spin up/down states, respectively. The positive spin state here means that the spin points in the direction parallel to the magnetic field, which means that the magnetic moment points in the opposite direction. Note that with this definition, the lower energy state is the spin state with negative index, i.e., \(n_{0-}>n_{0+}\) in case the background distribution \(f_{0}\) describes a thermodynamic equilibrium.
The full quantum mechanical expression of the thermodynamic equilibrium background in an external magnetic field is derived in Ref. (Zamanian et al. 2010), and reads
where \(L_n\) denotes Laguerre polynomials of order n and the particle energy \(E_n\) is given by
We note that, in general, the degree of spin polarization in the background \((n_{0+}-n_{0-})/((n_{0+}-n_{0-}))\) is obtained by performing momentum integrations of the expression (79).
Next, we follow Ref. Lundin and Brodin (2010) but with a slight generalization, allowing for a background distribution that is not necessarily isotropic, i.e., we also cover wave modes that are subject to Weibel type of instabilities. After linearization, Eq. (68) is written as
To proceed, we make a plane wave ansatz of the perturbed parameters according to \(f_{1}={\tilde{f}}_{1}\exp [i({\mathbf {k}}\cdot {\mathbf {r}}-\omega t)]\), etc. Without loss of generality, we define the wavevector as \({\mathbf {k}}=k_{\bot } \hat{{\mathbf {x}}}+k_{z}\hat{{\mathbf {z}}}\), where \(\hat{{\mathbf {x}}}\), and \(\hat{{\mathbf {z}}}\) are the unit vectors in the x and z-directions, respectively. We also choose to express the velocity in cylindrical coordinates \((v_{\perp },\varphi _{v},v_{z})\) such that \(d^{3}v=v_{\bot }dv_{\bot }d\varphi _{v}dv_{z}\), and expand \(f_{1}\) in eigenfunctions to the operator of the right-hand side
where
and \({\mathcal {J}}_{l}(x)\) is a Bessel function of the first kind. We may then note the following simplifying relations:
where \(\omega _{cg}=2\mu _{e}B_{0}/\hbar\) is the spin-precession frequency. Using the eigenfunction expansion of \({\tilde{f}}_{1}\) (Eq. (82)) in the linearized Vlasov equation (81), multiplying the resulting equation with \(\psi _{a}^{*}e^{ib\varphi _{s}}/ \sqrt{2\pi }\) (where the star denotes complex conjugate) and integrating over \(\varphi _{v}\) and \(\varphi _{s}\), we find the equation
where
The result coincides with Ref. Lundin and Brodin (2010), except that in our case \(f_{0}(v_{\bot },v_{z})\) is an arbitrary function, which means that the term in the integral \(\propto {\mathbf {v}}\times \tilde{{\mathbf {B}}}_{1}\) survives the integration \(\int _{0}^{2\pi }...d\varphi _{v}\). Writing out the dependence on \(\varphi _{v},\varphi _{s}\) and \(\theta _{s}\) explicitly, the integrals can be carried out, and the result substituted into the expression for the current density, which in turn give the conductivity tensor. Apart from the extra term \(\propto {\mathbf {v}}\times \tilde{{\mathbf {B}}}_{1}\), and the need to avoid some other slight simplifications for an isotropic background, the calculations are similar to those given in Ref. Lundin and Brodin (2010). Therefore, we proceed directly to the final result for the conductivity tensor, which may be written as
where
is the classical contribution, and the spin contributions are
together with
where
It can be noted that the term \(Y_{(\nu )ij}^{(\text {sp})}\) comes from the spin (magnetic dipole force) contribution to the free current density, whereas the terms \(X_{(\nu )ij}^{(\text {sp})}\) and \(Z_{(\nu )ij}^{(\text {sp} )}\) come from the magnetization current. Since the conductivity tensor (87) contains all plasma currents, the general dispersion relation is obtained in the same way as in the classical case, i.e., the dispersion relation is given by \(\text {det}D_{ij}=0\), with \(D_{ij}=\delta _{ij}(1-k^{2}c^{2}/\omega ^{2})+k_{i}k_{j}c^{2}/\omega ^{2}-i\sigma _{ij}/\varepsilon _{0}\omega\). Picking the special case of an isotropic distribution, i.e., letting \(F_{0\nu }=\) \(F_{0\nu }(v^{2})\), it is straightforward to show that the conductivity tensor reduces to the expression derived in Ref. Lundin and Brodin (2010).
Evaluating the dispersion relation is a complicated task in its own right. Generally, the spin contribution tends to be more significant if the background magnetic fields is strong, if the plasma density is high, and if the temperature is modest. There are numerous dimensionless parameters describing this, as discussed more thoroughly in Ref. Lundin and Brodin (2010). Here, we would just like to point out a few more consequences of the conductivity tensor. Since there are certain denominators in the expression (87) proportional to \(\omega -k_{z}v_{z}-\pm (\omega _{ce}-\omega _{cg})\), for almost perpendicular propagation (negligible \(k_z\)), certain spin terms will be magnified if the wave frequency matches the difference in the gyration frequency and the spin-precession frequency, \(\Delta \omega _c=(g/2-1)\omega _c\approx 0.00116 \omega _c\). Spin-induced wave modes with \(\omega \approx \Delta \omega _c\) have been studied by, e.g., Refs. Brodin et al. (2008); Asenjo et al. (2012). A closely related feature due to these denominators is the spin-induced wave–particle interaction. Even if the plasma parameters are more or less classical, such that the spin terms are small, for classical wave modes with \(\omega \sim \Delta \omega _c\), the smallness of the overall coefficients for the spin terms can be compensated by a larger number of resonant particles. Spin-induced damping due to this mechanism have been studied, e.g., by Refs. Zamanian et al. (2010); Ekman et al. (2021). For an extended treatment of the electrostatic limit, see Ref. Hussain et al. (2014).
Moreover, we note that since the expression for the conductivity tensor given here allows for an-isotropic distributions, it may be used for studying instabilities of the Weibel type. In a quantum plasma context, such instabilities have been previously been studied by, e.g., Refs. Haas (2008); Rightley and Uzdensky (2018), but without accounting for the spin dynamics. In addition to the classical free energy sources, the theory presented here allows for instabilities driven by a difference in the spin temperature and the kinetic temperature. Figure 3, reprinted with permission from J. Lundin and G. Brodin, Phys. Rev. E 82, 056407 (2010), copyright 2010 by the American Physical Society, shows that a rather small difference between the spin temperature \(T_{\mathrm{sp}}\) and the kinetic temperature \(T_{\mathrm{kin}}\) is enough to drive an instability in the absence of dissipation.
Finally, we note that in addition to the direct application of linear wave propagation, the conductivity tensor of a plasma plays an indirect but important role also for other phenomena. A particular example is the stopping power of particles in magnetized plasmas. This problem has been thoroughly studied, e.g., in the book by Ref. Nersisyan et al. (2007), including theoretical development of the dielectric tensor for both classical and quantum plasmas.
(Color online) The imaginary contribution of \(X_{ij}^{(sp)}\) to \(\sigma _{ij}\) plotted as a function of \(T_{\mathrm {sp}}/T_{\mathrm {kin}}\) for different values of \({\tilde{a}}\). A positive value corresponds to damping, while a negative value gives rise to a instability. We refer to Ref. Lundin and Brodin (2010) for the detailed definitions of \({{\tilde{a}}}\) and \(A_{ij}\) determining the instability growth rate
5 Conservation laws, Landau quantization, and nonlinear effects
Up to now, we have aimed for a clear logical structure of the review article, building up quantum kinetic theory by starting from elementary models, gradually progressing to more advanced ones. In this section, we will leave this route to some extent, and instead offer a smorgasbord of different results, to illustrate the diversity of quantum kinetic theory. In particular, we will consider quantum kinetic conservation laws, Landau quantization in a strong magnetic field, and we will use nonlinear perturbation theory to find the spin contribution to the ponderomotive force. Doing so, to present findings of a more general nature, we will apply models that to some degree extends those presented earlier. However, all of them can be derived similarly to the schemes presented above, i.e., by finding a proper Hamiltonian, using the von Neumann equation for the density matrix, and finally making a Wigner transform (and possibly also a Q-transform). The only additional feature is the need for a Foldy–Wouthuysen transform (Foldy and Wouthuysen 1950; Silenko 2008), to isolate the electron degrees of freedom from the positron degrees of freedom.
5.1 Conservation laws
Here, we will use a relativistic quantum kinetic model that comes from separating positive and negative energy solutions of the Dirac equation by means of a Foldy–Wouthuysen (F–W) transformation (Foldy and Wouthuysen 1950; Silenko 2008). Since we are decoupling electrons and positrons, the physical condition of applicability is that pair production is negligible. Quantitatively, the electric field should be much smaller than the critical field, \(E\ll E_{c}=m^{2}/e\hbar\) and similarly for the magnetic field (we use units with \(c=1\) in this section). Moreover, the typical scale lengths should be long compared to the Compton wavelength \(\hbar /m\). Apart from the F-W transformation, the derivation of the model is similar to Sect. 4 and we refer to Ref. Ekman et al. (2017) for the details.
The evolution equation for the scalar Wigner function f is
where \(\epsilon ^{2}={\mathbf {p}}^{2}+m^{2}\), \(\mu _{B}=q\hbar /2m\) is the Bohr magneton and
The system is closed with Maxwell’s equations, in units where \(c=\epsilon _{0}=\mu _{0}=1\),
where \({\mathbf {P}}\) and \({\mathbf {M}}\) are the polarization and magnetization densities, and \(\rho _{f}\) and \({\mathbf {j}}_{f}\) are the free charge and current densities. The source terms are slightly generalized, as compared to previous models, and given by
As the theory is relativistic, the integration element \(d\Omega\) of Sect. 4 is replaced by its relativistic counterpart, i.e., \(d\Omega \,=d^{3}pd^{2}s\). It follows from the evolution equation, Eq. (88), that the free charge is conserved, \(\partial _{t}\rho _{f}+\nabla \cdot {\mathbf {j}}_{f}=0\), and we interpret:
as the function on phase space corresponding to the velocity—it is in fact the Weyl transform of the velocity operator \(\hat{{\mathbf {v}}}=\frac{i}{ \hbar }[{\hat{H}},\hat{{\mathbf {x}}}]\) given by the Heisenberg equation of motion. The spin-dependent term is related to the hidden momentum (Shockley and James 1967; Shockley 1968; Coleman and Van Vleck 1968; Babson et al. 2009) of systems with magnetic moments. Here, we also note an important aspect of the relativistic theory, and that the spin magnetization current is complemented by polarization currents. This is natural, of course, as a magnetic dipole moment in the rest frame of a particle correspond to both a magnetic and electric dipole moment in any other frame.
The total energy density is given by
with the corresponding energy flux vector
where \({\mathbf {H}}={\mathbf {B}}-{\mathbf {M}}\). With these expression, we have a conservation law on divergence form
It is straightforward to confirm the above energy conservation law by carrying out a number of partial integrations.
Deriving the conservation law for momentum is somewhat more tedious, and we refer to Ref. (Ekman et al. 2019) for the details. Here, we just present the result, which can be written in standard form in terms of energy-momentum tensors for particles and fields
Here, the electromagnetic part of the energy–momentum tensor \(T_{ij}^{\text {EM }}\) is given by
where the usual relations \(\mathbf {D=E+P}\) and \({\mathbf {B}}={\mathbf {H}}- {\mathbf {M}}\) applies. Similarly, the electron contribution \(T_{ij}^{\text {e}}\) to the energy–momentum tensor is given by
where the momentum–velocity relation (96) apply.
A few things can be noted. First, the corresponding conservation laws for the nonrelativistic model in Sect. 4 can be obtained as expected from the above results, i.e., by dropping terms of higher order in an expansion \(\mathbf{p}/m\) (letting \(\epsilon = m(1+p^2/2)\), etc.). Second, with an expression for the energy momentum tensor, in principal, we can compute the gravitational source due to quantum relativistic electrons. In practice, this is complicated by the fact that the stress tensor is not necessarily symmetric; see Ref. (Ekman et al. 2019) for a more thorough discussion. Finally, we note that the conserved quantities will not be modified due to our neglect of short-scale effects (of the type contained in Eqs. (64)–(67)). The reason is that all the extra terms due to short-scale effects contain higher order derivatives whose contributions to the energy–momentum tensors vanish when integrating over momentum space.
5.2 Landau quantization
When the Zeeman energy in an external magnetic field is large, i.e., comparable to the kinetic energy of particles, the phenomenon of Landau quantization becomes crucial. This means that the energy levels for motion perpendicular to a magnetic field are quantized, and also that the energy difference between the spin states is significant. In particular, this tends to occur in astrophysical scenarios, where, in extreme cases, the Zeeman energy may be comparable to the electron rest mass energy. Specifically, this happens in the vicinity of magnetars, where the magnetic field strength can be of the order \(10^{10}\) \(\mathrm{T}\) (Harding and Lai 2006). Here, we will address the regime of fully relativistic Landau quantization, when the effect is most pronounced. A particular difficulty with relativistic Landau quantization, is that we can no longer use the inequality \(\mu _B B \ll m\), (or similarly for the electric field) which plays an important role when separating electron and positron states. In principle, this could be handled using the Dirac–Heisenberg–Wigner formalism (DHW) to be discussed in the next section, but this comes at the price of a considerably more complex theory. To focus solely on the problem of Landau quantization, we here takes a simpler route, and consider a strong constant magnetic field \(B_0\) (allowing for \(\mu _B B_0 \sim m\) or even larger), but limit the magnitude of electromagnetic field perturbations well beyond this.
A model focusing on the effect of Landau quantization may still neglect spin-dynamics, in case the validity condition \(\hbar k^{2}/m\omega \ll 1\) is fulfilled. (Here, k and \(\omega\) do not necessarily refer to plane waves; instead, they represent characteristic spatial and temporal gradients.) Also, assuming \(\hbar k\nabla _{p}\ll 1\), the previously studied short-scale effects can be dropped, and the model will be a slight generalization of the relativistic Vlasov equation, extended to account for Landau quantization in a strong (constant) magnetic field \(B_{0}\). The kinetic evolution equation derived in Ref. Al-Naseri et al. (2020) can be written as
where the main difference to the (relativistic) Vlasov equation lies in the energy expression \(\epsilon _{\pm }^{\prime }\), which now becomes an operator given by
We note that the first two terms inside the root sign just give the classical expression. The next term with a \({\mp }\) sign gives the magnetic dipole energy for spin up and spin down, respectively. Accordingly, the upper and lower signs are described by different evolution equations for \(W_{+}\) and \(W_{-}\), due to the different energies of the spin-up and spin-down particles. The final nonclassical feature comes from the last term under the root sign, which makes the energy an operator instead of just an algebraic expression. We note that the full operator is defined by its Taylor expansion. While one may worry that such a Taylor expansion will not behave well due to the root sign, in fact, for any valid Wigner function, the Taylor series will be well defined and convergent. Finally, to have a closed system, we need the source terms in Maxwell’s equations, which are given by summing over the spin-up and spin-down contribution, that is
In principle, there are also magnetization currents that can be added to the free sources above. However, such a contribution will be negligible in comparison, provided that the condition given above for neglecting the magnetic dipole force is fulfilled.
Next, we want to deduce the thermodynamic equilibrium state in a constant magnetic field. Noting that for a constant magnetic field, both the Dirac equation and the Pauli equation results in electrons obeying a quantum harmonic oscillator equation, we can make a straightforward generalization of the Pauli case (Zamanian et al. 2010). Both for the Pauli and the Dirac equations, the spatial dependence of the wave-function in Cartesian coordinates can be expressed as a Hermite polynomial times a Gaussian function (Melrose and Parle 1983) only the energy eigenvalues for the Landau quantized states are different. Specifically, applying the Dirac theory, the energy of the Landau quantized states becomes
where \(n=0,1,2,\ldots\) correspond to the different Landau levels for the perpendicular contribution to the kinetic energy, the index ± represents the contribution from the two spin states, and the term proportional to \(p_{z}^{2}\) gives the continuous dependence on the parallel kinetic energy. Since the Pauli and Dirac equations for individual particle states have the same spatial dependence for the wave function, we can adopt the expression for the Wigner function from Ref. Zamanian et al. (2010) (based on the Pauli equation) with some relatively minor adjustments.
-
1.
Contrary to Ref. Zamanian et al. (2010), we have made no Q-transform to introduce an independent spin variable, and thus, the spin dependence of Ref. Zamanian et al. (2010) reduces to \(W_\pm\).
-
2.
The Wigner function of Ref. Zamanian et al. (2010) must be expressed in terms of the momentum, i.e., \(m(v_{x}^{2}+v_{y}^{2})/2 \rightarrow (p_{x}^{2}+p_{y}^{2})/2m\).
-
3.
The nonrelativistic energy of Ref. Zamanian et al. (2010) is replaced by the relativistic expression (107) of the Dirac theory.
-
4.
The normalization of the Wigner function must be adopted to fit the present case.
With these changes, the background Wigner function \(W_{\pm }^{TB}\) for the case of electrons in thermodynamic equilibrium can be written as
where
\(n_0=n_{0+}+n_{0-} =\int (W_{+T}+W_{-T}) d^3 p\) is the electron number density of the plasma, \(\mu _{c}\) is the chemical potential, T is the temperature, and \(L_n\) denotes the Laguerre polynomial of order n.
That the factor \(\phi _n(p_{\perp })\) gives us the proper Wigner function for the Landau quantized eigenstates can be confirmed by an independent check. Since the expression (108) contains no dependence on the azimuthal angle in momentum space, we can write
when \(\epsilon ^{\prime }_{\pm }\) acts on \(\phi _n(p_\perp )\). Computing \(\epsilon ^{\prime }_{\pm }\phi _n(p_\perp )\) by Taylor-expanding the square root to infinite order, using the properties of the Laguerre polynomials, and then converting the sum back to a square root, it is straightforward to verify the relation
where \(\omega _{ce} = \frac{|qB_0 |}{m}\) is the electron cyclotron frequency, confirming that \(\phi _n(p_\perp )\) generates the proper energy eigenvalues for the perpendicular kinetic energy and the spin degrees of freedom.
While (108) gives the thermodynamic equilibrium expression \(W_{\pm }^{TB}\), we note that the plasma background state is not necessarily in thermodynamic equilibrium. Making use of the property (111), we note that the most general time-independent solution \(W_{0\pm }\) to (103) of physical significance can be written in the form
where \(g_{n\pm }(p_{z})\) is a function that is normalizable, but otherwise arbitrary, and the number of particles in each Landau quantized eigenstate \(n_{n,\pm }\) obeys the condition
Naturally, the expressions for \(W_{0\pm }\) and \(W_{\pm }^{TB}\) presented here are of most significance for relativistically strong magnetic fields, when Landau quantization is pronounced. As a consequence, the above formulas will reduce to more well-known expressions when the limit \(\hbar \omega _{ce}/m\ll 1\) is taken. Specifically, Eq. (108) will become a relativistically degenerate Fermi-Dirac distribution in case we let \(T=0\) and \(\mu _{c}=E_{F}\gg \hbar \omega _{ce}\), where \(E_{F}\) is the Fermi energy. Alternatively, for \(k_{B}T\gg E_{F}\) and \(k_{B}T\gg \hbar \omega _{ce}\), Eq. (108) reduces to a Synge-Juttner distribution.
To give a concrete illustration, in Fig. 4, reprinted with permission from Al-Naseri et al. (2021) copyright 2021 by the American Physical Society, we show a bar chart for the normalized number density \(n_{0n\pm }/n_0\) in the different energy states, for a few values of the temperature and magnetic field, under the assumption that the density is low enough for the system to be nondegenerate, i.e., assuming \(T>T_\mathrm{F}\).
As a result of the background dependence, Eq. (112), in the Landau quantized regime, the electrons behave as a multi-species system, where each particle species has its own rest mass, as given by Eq. (107) but with \(p_{z}=0\). This is because the separation between Landau levels is of the order of the rest mass, and all excitations by quanta with energies of that order have been neglected. If we define the effective number density of each "species" (discrete energy-state) as
we see that \(n_{0n\pm }\) to a large degree will be determined by the Boltzmann factors of Eq. (108). For a study of Langmuir waves in a Landau quantized plasma, see Ref. Al-Naseri et al. (2020).
While we have here focused on the extreme case of relativistic Landau quantization, we note that the thermodynamics is much affected also in the nonrelativistic regime, provided that the Zeeman energy is of the same magnitude or larger than the characteristic kinetic energy in the background plasma. For applications of Landau quantization in the nonrelativistic regime, see e.g. (Eliezera et al. 2005; Shaukat 2017)
5.3 Nonlinear effects
Not surprisingly, quantum kinetic models can describe a great variety of nonlinear phenomena. Just like for classical plasmas, a fair share of these phenomena is induced by the ponderomotive force. For example, the ponderomotive force is the driver of plasma wake field generation [93], the key mechanism in soliton formation (Shukla et al. 1986), and the main source of nonlinear self-focusing (Kurki-Suonio et al. 1989). While the main features of classical and quantum kinetic models driven by the ponderomotive force are similar, nevertheless, there are important differences. For one thing, in a magnetized plasma, the classical ponderomotive force has cyclotron resonances (Karpman and Washimi 1977). In quantum kinetic theory, the classical terms are still present, but they are complemented by terms containing extra quantum resonances (Brodin et al. 2010; Stefan et al. 2011).
The concept of a ponderomotive force in quantum kinetic theory is not as straightforward as in a fluid theory. Depending on definition, some low-frequency nonlinearities induced by quadratic nonlinearities may be included as a ponderomotive force term or not. To avoid ambiguities, we will focus on the regime where the phase velocity of the high-frequency wave is much higher than the thermal velocity (or characteristic velocity, in case of degeneracy effects).
As a starting point, we will base our study on the long-scale version of the model put forward in Sect. 4, that is, Eq. (68). Next, we consider circularly polarized electromagnetic waves of high frequency propagating parallel to an external magnetic field, \({\mathbf {B}}_{0}=B_{0} {\hat{z}}\), and use the following ansatz:
The amplitudes are assumed to vary much slower than the exponential phase factors, and the star denotes complex conjugates. Since the basic wave modes propagating parallel to \({\mathbf {B}}_{0}\) are either left- or right-circularly polarized, we have \(\tilde{{\mathbf {E}}},\tilde{{\mathbf {B}}} \propto\) \(\widehat{{\mathbf {x}}}\pm i\widehat{{\mathbf {y}}}\). Furthermore, all perturbations are small, such that weakly nonlinear perturbation theory is applicable, and we will focus on the ponderomotive contribution, that is the quadratically nonlinear low-frequency terms.
To calculate the weakly nonlinear low-frequency response to an incoming transverse wave packet, we make the ansatz
where \(f_{0}\) is the background distribution, \(f_{\mathrm {lf}}\) is a low-frequency part due to quadratic nonlinearities, and \({\tilde{f}}_{1}\) is a slowly modulated high-frequency wave. The background distribution will be taken to be of the form
where \(n_{0}\) is the equilibrium density, and the thermal velocity \(v_{T}\) is defined as \(v_{T}=\sqrt{2k_{B}T/m}\). It should be stressed that the background distribution (117) has been picked mostly for convenience. In fact, the results below are not depending sensitively on the background, as long as the phase velocity is larger than the characteristic velocity. For example, a degenerate distribution, but with the Fermi velocity smaller than the phase velocity would produce identical results.
Given the ansatz (115) and (116), the aim is then to find an equation for the low-frequency part of the distribution function. From such an equation, we can then calculate the low-frequency response in the current density and magnetization, and compare with the results for a ponderomotive force, as defined from a fluid theory. First, we deduce the high-frequency linear perturbation of the distribution function, which is given by \(f_{1}=f_{+}\) (\(f_{-})\) for left-hand (right-hand) circularly polarized waves. The expressions for \(f_{\pm }\) found from Eq. (68) to linear order can be easily computed from Eq. (9) in Ref. (Lundin and Brodin 2010), and the result is
Next, allowing for slow modulations and solving the equation to first order in \(\partial _{z}/k\), \(\partial _{t}/\omega\), we note that the zero-order solution applies after making the substitution \(\omega \rightarrow \omega +i\partial _{t}\) and \(k\rightarrow k-i\partial _{z}\) in Eq. (118), and then expanding to first order in the slow derivatives. Inserting the ansatz above into the evolution equation and considering the slow-time scale and keeping only up to quadratic nonlinearities, we obtain the equation
where c.c. stands for complex conjugate. Here, we have also added a low-frequency electric field in the z-direction, \(E_{z\mathrm {lf}}\), which has \(f_{\mathrm {lf}}\) as source. Equations (119) and (118) now constitute a basis for calculating the nonlinear response in the current density and magnetization.
After some algebra (described more closely in Ref. Stefan et al. 2011), based on the low-frequency part of Ampere’s law, we end up with the final expression for the induced low-frequency field, which can be written in terms of the ponderomotive force \(f_{p}\) as
where \(f_{p}\) can be divided into its classical and its spin contribution according to
with the different parts given by
and
The classical ponderomotive term (121) agrees with an expression first derived by Ref. Karpman and Washimi (1977). The spin ponderomotive term (122) was first derived in Ref. Stefan et al. (2011). Our spin term agrees with that work, although, in contrast to that expression, we have integrated the contribution over the spin-up and the spin-down term. Note that although the modest scale lengths assumed tend to limit the magnitude of the spin terms, the quantum contribution can still be larger or comparable to the classical terms, in particular close to resonances \(\omega \simeq \omega _{c}\) or \(\omega \simeq \omega _{cg}\). Note that due to the closeness of the spin-precession frequency \(\omega _{cg}\) and the cyclotron frequency \(\omega _{c}\), these resonances can be more or less overlapping.
An interesting feature of the above expression is the second term in Eq. (122), containing the \(\tanh -\)factor. If we had not averaged over the spin states, spin-up and spin-down electrons would be affected in opposite direction (recall that we get the \(\tanh -\)factor from the difference in the number of spin-up and down particles), and hence, a part of the spin contribution to the ponderomotive force leads to a spin polarization being induced by the high-frequency wave. We will not explore the consequences of the expression (122) further, however, but refer to Refs Brodin et al. (2010), Stefan et al. (2011), Misra et al. (2010a), Misra et al. (2010b) that have studied various types of nonlinear dynamics induced by the spin ponderomotive force.
Before ending the description of spin ponderomotive physics, it is worth noting that in certain cases, weakly relativistic contributions, in particular the spin-orbit correction, can be important for the end result. To explore this fact, we will make use of the weakly relativistic limit of Eq. (88). obtained by letting \(\varepsilon \rightarrow m\). This model was first derived by Ref. Asenjo et al. (2012), and is given by
While we still use put gamma factors to unity (or \(\varepsilon \rightarrow m\) ), the model keeps terms linear in a v/c-expansion, such that Thomas precession, spin-orbit terms, and a nontrivial velocity–momentum relation (including spin) are kept. Taking the appropriate limit, the source terms used in Sect. 4 are replaced by
Here, \(\rho _{F} = q\int \!d\Omega \,f\) is the free charge density and the free current density, the polarization and magnetization are given by
Next, we make the same calculation as for the simpler (nonrelativistic) model (given by Eq. (68)), considering a quasi-monchromatic circularly polarized electromagnetic wave. However, to reduce the algebra, we consider a nonmagnetized plasma, i.e., we let \(B_{0}\rightarrow 0\). We refer the reader to Ref. Stefan and Brodin (2013) for the algebraical details, and move on to the end result for the ponderomotive force
where, due to the technicalities of the model, we have a result for the time-derivative of the ponderomotive force, rather than the ponderomotive force \(f_p\) itself. The expression is
The last term is the classical contribution, and the second-to-last term in the square bracket is what is obtained without the weakly relativistic effects. However, if we assume that \(k/\omega\) is roughly of order unity, we see that all terms in the square brackets are of the same order. This implies that when dealing with an unmagnetized plasma where spin effects are important, the spin-orbit coupling contributions must be taken into account, as well. However, the previous result for the ponderomotive force, Eq. (122), is still relevant, as spin terms tend to be more important in magnetized plasmas, and hence the simpler model (68) can still be justified.
6 The full Dirac theory: the DHW equations
Quantum relativistic treatments are of interest in several different contexts (Zhang et al. 2020; Elkamash et al. 2017; Shi et al. 2018). Dense astrophysical objects can have a Fermi energy approaching or exceeding the electron rest mass energy, and the strong magnetic fields of magnetars give rise to relativistic Landau quantization. Importantly, the continuous evolution of laser intensity brings a variety of quantum relativistic phenomena accessible to experimentalists. Upcoming laser facilities of interest in this context include, e.g., the extreme light infrastructure (ELI) [105], (Dunne 2009) and the European X-ray free electron laser (XFEL) [107], (Ringwald 2001).
The quantum kinetic models of previous sections have all made various simplifications as compared to the full quantum relativistic theory. In particular, to avoid the mixed electron–positron states of the Dirac theory, up to now, we have imposed limitations on the electric field. Specifically, we have demanded \(E\ll E_{\mathrm{cr}}\) where \(E_{\mathrm{cr}}=m^2c^3/e\hbar\) is the critical field, to avoid the complications associated with significant pair production due to the Schwinger mechanism. In this section, however, we will take on the full complexity of the Dirac theory using the so-called Dirac–Heisenberg–Wigner (DHW) formalism (Bialynicki-Birula et al. 1991). Compared to previous sections, new features of the theory include Zitterbewegung (a rapid (speed of light) particle motion associated with interference between positive and negative energy states), vacuum polarization, and electron–positron pair creation. Also, the previous 2-by-2 Wigner matrix will be replaced by 16 components, due to the 4 components of the Dirac spinors. Nevertheless, many other aspects of the quantum kinetic theory will be familiar and we will point out how the DHW formalism can be related to the quantum kinetic approximations presented earlier.
6.1 The DHW model
The DHW model was first derived by Ref. (Bialynicki-Birula et al. 1991). Moreover, some relatively minor variations of this derivation have been published in the literature more recently, see e.g. (Hebenstreit et al. 2010; Sheng et al. 2019). As all these treatments are fully satisfactory, we will not repeat the calculations, but just point out a few of the main features.
-
1.
The derivation is based on the Dirac equation, which gives the time evolution of Dirac four spinors, generally describing mixed electron–positron states.
-
2.
Just like in previous theories, a gauge-invariant Wigner transformation is made, which here produce a 4-by-4 Wigner matrix, with the components depending on phase-space variables just like in standard kinetic theory.
-
3.
The main omission is made when using the Hartree approximation where the electromagnetic field is treated as a nonquantized field. This approximation amounts to neglecting the quantum fluctuations. We will come back to the consequences of this approximation.
-
4.
To write the equations in a physically more transparent form, the 16 components of the Wigner matrix are decomposed into 4 different four vectors, which in turn is split into temporal and spatial components. Most of these quantities have a clear physical meaning, which helps forming a physical understanding of the theory.
-
5.
The (phase-space) current density and charge density are parts of the DHW unctions, which makes it straightforward to close the system using Maxwell’s equations.
With these preliminaries, we jump directly to the DHW quations, which in units where \(c=\hbar =1\) can be written in the form
Due to the Wigner transform, we cover short-scale quantum phenomena in much the same way as in the previous sections. This is illustrated by the appearance of the nonlocal operators in Eq. (131), which are given by
As before, the operators reduce to their local approximations (i.e., \(D_t\rightarrow \partial /\partial t + e {\mathbf {E}} \cdot \nabla _p\), \({\mathbf {D}} \rightarrow \nabla _r + e {\mathbf {B}} \times \nabla _p\), \(\tilde{{\mathbf {E}}} \rightarrow {\mathbf {E}}\), and \(\tilde{{\mathbf {p}}}\rightarrow {\mathbf {p}}\)) for scale lengths much longer than the characteristic de Broglie length.
To close the system, we need the source terms in Maxwell’s equations, which are given by
and
Thus, \(v_0\) is the time component of the four-vector phase-space function that gives the four current density, and \(\mathbf{v}\) is the spatial component, i.e.,the current density. Most, if not all, DHW unctions have fairly concrete interpretations which helps guiding the physical intuition. To gain a better understanding, we take a look at some of the conserved quantities of the DHW ystem (for a derivation, see Ref. Bialynicki-Birula et al. 1991). First, the total energy W is given by
second, the linear momentum is
and, finally, the total angular momentum \(\mathbf{M}\) is
We can see in Eq. (138) that the current density can be related to the kinetic energy, as expected. However, the role of mass density is played by another function s, with no trivial relation to the charge density. As the Dirac field contains both electrons and positrons, the lack of a simple relation between the mass density and the charge density should not be surprising. Nevertheless, in the expression for momentum (139), we see that \(\mathbf{p} v_0\) acts as a phase-space momentum density. Since electrons and positrons contribute with opposite signs to \(v_0\), we realize that electrons and positrons must have a different dependence on \(\mathbf{p}\). To be concrete, for electrons and positrons moving in the same direction, we need to shift the momentum dependence for the dependent variables according to \(\mathbf{p} \rightarrow \mathbf{-p}\), as will be illustrated more explicitly below. This is not an issue when solving the DHW quations, as the DHW variables generally describe coupled electron and positron states anyway. However, this insight can be of some importance, e.g., when interpreting results, in particular when numerical calculations have been made. The shift in momentum dependence is consistent with the common interpretation of positrons as being electrons moving backwards in time.
Another observation that can be made based on the conserved quantities is that the term \(\propto (1/2) \mathbf{a}\) can be identified as the spin contribution to angular momentum, i.e., \(\mathbf{a}\) gives the spin density. Finally, the equation for \(D_t\mathbf{t}_1\) in Eq. (131) shows a division of the total current density into its free part, magnetization part, and polarization part. To be specific, we can deduce that \(\mathbf{t}_2\) gives the magnetization, and \(\mathbf{t}_1\) gives the polarization. For some further discussion of the physical interpretation of the DHW functions, see Ref. (Bialynicki-Birula et al. 1991).
Contrary to previous kinetic theories, in the DHW formalism, the kinetic variables are not zero even in vacuum; in older terminology, we would say that the vacuum is filled with the particles of the Dirac sea. However, in the absence of a spin polarizing magnetic field, the only DHW functions with nonzero vacuum values are the mass density and current density, which are given by
where \(\epsilon =\sqrt{m^2+p^2}\). The expressions above are obtained by calculating the Wigner operator for the free particle Dirac equation and taking the vacuum expectation value. Note that while the charge density is zero (due to the cancellation of the electron and positron vacuum fluctuations), the same is not true for the current density. The reason is that there are two signs that enter the picture—first, electrons and positrons have opposite signs of the charge, but second, switching electrons for positrons means letting \(\mathbf{p} \rightarrow \mathbf{-p}\), such that the vacuum contributions are additive. Nevertheless, when integrating over momentum to get the total current density, we still get zero as one would expect. The substitution \({\mathbf {p}} \rightarrow - {\mathbf {p}}\) when switching between electrons and positrons also holds for real particles as well as the vacuum contribution. In particular, for beam systems, this is important to keep in mind, as is illustrated in Fig. 5.
When adding the real particles of the Dirac field (electrons and/or positrons) into the picture, we can add distribution functions much like in the theories of the previous sections. Specifically, we could start from a background
with a nonzero charge density
The function \(f_{e,p}(\mathbf{p})\) can be picked as any common background distribution function from classical kinetic theory, i.e. a Maxwell–Boltzmann, Synge–Juttner, or Fermi-Dirac distribution, depending on whether the characteristic kinetic energy is relativistic and whether the particles are degenerate.
Note that for a completely degenerate (\(T=0\)) Fermi-Dirac background of electrons (and no positrons \(f_{p}=0\)), the electron and vacuum contributions for the mass density and current density cancel inside the Fermi sphere. Consequently, for momenta \(p\le p_{F}\), where \(p_{F}=\hbar (3\pi ^2n_{0})^{1/3}\) is the Fermi momentum, we have \(s=\mathbf{v}=0\). Furthermore, note that in the presence of a strong field in the background state (e.g., a strong constant magnetic field), these fairly simple background expressions need to be modified. For example, in a case with \(\mu _B B_0 \sim mc^2\), also the vacuum states will be subject to Landau quantization. Moreover, the spin density and magnetization (as described by the functions \(\mathbf{a}\) and \(\mathbf{t}_{\mathbf{1}}\), respectively) will no longer vanish in the background state, due to the contribution from real particles.
6.2 The electrostatic one-dimensional case
To illustrate some features of the DHW theory, we will consider the case of a one-dimensional electrostatic field, i.e., \(\mathbf{E}=E(z,t){{{\hat{\mathbf{z}}}}}\). At the same time, the DHW functions depend on \((\mathbf{p},z,t)\), but where the momentum dependence can be reduced to two independent variables (\(p_{\perp },p_z\)), due to the rotational symmetry.
Due to the simplified geometry, only half of the 16 scalar DHW functions will be nonzero. Moreover, only four of these variables will be independent. There are different ways of finding these nonzero variables. Here, we will just present the result, which is straightforward to verify by direct substitutions into the DHW equations, Eq. (131). For a more systematic derivation of the reduced electrostatic equations, see Ref. (Al-Naseri et al. 2021). As it turns out, the DHW equations can be expressed in terms of four variables \(\chi _1-\chi _4\), related to the original DHW functions as follows:
where \(\epsilon _{\perp }=\sqrt{m^2+p_{\perp }^2}\). Taking this as an ansatz for the variables \(\chi _1-\chi _4\) and substituting the expressions into Eq. (131), we obtain the electrostatic equations
where, in the 1D-case of study, \(D_t=\partial _t+eE\partial _{p_z}\) The above system is closed by Ampére’s law, which in terms of the \(\chi\) variables is written
While Eqs. (145)-(146) represent a huge simplification compared to the full DHW theory, they can still describe a host of different phenomena. As an example, Ref. (Hebenstreit et al. 2011) has used a similar set to study Schwinger pair-production for given electrostatic pulses. From a plasma physics perspective, studies of Langmuir waves in a high-density plasma are a natural problem. While the nonlinear strong field regime is interesting to study (allowing for the Schwinger mechanism), we leave that for a future numerical investigation. Instead, we will focus here on the problem of linearized Langmuir waves, as this is straightforward to study analytically.
The nonzero background quantities for the \(\chi _{i}\)-variables can be written as
using upper index 0 for the unperturbed background values, and letting the variables have both electron and positron contributions. Next, we divide the variables into unperturbed and perturbed variables according to
(with \(\chi _{3}^{0}(\mathbf{p})=0\) and only a perturbed electric field E) and linearize (145) and (146). Making use of the relation
the problem is reduced to linear algebra. Solving for \(\chi _{i}^{1}\), and restoring \(\hbar\) to identify the quantum contributions (e.g. letting \((2\pi )^3\rightarrow (2\pi \hbar )^3\) in the denominator of Eq. (146)), we obtain
where
Note that \(F(p_{\pm })\) and \(f_{e,p}(p_{\pm })\) depend on the full momentum, but we suppressed the perpendicular momentum to simplify the notation. Combining the above results for \(\chi _i(\mathbf{p})\) with Ampere’s law (146), we obtain the dispersion relation \(D(k,\omega )=0\) with
The classical, but relativistic, limit of the dispersion relation is obtained by letting \(\hbar \rightarrow 0\). Taking this limit, the dispersion function (156) reduces to
which can be shown to agree with the standard result after some straightforward algebra. Note that the appearance of \(\hbar\) in the integration measure \(\frac{d^3p}{(2\pi \hbar )^3}\) is just a matter of normalization, and not a sign of any remaining quantum features.
The main purpose here as been to demonstrate the usefulness of the DHW equation for practical plasma calculations. However, before ending the discussion, without going into details, let us point out a few features of the general dispersion relation.
-
1.
Apart from the effect of a relativistic Fermi velocity, in the relativistic regime, the quantum contribution to the real part of the plasma frequency will actually decrease with increasing density, since quantum terms are compared with the (high) relativistic Fermi energies and Fermi momenta.
-
2.
The main new effect due to the quantum relativistic regime, comes from the new types of resonant denominators, associated with wave damping. In particular, even for \(k=0\), we may still have a resonant denominator (corresponding to electron–positron pair-production), provided the pair-creation condition \(\hbar \omega \ge 2mc^2\) is fulfilled.
-
3.
Due to the vacuum background, the integrand is nonzero even in the absence of particles, giving raise to the effect of vacuum polarization contribution. While this term typically gives a contribution that is much smaller than that from the real particles, the given expression is subject to ultra-violet divergences that must be handled using a renormalization scheme, see, e.g., Ref. Bialynicki-Birula et al. (1991).
Naturally, the above points only give the principal features. A more thorough study of the quantum relativistic dispersion relation for Langmuir waves has to be done numerically. This will be the subject of a future paper.
6.3 Limiting cases of the DHW theory
Apart from exchange effects, the DHW equations covers all the physical phenomena presented in the previous sections. Thus, ideally, we should be able to recover all the previous models (except the parts presented in Sect. 3) as special cases of the DHW formalism. However, demonstrating the equivalence in appropriate limiting cases is somewhat nontrivial. First of all, the DHW equations do not only describe electrons, since a Foldy–Wouythuysen transformation cannot be made in the fully quantum relativistic regime. Furthermore, the equations with a spin-dependent Wigner function uses a Q-transform to get a scalar theory, which further complicates a comparison. Nevertheless, though a complete investigation is yet to be made, showing the equivalence of the DHW formalism with the models of Sect. IV (i.e., the nonrelativistic Pauli limit) is relatively straightforward.
First, we note that for fields well below the critical field, there is little ambiguity whether we have electron or positron states. Considering the case of electrons only, ignoring relativistic effects, the charge and mass density are the same (due to the normalization, the constant factors involving e and m do not enter), i.e., \(s=v_0\). As a first exercise, let us recover the model based on the Schrödinger Hamiltonian. This implies dropping the effects of the electron spin, i.e., the spin density, magnetization, and spin polarization are zero, and thus, we let \(\mathbf{a}=\mathbf{t_2}=\mathbf{t}_{\mathbf{1}}=0\) in the DHW equations. As a result of the above approximations, we get \(\mathbf{v}={{{\tilde{\mathbf{p}}}}}s={{{\tilde{\mathbf{p}}}}}v_0\), which immediately lead to a closed equation for \(v_0\)
Identifying \(v_0\) with the Wigner function of section 4, using the definitions of the nonlocal variables to write the more explicitly, Eq. (158) gives us
The definitions of \(\Delta {{{\tilde{\mathbf{v}}}}}\), etc., are the same as those in Sect. 4. We note that Eq. (159) coincides with Eq. (37). Thus, Eq. (159) generalizes the results for the electrostatic version of the Schrödinger Hamiltonian to also cover electromagnetic fields, as follows naturally using the gauge-invariant Wigner transform, as discussed in Sect. 2.3. Alternatively, we could re-derive the same equation by dropping the spin terms in Eq. (63) (all terms proportional to \(\mu _B\)), and integrate the equation over spin space.
Next, our aim is to recover the model of Section IV, based on the Pauli Hamiltonian. As the short-scale physics associated with the nonlocal expressions (132)–(135) has already been established above, for convenience, we restrict ourselves to the case of long-scale lengths (\(\hbar \nabla \nabla _p \ll 1\)), such that the local approximations (i.e., dropping the variables with tilde) can be used. For the nonrelativistic case, we can still put the charge and mass density equal, i.e., \(s=v_0\). Second, in the absence of relativistic effects (and for the given normalizations) and for the case of electrons only, the spin density and the magnetization are the same, i.e., \(\mathbf{a}=\mathbf{t}_2\). Third, a nonvanishing polarization due to the spin only enters in the relativistic theory, and thus, we can put \(\mathbf{t}_1=0\). Finally, the term \(\propto D_t \rho\) in Eq. (131) is a small correction (in a quantum relativistic expansion \(\hbar \partial _t/mc^2\)), and hence, we can use the approximation \(a_0=\mathbf{p}\cdot \mathbf{t}_1/m\). With these simplifications as a starting point, the DHW equations can be combined to give the following evolution equation for the magnetization:
Normally, we should drop the term \(\propto \mathbf{p}\times \mathbf{p}\), since such a term is identically zero. However, recall that before introducing approximations, this term would rather be proportional to \({{{\tilde{\mathbf{p}}}}}\times {{{\tilde{\mathbf{p}}}}}\). As it turns out, the local approximations are applicable everywhere else, as in those cases, the corrections are compared with larger surviving terms. Here, however, we need to use the full expression \(\propto {{{\tilde{\mathbf{p}}}}}\times {{{\tilde{\mathbf{p}}}}}\), and evaluate the term to the first nonvanishing order in an expansion in the small parameter \(\hbar \nabla \nabla _p\). Performing this expansion and identifying \(\mathbf{t}_2\) with \(\mathbf{f}\) and \(v_0\) with \(f_0\), after some algebra, we can confirm the exact agreement of Eq. (160) with Eq. (75).
Next, to establish agreement with the model based on the Pauli Hamiltonian, we need to re-derive Eq. (74). Using the same approximations as before, we immediately get
While there is a little bit of algebra involved (since the operator \(\mathbf{D}\) contains the magnetic field), it is straightforward to show that Eq. (161) reduces to Eq. (74). Finally, we note that the current sources to be used in the DHW equations are the same as in the Pauli limit, given that polarizations currents are dropped in nonrelativistic theory. Furthermore, as the agreement between Eqs. (74)–(75) and (68) has already been established, and the short-scale physics (as described by Eq. (159)) have been recovered, for most practical purposes, the full model based on the Pauli Hamiltonian (Eq. (54)) have also been verified, although not in a strict sense.
While the above confirmation is reassuring, the main purpose of studying approximate versions of the DHW model is to find models that are easier to analyze in specific cases. The DHW equations allow for systematic expansions in numerous quantum and relativistic parameters, \(\hbar \omega /mc^2\), \(\hbar e{F}/m^2c^2\) (where F represents electric and/or magnetic fields), \(\hbar \nabla \nabla _p\), p/mc, and \(\hbar k^2/m\omega\) to name a few. Here, \(\omega\) and k represent general temporal and spatial scales, rather than specific frequencies and wave numbers. Depending on the ordering of the dimensionless parameters, there are several possibilities for approximate models containing different combinations of expansion parameters. A systematic search for consistent approximations of the DHW system is a project for further research.
7 Concluding remarks
While the aim of this review has been to cover many aspects of quantum kinetic theory, naturally, there are many interesting and important topics that we have not touched upon. While, undoubtedly, many things will be left out altogether, let us here at least partially remedy some of the omissions made, by pointing to a few relevant aspects of quantum kinetic theory that we have not covered.
Firstly, as is well known, there are close connections between hydrodynamic and kinetic theories. In particular, a common approach to derive accurate fluid theories is by making moment expansions of kinetic theories. In a quantum context, this scheme has been used to derive fluid theories from kinetic theories, e.g., by Refs. Cai et al. (2012); Haas et al. (2010a, 2010b) for the model defined by the Schrödinger Hamiltonian and by Refs. Hurst et al. (2014); Zamanian et al. (2010) for the Pauli Hamiltonian model, and also by Ref. Hurst et al. (2017) for the model where the Pauli Hamiltonian is extended by the spin-orbit term. Moreover, moment expansion for models including exchange effects has been made by, e.g., Refs. Haas (2021); Manfredi (2020).
Second, we note that for completely degenerate systems, in certain cases, kinetic models may be simplified. This happens in situations when the phase-space density is conserved, in which case the dynamics is determined by the Fermi surface. This has been explored in the so-called waterbag models of plasmas (Manfredi 2020, 2005) and also for the case of a semiclassical model based on the Pauli Hamiltonian (Brodin and Stefan 2013).
Thirdly, we stress that we here have focused on nondissipative quantum kinetic models, ignoring the effects of higher order correlation in the BBGKY-hierarchy, neglecting all the influence of collisions, as can be covered, e.g., by path integral quantum monte carlo methods (Dornheim et al. 2018; Hamann et al. 2020; Zhang et al. 2016). However, the effect of dissipation is a broad research topic in its own right, of particular importance in the strong coupling regime. For references covering this field, see e.g. (Bonitz 2016; Ichimaru 1982; Bonitz et al. 2015).
As our review has focused on quantum kinetic models, and the worked out examples has served the purpose of illustrating the applicability of the theory, many aspects of quantum kinetic theory have still been ignored; in particular, interesting theoretical aspects involving wave–particle interaction, spin-polarization dynamics, numerical computation schemes, and the interesting interplay with single-particle dynamics (Dinu et al. 2016)
References
The extreme light infrastructure project (2020) https://eli-laser.eu/
The European X-Ray Free-Electron Laser Facility (2020) https://www.xfel.eu/
I.A. Aleksandrov, C. Kohlfurst, Phys. Rev. D 101, 096009 (2020)
H. Al-Naseri, J. Zamanian, R. Ekman, G. Brodin, Phys. Rev. E 102, 043203 (2020)
H. Al-Naseri, J. Zamanian, G. Brodin, Phys. Rev. E 104, 015207 (2021)
P.A. Andreev, Ann. Phys. 350, 198 (2014)
P.A. Andreev, Phys. Plasmas 23, 062103 (2016)
P.A. Andreev, Phys. Plasmas 24, 022115 (2017)
P.A. Andreev, Phys. Plasmas 25, 032116 (2018)
P.A. Andreev, L.S. Kuzmenkov, Phys. Plasmas 24, 112108 (2017)
F.A. Asenjo, J. Zamanian, M. Marklund, G. Brodin, P. Johansson, New J. Phys. 14, 073042 (2012)
H.A. Atwater, Sci. Am. 296, 56 (2007)
D. Babson, S.P. Reynolds, R. Bjorkquist, D.J. Griffiths, Am. J. Phys. 77, 826 (2009)
I. Bialynicki-Birula, P. Gornicki, J. Rafelski, Phys. Rev. D 44, 1825 (1991)
D.B. Boercker, J.W. Dufty, Ann. Phys. 119, 43 (1979)
N.N. Bogolyubov, Z. Eksp, Teor. Fiz. 16, 691 (1946). ([JETP 10, 265 (1946)])
M. Bonitz, Quantum Kinetic Theory, 2nd edn. (Springer, Cham, 2016)
M. Bonitz, N. Schlunzen, S. Hermanns, Contrib. Plasma Phys. 55, 152 (2015)
M. Bonitz, Z.H.A. Moldabekov, T.S. Ramazanov, Phys. Plasmas 26, 090601 (2019)
T.J.M. Boyd, J.J. Sanderson, The Physics of Plasmas (Cambridge University Press, Cambridge, 2003)
G. Brodin, M. Stefan, Phys. Rev. E 88, 023107 (2013)
G. Brodin, M. Marklund, J. Zamanian, A. Ericsson, P.L. Mana, Phys. Rev. Lett. 101, 245002 (2008)
G. Brodin, A.P. Misra, M. Marklund, Phys. Rev. Lett. 105, 105004 (2010)
G. Brodin, R. Ekman, J. Zamanian, Phys. Plasmas 26, 092113 (2019)
Z. Cai, Y. Fan, R. Li, T. Lu, Y. Wang, J. Math. Phys. 53, 103503 (2012)
G. Chabrier, F. Douchin, A. Potekhin, J. Phys.: Condens. Matter 14, 9133 (2002)
S. Coleman, J.H. Van Vleck, Phys. Rev. 171, 1370 (1968)
N. Crouseilles, G. Manfredi, Comput. Phys. Commun. 185, 448 (2014)
N. Crouseilles, P.-A. Hervieux, G. Manfredi, Phys. Rev. B 78, 155412 (2008)
N. Crouseilles, P. Hervieux, Y. Li, G. Manfredi, Y. Sun, J. Plasma Phys. 87, 825870301 (2021)
D. Del Sorbo, D. Seipt, T.G. Blackburn, A.G.R. Thomas, C.D. Murphy, J.G. Kirk, C.P. Ridgers, Phys. Rev. A 96, 043407 (2017)
V. Dinu, C. Harvey, A. Ilderton, M. Marklund, G. Torgrimsson, Phys. Rev. Lett. 116, 044801 (2016)
T. Dornheim, S. Groth, J. Vorberger, M. Bonitz, Phys. Rev. Lett. 121, 255001 (2018)
G. Dunne, Eur. Phys. J. D 55, 327 (2009)
R. Ekman, J. Zamanian, G. Brodin, Phys. Rev. E 92, 013104 (2015)
R. Ekman, F.A. Asenjo, J. Zamanian, Phys. Rev. E 96, 023207 (2017)
R. Ekman, H. Al-Naseri, J. Zamanian, G. Brodin, Phys. Rev. E 100, 023201 (2019)
R. Ekman, H. Al-Naseri, J. Zamanian, G. Brodin, Eur. Phys. J. D 75, 29 (2021)
B. Eliasson, P.K. Shukla, J. Plasma Phys. 76, 7 (2009)
S. Eliezera, P. Norreys, J.T. Mendonça, K. Lancaster, Phys. Plasmas 12, 052115 (2005)
I.S. Elkamash, F. Haas, I. Kourakis, Phys. Plasmas 24, 092119 (2017)
A. Foldy, L. Wouthuysen, Phys. Rev. 78, 29 (1950)
P. Giannozzi, S. Baroni, N. Bonin et al., J. Phys.: Condens. Matter 21, 395502 (2009)
S.H. Glenzer, R. Redmer, Rev. Mod. Phys. 81, 1625 (2009)
F. Haas, Phys. Plasmas 15, 022104 (2008)
F. Haas, Quantum Plasmas, A Hydrodynamics Approach, Chap 2 (Springer, New York, 2011)
F. Haas, Contrib. Plasma Phys. 2021, e202100046 (2021)
F. Haas, P.K. Shukla, Phys. Plasmas 15, 112302 (2008)
F. Haas, B. Eliasson, P.K. Shukla, G. Manfredi, Phys. Rev. E 78, 056407 (2008)
F. Haas, M. Marklund, G. Brodin, J. Zamanian, Phys. Lett. A 374, 481 (2010)
F. Haas, M. Marklund, G. Brodin, J. Zamanian, NJP 12, 073027 (2010)
P. Hamann, J. Vorberger, T. Dornheim, Z.A. Moldabekov, M. Bonitz, Contr. Plasma Phys. 60, e202000147 (2020)
A.K. Harding, D. Lai, Rep. Prog. Phys. 69, 2631 (2006)
P.J. Hasnip, K. Refson, M.I.J. Probert, J.R. Yates, S.J. Clark, C.J. Pickard, Phil. Trans. R. Soc. A 372, 20130270 (2014)
F. Hebenstreit, R. Alkofer, H. Gies, Phys. Rev. D 82, 105026 (2010)
F. Hebenstreit, R. Alkofer, H. Gies, Phys. Rev. Lett. 107, 180403 (2011)
J. Hurst, O. Morandi, G. Manfredi et al., Eur. Phys. J. D 68, 176 (2014)
J. Hurst, P.A. Hervieux, G. Manfredi, Phil. Trans. R. Soc. A 375, 20160199 (2017)
A. Hussain, M. Stefan, G. Brodin, Phys. Plasmas 21, 032104 (2014)
S. Ichimaru, Rev. Mod. Phys. 54, 1017 (1982)
V.I. Karpman, H. Washimi, J. Plasma Phys. 18, 173 (1977)
W. Kohn, L.J. Sham, Phys. Rev. 140, 1133 (1965)
T. Kurki-Suonio, P.J. Morrison, T. Tajima, Phys. Rev. A 40, 3230 (1989)
Y.-F. Li, R. Shaisultanov, K.Z. Hatsagortsyan, F. Wan, C.H. Keitel, J.-X. Li, Phys. Rev. Lett. 122, 154801 (2019)
D. Liu et al., Nat. Commun. 9, 193 (2018)
J. Lundin, G. Brodin, Phys. Rev. E 82, 056407 (2010)
A.H. MacDonald, G.W. Bryant, Phys. Rev. Lett. 58, 515 (1987)
G. Manfredi, Fields Inst. Commun. 46, 263 (2005)
G. Manfredi, J. Plasma Phys. 86, 825860201 (2020)
G. Manfredi, P.-A. Hervieux, Appl. Phys. Lett. 91, 61108 (2007)
G. Manfredi, J. Hurst, Plasma Phys. Control. Fus. 57, 054004 (2015)
G. Manfredi, P.-A. Hervieux, J. Hurst, Rev. Mod. Plasma Phys. 3, 13 (2019)
G. Manfredi, P.A. Hervieux, J. Hurst, Rev. Mod. Plasma Phys. 5, 7 (2021)
D.B. Melrose, Rev. Mod. Plasma Phys. 4, 8 (2020)
D.B. Melrose, A.J. Parle, Aust. J. Phys. 36, 755 (1983)
J.T. Mendonça, Symmetry 13, 1361 (2021)
A.P. Misra, G. Brodin, M. Marklund, P.K. Shukla, Phys. Plasmas 17, 122306 (2010)
A.P. Misra, G. Brodin, M. Marklund, P.K. Shukla, Phys. Rev. E 82, 056406 (2010)
Z.A. Moldabekov, M. Bonitz, T.S. Ramazanov, Phys. Plasmas 25, 031903 (2018)
A. Moradi, J. Phys.: Condens. Matter 21, 045303 (2008)
J.E. Moyal, Math. Proc. Cambr. Phil. Soc. 45, 99 (1949)
H. Nersisyan, C. Toepffer, G. Zwicknagel, Interactions Between Charged Particles in a Magnetic Field (Springer, Berlin, 2007)
S. Rightley, D. Uzdensky, J. Plasma Phys. 84, 905840408 (2018)
A. Ringwald, Phys. Lett. B 510, 107 (2001)
J.J. Sakurai, J. Napolitano, Modern Quantum Mechanics, 2nd edn. (Cambridge University Press, Cambridge, 2017)
M.O. Scully, K. Wódkiewicz, Found. Phys. 24, 85 (1994)
O.T. Serimaa, J. Javanainen, S. Varró, Phys. Rev. A 33, 2913 (1986)
M.I. Shaukat, Phys. Plasmas 24, 062305 (2017)
X.L. Sheng, R.H. Fang, Q. Wang, D.H. Rischke, Phys. Rev. D 99, 056004 (2019)
Y. Shi, J. Xiao, H. Qin, N.J. Fisch, Phys. Rev. E 97, 053206 (2018)
W. Shockley, Phys. Rev. Lett. 20, 343 (1968)
W. Shockley, R.P. James, Phys. Rev. Lett. 18, 876 (1967)
P.K. Shukla, B. Eliasson, Phys.-Usp. 53, 51 (2010)
P.K. Shukla, B. Eliasson, Rev. Mod. Phys. 83, 885 (2011)
P.K. Shukla, N.N. Rao, M.Y. Yu, N.L. Tsintsadze, Phys. Rep. 138, 1 (1986)
A.J. Silenko, Phys. Rev. A 77, 012116 (2008)
D.D. Sorbo, D. Seipt, A.G.R. Thomas, C.P. Ridgers, Plasma Phys. Control. Fusion 60, 064003 (2018)
M. Stefan, G. Brodin, Phys. Plasmas 20, 012114 (2013)
M. Stefan, J. Zamanian, G. Brodin, A.P. Misra, M. Marklund, Phys. Rev. E 83, 036410 (2011)
R.L. Stratonovic, Z. Eksp, Teor. Fiz. 58, 1612 (1970). ([Sov. Phys. -JETP 31, 864 (1970)])
G. Swanson, Plasma Waves (Taylor & Francis, Routledge, 2003)
T. Tajima, J.M. Dawson, Phys. Rev. Lett. 43(4), 267 (2020)
L.C. Thomas, T. Dezen, E.B. Grohs, C.T. Kishimoto, Phys. Rev. D 101, 063507 (2020)
Yu. Tyshetskiy, S.V. Vladimirov, R. Kompaneets, J. Plasma Phys. 79, 387 (2013)
Yu. Tyshetskiy, S.V. Vladimirov, R. Kompaneets, Phys. Plasmas 21, 122114 (2014)
D.A. Uzdensky, S. Rightley, Rep. Prog. Phys. 77, 036902 (2014)
S.V. Vladimirov, Y.O. Tyshetskiy, Phys.-Usp. 54, 1243 (2011)
O. Von Roos, J. Zmuidzinas, Phys. Rev. 121, 941 (1961)
S.J. Wang, W. Cassing, Ann. Phys. 159, 328 (1985)
E. Wigner, Phys. Rev. 40, 749 (1932)
S.A. Wolf, D.D. Awschalom, R.A. Buhrman, J.M. Daughton, S. Von Molnar, M.L. Roukes, A.Y. Chtchelkanova, D.M. Treger, Science 294, 1488 (2001)
C. Zachos, D. Fairlie, T. Curtright, Quantum Mechanics in Phase Space (World Scientific, Singapore, 2005)
J. Zamanian, M. Stefan, M. Marklund, G. Brodin, Phys. Plasmas 17, 102109 (2010)
J. Zamanian, M. Marklund, G. Brodin, New J. Phys. 12, 043019 (2010)
J. Zamanian, M. Marklund, G. Brodin, Phys. Rev. E 88, 63105 (2013)
J. Zamanian, M. Marklund, G. Brodin, Eur. Phys. J. D 69, 25 (2015)
S. Zhang, K.P. Driver, F. Soubiran, B. Militzer, HEDP 21, 16 (2016)
P. Zhang, S.S. Bulanov, D. Seipt, A.V. Arefiev, A.G.R. Thomas, Phys. Plasmas 27, 050601 (2020)
Funding
Open access funding provided by Umea University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A BBGKY-hierarchy and the mean-field approximation
A BBGKY-hierarchy and the mean-field approximation
The N-particle density matrix is not directly applicable in the case where we have a large number of particles, as is typically the case for plasmas. It is, therefore, necessary to make some approximations to reduce the complexity of the equations. One commonly used approximations when dealing with plasmas is the mean-field approximation, which we will consider here. Since it is more convenient for this type of considerations, we will here use the operator representation of the density matrix (as opposed to using the position representation as was done in Sect. 2. Using the bra-ket notation, we can define the density operator as
where \(|\psi _i \rangle\) are N-particle states. The evolution equation can then be written as
where \(\left[ \cdot , \cdot \right]\) denotes the commutator. Assume that we have an Hamiltonian in the form
where
is the kinetic energy operator, with \(\hat{{\mathbf {p}}}_i\) being the momentum operator acting on the i:th particle. The operator in the last term \({\hat{V}}_{ij}\) corresponds to particle–particle interactions, which we will later take as the Coulomb interaction. However, for now, we only need to assume that the interaction is symmetric under exchange of particles, i.e., \({\hat{V}}_{ij} = {\hat{V}}_{ji}\). We note that the density matrix is symmetric with respect to change of particles, that is
This is true, as long as the particles are indistinguishable, and hence both for fermions and bosons. We may now define the s-particle reduced density matrix as
where we, for convenience, have multiplied by the number of particles i times. Now, using the above, we can derive the so-called BBGKY-hierarchy for the reduced density matrices
Here, we have assumed that N is large, so that we may use \(N-s \approx N\) to any order s where the above equation is of any practical use. We note that the one-particle density matrix couples to the two-particle density matrix, etc. Now, we are only interested in the lowest equation which is
To make progress from this, we write the two-particle density matrix as
where \({\hat{g}}_{12}\) is the two-particle correlations defined by the equation above. In the lowest order approximation, we completely neglect the two-particle correlations \({\hat{g}}_{12} \approx 0\). We then get the so-called mean-field, or Hartree approximation
We note that the normalization of the density matrix is such that
i.e., the number of particles. The diagonal elements can then be identified as the local density of particles \(\rho ({\mathbf {r}}, {\mathbf {r}}) = n({\mathbf {r}})\). In particular, in the case of a plasma interacting via the Coulumb interaction
and the last term is
where the last step is written in terms of the mean-field potential, i.e., the potential created by all particles interacting with particle 1. Here, we have only considered particles which are indistinguishable, but we have not yet taken into account the correct symmetry. For fermions, we need to modify the procedure slightly to account for the antisymmetry of the wave function, but the basic principle is the same. We will do this modification in Sect. 3 where we consider exchange effects. The conclusion from the above considerations is that if we can assume that particle correlations are negligible, we may describe the plasma as particles moving in the mean field created by all the other particles.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brodin, G., Zamanian, J. Quantum kinetic theory of plasmas. Rev. Mod. Plasma Phys. 6, 4 (2022). https://doi.org/10.1007/s41614-022-00065-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41614-022-00065-5