Introduction

The spin and pseudospin symmetry concepts introduced in nuclear theory [1, 2] have been used to explain the features of deformed nuclei [3] and superdeformation [4], and to establish an effective shell-model coupling scheme [5]. Within the framework of the relativistic mean field theory, Ginocchio [6, 7] has found that a Dirac Hamiltonian with scalar and vector harmonic oscillator potentials in the case of (V(r) − S(r) = 0) possesses not only a spin symmetry but also a U(3)symmetry, but a Dirac Hamiltonian in the case of (V(r) + S(r) = 0) possesses a pseudospin symmetry and a pseudo-U(3)symmetry. Meng et al. [8] have showed that the pseudospin symmetry is exact under the condition (d(V(r) + S(r))/dr = 0). In addition, Alhaidari et al. [9] have investigated in detail physical interpretation on the three-dimensional Dirac equation in the case of spin symmetry limit (V(r) − S(r) = 0) and pseudospin symmetry limit (V(r) + S(r) = 0). In recent years, by considering the importance of spin and pseudospin symmetries, some authors have contributed many works in this field. For more review of this, one can read the recent works by Wei and Dong [10–13].

The p-spin symmetry refers to a quasidegeneracy of single nucleon doublets with non-relativistic quantum number (n, l, j = l + 1/2) and (n − 1, l + 2, j = l + 3/2), where n, l and j are single nucleon radial, orbital and total angular quantum numbers, respectively [1, 2]. The total angular momentum \( j = \tilde{l} + \tilde{s} \) with \( \tilde{l} = l + 1 \) is a pseudoangular momentum and \( \tilde{s} \) is p-spin angular momentum [14–18].

In this paper, we attempt to study the spin and pseudospin symmetry solutions of the Dirac equation for arbitrary quantum number κ with the Pöschl–Teller-like potential. This is given by

$$ V(r) = \frac{{V_{1} - V_{2} \cos \,h\,\alpha r}}{{\sin \,h^{2} \alpha r}}. $$
(1)

The potential parameters V 1 and V 2 describe the property of the potential well, V 1 > V 2, while α is related to the range of the potential [19–24]. The behavior of this potential with respect to four different values of α is shown in Fig. 1.

Fig. 1
figure 1

The behavior of the Pöschl–Teller-like potential with respect to four different values of α, and for V 1 = 0.5, V 2 = 0.1

Full size image

Also Tensor potentials have been introduced into the Dirac equation with the substitution \( \vec{p} \to \vec{p} - im\,\omega \,\beta \cdot \hat{r}\,U\left( r \right) \) and a spin–orbit coupling is added to the Dirac Hamiltonian [25, 26]. For more review of tensor interaction, one can refer to the [27–34] that authors used different potential and different kinds of tensor potential. Here we study a tensor potential in the Coulomb-like form as follows:

$$ U(r) = - \frac{{U_{{0{\text{C}}}} }}{r},\quad U_{{0{\text{C}}}} = \frac{{Z_{a} Z_{b} e^{2} }}{{4\pi \varepsilon_{0} }},\quad r \ge R_{\text{C}} , $$
(2)

where R C = 7.78 fm is the coulomb radius, and Z a and Z b denote the charges of the projectile a and the target nuclei b, respectively.

The Potential in Eq. (1) is also one of the important examples for the special case of the multiparameter exponential-type potential model [35, 36]. By solving the Klein–Gordon equation and Dirac equation with equal scalar and vector Pöschl–Teller-like potentials, the exact relativistic energy equations have been obtained for the s-wave bound states (l = 0) [37, 38]. Using the conventional approximation scheme proposed by Greene and Aldrich [39] to deal with the centrifugal term, Dong et al. [40, 41] have investigated the arbitrary l-wave bound-state solutions of the Schrödinger equation and Klein–Gordon equation with the Pöschl–Teller-like potential in terms of the standard function analysis method. However, as far as we know, one has not reported the investigation of the spin and pseudospin symmetries solutions of the Dirac equation with the Pöschl–Teller-like potential including a Coulomb-like potential as a tensor interaction for the arbitrary spin–orbit quantum number κ. In this paper, we solve approximately the Dirac equation with the Pöschl–Teller-like potential for the spin–orbit quantum number κ. Under the condition of spin and pseudospin symmetries, we study the bound-state energy equation and corresponding spinor wave functions in terms of the basic concept of the supersymmetric shape invariance formalism [42, 43] and the function analysis method.

Dirac equation including tensor coupling

The Dirac equation for fermionic massive spin-1/2 particles moving in attractive scalar S(r),  repulsive vector V(r) and tensor U(r) potentials is (in units ℏ = c = 1)

$$ \left[ {\vec{\alpha } \cdot \vec{p} + \beta \left( {M + S\left( r \right)} \right) - i\,\beta \,\vec{\alpha } \cdot \hat{r}\,U\left( r \right)} \right]\psi \left( {\vec{r}} \right) = \left[ {E - V\left( r \right)} \right]\psi \left( {\vec{r}} \right), $$
(3)

where E is the relativistic energy of the system, \( \vec{p} = - i\,\vec{\nabla } \) is the three-dimensional momentum operator and M is the mass of the fermionic particle. Further, \( \vec{\alpha } \) and β are the 4 × 4 Dirac matrices given by

$$ \vec{\alpha } = \left( {\begin{array}{*{20}c} 0 & {\vec{\sigma }} \\ {\vec{\sigma }} & 0 \\ \end{array} } \right),\quad \beta = \left( {\begin{array}{*{20}c} I & 0 \\ 0 & { - I} \\ \end{array} } \right), $$
(4)

where I is 2 × 2 unitary matrix and \( \vec{\sigma } \) are three-vector spin matrices

$$ \sigma_{1} = \left( {\begin{array}{*{20}c} 0 & 1 \\ 1 & 0 \\ \end{array} } \right),\quad \sigma_{2} = \left( {\begin{array}{*{20}c} 0 & { - i} \\ i & 0 \\ \end{array} } \right),\quad \sigma_{3} = \left( {\begin{array}{*{20}c} 1 & 0 \\ 0 & { - 1} \\ \end{array} } \right). $$
(5)

The total angular momentum operator \( \vec{J} \) and spin–orbit \( K = \left( {\vec{\sigma } \cdot \vec{L} + 1} \right) \), where \( \vec{L} \) is orbital angular momentum of the spherical nucleons, commute with the Dirac Hamiltonian. The eigenvalues of spin–orbit coupling operator are \( \kappa = \left( {j + \frac{1}{2}} \right) > 0 \) and \( \kappa = - \left( {j + \frac{1}{2}} \right) < 0 \) for unaligned spin \( j = l - \frac{1}{2} \) and the aligned spin \( j = l + \frac{1}{2} \), respectively. (H 2, K, J 2, J z ) can be taken as the complete set of the conservative quantities. Thus, the spinor wave functions can be classified according to their angular momentum j; spin–orbit quantum number κ and the radial quantum number n can be written as follows:

$$ \psi_{n\kappa } \left( {\vec{r}} \right) = \left( {\begin{array}{*{20}c} {f_{n\kappa } \left( {\vec{r}} \right)} \\ {g_{n\kappa } \left( {\vec{r}} \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{{F_{n\kappa } \left( r \right)}}{r}Y_{jm}^{l} \left( {\theta ,\varphi } \right)} \\ {i\frac{{G_{n\kappa } \left( r \right)}}{r}Y_{jm}^{{\tilde{l}}} \left( {\theta ,\varphi } \right)} \\ \end{array} } \right), $$
(6)

where \( f_{n\kappa } \left( {\vec{r}} \right) \) is the upper (large) component and \( g_{n\kappa } \left( {\vec{r}} \right) \) is the lower (small) component of the Dirac spinors. Y l jm (θ, ϕ) and \( Y_{jm}^{{\tilde{l}}} \left( {\theta ,\phi } \right) \) are spin and p-spin spherical harmonics, respectively, and m is the projection of the angular momentum on the z-axis. Substituting Eq. (6) into Eq. (3) and using the following relations:

$$ \left( {\vec{\sigma } \cdot \vec{A}} \right)\left( {\vec{\sigma } \cdot \vec{B}} \right) = \vec{A} \cdot \vec{B} + i\vec{\sigma } \cdot \left( {\vec{A} \times \vec{B}} \right), $$
(7a)
$$ \left( {\vec{\sigma } \cdot \vec{P}} \right) = \vec{\sigma } \cdot \hat{r}\left( {\hat{r} \cdot \vec{P} + i\frac{{\vec{\sigma } \cdot \vec{L}}}{r}} \right) $$
(7b)

together with the following properties:

$$ \begin{aligned} \left( {\vec{\sigma } \cdot \vec{L}} \right)Y_{jm}^{{\tilde{l}}} \left( {\theta ,\phi } \right) & = \left( {\kappa - 1} \right)Y_{jm}^{{\tilde{l}}} \left( {\theta ,\phi } \right), \\ \left( {\vec{\sigma } \cdot \vec{L}} \right)Y_{jm}^{l} \left( {\theta ,\phi } \right) & = - \left( {\kappa - 1} \right)Y_{jm}^{l} \left( {\theta ,\phi } \right), \\ \left( {\vec{\sigma } \cdot \hat{r}} \right)Y_{jm}^{{\tilde{l}}} \left( {\theta ,\phi } \right) & = - Y_{jm}^{l} \left( {\theta ,\phi } \right), \\ \left( {\vec{\sigma } \cdot \hat{r}} \right)Y_{jm}^{l} \left( {\theta ,\phi } \right) & = - Y_{jm}^{{\tilde{l}}} \left( {\theta ,\phi } \right),\, \\ \end{aligned} $$
(8)

one obtains two coupled differential equations for upper and lower radial wave functions F nκ (r) and G nκ (r) as:

$$ \left( {\frac{\text{d}}{{{\text{d}}r}} + \frac{\kappa }{r} - U\left( r \right)} \right)F_{n\kappa } \left( r \right) = \left( {M + E_{n\kappa } -\Delta \left( r \right)} \right)G_{n\kappa } \left( r \right), $$
(9a)
$$ \left( {\frac{\text{d}}{{{\text{d}}r}} - \frac{\kappa }{r} + U\left( r \right)} \right)G_{n\kappa } \left( r \right) = \left( {M - E_{n\kappa } + \varSigma \left( r \right)} \right)F_{n\kappa } \left( r \right). $$
(9b)

where

$$ \Delta \left( r \right) = V\left( r \right) - S\left( r \right), $$
(10a)
$$ \varSigma \left( r \right) = V\left( r \right) + S\left( r \right), $$
(10b)

are the difference and the sum potentials, respectively. Eliminating F nκ (r) and G nκ (r) from Eqs. (9), we finally obtain the following two Schrödinger-like differential equations for the upper and lower radial spinor components, respectively:

$$ \begin{gathered} \left[ {\frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} - \frac{{\kappa \left( {\kappa + 1} \right)}}{{r^{2} }} + \frac{2\kappa }{r}U\left( r \right) - \frac{{{\text{d}}U\left( r \right)}}{{{\text{d}}r}} - U^{2} \left( r \right)} \right]F_{n\kappa } \left( r \right) \hfill \\ \quad \quad + \frac{{\frac{{{\text{d}}\Delta \left( r \right)}}{{{\text{d}}r}}}}{{M + E_{n\kappa } -\Delta \left( r \right)}}\left( {\frac{\text{d}}{{{\text{d}}r}} + \frac{\kappa }{r} - U\left( r \right)} \right)F_{n\kappa } \left( r \right) \hfill \\ \quad \quad = \left[ {\left( {M + E_{n\kappa } -\Delta \left( r \right)} \right)\left( {M - E_{n\kappa } + \varSigma \left( r \right)} \right)} \right]F_{n\kappa } \left( r \right), \hfill \\ \end{gathered} $$
(11)
$$ \begin{gathered} \left[ {\frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} - \frac{{\kappa \left( {\kappa - 1} \right)}}{{r^{2} }} + \frac{2\kappa }{r}U\left( r \right) + \frac{{{\text{d}}U\left( r \right)}}{{{\text{d}}r}} - U^{2} \left( r \right)} \right]G_{n\kappa } \left( r \right) \hfill \\ \quad + \frac{{\frac{{{\text{d}}\varSigma \left( r \right)}}{{{\text{d}}r}}}}{{M - E_{n\kappa } + \varSigma \left( r \right)}}\left( {\frac{\text{d}}{{{\text{d}}r}} - \frac{\kappa }{r} + U\left( r \right)} \right)G_{n\kappa } \left( r \right) \hfill \\ \quad = \left[ {\left( {M + E_{n\kappa } -\Delta \left( r \right)} \right)\left( {M - E_{n\kappa } + \varSigma \left( r \right)} \right)} \right]G_{n\kappa } \left( r \right) \hfill \\ \end{gathered} $$
(12)

where \( \kappa \left( {\kappa - 1} \right) = \tilde{l}\left( {\tilde{l} + 1} \right) \) and κ(κ + 1) = l(l + 1).

The quantum number κ is related to the quantum numbers for spin symmetry l and p-spin symmetry \( \tilde{l} \) as:

$$ \kappa = \left\{ {\begin{array}{*{20}l} { - (l + 1) = - \left( {j + \frac{1}{2}} \right)} \hfill & {(s_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,p_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} ,{\text{etc}}.)} \hfill & {j = l + \frac{1}{2},} \hfill & {{\text{aligned spin}}\,(\kappa < 0)} \hfill \\ { + l = + \left( {j + \frac{1}{2}} \right)} \hfill & {(p_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,d_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} ,{\text{etc}}.)} \hfill & {j = l - \frac{1}{2},} \hfill & {{\text{unaligned spin}}\,(\kappa > 0),} \hfill \\ \end{array} } \right. $$

and the quasidegenerate doublet structure can be expressed in terms of a p-spin angular momentum \( \tilde{s} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2} \) and pseudoorbital angular momentum \( \tilde{l} \), which can be defined as:

$$ \kappa = \left\{ {\begin{array}{*{20}l} { - \tilde{l} = - \left( {j + \frac{1}{2}} \right)} \hfill & {(s_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,p_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} ,{\text{etc}}.)} \hfill & {j = \tilde{l} - \frac{1}{2},} \hfill & {{\text{alinged p}} - {\text{spin}}\,(\kappa < 0),} \hfill \\ { + (\tilde{l} + 1) = + \left( {j + \frac{1}{2}} \right)} \hfill & {(d_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} ,f_{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} ,{\text{etc}}.)} \hfill & {j = \tilde{l} + \frac{1}{2},} \hfill & {{\text{unaligned p}} - {\text{spin}}\,(\kappa > 0),} \hfill \\ \end{array} } \right. $$

where κ = ± 1, ± 2, …. For example, (1s 1/2, 0d 3/2) and (1p 3/2, 0f 5/2) can be considered as p-spin doublets.

Spin symmetry limit

In this section, we will solve Dirac equation under spin symmetry limit with Pöschl–Teller-like potential and Coulomb-like potential as a tensor interaction. The exact spin symmetry occurs in Dirac equation when (d[V(r) − S(r)]/dr = dΔ(r)/dr = 0) or Δ(r) = C s = constant [44–47]. Substituting Eqs. (1), (2) into Eq. (11) and taking Σ(r) as the Pöschl–Teller-like potential, the equation obtained for the upper component of the Dirac spinor, F nκ (r), becomes

$$ \left[ {\frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} - } \right.\left. {\frac{{\lambda_{\kappa } \left( {\lambda_{\kappa } + 1} \right)}}{{r^{2} }} - \gamma \left( {\frac{{V_{1} - V_{2} \cos \,h\,\alpha r}}{{\sin \,h^{2} \alpha r}}} \right) - \beta^{2} } \right]F_{n\kappa } \left( r \right) = 0, $$
(13)

where λ κ  = κ + U 0C, γ = M + E nκ  − C s and β 2 = (M − E nκ )(M + E nκ  − C s). Also, κ = l and κ = −l − 1 for κ < 0 and κ > 0, respectively.

P-spin symmetry limit

Within the pseudospin symmetry case, (d[V(r) + S(r)]/dr = dΣ(r)/dr = 0) or Σ(r) = C ps = constant and p-spin symmetry is exact in the Dirac equation [8, 48–50]. In this part, we consider Δ(r) as the Pöschl–Teller-like potential, the equation obtained for the lower component of the Dirac spinor, G nκ (r), becomes

$$ \left[ {\frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} - } \right.\left. {\frac{{\lambda_{\kappa } \left( {\lambda_{\kappa } - 1} \right)}}{{r^{2} }} - \tilde{\gamma }\left( {\frac{{V_{1} - V_{2} \cos \,h\alpha r}}{{\sin \,h^{2} \alpha r}}} \right) - \tilde{\beta }^{2} } \right]G_{n\kappa } \left( r \right) = \,0\,, $$
(14)

where λ κ  = κ + U 0C, \( \tilde{\gamma } = M - E_{n\kappa } + C_{\text{ps}} \), \( \tilde{\beta }^{2} = \left( {M + E_{n\kappa } } \right)\left( {M - E_{n\kappa } + C_{\text{ps}} } \right) \). Also, \( \kappa = - \tilde{l} \) and \( \kappa = \tilde{l} + 1 \) for κ < 0 and κ > 0, respectively.

Equations (13) and (14) can be solved analytically only for the case of λ κ  = − 1 and λ κ  = 1 due to the pseudocentrifugal terms, λ κ (λ κ  + 1)/r 2 and λ κ (λ κ  − 1)/r 2, respectively. Using the approximation scheme suggested by Greene and Aldrich [39], we can express approximately the pseudocentrifugal term in the following form [51–54]:

$$ \frac{1}{{r^{2} }} \approx \alpha^{2} \frac{{{\text{e}}^{ - \alpha r} }}{{(1 - {\text{e}}^{ - \alpha r} )^{2} }} $$
(15)

This is a good approximation for small values of the parameter α and it breaks down for large values of α. For the case of αr ≪ 1, one can show that (see Fig. 2)

$$ \alpha^{2} \left( {c_{0} + \frac{{{\text{e}}^{ - \alpha r} }}{{(1 - {\text{e}}^{ - \alpha r} )^{2} }}} \right) = \alpha^{2} \left( {c_{0} + \frac{1}{{4\sin \,h^{2} \tfrac{\alpha r}{2}}}} \right) \to \frac{1}{{r^{2} }} $$
(16)

where c 0 = 1/12 is a dimensionless constant.

Fig. 2
figure 2

1/r 2 and its approximations for α = 1/2

Full size image

Bound States of the Pöschl–Teller-like potential with Coulomb tensor interaction

Spin symmetry solution

Substituting Eq. (16) into Eq. (13) leads us to obtain the following Schrödinger-like equation for the upper spinor component:

$$ \left[ { - \frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} + } \right.\left. {\frac{{\lambda_{\kappa } \left( {\lambda_{\kappa } + 1} \right)\alpha^{2} + \gamma (V_{1} - V_{2} )}}{{4\sin \,h^{2} \tfrac{\alpha r}{2}}} - \frac{{\gamma (V_{1} + V_{2} )}}{{4\cos \,h^{2} \tfrac{\alpha r}{2}}}} \right]F_{n\kappa } \left( r \right) = \tilde{E}_{n\kappa } F_{n\kappa } \left( r \right) $$
(17)

where \( \tilde{E}_{n\kappa } \) is defined as \( \tilde{E}_{n\kappa } = \left( {E_{n\kappa } - M} \right)\left( {M + E_{n\kappa } - C_{\text{s}} } \right) - \lambda_{\kappa } \left( {\lambda_{\kappa } + 1} \right)\alpha^{2} c_{0} \). Using the basic concept of the supersymmetric shape invariance formulism [42, 43], we solve Eq. (17). The ground-state upper component F 0,κ (r) can be written as:

$$ F_{0,\kappa } \left( r \right) = \exp \left( { - \int {W\left( r \right)} {\text{d}}r} \right), $$
(18)

where W(r) is called a superpotential in supersymmetric quantum mechanics [43]. Substituting Eq. (18) into Eq. (17), we have the following equation for W(r)

$$ W^{2} \left( r \right) - \frac{{{\text{d}}W\left( r \right)}}{{{\text{d}}r}} = \frac{{\lambda_{\kappa } \left( {\lambda_{\kappa } + 1} \right)\alpha^{2} + \gamma (V_{1} - V_{2} )}}{{4\sin \,h^{2} \tfrac{\alpha r}{2}}} - \frac{{\gamma (V_{1} + V_{2} )}}{{4\cos \,h^{2} \tfrac{\alpha r}{2}}} - \tilde{E}_{0,\kappa } , $$
(19)

where \( \tilde{E}_{0,\kappa } \) is the ground-state energy. Considering the compatibility between the superpotential function W(r) and the right-hand side of Eq. (19), we write the superpotential W(r) in the following form:

$$ W\left( r \right) = A\tan \,h\frac{\alpha r}{2} + B\cot \,h\frac{\alpha r}{2} $$
(20)

Substituting Eq. (20) into (18) leads us to obtain the ground-state upper component

$$ F_{0,\kappa } \left( r \right),\quad F_{0,\kappa } \left( r \right) = \left( {\cos \,h\frac{\alpha r}{2}} \right)^{{{{ - 2A} \mathord{\left/ {\vphantom {{ - 2A} \alpha }} \right. \kern-0pt} \alpha }}} \left( {\sin \,h\frac{\alpha r}{2}} \right)^{{{{ - 2B} \mathord{\left/ {\vphantom {{ - 2B} \alpha }} \right. \kern-0pt} \alpha }}} $$
(21)

For the bound-state solutions, the upper component F nκ (r) must satisfy the boundary conditions that F nκ (r)/r becomes zero when r → ∞, and F nκ (r)/r is finite if r = 0. In view of these regularity conditions, we have the restriction conditions: A > 0, B < 0 and A > −B.

Substituting Eq. (20) into Eq. (19) and comparing equal powers of two sides in Eq. (19), we obtain the following relationships:

$$ \left( {A + B} \right)^{2} = - \tilde{E}_{0,\kappa } $$
(22)
$$ A^{2} + \frac{\alpha }{2}A = \frac{{\gamma (V_{1} + V_{2} )}}{4} $$
(23)
$$ B^{2} + \frac{\alpha }{2}B = \frac{{\gamma (V_{1} - V_{2} ) + \lambda_{\kappa } \left( {\lambda_{\kappa } + 1} \right)\alpha^{2} }}{4} $$
(24)

Considering the regularity conditions, A > 0 and B < 0, we obtain the coefficients A and B by solving Eqs. (23) and (24),

$$ A = \frac{\alpha }{4}\left[ { - 1 + \sqrt {1 + \frac{{4\gamma (V_{1} + V_{2} )}}{{\alpha^{2} }}} } \right] $$
(25)
$$ B = \frac{\alpha }{4}\left[ { - 1 - \sqrt {\left( {1 + 2\lambda_{\kappa } } \right)^{2} + \frac{{4\gamma (V_{1} - V_{2} )}}{{\alpha^{2} }}} } \right] $$
(26)

Using the expression given in Eq. (20), we construct the following two supersymmetric partner potentials:

$$ V_{ \pm } \left( r \right) = W^{2} \left( r \right) \pm \frac{{{\text{d}}W\left( r \right)}}{{{\text{d}}r}} = \left( {A + B} \right)^{2} + \frac{{B^{2} \mp \tfrac{1}{2}\alpha B}}{{\sin \,h^{2} \tfrac{\alpha r}{2}}} - \frac{{A^{2} \mp \tfrac{1}{2}\alpha A}}{{\cos \,h^{2} \tfrac{\alpha r}{2}}} $$
(27)

Setting (a 0, b 0) = (A, B), one can get the following shape-invariant relationship,

$$ V_{ + } \left( {r,a_{0} ,b_{0} } \right) = V_{ - } \left( {r,a_{1} ,b_{1} } \right) + R\left( {a_{1} ,b_{1} } \right), $$
(28)

where a 1 and b 1 are the functions of a 0 and b 0, respectively, i.e., a 1 = f(a 0) = a 0 − α/2, b 1 = f(b 0) = b 0 − α/2, and the remainder R(a 1, b 1) is independent of r, R(a 1, b 1) = (a 0 + b 0)2 − (a 1 + b 1)2 = (A + B)2 − (A + B − α)2.

The energy eigenvalues of the potential V −(r) can be determined using the shape invariance approach [42]. The energy eigenvalues of the potential V −(r) are given by

$$ \tilde{E}_{0,\kappa }^{( - )} = 0, $$
(29)
$$ \begin{aligned} \tilde{E}_{n\kappa }^{( - )} & = \sum\limits_{k = 1}^{n} {R\left( {a_{k} ,b_{k} } \right)} = R\left( {a_{1} ,b_{1} } \right) + R\left( {a_{2} ,b_{2} } \right) + \cdot \cdot \cdot + R\left( {a_{n} ,b_{n} } \right) \\ & = \left( {a_{0} + b_{0} } \right)^{2} - \left( {a_{1} + b_{1} } \right)^{2} + \left( {a_{1} + b_{1} } \right)^{2} - \left( {a_{2} + b_{2} } \right)^{2} + \cdot \cdot \cdot + \left( {a_{n - 1} + b_{n - 1} } \right)^{2} - \left( {a_{n} + b_{n} } \right)^{2} \\ & = \left( {a_{0} + b_{0} } \right)^{2} - \left( {a_{n} + b_{n} } \right)^{2} = \left( {A + B} \right)^{2} - \left( {A + B - n\alpha } \right)^{2} , \\ \end{aligned} $$
(30)

where the quantum number n = 0, 1, 2, …. From Eqs. (19) and (27), we have the following relation:

$$ \frac{{\lambda_{\kappa } \left( {\lambda_{\kappa } + 1} \right)\alpha^{2} + \gamma (V_{1} - V_{2} )}}{{4\sin \,h^{2} \tfrac{\alpha r}{2}}} - \frac{{\gamma (V_{1} + V_{2} )}}{{4\cos \,h^{2} \tfrac{\alpha r}{2}}} = V_{ - } \left( r \right) + \tilde{E}_{0,\kappa } . $$
(31)

From Eqs. (17) and (31), we can find the solution for \( \tilde{E}_{n\kappa } \) in Eq. (17),

$$ \tilde{E}_{n\kappa } = \tilde{E}_{0,\kappa } + \tilde{E}_{n\kappa }^{( - )} = - \left( {A + B - n\alpha } \right)^{2} , $$
(32)

where we have employed the relation \( \tilde{E}_{0,\kappa } = - \left( {A + B} \right)^{2} \). Substituting Eqs. (25) and (26) into Eq. (32) and using \( \tilde{E}_{n\kappa } = \left( {E_{n\kappa } - M} \right)\left( {M + E_{n\kappa } - C_{s} } \right) - \lambda_{\kappa } \left( {\lambda_{\kappa } + 1} \right)\alpha^{2} c_{0} \), we can find the energy eigenvalue equation of the relativistic Pöschl–Teller-like potential under the condition of spin symmetry,

$$ \begin{gathered} E_{n\kappa }^{2} - M^{2} - C_{\text{s}} \left( {E_{n\kappa } - M} \right) - \left( {\kappa + U_{{0{\text{C}}}} } \right)\left( {\kappa + U_{{0{\text{C}}}} + 1} \right)\alpha^{2} c_{0} = - \alpha^{2} \left( { - n - \frac{1}{2}} \right. \hfill \\ \quad + \frac{1}{4}\sqrt {1 + \frac{{4\left( {M + E_{n\kappa } - C_{\text{s}} } \right)(V_{1} + V_{2} )}}{{\alpha^{2} }}} \left. { - \frac{1}{4}\sqrt {\left( {1 + 2\left( {\kappa + U_{{0{\text{C}}}} } \right)} \right)^{2} + \frac{{4\left( {M + E_{n\kappa } - C_{\text{s}} } \right)(V_{1} - V_{2} )}}{{\alpha^{2} }}} } \right)^{2} \hfill \\ \end{gathered} $$
(33)

where the quantum number \( n = 0,1,2, \ldots , < \tfrac{1}{\alpha }\left( {A + B} \right) \). Using the recursion operator approach [55, 56], we can determine the excited state upper components from the superpotential W(r) given in Eq. (20) and the ground-state upper component, F 0,κ (r) given in Eq. (21).

To find the corresponding wave functions, we take the function analysis method to calculate the unnormalized excited state upper components. Substituting Eq. (32) into Eq. (17), we obtain

$$ \left( { - \frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} + \frac{{\lambda_{\kappa } \left( {\lambda_{\kappa } + 1} \right)\alpha^{2} + \gamma (V_{1} - V_{2} )}}{{4\sin \,h^{2} \tfrac{\alpha r}{2}}} - \frac{{\gamma (V_{1} + V_{2} )}}{{4\cos \,h^{2} \tfrac{\alpha r}{2}}}} \right)F_{n\kappa } \left( r \right) = - \left( {A + B - n\alpha } \right)^{2} F_{n\kappa } \left( r \right). $$
(34)

Defining a new variable of the form \( s = - \sin \,h^{2} \tfrac{\alpha r}{2} \) and making a transformation of the upper spinor component of the form \( F_{n\kappa } \left( r \right) = (1 - s)^{{\frac{ - A}{\alpha }}} s^{{\frac{ - B}{\alpha }}} f_{n\kappa } \left( s \right) \), Eq. (34) can be written as follows:

$$ \left( {1 - s} \right)s\frac{{{\text{d}}^{2} f_{n\kappa } \left( s \right)}}{{{\text{d}}s^{2} }} + \left[ {\frac{1}{2} - \frac{2B}{\alpha } - \left( {1 - \frac{2A}{\alpha } - \frac{2B}{\alpha }} \right)s} \right]\frac{{{\text{d}}f_{n\kappa } \left( s \right)}}{{{\text{d}}s}} + n\left( {n - \frac{2A}{\alpha } - \frac{2B}{\alpha }} \right)f_{n\kappa } \left( s \right) = 0. $$
(35)

This equation is the well-known differential equation satisfied by the hypergeometric function 2 F 1(a, b; c; s), i.e.,

$$ f_{n\kappa } \left( s \right) = {}_{2}F_{1} \left( {a,b;c;s} \right) = \frac{\varGamma \left( c \right)}{\varGamma \left( a \right)\varGamma \left( b \right)}\sum\limits_{k = 0}^{\infty } {\frac{{\varGamma \left( {a + k} \right)\varGamma \left( {b + k} \right)}}{{\varGamma \left( {c + k} \right)}}\,\frac{{s^{k} }}{k!}} , $$
(36)

where \( a = - n,\quad b = n - \frac{2A}{\alpha } - \frac{2B}{\alpha } \), and \( c = \frac{1}{2} - \frac{2B}{\alpha } \). Using the original variable r, the upper component F nκ (r) corresponding to energy level E nκ can be expressed as follows:

$$ F_{n\kappa } \left( r \right) = \left( {1 + \sin \,h^{2} \frac{\alpha r}{2}} \right)^{{ - \frac{A}{\alpha }}} \left( { - \sin \,h^{2} \frac{\alpha r}{2}} \right)^{{ - \frac{B}{\alpha }}} \,{}_{2}F_{1} \left( { - n,n - \frac{2A}{\alpha } - \frac{2B}{\alpha };\frac{1}{2} - \frac{2B}{\alpha }; - \sin \,h^{2} \frac{\alpha r}{2}} \right), $$
(37)

where A and B are given in Eqs. (25) and (26), respectively. Using Eq. (9a) and the expression of F nκ (r) given in Eq. (37), we obtain the lower spinor component G nκ (r) corresponding to the upper component F nκ (r) and energy level E nκ ,

$$ \begin{gathered} G_{n\kappa } (r) = \frac{1}{{\left( {M + E_{n\kappa } - C_{s} } \right)}}\left( {\frac{\text{d}}{{{\text{d}}r}} + \frac{\kappa }{r} - U(r)} \right)F_{n\kappa } (r) \hfill \\ = \frac{1}{{\left( {M + E_{n\kappa } - C_{s} } \right)}}\left( {1 + \sin \,h^{2} \frac{\alpha r}{2}} \right)^{{ - \frac{A}{\alpha }}} \left( { - \sin \,h^{2} \frac{\alpha r}{2}} \right)^{{ - \frac{B}{\alpha }}} \left[ { - \left( {\frac{A\sin \,h\alpha r}{{2\left( {1 + \sin \,h^{2} \frac{\alpha r}{2}} \right)}} + \frac{{B\cos \,h\frac{\alpha r}{2}}}{{\sin \,h\frac{\alpha r}{2}}} - \frac{{\kappa + U_{0C} }}{r}} \right)} \right. \hfill \\ \times {}_{2}F_{1} \left( { - n,n - \frac{2A}{\alpha } - \frac{2B}{\alpha };\frac{1}{2} - \frac{2B}{\alpha }; - \sin \,h^{2} \frac{\alpha r}{2}} \right) + \frac{{n\alpha \sin \,h\alpha r\left( {n - \frac{2A}{\alpha } - \frac{2B}{\alpha }} \right)}}{{2\left( {\frac{1}{2} - \frac{2B}{\alpha }} \right)}} \hfill \\ \left. { \times {}_{2}F_{1} \left( { - n + 1,n + 1 - \frac{2A}{\alpha } - \frac{2B}{\alpha };\frac{3}{2} - \frac{2B}{\alpha }; - \sin \,h^{2} \frac{\alpha r}{2}} \right)} \right], \hfill \\ \end{gathered} $$
(38)

where E nκ  ≠ − M + C s. From Eqs. (37) and (38), we can observe that the upper component F nκ (r) and lower component G nκ (r) can satisfy the regularity conditions for the bound states when A > 0 and B < 0 and A > −B.

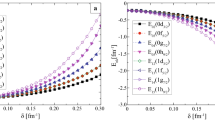
The energy level E nκ is given implicitly by energy eigenvalue Eq. (33) which is a rather complicated transcendental equation. To show the procedure of determining the bound-state energy eigenvalues from Eq. (33), we take a set of physical parameter values, C s = 2, α = 1.2, M = 10, V 1 = 5, V 2 = 3, and c 0 = 1/12, to give a numerical example. When n = 0 and κ = 1, Eq. (33) yields the following values of E 0,1: 9.727533, −7.948904. We choose E 0,1 = 9.727533 as the solution of Eq. (33), and find that the values of A and B are A = 5.66197 and B = −3.41027, respectively. These values satisfy the regularity conditions: A > 0, B < 0 and A > − B. If we take E 0,1 = −7.948904 as the solution of Eq. (33), the values of A and B are A = 0.138395 and B = −1.21408, which do not satisfy the regularity condition: A > − B. Therefore, we can only take the positive energy value E 0,1 = 9.727533 as the solution of Eq. (33). Using the same parameter values of α, M, V 1, V 2 and C s, the numerical solutions of Eq. (33) for the other values of n and κ are presented in Table 1. In Fig. 3, we have investigated the effect of the tensor potential on the bound states.

Table 1 The spin symmetric bound-state energy levels (in unit of fm −1) of the Coulomb potential taking several values of n and κ
Full size table
Fig. 3
figure 3

(color online) Contribution of the tensor Coulomb potential parameter to the energy levels in the case of spin symmetry

Full size image

P-spin symmetry solution

In this subsection, we will obtain the energy eigenvalues and the corresponding wave functions for the p-spin symmetric limit by substituting Eq. (16) into Eq. (14) that leads us to obtain the following Schrödinger-like equation for the lower spinor component:

$$ \left[ { - \frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} + } \right.\left. {\frac{{\lambda_{\kappa } \left( {\lambda_{\kappa } - 1} \right)\alpha^{2} + \tilde{\gamma }(V_{1} - V_{2} )}}{{4\sin \,h^{2} \tfrac{\alpha r}{2}}} - \frac{{\tilde{\gamma }(V_{1} + V_{2} )}}{{4\cos \,h^{2} \tfrac{\alpha r}{2}}}} \right]G_{n\kappa } \left( r \right) = \tilde{E}_{n\kappa } G_{n\kappa } \left( r \right), $$
(39)

where \( \tilde{E}_{n\kappa } \) is defined as\( \tilde{E}_{n\kappa } = \left( {E_{n\kappa } + M} \right)\left( {E_{n\kappa } - M - C_{\text{ps}} } \right) - \lambda_{\kappa } \left( {\lambda_{\kappa } - 1} \right)\alpha^{2} c_{0} \). We write the super-potential \( \tilde{W}\left( r \right) \) in the following form:

$$ W\left( r \right) = \tilde{A}\tan \,h\frac{\alpha r}{2} + \tilde{B}\cot \,h\frac{\alpha r}{2}\,, $$
(40)

that leads us to obtain the ground-state upper component

$$ G_{0,\kappa } \left( r \right),\quad G_{0,\kappa } \left( r \right) = \left( {\cos \,h\frac{\alpha r}{2}} \right)^{{{{ - 2\tilde{A}} \mathord{\left/ {\vphantom {{ - 2\tilde{A}} \alpha }} \right. \kern-0pt} \alpha }}} \left( {\sin \,h\frac{\alpha r}{2}} \right)^{{{{ - 2\tilde{B}} \mathord{\left/ {\vphantom {{ - 2\tilde{B}} \alpha }} \right. \kern-0pt} \alpha }}} , $$
(41)

where

$$ \tilde{A} = \frac{\alpha }{4}\left[ { - 1 + \sqrt {1 + \frac{{4\tilde{\gamma }(V_{1} + V_{2} )}}{{\alpha^{2} }}} } \right], $$
(42)
$$ \tilde{B} = \frac{\alpha }{4}\left[ { - 1 - \sqrt {\left( {1 - 2\lambda_{\kappa } } \right)^{2} + \frac{{4\tilde{\gamma }(V_{1} - V_{2} )}}{{\alpha^{2} }}} } \right], $$
(43)

To avoid repetition in our solution to Eq. (14), We follow the same procedures explained in the previous section to obtain the energy eigenvalue equation,

$$ \begin{gathered} E_{n\kappa }^{2} - M^{2} - C_{\text{ps}} \left( {E_{n\kappa } + M} \right) - \left( {\kappa + U_{{0{\text{C}}}} } \right)\left( {\kappa + U_{{0{\text{C}}}} - 1} \right)\alpha^{2} c_{0} = - \alpha^{2} \left( { - n - \frac{1}{2}} \right. \hfill \\ + \frac{1}{4}\sqrt {1 + \frac{{4\left( {M - E_{n\kappa } + C_{\text{ps}} } \right)(V_{1} + V_{2} )}}{{\alpha^{2} }}} \left. { - \frac{1}{4}\sqrt {\left( {1 - 2\left( {\kappa + U_{{0{\text{C}}}} } \right)} \right)^{2} + \frac{{4\left( {M - E_{n\kappa } + C_{\text{ps}} } \right)(V_{1} - V_{2} )}}{{\alpha^{2} }}} } \right)^{2} \hfill \\ \end{gathered} $$
(44)

and the corresponding wave functions for the lower Dirac spinor as:

$$ G_{n\kappa } \left( r \right) = \left( {1 + \sin \,h^{2} \frac{\alpha r}{2}} \right)^{{ - \frac{{\tilde{A}}}{\alpha }}} \left( { - \sin \,h^{2} \frac{\alpha r}{2}} \right)^{{ - \frac{{\tilde{B}}}{\alpha }}} {}_{2}F_{1} \left( { - n,n - \frac{{2\tilde{A}}}{\alpha } - \frac{{2\tilde{B}}}{\alpha };\frac{1}{2} - \frac{{2\tilde{B}}}{\alpha }; - \sin \,h^{2} \frac{\alpha r}{2}} \right). $$
(45)

Finally, the upper-spinor component of the Dirac equation can also be obtained via Eq. (9b) as:

$$ \begin{aligned} F_{n\kappa } \left( r \right) = & \frac{1}{{\left( {M - E_{n\kappa } + C_{\text{ps}} } \right)}}\left( {\frac{\text{d}}{{{\text{d}}r}} - \frac{\kappa }{r} + U\left( r \right)} \right)G_{n\kappa } \left( r \right) \\ = & \frac{1}{{\left( {M - E_{n\kappa } + C_{\text{ps}} } \right)}}\left( {1 + \sin \,h^{2} \frac{\alpha r}{2}} \right)^{{ - \frac{{\tilde{A}}}{\alpha }}} \left( { - \sin \,h^{2} \frac{\alpha r}{2}} \right)^{{ - \frac{{\tilde{B}}}{\alpha }}} \left[ { - \left( {\frac{{\tilde{A}\sin \,h\,\alpha r}}{{2\left( {1 + \sin \,h^{2} \frac{\alpha r}{2}} \right)}} + \frac{{\tilde{B}\cos \,h\frac{\alpha r}{2}}}{{\sin \,h\frac{\alpha r}{2}}} + \frac{{\kappa + U_{0C} }}{r}} \right)} \right. \\ \quad \times {}_{2}F_{1} \left( { - n,n - \frac{{2\tilde{A}}}{\alpha } - \frac{{2\tilde{B}}}{\alpha };\frac{1}{2} - \frac{{2\tilde{B}}}{\alpha }; - \sin \,h^{2} \frac{\alpha r}{2}} \right) + \frac{{n\alpha \sin \,h\,\alpha r\left( {n - \frac{{2\tilde{A}}}{\alpha } - \frac{{2\tilde{B}}}{\alpha }} \right)}}{{2\left( {\frac{1}{2} - \frac{{2\tilde{B}}}{\alpha }} \right)}} \\ \left. {\quad \times {}_{2}F_{1} \left( { - n + 1,n + 1 - \frac{{2\tilde{A}}}{\alpha } - \frac{{2\tilde{B}}}{\alpha };\frac{3}{2} - \frac{{2\tilde{B}}}{\alpha }; - \sin \,h^{2} \frac{\alpha r}{2}} \right)} \right] ,\\ \end{aligned}$$
(46)

where E nκ  ≠ M + C ps.

By taking a set of physical parameter values, C ps = 2, α = 1.2, M = 10, V 1 = 5, V 2 = 3, c 0 = 1/12, when n = 1 and κ = 2, Eq. (44) yields the following values of E 1,2: −9.92187466, 11.814382. We choose E 1,2 = −9.92187466 as the solution of Eq. (44), and find that the values of \( \tilde{A} \) and \( \tilde{B} \) are \( \tilde{A} = 6.32825 \) and \( \tilde{B} = - 3.73088 \), respectively. These values satisfy the regularity conditions: \( \tilde{A} > 0,\,\,\tilde{B} < 0 \) and \( \tilde{A} > - \tilde{B} \). If we take E 1,2 = 11.814382 as the solution of Eq. (44), the values of \( \tilde{A} \) and \( \tilde{B} \) are \( \tilde{A} = 0.379142 \) and \( \tilde{B} = - 1.25016 \), which do not satisfy the regularity condition: \( \tilde{A} > - \tilde{B} \). Therefore, we can only take the negative energy value E 1,2 = −9.92187466 as the solution of Eq. (44). Using the same parameter values of α, M, V 1, V 2 and C ps , the numerical solutions of Eq. (44) for the other values of n and κ are presented in Table 2.

Table 2 The p-spin symmetric bound-state energy levels (in unit of fm −1) of the Coulomb potential taking several values of n and κ
Full size table

Also in Fig. 4, we have investigated the effect of the tensor potential on the p-spin doublet splitting by considering some pairs of orbitals.

Fig. 4
figure 4

(color online) Contribution of the tensor Coulomb potential parameter to the energy levels in the case of p-spin symmetry

Full size image

Conclusion

In this paper, we have approximately studied the bound-state solutions of the Dirac equation for the Pöschl–Teller-like potential with a Coulomb-like tensor interaction within the framework of spin and pseudospin symmetry limits. By employing an improved approximation scheme to deal with the pseudocentrifugal term 1/r 2 and the SUSYQUM technique, We have obtained the energy levels in a closed form and the corresponding wave functions in terms of the hypergeometric function 2 F 1(a, b; c; s). Some numerical values of the energy levels are reported in Tables 1 and 2 under the condition of the spin and p-spin symmetries, respectively. Obviously, the degeneracy between the members of doublet states in spin and p-spin symmetries is removed by tensor interaction. The p-spin spectra of the present potential are identical to those ones obtained in Ref. [57] as the potential parameters U 0C = 0, α = 0.15, M = 1.0, C ps = −5.