Evolution of solitons and their reflection and transmission in a plasma having negatively charged dust grains

Abstract

Theoretical calculations are carried out for studying soliton’s reflection and transmission in an inhomogeneous plasma comprising ions, two temperature electrons and negatively charged dust grains. Using reductive perturbation technique, relevant modified KdV equations are derived for the incident, reflected and transmitted solitons. Then a coupled equation is obtained based on these mKdV equations, which is solved for the reflected soliton under the use of solutions of mKdV equations corresponding to the incident and transmitted solitons. Based on the ratio of amplitudes of reflected and incident solitons, reflection coefficient is examined under the effect of dust grain density; the same is done for the transmission coefficient which is the ratio of amplitudes of transmitted and incident solitons. The transmission of the solitons becomes weaker under the effect of stronger magnetic field and higher dust density. However, this leads to the stronger reflection of the soliton.

Introduction

The solitary structure is formed from an ion acoustic wave when the effects of nonlinearity and dispersion are balanced in the plasma. Washimi and Taniuti [1] were the first to derive the well-known Korteweg-deVries (KdV) equation with the help of reductive perturbation technique (RPT) to describe the soliton behavior in the homogeneous plasma. However, plasma contributes an extra term in the usual KdV equation [2–5], when the density inhomogeneity is taken into account, and then modified KdV (mKdV) equation is realized. Accordingly, the soliton behavior is modified in the inhomogeneous plasmas. There are a large number of studies on the ion acoustic solitary waves in homogeneous plasmas [6–8], inhomogeneous plasmas [2, 9] and magnetized plasmas [10–13]. The ion acoustic waves and hence, the solitons are found to reflect from a density gradient or the metal surface present in the plasma. There have been a lot of experimental observations concerning solitons in different plasma models [14–23]. The reflection of a planar ion acoustic soliton has been studied by Nishida [19] from a finite plane boundary. The soliton propagation, collision and reflection have been experimentally observed by Cooney et al. [21] at a sheath in a multicomponent plasma; they discussed a conservation law of soliton reflection and transmission. Nagasawa and Nishida [20] studied the nonlinear reflection and refraction of the soliton from a metallic electrode in a double-plasma (DP) device.

Most of the experiments on soliton reflection were conducted in plasmas by neglecting the dust grains which are charged by ions and electrons, and are available in laboratory plasmas or space-related plasmas such as in planetary rings, asteroid zones, cometary tails and in lower parts of Earth’s ionosphere. In addition, low-temperature technological plasmas are also contaminated by highly charged dust impurities. Interestingly, the dust grains may acquire either negative charge or positive charge [24–26], but the chances are higher that the grains acquire negative charge. In most general situations, the temperature of all the electrons does not remain the same and two groups of electrons with lower and higher temperature are found in the plasmas [27–29]. In the two electron temperature plasmas, the characteristics of ion acoustic waves and solitons are modified [27–31] due to different distributions of these electrons.

In the present work, we investigate the soliton propagation, reflection and transmission in an inhomogeneous plasma, which has two temperature electrons and negatively charged dust grains. To study this, we derive relevant mKdV equations for the incident, reflected and transmitted waves and couple them at the point of reflection. Finally, the coupled equation is solved for finding the reflection and transmission coefficients.

Basic fluid equations and reductive perturbation technique

We consider a weakly inhomogeneous plasma containing heavy dust grains of density n_d0 and initial charge number Z_d0, and inertial warm positive ions of density n, velocity $\overrightarrow{v}$ and temperature T _i . Low-temperature trapped electrons (density n_el and temperature T_el) are taken to follow the vortex-like distribution. The higher temperature isothermal electrons are considered with density n_eh and temperature T_eh. An external magnetic field (magnitude B₀) is taken at an angle θ with the direction of wave propagation in the (x, z) plane. Under this situation, for studying the ion acoustic waves and their evolution into solitons

$$\left(\frac{\mathit{\partial }n}{\mathit{\partial }t}\right)+\frac{\mathit{\partial }}{\mathit{\partial }x}\left(n{v}_x\right)+\frac{\mathit{\partial }}{\mathit{\partial }z}\left(n{v}_z\right)=0,$$

(1)

$$n\left(\frac{\mathit{\partial }{v}_x}{\mathit{\partial }t}\right)+n{v}_x\left(\frac{\mathit{\partial }{v}_x}{\mathit{\partial }x}\right)+n{v}_z\left(\frac{\mathit{\partial }{v}_x}{\mathit{\partial }z}\right)=n{\mathit{\Omega }}_R{v}_y-n\left(\frac{\mathit{\partial }\mathit{\phi }}{\mathit{\partial }x}\right)-2\frac{T_i}{T_{\text{eff}}}\left(\frac{\mathit{\partial }n}{\mathit{\partial }x}\right),$$

(2)

$$n\left(\frac{\mathit{\partial }{v}_z}{\mathit{\partial }t}\right)+n{v}_x\left(\frac{\mathit{\partial }{v}_z}{\mathit{\partial }x}\right)+n{v}_z\left(\frac{\mathit{\partial }{v}_z}{\mathit{\partial }z}\right)=-n\left(\frac{\mathit{\partial }\mathit{\phi }}{\mathit{\partial }z}\right)-2\frac{T_i}{T_{\text{eff}}}\left(\frac{\mathit{\partial }n}{\mathit{\partial }z}\right),$$

(3)

$$\left(\frac{\mathit{\partial }{v}_y}{\mathit{\partial }t}\right)+v_x\left(\frac{\mathit{\partial }{v}_y}{\mathit{\partial }x}\right)+v_z\left(\frac{\mathit{\partial }{v}_y}{\mathit{\partial }z}\right)=-{\mathit{\Omega }}_R{v}_x,$$

(4)

$$\left(\frac{{\mathit{\partial }}^2\mathit{\phi }}{\mathit{\partial }{x}^2}\right)+\left(\frac{{\mathit{\partial }}^2\mathit{\phi }}{\mathit{\partial }{z}^2}\right)=n_{\text{el}}+n_{\text{eh}}-n+n_{\text{d0}}{Z}_{\text{d0}},$$

(5)

$$n_{\text{el}}=n_{\text{el0}}\left\{1+\frac{T_{\text{eff}}}{T_{\text{el}}}\mathit{\phi }-\frac{4}{3}{b}_l{\left(\frac{T_{\text{eff}}}{T_{\text{el}}}\mathit{\phi }\right)}^{3/2}+\frac{1}{2}{\left(\frac{T_{\text{eff}}}{T_{\text{el}}}\mathit{\phi }\right)}^2+\dots \right\},$$

(6)

$$n_{\text{eh}}=n_{\text{eh0}}exp\left(\frac{T_{\text{eff}}\mathit{\phi }}{T_{\text{eh}}}\right),$$

(7)

In the above equations, the motion of dust grains has been neglected in view of their very-low-frequency oscillations compared to the oscillations of ions and electrons. The nonisothermality is taken through the expansion of n_el, where the parameter b _l is given by $b_l=\left[1-T_{\text{el}}/T_{\text{eff}}\right]/\sqrt{\mathit{\pi }}$ [27–30]. ${\mathit{\Omega }}_R=\sqrt{\frac{{\mathit{\epsilon }}_0}{m_i{n}_0^0}}{B}_0$ and $T_{\text{eff}}$ is the effective temperature of the plasma, given by $T_{\text{eff}}=\left(n_{\text{elo}}+n_{\text{eho}}\right)T_{\text{el}}{T}_{\text{eh}}/\phantom{\left(n_{\text{elo}}+n_{\text{eho}}\right)T_{\text{el}}{T}_{\text{eh}}\left(n_{\text{elo}}{T}_{\text{eh}}+n_{\text{eho}}{T}_{\text{el}}\right)}\left(n_{\text{elo}}{T}_{\text{eh}}+n_{\text{eho}}{T}_{\text{el}}\right)$ in view of two temperature electrons. In Eqs. (1)–(7) all the densities are normalized by the unperturbed plasma density $n_0^0$ at some arbitrary reference point (say x = z = 0), space coordinates x and z by the Debye length ${\left({\mathit{\epsilon }}_0{T}_{\text{eff}}/n_0^0{e}^2\right)}^{1/2}$, ion flow velocity by the ion acoustic speed ${\left(T_{\text{eff}}/m_i\right)}^{1/2}$ and time $t$ by the inverse of ion plasma frequency ${\mathit{\omega }}_{pi}={\left(n_0^0{e}^2/{\mathit{\epsilon }}_0{m}_i\right)}^{1/2}$, where $m_i$ is the mass of the ion. Finally, the electric potential ϕ is normalized by $T_{\text{eff}}/e$.

As per the requirement of RPT, we expand the densities, fluid velocities and electric potential in terms of a smallness parameter $\mathit{\epsilon }$. The oblique incidence of the wave with respect to the magnetic field causes the perturbations in longitudinal and transverse components of velocity to be different. Hence, the expansions of physical quantities are given by

$$\begin{array}{c}S=S_o(x,z)+\mathit{\epsilon }{S}_1(x,z,t)+{\mathit{\epsilon }}^{3/2}{S}_2(x,z,t)+{\mathit{\epsilon }}^2{S}_3(x,z,t)+\dots ,S\equiv n,n_{el},n_{eh},v_z,\\ V=V_0(x,z)+{\mathit{\epsilon }}^{5/4}{V}_1(x,z,t)+{\mathit{\epsilon }}^{3/2}{V}_2(x,z,t)+{\mathit{\epsilon }}^2{V}_3(x,z,t)+\dots \\ V\equiv v_x,v_y,\mathit{\phi }=\mathit{\epsilon }{\mathit{\phi }}_1(x,z,t)+{\mathit{\epsilon }}^{3/2}{\mathit{\phi }}_2(x,z,t)+{\mathit{\epsilon }}^2{\mathit{\phi }}_3(x,z,t)+\dots ,\\ \end{array}$$

(8)

mKdV equations for incident, reflected and transmitted waves

To derive mKdV equations for the incident, reflected and transmitted waves in the said inhomogeneous plasma, we employ stretched coordinates based on the proposal of Asano and Taniuti [32]. We use the subscripts I, R and T for the cases of incident, reflected and transmitted waves, respectively. In general, the angles of incidence, reflection and transmission should be different. However, for the sake of simplicity we assume that the direction of propagation of the reflected soliton is opposite to the directions of propagation of the incident and transmitted solitons, i.e., the transmission of the soliton is considered in the same direction as that of the incident soliton. Hence, the stretched coordinates for the incident wave are taken as [5, 11, 27, 33] $\mathit{\xi }={\mathit{\epsilon }}^{1/4}\left[\left(xsin\mathit{\theta }+zcos\mathit{\theta }\right)/{\mathit{\lambda }}_0-t\right],\mathit{\eta }={\mathit{\epsilon }}^{3/4}\left[xsin\mathit{\theta }+zcos\mathit{\theta }\right]$. Accordingly, the stretched coordinates for the transmitted wave are ${\mathit{\xi }}_T={\mathit{\epsilon }}^{1/4}\left[\left(xsin\mathit{\theta }+zcos\mathit{\theta }\right)/{\mathit{\lambda }}_{0T}-t\right],{\mathit{\eta }}_T={\mathit{\epsilon }}^{3/4}\left[xsin\mathit{\theta }+zcos\mathit{\theta }\right]$ and for the reflected wave ${\mathit{\xi }}_R=-{\mathit{\epsilon }}^{1/4}\left[\left(xsin\mathit{\theta }+zcos\mathit{\theta }\right)/{\mathit{\lambda }}_{0R}-t\right]$, ${\mathit{\eta }}_R=-{\mathit{\epsilon }}^{3/4}\left[xsin\mathit{\theta }+zcos\mathit{\theta }\right]$. The power of ε determines the order or perturbation, and higher (lower) power of ε means the slow (fast) variation of the physical quantities such as density, velocity and potential. This has been well established that these quantities should have fast variation in time and slow variation in space for the generation of solitary waves in inhomogeneous plasmas; however, opposite is true in homogeneous plasmas. In plasmas without nonisothermal electrons, the powers of ε are $\frac{1}{2}$ and $\frac{3}{2}$ for the time-like and space-like stretched coordinates, respectively. On the other hand, these powers are $\frac{1}{4}$ and $\frac{3}{4}$ in the inhomogeneous plasmas having nonisothermal electrons for the evolution of solitary waves, as the physical quantities should have relatively faster variation with the time and space in the plasmas having nonisothermal electrons. Under this situation only, the effects of nonlinearity and dispersion are balanced, which leads to the evolution of the solitons. The fast variation is required due to the fact that the nonisothermal electrons have lower thermal velocity and can be easily trapped by the potential of the ion acoustic wave.

The use of the above stretchings in Eqs. (1)–(7) along with the expansion (8) leads to various equations in zeroth-, first- and second-order equations, the same as is Ref. [40]. Then, the integration of first order equations yields the following phase velocity relations for the incident, reflected and transmitted waves

$${\mathit{\lambda }}_0=v_{x0}sin\mathit{\theta }+\left\{v_{z0}\pm \sqrt{\left(1+2\frac{T_i}{T_{\text{eff}}}\right)+\left(\frac{n_{\text{d0}}}{n_{\text{el0}}+n_{\text{eh0}}}\right)}\right\}cos\mathit{\theta },$$

(9)

$${\mathit{\lambda }}_{0R}=-v_{x0}sin\mathit{\theta }-\left\{v_{z0}\pm \sqrt{\left(1+2\frac{T_i}{T_{\text{eff}}}\right)+\left(\frac{n_{\text{d0}}}{n_{\text{el0}}+n_{\text{eh0}}}\right)}\right\}cos\mathit{\theta },$$

(10)

$${\mathit{\lambda }}_{0T}=v_{x0B}sin\mathit{\theta }+\left\{v_{z0B}\pm \sqrt{\left(1+2\frac{T_i}{T_{\text{eff}}}\right)+\left(\frac{n_{\text{d0}}}{n_{\text{el0}}+n_{\text{eh0}}}\right)}\right\}cos\mathit{\theta }.$$

(11)

The velocity components $v_{x0B}$ and $v_{z0B}$ correspond to the region where transmitted wave propagates. Depending upon the magnitudes, the phase velocity with positive sign in the above equations corresponds to the fast mode (velocity ${\mathit{\lambda }}_{0F}$) and the one for negative sign corresponds to the slow mode (velocity ${\mathit{\lambda }}_{0S}$). It means the present plasma supports two types of ion acoustic waves with different phase velocities.

The nonlinear analysis involves the second-order equations, which finally enable the mKdV equations for all the cases of incident, reflected and transmitted waves. A relevant mKdV equation for the incident wave is obtained as

$$\frac{\mathit{\partial }{v}_{1I}}{\mathit{\partial }\mathit{\eta }}+{\mathit{\alpha }}_{}{v}_{1I}^{1/2}\frac{\mathit{\partial }{v}_{1I}}{\mathit{\partial }\mathit{\xi }}+{\mathit{\beta }}_{}\frac{{\mathit{\partial }}^3{v}_{1I}}{\mathit{\partial }{\mathit{\xi }}^3}+{\mathit{\gamma }}_{}{v}_{1I}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }\mathit{\eta }}=0.$$

(12)

Here, various coefficients are given by

$$\begin{array}{c}\mathit{\alpha }=\frac{\sqrt{n_0}}{D_I}\left[-2b_l{n}_{\text{el0}}\left(n_{\text{el0}}+n_{\text{eh0}}\right){\mathit{\lambda }}_1^3{\left(\frac{n_{0}cos\mathit{\theta }}{{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)}\frac{T_{\text{eff}}}{T_{\text{el}}}\right)}^{3/2}\right],\\ \mathit{\beta }=\frac{n_{0}cos\mathit{\theta }{\mathit{\lambda }}_1^2}{D_I{\mathit{\lambda }}_0^2}\left[1+\left(\begin{array}{c}1\\ +2\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)T_i}{n_0{T}_{\text{eff}}}\\ \end{array}\right)\frac{1}{{\mathit{\lambda }}_1{\mathit{\Omega }}_R^2}\left\{\begin{array}{c}{n}_0{\mathit{\lambda }}_1{sin}^2\mathit{\theta }+{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)\left(\begin{array}{c}2\frac{T_i}{T_{\text{eff}}}{sin}^2\mathit{\theta }\\ +{\mathit{\lambda }}_1\left\{v_{x0}-v_{x0}sin\mathit{\theta }-1\right\}\\ \end{array}\right)\\ +\left(1+2\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)T_i}{n_0{T}_{\text{eff}}}\right){\mathit{\lambda }}_0{cos}^2\mathit{\theta }\left({\mathit{\lambda }}_1-v_{x0}+v_{x0}sin\mathit{\theta }\right)\\ \end{array}\right\}\right],\\ \mathit{\gamma }=\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)cos\mathit{\theta }}{D_I{n}_0}\left[\begin{array}{c}\left(\begin{array}{c}2n_0{\mathit{\lambda }}_0{\mathit{\lambda }}_1^2\\ -n_0{\mathit{\lambda }}_0^2{\mathit{\lambda }}_1\\ \end{array}\right)+\left(n_{\text{el0}}+n_{\text{eh0}}\right){\mathit{\lambda }}_1\left\{\begin{array}{c}2\frac{T_i}{T_{\text{eff}}}\left(2{\mathit{\lambda }}_0{\mathit{\lambda }}_1-{\mathit{\lambda }}_0^2\right)\\ +{\mathit{\lambda }}_1^3\left(1-{\mathit{\lambda }}_0\right)+{\mathit{\lambda }}_1^2\left(2{\mathit{\lambda }}_0^2-{\mathit{\lambda }}_0\right)-{\mathit{\lambda }}_1{\mathit{\lambda }}_0^3\\ \end{array}\right\}\\ +\left({\mathit{\lambda }}_0^2-{\mathit{\lambda }}_0\right){\left({\mathit{\lambda }}_1-{\mathit{\lambda }}_0\right)}^2{cos}^2\mathit{\theta }\left\{n_0+2\frac{T_i}{T_{\text{eff}}}\left(n_{\text{el0}}+n_{\text{eh0}}\right)\right\}\\ \end{array}\right],\\ \end{array}$$

together with

$$\begin{array}{c}{D}_I={\mathit{\lambda }}_0{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)\left[2\left(n_{\text{el0}}+n_{\text{eh0}}\right)\frac{T_i}{T_{\text{ef}f}}\left(\frac{1}{n_0}+{\mathit{\lambda }}_1\right)+n_0\left({\mathit{\lambda }}_1+{\mathit{\lambda }}_{0}cos\mathit{\theta }\right)\right]\\ +\left(\begin{array}{c}{n}_0\\ +2\left(n_{\text{el0}}+n_{\text{eh0}}\right)\frac{T_i}{T_{\text{eff}}}\\ \end{array}\right){\mathit{\lambda }}_{0}cos\mathit{\theta }\left[n_0+\left(n_{\text{el0}}+n_{\text{eh0}}\right)\left\{2\frac{T_i}{T_{\text{eff}}}\left\{\left({cos}^2\mathit{\theta }-{\mathit{\lambda }}_0{cos}^2\mathit{\theta }\right)+{\mathit{\lambda }}_1{\mathit{\lambda }}_0-{\mathit{\lambda }}_1^2\right\}\right\}\right],\\ \end{array}$$

and ${\mathit{\lambda }}_1=cos\mathit{\theta }{\sqrt{\left[\left(1+2\frac{T_i}{T_{\text{eff}}}\right)+\left(\frac{n_{\text{d0}}}{n_{\text{el0}}+n_{\text{eh0}}}\right)\right]}}^{}$.

Similarly, a relevant mKdV equation for the reflected wave is obtained as

$$\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\alpha }}_R{v}_{z1}^{1/2}\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R^3}+{\mathit{\gamma }}_R{v}_{z1}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}=0,$$

(13)

where

$$\begin{array}{c}{\mathit{\alpha }}_R=-\frac{\sqrt{n_0}}{D_R}{\left(2b_l{n}_{\text{el0}}\left(n_{\text{el0}}+n_{\text{eh0}}\right){\mathit{\lambda }}_1^3\frac{n_{0}cos\mathit{\theta }}{{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)}\frac{T_{\text{eff}}}{T_{\text{el}}}\right)}^{3/2},\\ {\mathit{\beta }}_R=\frac{n_{0}cos\mathit{\theta }{\mathit{\lambda }}_1^2}{D_R{\mathit{\lambda }}_{0R}^2}\left[1+\left(\begin{array}{c}1\\ +2\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)T_i}{n_0{T}_{\text{eff}}}\\ \end{array}\right)\frac{1}{{\mathit{\lambda }}_1{\mathit{\Omega }}_R^2}\left\{\begin{array}{c}{n}_0{\mathit{\lambda }}_1{sin}^2\mathit{\theta }+{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)\left(\begin{array}{c}2\frac{T_i}{T_{\text{eff}}}{sin}^2\mathit{\theta }\\ -{\mathit{\lambda }}_1\left\{v_{x0}-v_{x0}sin\mathit{\theta }-1\right\}\\ \end{array}\right)\\ +\left(1+2\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)T_i}{n_0{T}_{\text{eff}}}\right){\mathit{\lambda }}_{0R}{cos}^2\mathit{\theta }\left\{{\mathit{\lambda }}_1+v_{x0}-v_{x0}sin\mathit{\theta }\right\}\\ \end{array}\right\}\right],\\ {\mathit{\gamma }}_R=\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)cos\mathit{\theta }}{D_R{n}_0}\left[\begin{array}{c}\left(\begin{array}{c}2n_0{\mathit{\lambda }}_{0R}{\mathit{\lambda }}_1^2\\ -n_0{\mathit{\lambda }}_1{\mathit{\lambda }}_{0R}^2\\ \end{array}\right)+\left(n_{\text{el0}}+n_{\text{eh0}}\right){\mathit{\lambda }}_1\left\{\begin{array}{c}2\frac{T_i}{T_{\text{eff}}}\left(2{\mathit{\lambda }}_{0R}{\mathit{\lambda }}_1-{\mathit{\lambda }}_{0R}^2\right)\\ +{\mathit{\lambda }}_1^3\left(1-{\mathit{\lambda }}_{0R}\right)+{\mathit{\lambda }}_1^2\left(2{\mathit{\lambda }}_{0R}^2-{\mathit{\lambda }}_{0R}\right)-{\mathit{\lambda }}_1{\mathit{\lambda }}_{0R}^3\\ \end{array}\right\}\\ +\left({\mathit{\lambda }}_{0R}^2-{\mathit{\lambda }}_{0R}\right){\left({\mathit{\lambda }}_1-{\mathit{\lambda }}_{0R}\right)}^2{cos}^2\mathit{\theta }\left\{n_0+2\frac{T_i}{T_{\text{eff}}}\left(n_{\text{el0}}+n_{\text{eh0}}\right)\right\}\\ \end{array}\right],\end{array}$$

together with

$$\begin{array}{c}{D}_R={\mathit{\lambda }}_{0R}{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)\left[2\left(n_{\text{el0}}+n_{\text{eh0}}\right)\frac{T_i}{T_{\text{eff}}}\left(\frac{1}{n_0}+{\mathit{\lambda }}_1\right)+n_0\left({\mathit{\lambda }}_1+{\mathit{\lambda }}_{0R}cos\mathit{\theta }\right)\right]\\ +\left(\begin{array}{c}{n}_0\\ +2\left(n_{\text{el0}}+n_{\text{eh0}}\right)\frac{T_i}{T_{\text{eff}}}\\ \end{array}\right){\mathit{\lambda }}_{0R}cos\mathit{\theta }\left[n_0+\left(n_{\text{el0}}+n_{\text{eh0}}\right)\left\{2\frac{T_i}{T_{\text{eff}}}\left\{\left({cos}^2\mathit{\theta }-{\mathit{\lambda }}_{0R}{cos}^2\mathit{\theta }\right)+{\mathit{\lambda }}_1{\mathit{\lambda }}_{0R}-{\mathit{\lambda }}_1^2\right\}\right\}\right].\end{array}$$

The mKdV equation for the transmitted wave is the following

$$\frac{\mathit{\partial }{v}_{1T}}{\mathit{\partial }{\mathit{\eta }}_T}+{\mathit{\alpha }}_T{v}_{1T}^{1/2}\frac{\mathit{\partial }{v}_{1T}}{\mathit{\partial }{\mathit{\xi }}_T}+{\mathit{\beta }}_T\frac{{\mathit{\partial }}^3{v}_{1T}}{\mathit{\partial }{\mathit{\xi }}_T^3}+{\mathit{\gamma }}_T{v}_{1T}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_T}=0,$$

(14)

where

$${\mathit{\alpha }}_T=\frac{\sqrt{n_0}}{D_T}\left[-2b_l{n}_{\text{el0}}{\mathit{\lambda }}_1^3\left(n_{\text{el0}}+n_{\text{eh0}}\right){\left(\frac{n_{0}cos\mathit{\theta }}{{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)}\frac{T_{\text{ef}f}}{T_{\text{el}}}\right)}^{3/2}\right],$$

$$\begin{array}{c}{\mathit{\beta }}_T=\frac{n_{0}cos\mathit{\theta }{\mathit{\lambda }}_1^2}{D_T{\mathit{\lambda }}_{0T}^2}\left[1+\left(\begin{array}{c}1\\ +2\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)T_i}{n_0{T}_{\text{eff}}}\\ \end{array}\right)\frac{1}{{\mathit{\lambda }}_1{\mathit{\Omega }}_R^2}\left\{\begin{array}{c}{n}_0{\mathit{\lambda }}_1{sin}^2\mathit{\theta }+{\mathit{\lambda }}_1\left(n_{el0}+n_{eh0}\right)\left(\begin{array}{c}2\frac{T_i}{T_{eff}}{sin}^2\mathit{\theta }\\ +{\mathit{\lambda }}_1\left\{v_{x0B}-v_{x0B}sin\mathit{\theta }-1\right\}\\ \end{array}\right)\\ +\left(1+2\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)T_i}{n_0{T}_{\text{eff}}}\right){\mathit{\lambda }}_{0T}{cos}^2\mathit{\theta }\left({\mathit{\lambda }}_1-v_{x0B}+v_{x0B}sin\mathit{\theta }\right)\\ \end{array}\right\}\right],\\ {\mathit{\gamma }}_T=\frac{\left(n_{\text{el0}}+n_{\text{eh0}}\right)cos\mathit{\theta }}{D_T{n}_0}\left[\begin{array}{c}\left(\begin{array}{c}2n_0{\mathit{\lambda }}_{0T}{\mathit{\lambda }}_1^2\\ -n_0{\mathit{\lambda }}_{0T}^2{\mathit{\lambda }}_1\\ \end{array}\right)+\left(n_{\text{el0}}+n_{\text{eh0}}\right){\mathit{\lambda }}_1\left\{\begin{array}{c}2\frac{T_i}{T_{\text{eff}}}\left(2{\mathit{\lambda }}_{0T}{\mathit{\lambda }}_1-{\mathit{\lambda }}_{0T}^2\right)\\ +{\mathit{\lambda }}_1^3\left(1-{\mathit{\lambda }}_{0T}\right)+{\mathit{\lambda }}_1^2\left(2{\mathit{\lambda }}_{0T}^2-{\mathit{\lambda }}_{0T}\right)-{\mathit{\lambda }}_1{\mathit{\lambda }}_{0T}^3\\ \end{array}\right\}\\ +\left({\mathit{\lambda }}_{0T}^2-{\mathit{\lambda }}_{0T}\right){\left({\mathit{\lambda }}_1-{\mathit{\lambda }}_{0T}\right)}^2{cos}^2\mathit{\theta }\left\{n_0+2\frac{T_i}{T_{\text{eff}}}\left(n_{el0}+n_{\text{eh0}}\right)\right\}\\ \end{array}\right],\end{array}$$

together with

$$\begin{array}{c}{D}_T={\mathit{\lambda }}_{0T}{\mathit{\lambda }}_1\left(n_{\text{el0}}+n_{\text{eh0}}\right)\left[2\left(n_{\text{el0}}+n_{\text{eh0}}\right)\frac{T_i}{T_{\text{eff}}}\left(\frac{1}{n_0}+{\mathit{\lambda }}_1\right)+n_0\left({\mathit{\lambda }}_1+{\mathit{\lambda }}_{0T}cos\mathit{\theta }\right)\right]\\ +\left(\begin{array}{c}{n}_0\\ +2\left(n_{\text{el0}}+n_{\text{eh0}}\right)\frac{T_i}{T_{\text{eff}}}\\ \end{array}\right){\mathit{\lambda }}_{0T}cos\mathit{\theta }\left[n_0+\left(n_{\text{el0}}+n_{\text{eh0}}\right)\left\{2\frac{T_i}{T_{\text{eff}}}\left\{\left({cos}^2\mathit{\theta }-{\mathit{\lambda }}_{0T}{cos}^2\mathit{\theta }\right)+{\mathit{\lambda }}_1{\mathit{\lambda }}_{0T}-{\mathit{\lambda }}_1^2\right\}\right\}\right].\end{array}$$

Soliton solution of Eqs. (12) and (14)

The mKdV Eq. (12) is obtained with the use of both the phase velocity relations λ _0F and λ _0S , which means both the waves evolve into solitary structures determined by Eq. (12). To analyze these structures, we use a sine–cosine method [4, 5, 34] because the solution of mKdV equations cannot be determined by ordinary methods due to presence of variable coefficients. For this, we put $v_{1I}=L\left(\mathit{\eta }\right){\tilde{v}}_I\left(\mathit{\xi },\mathit{\eta }\right)$ with $L\left(\mathit{\eta }\right)=e^{-{\int }_{}^{\mathit{\eta }}{\mathit{\gamma }}_{}\left(\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}^{\prime }}\right)d{\mathit{\eta }}^{\prime }}$in Eq. (12) and get

$$\frac{\mathit{\partial }{\tilde{v}}_I}{\mathit{\partial }\mathit{\eta }}+{\mathit{\alpha }}_{}{\tilde{v}}_I^{1/2}\sqrt{L}\frac{\mathit{\partial }{\tilde{v}}_I}{\mathit{\partial }\mathit{\xi }}+{\mathit{\beta }}_{}\frac{{\mathit{\partial }}^3{\tilde{v}}_I}{\mathit{\partial }{\mathit{\xi }}^3}=0.$$

(15)

Now, we put ${\tilde{v}}_I^{1/2}=v_I$ in the above equation to get

$$v_I\frac{\mathit{\partial }{v}_I}{\mathit{\partial }\mathit{\eta }}+{\mathit{\alpha }}_{}{v}_I^2\sqrt{L}\frac{\mathit{\partial }{v}_I}{\mathit{\partial }\mathit{\xi }}+{\mathit{\beta }}_{}\left(3\frac{\mathit{\partial }{v}_I}{\mathit{\partial }\mathit{\xi }}\frac{{\mathit{\partial }}^2{v}_I}{\mathit{\partial }{\mathit{\xi }}^2}+v_I\frac{{\mathit{\partial }}^3{v}_I}{\mathit{\partial }{\mathit{\xi }}^3}\right)=0.$$

(16)

The solution of this equation can be written as $v_I\left(\mathit{\theta }\right)={\sum }_{j=1}^r\left\{P_{j}sin\mathit{\theta }+Q_{j}cos\mathit{\theta }\right\}{cos}^{j-1}\mathit{\theta }+Q_0$, if $\frac{d\mathit{\theta }}{d{\mathit{\zeta }}_{}}=sin\mathit{\theta }$. In the form of hyperbolic functions, this solution reads

$$v_I\left({\mathit{\zeta }}_{}\right)=Q_0+\sum _{j=1}^r{tanh}^{j-1}\left({\mathit{\zeta }}_{}\right)\left\{P_{j}sech\left({\mathit{\zeta }}_{}\right)+Q_{j}tanh\left({\mathit{\zeta }}_{}\right)\right\}.$$

(17)

To get a stationary solution, we now transform the coordinates to the frame of reference of soliton through $\mathit{\zeta }=g_I\left(\mathit{\eta }-U\mathit{\xi }\right)$, where $g_I^{-1}$ is the width and U is the shift [35] in the velocity when the wave evolves as a soliton. For the present case, we get r = 2. With this, the solution in the form of intermediate variable θ is written as

$$v_I\left(\mathit{\theta }\right)=Q_0+Q_{1}cos\mathit{\theta }+P_{1}sin\mathit{\theta }+Q_2{cos}^2\mathit{\theta }+P_{2}cos\mathit{\theta }sin\mathit{\theta }.$$

(18)

Now, solution (18) is substituted in Eq. (16) to obtain coefficients of the various trigonometric identities. Based on the values of the coefficients Q ₀ , Q ₁ , Q ₂ , P ₁ and P ₂ , we will have different soliton solutions corresponding to Eq. (16). For a single soliton solution, we find $Q_1=P_1=P_2$ = 0, then we obtain $Q_0=-Q_2=\frac{15}{8\mathit{\alpha }\sqrt{L}U}$ and ${\text{g}}_{\text{I}}=\sqrt{\frac{1}{16\mathit{\beta }{U}^3}}$. With these coefficients, the soliton solution is realized as

$$v_I=A_{I}sec{h}^2\left[\frac{\left(\mathit{\eta }-U\mathit{\xi }\right)}{W_I}\right].$$

(19)

This equation represents the incident soliton having peak amplitude $A_I\left(\equiv \frac{15}{8{\mathit{\alpha }}_{}U\sqrt{L}}\right)$ and the width $W_I=g_I^{-1}=\sqrt{16{\mathit{\beta }}_{}{U}^3}$. It is clear that the soliton width would be real only when the coefficient β is positive for the positive velocity shift U. Our calculations infer that the fast and slow waves evolve as density hill type structures only. It means the plasma supports only the compressive solitary structures.

Following the same procedure, we obtain the solution of Eq. (14) as

$$v_T=A_{T}sec{h}^2\left[\frac{\left({\mathit{\eta }}_T-U_T{\mathit{\xi }}_T\right)}{W_T}\right].$$

(20)

This equation represents the transmitted soliton having peak amplitude $A_T\left(\equiv \frac{15}{8{\mathit{\alpha }}_T{U}_T\sqrt{L_T}}\right)$ and the width $W_T=g_T^{-1}=\sqrt{16{\mathit{\beta }}_T{U}_T^3}$.

Coupling of mKdV equations and reflected soliton

After getting the profiles of the incident and transmitted solitons, now we find the solution to the mKdV Eq. (13) for the reflected soliton. Since at the point of reflection all the solitons (incident, reflected and transmitted solitons) evolve, we couple all the mKdV equations at the point of reflection by replacing v _1I in Eq. (13) by v _1I  + v _z1  + v _1T , i.e., by the total ion fluid velocity [36–38]

$$\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\alpha }}_R{\left(v_{1I}+v_{1T}+v_{z1}\right)}^{1/2}\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R^3}+{\mathit{\gamma }}_R{\left(v_{1I}+v_{1T}+v_{z1}\right)}^{}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}=0.$$

(21)

In view of the reflection and transmission of incident solitary wave only, we use $v_{z1}<<v_{1I}+v_{1T}$ and also assume $v_{1T}<<v_{1I}$, [19, 36, 39]. Then the above equation takes the form

$$\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\alpha }}_R{P}_R\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\alpha }}_R\frac{P_R}{Q_R}{v}_{z1}\frac{\mathit{\partial }{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{v}_{z1}}{\mathit{\partial }{\mathit{\xi }}_R^3}+{\mathit{\gamma }}_R{\left(v_{1I}+v_{1T}\right)}^{}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\gamma }}_R{v}_{z1}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}=0,$$

(22)

where $P_R=\frac{2v_{1I}+v_{1T}}{2\sqrt{v_{1I}}}$ and $Q_R=2\left(v_{1I}+v_{1T}\right)$.

Now, we apply a transformation $v_{z1}=L_R\left({\mathit{\eta }}_R\right){\tilde{v}}_R\left({\mathit{\eta }}_R,{\mathit{\xi }}_R\right)$ with $L_R\left(\mathit{\eta }\right)=e^{-{\int }_{}^{{\mathit{\eta }}_R}{\mathit{\gamma }}_R\left(\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R^{\prime }}\right)d{\mathit{\eta }}_R^{{}^{\prime }}}$ in the above equation to obtain

$$\frac{\mathit{\partial }{\tilde{v}}_R}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\alpha }}_R{P}_R\frac{\mathit{\partial }{\tilde{v}}_R}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\alpha }}_R{L}_R\frac{P_R}{Q_R}{\tilde{v}}_R\frac{\mathit{\partial }{\tilde{v}}_R}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{\tilde{v}}_R}{\mathit{\partial }{\mathit{\xi }}_R^3}+{\mathit{\gamma }}_R{\frac{\left(v_{1I}+v_{1T}\right)}{L_R}}^{}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R}=0.$$

We employ another transformation ${\tilde{v}}_R\left({\mathit{\eta }}_R,{\mathit{\xi }}_R\right)=h_R\left({\mathit{\eta }}_R\right)+v_R\left({\mathit{\eta }}_R,{\mathit{\xi }}_R\right)$, where $h_R\left({\mathit{\eta }}_R\right)={\int }_{}^{{\mathit{\eta }}_R}-\left(\frac{{\mathit{\gamma }}_R}{L_R}\right)\left(v_{1I}+v_{1T}\right)\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\eta }}_R^{{}^{\prime }}}d{\mathit{\eta }}_R^{{}^{\prime }}$ in the above equation. This yields

$$\frac{\mathit{\partial }{v}_R}{\mathit{\partial }{\mathit{\eta }}_R}+{\mathit{\alpha }}_R{P}_R\frac{\mathit{\partial }{v}_R}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\alpha }}_R{L}_R\frac{P_R}{Q_R}{h}_R\frac{\mathit{\partial }{v}_R}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\alpha }}_R{L}_R\frac{P_R}{Q_R}{v}_R\frac{\mathit{\partial }{v}_R}{\mathit{\partial }{\mathit{\xi }}_R}+{\mathit{\beta }}_R\frac{{\mathit{\partial }}^3{v}_R}{\mathit{\partial }{\mathit{\xi }}_R^3}=0.$$

(23)

This equation can be solved by following the same method as adopted for the incident soliton. Hence, we get

$$v_R=\frac{3}{L_R}\left(\frac{4}{U_R{\mathit{\alpha }}_R\tilde{V}}-2\left(v_{1I}+v_{1T}\right)-h_R{L}_R\right)sec{h}^2\left[\frac{\left({\mathit{\eta }}_R-U_R{\mathit{\xi }}_R\right)}{W_R}\right].$$

(24)

Here, $\tilde{V}=\frac{2v_{1I}+v_{1T}}{\sqrt{v_{1I}}\left(v_{1I}+v_{1T}\right)}$ and $W_R\equiv \frac{5L_R}{2\mathit{\alpha }}\sqrt{\frac{\mathit{\beta }U}{L}}{\left[\frac{4}{U_R{\mathit{\alpha }}_R\tilde{V}}-2\left(v_{1I}+v_{1T}\right)-h_R{L}_R\right]}^{-1}$. The symbol $W_R$ represents the width of the reflected soliton and the first term $\frac{3}{L_R}\left(\frac{4}{U_R{\mathit{\alpha }}_R\tilde{V}}-2\left(v_{1I}+v_{1T}\right)-h_R{L}_R\right)$ is the peak amplitude of the soliton. The symbol U _R is the velocity shift that is realized when the wave takes the form of reflected soliton. This shift is different from the shift that was observed during the soliton reflection, as that shift means the fall or rise of the path of propagation of the incident soliton.

Energy conservation of solitons

The previous studies of the soliton reflection discuss that the soliton after its reflection gets shifted and this shift amounts to the energy difference between the incident and reflected solitons. However, unlike this case, Eqs. (19), (20) and (24) reveal that in the case of reflection and transmission of the solitons this energy is balanced. Hence, considering the energy balance we can obtain an expression between the parameters U, U _R and U _T . For this, we follow Malik [8] in view of the weak density gradient so that the unperturbed quantities can be treated as slow varying functions, and use the integral $E={\int }_{-\infty }^{\infty }{v}^2\left(\mathit{\varsigma }\right)d\mathit{\varsigma }$, where $v\equiv v_I,v_R,v_T$ and $\mathit{\varsigma }\equiv \mathit{\varsigma },{\mathit{\varsigma }}_R,{\mathit{\varsigma }}_T$. Based on this integral the energies of the incident, reflected and transmitted solitons are obtained as $E_I=\frac{4}{3}{A}_I^2{W}_I$, $E_R=\frac{4}{3}{A}_R^2{W}_R$ and $E_T=\frac{4}{3}{A}_T^2{W}_T$. The conservation of energy shall require $E_I=E_R+E_T$. Further, based on the experimental investigations we can assume $A_I{W}_I=A_R{W}_R=A_T{W}_T$ for the modified KdV solitons. All these equations give the following relation between U, U _R and U _T

$$\frac{{\mathit{\alpha }}_T{L}_T^{1/2}{U}_T-{\mathit{\alpha }}_{}{L}_{}^{1/2}{U}_{}}{8{\mathit{\alpha }}_{}{L}_{}^{1/2}{U}_{}{\mathit{\alpha }}_T{L}_T^{1/2}{U}_T}+\frac{2\left(v_{1I}+v_{1T}\right)+h_R{L}_R}{5L_R}=\frac{4}{5{\mathit{\alpha }}_R{U}_R\tilde{V}{L}_R}.$$

(25)

The above relation shows that the velocity shift of the reflected and transmitted solitons is in accordance with the velocity U of the incident soliton.

Results and discussion

The present plasma supports two types of the waves governed by Eq. (9), which evolve into two types of compressive solitons governed by Eq. (12). However, Eq. (10) shows that only the wave corresponding to plus sign propagates in the plasma. Since this wave belongs to the reflected soliton governed by Eq. (13), it is inferred that only the soliton corresponding to plus sign in Eq. (9) reflects. This is justified in view of the fact the soliton requires a minimum energy to reflect from the density gradient during the reflection mechanism.

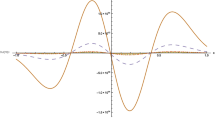
Figure 1 shows the profiles of the incident, reflected and transmitted solitons in the magnetized and inhomogeneous plasma having negatively charged dust grains. This can be seen that the perturbations are localized as the soliton amplitude approaches zero as we move away from ζ = 0. As is obvious, the incident soliton carries largest size with highest amplitude and hence, the largest energy. The reflected soliton carries opposite profile to the incident soliton [40], which means the soliton changes its polarity after its reflection. This is the similar result as obtained by Nishida and Nagasawa [18] in an experiment conducted in a plasma with two temperature electrons. So our theoretical calculations confirm their findings. However, the transmitted soliton carries lower size and does not change its polarity. The sizes of the reflected and transmitted solitons are smaller compared with the size of the incident soliton. This is plausible, as the energy corresponding to the incident soliton is bifurcated in the reflection and transmission of the soliton.

Fig. 1

Profiles of the incident, reflected and transmitted solitons, when B₀ = 0.05T, n₀ = 0.8, n_el0 = 0.1, n_eh0 = 0.12, T_el = 0.5 eV, T _i  = 0.05 eV, T_eh = 3 eV, v_x0 = 0.45, v_z0 = 0.30, U = 0.5, U _R  = 0.5 and m _i /m_e = 1,836

To study the effect of magnetic field on the transmission of the soliton, we have plotted Fig. 2, which shows the variation of energy of transmitted soliton with the magnetic field (B₀) for two different values of the wave propagation angle θ (15 and 20 °C). This is evident from the figure that the transmitted soliton loses its energy under the effect of stronger magnetic field. This is consistent with the observations made by other investigators [3, 7, 8, 10, 11, 13, 35, 38], who found that the solitons with smaller width propagate in the plasma under the effect of higher magnetic field. Since the energy of the soliton is directly proportional to its width, the solitons are expected to evolve with lower energy in the presence of stronger magnetic field. On the other hand, we observe that the soliton carries lower energy when the magnetic field is applied at a larger angle with the direction of wave propagation. This is plausible, as the Lorentz force becomes larger for the larger obliqueness of the wave propagation and hence, the soliton with smaller width would evolve. Further, this is noticed that the soliton energy sharply decreases with the magnetic field when it is applied at a smaller angle with the direction of wave propagation. The reduction in soliton energy is attributed to the change in dispersive properties of the plasma with the application of magnetic field. Since the plasma becomes more dispersive under the effect of stronger magnetic field, the nonlinear effect ought to be enhanced for the generation of solitary structure. This modification leads to the smaller width of the soliton and hence, the smaller energy.

Fig. 2

Dependence of the transmitted soliton energy (E _T ) on magnetic field (B₀), when n₀ = 0.8, n_el0 = 0.1, n_eh0 = 0.12, T_el = 0.5 eV, T _i  = 0.05 eV, T_eh = 3 eV, v_x0 = 0.45, v_z0 = 0.30, U = 0.5, U _R  = 0.5 and m _i /m _e  = 1,836

The role of dust grains to the soliton transmission is clarified in Fig. 3, where the variation of soliton amplitude is shown with the dust grain density. Clearly, the transmitted soliton attains lower amplitude under the presence of higher density of the dust grains. Since the energies of the solitons follow Eq. (25), this is obvious that the reflection of soliton would be stronger under the presence of more dust grains in the plasma. Hence, the reflection coefficient (RC: ratio of reflected-to-incident soliton amplitudes) enhances whereas the transmission coefficient (TC: ratio of transmitted-to-incident soliton amplitudes) is lowered under the effect of higher density of dust grains (Fig. 4). The opposite behavior of RC and TC with the dust density is admissible in view of the energy balance of the incident, reflected and transmitted solitons. This is also in accordance with the mechanism of soliton reflection. As the incident soliton is accelerated by the gradient and then reflected, there is a partial transmission of the soliton. Since the reflected and transmitted solitons propagate in opposite directions, it is plausible that these structures see opposite effects of the dust grains due to the fixed direction of the density gradient. It appears that the transmitted soliton is slowed down in the presence of higher density of the dust grains. Hence, it evolves with smaller amplitude. This leads to the weaker transmission and stronger reflection of the soliton in view of the energy balance.

Fig. 3

Variation of the transmitted soliton amplitude (A _T ) with dust density (n_d0Z_d0), when B₀ = 0.05T, n₀ = 0.8, n_eh0 = 0.12, T_el = 0.5 eV, T _i  = 0.05 eV, T_eh = 3 eV, v_x0 = 0.45, v_z0 = 0.30, U = 0.5, U _R  = 0.5 and m _i /m_e = 1,836

Fig. 4

Variation of the transmission coefficient (TC) and reflection coefficient (RC) with the dust density (n_d0Z_d0), when B₀ = 0.05T, n₀ = 0.8, n_eh0 = 0.12, T_el = 0.5 eV, T _i  = 0.05 eV, T_eh = 3 eV, v_x0 = 0.45, v_z0 = 0.30, U = 0.5, U _R  = 0.5 and m _i /m_e = 1,836

Conclusions

The problem of reflection and transmission of a soliton was solved in an inhomogeneous dusty plasma having two temperature electrons under the effect of an external static magnetic field. Two types of the waves, corresponding to plus sign (fast wave) and minus sign (slow wave) in Eq. (9), were found to propagate and evolve into solitons in this plasma. However, the soliton corresponding to only the fast wave was found to reflect and transmit in the plasma and the soliton corresponding to the slow wave was transmitted only. The effect of higher dust density was found to lower the amplitude and energy of the transmitted soliton. However, opposite effect of these parameters was realized on the soliton reflection. The nonlinear terms of Eqs. (12)–(14) revealed lower order nonlinearity in the present plasma, compared to the usual plasma without nonisothermal electrons, for the generation of solitons. Hence, the smaller amplitude solitons are expected to evolve in the present plasma in comparison with the case of ordinary plasma.