1 Introduction

In recent times, considerable interest has been shown in exploring universal relations constructed from the area product and sum relations of multi-horizon stationary black holes in super gravity, Einstein gravity and other modified theories of gravity [1,2,3,4,5,6]. In most cases, whereas the area product and sum relations are mass independent, they depend on various black hole parameters including charge, angular momentum, and cosmological constant. However, in some cases such as asymptotically non-flat spacetime, these relations fail to execute mass-independent relations [7,8,9,10]. Visser [11] found that the mass-independent area product relations fail in Schwarzschild-de Sitter black hole even if the contributions of the virtual horizon is included.

Several authors [12,13,14] argued that the contribution of virtual horizon area should be added to build up mass-independent area-product and sum relations. However, in some cases, such contributions of virtual horizon could not sustain significantly [11]. It is known that a class of black holes admits more than one horizons, such as black hole event horizon (outer horizon), cauchy horizon (inner horizon), and virtual horizon (un-physical horizon). It has been argued [15,16,17,18] that like event horizon, other horizons are also associated with the notion of temperature and entropy. An extension of these notions has also been made for dynamical apparent horizon of FRW universe [19,20,21,22,23,24,25,26,27,28]. Despite the multiple horizons of stationary black holes, there are dynamical spacetime metrics containing dynamic multiple horizons. The universal relations for dynamical multi-horizons geometries need to be investigated for more physical interest. In this context, we consider McVittie universe carrying a central mass describing black hole embedded in expanding flat FRW universe. The McVittie universe holds dynamic multiple horizons, namely the black hole event horizon, \(R_{{\text {E}}}\), the cosmological horizon, \(R_{{\text {C}}}\), and the virtual horizon, \(R_{{\text {V}}}\). Analogous to the multi-horizon of stationary black holes, in this paper, we investigate the explicit mass-dependent and mass-independent relations over the dynamical horizons of McVittie spacetime.

The Bekenstein–Hawking area-entropy law [29] is defined at the black hole horizon \((H_{+})\)

$$\begin{aligned} S_{+} = \frac{A_{+}}{4}. \end{aligned}$$
(1)

Another striking discovery was made by Hawking [30] in which thermal radiation was predicted near the black hole horizon with a temperature given by

$$\begin{aligned} T_{+} = \frac{\kappa _{+}}{2\pi } , \end{aligned}$$
(2)

where \(T_{+}\), \(\kappa _{+}\), and \(A_{+}\) are the Hawking temperature, the surface gravity, and the horizon area computed at black hole horizon called outer horizon \((H_{+})\), respectively. Note that the units are such that \(c=G=\kappa = \hbar =1\). In general, the above-mentioned quantities are held at the event horizon but, on the other hand, certain black holes contain two or more horizons, such as cauchy and virtual horizons. There might be an indication that aforementioned relations may also hold for these horizons. In the case of stationary black holes, it has been argued [31, 32] that these thermodynamics quantities are also associated with the same proportionalities as in the case of event horizon. In this paper, we advocate assigning the notion of entropy and temperature at the multiple horizons of the dynamical spacetime, namely McVittie universe. In addition, we investigate the product area and sum relations for multi-horizon of McVittie universe. We start by solving the cubic horizon equation (5) to obtain three roots exhibiting the event horizon, the cosmological apparent horizon and the virtual horizon of McVittie metric. Then, we obtain the area product relations comprising explicit mass dependent and mass independent from the areas of dynamical event horizon, the cosmological horizon, and the virtual horizon. Through this method, we establish that the product of the event horizon area, the cosmological horizon area, and the virtual horizon area are not universal but are explicitly mass dependent. On the other hand, the sum of horizon areas is mass independent. Furthermore, the Hawking temperature products and sum relations are also obtained and analyzed. In addition, we also discussed the validity conditions of Generalized Second Law (GSL) of thermodynamics.

2 Horizons of McVittie universe

Let us now start with the expanding McVittie universe holding a black hole embedded in a flat FRW background. The line element of the McVitte universe [33] (with units \(G = c = \kappa = \hbar =1\)) is given by

$$\begin{aligned} {\text {d}}s^{2}=-\frac{\left( 1-\frac{M}{2a(t)r}\right) ^{2}}{\left( 1+\frac{M}{2a(t)r}\right) ^{2}}{\text {d}}t^{2}+ a^{2}(t)\left( 1+\frac{M}{2a(t)r}\right) ^{4}({\text {d}}r^{2}+r^{2}{\text {d}}\Omega ^{2}), \end{aligned}$$
(3)

where \({\text {d}}\Omega ^{2}\) represents the metric of a unit 2-sphere, M is the mass of the black hole and a(t) represents the cosmic scale factor. To calculate the apparent horizons of the McVittie universe, it is convenient to re-write the above metric (3) in a spherical symmetric form

$$\begin{aligned} {\text {d}}s^{2}=h^{ab}{\text {d}}x_{a}{\text {d}}x_{b}+ R^{2}{\text {d}}\Omega ^{2}, \end{aligned}$$
(4)

where \(R(t, r) = a(t)r(1+\frac{M}{2a(t)r})^{2}\) is called areal radius, the coordinates \(x_{0} = t\), \(x_{1} = r,\) and \(h^{ab} = {\text {diag}}\left( -\frac{(1-\frac{M}{2a(t)r})^{2}}{(1+\frac{M}{2a(t)r})^{2}}, ~a(t)^{2}(1+\frac{M}{2a(t)r})^{4}\right) \) represents two dimensional metric. The apparent horizon is a marginally trapped surface with vanishing expansion. Mathematically \(h^{ab}\partial _{a}R \partial _{b}R =0\), which admits a cubic equation in terms of apparent horizon radius given by

$$\begin{aligned} H^{2}R^{3}_{{\text {A}}}-R_{{\text {A}}}+2M=0, \end{aligned}$$
(5)

where H is the time varying Hubble parameter and \(R_{{\text {A}}}\) denotes the dynamic apparent horizon radius. It is evident from equation (5) that when \(M=0\), it admits cosmological horizon, \(R_{{\text {A}}}=R_{{\text {C}}}=\frac{1}{H}\), of flat FRW universe, on the other hand when \(a(t) ={\text {constant}} ~~{\text {i.e,}}~~ H=0\), it turns out black hole event horizon located at \(R_{{\text {A}}}=R_{{\text {E}}}=2M\). The various horizons of McVittie universe are obtained by finding the roots of Eq. (5). These roots are presented below [34]

$$\begin{aligned} R_{{\text {E}}}= & {} \frac{2}{\sqrt{3}H} \sin \theta , \end{aligned}$$
(6)
$$\begin{aligned} R_{{\text {C}}}= & {} \frac{1}{H} \cos \theta -\frac{1}{\sqrt{3}H} \sin \theta , \end{aligned}$$
(7)

and

$$\begin{aligned} R_{{\text {V}}} = -\frac{1}{H} \cos \theta -\frac{1}{\sqrt{3}H} \sin \theta , \end{aligned}$$
(8)

where \(\sin 3 \theta = 3\sqrt{3}MH(t)\). Obviously, \(R_{{\text {V}}}<0\) which is unphysical and referred to as a virtual horizon. The remaining two real positive roots correspond to two horizons, \(R_{{\text {E}}}\), and \(R_{{\text {C}}}\), of McVittie universe, where the horizon \(R_{{\text {E}}}\) is named as a black hole event horizon as it turns out to be the Schwarzschild black hole horizon, \(R=2M\), when \(H \rightarrow 0\). On the other hand, the horizon, \(R_{{\text {C}}}\), is to referred as a cosmological horizon since it reduces to the cosmological horizon \(\frac{1}{H}\) of flat FRW universe when there is no point mass present in McVittie universe.

Let us define entropies \(S_{{\text {E}}}\), \(S_{{\text {C}}}\), and \(S_{{\text {V}}}\) associated with the Event horizon \(R_{{\text {E}}}\), cosmological horizon \(R_{{\text {C}}}\) and virtual horizon \(R_{{\text {V}}}\) of McVittie via area law of entropy (1), respectively

$$\begin{aligned} S_{{\text {E}}} = \frac{A_{{\text {E}}}}{4}= \pi R^{2}_{{\text {E}}},S_{{\text {C}}} = \frac{A_{{\text {C}}}}{4}= \pi R^{2}_{{\text {C}}}, {\text {and}}~ S_{{\text {V}}} = \frac{A_{{\text {V}}}}{4}= \pi R^{2}_{{\text {V}}}. \end{aligned}$$
(9)

Another thermodynamic quantity is the Hawking temperature associated with the horizons of the McVittie universe and is defined via surface gravity using the relation \(T_{i} = \frac{\kappa _{i}}{2\pi }\), where \(i = {\text {E, C, V}}\) and \(\kappa _{i}\) is the surface gravity associated with \(R_{i{\text {th}}}\) horizon. Mathematically the surface gravity associated with \(R_{i{\text {th}}}\) horizon is determined via relation [19]

$$\begin{aligned} \kappa _{i}=\frac{1}{2\sqrt{-h}}\frac{\partial }{\partial _{a}} \left( \sqrt{-h}h^{ab}\frac{\partial }{\partial _{b}}{R_{i}}\right) , \end{aligned}$$
(10)

where \(-h\) is the determinant of \(h_{ab}={\text {diag}}(g_{00}, g_{11})\) with \(g_{00}\) and \(g_{11}\)t–r components of McVittie metric (3) and \(R=a(t)r\left( 1+\frac{M}{2a(t)r}\right) ^{2}\) is the apparent radius of the universe. The above expression (10) is evaluated at the apparent horizon \(R_{i}\) of the McVittie metric which turns out to be

$$\begin{aligned} \kappa _{i} = \frac{M}{R^{2}_{i}}-\frac{R_{i}}{4}(H^{2}-8\pi P), \end{aligned}$$
(11)

where \(\kappa _{i}\) is the surface gravity associated with the horizons, \(R_{{\text {E}}}\), \(R_{{\text {C}}}\), and \(R_{{\text {V}}}\). The temperature \(T_{i}\) associated with each horizon of the universe is given by

$$\begin{aligned} T_{i} =\frac{1}{2\pi } \left( \frac{M}{R^{2}_{i}}-\frac{R_{i}}{4}(H^{2}-8\pi P)\right) , \end{aligned}$$
(12)

where \(T_{i}\) is the temperature associated with the \(R_{i{\text {th}}}\) horizon of the universe.

3 Generalized second law of thermodynamics

It has been shown in Ref. [19] that the first law of black hole thermodynamics holds on the horizon of McVittie universe, it is natural to investigate the validity of GSLT in this model. In the cosmological context, the generalized second law (GSL) of thermodynamics states that the sum of the entropy, \(S_{{\text {H}}}\), of the geometrical horizon, plus the entropy, \(S_{{\text {R}}}\), of the matter and radiation fields inside the horizon is a nondecreasing function of time [15]. Mathematically, GSL can be communicated as

$$\begin{aligned} \dot{S_{H}} + \dot{S_{R}}\ge 0. \end{aligned}$$
(13)

It has been argued in Refs. [35, 36] that GSL confirms particular connection between thermodynamics, gravitation, and quantum theory; therefore, GSL has been studied extensively for both black holes and cosmological spacetimes [37,38,39,40]. Eventually, in this section we investigate the validity conditions of GSL at the apparent horizon of McVittie universe. To achieve this task, we make the differential of Eq. (3) with respect to time which after algebraic simplification turns out

$$\begin{aligned} \dot{R_{{\text {A}}}} = \frac{2H\dot{H}R_{{\text {A}}}^{3}}{1-3H^{2}R_{{\text {A}}}^{2}}. \end{aligned}$$
(14)

It is interesting to know that as \(\dot{R_{{\text {A}}}} \rightarrow \infty \), \(R_{{\text {A}}} \rightarrow \frac{1}{\sqrt{3}H}\). This result indicates that apparent horizon speeds up expanding towards infinity when apparent horizon approaches at its minimum value \(R_{{\text {A}}} \rightarrow \frac{1}{\sqrt{3}H}\) and \(\dot{R_{{\text {A}}}} \rightarrow 0\) when \(R_{{\text {A}}} \rightarrow \infty \). To achieve our task, let us differentiate Eq. (7) which admits

$$\begin{aligned} T_{H}\dot{S_{H}} = \frac{1}{4}(2-3H^{2}R_{{\text {A}}}^{2}+8\pi P R_{{\text {A}}}^{2})\dot{R_{{\text {A}}}}, \end{aligned}$$
(15)

where P describes the pressure of the perfect fluid. The fluid energy density \(E_{m} = \rho V\), entropy \(S_{m}\) and the its temperature \(T_{m}\) hold the Gibbs identity \(T_{m}{\text {d}}S_{m} = {\text {d}}E_{m} + P{\text {d}}V\) on the apparent horizon. By solving Gibbs identity on the apparent horizon \(R_{{\text {A}}}\) of McVittie universe, it turns out

$$\begin{aligned} T_{m}\dot{S_{m}} = \frac{1}{2}(1+8\pi P R^{2}_{{\text {A}}})\dot{R_{{\text {A}}}}. \end{aligned}$$
(16)

To acquire thermal equilibrium near the apparent horizon, we assume that \(T_{H} = T_{m} = T\). Using Eqs. (34) and (35) together with assumption of the thermal equilibrium near apparent horizon, we get

$$\begin{aligned} T(\dot{S_{H}}+ \dot{S_{m}}) = \frac{1}{4}(4-3H^{2}R^{2}_{H}+24\pi P R^{2}_{H})\dot{R_{{\text {A}}}}. \end{aligned}$$
(17)

By introducing horizon temperature \(T_{H}\) from Eq. (20) in the above equation, one can get

$$\begin{aligned} T(\dot{S_{H}}+ \dot{S_{m}}) = \frac{1}{2}(1+4\pi R_{{\text {A}}} T_{H}+8\pi P R^{2}_{{\text {A}}})\dot{R_{{\text {A}}}}. \end{aligned}$$
(18)

Assuming \(P > 0\), it is easy to show that GSL holds near the apparent horizon only if \(\dot{R_{{\text {A}}}}> 0\). From equation (14), there are two possibilities for which \(\dot{R_{{\text {A}}}}> 0\).

(a) \(\dot{H}>0\) and \(1-3H^{2} R_{{\text {A}}}^{2}>0\) and (b) \(\dot{H}<0\) and \(1-3H^{2} R_{{\text {A}}}^{2}<0\). From condition (a), we get the validity region of GSL where \(R_{{\text {A}}}<\frac{1}{\sqrt{3}H}\), and \(H(t) > H_{0}\), where \(H_{0}\) is the hubble constant. In addition, the possibility (b) admits validity region of GSL for which \(R_{{\text {A}}}>\frac{1}{\sqrt{3}H}\), and \(H(t) < H_{0}\).

4 Mass dependent area product relations

The Mcvittie universe contains two physical horizons corresponding to real positive roots of the cubic Eq. (5) and one virtual horizon. If one considers two physical horizons of the universe, then the area product relation turns out

$$\begin{aligned} R_{{\text {E}}}^{2}R_{{\text {C}}}^{2} = \frac{4 \sin ^{2}\theta }{3H^{4}}\Big (1-\frac{2 \sin \theta }{3}(\sin \theta -\sqrt{3} \cos \theta )\Big ), \end{aligned}$$
(19)

which is not a explicit mass-dependent/mass-independent relation. On the other hand, if one includes the area of virtual horizon \('R_{{\text {V}}}'\) in the above equation (13), then the area product relation is presented below

$$\begin{aligned} R_{{\text {E}}}^{2}R_{{\text {C}}}^{2}R_{{\text {V}}}^{2} = \frac{4M^{2}}{H^{4}}, \end{aligned}$$
(20)

which is, however, explicitly mass-dependent relation including time varying Hubble parameter. The comparison of these two relations suggests the important role of virtual horizon as supported in Ref. [12]. The above relation (14) can be rewritten in terms of entropies associated with the horizons of Mcvittie metric which admits

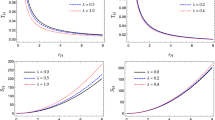
$$\begin{aligned} S_{{\text {E}}}S_{{\text {C}}}S_{{\text {V}}}= \frac{4\pi ^{3} M^{2}}{H^{4}}. \end{aligned}$$
(21)

The above Eq. (14) involves a constant mass parameter M and time varying Hubble parameter H. The validity of this relation (14) is entirely based on the variation of time-dependent Hubble parameter H of the expanding universe. In the early stages of the universe, the Hubble parameter \(H \rightarrow \infty \) which asserts that the entropy of the universe approaches to zero. On the other hand, at the late stages of universe evolution,the Hubble parameter \(H \rightarrow 0\) which predicts the divergence of the entropy, named as “Heat Death” of the universe. This analysis of the above Eq. (14) is also supported by the Big Bang theory. According to the Big Bang, the universe started in a compact and ordered state holding zero entropy in the early stage. While with passage of time, the universe started expanding and cooling down and growing into less ordered and eventually end in the ’Heat Death’ when all the matter attained equilibrium and the entropy approaches its maximum. Let us write down other useful mass-dependent relations

$$\begin{aligned} \frac{R_{{\text {E}}}^2R_{{\text {C}}}^2 + R_{{\text {C}}}^2R_{{\text {V}}}^2 + R_{{\text {V}}}^2 R_{{\text {E}}}^2}{R_{{\text {E}}}^2 R_{{\text {C}}}^2R_{{\text {V}}}^2}= & {} \frac{H^2}{4M^2}, \end{aligned}$$
(22)
$$\begin{aligned} \frac{R_{{\text {E}}}^2 + R_{{\text {C}}}^2 + R_{{\text {V}}}^2}{R_{{\text {E}}}^2 R_{{\text {C}}}^2 R_{{\text {V}}}^2}= & {} \frac{H^2}{2M^2}, \end{aligned}$$
(23)

and

$$\begin{aligned} \frac{1}{R_{{\text {E}}} R_{{\text {C}}} R_{{\text {V}}}}=\frac{2M}{H^2}. \end{aligned}$$
(24)

Note that one can rewrite the above relations in terms of entropies by substituting \(R_{{\text {E}}} = \sqrt{S_{{\text {E}}} / \pi }\), \(R_{{\text {C}}} = \sqrt{S_{{\text {C}}} / \pi }\) and \(R_{{\text {V}}} = \sqrt{S_{{\text {V}}} / \pi }\). Some more explicit mass-dependent relations are given below

$$\begin{aligned} \frac{1}{R_{{\text {E}}}}+\frac{1}{R_{{\text {C}}}}+\frac{1}{R_{{\text {V}}}}= & {} \frac{-1}{2M}, \end{aligned}$$
(25)
$$\begin{aligned} \frac{1}{R_{{\text {E}}}^{2}}+\frac{1}{R_{{\text {C}}}^{2}}+\frac{1}{R_{{\text {V}}}^{2}}= & {} \frac{H^{2}}{4M^{2}}, \end{aligned}$$
(26)
$$\begin{aligned} \frac{1}{R_{{\text {E}}}^{2}R_{{\text {C}}}^{2}}+\frac{1}{R_{{\text {C}}}^{2}R_{{\text {V}}}^{2}}+\frac{1}{R_{{\text {V}}}^{2}R_{{\text {E}}}^{2}}= & {} \frac{H^{2}}{2M^{2}}, \end{aligned}$$
(27)
$$\begin{aligned} \frac{1}{R_{{\text {E}}}R_{{\text {C}}}}+\frac{1}{R_{{\text {C}}}R_{{\text {V}}}}+\frac{1}{R_{{\text {V}}}R_{{\text {E}}}}= & {} 0. \end{aligned}$$
(28)

As a special case of Schwarzschild-de Sitter–Kottler universe, the above relations also hold true by replacing Hubble parameter, \(H = \sqrt{\frac{\Lambda }{3}}\) as discussed in Ref. [11].

5 Mass-independent area product relations

In contrast with the mass-dependent relations, there are also exact mass-independent relations arising from the area product and the area sum determined via all three horizons of the universe. For example

$$\begin{aligned} R_{{\text {E}}}^{2} + R_{{\text {C}}}^{2} + R_{{\text {V}}}^{2} = \frac{2}{H^2}, \end{aligned}$$
(29)

is a mass-independent relation arising from the horizon-area sum. By substituting \(R_{{\text {V}}} = -R_{{\text {E}}}-R_{{\text {C}}}\), in the above Eq. (23), one can rewrite this relation in terms of physical horizons which admits

$$\begin{aligned} R_{{\text {E}}}^{2} + R_{{\text {C}}}^{2} + R_{{\text {E}}}R_{{\text {C}}} = \frac{1}{H^2}, \end{aligned}$$
(30)

this is a universal relation in terms of physical roots of the McVittie universe. In terms of entropies, the above relation represents the total entropy \(S_{{\text {T}}}=S_{{\text {E}}} + S_{{\text {C}}} + S_{{\text {V}}} = \frac{2\pi }{H^2}\) of the universe. Obviously, the total entropy \(T_{{\text {T}}}\) is inversely proportional to the square of time varying Hubble parameter. It vanishes as \(H\rightarrow \infty \) in the beginning of the universe and grows up to its maximum value when \(H\rightarrow 0\) with a result named as ’Heat Death’ of the universe.

Another universal relation is determined via the product sum of the square entropies which admits

$$\begin{aligned} S_{{\text {E}}}^2 S_{{\text {C}}}^2 + S_{{\text {C}}}^2 S_{{\text {V}}}^2 + S_{{\text {V}}}^2 S_{{\text {E}}}^2 = \frac{\pi ^2}{H^4}. \end{aligned}$$
(31)

One can also get a universal via product sum of entropies given by

$$\begin{aligned} \sqrt{S_{{\text {E}}} S_{{\text {C}}}} +\sqrt{S_{{\text {E}}} S_{{\text {V}}}} +\sqrt{S_{{\text {C}}} S_{{\text {V}}}}=\frac{-\pi }{H^2}. \end{aligned}$$
(32)

On the other hand, one can determine universal relation through the use of Hawking temperatures associated with the various horizons of the McVittie universe. One of such a relation is obtained by the product-sum of the temperatures associated with the various horizons of the McVittie universe which admits

$$\begin{aligned} T_{{\text {E}}} T_{{\text {C}}} + T_{{\text {C}}} T_{{\text {V}}} + T_{{\text {V}}} T_{{\text {E}}} = \frac{5 H^{2}}{64\pi ^{2}}. \end{aligned}$$
(33)

It is evident from the previous equation that in the early stage of the universe when \(H \rightarrow \infty \), the above temperature relation (27) diverges when \(t \rightarrow 0\), indicating very high temperature in the early stage of the universe. At the late stage of the universe when \(H \rightarrow 0\), the universe temperature reduces to absolute zero. Analogous to the mass-dependent area product and sum relations, the mass-dependent temperature product/sum relations are listed below

$$\begin{aligned} T_{{\text {E}}} T_{{\text {C}}}T_{{\text {V}}}= & {} \frac{H^{2}}{256}\left( \frac{1}{2M}-27H^{2}M\right) , \end{aligned}$$
(34)
$$\begin{aligned} T_{{\text {E}}} +T_{{\text {C}}}+T_{{\text {V}}}= & {} \frac{H^{2}}{8\pi M}, \end{aligned}$$
(35)
$$\begin{aligned} \frac{1}{T_{{\text {E}}}} + \frac{1}{T_{{\text {C}}}} + \frac{1}{T_{{\text {V}}}}= & {} \frac{40\pi M}{1-54H^{2}M^{2}}, \end{aligned}$$
(36)
$$\begin{aligned} T_{{\text {E}}}^{2} +T_{{\text {C}}}^{2}+T_{{\text {V}}}^{2}= & {} \frac{1-10H^{2}M^{2}}{64\pi ^{2} M^{2}}. \end{aligned}$$
(37)

6 Conclusion

In this paper, we have investigated the area product and the area sum relations when evaluated at the event horizon, the cosmological horizon and the virtual horizon of the expanding McVittie universe. Analogous to the mass independent and mass-dependent relations of multi-horizon stationary black holes, we employed the notion of entropy and temperature at the multi-horizons of the McVittie universe and determined various mass-independent and explicit mass dependent relations. Mainly, all these relations also depend on the time-varying Hubble parameter. It is found that the product area relation is not universal when evaluated at multi-horizon even including virtual horizon area. On the other hand, the horizon areas sum including virtual horizon area is mass independent (a universal relation) but is a function of the time varying Hubble parameter H. We also discussed and analyzed these horizon area relations. It is found that the total entropy of the McVittie universe approaches to zero during the beginning of the universe and grows up till it diverges at the end of the universe possessing "The heat Death" scenario. Another universal relation is obtained by the product-sum of the temperatures associated with the event, cosmological and virtual horizons.