Abstract
Small Bénabou’s bicategories and, in particular, Mac Lane’s monoidal categories, have well-understood classifying spaces, which give geometric meaning to their cells. This paper contains some contributions to the study of the relationship between bicategories and the homotopy types of their classifying spaces. Mainly, generalizations are given of Quillen’s Theorems A and B to lax functors between bicategories.
Similar content being viewed by others
1 Introduction and summary
Categorical structures have numerous applications outside of category theory proper as they occur naturally in many branches of mathematics, physics and computer science. In particular, higher-dimensional categories provide a suitable tool for the treatment of an extensive list of issues with recognized mathematical interest in algebraic topology, algebraic geometry, algebraic \(K\)-theory, string field theory, conformal field theory and statistical mechanics, as well as in the study of geometric structures on low-dimensional manifolds. See the recent book Towards Higher Categories [1], which provides a useful background for this subject.
Like small categories [28], small Bénabou’s bicategories and, in particular, Mac Lane’s monoidal categories, are closely related to topological spaces through the classifying space construction. This assigns to each bicategory \(\mathcal {B}\) a CW-complex \(\mathrm {B}\mathcal {B}\) whose cells give a natural geometric meaning to the cells of the bicategory [9]. By this correspondence, for example, bigroupoids correspond to homotopy 2-types (CW-complexes whose \(n\)th homotopy group at any base point vanishes for \(n\ge 3\)), and certain monoidal categories to delooping of the classifying spaces of the underlying categories (up to group completion). The process of taking classifying spaces of bicategories reveals a way to transport categorical coherence to homotopical coherence since the construction \(\mathcal {B}\mapsto \mathrm {B}\mathcal {B}\) preserves products, any lax or oplax functor between bicategories, \(F:\mathcal {A}\rightarrow \mathcal {B}\), induces a continuous map on classifying spaces \(\mathrm {B}F:\mathrm {B}\mathcal {A}\rightarrow \mathrm {B}\mathcal {B}\), any lax or oplax transformation between these, \(\alpha :F\Rightarrow F'\), induces a homotopy between the corresponding induced maps \(\mathrm {B}\alpha :\mathrm {B}F\Rightarrow \mathrm {B}F'\), and any modification between these, \(\varphi :\alpha \Rrightarrow \beta \), a homotopy \(\mathrm {B}\varphi :\mathrm {B}\alpha \Rrightarrow \mathrm {B}\beta \) between them. Thus, if \(\mathcal {A}\) and \(\mathcal {B}\) are biequivalent bicategories or if a homomorphism \(\mathcal {A}\rightarrow \mathcal {B}\) has a biadjoint, then their associated classifying spaces are homotopy equivalent.
In this paper we show the subtlety of this theory by analyzing the homotopy fibers of the map \(\mathrm {B}F:\mathrm {B}\mathcal {A}\rightarrow \mathrm {B}\mathcal {B}\), which is induced by a lax functor between small bicategories \(F:\mathcal {A}\rightarrow \mathcal {B}\), such as Quillen did in [28] where he stated his celebrated Theorems A and B for the classifying spaces of small categories. Every object \(b\in \mathrm {Ob}\mathcal {B}\) has an associated homotopy fiber bicategory \(F\!\!\downarrow {\!_b}\) whose objects are the 1-cells \(f:Fa\rightarrow b\) in \(\mathcal {B}\), with \(a\) an object of \(\mathcal {A}\); the 1-cells consist of all triangles

with \(u:a\rightarrow a'\) a 1-cell in \(\mathcal {A}\) and \(\beta :f\Rightarrow f'\circ Fu\) a 2-cell in \(\mathcal {B}\), and the 2-cells of this bicategory are commutative diagrams of 2-cells in \(\mathcal {B}\) of the form

with \(\alpha :u\Rightarrow u'\) a 2-cell in \(\mathcal {A}\). Compositions, identities, and the structure associativity and unit constraints in \(F\!\!\downarrow {\!_b}\) are canonically provided by those of the involved bicategories and the structure 2-cells of the lax functor (see Sect. 5 for details). For the case \(F=1_\mathcal {B}\), we have the comma bicategory \(\mathcal {B}\!\!\downarrow {\!_b}\). Then, we prove (see Theorem 5.4):
“For every object \(b\) of the bicategory \(\mathcal {B}\), the induced square

is homotopy cartesian if and only if all the maps \(\mathrm {B}p:\mathrm {B}(F\!\!\downarrow {\!_b})\rightarrow \mathrm {B}(F\!\!\downarrow {\!_{b'}})\), induced by the 1-cells \(p:b\rightarrow b'\) of \(\mathcal {B}\), are homotopy equivalences.”
Since the spaces \(\mathrm {B}(\mathcal {B}\!\!\downarrow {\!_b})\) are contractible (Lemma 5.2), the result above tells us that, under the minimum necessary conditions, the classifying space of the homotopy fiber bicategory \(F\!\!\downarrow {\!_b}\) is homotopy equivalent to the homotopy fiber of \(\mathrm {B}F:\mathrm {B}\mathcal {A}\rightarrow \mathrm {B}\mathcal {B}\) at its 0-cell \(\mathrm {B}b\in \mathrm {B}\mathcal {B}\). Thus, the name ‘homotopy fiber bicategory’ is well chosen. Furthermore, as a corollary, we obtain (see Theorem 5.6):
“If all the spaces \(\mathrm {B}(F\!\!\downarrow {\!_b})\) are contractible, then the map \(\mathrm {B}F:\mathrm {B}\mathcal {A}\rightarrow \mathrm {B}\mathcal {B}\) is a homotopy equivalence.”
When the bicategories \(\mathcal {A}\) and \(\mathcal {B}\) involved in the results above are actually categories, then they are reduced to the well-known Theorems A and B by Quillen [28]. Indeed, the methods used in the proof of Theorem 5.4 we give follow similar lines to those used by Quillen in his proof of Theorem B. However, the situation with bicategories is more complicated than with categories. Let us stress the two main differences between both situations: On one hand, every 2-cell \(\sigma :p\Rightarrow q:b\rightarrow b'\) in \(\mathcal {B}\) gives rise to a homotopy
that must be taken into account. On the other hand, for \(p:b\rightarrow b'\) and \(p':b'\rightarrow b^{\prime \prime }\) any two composable 1-cells in \(\mathcal {B}\), we have a homotopy
rather than the identity \(\mathrm {B}p'\circ \mathrm {B}p = \mathrm {B}(p'\circ p)\), as it happens in the category case. This unfortunate behavior is due to the fact that neither is the horizontal composition of 1-cells in the bicategories involved (strictly) associative nor does the lax functor preserve (strictly) that composition. Therefore, in the process of taking homotopy fiber bicategories, \(F\!\!\downarrow \,: b\mapsto F\!\!\downarrow {\!_b}\), we are forced to deal with lax bidiagrams of bicategories
which are a type of lax functors in the sense of Gordon et al. [18] from the bicategory \(\mathcal {B}\) to the tricategory of small bicategories, rather than ordinary diagrams of small categories, that is, functors \(\mathfrak {F}:\mathcal {B}\rightarrow \mathbf{Cat}\), as it happens when both \(\mathcal {A}\) and \(\mathcal {B}\) are categories.
After this introductory Sect. 1, the paper is organized in four sections. Section 2 is an attempt to make the paper as self-contained as possible; hence, at the same time as we set notations and terminology, we define and describe in detail the kind of lax functors \(\mathfrak {F}:\mathcal {B}\rightarrow \mathbf{Bicat}\) we are going to work with. Section 3 is very technical but crucial to our discussions. It is mainly dedicated to describing in detail a bicategorical Grothendieck construction, which assembles any lax bidiagram of bicategories \(\mathfrak {F}:\mathcal {B}\rightarrow \mathbf{Bicat}\) into a bicategory \(\int _\mathcal {B}\mathfrak {F}\). This is similar to what the ordinary construction, due to Grothendieck [20, 21], Giraud [15, 16], and Thomason [32] on lax diagrams of categories with the shape of any given category. By means of this higher Grothendieck construction, in Sect. 4 we establish the third relevant result of the paper, namely (see Theorem 4.3):
“If \(\mathfrak {F}:\mathcal {B}\rightarrow \mathbf{Bicat}\) is a lax bidiagram of bicategories such that each 1-cell \(p:b\rightarrow b'\) in the bicategory \(\mathcal {B}\) induces a homotopy equivalence \(\mathrm {B}\mathfrak {F}_b\simeq \mathrm {B}\mathfrak {F}_{b'}\), then, for every object \(b\in \mathrm {Ob}\mathcal {B}\), there is an induced homotopy cartesian square

That is, the classifying space \(\mathrm {B}\mathfrak {F}_b\) is homotopy equivalent to the homotopy fiber of the map induced on classifying spaces by the projection homomorphism \(\int _\mathcal {B}\mathfrak {F}\rightarrow \mathcal {B}\) at the 0-cell corresponding to the object \(b\).”
Thanks to Thomason’s Homotopy Colimit Theorem [32], when \(\mathcal {B}\) is a small category and \(\mathfrak {F}\) values in \(\mathbf{Cat}\), the result above is equivalent to the relevant lemma used by Quillen in his proof of Theorem B. Similarly here, the proof of the bicategorical Theorem B, given in the last Sect. 5, essentially consists of two steps: First, to apply that key result above to the lax bidiagram of homotopy fiber bicategories, \(F\!\!\downarrow \,:\mathcal {B}\rightarrow \mathbf{Bicat}\), of a lax functor \(F:\mathcal {A}\rightarrow \mathcal {B}\). Second, to prove that there is a homomorphism \(\int _\mathcal {B}F\!\!\downarrow \,\, \rightarrow \mathcal {A}\) inducing a homotopy equivalence \(\mathrm {B}(\int _\mathcal {B}F\!\!\downarrow )\simeq \mathrm {B}\mathcal {A}\), so that the bicategory \(\int _\mathcal {B}F\!\!\downarrow \) may be thought of as the “total bicategory” of the lax functor \(F\). Section 5 also includes some applications to classifying spaces of monoidal categories. For instance, we find a new proof of the well-known result by Mac Lane [26] and Stasheff [29]:
“Let \(({\mathcal M},\otimes )=({\mathcal M},\otimes ,I,\varvec{a},\varvec{l},\varvec{r})\) be a monoidal category. If multiplication for each object \(x\in \mathrm {Ob}{\mathcal M}\), \(y\mapsto y\otimes x\), induces a homotopy autoequivalence on \(\mathrm {B}{\mathcal M}\), then there is a homotopy equivalence
between the classifying space of the underlying category and the loop space of the classifying space of the monoidal category.”
2 Bicategorical preliminaries: Lax bidiagrams of bicategories
In this paper we shall work with small bicategories, and we refer the reader to the papers by Bénabou [4], Street [30], Gordon et al. [18], Gurski [22], and Leinster [25], for the background. The bicategorical conventions and the notations that we use along the paper are the same as in [10, Sect. 2.1] and [9, Sect. 2.4]. Thus, given any bicategory \(\mathcal {B}\), the composition in each hom-category \(\mathcal {B}(a,b)\), that is, the vertical composition of 2-cells, is denoted by \(\beta \cdot \alpha \), while the symbol \(\circ \) is used to denote the horizontal composition functors \(\mathcal {B}(b,c)\times \mathcal {B}(a,b) \overset{\circ }{\rightarrow }\mathcal {B}(a,c)\). Identities are denoted as \(1_f:f\Rightarrow f\), for any 1-cell \(f:a\rightarrow b\), and \(1_a:a\rightarrow a\), for any object \(a\in \mathrm {Ob}\mathcal {B}\). The associativity, right unit, and left unit constraints of the bicategory are respectively denoted by the letters \(\varvec{a}\), \(\varvec{r}\), and \(\varvec{l}\).
We will use that, in any bicategory, the commutativity of the two triangles

and the equality
are consequence of the other axioms (this is not obvious, but a proof can be done paralleling the given, for monoidal categories, by Joyal and Street in [24, Proposition 1.1]).
A lax functor is usually written as a pair \( F=(F,\widehat{F}):\mathcal {A}\rightarrow \mathcal {B}\) since we will generally denote its structure constraints by
The lax functor is termed a pseudo functor or homomorphism whenever all the structure constraints \(\widehat{F}\) are invertible. If the unit constraints \(\widehat{F}_a\) are all identities, then the lax functor is qualified as (strictly) unitary or normal and if, moreover, the constraints \(\widehat{F}_{g,f}\) are also identities, then \(F\) is called a \(2\)-functor.
If \(F,G:\mathcal {A}\rightarrow \mathcal {B}\) are lax functors, then we follow the convention of [18] in what is meant by a lax transformation \({\alpha =(\alpha ,\widehat{\alpha }):F\Rightarrow G}\). Thus, \(\alpha \) consists of morphisms \({\alpha a:Fa\rightarrow Ga}\), \(a\in \mathrm {Ob}\mathcal {A}\), and of 2-cells \(\widehat{\alpha }_f:\alpha b\circ Ff\Rightarrow Gf\circ \alpha a\), subject to the usual axioms. When the 2-cells \(\widehat{\alpha }\) are all invertible, we say that \(\alpha :F\Rightarrow G\) is a pseudo transformation.
In accordance with the orientation of the naturality 2-cells chosen, if \({\alpha ,\beta :F\Rightarrow G}\) are two lax transformations, then a modification \(\sigma :\alpha \Rrightarrow \beta \) will consist of 2-cells \(\sigma a:\alpha a\Rightarrow \beta a\), \(a\in \text{ Ob }\mathcal {A}\), subject to the commutativity condition, for any morphism \(f:a\rightarrow b\) of \(\mathcal {A}\):

\(\mathbf{Bicat}\) denotes the tricategory of bicategories, homomorphisms, pseudo natural transformations, and modifications. In the structure of \(\mathbf{Bicat}\) we use, the composition of pseudo transformations is taken to be

where  , but note the existence of the useful invertible modification
, but note the existence of the useful invertible modification

whose component at an object \(a\) of \(\mathcal {A}\), is \(\widehat{\beta }_{\alpha a}\), the component of \(\beta \) at the morphism \(\alpha a\).
2.1 Lax bidiagrams of bicategories
The next concept of fibered bicategory in bicategories is the basis of most of our subsequent discussions. Let \(\mathcal {B}\) be a bicategory. Regarding \(\mathcal {B}\) as a tricategory in which the \(3\)-cells are all identities, we define a lax bidiagram of bicategories
to be a contravariant lax functor of tricategories from \(\mathcal {B}\) to \(\mathbf{Bicat}\), all of whose coherence modifications are invertible. More explicitly, a lax bidiagram of bicategories \(\mathfrak {F}\) as above consists of the following data:
(D1) for each object \(b\) in \(\mathcal {B}\), a bicategory \(\mathfrak {F}_b\);
(D2) for each 1-cell \(f:a\rightarrow b\) of \(\mathcal {B}\), a homomorphism \(f^*:\mathfrak {F}_b\rightarrow \mathfrak {F}_a\);
(D3) for each 2-cell  of \(\mathcal {B}\), a pseudo transformation \(\alpha ^*:f^*\Rightarrow g^*\);
of \(\mathcal {B}\), a pseudo transformation \(\alpha ^*:f^*\Rightarrow g^*\);

(D4) for each two composable 1-cells  in the bicategory \(\mathcal {B}\), a pseudo transformation \(\chi _{_{g,f}}:f^*g^*\Rightarrow (g\circ f)^*\);
in the bicategory \(\mathcal {B}\), a pseudo transformation \(\chi _{_{g,f}}:f^*g^*\Rightarrow (g\circ f)^*\);

(D5) for each object \(b\) of \(\mathcal {B}\), a pseudo transformation \(\chi _{_b}: 1_{\mathfrak {F}_b}\Rightarrow 1_b^*\);

(D6) for any two vertically composable 2-cells  and
and  in \(\mathcal {B}\), an invertible modification \(\xi _{_{\beta ,\alpha }}\!:\beta ^*\circ \alpha ^* \Rrightarrow (\beta \cdot \alpha )^*\);
in \(\mathcal {B}\), an invertible modification \(\xi _{_{\beta ,\alpha }}\!:\beta ^*\circ \alpha ^* \Rrightarrow (\beta \cdot \alpha )^*\);

(D7) for each 1-cell \(f:a\rightarrow b\) of \(\mathcal {B}\), an invertible modification \(\xi _{_f}:1_{f^*}\Rrightarrow 1_f^*\);

(D8) for every two horizontally composable 2-cells  , an invertible modification \(\chi _{_{\beta ,\alpha }}:(\beta \circ \alpha )^*\!\circ \chi _{_{g,f}}\Rrightarrow \chi _{_{k,h}}\circ (\alpha ^*\beta ^*)\);
, an invertible modification \(\chi _{_{\beta ,\alpha }}:(\beta \circ \alpha )^*\!\circ \chi _{_{g,f}}\Rrightarrow \chi _{_{k,h}}\circ (\alpha ^*\beta ^*)\);

(D9) for every three composable 1-cells  in \(\mathcal {B}\), an invertible modification \(\omega _{_{h,g,f}}:\, \varvec{a}^*\!\circ (\chi _{_{h\circ g,f}}\circ f^*\chi _{_{h,g}} )\Rrightarrow \chi _{_{h,g\circ f}}\circ \chi _{_{g,f}}h^*\);
in \(\mathcal {B}\), an invertible modification \(\omega _{_{h,g,f}}:\, \varvec{a}^*\!\circ (\chi _{_{h\circ g,f}}\circ f^*\chi _{_{h,g}} )\Rrightarrow \chi _{_{h,g\circ f}}\circ \chi _{_{g,f}}h^*\);

(D10) for any 1-cell \(f:a\rightarrow b\) of \(\mathcal {B}\), two invertible modifications

These data must satisfy the following coherence conditions:
(C1) for any three composable \(2\)-cells  in \(\mathcal {B}\), the equation on modifications below holds;
in \(\mathcal {B}\), the equation on modifications below holds;

(C2) for any 2-cell  of \(\mathcal {B}\),
of \(\mathcal {B}\),

Notation 2.1
Thanks to conditions (C1) and (C2), for each objects \(a,b\in \mathrm {Ob}\mathcal {B}\), we have a homomorphism \(\mathcal {B}(a,b)\rightarrow \mathbf{Bicat}(\mathfrak {F}_b,\mathfrak {F}_a)\) such that

and whose structure constraints are the deformations \(\xi \) in \((\mathbf{D6})\) and \((\mathbf{D7})\). Then, whenever it is given a commutative diagram in the category \(\mathcal {B}(a,b)\) of the form

we will denote by

the invertible modification obtained by an (any) appropriate composition of the modifications \(\xi \) and their inverses \(\xi ^{-1}\), once any particular bracketing in the strings \(\alpha _0^*,\ldots ,\alpha _m^*\) and \(\beta _0^*,\ldots ,\beta _n^*\) has been chosen. That diagram (6) is well defined from diagram (5) is a consequence of the coherence theorem for homomorphisms of bicategories [18, Theorem 1.6].
Furthermore, for any diagram  in \(\mathcal {B}\), we shall denote by
in \(\mathcal {B}\), we shall denote by

the modifications obtained, respectively, by pasting the diagrams in \(\mathbf{Bicat}\) below.

(C3) for every diagram of 2-cells  in \(\mathcal {B}\),
in \(\mathcal {B}\),

(C4) for every pair of composable 1-cells  ,
,

(C5) for every \(2\)-cells  , the equation \(A=A'\) holds, where
, the equation \(A=A'\) holds, where

(C6) for every four composable 1-cells  , the equation \(B=B'\) holds, where
, the equation \(B=B'\) holds, where

(C7) for every 2-cell  , the following two equations on modifications hold:
, the following two equations on modifications hold:

(C8) for every pair of composable 1-cells  , the following equation holds:
, the following equation holds:

A lax bidiagram of bicategories \(\mathfrak {F}:\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) is called a pseudo bidiagram of bicategories whenever each of the pseudo transformations \(\chi \), in \((\mathbf{D4})\) and \((\mathbf{D5})\), is a pseudo equivalence; that is, regarding \(\mathcal {B}\) as a tricategory whose 3-cells are all identities, a trihomomorphism \(\mathfrak {F}:\mathcal {B}^{^{\mathrm {op}}}\rightarrow \mathbf{Bicat}\) in the sense of Gordon et al. [18, Definition 3.1].
Example 2.2
If \(\mathcal {C}\) is any small category viewed as a bicategory, then a lax bidiagram of bicategories over \(\mathcal {C}\), as above, in which the deformations \(\xi \) in \((\mathbf{D6})\) and \((\mathbf{D7})\), and \(\chi \) in \((\mathbf{D8})\), are all identities is the same thing as a lax diagram of bicategories \(\mathfrak {F}:\mathcal {C}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) as in [10, Sect. 2.2].
For instance, let \(X\) be any topological space and let \(\mathcal {C}(X)\) denote its poset of open subsets, regarded as a category. Then a fibered bicategory in bigroupoids above X is a lax diagram of bicategories
such that all the bicategories \(\mathfrak {F}_U\) are bigroupoids, that is, bicategories whose 1-cells are invertible up to a 2-cell, and whose 2-cells are strictly invertible. In particular, when all the bigroupoids \(\mathfrak {F}_U\) are strict, that is, 2-categories, and all the homomorphisms \(f^*:\mathfrak {F}_U\rightarrow \mathfrak {F}_V\) associated to the inclusions of open sets \(f:V\hookrightarrow U\) are 2-functors, we have the notion of fibered 2-category in 2-groupoids above the space \(X\). Thus, 2-stacks and 2-gerbes on spaces are relevant examples of lax diagrams of bicategories (see e.g. Breen [5, Definitions 6.1, 6.2, and 6.3]).
For another example, if \(\mathcal {T}\) is any small tricategory, as in [18, Definition 2.2], then its Grothendieck nerve
whose bicategory of \(p\)-simplices is
[12, Theorem 3.3.1] gives a striking example of a pseudo diagram of bicategories.
Example 2.3
For any bicategory \(\mathcal {B}\), a lax bidiagram of categories over \(\mathcal {B}\), that is, a lax bidiagram \(\mathfrak {F}:\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) in which every bicategory \(\mathfrak {F}_a\), \(a\in \mathrm {Ob}\mathcal {B}\), is a category (i.e., a bicategory where all the 2-cells are identities) is the same thing as a contravariant lax functor \(\mathfrak {F}:\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Cat}\) to the 2-category \(\mathbf{Cat}\) of small categories, functors, and natural transformations, since the condition of all \(\mathfrak {F}_a\) being categories forces all the modifications in \((\mathbf{D6})- (\mathbf{D10})\) to be identities.
For example, any object \(b\) of a bicategory \(\mathcal {B}\) defines a pseudo bidiagram of categories [30, Example 10]
which carries an object \(x\in \mathrm {Ob}\mathcal {B}\) to the hom-category \(\mathcal {B}(x,b)\), a 1-cell \(g:x\rightarrow y\) to the functor \(g^*:\mathcal {B}(y,b)\rightarrow \mathcal {B}(x,b)\) defined by

and a 2-cell \(\alpha :g\Rightarrow g'\) is carried to the natural transformation \(\alpha ^*:g^*\Rightarrow g^{\prime *}\) that assigns to each 1-cell \(f:y\rightarrow b\) in \(\mathcal {B}\) the 2-cell \(1_{\!f}\circ \alpha :f\circ g\Rightarrow f\circ g'\). For \(x\overset{g}{\rightarrow }y\overset{h}{\rightarrow }z\) any two composable 1-cells of \(\mathcal {B}\), the structure natural equivalence \(\chi : g^*h^*\cong (h\circ g)^*\), at any \(f:z\rightarrow b\), is provided by the associativity constraint \(\varvec{a}:(f\circ h)\circ g\cong f\circ (h\circ g)\), whereas for any \(x\in \mathrm {Ob}\mathcal {B}\), the structure natural equivalence \(\chi :1_{\mathcal {B}(x,b)}\cong 1_{x}^*\), at any \(f:x\rightarrow b\), is the right unit isomorphism \(\varvec{r}^{-1}:f\cong f\circ 1_{x}\).
3 The Grothendieck construction on lax bidiagrams of bicategories
The well-known ‘Grothendieck construction’, due to Grothendieck [20, 21] and Giraud [15, 16], on pseudo diagrams \((\mathfrak {F},\chi ):\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Cat}\) of small categories with the shape of any given small category, was implicitly used in the proof given by Quillen of his famous Theorems A and B for the classifying spaces of small categories [28]. Subsequently, since Thomason established his celebrated Homotopy Colimit Theorem [32], the Grothendieck construction has become an essential tool in homotopy theory of classifying spaces.
In this section, our work is dedicated to extending the Grothendieck construction to lax bidiagrams of bicategories \(\mathfrak {F}=(\mathfrak {F}, \chi ,\xi ,\omega ,\gamma ,\delta ):\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\), where \(\mathcal {B}\) is any bicategory, since its use is a key for proving our main results in the paper. But we are not claiming here much originality, since extensions of the ubiquitous Grothendieck construction have been developed in many general frameworks. In particular, we should mention here three recent approaches to our construction: In [10], Carrasco, Cegarra, and Garzón study the bicategorical Grothendieck construction on lax diagrams of bicategories, as in Example 2.2. In [2, 3], Baković performs the Grothendieck construction on normal pseudo bidiagrams of bicategories, that is, lax bidiagrams \(\mathfrak {F}\) whose modifications \(\chi _b\) in \((\mathbf{D5})\) and \(\xi _f\) in \((\mathbf{D7})\) are identities, and whose pseudo transformations \(\chi _{g,f}\) in \((\mathbf{D4})\) are pseudo equivalences. Buckley, in [6], presents the more general case of pseudo bidiagrams, that is, when all the pseudo transformations \(\chi _{g,f}\) and \(\chi _b\) in \((\mathbf{D4})\) and \((\mathbf{D5})\) are pseudo equivalences.
The Grothendieck construction on a lax bidiagram of bicategories \(\mathfrak {F}:\mathcal {B}^{\mathrm {op}} \rightarrow \mathbf{Bicat}\), as in (4), assembles it into a bicategory, denoted by

which is defined as follows:
The objects are pairs \((x,a)\), where \(a\in \mathrm {Ob}\mathcal {B}\) and \(x\in \mathrm {Ob}\mathfrak {F}_a\).
The 1-cells are pairs \((u,f):(x,a)\rightarrow (y,b)\), where \(f:a\rightarrow b\) is a 1-cell in \(\mathcal {B}\) and \(u:x\rightarrow f^*y\) is a 1-cell in \(\mathfrak {F}_a\).
The 2-cells are pairs  consisting of a 2-cell
consisting of a 2-cell  of \(\mathcal {B}\) together with a 2-cell \(\phi :\alpha ^*y\circ u\Rightarrow v\) in \(\mathfrak {F}_a\),
of \(\mathcal {B}\) together with a 2-cell \(\phi :\alpha ^*y\circ u\Rightarrow v\) in \(\mathfrak {F}_a\),

The vertical composition of 2-cells in \(\int _\mathcal {B}\mathfrak {F}\),  and
and  , is the 2-cell
, is the 2-cell

where \(\beta \cdot \alpha \) is the vertical composition of \(\beta \) with \(\alpha \) in \(\mathcal {B}\), and \(\psi \odot \phi :(\beta \cdot \alpha )^*\!y\circ u\Rightarrow w\) is the 2-cell of \(\mathfrak {F}_a\) obtained by pasting the diagram below.

The vertical composition of 2-cells so defined is associative and unitary thanks to the coherence conditions \((\mathbf{C1})\) and \((\mathbf{C2})\). The identity 2-cell, for each 1-cell \((u,f):(x,a)\rightarrow (y,b)\), is

Hence, we have defined the hom-category \(\int _\mathcal {B}\mathfrak {F}\big ((x,a),(y,b)\big )\), for any two objects \((x,a)\) and \((y,b)\) of \(\int _\mathcal {B}\mathfrak {F}\). Before continuing the description of this bicategory, we shall do the following useful observation:
Lemma 3.1
A \(2\)-cell \((\phi ,\alpha ):(u,f)\Rightarrow (v,g)\) in \(\int _\mathcal {B}\mathfrak {F}\big ((x,a),(y,b)\big )\) is an isomorphism if and only if both \(\alpha :f\Rightarrow g\), in \(\mathcal {B}(a,b)\), and \(\phi :\alpha ^*y\circ u\Rightarrow v\), in \(\mathfrak {F}_a(x,g^*y)\), are isomorphisms.
Proof
It is quite straightforward, and we leave it to the reader. \(\square \)
We return now to the description of the bicategory \(\int _\mathcal {B}\mathfrak {F}\).
The horizontal composition of two 1-cells  is the 1-cell
is the 1-cell
where \(f'\circ f:a\rightarrow c\) is the composite in \(\mathcal {B}\) of the 1-cells \(f\) and \(f'\), while
is the composite in \(\mathfrak {F}_a\) of  .
.
The horizontal composition of 2-cells is defined by

where \(\alpha '\circ \alpha \) is the horizontal composition in \(\mathcal {B}\) of \(\alpha '\) with \(\alpha \), and \(\phi '\circledcirc \phi \) is the 2-cell in \(\mathfrak {F}_a\) canonically obtained by pasting the diagram below.

Owing to the coherence conditions \((\mathbf{C3})\) and \((\mathbf{C4})\), the horizontal composition so defined truly gives, for any three objects \((x,a),(y,b),(z,c)\) of \(\int _{\mathcal {B}}\!\mathfrak {F}\), a functor

The structure associativity isomorphism, for any three composable morphisms
is provided by the associativity constraint \(\varvec{a}:(h\circ g)\circ f\cong h\circ (g\circ f)\) of the bicategory \(\mathcal {B}\), together with the isomorphism in the bicategory \(\mathfrak {F}_a\)
canonically obtained from the 2-cell pasted of the diagram

By Lemma 3.1, these associativity 2-cells are actually isomorphisms in  . Furthermore, they are natural thanks to the coherence condition \((\mathbf{C5})\), while the pentagon axiom for them holds because of condition \((\mathbf{C6})\).
. Furthermore, they are natural thanks to the coherence condition \((\mathbf{C5})\), while the pentagon axiom for them holds because of condition \((\mathbf{C6})\).
The identity 1-cell for each object \((x,a)\) in  , is provided by the pseudo transformation \(\chi _a:1_{\mathfrak {F}_a}\Rightarrow 1_a^*\), by
, is provided by the pseudo transformation \(\chi _a:1_{\mathfrak {F}_a}\Rightarrow 1_a^*\), by
The left and right unit constraints for each morphism \((u,f):(x,a)\rightarrow (y,b)\) in  ,
,
are respectively given by the 2-cells \(\varvec{l}:1_b\circ f\Rightarrow f\) and \(\varvec{r}:f\circ 1_a\Rightarrow f\) of \(\mathcal {B}\), together with the 2-cells in \(\mathfrak {F}_a\) obtained by pasting the diagrams below.

These unit constraints in  are isomorphisms by Lemma 3.1, natural due to coherence condition \((\mathbf{C7})\), and the coherence triangle for them follows from condition \((\mathbf{C8})\). Hence,
are isomorphisms by Lemma 3.1, natural due to coherence condition \((\mathbf{C7})\), and the coherence triangle for them follows from condition \((\mathbf{C8})\). Hence,  is actually a bicategory.
is actually a bicategory.
As a consequence of the above construction we obtain the following equalities on lax bidiagram of bicategories, which is used many times along the paper for several proofs:
Lemma 3.2
Let \(\mathfrak {F}=(\mathfrak {F}, \chi ,\xi ,\omega ,\gamma ,\delta ):\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) be a lax bidiagram of bicategories. The equations on modifications below hold.
-
(i)
For any object \(a\) of \(\mathcal {B}\),

-
(ii)
for every pair of composable 1-cells
 in \(\mathcal {B}\),
in \(\mathcal {B}\), 
Proof
-
(i)
follows from the equality (2) in the bicategory \(\int _\mathcal {B}\mathfrak {F}\), that is, \(\varvec{r}_{1_{(x,a)}}=\varvec{l}_{1_{(x,a)}}\), for any \(x\in \mathfrak {F}_a\). Similarly, \((ii)\) is consequence of the commutativity of triangles (1) in \(\int _\mathcal {B}\mathfrak {F}\), for any pair of composable 1-cells of the form

for any \(x\in \mathrm {Ob}\mathfrak {F}_c\). \(\square \)
3.1 A cartesian square
Let \(\mathfrak {F}=(\mathfrak {F}, \chi ,\xi ,\omega ,\gamma ,\delta ):\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) be any given lax bidiagram of bicategories. For any bicategory \(\mathcal {A}\) and any lax functor \(F:\mathcal {A}\rightarrow \mathcal {B}\), we shall denote by
the lax bidiagram of bicategories obtained by composing, in the natural sense, \(\mathfrak {F}\) with \(F\); that is, the lax bidiagram consisting of the following data:
(D1) for each object \(a\) in \(\mathcal {A}\), the bicategory \(\mathfrak {F}_{Fa}\);
(D2) for each 1-cell \(f:a\rightarrow b\) of \(\mathcal {A}\), the homomorphism \((Ff)^*:\mathfrak {F}_{Fb}\rightarrow \mathfrak {F}_{Fa}\);
(D3) for each 2-cell  of \(\mathcal {A}\), the pseudo transformation \((F\alpha )^*:(Ff)^*\Rightarrow (Fg)^{*}\);
of \(\mathcal {A}\), the pseudo transformation \((F\alpha )^*:(Ff)^*\Rightarrow (Fg)^{*}\);
(D4) for each two composable 1-cells  in the bicategory \(\mathcal {A}\), the pseudo transformation \({\chi _F} _{_{\!g,f}}:(Ff)^*(Fg)^*\Rightarrow F(g\circ f)^*\) obtained by pasting
in the bicategory \(\mathcal {A}\), the pseudo transformation \({\chi _F} _{_{\!g,f}}:(Ff)^*(Fg)^*\Rightarrow F(g\circ f)^*\) obtained by pasting

(D5) for each object \(a\) of \(\mathcal {A}\), the pseudo transformation 
(D6) for any two vertically composable 2-cells  in \(\mathcal {A}\), the invertible modification \({\xi _F}_{_{\beta ,\alpha }}=\xi _{_{F\beta ,F\alpha }}\!:F(\beta )^*\circ F(\alpha )^* \Rrightarrow F(\beta \cdot \alpha )^*\);
in \(\mathcal {A}\), the invertible modification \({\xi _F}_{_{\beta ,\alpha }}=\xi _{_{F\beta ,F\alpha }}\!:F(\beta )^*\circ F(\alpha )^* \Rrightarrow F(\beta \cdot \alpha )^*\);
(D7) for each 1-cell \(f:a\rightarrow b\) of \(\mathcal {A}\), the invertible modification \({\xi _F}_{_f}=\xi _{_{Ff}}\!:1_{{F(f)}^*}\Rrightarrow 1_{Ff}^*\);
(D8) for every two horizontally composable 2-cells  in \(\mathcal {A}\),
in \(\mathcal {A}\),
is the invertible modification obtained by pasting the diagram below;

(D9) for every three composable 1-cells  in \(\mathcal {A}\), the invertible modification
in \(\mathcal {A}\), the invertible modification
is obtained from the modification pasted of the diagram below;

(D10) for any 1-cell \(f:a\rightarrow b\) of \(\mathcal {A}\), the invertible modifications
are, respectively, canonically obtained from the modification pasted of the diagrams below.

There is an induced lax funtor

given on cells by

and whose structure constraints are canonically given by those of \(F\), namely: For every two composable 1-cells  in \(\int _\mathcal {A}\mathfrak {F}F\), the corresponding structure 2-cell of \(\bar{F}\) for their composition is
in \(\int _\mathcal {A}\mathfrak {F}F\), the corresponding structure 2-cell of \(\bar{F}\) for their composition is
where \(\widehat{F}=\widehat{F}_{g,f}:Fg\circ Ff\Rightarrow F(g\circ f)\) is the structure 2-cell of \(F\), and
is the associativity isomorphism in the bicategory \(\mathfrak {F}_{Fa}\). For \((x,a)\) any object of the bicategory \(\int _\mathcal {A}\mathfrak {F}F\), the corresponding structure 2-cell of \(\bar{F}\) for its identity is
where \(\widehat{F}=\widehat{F}_a:1_{Fa}\Rightarrow F(1_a)\) is the structure 2-cell of \(F\), and \(1\) is the is the identity 2-cell of the 1-cell \(\widehat{F}_a^*x\circ \chi _{Fa}x:x\rightarrow F(1_a)^*x\) in the bicategory \(\mathfrak {F}_{Fa}\).
Then, although the category of bicategories and lax functors has no pullbacks in general, if, for any lax bidiagram of bicategories \(\mathfrak {F}:\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) as above, we denote by

the canonical projection 2-functor, which is defined by

the following fact holds:
Lemma 3.3
Let \(\mathfrak {F}:\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) be a lax bidiagram of bicategories. For any lax functor \(F:\mathcal {A}\rightarrow \mathcal {B}\), the induced square

is cartesian in the category of bicategories and lax functors.
Proof
Any pair of lax functors, say \(L:\mathcal {C}\rightarrow \mathcal {A}\) and \(M:\mathcal {C}\rightarrow \int _\mathcal {B}\mathfrak {F}\), such that \(FL=PM\) determines a unique lax functor \(N:\mathcal {C}\rightarrow \int _\mathcal {A}\mathfrak {F}F\)

such that \(PN=L\) and \(\bar{F}N=M\), which is defined as follows: Observe that the lax functor \(M\) carries any object \(a\in \mathrm {Ob}\mathcal {C}\) to an object of \(\int _\mathcal {B}\mathfrak {F}\) which is necessarily written in the form \(Ma=(Da, FLa)\) for some object \(Da\) of the bicategory \(\mathfrak {F}_{FLa}\). Similarly, for any 1-cell \(f:a\rightarrow b\) in \(\mathcal {C}\), we have \(Mf=(Df,FLf)\), for some 1-cell \(Df:Da\rightarrow FL(f)^*Db\) in \(\mathfrak {F}_{FLa}\), and, for any 2-cell \(\alpha :f\Rightarrow g\in \mathcal {C}(a,b)\), we have \(M\alpha =(D\alpha ,FL\alpha )\), for \(D\alpha :FL(\alpha )^*Db\circ Df\Rightarrow Dg\) a 2-cell in \(\mathfrak {F}_{FLa}\). Also, for any pair of composable 1-cells \(a\overset{f}{\rightarrow }b\overset{g}{\rightarrow }c\) and any object \(a\) in \(\mathcal {C}\), the structure 2-cells of \(M\) can be respectively written in a similar form as
for some 2-cells \(\widehat{D}_{g,f}\) and \(\widehat{D}_{a}\) of the bicategory \(\mathfrak {F}_{FLa}\). Then, the claimed \(N:\mathcal {C}\rightarrow \int _\mathcal {A}\mathfrak {F}F\) is the lax functor which acts on cells by

and whose respective structure 2-cells, for any pair of composable 1-cells \(a\overset{f}{\rightarrow }b\overset{g}{\rightarrow }c\) and any object \(a\) in \(\mathcal {C}\), are
\(\square \)
Remark 3.4
There exist different other ‘dual’ notions of bidiagrams of bicategories, depending on the covariant or contravariant choices for \((\mathbf{D2})\) and \((\mathbf{D3})\), and the direction of the pseudo transformations \(\chi \) in \((\mathbf{D4})\) and \((\mathbf{D5})\), but the results we present about lax bidiagrams are similarly proved for the different cases. For example, in a covariant oplax bidiagram of bicategories \(\mathfrak {F}:\mathcal {B}\rightarrow \mathbf{Bicat}\) the data in \((\mathbf{D2})\) are specified with homomorphisms \(f_*:\mathfrak {F}_a\rightarrow \mathfrak {F}_b\) for the \(1\)-cells \(f:a\rightarrow b\) of \(\mathcal {B}\), while in \((\mathbf{D4})\), the pseudo transformations are of the form \(\chi _{g,f}:(g\circ f)_*\Rightarrow g_*f_*\). The corresponding data in \((\mathbf{D5}), (\mathbf{D8}), (\mathbf{D9})\) and \((\mathbf{D10})\) change in a natural way. The Grothendieck construction on such a bidiagram, has now \(1\)-cells \((u,f):(x,a)\rightarrow (y,b)\) given by \(f:a\rightarrow b\) a \(1\)-cell in \(\mathcal {B}\) and \(u:f_*x\rightarrow y\) a \(1\)-cell in \(\mathfrak {F}_b\). The \(2\)-cells \((\phi ,\alpha ):(u,f)\Rightarrow (v,g)\) are now given by a \(2\)-cell \(\alpha : f\Rightarrow g\) in \(\mathcal {B}\) and a \(2\)-cell \(\phi :u\Rightarrow v\circ \alpha _*x\). The compositions and constraints of this bicategory are defined in the same way as in the contravariant lax case.
4 The homotopy cartesian square induced by a lax bidiagram
For the general background on simplicial sets we mainly refer to the book by Goerss and Jardine [17]. In particular, we will use the following result, which can be easily proved from the discussion made in [17, IV, 5.1] and Quillen’s Lemma [28, Lemma in p. 14] (or [17, IV, Lemma 5.7]):
Lemma 4.1
Let \(p: E\rightarrow B\) be an arbitrary simplicial map. For any \(n\)-simplex \(x\in B_n\), let \(p^{-1}(x)\) be the simplicial set defined by the pullback diagram

where \(\Delta [n]=\Delta (-,[n])\) is the standard simplicial \(n\)-simplex, whose \(m\)-simplices are the maps \([m]\rightarrow [n]\) in the simplicial category \(\Delta \), and \(\Delta x: \Delta [n]\rightarrow B\) denotes the simplicial map such that \(\Delta x(1_{[n]})=x\).
Suppose that, for every \(n\)-simplex \(x\in B_n\), and for any map \(\sigma :[m]\rightarrow [n]\) in the simplicial category, the induced simplicial map \(p^{-1}(\sigma ^*x)\rightarrow p^{-1}(x)\)

gives a homotopy equivalence on geometric realizations \(|p^{-1}(\sigma ^*x)|\simeq |p^{-1}(x)|\). Then, for each vertex \(v\in B_0\), the induced square of spaces

is homotopy cartesian, that is, \(|p^{-1}(v)|\) is homotopy equivalent to the homotopy fiber of the map \(|p|:|E|\rightarrow |B|\) over the 0-cell \(|v|\) of \(|B|\).
Like categories, bicategories are closely related to spaces through the classifying space construction. We shall recall briefly from [9, Theorem 6.1] that the classifying space of a (small) bicategory can be defined by means of several, but always homotopy equivalent, simplicial and pseudo simplicial objects that have been characteristically associated to it. For instance, the classifying space \(\mathrm {B}\mathcal {B}\) of the bicategory \(\mathcal {B}\) may be thought of as
the geometric realization of its (non-unitary) geometric nerve [9, Definition 4.3]; that is, the simplicial set
whose \(n\)-simplices are all lax functors \({\mathbf{z}:[n]\rightarrow \mathcal {B}}\). Here, the ordered sets \({[n]=\{0,1,\dots ,n\}}\) are considered as categories with only one morphism \((i,j):i\rightarrow j\) when \(0\le i\le j\le n\), so that a non-decreasing map \([m]\rightarrow [n]\) is the same as a functor. Hence, a geometric \(n\)-simplex of \(\mathcal {B}\) is a list of cells of the bicategory
which is geometrically represented by a diagram in \(\mathcal {B}\) with the shape of the 2-skeleton of an oriented standard \(n\)-simplex, whose faces are triangles

with objects \(\mathbf{z}_i\) placed on the vertices, 1-cells \(\mathbf{z}_{i,j}:\mathbf{z}_i\rightarrow \mathbf{z}_j\) on the edges, and 2-cells \(\widehat{\mathbf{z}}_{i,j,k}:\mathbf{z}_{j,k}\circ \mathbf{z}_{i,j}\Rightarrow \mathbf{z}_{i,k}\) in the inner, together with 2-cells \(\widehat{\mathbf{z}}_i: 1_{\mathbf{z}_i}\Rightarrow \mathbf{z}_{i,i}\). These data are required to satisfy the condition that, for \(0\le i\le j\le k\le l\le n\), each tetrahedron is commutative in the sense that

and, moreover,

If \(\sigma :[m]\rightarrow [n]\) is any map in \(\Delta \), that is, a functor, the induced \(\sigma ^*:\Delta \mathcal {B}_n\rightarrow \Delta \mathcal {B}_m\) carries any \({\mathbf{z}:[n]\rightarrow \mathcal {B}}\) to \({\sigma ^*\mathbf{z}=\mathbf{z}\sigma :[m]\rightarrow \mathcal {B}}\), the composite lax functor of \(\mathbf{z}\) with \(\sigma \).
On a small category \(\mathcal {C}\), viewed as a bicategory in which all 2-cells are identities, the geometric nerve construction \(\Delta \mathcal {C}\) gives the usual Grothendieck nerve of the category [20], since, for any integer \(n\ge 0\), we have \(LaxFunc([n],\mathcal {C})=\mathrm {Func}([n],\mathcal {C})\). Hence, the space \(\mathrm {B}\mathcal {C}=|\Delta \mathcal {C}|\) of a category \(\mathcal {C}\), is the usual classifying space of the category, as considered by Quillen in [28]. In particular, the geometric nerve of the category \([n]\) is precisely \(\Delta [n]\), the standard simplicial \(n\)-simplex, so the notation is not confusing. Furthermore, for any bicategory \(\mathcal {B}\), the simplicial map \(\Delta \mathbf{z}:\Delta [n]\rightarrow \Delta \mathcal {B}\) defined by a \(n\)-simplex \(\mathbf{z}\in \Delta \mathcal {B}_n\), that is, such that \(\Delta \mathbf{z}(1_{[n]})=\mathbf{z}\), is precisely the simplicial map obtained by taking geometric nerves on the lax functor \(\mathbf{z}:[n]\rightarrow \mathcal {B}\). Thus, if \(\sigma :[m]\rightarrow [n]\) is any map in \(\Delta \), then
The following fact, which is proved in [9, Proposition 7.1], will be used repeatedly in our subsequent discussions:
Lemma 4.2
If \(F,G:\mathcal {A}\rightarrow \mathcal {B}\) are two lax functors between bicategories, then any lax or oplax transformation, \(\varepsilon :F\Rightarrow G\), canonically defines a homotopy \(\mathrm {B}\varepsilon :\mathrm {B}F\simeq \mathrm {B}G\) between the induced maps on classifying spaces \(\mathrm {B}F,\mathrm {B}G:\mathrm {B}\mathcal {A}\rightarrow \mathrm {B}\mathcal {B}\).
Suppose that \(\mathfrak {F}:\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Cat}\) is a functor, where \(\mathcal {B}\) is any small category, such that for every morphism \(f:b\rightarrow c\) of \(\mathcal {B}\) the induced map \(\mathrm {B}f^*:\mathrm {B}\mathfrak {F}_c\rightarrow \mathrm {B}\mathfrak {F}_b\) is a homotopy equivalence. Then, by Quillen’s Lemma [28, Lemma in p. 14], the induced commutative square of spaces

is homotopy cartesian. By Thomason’s Homotopy Colimit Theorem [32], there is a natural homotopy equivalence \(\mathrm {hocolim}_\mathcal {B}\mathrm {B}\mathfrak {F}\simeq \mathrm {B}\int _\mathcal {B}\mathfrak {F}\). Therefore, there is a homotopy cartesian square

We are now ready to state and prove the following important result in this paper, which generalizes the result above, as well as the results in [9, Theorem 7.4] and [11, Theorem 4.3]:
Theorem 4.3
Let \(\mathfrak {F}=(\mathfrak {F}, \chi ,\xi ,\omega ,\gamma ,\delta ):\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) be any given lax bidiagram of bicategories. For any object \(a\in \mathrm {Ob}\mathcal {B}\), there is a commutative square in \(\mathbf{Bicat}\)

where \(P\) is the projection \(2\)-functor (9), \(a\) denotes the normal lax functor carrying \(0\) to \(a\), and \(J\) is the natural embedding homomorphism (12) described below, such that, whenever each 1-cell \(f:b\rightarrow c\) in \(\mathcal {B}\) induces a homotopy equivalence \(\mathrm {B}f^*\!:\mathrm {B}\mathfrak {F}_c\simeq \mathrm {B}\mathfrak {F}_b\), then the square of spaces induced on classifying spaces below is homotopy cartesian.

Proof
This is divided into four parts.
Part 1. Here we exhibit the embedding homomorphism in the square (10)

It is defined on cells of \(\mathfrak {F}_a\) by

where \(\chi y\circ u\) is the 1-cell of \(\mathfrak {F}_a\) composite of  , \(1=1_{1_a}\), the identity 2-cell in \(\mathcal {B}\) of the identity 1-cell of \(a\), and \(\tilde{\phi }\) is the \(2\)-cell given by the pasting in the diagram below.
, \(1=1_{1_a}\), the identity 2-cell in \(\mathcal {B}\) of the identity 1-cell of \(a\), and \(\tilde{\phi }\) is the \(2\)-cell given by the pasting in the diagram below.

For  , two composable 1-cells in \(\mathfrak {F}_a\), the corresponding constraint \(2\)-cell for their composition is \((\widehat{J},\varvec{l}):Jv\circ Ju\cong J(v\circ u)\), where \(\varvec{l}=\varvec{l}_{1_a}:1_a\circ 1_a\cong 1_a\), while \(\widehat{J}=\widehat{J}_{v,u}\) is the \(2\)-cell of \(\mathfrak {F}_a\) given by pasting the diagram
, two composable 1-cells in \(\mathfrak {F}_a\), the corresponding constraint \(2\)-cell for their composition is \((\widehat{J},\varvec{l}):Jv\circ Ju\cong J(v\circ u)\), where \(\varvec{l}=\varvec{l}_{1_a}:1_a\circ 1_a\cong 1_a\), while \(\widehat{J}=\widehat{J}_{v,u}\) is the \(2\)-cell of \(\mathfrak {F}_a\) given by pasting the diagram

and, for any object \(x\) of \(\mathfrak {F}_a\), the structure isomorphism for its identity is \((\widehat{J},1):1_{Jx}\cong J(1_x)\), where \(1=1_{1_a}\), and \(\widehat{J}=\widehat{J}_{x}\) is provided by pasting the diagram in \(\mathfrak {F}_a\) below.

So defined, it is straightforward to verify that \(J\) is functorial on vertical composition of 2-cells in \(\mathfrak {F}_a\). The naturality of the structure 2-cells \(Jv\circ Ju\cong J(v\circ u)\) follows from the coherence conditions in (C1) and (C2), whereas the hexagon coherence condition for them is verified thanks to conditions (C1), (C2), and (C7), and the result in Lemma 3.2\((ii)\) relating \(\gamma \) with \(\omega \). As for the other two coherence conditions, one amounts to the equality in Lemma 3.2\((i)\), and the other is easily checked.
Part 2. Let \(\mathbf{z}:[n]\rightarrow \mathcal {B}\) be any given geometric \(n\)-simplex of the bicategory, \(n\ge 0\). Then, as in (7), we have a composite lax bidiagram of bicategories \(\mathfrak {F}\mathbf{z}:[n]\rightarrow \mathbf{Bicat}\). In this part of the proof, we prove that the homomorphism

induces a homotopy equivalence on classifying spaces:

\(\square \)
This is a direct consequence of the following general observation:
Lemma 4.4
Suppose \(\mathcal {C}\) is a small category with an initial object \(0\), and let us regard \(\mathcal {C}\) as a bicategory whose \(2\)-cells are all identities. Then, for any lax bidiagram of bicategories \(\mathfrak {L}:\mathcal {C}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\), the homomorphism \(J\!=\!J(\mathfrak {L},0):\mathfrak {L}_0\rightarrow \int _{\mathcal {C}}\!\mathfrak {L}\) induces a homotopy equivalence on classifying spaces, \(\mathrm {B}J\!:\mathrm {B}\mathfrak {L}_0\simeq \mathrm {B}\!\int _{\mathcal {C}}\mathfrak {L}\).
Proof
For any object \(a\in \mathrm {Ob}\mathcal {C}\), let \(0_a:0\rightarrow a\) denote the unique morphism in \(\mathcal {C}\) from the initial object to \(a\). There is a homomorphism

which carries any object \((x,a)\) to \(K(x,a)=0_a^*x\), the image of \(x\) by the homomorphism \(0_a^*:\mathfrak {L}_a\rightarrow \mathfrak {L}_0\), a 1-cell \((u,f):(x,a)\rightarrow (y,b)\) to

and a 2-cell  to the 2-cell \(K(\phi ,1)\!:\!K(u,f)\!\Rightarrow \! K(v,f)\) obtained by pasting the diagram below, where
to the 2-cell \(K(\phi ,1)\!:\!K(u,f)\!\Rightarrow \! K(v,f)\) obtained by pasting the diagram below, where  .
.

For each object \((x,a)\) of \(\int _{\mathcal {C}}\mathfrak {L}\), the structure isomorphism \(\widehat{K}:1_{K(x,a)}\cong K1_{(x,a)}\) is

while the constraint \(\widehat{K}:K(v,g)\circ K(u,f)\cong K((v,g)\circ (u,f))\), for each pair of composable 1-cells  of \(\int _{\mathcal {C}}\mathfrak {L}\), is given by pasting in \(\mathfrak {L}_0\) the diagram below.
of \(\int _{\mathcal {C}}\mathfrak {L}\), is given by pasting in \(\mathfrak {L}_0\) the diagram below.

There are also two pseudo transformations
which are defined as follows: The component of \(\varepsilon \) at an object \((x,a)\) of \(\int _\mathcal {C}\mathfrak {L}\) is
and its naturality component at a morphism \((u,f):(x,a)\rightarrow (y,b)\) is
where \(\widehat{\varepsilon }\) is the 2-cell of \(\mathfrak {L}_0\) pasted of the diagram below.

The pseudo transformation \(\eta : 1 \Rightarrow KJ\) assigns to each object \(x\) of the bicategory \(\mathfrak {L}_0\) the 1-cell \( \eta x=\chi x: x\rightarrow 1_0^*x\), while its naturality isomorphism at any 1-cell \(u:x\rightarrow y\),
is obtained by pasting the diagram below.

Hence, by Lemma 4.2, there are induced homotopies \(\mathrm {B}\varepsilon :\mathrm {B}J\,\mathrm {B}K =\mathrm {B}(JK)\simeq \mathrm {B}1_{\int _{\mathcal {C}}\!\mathfrak {L}}=1_{\mathrm {B}\!\int _{\mathcal {C}}\mathfrak {L}}\) and \(\mathrm {B}\eta : 1_{\mathrm {B}\mathfrak {L}_0}= \mathrm {B}1_{\mathfrak {L}_0}\simeq \mathrm {B}(KJ)=\mathrm {B}K\,\mathrm {B}J \), and it follows that both maps \(\mathrm {B}J\) and \(\mathrm {B}K\) are actually homotopy equivalences. \(\square \)
Part 3. Let \(\sigma :[m]\rightarrow [n]\) be a map in the simplicial category. By Lemma 3.3, for any geometric \(n\)-simplex \(\mathbf{z}:[n]\rightarrow \mathcal {B}\) of the bicategory \(\mathcal {B}\), we have the square

which is cartesian in the category of bicategories and lax functors. This part has the goal of proving that the lax functor \(\bar{\sigma }\) induces a homotopy equivalence on classifying spaces:

To do that, let us consider the square of lax functors

where \(\mathbf{z}_{0,\sigma 0}^*\) is the homomorphism attached by the lax diagram \(\mathfrak {F}:\mathcal {B}^{\mathrm {op}}\rightarrow \mathbf{Bicat}\) to the 1-cell \(\mathbf{z}_{0,\sigma 0}:\mathbf{z}_0\rightarrow \mathbf{z}_{\sigma 0}\) of \(\mathcal {B}\), and the homomorphisms \(J\) are defined as in (12). This square is not commutative, but there is a pseudo transformation \(\theta : J\mathbf{z}_{0,\sigma 0}^*\Rightarrow \bar{\sigma }J\), whose component at any object \(x\) of \(\mathfrak {F}_{\mathbf{z}\sigma 0}\) is the 1-cell of \(\int _{[n]}\mathfrak {F}\mathbf{z}\)
and whose naturality isomorphism, at any 1-cell \(u:x\rightarrow y\) in \(\mathfrak {F}_{\mathbf{z}\sigma 0}\), is
where \(\tilde{\theta }\) is given by pasting in \(\mathfrak {F}_{\mathbf{z}_0}\) the diagram below.

Hence, by Lemma 4.2, the induced square on classifying spaces

is homotopy commutative. Moreover, both maps \(\mathrm {B}J\) in the square are homotopy equivalences, as we showed in the proof of Lemma 4.4 above. Since, by hypothesis, the map \(\mathrm {B}\mathbf{z}_{0,\sigma 0}^*:\mathrm {B}\mathfrak {F}_{\mathbf{z}_{\sigma 0}}\rightarrow \mathrm {B}\mathfrak {F}_{\mathbf{z}_{0}}\) is also a homotopy equivalence, it follows that the remaining map in the square have the same property, that is, the map \(\mathrm {B}\bar{\sigma }: \) is a homotopy equivalence.
Part 4. Finally, we are ready to complete here the proof of the theorem as follows: Let us consider the induced simplicial map on geometric nerves \(\Delta P:\Delta \int _\mathcal {B}\mathfrak {F}\rightarrow \Delta \mathcal {B}\). This verifies the hypothesis in Lemma 4.1. In effect, thanks to Lemma 3.3, for any geometric \(n\)-simplex of \(\mathcal {B}\), \(\mathbf{z}:[n]\rightarrow \mathcal {B}\), the square

is a pullback in the category of bicategories and lax functors, whence the square induced by taking geometric nerves

is a pullback in the category of simplicial sets. Thus,  .
.
Furthermore, for any map \(\sigma :[m]\rightarrow [n]\) in the simplicial category, since the diagram of lax functors

is commutative, the induced diagram of simplicial maps

is also commutative. Then, as \(\sigma ^*\mathbf{z}=\mathbf{z}\sigma \), the induced simplicial map \(\Delta P^{-1}(\sigma ^*\mathbf{z})\rightarrow \Delta P^{-1}(\mathbf{z})\) is precisely the map \(\Delta \bar{\sigma }:\Delta \int _{[m]}\mathfrak {F}\mathbf{z}\sigma \rightarrow \Delta \int _{[n]}\mathfrak {F}\mathbf{z}\), whose induced map on geometric realizations is the homotopy equivalence (14),  .
.
Hence, by Lemma 4.1, for each object \(a\in \mathrm {Ob}\mathcal {B}\), the square

is homotopy cartesian. Furthermore, since the diagram of lax functors

commutes, it follows that the square (11) is homotopy cartesian as it is the composite of the squares

where the map \(\mathrm {B}J(\mathfrak {F}a,0)\!:\mathrm {B}\mathfrak {F}_a \simeq \mathrm {B}\!\int _{[0]}\mathfrak {F}a\) in the left square is one of the homotopy equivalences (13), while the square on the right is homotopy cartesian.
5 The homotopy cartesian square induced by a lax functor
In this section we prove the main theorem of this paper, that is, a generalization to lax functors (monoidal functors, for instance) of the well-known Quillen’s Theorem B [28]. We shall first extend Gray’s construction [19, Section 3.1] of homotopy fiber 2-categories to homotopy fiber bicategories of an arbitrary lax functor between bicategories, so we can state the corresponding ‘Theorem B’ in terms of them.
Let \(F:\mathcal {A}\rightarrow \mathcal {B}\) be any given lax functor between bicategories. As in Example 2.3, each object \(b\) of \(\mathcal {B}\) gives rise to a pseudo bidiagram of categories
which carries an object \(x\in \mathrm {Ob}\mathcal {B}\) to the hom-category \(\mathcal {B}(x,b)\), and then also to the lax bidiagram of categories
obtained, as in (7), by composing \(\mathcal {B}(-,b)\) with \(F\). The Grothendieck construction on these lax bidiagrams leads to the notions of homotopy fiber and comma bicategories:
Definition 5.1
The homotopy fiber, \(F\!\!\downarrow {\!_b}\), of a lax functor between bicategories \(F:\mathcal {A}\rightarrow \mathcal {B}\) over an object \(b\in \mathrm {Ob}\mathcal {B}\), is the bicategory obtained as the Grothendieck construction on the lax bidiagram (15), that is,

In particular, when \(F=1_\mathcal {B}\) is the identity functor on \(\mathcal {B}\),

is the comma bicategory of objects over \(b\) of the bicategory \(\mathcal {B}\).
It will be useful to develop here the Grothendieck construction, exposed in Sect. 3, in this particular case. Its objects are pairs
with \(a\) a 0-cell of \(\mathcal {A}\) and \(f\) a 1-cell of \(\mathcal {B}\) whose source is \(Fa\) and target the fixed object \(b\). The 1-cells
consist of a \(1\)-cell \(u:a\rightarrow a'\) in \(\mathcal {A}\), together with a \(2\)-cell \(\beta \!:f\Rightarrow f'\circ Fu\) in the bicategory \(\mathcal {B}\),

A 2-cell in \(F\!\!\downarrow {\!_b}\),

is a 2-cell \(\alpha :u\Rightarrow u'\) in \(\mathcal {A}\), such that the equation below holds in the category \(\mathcal {B}(Fa,b)\).

Compositions, identities, and the structure associativity and unit constraints in \(F\!\!\downarrow {\!_b}\) are as follows: For any given objects \((f,a)\) and \((f',a')\) as in (16), the vertical composition of 2-cells

is given by the vertical composition \(\alpha '\cdot \alpha \) of 2-cells in \(\mathcal {A}\). The horizontal composition of two 1-cells in \(F\!\!\downarrow {\!_b}\),

is the 1-cell
where the second component is the horizontal composition \(v \circ u\) in \(\mathcal {A}\), while the first one is the 2-cell in \(\mathcal {B}\) obtained by pasting the diagram below.

The horizontal composition of 2-cells is simply given by the horizontal composition of 2-cells in \(\mathcal {B}\),

and the identity 1-cell of each 0-cell \((f:Fa\rightarrow b, a)\) is

Finally, the associativity, left and right unit constraints are obtained from those of \(\mathcal {A}\) by the formulas
We shall prove below that, under reasonable necessary conditions, the classifying spaces of the homotopy fiber bicategories \(\mathrm {B}(F\!\!\downarrow {\!_b})\), of a lax functor \(F:\mathcal {A}\rightarrow \mathcal {B}\), realize the homotopy fibers of the induced map on classifying spaces, \(\mathrm {B}F:\mathrm {B}\mathcal {A}\rightarrow \mathrm {B}\mathcal {B}\). This fact will justify the name of ‘homotopy fiber bicategories’ for them. As a first step to do it, we state the following particular case, when \(F=1_\mathcal {B}\) is the identity homomorphism:
Lemma 5.2
For any object \(b\) of a bicategory \(\mathcal {B}\), the classifying space of the comma bicategory \(\mathcal {B}\!\!\downarrow {\!_b}\) is contractible, that is, \(\mathrm {B}(\mathcal {B}\!\!\downarrow {\!_b})\simeq pt\).
Proof
Let \([0]\rightarrow \mathcal {B}\!\!\downarrow {\!_b}\) denote the normal lax functor that carries \(0\) to the object \((1_b,b)\), and let \(\mathrm {Ct}:\mathcal {B}\!\!\downarrow {\!_b}\rightarrow \mathcal {B}\!\!\downarrow {\!_b}\) be the composite of \(\mathcal {B}\!\!\downarrow {\!_b}\rightarrow [0] \rightarrow \mathcal {B}\!\!\downarrow {\!_b}\). Then, the induced map on classifying spaces

is a constant map. Now, let us observe that there is a canonical oplax transformation \(1_{\mathcal {B}\downarrow {_b}}\Rightarrow \mathrm {Ct}\), whose component at any object \((f:a\rightarrow b,a)\) is the 1-cell \((\varvec{l}^{-1}_f,f):(f,a)\rightarrow (1_b,b)\), and whose naturality component at a 1-cell \((\beta ,u):(f,a)\rightarrow (f',a')\) is

This oplax transformation gives, thanks to Lemma 4.2, a homotopy between \(\mathrm {B}(1_{\mathcal {B}\downarrow {_b}})=1_{\mathrm {B}(\mathcal {B}\downarrow {_b})}\) and the constant map \(\mathrm {B}\mathrm {Ct}\), and so we obtain the result. \(\square \)
Example 5.3
Let \(\mathcal {B}\) be a bicategory, and suppose \(b\in \mathrm {Ob}\mathcal {B}\) is an object such that the induced maps \(\mathrm {B}p^*:\mathrm {B}\mathcal {B}(y,b)\rightarrow \mathrm {B}\mathcal {B}(x,b)\) are homotopy equivalences for the different morphisms \(p:x\rightarrow y\) in \(\mathcal {B}\) (for instance, any object of a bigroupoid). By Theorem 4.3, we have the homotopy fiber sequence
in which the space \(\mathrm {B}\mathcal {B}\!\!\downarrow {\!_{b}}\) is contractible by Lemma 5.2. Hence, we conclude the existence of a homotopy equivalence
between the loop space of the classifying space of the bicategory with base point \(\mathrm {B}b\) and the classifying space of the category of endomorphisms of \(b\) in \(\mathcal {B}\).
The homotopy equivalence above is already known when the bicategory is strict, that is, when \(\mathcal {B}\) is a 2-category. It appears as a main result in the paper by Del Hoyo [14, Theorem 8.5], and it was also stated at the same time by Cegarra in [11, Example 4.4]. Indeed, that homotopy equivalence (21), for the case when \(\mathcal {B}\) is a 2-category, can be deduced from a result by Tillman about simplicial categories in [31, Lemma 3.3].
Returning to an arbitrary lax functor \(F:\mathcal {A}\rightarrow \mathcal {B}\), we shall now pay attention to two constructions with fiber homotopy bicategories. First, we have that any 1-cell \(p:b\rightarrow b'\) in \(\mathcal {B}\) determines a 2-functor
whose function on objects is defined by
A 1-cell \((\beta ,u):(f,a)\rightarrow (f',a')\) of \(F\!\!\downarrow {\!_b}\), as in (17), is carried to the 1-cell of \(F\!\!\downarrow {\!_{b'}}\)

while, for \(\alpha :(\beta ,u)\Rightarrow (\beta ',u')\) any 2-cell in \(F\!\!\downarrow {\!_b}\) as in (18),
Secondly, by Lemma 3.3, we have a pullback square in the category of bicategories and lax functors for any \(b\in \mathrm {Ob}\mathcal {B}\)

where, recall, the 2-functors \(P\) are the canonical projections (9), and \(\bar{F}\) is the induced lax functor (8), which acts on cells by

and whose structure constraints are canonically given by those of \(F\).
We are now ready to state and prove the following theorem, which is just the well-known Quillen’s Theorem B [28] when the lax functor \(F\) in the hypothesis is an ordinary functor between categories. The result therein also generalizes a similar result by Cegarra [11, Theorem 3.2], which was stated for the case when \(F\) is a 2-functor between 2-categories, but the extension to arbitrary lax functors between bicategories is highly nontrivial and the proof we give here uses different tools.
Theorem 5.4
Let \(F:\mathcal {A}\rightarrow \mathcal {B}\) be a lax functor between bicategories. The following statements are equivalent:
-
(i)
For every 1-cell \(p:b\rightarrow b'\) in \(\mathcal {B}\), the induced map \(\mathrm {B}p_*:\mathrm {B}(F\!\!\downarrow {\!_b})\rightarrow \mathrm {B}(F\!\!\downarrow {\!_{b'}})\) is a homotopy equivalence.
-
(ii)
For every object \(b\) of \(\mathcal {B}\), the induced square by (23) on classifying spaces
 (24)
(24)is homotopy cartesian. Therefore, in such a case, for each object \(a\in \mathrm {Ob}\mathcal {A}\) such that \(Fa=b\), there is a homotopy fibre sequence
$$\begin{aligned} \mathrm {B}(F\!\!\downarrow {\!_b})\rightarrow \mathrm {B}\mathcal {A}\rightarrow \mathrm {B}\mathcal {B}, \end{aligned}$$relative to the base 0-cells \(\mathrm {B}a\) of \(\mathrm {B}\mathcal {A}\), \(\mathrm {B}b\) of \(\mathrm {B}\mathcal {B}\) and \(\mathrm {B}(1_b,a)\) of \(\mathrm {B}(F\!\!\downarrow {\!_b})\), that induces a long exact sequence on homotopy groups
$$\begin{aligned} \cdots \rightarrow \pi _{n+1}\mathrm {B}\mathcal {B}\rightarrow \pi _n\mathrm {B}(F\!\!\downarrow {\!_b})\rightarrow \pi _n\mathrm {B}\mathcal {A}\rightarrow \pi _n\mathrm {B}\mathcal {B}\rightarrow \cdots . \end{aligned}$$
Proof \((ii)\Rightarrow (i)\) Suppose that \(p:b\rightarrow b'\) is any 1-cell of \(\mathcal {B}\). Then, taking \(\mathbf{z}:[1]\rightarrow \mathcal {B}\) the normal lax functor such that \(\mathbf{z}_{0,1}=p\), we have the path \(\mathrm {B}\mathbf{z}:\mathrm {B}[1]\!=\!I\rightarrow \mathrm {B}\mathcal {B}\), whose origen is the point \(\mathrm {B}a\) and whose end is \(\mathrm {B}b\) (actually, \(\mathrm {B}b^{\prime }\) is a CW-complex and \(\mathrm {B}\mathbf{z}\) is one of its 1-cells). Since the homotopy fibers of a continuous map whose over points are connected by a path are homotopy equivalent, the result follows.
\((i)\Rightarrow (ii)\) This is divided into three parts.
Part 1. We begin here by noting that the bicategorical homotopy fiber construction is actually the function on objects of a covariant oplax bidiagram of bicategories
consisting of the following data:
(D1) for each object \(b\) in \(\mathcal {B}\), the homotopy fiber bicategory \(F\!\!\downarrow {\!_b}\);
(D2) for each 1-cell \(p:b\rightarrow b'\) of \(\mathcal {B}\), the 2-functor \(p_*\!:\, F\!\!\downarrow {\!_b}\rightarrow F\!\!\downarrow {\!_{b'}}\) in (22);
(D3) for each 2-cell  of \(\mathcal {B}\), the pseudo transformation \(\sigma _*:p_*\Rightarrow p'_*\), whose component at an object \((f,a)\) of \(F\!\!\downarrow {\!_{b}}\), is the 1-cell
of \(\mathcal {B}\), the pseudo transformation \(\sigma _*:p_*\Rightarrow p'_*\), whose component at an object \((f,a)\) of \(F\!\!\downarrow {\!_{b}}\), is the 1-cell

and whose naturality component at any 1-cell \((\beta ,u):(f,a)\rightarrow (f',a')\), as in (17), is the canonical isomorphism \(\varvec{r}^{-1}\cdot \varvec{l}:1_{a'}\circ u\cong u\circ 1_a\);

(D4) for each two composable 1-cells  in the bicategory \(\mathcal {B}\), the pseudo transformation \({\chi } _{_{\!p',p}}:(p'\circ p)_*\Rightarrow p'_*p_*\) has component, at an object \((f,a)\) of \(F\!\!\downarrow {\!_{b}}\), the 1-cell
in the bicategory \(\mathcal {B}\), the pseudo transformation \({\chi } _{_{\!p',p}}:(p'\circ p)_*\Rightarrow p'_*p_*\) has component, at an object \((f,a)\) of \(F\!\!\downarrow {\!_{b}}\), the 1-cell

and whose naturality component at a 1-cell \((\beta ,u):(f,a)\rightarrow (f',a')\), is

(D5) for each object \(b\) of \(\mathcal {B}\), \(\chi _{_b}:{1_{b}}_*\Rightarrow 1_{F\downarrow {_{b}}}\) is the pseudo transformation whose component at any object \((f,a)\) is the 1-cell

and whose naturality component, at a 1-cell \((\beta ,u):(f,a)\rightarrow (f',a')\), is

(D6) for any two vertically composable 2-cells  in \(\mathcal {B}\), the invertible modification \({\xi }_{\tau ,\sigma }:\tau _*\circ \sigma _* \Rrightarrow (\tau \cdot \sigma )_*\) has component, at any object \((f,a)\), the canonical isomorphism \(\varvec{l}:1_a\circ 1_a\cong 1_a\)
in \(\mathcal {B}\), the invertible modification \({\xi }_{\tau ,\sigma }:\tau _*\circ \sigma _* \Rrightarrow (\tau \cdot \sigma )_*\) has component, at any object \((f,a)\), the canonical isomorphism \(\varvec{l}:1_a\circ 1_a\cong 1_a\)

(D7) for each 1-cell \(p:b\rightarrow b'\) of \(\mathcal {B}\), \({(1_p)}_*=1_{p_*}\), and \({\xi }_{_p}\) is the identity modification;
(D8) for every two horizontally composable 2-cells  in \(\mathcal {B}\), the equality \( (\tau _*\sigma _*)\!\circ {\chi }{_{p',p}}={\chi }{_{q',q}}\circ (\tau \circ \sigma )_* \) holds and the modification \({\chi }_{_{\tau ,\sigma }}\) is the identity;
in \(\mathcal {B}\), the equality \( (\tau _*\sigma _*)\!\circ {\chi }{_{p',p}}={\chi }{_{q',q}}\circ (\tau \circ \sigma )_* \) holds and the modification \({\chi }_{_{\tau ,\sigma }}\) is the identity;
(D9) for every three composable 1-cells  in \(\mathcal {B}\), the invertible modification \({\omega }_{_{p^{\prime \prime },p',p}}\), at any object \((f,a)\), is the canonical isomorphism \(\varvec{r}:(1_a\circ 1_a)\circ 1_a\cong 1_a\circ 1_a\),
in \(\mathcal {B}\), the invertible modification \({\omega }_{_{p^{\prime \prime },p',p}}\), at any object \((f,a)\), is the canonical isomorphism \(\varvec{r}:(1_a\circ 1_a)\circ 1_a\cong 1_a\circ 1_a\),

(D10) for any \(1\)-cell \(p:b\rightarrow b'\) of \(\mathcal {B}\), the invertible modifications \(\gamma _p\) and \(\delta _p\), at any object \((f,a)\) are given by the canonical isomorphism \(1_a\circ (1_a\circ 1_a)\cong 1_a\),

Observe that all the 2-cells given above are well defined since all the data is obtained from the constraints of the bicategories involved and the lax functor \(F\). Then the coherence conditions of these give us the equality (19) in each case. For the same reason the axioms (C1)–(C8) hold.
Part 2. In this part, we consider the Grothendieck construction on the oplax bidiagram of homotopy fibers \(F\!\!\downarrow \,:\mathcal {B}\rightarrow \mathbf{Bicat}\), and we shall prove the following:
Lemma 5.5
There is a homomorphism

inducing a homotopy equivalence on classifying spaces, \(\mathrm {B}Q:\mathrm {B}\!\int _{\mathcal {B}}\!F\!\!\downarrow \ \simeq \mathrm {B}\mathcal {A}\).
Before starting the proof of the lemma, we shall briefly describe the bicategory \(\int _{\mathcal {B}}\!F\!\!\downarrow \). It has objects the triplets \((f,a,b)\), with \(a\in \mathrm {Ob}\mathcal {A}\), \(b\in \mathrm {Ob}\mathcal {B}\), and \(f:Fa\rightarrow b\) a 1-cell of \(\mathcal {B}\). Its 1-cells
consist of a \(1\)-cell \(p:b\rightarrow b'\) in \(\mathcal {B}\), together with a \(1\)-cell \((\beta ,u):p_*(f,a)=(p\circ f,a)\rightarrow (f',a')\) in \(F\!\!\downarrow \!_{b'}\), that is, a 1-cell \(u:a\rightarrow a'\) in \(\mathcal {A}\) and a 2-cell \(\beta : p\circ f\Rightarrow f'\circ Fu\) in \(\mathcal {B}\)

A 2-cell in \(\int _{\mathcal {B}}\!F\!\!\downarrow \),

consists of a 2-cell \(\sigma :p\Rightarrow p'\) in \(\mathcal {B}\), together with a 2-cell \(\alpha :(\beta ,u)\Rightarrow (\beta ',u')\circ \sigma _*(f,a)\) in \(F\!\!\downarrow \!_{b'}\), that is, (after some work using coherence equations) a 2-cell \(\alpha : u\Rightarrow u'\circ 1_a\) in \(\mathcal {A}\), such that the equation below holds.

We shall look carefully at the vertical composition of \(2\)-cells and the horizontal composition of \(1\)-cells in \(\int _\mathcal {B}F\!\!\downarrow \) since we will use them later: Given two vertically composable \(2\)-cells, say \((\alpha ,\sigma )\) as above and \((\alpha ',\sigma '):(\beta ',u',p')\Rightarrow (\beta ^{\prime \prime },u^{\prime \prime },p^{\prime \prime })\), their vertical composition is given by the formula
Given two composable \(1\)-cells, say \((\beta ,u,p)\) as above and \((\beta ',u',p'):(f',a',b')\rightarrow (f^{\prime \prime },a^{\prime \prime },b^{\prime \prime })\), their horizontal composition is
where \(\beta '\circledcirc (1_{p'}\circ \beta )\) is as in (20), thus

The identity \(1\)-cell at an object \((f,a,b)\) is

Proof of Lemma 5.5
The homomorphism \(Q\) in (25) is defined on cells by

This homomorphism \(Q\) is strictly unitary, and its structure isomorphism at any two composable 1-cells, say \((\beta ,u,p)\) as above and \((\beta ',u',p'): (f',a',b')\rightarrow (f^{\prime \prime },a^{\prime \prime },b^{\prime \prime })\), is
To prove that this homomorphism \(Q\) induces a homotopy equivalence on classifying spaces, let us observe that there is also a lax functor \(L:\mathcal {A}\rightarrow \int _{\mathcal {B}}\!F\!\!\downarrow \), such that \(Q\,L=1_{\mathcal {A}}\). This is defined on cells of \(\mathcal {A}\) by

where the first component of \((\varvec{l}^{-1}\cdot \varvec{r},u,Fu)\) is the canonical isomorphism \(Fu\circ 1_{Fa}\cong 1_{Fa'}\circ Fu\). Its structure 2-cells, at any pair of composable 1-cells \(a\overset{u}{\rightarrow }a'\overset{u'}{\rightarrow }a^{\prime \prime }\) and at any object \(a\) of \(\mathcal {A}\), are respectively defined by
The equality \(QL=1_{\mathcal {A}}\) is easily checked. Furthermore, there is an oplax transformation \(\iota :LQ\Rightarrow 1_{\int _{\mathcal {B}}\!F\downarrow }\) assigning to each object \((f,a,b)\) of the bicategory \(\int _{\mathcal {B}}\!F\!\!\downarrow \) the 1-cell
and whose naturality component at any 1-cell \((\beta ,u,p):(f,a,b)\rightarrow (f',a',b')\) is the 2-cell

Therefore, by taking classifying spaces, we have \(\mathrm {B}Q\,\mathrm {B}L{=}1_{\mathrm {B}\mathcal {A}}\) and, by Lemma 4.2, \(\mathrm {B}L\,\mathrm {B}Q\simeq 1_{\mathrm {B}\int _{\mathcal {B}}\!F\downarrow }\), whence \(\mathrm {B}Q\) is actually a homotopy equivalence.
Part 3. We complete here the proof of the theorem as follows: There is a canonical homomorphism

making commutative, for any object \(b\in \mathrm {Ob}\mathcal {B}\), the diagrams

in which \(Q:\int _\mathcal {B}F\!\!\downarrow \rightarrow \mathcal {A}\) is the homomorphism in (25) and \(Q:\int _\mathcal {B}\mathcal {B}\!\!\downarrow \rightarrow \mathcal {B}\) is the corresponding one for \(F=1_{\mathcal {B}}\), all the 2-functors \(P\) are the canonical projections (9), and the embedding homomorphisms \(J\) are the corresponding ones defined as in (12). This homomorphism (26) is defined on cells by

Its composition constraint at a pair of composable \(1\)-cells, say \((\beta ,u,p)\) as above and \((\beta ',u',p'):(f',a',b')\rightarrow (f^{\prime \prime },a^{\prime \prime },b^{\prime \prime })\), is the 2-cell

while its unit constraint at an object \((f,a,b)\) is

Let us now observe that (the covariant and oplax version of) Theorem 4.3 applies both to the bidiagram of homotopy fibres \(F\!\!\downarrow \), by hypothesis, and to the bidiagram of comma bicategories \(\mathcal {B}\!\!\downarrow \), since the spaces \(\mathrm {B}\mathcal {B}\!\!\downarrow {\!_{b}}\) are contractible by Lemma 5.2 and therefore any 1-cell \(p:b\rightarrow b'\) in \(\mathcal {B}\) obviously induces a homotopy equivalence \(\mathrm {B}p_*:\mathrm {B}\mathcal {B}\!\!\downarrow {\!_{b}}\simeq \mathrm {B}\mathcal {B}\!\!\downarrow {\!_{b'}}\). Hence, the squares

induce homotopy cartesian squares on classifying spaces

By [17, II, Lemma 8.22 (2)(b)], it follows from the commutativity of diagram \((B)\) above that the induced square

is homotopy cartesian. Then, by [17, II, Lemma 8.22 (1), (2)(a)], the theorem follows from the commutativity of diagram \((A)\), since, by Lemma 5.5, in the induced square

both maps \(\mathrm {B}Q\) are homotopy equivalences and therefore it is homotopy cartesian. \(\square \)
The following corollary generalizes Quillen’s Theorem A in [28]:
Theorem 5.6
Let \(F:\mathcal {A}\rightarrow \mathcal {B}\) be a lax functor between bicategories. The induced map on classifying spaces \(\mathrm {B}F:\mathrm {B}\mathcal {A}\rightarrow \mathrm {B}\mathcal {B}\) is a homotopy equivalence whenever the classifying spaces of the homotopy fiber bicategories \(\mathrm {B}F\!\!\downarrow {\!_{b}}\) are contractible for all objects \(b\) of \(\mathcal {B}\).
Particular cases of the result above have been also stated in [7, Theorem 1.2], for the case when \(F:\mathcal {A}\rightarrow \mathcal {B}\) is any 2-functor between 2-categories, and in [14, Theorem 6.4], for the case when \(F\) is a lax functor from a category \(\mathcal {A}\) to a 2-category \(\mathcal {B}\). In [13, Théorème 6.5], it is stated a relative Theorem A for lax functors between 2-categories, which also implies the particular case of Theorem 5.6 above when \(F\) is any lax functor between 2-categories.
Example 5.7
Let \(({\mathcal M},\otimes )=({\mathcal M},\otimes ,I,\varvec{a},\varvec{l},\varvec{r})\) be a monoidal category (see e.g. [27]), and let \(\Sigma ({\mathcal M},\otimes )\) denote its suspension or delooping bicategory. That is, \(\Sigma ({\mathcal M},\otimes )\) is the bicategory with only one object, say \(\star \), whose hom-category is \({\mathcal M}\), and whose horizontal composition is given by the tensor functor \(\otimes :{\mathcal M}\times {\mathcal M}\rightarrow {\mathcal M}\). The identity 1-cell on the object is the unit object \(I\) of the monoidal category, and the constraints \(\varvec{a}\), \(\varvec{l}\), and \(\varvec{r}\) for \(\Sigma ({\mathcal M},\otimes )\) are just those of the monoidal category.
By [7, Theorem 1],
that is, the classifying space of the monoidal category is the classifying space of its suspension bicategory. Then, Theorem 5.4 is applicable to monoidal functors between monoidal categories.
However, we should stress that the homotopy fiber bicategory of the homomorphism between the suspension bicategories that a monoidal functor \(F:({\mathcal M},\otimes )\rightarrow ({\mathcal M}',\otimes )\) defines, \(\Sigma F:\Sigma ({\mathcal M},\otimes )\rightarrow \Sigma ({\mathcal M}',\otimes )\), at the unique object of \(\Sigma ({\mathcal M}',\otimes )\), is not a monoidal category but a genuine bicategory: The 0-cells of \(\Sigma F\!\!\downarrow _\star \) are the objects \(x'\in {\mathcal M}'\), its 1-cells \((u',x):x'\rightarrow y'\) are pairs with \(x\) an object in \({\mathcal M}\) and \(u':x'\rightarrow y'\otimes F(x)\) a morphism in \({\mathcal M}'\), and its 2-cells

are those morphisms \(u:x\rightarrow y\) in \({\mathcal M}\) making commutative the triangle

The vertical composition of 2-cells is given by the composition of arrows in \({\mathcal M}\). The horizontal composition of two 1-cells  is the 1-cell \( (v' \circledcirc u', y\otimes x): x'\rightarrow z' \),
is the 1-cell \( (v' \circledcirc u', y\otimes x): x'\rightarrow z' \),

and the horizontal composition of 2-cells is given by tensor product of arrows in \({\mathcal M}\). The identity 1-cell of any 0-cell \(x\) is \( (\overset{_\circ }{1}_x,I):x\rightarrow x\), where \( \overset{_\circ }{1}_x=(x'\cong x'\otimes I'\cong x'\otimes FI) \). The associativity, left and right constraints are obtained from those of \(({\mathcal M},\otimes )\) by the formulas
Following the terminology of [8, p. 228], we shall call this bicategory \(\Sigma F\!\!\downarrow _\star \) the homotopy fiber bicategory of the monoidal functor \(F:({\mathcal M},\otimes )\rightarrow ({\mathcal M}',\otimes )\), and write it by \(\mathcal {K}_F\).
Every object \(z'\) of \({\mathcal M}'\), determines a 2-endofunctor \(z'\otimes -:\mathcal {K}_F\rightarrow \mathcal {K}_F\), which is defined on cells by

where  , and from Theorems 5.4 and 5.6, we get the following:
, and from Theorems 5.4 and 5.6, we get the following:
Theorem 5.8
For any monoidal functor \(F:({\mathcal M},\otimes )\rightarrow ({\mathcal M}',\otimes )\), the following statements hold:
-
(i)
There is an induced homotopy fiber sequence
$$\begin{aligned} \mathrm {B}\mathcal {K}_F\rightarrow \mathrm {B}({\mathcal M},\otimes )\overset{\mathrm {B}F}{\longrightarrow }\mathrm {B}({\mathcal M}',\otimes ), \end{aligned}$$whenever the induced maps \(\mathrm {B}(z'\otimes -):\mathrm {B}\mathcal {K}_F\rightarrow \mathrm {B}\mathcal {K}_F\) are homotopy autoequivalences, for all \(z'\in \text{ Ob }{\mathcal M}'\).
-
(ii)
The induced map \(\mathrm {B}F: \mathrm {B}({\mathcal M},\otimes )\rightarrow \mathrm {B}({\mathcal M}',\otimes )\) is a homotopy equivalence if the space \(\mathrm {B}\mathcal {K}_F\) is contractible.
For any monoidal category \(({\mathcal M},\otimes )\), pseudo bidiagrams of categories over its suspension bicategory,
are interesting to consider, since they can be regarded as a category \({\mathcal N}\) (the one associated to the unique object of the suspension bicategory) endowed with a coherente right pseudo action of the monoidal category \(({\mathcal M},\otimes )\) (see e.g. [23, Sect. 1]). Namely, by the functor \(\otimes :{\mathcal N}\times {\mathcal M}\rightarrow {\mathcal N}\), which is defined on objects by \(a\otimes x=x^*a\) and on morphism by

together with the coherent natural isomorphisms

For each such \(({\mathcal M},\otimes )\)-category \({\mathcal N}\), the cells of the bicategory \(\int _{\Sigma ({\mathcal M},\otimes )}{\mathcal N}\) has the following easy description: Its objects are the same as the objects of the category \({\mathcal N}\). A 1-cell \((f,x):a\rightarrow b\) is a pair with \(x\) an object of \({\mathcal M}\) and \(f:a\rightarrow b\otimes x\) a morphism in \({\mathcal N}\), and a 2-cell

is a morphism \(u:x\rightarrow y\) in \({\mathcal M}\) such that the triangle

is commutative. Many of the homotopy theoretical properties of the classifying space of the monoidal category, \(\mathrm {B}({\mathcal M},\otimes )\), can actually be more easily reviewed by using Grothendieck bicategories \(\int _{\Sigma ({\mathcal M},\otimes )}{\mathcal N}\), instead of the Borel pseudo simplicial categories
as, for example, Jardine did in [23] for \(({\mathcal M},\otimes )\)-categories \({\mathcal N}\).
Thus, one sees, for example, that if the action is such that multiplication by each object \(x\) of \({\mathcal M}\), that is, the endofunctor \(-\otimes x:{\mathcal N}\rightarrow {\mathcal N}\), induces a homotopy equivalence \(\mathrm {B}{\mathcal N}\simeq \mathrm {B}{\mathcal N}\), then, by Theorem 4.3, one has an induced homotopy fiber sequence (cf. [23, Proposition 3.5])

In particular, the right action of \(({\mathcal M},\otimes )\) on the underlying category \({\mathcal M}\) leads to the bicategory

the comma bicategory of the suspension bicategory over its unique object, whose classifying space is contractible by Lemma 5.2 (cf. [23, Proposition 3.8]). Then, it follows the well-known result by Mac Lane [26] and Stasheff [29] that there is a homotopy equivalence
between the classifying space of the underlying category and the loop space of the classifying space of the monoidal category, whenever multiplication by each object \(x\in \mathrm {Ob}{\mathcal M}\), \(y\mapsto y\otimes x\), induces a homotopy autoequivalence on \(\mathrm {B}{\mathcal M}\) (cf. Example 5.3).
References
Baez, J.C., May, P (eds.) Towards Higher Categories. The IMA Volumes in Mathematics and its Applications, vol. 152. Springer, Berlin (2010)
Baković, I.: Fibrations of bicategories. Preprint available at http://www.irb.hr/korisnici/ibakovic/groth2fib.pdf
Baković, I.: Grothendieck construction for bicategories. Preprint available at http://www.irb.hr/users/ibakovic/sgc.pdf
Bénabou, J.: Introduction to bicategories. In: Reports of the Midwest Category Seminar. In: Lecture Notes in Math., vol. 47, pp. 1–77. Springer, Berlin (1967)
Breen, L.: Notes on 1- and 2-gerbes. In: Towards Higher Categories. IMA Volumes in Mathematics and its Applications, vol. 152, pp. 193–235. Springer, New York (2010)
Buckley, M.: Fibred 2-categories and bicategories. Preprint available at http://arxiv.org/abs/1212.6283
Bullejos, M., Cegarra, A.M.: On the geometry of 2-categories and their classifying spaces. \(K\)-Theory 29, 211–229 (2003)
Bullejos, M., Cegarra, A.M.: Classifying spaces for monoidal categories through geometric nerves. Canad. Math. Bull. 47, 321–331 (2004)
Carrasco, P., Cegarra, A.M., Garzón, A.R.: Nerves and classifying spaces for bicategories. Algebr. Geom. Topol. 10, 219–274 (2010)
Carrasco, P., Cegarra, A.M., Garzón, A.R.: Classifying spaces for braided monoidal categories and lax diagrams of bicategories. Adv. Math. 226, 419–483 (2011)
Cegarra, A.M.: Homotopy fiber sequences induced by 2-functors. J. Pure Appl. Algebra 215, 310–334 (2011)
Cegarra, A.M., Heredia, B.A.: Geometric realizations of tricategories. Preprint available at http://arxiv.org/abs/1203.3664
Chiche, J.: Un théorème A de Quillen pour les 2-foncteurs lax. Preprint available at http://arxiv.org/abs/1211.2319
del Hoyo, M.L.: On the loop space of a 2-category. J. Pure Appl. Algebra 216, 28–40 (2012)
Giraud, J.: Méthode de la descente. Bull. Soc. Math. France Mém. 2 (1964)
Giraud, J.: Cohomologie non abélienne. Die Grundlehren der mathematischen Wissenschaften, Band bf 179. Springer, Berlin (1971)
Goerss, P.G., Jardine, J.F.: Simplicial homotopy theory. In: Progress in Mathematics, vol. 174. Birkhäuser Verlag, Basel (1999)
Gordon, R., Power, A.J., Street, R.: Coherence for tricategories. In: Mem. Am. Math. Soc., vol. 117 (1995)
Gray, J.: Closed categories, lax limits and homotopy limits. J. Pure Appl. Algebra 19, 127–158 (1980)
Grothendieck, A.: Techniques de construction et théorèmes d’existence en géométrie algébrique. III. Préschemas quotients. Séminaire Bourbaki, 13e année, 1960/61, no 212, Février (1961)
Grothendieck, A.: Catégories Fibrées et Déscente, (SGA I, exposé VI). Lecture Notes in Math., vol. 224, pp. 145–194. Springer, Berlin (1971)
Gurski, N.: An algebraic theory of tricategories. Ph.D. thesis, March 9 (2007)
Jardine, J.F.: Supercoherence. J. Pure Appl. Algebra 75, 103–194 (1991)
Joyal, A., Street, R.: Braided tensor categories. Adv. Math. 102, 20–78 (1993)
Leinster, T.: Higher operads, higher categories. London Math. Soc. Lect. Notes Series 298. Cambridge Univ. Press, Cambridge (2004)
Mac Lane, S.: Categorical algebra. Bull. Am. Math. Soc. 71, 40–106 (1965)
Mac Lane, S.: Categories for the Working Mathematician. GTM 5, 2nd edn. Springer, Berlin (1998)
Quillen, D.: Higher algebraic K-theory: I. In: Algebraic K-theory, I: Higher K-theories. In: Lecture Notes in Math. vol. 341, pp. 85–147. Springer, Berlin (1973)
Stasheff, J.D.: Homotopy associativity of H-spaces I. Trans. Am. Math. Soc. 108, 275–292 (1963)
Street, R.: Categorical structures. Handbook of Algebra, vol. 1, pp. 529–577. North-Holland, Amsterdam (1996)
Tillmann, U.: On the homotopy of the stable mapping class group. Invent. Math. 130, 257–275 (1997)
Thomason, R.W.: Homotopy colimits in the category of small categories. Math. Proc. Camb. Philos. Soc. 85, 91–109 (1979)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nick Inassaridze.
Dedicated to Hvedri Inassaridze on his 80th birthday.
This work has been supported by DGI of Spain, Project MTM2011-22554. Also, the first author by FPU grant FPU12-01112, and third author by FPU grant AP2010-3521.
Rights and permissions
About this article
Cite this article
Calvo, M., Cegarra, A.M. & Heredia, B.A. Bicategorical homotopy fiber sequences. J. Homotopy Relat. Struct. 9, 125–173 (2014). https://doi.org/10.1007/s40062-013-0059-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-013-0059-y



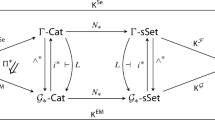

 in
in 

