Optimal dividend strategies in a Cramer–Lundberg model with capital injections and administration costs

Abstract

In this paper, we consider a classical risk model with dividend payments and capital injections in the presence of both fixed and proportionals administration costs. Negative surplus or ruin is not allowed. We measure the value of a strategy by the discounted value of the dividends minus the costs. It turns out, capital injections are only made if the claim process falls below zero. Further, at the time of an injection the company may not only inject the deficit, but inject additional capital C ≥ 0 to prevent future capital injections. We derive the associated Hamilton–Jacobi–Bellman equation and show that the optimal strategy is of band type. By using Gerber–Shiu functions, we derive a method to determine numerically the solution to the integro-differential equation and the unknown value C.

Appendix

Proof of Theorem 1

Let h > 0 and fix $u\in [0,u_0].$ If x = 0 we suppose u ≤ c, if x > 0 we let h be small enough such that x + (c − u)h ≥ 0, i.e. the reserve process does not fall below zero because of the dividend payments. Let K > 0 be the Lipschitz-constant. Choose $\varepsilon > 0$ and ${n\in\mathbb{N} }$ such that $K (x+(c-u)h)/n<\varepsilon/2$ and let x _k  = k(x + (c − u)h)/n for 0 ≤ k ≤ n. For initial capital $x^{\prime}$ where $x_k\leq x^{\prime}< x_{k+1},$ we choose a strategy {U ^k _t } with $V^{U^k}(x_k)> V(x_k)-\varepsilon/2.$ Then, by the Lipschitz continuity of V(x), it holds that

$$ V^{U^k} (x^{\prime})\geq V^{U^k}(x_k)> V(x_k)-\varepsilon/2 > V(x^{\prime}) - K (x^{\prime} -x_k)-\varepsilon/2 > V(x^{\prime}) - \varepsilon. $$

Thus, for all $x^{\prime}\in[0, x+(c-u)h]$ we can find a measurable strategy $\tilde{U}$ such that $V^{\tilde{U}}(x^{\prime})> V(x^{\prime})-\varepsilon.$

Consider now the strategy

$$ U_t=\left\{ \begin{array}{ll} u, & 0\leq t< h\wedge T_1,\\ \tilde{U}_{t-h}, & t\geq h\wedge T_1, \end{array}\right. \qquad Z_t=\left\{ \begin{array}{ll} 0, & 0\leq t< h\wedge T_1, \\ \tilde{Z}_{t-h}, & t\geq h\wedge T_1. \end{array}\right. $$

Conditioning on ${{\mathcal F}_{h\wedge T_1}}$ yields

$$ \begin{aligned} V(x) & \geq V^{U}(x)= {\mathbb{E}}\left[\int\limits_{0}^{h\wedge T_1-} e^{-\delta t}u \;\hbox{d} t +e^{-\delta (h\wedge T_1)}V^{\tilde{U}}(X_{h\wedge T_1})\right] \\ & ={\mathbb{E}}\left[\left(\int\limits_{0}^{h} e^{-\delta t}u \;\hbox{d} t +e^{-\delta h}V^{\tilde{U}}(X_{h})\right){\rm 1\!\!I}_{T_1> h}\right.\\ & \quad \left. +\left(\int\limits_{0}^{ T_1-} e^{-\delta t}u \;\hbox{d} t +e^{-\delta T_1}V^{\tilde{U}}(X_{ T_1})\right){\rm 1\!\!I}_{T_1\leq h} \right]\\ & =\left. e^{-\lambda h}\int\limits_0^{h}u e^{-\delta t}\;\hbox{d} t +e^{-(\delta+\lambda) h}V^{\tilde{U}}(x+(c-u)h)\right.\\ & \quad +\int\limits_0^h\lambda e^{-\lambda t}\left\{\int\limits_0^{t}u e^{-\delta s}\;\hbox{d} s\right.\\ & \quad \left. +e^{-\delta t}\int\limits_0^\infty V^{\tilde{U}}(x+(c-u)t-y) \;\hbox{d} G(y)\right\}\;\hbox{d} t\;\\ &\left.\geq e^{-\lambda h}\int\limits_0^{h}u e^{-\delta t}\;\hbox{d} t +e^{-(\delta+\lambda) h}V(x+(c-u)h)\right.\\ & \quad +\int\limits_0^h\lambda e^{-\lambda t}\left\{\int\limits_0^{t}u e^{-\delta s}\;\hbox{d} s\right. \\ & \quad \left. +e^{-\delta t}\int\limits_0^\infty V(x+(c-u)t-y) \;\hbox{d} G(y)\right\}\;\hbox{d} t- \varepsilon. \end{aligned} $$

The constant $\varepsilon$ is arbitrary, thus, we let tend it to zero. If we rearrange the terms and divide them by h, then we get

$$ \begin{aligned} 0 & \geq {\frac{V(x+(c-u)h)-V(x)}{h}}-{\frac{1-e^{-(\lambda+\delta) h}}{h}}V(x+(c-u)h)\\ & \quad +e^{-\lambda h}{\frac{1}{h}}\int\limits_0^h u e^{-\delta t} \;\hbox{d} t + {\frac{1}{h}}\int\limits_0^h \lambda e^{-\lambda t}\left[\int\limits_0^t u e^{-\delta s}\;\hbox{d} s\right.\\ & \quad \left. +e^{-\delta t}\int\limits_{0}^{\infty}V(x+(c-u)t-y)\; d G(y)\right]\;\hbox{d} t. \end{aligned} $$

(12)

Now we choose a strategy W(h) = {W _t (h)} with V ^W(h)(x) ≥ V(x) − h ². There exists w _h such that ${{\mathbb{E}}[\int_0^{h\wedge T_1}(W_s(h)-w_h)e^{-\delta s}\;\hbox{d} s]=0}.$ Let $w_t^{\prime}$ denote W _t (h) conditioned on T ₁ > t and $a(t)=\int_0^t(c-w_s^{\prime})\;\hbox{d} s$. In the same way as above, we can derive

$$ \begin{aligned} &0 \leq h+ {\frac{V(x+a(h))-V(x)}{h}}-{\frac{1-e^{-(\lambda+\delta) h}} {h}}V(x+a(h))\\ & \quad +e^{-\lambda h}{\frac{1}{h}}\int\limits_0^h w_h e^{-\delta t} \;\hbox{d} t + {\frac{1}{h}}\int\limits_0^h \lambda e^{-\lambda t}\left[\int\limits_0^t w_h e^{-\delta s}\;\hbox{d} s \right.\\ & \quad \left. +e^{-\delta t}\int\limits_{0}^{\infty}V(x+a(t)-y) \;\hbox{d} G(y)\right]\;\hbox{d} t. \end{aligned} $$

All terms with exception of the second and the forth one converge. We choose a sequence h _n  → 0 such that

$$ \lim_{n\to \infty}{\frac{V(x+a(h_n))-V(x)} {h_n}}=\limsup_{h\downarrow 0}{\frac{V(x+a(h))-V(x)}{h}}. $$

This limit is finite by the local Lipschitz continuity. Without loss of generality, we can assume that $w_{h_n}$ converges to some value $\tilde{u}$. Then a(h _n )/h _n converges to $c-\lim w_{h_n}^{\prime}=c-\lim w_{h_n}=c-\tilde{u}$ and

$$ \begin{aligned} \lim_{n\to \infty}{\frac{V(x+a(h_n))-V(x)}{h_n}}=& \lim_{n\to \infty}{\frac{V(x+a(h_n))-V(x)}{a(h_n)}}\;{\frac{a(h_n)}{h_n}}\\ =& (c-\tilde{u})V^{\prime}(x). \end{aligned} $$

The sequence {$w_{j_n}$} fulfils (12), and so equality holds for $u=\tilde{u}$.

We can repeat the above procedure for any subsequence $w_{j_n}$ that converges to $\hat{u},$ say. Then for the limit

$$ \lim_{n\to\infty}{\frac{V(x+a(j_n))-V(x)}{j_n}} $$

we get

$$ \limsup_{h\downarrow 0}{\frac{V(x+a(h))-V(x)} {h}}+\hat{u}=(\lambda+\delta)V(x)-\lambda \int\limits_{0}^{\infty}V(x-y) \;\hbox{d} G(y) $$

such that $\tilde{u}=\hat{u}$ and the limit

$$ \limsup_{h\downarrow 0}{\frac{V(x+a(h))-V(x)} {h}}=(c-\tilde{u})\lim_{h\downarrow 0}{\frac{V(x+(c-\tilde{u})h)-V(x)}{(c-\tilde{u})h}} $$

is unique. If now ${x\in{\mathcal D},}$ the above limit is $(c-\tilde{u})V^{\prime}(x)$. Otherwise we have shown the differentiability at x from the right if $c>\tilde{u}$ and the differentiability at x from the left if $c<\tilde{u}$. We do not distinguish the notation first and write for both derivatives the Hamilton–Jacobi–Bellman equation

$$ \sup_{0\leq u\leq u_0}\left\{(c-u)V^{\prime}(x)+u-(\lambda+\delta)V(x) +\lambda \int\limits_0^{\infty}V(x-y) \;\hbox{d} G(y)\right\}=0 , $$

(13)

where we have

$$ \begin{aligned} &\int\limits_0^{\infty}V(x-y) \;\hbox{d} G(y)\\ & \quad = \int\limits_0^x V(x-y) \;\hbox{d} G(y) + \int\limits_x^\infty (V(C)- \phi(y-x+C)-L)\;\hbox{d} G(y)\\ & \quad = \int\limits_0^x V(x-y) \;\hbox{d} G(y)\\ &\qquad + (V(C)-\phi C-L)(1-G(x))- \phi\int\limits_x^\infty (1-G(y))\;\hbox{d} y, \end{aligned} $$

(14)

because of the property (1).

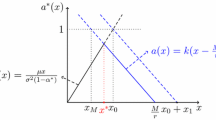
Equation 13 is linear in u, thus, the argument $\tilde{u}=u(x)$ maximising the left-hand side of Eq. 13 is

$$ u(x)=\left\{ \begin{array}{ll} 0, & \hbox {if} \quad V^{\prime}(x)>1,\\ \in[0, u_0], & \hbox {if}\quad V^{\prime}(x)=1,\\ u_0, & \hbox {if} \quad V^{\prime}(x)<1. \end{array}\right. $$

Consider now the function

$$ H(x):= (\lambda+\delta)V(x)-\lambda \int\limits_0^{\infty}V(x-y) \;\hbox{d} G(y). $$

(15)

Since V(x − y) ≤ V(x) for y ≥ 0, it follows by the bounded convergence theorem and continuity of V(x) that H(x) is a continuous function on ${\mathbb{R}}.$ The HJB equation (13) reads

$$ (c-\tilde{u})V^{\prime}(x)+\tilde{u} - H(x)=0. $$

(16)

for any ${x\in {\mathcal D}}$ and $\tilde{u}=u(x).$

Let u ₀ < c. Then we have shown the differentiability from the right with

$$ \begin{array}{lllll} V^{\prime}(x+)> 1 &\Leftrightarrow& \tilde{u}=0 &\Leftrightarrow& H(x)> c,\\ V^{\prime}(x+)<1 &\Leftrightarrow& \tilde{u}=u_0 &\Leftrightarrow& H(x)< c,\\ V^{\prime}(x+)=1 &\Leftrightarrow& \tilde{u}\;\hbox{arbitr.} &\Leftrightarrow& H(x)=c. \end{array} $$

Suppose, H(x) > c. Then, by continuity, there exist $\varepsilon>0$ and an interval ${{\mathcal U}_\varepsilon(x)}$ such that H(z) > c for any ${z\in {\mathcal U}_\varepsilon(x)}.$ Let {x _n } be a sequence in ${{\mathcal U}_\varepsilon(x)\cap {\mathcal D}}$ tending to x from left. For any x _n Eq. 16 holds. Denote $\tilde{u}_n= u(x_n)$. Then, H(x _n ) > c and from Eq. 16 $\tilde{u}_n=0$ follows. Therefore, $u=\lim_{n\to\infty}\tilde{u}_n=0$ and we get that V is differentiable from the left with

$$ V^{\prime}(x-)=\lim_{n\to\infty}{\frac{H(x_n)-\tilde{u}_n} {c-\tilde{u}_n}}={\frac{H(x)}{c}}=V^{\prime}(x+)>1. $$

If H(x) < c, in an analogous way we get $H(x_n)<c, \tilde{u}_n=u_0$ and therefore u = u ₀ such that $V^{\prime}(x-)=V^{\prime}(x+)<1$.

If H(x) = c, differentiability follows because we can choose u arbitrarily.

Thus, for u ₀ < c, we have proved that V is continuously differentiable and fulfils Eq. 13. We denote this solution by $V_{u_0} (x)$.

We consider now the case u ₀ = c. We can follow from Eq. 16 that

$$ \begin{array}{lll} V^{\prime}(x+)>1 \Leftrightarrow \tilde{u}=0 &\Leftrightarrow& H(x)>c,\\ ((V^{\prime}(x-)<1 \Leftrightarrow \tilde{u}=u_0) \;\;{or}\;\; (V^{\prime}(x)=1 \Leftrightarrow \tilde{u}\;\hbox{arbitr.})) &\Leftrightarrow& H(x)=c. \end{array} $$

If H(x) > c, then, by similar arguments as above, we derive that V is differentiable at x with $V^{\prime}(x)>1$ and HJB equation (13) is fulfilled with u = 0.

Let now H(x) = c. Then, H(z) ≥ c for any ${z\in {\mathcal U}_\varepsilon(x)}$. Suppose, $V^{\prime}(x-)<1$. For a sequence x _n ↓ x with H(x _n ) > c we get that $\tilde{u}_n=0$ and therefore V is differentiable from the right with $V^{\prime}(x+)=1$. In this case (13) is again fulfilled. If there is a sequence with H(x _n ) = c, then we get differentiability at x.

The last case to consider is u ₀ > c. Then

$$ \begin{array}{lll} V^{\prime}(x)=1 \Leftrightarrow \tilde{u}\;\hbox{arbitr.} &\Leftrightarrow& H(x)=c,\\ ((V^{\prime}(x-)<1 \Leftrightarrow \tilde{u}=u_0) \;\;{or}\;\; (V^{\prime}(x+)>1 \Leftrightarrow \tilde{u}=0)) &\Leftrightarrow& H(x)>c. \end{array} $$

If H(x) = c, then differentiability follows similarly to above.

Let H(x) > c. Suppose that $V^{\prime}(x+)>1$ and $\tilde{u}=0$. Let {x _n } be a sequence in ${{\mathcal U}_\varepsilon(x)\cap{\mathcal D}}$ with x _n ↑ x. If $u=\lim_{n\to\infty}\tilde{u}_n=0,$ then we get differentiability with $V^{\prime}(x)>1$. If u = u ₀, then V is differentiable from the left with $V^{\prime}(x-)<V^{\prime}(x+)$ and both derivatives solve Eq. 13.

Suppose that V′(x −) < 1 and $\tilde{u}=u_0$. For a sequence x _n ↓ x we again have to choose either u = 0 or u = u ₀. The choice u = 0 shows that V is differentiable from the right with $V^{\prime}(x+)>1$ and both derivatives solve Eq. 13. If u = u ₀, then differentiability follows with $V^{\prime}(x)<1$.

Proof of Lemma 6

The proof is based on Schmidli [20, Section 2.4.2].

• 1. Since H is continuous, H(x) ≥ c for all $x\in[0,\infty)$ and {c} is closed, the set $\{x\in[0,\infty): H(x)=c\}$ is closed.

• 2. Let ${x\in {\mathcal B}}$. Since ${{\mathcal A}}$ is closed, there must be $\varepsilon>0$ such that ${(x-\varepsilon, x)\subset {\mathcal A}^c}$ because, otherwise, ${x\in {\mathcal A}}$. Since ${(x-\varepsilon, x)\subset{\mathcal C}^c,}$ we get ${(x-\varepsilon, x)\subset{\mathcal B}}$.

• 3. Let $\{x_n\}\subset (x_0, x]$ such that x _n ↓ x ₀. Then, $V^{\prime}(x_n)=1$ and H(x _n ) > c. By continuity, $V^{\prime}(x_0)=1$ and H(x ₀) = c, since, otherwise, ${x_0\in {\mathcal B}}$.

• 4. If ${x\in{\mathcal C},}$ then, by the continuity of H, there must be a δ > 0 such that ${[x,x+\delta)\subset {\mathcal A}^c}$. If there would be some ${x_1\in {\mathcal B}}$ within this interval, we could follow the existence of an ${x_0\in {\mathcal A}}$ with x ₀ < x ₁ such that ${(x_0,x_1] \subset {\mathcal B}}$. Since ${x\notin {\mathcal B}}$ this x ₀ has also to be in the interval [x, x + δ) which is a contradiction. Therefore, ${[x,x+\delta)\subset {\mathcal B}^c}$ and ${[x,x+\delta)\subset {\mathcal C}}$.

• 5. Let C be chosen optimally. Since V(x) is strictly increasing, we get $V(x)-\int\limits_0^x V(x-y)\;{\text{d}} G(y)\geq V(x)(1-G(x))$ and therefore

  $$ \begin{aligned} & (\lambda+\delta)V(x)-\lambda\int\limits_0^x V(x-y)\hbox{d} G(y)\\ & \qquad -\lambda(V(C)-\phi C-L)(1-G(x))+\lambda\phi\int\limits_x^\infty (1-G(y))\hbox{d} y\\ & \quad \geq \lambda V(x)(1-G(x))+\delta V(x)-\lambda (V(C)-\phi C-L)(1-G(x))\\ & \quad = \delta V(x)+\lambda(1-G(x))(V(x)-V(C)+\phi C+L)\\ &\quad \geq \delta V(x). \end{aligned} $$

  The last inequality holds because obviously V(x) − V(C) ≥ 0 for x ≥ C. For x < C we have by Lemma 4 that V(x) − V(C) ≥  − ϕ(C − x) − L and thus V(x) − V(C) + ϕC + L ≥ ϕx ≥ 0.

  From Lemma 4 we can follow that for any $x>\lambda(\phi\mu+\phi C+L)/\delta$

  $$V(x)\geq x+ \frac{c- \lambda(\phi\mu+\phi C+L)}{\delta}>\frac{\lambda(\phi\mu+\phi C+L)}{\delta}+\frac{c- \lambda(\phi\mu+\phi C+L)}{\delta}=\frac{c}{\delta}$$

  holds. Assume now that there is $x>\lambda(\phi\mu+\phi C+L)/\delta$ with $V^\prime(x-)>1.$ Then $V^\prime(z)>1$ for all z ≥ x. To prove this claim, we suppose that there is $z={\text{inf}}\{y>x:V^\prime(y)=1\}<\infty.$ For this point we have

  $$1=V^\prime(z)=\frac{(\lambda+\delta)V(x)-\lambda\int_0^\infty V (x-y) \text{d}G(y)}{c}\geq \frac{\delta V(z)}{c}\\>\frac{\delta V(x)}{c}>1,$$

  which is a contradiction. Thus,

  $$V^\prime(z)\geq \frac{\delta}{c}V(z)$$

  for all z ≥ x, or equivalently, $\log(V(z)/V(x))\geq (z-x)\delta/c,$ i.e. V(x) is exponentially increasing on $[x,\infty).$ This is a contradiction to Lemma 4. Thus, $V^\prime(x-)=1.$

• 6. The assertion follows from the forth and fifth point.

Proof of Lemma 7

Let $\varepsilon={\frac{c}{2(2\lambda+\delta)}}$ and denote by $CI[x_0,x_0+\varepsilon)$ the set of all continuous and increasing functions $u:[x_0,x_0+\varepsilon)\rightarrow [0,\infty)$. For a $u\in CI[x_0,x_0+\varepsilon),$ let

$$ \begin{aligned} \bar{u}(x)& = {\frac{1} {c}}\left[(\lambda+\delta)u(x)-\lambda\int\limits_{x-x_0}^x v(x-y)\hbox{d} G(y)-\lambda\int\limits_0^{x-x_0}u(x-y)\hbox{d} G(y)\right.\\& \quad \left.-\lambda (v(C)-\phi C-L)(1-G(x))+\lambda\phi\int\limits_x^\infty(1-G(y))\hbox{d} y\right]. \end{aligned} $$

By the continuity of u and $v, \bar{u}$ is continuous for x ≥ 0. Define now for $u\in CI[x_0,x_0+\varepsilon)$

$$ T_u(x)=\int\limits_{x_0}^x \bar{u}(s)\;{\text{d}} s + v(x_0)\;. $$

Because of the monotonicity of u and v and v(x ₀) = u(x ₀) we get

$$ \begin{aligned} c\bar{u}(x)& = (\lambda+\delta)u(x)-\lambda\int\limits_{x-x_0}^x v(x-y)\hbox{d} G(y)-\lambda\int\limits_0^{x-x_0}u(x-y)\hbox{d} G(y)\\ & \quad -\lambda (v(C)-\phi C-L)(1-G(x))+\lambda\phi\int\limits_x^\infty (1-G(y))\hbox{d} y\\ &\geq (\lambda+\delta)u(x)-\lambda v(x_0)(G(x)-G(x-x_0))-\lambda u(x)G(x-x_0) \\ & \quad -\lambda v(C)(1-G(x))\\ &\geq \delta u(x)+\lambda u(x)-\lambda u(x)G(x)-\lambda v(C)(1-G(x))\\ & = \delta u(x)+\lambda (1-G(x))(u(x)- v(C))\\ &\geq \delta u(x)\\ & > 0. \end{aligned} $$

By the positivity of u and v, we get the upper bound for $\bar{u}(x)$

$$ c\bar{u}(x)\leq (\lambda+\delta)u(x)+\lambda(\phi C +L+\phi\mu). $$

It follows that T _u is increasing, positive and continuous for $x\in [x_0, x_0+\varepsilon)$. For $u_1, u_2\in CI[x_0,x_0+\varepsilon)$ holds

$$ \begin{aligned} &c(\bar{u}_1(x)-\bar{u}_2(x))\\ &=(\lambda+\delta)(u_1(x)-u_2(x))-\lambda \int\limits_0^{x-x_0}(u_1(x-y)-u_2(x-y))\hbox{d} G(y)\\ & \leq (\lambda+\delta)\left\|u_1-u_2\right\|+\lambda \left\|u_1-u_2\right\|G(x-x_0)\\ & \leq(2\lambda+\delta)\left\|u_1-u_2\right\|, \end{aligned} $$

where $\left\|\cdot\right\|$ is the supremum norm. It follows

$$ T_{u_1}(x)-T_{u_2}(x)\leq \varepsilon {\frac{2\lambda+\delta} {c}}\left\|u_1-u_2\right\|\leq {\frac{1} {2}}\left\|u_1-u_2\right\|\;. $$

Interchanging u ₁ and u ₂ yields $\left\|T_{u_1}-T_{u_2}\right\|\leq {\frac{1} {2}}\left\|u_1-u_2\right\|,$ i.e. T is a contraction on $CI[x_0,x_0+\varepsilon)$. This proves the existence of a $u\in CI[x_0,x_0+\varepsilon)$ such that

$$ u(x)=T_u(x)=\int\limits_{x_0}^x \bar{u}(s)\hbox{d} s + v(x_0). $$

This provides $u^{\prime}(x)=\bar{u}(x)$ everywhere in $[x_0, x_0+\varepsilon)$. Thus we get the existence of a unique solution to Eq. 10 with the required properties on $[x_0, x_0+\varepsilon)$.

Since $\varepsilon$ does not depend on x ₀, we have shown the existence of a unique solution on $[x_0,\infty)$.