Dividend and Capital Injection Optimization with Transaction Cost for Lévy Risk Processes

Abstract

The optimal dividends problem has remained an active research field for decades. For an insurance company with reserve modelled by a spectrally negative Lévy process having finite first-order moment, we study the optimal impulse dividend and capital injection (IDCI) strategy for maximizing the expected accumulated discounted net dividend payment subtracted by the accumulated discounted cost of injecting capital. In this setting, the beneficiary of the dividends injects capital to ensure a non-negative risk process so that the insurer never goes bankrupt. The optimal IDCI strategy together with its value function is obtained. Besides, two numerical examples are provided to illustrate the features of the optimal strategies. The impacts of model parameters are also studied.

1 Introduction

Dividends, known as the distribution of corporate profits to shareholders, have attracted broad arguments across the academic and nonacademic literature on corporate financial policies. From the shareholder’s point of view, dividends are a form of cash flow to the investor, and hence they are an important reflection of a company’s value. Consequently, the boards of the company declare dividends regularly and raise them from time to time or face discontentment from investors. It is nearly universal policy of paying substantial dividends to investors, in spite of its significant tax penalty comparing to the lower tax rate on capital gains, which is one of the primary puzzles in the economics of corporate finance. [19] reviewed five kinds of explanations and provided a market equilibrium model to explain why companies pay dividends.

As pointed out by [18], it is a common business to raise new capital at or around the time companies pay dividends. One of the most common ways companies raise capital is through issuing new debts, often in the form of bank loans. In the academic literature, this procedure of raising new capital for the company is the so-called “capital injection”. As a result of paying dividends, it seems attractive for investors looking to generate income, which creates more demands for the company’s stock. However, from the company manager’s point of view, neither paying dividend nor raising new capital is free. In addition to the administrative costs of distributing dividends such as the cost of paperwork and the utilization of the communication network, two sources of agency cost on the part of managers who directly control the dividend strategy should also be taken into consideration, see [18] for more details. In this paper we bundle all these as transaction costs and model them as having a fixed size c per distribution of dividends. On the other side, the cost of capital injections can be understood as the cost of debts, the amount of which depends on the amount of new capital raised. This paper uses $\phi$ to model the cost of per unit capital injected.

Based on these considerations, this paper aims to discuss the optimal impulse dividend and capital injection (IDCI) strategy for an insurance company. The surplus level is modelled by a spectrally negative Lévy (SNL) risk process, a widely used model in the literature of actuarial studies. To imitate the real-world procedure of dividend payments, we consider two real-life factors as mentioned above: the capital injections and the transaction costs involved in the dividend distribution and capital injection. Allowing capital injections can protect the insurance company against the bankruptcy, thereby sustaining dividend payments in the long run. Transaction costs also play an important role in the selection of dividend policy. Through maximizing the expected accumulated discounted net dividend payments subtracted by the accumulated discounted cost of injecting capital under the proposed surplus process, we obtain the optimal IDCI strategy, which provides a useful reference for insurance companies when designing their long-term profit-sharing strategies.

The optimal dividend payout strategies have remained an active research field in the actuarial science literature for almost 60 years. Two survey papers, [1, 3], provide thorough and insightful reviews on the classical contributions and recent progress in the field. The earliest paper in the field, [17], proved that with the option to pay out dividends from its surplus to the beneficiary until the discrete time of ruin, an insurance company should adopt a barrier dividend strategy to maximize the expected total amount of discounted dividends until ruin. However, when dividends are imposed with fixed transaction costs, recent research findings in the literature suggest that the dividend optimization problem becomes an impulse (dividend) control problem and the optimal dividend strategy is an optimal impulse dividend (OID) strategy.

Research on OID strategies has attracted much attention for a decade and has progressed well under various surplus processes. In the classical Cramér-Lundberg (CL) risk model, [10] studied an OID problem with transaction cost and tax on dividends as well as exponentially distributed claims. The obtained OID strategy reduces the reserve to level $u_{1}\in [0,u_{2})$ whenever it is above or equal to level $u_{2}$, also called a $(u_{1},u_{2})$ strategy. In the dual classical CL risk model, [58] also considered an OID problem with fixed/proportional transaction cost on dividends and derived the OID strategy via a quasi-variational inequality argument. [11] studied the OID problem with transaction costs on dividends for a class of general diffusion risk processes and derived the $(u_{1},u_{2})$ OID strategy. In the context of SNL risk process, [36] discussed an OID problem with transaction cost and showed that a $(u_{1},u_{2})$ strategy maximizes the expected accumulated present value of the net dividends. For the spectrally positive Lévy (SPL) risk process with fixed transaction costs on dividends, [13] proved that a $(u_{1},u_{2})$ strategy is again the OID strategy. For more results on impulse dividend control problems, we refer readers to [4, 22, 23, 25, 41, 52, 57] and the references therein.

In the literature, capital injection is another factor to consider when designing dividend payout. Under risk models with dividends as well as fixed transaction costs imposed on the capital injections, the corresponding optimization problem is also an impulse (capital injection) control problem. In the setting of the dual classical CL risk model, [52] found that the optimal dividend and capital injection (ODCI) strategy, which maximizes the expected present value of the dividends subtracted by the discounted cost of capital injections, pays out dividends according to a barrier strategy and injects capitals to bring the reserve up to a critical level whenever it falls below 0. Under the drifted diffusion risk model, [41] investigated the optimal dividend problem of an insurance company which controls risk exposure by reinsurance and by issuing new equity to protect the insurance company from bankruptcy. The corresponding ODCI strategy also pays dividends by a barrier strategy and injects capital to bring reserve up to a critical level whenever it falls below 0. In the setting of SPL risk process with the dividend rate restricted, [55, 57] considered an ODCI problem and found that the optimal method of paying dividends is a threshold strategy. For more information on dividend optimization in risk models with capital injection being imposed with proportional or fixed transaction cost, we refer readers to [5, 6, 12, 25, 34, 54] and the references therein.

Regarding SNL risk processes, the majority of dividend optimization problems are formulated as non-impulse stochastic control problems. Using the expected present value of dividends until ruin (the expected present value of the dividends subtracted by the discounted costs of capital injections) as the value function, [6] identified the condition under which the barrier strategy (respectively, the barrier dividend strategy together with capital injection strategy that reflects the reserve process at 0) is optimal among all admissible strategies. More results of non-impulse dividend optimization under the SNL risk processes can be found in [7, 9, 15, 16, 20, 21, 28, 31, 32, 34, 37, 38, 45,46,47,48,49,50, 53] and the references therein. The non-impulse dividends optimization under the SPL risk processes can be found in [4, 5, 12, 13, 53, 55, 57] and others.

Motivated by [6, 36], this paper studies a general optimal IDCI problem through maximizing the expected accumulated discounted net dividend payment subtracted by the accumulated discounted cost of injecting capital in the setup of the SNL process that is assumed to have finite first-order moment, an important restriction that appears commonly in the literature on Lévy risk processes where capital injections are required to keep the surplus process non-negative; see, for example, [6, 39, 40] where it is called Assumption ($\mathbb {M}$). The novelty in this paper lies as follows: (i) compared with the existing OID results under diffusion or general Lévy setup, the present model brings in the capital injection in an optimal way to reflect the corresponding risk process at 0; and (ii) compared with the existing OID results concerning capital injections, the present model studies the Lévy setup, a more general driven process. In this paper, the discussion follows the standard treatment of Hamilton–Jacobi–Bellman (HJB) inequality in the control theory. We first find the optimal strategy among all $(z_{1},z_{2})$ IDCI strategies, and then we prove that it is optimal among all IDCI strategies via a verification argument. To facilitate the standard HJB framework, we employ subtle approaches within each step, for example, the novel technique to derive Proposition 3.3 and Lemma 4.6, and the mollifying argument to prove the modified verification lemma (see, Lemma 4.3 and 4.4).

We acknowledge that there is a parallel paper in the literature, [28], which was also finished independently around the same time. The first version of both papers were available on internet in the middle of 2018. The authors of [28] considered the bail-out optimal dividend problem under fixed transaction costs for a Lévy risk model with a constraint on the expected net present value of injected capital. While the main results in this paper and those in [28] appear to be very similar, the primary objectives of these two papers are notably different as well as the methods adopted in the proof of certain main results (for instance, the verification Lemma 4.3 and 4.4 in this paper vs Theorem 4.10 in [28]). We believe both papers make interesting contributions to the literature.

The remainder of this paper is organized as follows: Sect. 2 comprises preliminaries concerning the SNL process and the mathematical setup of the dividend optimization problem. In Sect. 3 we represent the value function of a $(z_{1},z_{2})$ IDCI strategy using the scale function associated with the SNL process. This facilitates the characterization of the optimal strategy among all $(z_{1},z_{2})$ IDCI strategies, which is further proved to be optimal among all admissible IDCI strategies. In Sect. 4, we first prove that a solution to the HJB inequalities coincides with the optimal value function via a verification lemma. Next, the solution to the HJB inequality is constructed, and the optimal strategy is found to be a $(z_{1},z_{2})$ IDCI strategy under which the risk process is reflected at 0. In Sect. 5, we illustrate the optimal IDCI strategy by using two numerical examples. Section 6 concludes this paper.

2 Formulation of the Dividend Optimization Problem

Let $X=\{X(t);t\ge 0\}$ with probability laws $\{\mathrm {P}_{x};x\in \left[ 0,\infty \right) \}$ and natural filtration $\mathcal {F}=\{\mathcal {F}_{t};t\ge 0\}$ satisfying the usual condition be a spectrally negative Lévy (SNL) process, i.e., a càdlàg $\mathcal {F}$-adapted stochastic process that has stationary and independent increments, and has no positive jumps. Under $\mathrm {P}_{x}$ the SNL process X starts from x, i.e., $X(0)=x$ almost surely. We exclude the trivial case of a pure increasing linear drift or the negative of a subordinator. Denote the running supremum $\overline{X}(t):=\sup \{X(s);s\in [0,t]\}$ for $t\ge 0$. Assume that in the case of no control (dividend is not deducted and capital is not injected), the risk process evolves as X(t) for $t\ge 0$. An impulse dividend strategy, denoted by $D=\{D(t);t\ge 0\}$, is a one-dimensional, non-decreasing, left-continuous, $\mathcal {F}$-adapted, and pure jump process started at 0, i.e., $D(0)=0$ and D(t) defines the cumulative dividend that the company has paid out until time $t\ge 0$. For the insurance company not to go bankrupt, the beneficiary of the dividend is required to inject capital into the insurance company to ensure that the risk process is non-negative. A capital injection strategy, denoted by $R=\{R(t);t\ge 0\}$, is a one-dimensional, non-decreasing, càdlàg, $\mathcal {F}$-adapted process started at 0, i.e., $R(0)=0$ and R(t) defines the cumulative capital that the beneficiary has injected until time $t\ge 0$. The combined pair (D, R) is called an IDCI strategy. More explicitly, an impulse dividend strategy D is characterized by

$$\begin{aligned} \left( \tau _n^{D},\eta _{n}^{D}\right) ,\quad n=1,2,\cdots , \end{aligned}$$

where $(\tau _{n}^{D})_{n\ge 1}$ and $(\eta _{n}^{D})_{n\ge 1}$ are the times and amounts of dividend lump sum payments, respectively. With dividends deducted according to D and capital injected according to R, the controlled aggregate reserve process is then given by

$$\begin{aligned} U(t)=X(t)-D(t)+R(t), \quad t\ge 0. \end{aligned}$$

An IDCI strategy (D, R) is defined to be admissible if $U(t)\ge 0$ for all $t\ge 0$ and $\int _{0}^{\infty }\mathrm {e}^{-qt}\mathrm {d}R(t)<\infty$ almost sure in the sense of $\mathrm {P}_{x}$, where $q>0$ is a discount factor.

Let $\mathcal {D}$ be the set of all admissible dividend and capital injection strategies. For an IDCI strategy $(D,R)\in \mathcal {D}$, denote its value function as

$$\begin{aligned}&V_{(D,R)}(x)=\mathrm {E}_{x}\left( \sum _{n=1}^{\infty } \mathrm {e}^{-q \tau _{n}^{D}}\left( \eta _{n}^{D}-c\right) \right. \\&\quad \left. -\phi \int _{0}^{\infty }\mathrm {e}^{-qt}\mathrm {d}R(t)\right) ,\quad x\in [0,\infty ), \end{aligned}$$

where $c>0$ is the transaction cost for each lump sum dividend payment and $\phi >1$ is the cost per unit capital injected. The goal is to identify the optimal strategy $(D^*,R^*)$ and the corresponding optimal value function

$$\begin{aligned} V(x)=V_{(D^*,R^*)}(x)=\sup \limits _{(D,R)\in \mathcal {D}}V_{(D,R)}(x),\quad x\in [0,\infty ). \end{aligned}$$

Intuitively speaking, because of $\phi >0$ and $q>0$, it would be better if the capital is injected as late as possible with no further capital injection being made rather than just injecting enough amounts to keep the corresponding risk process non-negative.

The Laplace exponent of X is

$$\begin{aligned} \psi (\theta )= & {} \ln \mathrm {E}_{0}\left[ \mathrm {e}^{\theta X(1)}\right] \\= & {} \gamma \theta +\frac{1}{2}\sigma ^{2}\theta ^{2}-\int _{(0,\infty )}(1-\mathrm {e}^{-\theta x}-\theta x\mathbf {1}_{(0,1)}(x))\upsilon (\mathrm {d}x), \end{aligned}$$

where $\upsilon$ is the Lévy measure with $\int _{(0,\infty )}(1\wedge x^{2})\upsilon (\mathrm {d}x)<\infty$. In this paper, we need to further assume that $\upsilon$ has finite first-order moment, i.e., $\int _1^\infty y\upsilon (dy)<\infty$, in which case the process X satisfies the Assumption ($\mathbb {M}$) in [40]. Actually, we have the following representation

$$\begin{aligned} X(t)=\gamma t+\sigma B(t)-\int _{0}^{t}\int _{(0,1)}x \overline{N}(\mathrm {d}s,\mathrm {d}x)-\int _{0}^{t}\int _{[1,\infty )}x N(\mathrm {d}s,\mathrm {d}x), \quad t\ge 0, \end{aligned}$$

where B(t) is the standard Brownian motion, $N(\mathrm {d}s,\mathrm {d}x)$ is an independent Poisson random measure on $[0, \infty )\times (0, \infty )$ with intensity measure $\mathrm {d}s\upsilon (\mathrm {d}x)$, and $\overline{N}(\mathrm {d}s,\mathrm {d}x)=N(\mathrm {d}s,\mathrm {d}x)-\mathrm {d}s\upsilon (\mathrm {d}x)$ denotes the compensated random measure.

It is known that $\psi (\theta )<\infty$ for $\theta \in [0,\infty )$, in which case it is strictly convex and infinitely differentiable. As in [14], the q-scale function of X, for each $q\ge 0$, $W^{(q)}:[0,\infty )\mapsto [0,\infty )$ is the unique strictly increasing and continuous function with Laplace transform

$$\begin{aligned} \int _{0}^{\infty }\mathrm {e}^{-\theta x}W^{(q)}(x)\mathrm {d}x=\frac{1}{\psi (\theta )-q},\quad \theta >\Phi _{q}, \end{aligned}$$

where $\Phi _{q}$ is the largest solution of the equation $\psi (\theta )=q$. Further, let $W^{(q)}(x)=0$ for $x<0$ and write W for the 0-scale function $W^{(0)}$. By Lemma 1 in [42] we know that the scale function $W^{(q)}$ is right and left differentiable over $(0,\infty )$. By $W^{(q)\prime }_{\pm }(x)$, we will denote the right and left-derivative of $W^{(q)}$ in x, respectively. For any $x\in \mathbb {R}$ and $\vartheta \ge 0$, there exists the well-known exponential change of measure for an SNL process

$$\begin{aligned} \left. \frac{\mathrm {P}_{x}^{\vartheta }}{\mathrm {P}_{x}}\right| _{\mathcal {F}_{t}}=\mathrm {e}^{\vartheta \left( X(t)-x\right) -\psi (\vartheta )t}. \end{aligned}$$

Under the probability measure $\mathrm {P}_{x}^{\vartheta }$, X remains an SNL process with Laplace exponent $\psi _{\vartheta }$ and scale function $W_{\vartheta }^{(q)}$ as follows: for $\vartheta \ge 0$ and $q+\psi (\vartheta )\ge 0$

$$\begin{aligned} \psi _{\vartheta }(\theta )=\psi (\vartheta +\theta )-\psi (\vartheta )\,\,\,\text { and }\,\,\, W_{\vartheta }^{(q)}(x)=\mathrm {e}^{-\vartheta x}W^{(q+\psi (\vartheta ))}(x). \end{aligned}$$

(1)

In addition, denote by $W_{\vartheta }$ the 0-scale function for X under $\mathrm {P}_{x}^{\vartheta }$. For more detailed properties concerning the exponential change of measure, we are referred to Chapter 3 of [30].

Note that we do not impose the safety loading condition $\psi ^{\prime }(0+)\ge 0$. Instead, $\psi ^{\prime }(0+)\in (-\infty ,\infty )$ is assumed throughout the paper.

3 The $(z_{1},z_{2})$ Type Dividend and Capital Injection Strategy

For the Lévy process X, denote the reflected process at infimum (or at 0)

$$\begin{aligned} Y(t)=X(t)-\inf _{0\le s\le t}\left( X(s)\wedge 0\right) ,\quad t\ge 0. \end{aligned}$$

Define $T_{a}^{+}=\inf \{t\ge 0;Y(t)> a\}$ and $\tau _{a}^{+}=\inf \{t\ge 0;U(t)> a\}$, respectively, to be the up-crossing times of level $a\ge x$ of the processes Y and U, with the convention $\inf \emptyset =\infty$. Define further

$$\begin{aligned}&\overline{W}^{(q)}(x)=\int _{0}^{x}W^{(q)}(z)\mathrm {d}z,\,\, Z^{(q)}(x)\\&\quad =1+q \,\overline{W}^{(q)}(x),\,\,\overline{Z}^{(q)}(x)=\int _{0}^{x}Z^{(q)}(z)\mathrm {d}z. \end{aligned}$$

Then, for $x\in [0,b]$ and $q\ge 0$, Proposition 2 of [42] gives that

$$\begin{aligned} \mathrm {E}_x\left( \mathrm {e}^{-qT_{b}^{+}}\right) =Z^{(q)}(x)/Z^{(q)}(b). \end{aligned}$$

(2)

For $z_{1}<z_{2}$, let us consider an important type of IDCI strategy, that is the $(z_{1},z_{2})$ strategy $\{(D_{z_{1}}^{z_{2}}(t),R_{z_{1}}^{z_{2}}(t));t\ge 0\}$: a lump sum of dividend payment is made to bring the reserve level down to the level $z_{1}$ once the reserve hits or is above the level $z_{2}$, while no dividend payment is made whenever the reserve level is below $z_{2}$. Capital is injected in such a way that the reserve process is reflected at 0 , i.e., $R_{z_{1}}^{z_{2}}(t)=-\inf \limits _{0\le s\le t}\left( X(s)-D_{z_{1}}^{z_{2}}(s)\right) \wedge 0$. To be precise, we define recursively $T_{0}^{+}=0,\,\,T_{1}^{+}=T_{z_{2}}^{+}$ and

$$\begin{aligned} T^{+}_{n+1}= & {} \inf \bigg \{t> T^{+}_{n}; X(t)-(x\vee z_{2}-z_{1})-(n-1)(z_{2}-z_{1}) \nonumber \\&\quad -\inf \limits _{ s\le t}\bigg [X(s)-\sum _{k=1}^{n-1} \left( x\vee z_{2}-z_{1}+(k-1)(z_{2}-z_{1})\right) \mathbf {1}_{(T_{k}^{+},T_{k+1}^{+}]}(s) \nonumber \\&\quad -\left( x\vee z_{2}-z_{1}+(n-1)(z_{2}-z_{1})\right) \mathbf {1}_{(T_{n}^{+},\infty )}(s) \bigg ]\wedge 0>z_{2}\bigg \},\,\, n\ge 1.\nonumber \\ \end{aligned}$$

(3)

Then, the $(z_{1},z_{2})$ strategy can be re-expressed as

$$\begin{aligned} D_{z_{1}}^{z_{2}}(t)= & {} \sum _{n=1}^{\infty }\left( x\vee z_{2}-z_{1}+(n-1)(z_{2}-z_{1})\right) \mathbf {1}_{(T_{n}^{+},T_{n+1}^{+}]}(t) ,\quad t\ge 0, \end{aligned}$$

(4)

and

$$\begin{aligned} R_{z_{1}}^{z_{2}}(t)= & {} -\inf \limits _{ s\le t}\bigg (X(s)-\sum _{n=1}^{\infty } \left( x\vee z_{2}-z_{1}+(n-1)(z_{2}-z_{1})\right) \\&\quad \times \mathbf {1}_{(T_{n}^{+},T_{n+1}^{+}]}(s) \bigg )\wedge 0 ,\quad t\ge 0. \end{aligned}$$

In the following result, the value function of a $(z_{1},z_{2})$ strategy, denoted by $V_{z_{1}}^{z_{2}}$, is expressed in terms of the scale functions.

Proposition 3.1

Given $q>0$ and $c>0$, we have

$$\begin{aligned} V_{z_{1}}^{z_{2}}(x)= & {} Z^{(q)}(x)\left( \frac{z_{2}\!-\!z_{1}\!-\!c}{Z^{(q)}(z_{2})\!-\!Z^{(q)}(z_{1})} \!-\!\phi \frac{\overline{Z}^{(q)}(z_{2})\!-\!\overline{Z}^{(q)}(z_{1})}{Z^{(q)}(z_{2})\!-\!Z^{(q)}(z_{1})}\right) \nonumber \\&\quad +\phi \left( \overline{Z}^{(q)}(x)+\frac{\psi ^{\prime }(0+)}{q}\right) , \quad x\in [0,z_{2}],\,z_{1}+c\le z_{2}<\infty , \end{aligned}$$

(5)

and

$$\begin{aligned} V_{z_{1}}^{z_{2}}(x)= & {} x+\frac{Z^{(q)}(z_{2})\left( z_{2}-z_{1}-c\right) }{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})} -\phi \frac{\overline{Z}^{(q)}(z_{2})Z^{(q)}(z_{1})-\overline{Z}^{(q)}(z_{1})Z^{(q)}(z_{2})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})} \nonumber \\&\quad -z_{2}+\phi \frac{\psi ^{\prime }(0+)}{q} \nonumber \\= & {} x-z_{2}+V_{z_{1}}^{z_{2}}(z_{2}),\quad x\in (z_{2},\infty ),\,z_{1}+c\le z_{2}<\infty . \end{aligned}$$

(6)

Proof

Denote by f(x) the expected discounted total lump sum dividend payments minus the expected discounted total transaction costs for dividend payments, and we have

$$\begin{aligned} f(x)= x-z_{1}-c+f(z_{1}),\quad x\in (z_{2},\infty ), \end{aligned}$$

and

$$\begin{aligned} f(x)= \mathrm {E}_x\left( \mathrm {e}^{-q\tau _{z_{2}}^{+}}\right) f(z_{2}) =\frac{Z^{(q)}(x)}{Z^{(q)}(z_{2})}(z_{2}-z_{1}-c+f(z_{1})),\quad x\in [0, z_{2}], \end{aligned}$$

which yields $f(z_{1})=\frac{Z^{(q)}(z_{1})}{Z^{(q)}(z_{2})}(z_{2}-z_{1}-c+f(z_{1}))$, i.e.

$$\begin{aligned} f(z_{1})=\frac{Z^{(q)}(z_{1})\left( z_{2}-z_{1}-c\right) }{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}. \end{aligned}$$

Hence

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} \frac{Z^{(q)}(x)\left( z_{2}-z_{1}-c\right) }{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})},\quad &{} x\in [0,z_{2}],\\ x-z_{2}+\frac{Z^{(q)}(z_{2})\left( z_{2}-z_{1}-c\right) }{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})},\quad &{} x\in (z_{2},\infty ). \end{array}\right. \end{aligned}$$

(7)

Denote by g(x) the expected discounted total capital injections. By a similar argument to the one that derives an expression for (4.8) in [6] or by Theorem 3.3 of [51], one gets

$$\begin{aligned}&\mathrm {E}_x\left( \int _{0}^{\tau _{z_{2}}^{+}}\mathrm {e}^{-qt}\mathrm {d}R_{z_{1}}^{z_{2}}(t)\right) \nonumber \\&\quad =-\overline{Z}^{(q)}(x)-\frac{\psi ^{\prime }(0+)}{q}+\left( \overline{Z}^{(q)}(z_{2})+\frac{\psi ^{\prime }(0+)}{q}\right) \frac{Z^{(q)}(x)}{Z^{(q)}(z_{2})} ,\quad x\in [0,z_{2}]. \end{aligned}$$

(8)

Hence, by (8) one has for $x\in [0,z_{2}]$

$$\begin{aligned} g(x)= & {} \mathrm {E}_x\left( \int _{0}^{\tau _{z_{2}}^{+}}\mathrm {e}^{-qt}\mathrm {d}R_{z_{1}}^{z_{2}}(t)\right) +\mathrm {E}_x\left( \mathrm {e}^{-q\tau _{z_{2}}^{+}}\right) g(z_{1}) \\= & {} -\overline{Z}^{(q)}(x)-\frac{\psi ^{\prime }(0+)}{q}+\left( \overline{Z}^{(q)}(z_{2})+\frac{\psi ^{\prime }(0+)}{q}\right) \frac{Z^{(q)}(x)}{Z^{(q)}(z_{2})}+\frac{Z^{(q)}(x)}{Z^{(q)}(z_{2})}g(z_{1}), \end{aligned}$$

which gives

$$\begin{aligned} g(z_{1})=\frac{-\left( \overline{Z}^{(q)}(z_{1})+\frac{\psi ^{\prime }(0+)}{q}\right) Z^{(q)}(z_{2}) +\left( \overline{Z}^{(q)}(z_{2})+\frac{\psi ^{\prime }(0+)}{q}\right) Z^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}, \end{aligned}$$

and thus

$$\begin{aligned} g(x)= & {} \frac{Z^{(q)}(x)}{Z^{(q)}(z_{2})}\left( \overline{Z}^{(q)}(z_{2})\!-\! \frac{\overline{Z}^{(q)}(z_{1})Z^{(q)}(z_{2})\!-\!\overline{Z}^{(q)}(z_{2})Z^{(q)}(z_{1})}{Z^{(q)}(z_{2})\!-\!Z^{(q)}(z_{1})}\right) \nonumber \\&\quad \!-\overline{Z}^{(q)}(x)\!-\!\frac{\psi ^{\prime }(0+)}{q},\quad x\in [0,z_{2}]. \end{aligned}$$

(9)

For $x\in (z_{2},\infty )$, by (9) we have

$$\begin{aligned} g(x)=g(z_{1})=\frac{-\overline{Z}^{(q)}(z_{1})Z^{(q)}(z_{2})+\overline{Z}^{(q)}(z_{2})Z^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}-\frac{\psi ^{\prime }(0+)}{q}. \end{aligned}$$

(10)

Collecting $V_{z_{1}}^{z_{2}}(x)=f(x)-\phi g(x)$, (7), (9) and (10) yields (5) and (6) immediately. This completes the proof. $\square$

Define, for $0<c\le z_{1}+c< z_{2}<\infty$,

$$\begin{aligned} \xi (z_{1},z_{2}) =\frac{z_{2}-z_{1}-c}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}-\phi \frac{\overline{Z}^{(q)}(z_{2})-\overline{Z}^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}. \end{aligned}$$

(11)

Then, $V_{z_{1}}^{z_{2}}(x)=Z^{(q)}(x)\xi (z_{1},z_{2})+\phi \left( \overline{Z}^{(q)}(x)+\frac{\psi ^{\prime }(0+)}{q}\right) ,\,\, x\in [0,z_{2}]$. The set of maximizers of $\xi (z_{1},z_{2})$ is written as

$$\begin{aligned} \mathcal {M}:=\big \{(z_{1},z_{2});\, c\le z_{1}+c\le z_{2}, \inf \limits _{x\ge 0,\, x+c\le y}\left( \xi (z_{1},z_{2})-\xi (x,y)\right) \ge 0\big \}. \end{aligned}$$

(12)

Denote by

$$\begin{aligned} \hat{\tau }_{z_{2}}=\inf \{t\ge 0; \sup _{0\le s\le t}(X(s)\vee 0)-X(t)>z_{2}\} \end{aligned}$$

(13)

the first passage time of the Lévy process reflected at its supremum. The following result gives a useful link between the second partial derivative of $\xi$ (in $z_{2}$) and the Laplace transform of $\hat{\tau }_{z_{2}}$. Due to its log-concavity (see, Page 89 of [35]), the scale function $W^{(q)}$ is known to be differentiable over $(0,\infty )$ except for countably many points. In addition, $W^{(q)}$ has finite left- and right-derivatives at all $x\in (0,\infty )$ (see, Lemma 1 of [42]). Thence, in the sequel, for $x\in (0,\infty )$ where $W^{(q)}$ is not differentiable, $W^{(q)\prime }(x)$ shall be understood to be $W^{(q)\prime }_{+}(x)$, i.e., the right-derivative of $W^{(q)}$ at x.

Lemma 3.2

Let $\xi$ and $\hat{\tau }_{z_{2}}$ be defined respectively by (11) and (13). We have

$$\begin{aligned}&\frac{\partial }{\partial z_2}\left( \frac{[Z^{(q)}(z_{2})-Z^{(q)}(z_{1})]^{2}}{qW^{(q)}(z_{2})} \frac{\partial }{\partial z_{2}}\xi (z_{1},z_{2})\right) \nonumber \\&\quad =\frac{\left( Z^{(q)}(z_{2})-Z^{(q)}(z_{1})\right) W^{(q)\prime }(z_{2})}{[W^{(q)}(z_{2})]^{2}} \left( -\frac{1}{q}+\frac{\phi }{q}\mathrm {E}_{0}\left( \mathrm {e}^{-q\hat{\tau }_{z_{2}}}\right) \right) . \end{aligned}$$

(14)

Proof

It follows from Proposition 2 (ii) of [42] that

$$\begin{aligned}&\mathrm {E}_{0}\left( \mathrm {e}^{-q\hat{\tau }_{z_{2}}}\right) = Z^{(q)}(z_{2})- \frac{q[W^{(q)}(z_{2})]^{2}}{W^{(q)\prime }(z_{2})} . \end{aligned}$$

(15)

By algebraic manipulations one has

$$\begin{aligned}&\frac{\partial }{\partial z_2}\left[ \frac{\overline{Z}^{(q)}(z_{2}) -\overline{Z}^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}\right] \\&\quad =\frac{\frac{Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})} \left[ Z^{(q)}(z_{2})-Z^{(q)}(z_{1})\right] -\overline{Z}^{(q)}(z_{2})+\overline{Z}^{(q)}(z_{1})}{\left[ Z^{(q)}(z_{2})-Z^{(q)}(z_{1})\right] ^{2}\big /qW^{(q)}(z_{2})}, \end{aligned}$$

and

$$\begin{aligned}&\left[ \frac{Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})} \left[ Z^{(q)}(z_{2})-Z^{(q)}(z_{1})\right] -\overline{Z}^{(q)}(z_{2})+\overline{Z}^{(q)}(z_{1})\right] ^{\prime }_{z_{2}}\\&\quad =qW^{(q)}(z_{2})\frac{Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})} +[Z^{(q)}(z_{2})-Z^{(q)}(z_{1})]\frac{\partial }{\partial z_2} \left[ \frac{Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}\right] -Z^{(q)}(z_{2})\\&\quad =\left( Z^{(q)}(z_{2})-Z^{(q)}(z_{1})\right) \left( 1-\frac{Z^{(q)}(z_{2})W^{(q)\prime }(z_{2})}{q[W^{(q)}(z_{2})]^{2}}\right) \\&\quad =\left( Z^{(q)}(z_{2})-Z^{(q)}(z_{1})\right) \frac{W^{(q)\prime }(z_{2})}{[W^{(q)}(z_{2})]^{2}} \left( \frac{[W^{(q)}(z_{2})]^{2}}{W^{(q)\prime }(z_{2})}-\frac{Z^{(q)}(z_{2})}{q}\right) . \end{aligned}$$

One also has

$$\begin{aligned} \frac{\partial }{\partial z_2}\left[ \frac{z_{2}-z_{1}-c}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}\right] =\frac{\frac{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}{qW^{(q)}(z_{2})}-(z_{2}-z_{1}-c)}{\left[ Z^{(q)}(z_{2})-Z^{(q)}(z_{1})\right] ^{2}\big /qW^{(q)}(z_{2})}, \end{aligned}$$

and

$$\begin{aligned}&\frac{\partial }{\partial z_2}\left[ \frac{ Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}{qW^{(q)}(z_{2})}-z_{2}+z_{1}+c\right] \\&\quad =\frac{\left[ Z^{(q)}(z_{2})-Z^{(q)}(z_{1})\right] W^{(q)\prime }(z_{2})}{-q[W^{(q)}(z_{2})]^{2}}. \end{aligned}$$

Combining the above facts, we obtain

$$\begin{aligned}&\frac{\partial }{\partial z_{2}}\xi (z_{1},z_{2}) = \frac{1}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}-\frac{Z^{(q)\prime }(z_{2})(z_{2}-z_{1}-c)}{[Z^{(q)}(z_{2})-Z^{(q)}(z_{1})]^{2}} \nonumber \\&\quad -\phi \frac{Z^{(q)}(z_{2})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})} +\phi \frac{Z^{(q)\prime }(z_{2})[\overline{Z}^{(q)}(z_{2})-\overline{Z}^{(q)}(z_{1})]}{[Z^{(q)}(z_{2})-Z^{(q)}(z_{1})]^{2}}, \end{aligned}$$

(16)

which together with (15) yields (14). $\square$

The following result characterizes the optimal IDCI strategy among all $(z_{1},z_{2})$ strategies.

Proposition 3.3

The set $\mathcal {M}$ is nonempty, i.e. $\mathcal {M}\ne \emptyset$. For $(z_{1},z_{2})\in \mathcal {M}$, we have

$$\begin{aligned} \frac{z_{2}-z_{1}-c}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}-\phi \frac{\overline{Z}^{(q)}(z_{2})-\overline{Z}^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})} =\frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}. \end{aligned}$$

(17)

Proof

By the definition of $\hat{\tau }_{z_{2}}$ one knows that it is increasing with respect to $z_{2}$ and $\lim \limits _{z_{2}\rightarrow \infty }\hat{\tau }_{z_{2}}=\infty$, implying $\lim \limits _{z_{2}\rightarrow \infty }\mathrm {E}_{0}\left( \mathrm {e}^{-q\hat{\tau }_{z_{2}}}\right) =0$. Hence there exists $\bar{z}_{0}\in [0,\infty )$ such that

$$\begin{aligned} -\frac{1}{q}+\frac{\phi }{q}\mathrm {E}_{0}\left( \mathrm {e}^{-q\hat{\tau }_{z_{2}}}\right) \le -\frac{1}{2q}, \quad z_{2}\in [\bar{z}_{0},\infty ). \end{aligned}$$

(18)

On the other hand, by (1) one can verify that

$$\begin{aligned} \frac{W^{(q)}(z)}{W^{(q)\prime }(z)}=\frac{\mathrm {e}^{\Phi _{q}z}W_{\Phi _{q}}(z)}{[\mathrm {e}^{\Phi _{q}z}W_{\Phi _{q}}(z)]^{\prime }} =\frac{1}{\Phi _{q}+\frac{W_{\Phi _{q}}^{\prime }(z)}{W_{\Phi _{q}}(z)}}\longrightarrow \frac{1}{\Phi _{q}}, \end{aligned}$$

where the fact that $\lim \limits _{z\rightarrow \infty }\frac{W_{\Phi _{q}}^{\prime }(z)}{W_{\Phi _{q}}(z)}=0$ (see the last paragraph of the proof of Lemma 2 in [43]) is used. Hence, by the rule of L’Hôpital, we have

$$\begin{aligned}&\lim _{z_{2}\rightarrow \infty }\frac{[Z^{(q)}(z_{2})-Z^{(q)}(z_{1})]W^{(q)\prime }(z_{2})}{[W^{(q)}(z_{2})]^{2}} \\&\quad =\lim _{z_{2}\rightarrow \infty }\frac{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}{W^{(q)}(z_{2})} \lim _{z_{2}\rightarrow \infty }\frac{W^{(q)\prime }(z_{2})}{W^{(q)}(z_{2})}\\&\quad =\lim _{z_{2}\rightarrow \infty }\frac{qW^{(q)}(z_{2})}{W^{(q)\prime }(z_{2})} \lim _{z_{2}\rightarrow \infty }\frac{W^{(q)\prime }(z_{2})}{W^{(q)}(z_{2})}=q. \end{aligned}$$

So, there exists $\bar{\bar{z}}_{0}\in [0,\infty )$ such that

$$\begin{aligned} \frac{[Z^{(q)}(z_{2})-Z^{(q)}(z_{1})]W^{(q)\prime }(z_{2})}{[W^{(q)}(z_{2})]^{2}}\ge \frac{q }{2},\quad z_{2}\in [\bar{\bar{z}}_{0},\infty ), \end{aligned}$$

which combined with (14) and (18) yields

$$\begin{aligned} \frac{\partial }{\partial z_2}\left( \frac{[Z^{(q)}(z_{2})-Z^{(q)}(z_{1})]^{2}}{qW^{(q)}(z_{2})} \frac{\partial }{\partial z_{2}}\xi (z_{1},z_{2})\right) \le -\frac{1}{4}, \quad z_{2}\in [\bar{z}_{0}\vee \bar{\bar{z}}_{0},\infty ), \end{aligned}$$

where $\xi$ is defined in (11). Owing to (16), it holds that

$$\begin{aligned} \frac{[Z^{(q)}(\bar{z}_{0}\vee \bar{\bar{z}}_{0})-Z^{(q)}(z_{1})]^{2}}{qW^{(q)}(\bar{z}_{0}\vee \bar{\bar{z}}_{0})} \frac{\partial }{\partial z_{2}}\xi (z_{1},\bar{z}_{0}\vee \bar{\bar{z}}_{0})<\infty . \end{aligned}$$

Thus, there exists $z_{0}\in (\bar{z}_{0}\vee \bar{\bar{z}}_{0},\infty )$ such that

$$\begin{aligned} \frac{[Z^{(q)}(z_{2})-Z^{(q)}(z_{1})]^{2}}{qW^{(q)}(z_{2})}\frac{\partial }{\partial z_{2}}\xi (z_{1},z_{2})<0,\quad z_{2}\in [z_{0},\infty ), \end{aligned}$$

which yields $\frac{\partial }{\partial z_{2}}\xi (z_{1},z_{2})<0$ for $z_{2}\in [z_{0},\infty )$. As a result,

$$\begin{aligned} \sup \limits _{0\le z_{1},z_{2}<\infty ,z_{1}+c\le z_{2}}\xi (z_{1},z_{2}) =\sup \limits _{0\le z_{1},z_{2}\le z_{0},z_{1}+c\le z_{2}}\xi (z_{1},z_{2}), \end{aligned}$$

(19)

which, plus the continuity of $\xi$ over $\{(z_{1},z_{2});z_{1},z_{2}\in [0, z_{0}],z_{1}+c\le z_{2}\}$, yields

$$\begin{aligned} \emptyset \ne \mathcal {M}\subseteq \{(z_{1},z_{2});z_{1},z_{2}\in [0, z_{0}],z_{1}+c\le z_{2}\}. \end{aligned}$$

For IDCI strategies $(z_{1}, z_{2})$ and $(z_{1}^{\prime }, z_{2}^{\prime })$ with $z_{2}-z_{1}=z_{2}^{\prime }-z_{1}^{\prime }=c$ and $z_{2}^{\prime }>z_{2}$, let $T_{n}^{+\prime }$ be defined via (3) with $z_{i}$ replaced by $z_{i}^{\prime }$ (i=1,2). Then, by (3), (4) and the technique of mathematical induction, we have, for $x\in [0,z_{2}]$,

$$\begin{aligned} T_{n}^{+\prime }> T_{n}^{+},\quad n\ge 1, \end{aligned}$$

and hence $D_{z_{1}^{\prime }}^{z_{2}^{\prime }}(t)\le D_{z_{1}}^{z_{2}}(t)$ for $t\ge 0$, which implies, for $t\ge 0$,

$$\begin{aligned} R_{z_{1}^{\prime }}^{z_{2}^{\prime }}(t)= -\inf \limits _{0\le s\le t}[X(s)-D_{z_{1}^{\prime }}^{z_{2}^{\prime }}(s)]\wedge 0 \le -\inf \limits _{0\le s\le t}[X(s)-D_{z_{1}}^{z_{2}}(s)]\wedge 0 =R_{z_{1}}^{z_{2}}(t) . \end{aligned}$$

Therefore, we have

$$\begin{aligned} \mathrm {E}_x\left( \int _{0}^{\infty }\mathrm {e}^{-qs}\mathrm {d}R_{z_{1}}^{z_{2}}(s)\right) \ge \mathrm {E}_x\left( \int _{0}^{\infty }\mathrm {e}^{-qs}\mathrm {d}R_{z_{1}^{\prime }}^{z_{2}^{\prime }}(s)\right) ,\,\, x\in [0,z_{2}]=[0,z_{2}]\cap [0,z_{2}^{\prime }], \end{aligned}$$

which, combined with (9) yields, for $z_{2}-z_{1}=z_{2}^{\prime }-z_{1}^{\prime }=c,\,z_{2}^{\prime }>z_{2}$,

$$\begin{aligned}&\frac{Z^{(q)}(x)}{Z^{(q)}(z_{2})}\Bigg [\overline{Z}^{(q)}(z_{2})- \frac{\overline{Z}^{(q)}(z_{1})Z^{(q)}(z_{2})- \overline{Z}^{(q)}(z_{2})Z^{(q)}(z_{1})}{Z^{(q)}(z_{2})- Z^{(q)}(z_{1})}\Bigg ]\!-\overline{Z}^{(q)}(x)-\frac{\psi ^{\prime }(0+)}{q} \\&\quad \ge \frac{Z^{(q)}(x)}{Z^{(q)}(z_{2}^{\prime })}\Bigg [\overline{Z}^{(q)}(z_{2}^{\prime })- \frac{\overline{Z}^{(q)}(z_{1}^{\prime })Z^{(q)}(z_{2}^{\prime }) - \overline{Z}^{(q)}(z_{2}^{\prime })Z^{(q)}(z_{1}^{\prime })}{Z^{(q)}(z_{2}^{\prime }) - Z^{(q)}(z_{1}^{\prime })}\Bigg ] -\overline{Z}^{(q)}(x) \\&\quad \quad -\frac{\psi ^{\prime }(0+)}{q}, \end{aligned}$$

which boils down to

$$\begin{aligned} \frac{\overline{Z}^{(q)}(z_{2})-\overline{Z}^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}\ge \frac{\overline{Z}^{(q)}(z_{2}^{\prime })-\overline{Z}^{(q)}(z_{1}^{\prime })}{Z^{(q)}(z_{2}^{\prime })-Z^{(q)}(z_{1}^{\prime })}. \end{aligned}$$

(20)

By (20) and the definition of $\xi$ in (11), we may rule out the possibility that $\xi$ attains its maximum value in the line $z_{2}=z_{1}+c$. Indeed, if $(z_{1},z_{2})$ is a maximum point of $\xi$ with $z_{2}=z_{1}+c$, then by (20) we should have $z_{2}=z_{1}=\infty$, contradicting (19).

Now, we have proved that $\emptyset \ne \mathcal {M}\subseteq \{(z_{1},z_{2});z_{1},z_{2}\in [0, z_{0}],z_{1}+c< z_{2}\}$. Thus, if $(z_{1},z_{2})$ is a maximizer of $\xi (z_{1},z_{2})$, then it holds that $\frac{\partial }{\partial z_{2}}\xi (z_{1},z_{2})=0$, i.e., (17) holds true. $\square$

For an IDCI strategy $(z_{1},z_{2})\in \mathcal {M}$, the following result, an immediate consequence of (5), (6), and (17), presents an alternative expression for the value function $V_{z_{1}}^{z_{2}}$. It is interesting to see that this expression is independent of $z_{1}$, which is not the case for arbitrary IDCI strategy $(z_{1},z_{2})$ (see (5) and (6)).

Proposition 3.4

For $(z_{1},z_{2})\in \mathcal {M}$, the value function of the $(z_{1},z_{2})$ IDCI strategy is

$$\begin{aligned} \,\,V_{z_{1}}^{z_{2}}(x)=\left\{ \begin{array}{ll} \phi \left[ \overline{Z}^{(q)}(x)+\frac{\psi ^{\prime }(0+)}{q}\right] + Z^{(q)}(x)\frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})},&{} x\in [0,z_{2}),\\ x-z_{2}+\phi \left[ \overline{Z}^{(q)}(z_{2})+\frac{\psi ^{\prime }(0+)}{q}\right] + Z^{(q)}(z_{2})\frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})},&{} x\in [z_{2},\infty ). \end{array}\right. \end{aligned}$$

Remark 3.5

Given $(z_{1},z_{2})\in \mathcal {M}$, one can verify that

$$\begin{aligned}{}[V_{z_{1}}^{z_{2}}(x)]^{\prime }=\left\{ \begin{array}{ll} \phi Z^{(q)}(x)+W^{(q)}(x)\frac{1-\phi Z^{(q)}(z_{2})}{W^{(q)}(z_{2})}, &{}x\in [0,z_{2}),\\ 1,&{}x\in (z_{2},\infty ), \end{array}\right. \end{aligned}$$

is continuous over $[0,\infty )$. By (15) we see that

$$\begin{aligned}&\phi Z^{(q)}(x)+W^{(q)}(x)\frac{1-\phi Z^{(q)}(z_{2})}{W^{(q)}(z_{2})} \\&\quad = W^{(q)}(x)\bigg [\frac{\phi Z^{(q)}(x) }{W^{(q)}(x)}-\frac{\phi Z^{(q)}(z_{2})}{W^{(q)}(z_{2})}\bigg ]+\frac{W^{(q)}(x)}{W^{(q)}(z_{2})} \\&\quad = \phi W^{(q)}(x) \int _{z_{2}}^{x}\frac{ q\left[ W^{(q)}(w)\right] ^{2}-W^{(q)\prime }(w)Z^{(q)}(w) }{\left[ W^{(q)}(w)\right] ^{2}} \mathrm {d}w+\frac{W^{(q)}(x)}{W^{(q)}(z_{2})} \\&\quad > \frac{W^{(q)}(x)}{W^{(q)}(z_{2})}, \quad x\in [0,z_{2}), \end{aligned}$$

which together with the above expression for $[V_{z_{1}}^{z_{2}}]^{\prime }$ implies that the function $V_{z_{1}}^{z_{2}}$ is strictly increasing over the non-negative real line. Furthermore, when the scale function is differentiable, one can also verify that

$$\begin{aligned} {[}V_{z_{1}}^{z_{2}}(x)]^{\prime \prime }=\left\{ \begin{array}{ll} q\phi W^{(q)}(x)+W^{(q)\prime }(x)\frac{1-\phi Z^{(q)}(z_{2})}{W^{(q)}(z_{2})}, &{}x\in [0,z_{2}),\\ 0, &{}x\in (z_{2},\infty ), \end{array}\right. \end{aligned}$$

is continuous on $[0,z_{2})$ and $(z_{2},\infty )$. However, $[V_{z_{1}}^{z_{2}}(x)]^{\prime \prime }$ is not evidently continuous at $z_{2}$. In fact, twice differentiability at $z_{2}$ is not guaranteed even if continuous differentiability is imposed on $W^{(q)}$. Furthermore, if the scale function is only assumed to be piece-wise continuously differentiable over all compact subsets of $[0,\infty )$ (as in Lemma 4.3, 4.4 and Theorem 4.8 ), then $[V_{z_{1}}^{z_{2}}(x)]^{\prime \prime }$ is well-defined and continuous over $[0,\infty )$ except for finitely many points of the compact set $[0,z_{2}]$. $\square$

The following result characterizes several desirable properties of $V_{z_{1}}^{z_{2}}$ for $(z_{1},z_{2})\in \mathcal {M}$.

Proposition 3.6

Given $(z_{1},z_{2})\in \mathcal {M}$, $V_{z_{1}}^{z_{2}}$ is continuously differentiable and $[V_{z_{1}}^{z_{2}}]^{\prime }(x)\le \phi$ over $[0,\infty )$, and

$$\begin{aligned} V_{z_{1}}^{z_{2}}(x)-V_{z_{1}}^{z_{2}}(y)\ge x-y-c,\quad 0\le y< y+c\le x. \end{aligned}$$

Proof

By the expression of $V_{z_{1}}^{z_{2}}$ given by Proposition 3.4, that $V_{z_{1}}^{z_{2}}$ is continuously differentiable over $[0,\infty )$ is trivial. A straightforward calculation shows that

$$\begin{aligned} \phi Z^{(q)}(z_{2})+W^{(q)}(z_{2})\frac{1-\phi Z^{(q)}(z_{2})}{W^{(q)}(z_{2})}=1<\phi . \end{aligned}$$

By $W^{(q)}(0)\ge 0$, $W^{(q)}(z_{2})>0$, and $1-\phi Z^{(q)}(z_{2})< 0$, one can verify

$$\begin{aligned} \phi Z^{(q)}(0)+W^{(q)}(0)\frac{1-\phi Z^{(q)}(z_{2})}{W^{(q)}(z_{2})} =\phi +W^{(q)}(0)\frac{1-\phi Z^{(q)}(z_{2})}{W^{(q)}(z_{2})}\le \phi . \end{aligned}$$

By Lemma 1 of [6] one has $W^{(q)}(x)\overline{W}^{(q)}(z_{2})\ge W^{(q)}(z_{2})\overline{W}^{(q)}(x)$ for $x\in [0,z_{2}]$, which, combined with $\phi >1$ and $W^{(q)}(x)>0$ for $x\in (0,z_{2})$, yields

$$\begin{aligned}&\phi -\left( \phi Z^{(q)}(x)+W^{(q)}(x)\frac{1-\phi Z^{(q)}(z_{2})}{W^{(q)}(z_{2})}\right) \\&\quad =-q\phi \overline{W}^{(q)}(x)-W^{(q)}(x)\frac{1-\phi -q\phi \overline{W}^{(q)}(z_{2})}{W^{(q)}(z_{2})}\\&\quad =\frac{1}{W^{(q)}(z_{2})}\left( q\phi \left( W^{(q)}(x)\overline{W}^{(q)}(z_{2})- W^{(q)}(z_{2})\overline{W}^{(q)}(x)\right) +W^{(q)}(x)(\phi -1)\right) \\&\quad >0,\quad x\in (0,z_{2}). \end{aligned}$$

In combination with these arguments, we reach $[V_{z_{1}}^{z_{2}}]^{\prime }(x)\le \phi$ for $x\in [0,z_{2}]$.

By (11), $(z_{1},z_{2})\in \mathcal {M}$, (12), and (17), we have

$$\begin{aligned}&\frac{x-y-c}{Z^{(q)}(x)-Z^{(q)}(y)}-\phi \frac{\overline{Z}^{(q)}(x)-\overline{Z}^{(q)}(y)}{Z^{(q)}(x)-Z^{(q)}(y)}\nonumber \\&\quad \le \frac{z_{2}-z_{1}-c}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}-\phi \frac{\overline{Z}^{(q)}(z_{2})-\overline{Z}^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}\nonumber \\&\quad =\frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})},\quad 0\le y,y+c\le x<\infty , \end{aligned}$$

(21)

from which one can get

$$\begin{aligned}&V_{z_{1}}^{z_{2}}(x)-V_{z_{1}}^{z_{2}}(y)\\&\quad =\phi \left( \overline{Z}^{(q)}(x)-\overline{Z}^{(q)}(y)\right) + \left( Z^{(q)}(x)-Z^{(q)}(y)\right) \frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}\\&\quad = \left( Z^{(q)}(x)-Z^{(q)}(y)\right) \left( \frac{z_{2}-z_{1}-c}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})} -\phi \frac{\overline{Z}^{(q)}(z_{2})-\overline{Z}^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})}\right) \\&\qquad +\phi \left( \overline{Z}^{(q)}(x)-\overline{Z}^{(q)}(y)\right) \\&\quad \ge \left( Z^{(q)}(x)-Z^{(q)}(y)\right) \left( \frac{x-y-c}{Z^{(q)}(x)-Z^{(q)}(y)} -\phi \frac{\overline{Z}^{(q)}(x)-\overline{Z}^{(q)}(y)}{Z^{(q)}(x)-Z^{(q)}(y)}\right) \\&\qquad +\phi \left( \overline{Z}^{(q)}(x)-\overline{Z}^{(q)}(y)\right) \\&\quad =x-y-c, \quad 0\le y\le x\le z_{2},\,y+c\le x. \end{aligned}$$

By Proposition 3.4, using (21) once again one can get

$$\begin{aligned} V_{z_{1}}^{z_{2}}(x)-V_{z_{1}}^{z_{2}}(y)= & {} x-z_{2}+\phi \left( \overline{Z}^{(q)}(z_{2})+\frac{\psi ^{\prime }(0+)}{q}\right) + Z^{(q)}(z_{2})\frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}\\&\quad -\phi \left( \overline{Z}^{(q)}(y)+\frac{\psi ^{\prime }(0+)}{q}\right) -Z^{(q)}(y)\frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}\\\ge & {} x-z_{2}+z_{2}-y-c, \quad x\ge z_{2}\ge y,\, y+c\le x. \end{aligned}$$

For $x\ge y\ge z_{2}$ with $y+c\le x$, by Proposition 3.4 one has $V_{z_{1}}^{z_{2}}(x)-V_{z_{1}}^{z_{2}}(y)=x-y> x-y-c$. The proof is completed. $\square$

4 Characterization of the Optimal IDCI Strategy

This section is devoted to verifying that an IDCI strategy $(z_{1},z_{2})\in \mathcal {M}$ serves as the optimal IDCI strategy dominating all other admissible IDCI strategies.

In the following Proposition 4.1, we first present a result characterizing the optimal value function V, which is helpful in motivating the HJB inequalities (i.e., (32)) in the verification Lemma 4.3 and 4.4.

Proposition 4.1

The function V(x) is continuous over $[0,\infty )$, and $V(y)-V(x)\ge y-x-c$ for $y\ge x\ge 0$. In addition, if V is differentiable over $[0,\infty )$, then $V^{\prime }(x)\le \phi$.

Proof

By definition, any admissible IDCI strategy associated with the initial reserve $x\ge 0$ also serves as an admissible IDCI strategy associated with the initial reserve $y\ge x$. Then it follows that V is non-decreasing.

For any $\varepsilon >0$ and $y\ge x\ge 0$, denote $(D_{x}^{\varepsilon },R_{x}^{\varepsilon })$ an admissible IDCI strategy associated with the initial reserve x such that $V_{(D_{x}^{\varepsilon },R_{x}^{\varepsilon })}(x)> V(x)-\varepsilon$. Without loss of generality, $D_{x}^{\varepsilon }$ is expressed as

$$\begin{aligned} \left( \tau _n^{D_{x}^{\varepsilon }},\eta _{n}^{D_{x}^{\varepsilon }}\right) ,\quad n=1,2,\cdots , \end{aligned}$$

where $\tau _{n}^{D_{x}^{\varepsilon }}$ and $\eta _{n}^{D_{x}^{\varepsilon }}$ are respectively the time and amount of dividend payouts, and $\tau _{1}^{D_{x}^{\varepsilon }}>0$ a.s.. Define a new admissible strategy $(D_{y}^{\varepsilon },R_{y}^{\varepsilon })$ associated with the initial reserve y such that $R_{y}^{\varepsilon }=R_{x}^{\varepsilon }$ and $D_{y}^{\varepsilon }$ are characterized as

$$\begin{aligned} \left( 0,\tau _{1}^{D_{x}^{\varepsilon }},\tau _{2}^{D_{x}^{\varepsilon }},\cdots ,\tau _{n}^{D_{x}^{\varepsilon }},\cdots ;\,y- x,\eta _{1}^{D_{x}^{\varepsilon }},\eta _{2}^{D_{x}^{\varepsilon }},\cdots ,\eta _{n}^{D_{x}^{\varepsilon }},\cdots \right) . \end{aligned}$$

According to $(D_{y}^{\varepsilon },R_{y}^{\varepsilon })$, we have

$$\begin{aligned} V(y)\ge V_{(D_{y}^{\varepsilon },R_{y}^{\varepsilon })}(y) =y-x-c+V_{(D_{x}^{\varepsilon },R_{x}^{\varepsilon })}(x)>y-x-c+V(x)-\varepsilon , \end{aligned}$$

which yields $V(y)-V(x)\ge y-x-c$ after setting $\varepsilon \downarrow 0$.

The inequality $V^{\prime }(x)\le \phi$ over $[0,\infty )$ can be proved if we have

$$\begin{aligned} V(x)-V(y)\le \phi (x-y),\quad 0\le y\le x<\infty , \end{aligned}$$

(22)

which, can be accomplished by considering an IDCI strategy that injects a capital of amount $x-y$ at time 0 to the reserve process starting from y.

Additionally, the continuity of V follows from (22) and the non-decreasing property of V. $\square$

Put $\Delta D(t)=D(t+)-D(t)$, $\Delta X(t)=X(t)-X(t-)$, and $\Delta R(t)=R(t)-R(t-)$. Define

$$\begin{aligned} \mathcal {D}_{1}= & {} \{(D,R)\in \mathcal {D}; \,\Delta D(t)>0 \mathrm {\, \,\,iff\,\,\,} c<\Delta D(t)\le U(t-)+\Delta X(t), \\&\quad \,\,\,\,\mathrm { and\,\,} R(t)=-\inf \limits _{0\le s\le t}\left( X(s)-D(s)\right) \wedge 0,\,\,t\ge 0\}, \end{aligned}$$

which is a proper subset of $\mathcal {D}$. Intuitively, the condition

$$\begin{aligned} c<\Delta D(t)\le U(t-)+\Delta X(t), \end{aligned}$$

requires that the lump sum dividend paid at time t is strictly greater than c and is no more than the available reserve after covering the down-ward jump of X at time t, i.e., $U(t-)+\Delta X(t)$. For $(D,R)\in \mathcal {D}_{1}$, it is seen that $\Delta R(t)=0$ whenever $\Delta D(t)>0$.

The following result tells us that we can confine ourselves within $\mathcal {D}_{1}$ when searching for the optimal IDCI strategy among $\mathcal {D}$. This finding is used in the proof of the verification Lemma 4.4.

Lemma 4.2

For any $(D,R)\in \mathcal {D}\setminus \mathcal {D}_{1}$, there exists one IDCI strategy $(\overline{D},\overline{R})\in \mathcal {D}_{1}$ that dominates (D, R), i.e., $V_{(D,R)}(x)< V_{(\overline{D},\overline{R})}(x)$ for all $x\in [0,\infty )$.

Proof

Given an admissible IDCI strategy $(D,R)\in \mathcal {D}\setminus \mathcal {D}_{1}$, denote by $\overline{D}(t)$ the pure jump dividend process whose jumps coincide in time and amount with those of D(t) with jump sizes strictly greater that c but less than the reserve available at the jump times (a lump sum dividend doesn’t lead to a deficit), and denote by $\overline{R}(t)$ the minimum non-decreasing capital injection process such that $X(t)-\overline{D}(t)+\overline{R}(t)\ge 0$ for $t\ge 0$, i.e.

$$\begin{aligned} \overline{D}(t)= & {} \sum _{s\in [0,t)}(\Delta D(s)\wedge (U(s-)+\Delta X(s))) \mathbf {1}_{\{\Delta D(s)\wedge (U(s-)+\Delta X(s))\ge c\}}, \nonumber \\ \overline{R}(t)= & {} -\inf \limits _{0\le s\le t}\left( X(s)-\overline{D}(s)\right) \wedge 0. \end{aligned}$$

(23)

By the definition of $\mathcal {D}_{1}$, one can claim that $(\overline{D},\overline{R})\in \mathcal {D}_{1}$ and

$$\begin{aligned} -\inf \limits _{0\le s\le t}\left( X(s)-D(s)\right) \wedge 0=\overline{R}(t)+D(t+)-\overline{D}(t+),\quad t\ge 0. \end{aligned}$$

(24)

Indeed, by the definition of $\overline{R}$ (i.e., $X(t)-\overline{D}(t)+\overline{R}(t)\ge 0$ for all $t\ge 0$), we have

$$\begin{aligned} \left( X(t)-D(t)\right) +\left( \overline{R}(t)+D(t)-\overline{D}(t)\right) \ge 0,\quad t\ge 0 \end{aligned}$$

which together with the fact that the non-decreasing capital injection process $-\inf \limits _{0\le s\le t}\left( X(s)-D(s)\right) \wedge 0$ is the minimum non-decreasing process such that

$$\begin{aligned} \left( X(t)-D(t)\right) +\left( -\inf \limits _{0\le s\le t}\left( X(s)-D(s)\right) \wedge 0\right) \ge 0,\quad t\ge 0, \end{aligned}$$

(25)

yields that

$$\begin{aligned} \overline{R}(t)+D(t)-\overline{D}(t)\ge -\inf \limits _{0\le s\le t}\left( X(s)-D(s)\right) \wedge 0,\quad t\ge 0. \end{aligned}$$

(26)

At the same time, one may note that (25) is equivalent to

$$\begin{aligned}&[X(t)-\overline{D}(t)]+\big [\overline{R}(t)-\big (\overline{R}(t)+D(t)-\overline{D}(t)+\inf \limits _{ s\le t}\big (X(s)-D(s)\big )\wedge 0\big )\big ] \ge 0, \end{aligned}$$

which together with the fact that the process $\overline{R}(t)$ is the minimum non-decreasing process such that $\left[ X(t)-\overline{D}(t)\right] +\overline{R}(t)\ge 0$ for all $t\ge 0$, implies that

$$\begin{aligned}&\overline{R}(t)-\left( \overline{R}(t)+D(t)-\overline{D}(t)+\inf \limits _{0\le s\le t}\left( X(s)-D(s)\right) \wedge 0\right) \ge \overline{R}(t), \quad t\ge 0, \end{aligned}$$

which combined with (26) and a choice of càdlàg version gives (24). Keeping only those lump sum dividends in D that satisfies $\Delta D(s)\ge c$, and then using the definition of $\overline{D}$ in (23), one can deduce

$$\begin{aligned}&D(t+)-\overline{D}(t+) \nonumber \\\ge & {} \sum _{s\in [0,t]}\Delta D(s)\Big [\mathbf {1}_{\{\Delta D(s)\wedge \left( U(s-)+\Delta X(s)\right) \ge c\}} +\mathbf {1}_{\{\Delta D(s)\ge c\ge U(s-)+\Delta X(s)\}}\Big ] \nonumber \\&-\sum _{s\in [0,t]}(\Delta D(s)\wedge (U(s-)+\Delta X(s))) \mathbf {1}_{\{\Delta D(s)\wedge (U(s-)+\Delta X(s))\ge c\}} \nonumber \\\ge & {} \sum _{s\in [0,t]}\left( \Delta D(s)-(U(s-)+\Delta X(s))\right) \mathbf {1}_{\{\Delta D(s)>U(s-)+\Delta X(s)\ge c\}} \nonumber \\&+\sum _{s\in [0,t]}\Delta D(s) \mathbf {1}_{\{\Delta D(s)\ge c\ge U(s-)+\Delta X(s)\}} \nonumber \\\ge & {} \sum _{s\in [0,t]}\left( \Delta D(s)-(U(s-)+\Delta X(s))\right) \mathbf {1}_{\{\Delta D(s)>U(s-)+\Delta X(s)\ge c\}} \nonumber \\&+\sum _{s\in [0,t]}\left( \Delta D(s)-\left( U(s-)+\Delta X(s)\right) \vee 0\right) \mathbf {1}_{\{\Delta D(s)\ge c\ge U(s-)+\Delta X(s)\}}, \end{aligned}$$

(27)

which combined with (24) and the minimum property of the non-decreasing process $-\inf \limits _{0\le s\le t}\left( X(s)-D(s)\right) \wedge 0$ yields

$$\begin{aligned}&\overline{R}(t) + \sum _{s\in [0,t]}\left( \Delta D(s)-(U(s-)+\Delta X(s))\right) \mathbf {1}_{\{\Delta D(s)>U(s-)+\Delta X(s)\ge c\}} \nonumber \\&\quad +\sum _{s\in [0,t]}\left( \Delta D(s)-\left( U(s-)+\Delta X(s)\right) \vee 0\right) \mathbf {1}_{\{\Delta D(s)\ge c\ge U(s-)+\Delta X(s)\}} \nonumber \\&\quad \le \overline{R}(t)+D(t+)-\overline{D}(t+) =-\inf _{0\le s\le t}\left( X(s)-D(s)\right) \wedge 0\le R(t). \end{aligned}$$

(28)

By the definitions of $V_{(D,R)}(x)$ and $V_{(\overline{D},\overline{R})}(x)$, we get

$$\begin{aligned} V_{(D,R)}(x)= & {} \sum _{t\ge 0} \mathrm {e}^{-qt} \left( \Delta D(t)-c\right) \Big [\mathbf {1}_{\{\Delta D(t)\wedge \left( U(t-)+\Delta X(t)\right) \ge c\}} \\&+\mathbf {1}_{\{\Delta D(t)\ge c\ge U(t-)+\Delta X(t)\}}+\mathbf {1}_{\{\Delta D(t)< c\}}\Big ] -\phi \int _{0}^{\infty }\mathrm {e}^{-qt}\mathrm {d}R(t), \end{aligned}$$

and

$$\begin{aligned} V_{(\overline{D},\overline{R})}(x)= & {} \sum _{t\ge 0} \mathrm {e}^{-qt} \left( \Delta D(t)\wedge \left( U(t-)+\Delta X(t)\right) -c\right) \\&\quad \times \mathbf {1}_{\{\Delta D(t)\wedge \left( U(t-)+\Delta X(t)\right) \ge c\}} -\phi \int _{0}^{\infty }\mathrm {e}^{-qt}\mathrm {d}\overline{R}(t), \end{aligned}$$

hence, by (28) we have

$$\begin{aligned}&V_{(D,R)}(x)-V_{(\overline{D},\overline{R})}(x) \\&\quad = \sum _{t\ge 0} \mathrm {e}^{-qt} \Big [\Delta D(t)-\Delta D(t)\wedge \left( U(t-)+\Delta X(t)\right) \Big ] \mathbf {1}_{\{\Delta D(t)\wedge \left( U(t-)+\Delta X(t)\right) \ge c\}} \\&\qquad +\sum _{t\ge 0} \mathrm {e}^{-qt} \left( \Delta D(t)-c\right) \mathbf {1}_{\{\Delta D(t)\ge c\ge U(t-)+\Delta X(t)\}} \\&\qquad +\sum _{t\ge 0} \mathrm {e}^{-qt} \left( \Delta D(t)-c\right) \mathbf {1}_{\{\Delta D(t)<c\}}-\phi \int _{0}^{\infty }\mathrm {e}^{-qt}\mathrm {d}\left( R(t)-\overline{R}(t)\right) \\&\quad \le \sum _{t\ge 0} \mathrm {e}^{-qt} \Big [\Delta D(t)-\left( U(t-)+\Delta X(t)\right) \Big ] \mathbf {1}_{\{\Delta D(t)>U(t-)+\Delta X(t)\ge c\}} \\&\qquad +\sum _{t\ge 0} \mathrm {e}^{-qt} \left( \Delta D(t)-c\right) \mathbf {1}_{\{\Delta D(t)\ge c\ge U(t-)+\Delta X(t)\}} \\&\quad +\sum _{t\ge 0} \mathrm {e}^{-qt} \left( \Delta D(t)-c\right) \mathbf {1}_{\{\Delta D(t)<c\}} \\&\quad -\phi \sum _{t\ge 0}\mathrm {e}^{-qt}\left( \Delta D(t)-(U(t-)+\Delta X(t))\right) \mathbf {1}_{\{\Delta D(t)>U(t-)+\Delta X(t)\ge c\}} \\&\quad -\phi \sum _{t\ge 0}\mathrm {e}^{-qt}\left( \Delta D(t)-c+c-\left( U(t-)+\Delta X(t)\right) \vee 0\right) \mathbf {1}_{\{\Delta D(t)\ge c\ge U(t-)+\Delta X(t)\}} \\= & {} \sum _{t\ge 0} \mathrm {e}^{-qt}\left( 1-\phi \right) \Big [\Delta D(t)-\left( U(t-)+\Delta X(t)\right) \Big ] \mathbf {1}_{\{\Delta D(t)>U(t-)+\Delta X(t)\ge c\}} \\&\quad +\sum _{t\ge 0} \mathrm {e}^{-qt} \left( 1-\phi \right) \Big [\Delta D(t)-c\Big ]\mathbf {1}_{\{\Delta D(t)\ge c\ge U(t-)+\Delta X(t)\}} \\&\quad +\sum _{t\ge 0} \mathrm {e}^{-qt} \Big [\Delta D(t)-c\Big ] \mathbf {1}_{\{\Delta D(t)<c\}} \\&\quad -\phi \sum _{t\ge 0}\mathrm {e}^{-qt}\Big [c-\left( U(t-)+\Delta X(t)\right) \vee 0\Big ] \mathbf {1}_{\{\Delta D(t)\ge c\ge U(t-)+\Delta X(t)\}} \\\le & {} 0, \end{aligned}$$

where one of the above two inequalities should be a strict inequality because there must be some $t_{0}\in (0,\infty )$ such that $\overline{D}(t_{0})< D(t_{0})$ or at least one inequality in (28) is a strict inequality at $t=t_{0}$. Otherwise, $\overline{D}(t)=D(t)$ and the inequality (28) becomes equality for all $t\ge 0$, hence $(D,R)=(\overline{D},\overline{R})\in \mathcal {D}_{1}$, contradicting the fact that $(D,R)\notin \mathcal {D}_{1}$. This completes the proof. $\square$

As pointed out in Remark 3.5, even if the continuous differentiability over $[0,\infty )$ is assumed on $W^{(q)}$, the twice differentiability of $V_{z_{1}}^{z_{2}}$ at $z_{2}$ is still absent in general, as is the continuity of $[V_{z_{1}}^{z_{2}}]^{\prime \prime }$ at $z_{2}$. Furthermore, imposing on $W^{(q)}$ the assumption of continuous differentiability over $[0,\infty )$ will exclude important sub-classes of spectrally negative Lévy processes. For example, for a spectrally negative compound Poisson process which has jumps of exact size $\alpha \in (0,\infty )$, the arrival rate $\lambda >0$, and a positive drift $\beta > 0$ such that $\beta -\lambda \alpha > 0$, the corresponding 0-scale function is identified by [2, 24] as

$$\begin{aligned} W(x)=\frac{1}{\beta }\sum _{n=1}^{[x/\alpha ]}\mathrm {e}^{-\lambda (\alpha n-x)/\beta }\frac{1}{n!}(\lambda /\beta )^{n}(\alpha n-x)^{n}, \end{aligned}$$

with $[x/\alpha ]$ being the integer part of $x/\alpha$. Note that the above example of scale function corresponds to a Lévy process that has sample paths of bounded variation and whose Lévy measure has atoms; otherwise, the scale function should be continuously differentiable over $(0,\infty )$.

In the sequel, it is assumed that $W^{(q)}$ is piece-wise continuously differentiable over all compact subsets of $[0,\infty )$, i.e., for every $x\in (0,\infty )$, $W^{(q)}$ is continuously differentiable over $[0,x]\setminus (d_{i})_{i\le m_{x}}$, where $(d_{i})_{i\le m_{x}}\subseteq [0,x]$ and the integer valued $m_{x}\ge 0$ is non-decreasing in x. Recalling that the function $V_{z_{1}}^{z_{2}}$ is linear over $[z_{2},\infty )$, one knows that $V_{z_{1}}^{z_{2}}$ is twice continuously differentiable over $[0,\infty )\setminus (d_{i})_{i\le m_{z_{2}}}$.

For any function $f\in C^{2}((-\infty ,\infty )\setminus (d_{i})_{i\le m})$ for some non-negative integer $m\ge 0$, define an operator $\mathcal {A}$ acting on f as

$$\begin{aligned}&\mathcal {A}f(x)=\gamma f^{\prime }(x)\\&\quad +\frac{1}{2}\sigma ^{2}f^{\prime \prime }(x) +\int _{(0,\infty )}\left( f(x-y)-f(x)+f^{\prime }(x) y\mathbf {1}_{(0,1)}(y)\right) \upsilon (\mathrm {d}y), \end{aligned}$$

where $x\in (-\infty ,\infty )\setminus (d_{i})_{i\le m}$. Also, define a sequence of mollified functions $f_{n}$ (of f) as

$$\begin{aligned} f_{n}(x)&\hat{=} \int _{-\infty }^{+\infty }\rho _{n}(x-y)f(y)\mathrm {d}y\nonumber \\&= \int _{-\infty }^{+\infty }\rho (z)f(x-\tfrac{z}{n}) \mathrm {d}z,\quad x\in (-\infty ,\infty ),\,n\ge 1, \end{aligned}$$

(29)

where $\rho _{n}(x)=n\rho (nx)$ and $\rho (x)=c\,\mathrm {e}^{\frac{1}{(x+1)^{2}-1}}\,\mathbf {1}_{(-2,0)}(x)$ with $\int _{-\infty }^{+\infty }\rho (x)\mathrm {d}x=1$.

In order to verify the optimality of a particular IDCI strategy $(z_{1},z_{2})\in \mathcal {M}$ producing the value function $V_{z_{1}}^{z_{2}}$, which lacks twice continuous differentiability at finitely many points $(d_{i})_{i\le m}\subseteq [0,z_{2}]$ for some integer $m\ge 0$, we need a modified version of verification argument, i.e., Lemma 4.4. Before presenting this verification argument, we show the following Lemma 4.3.

Lemma 4.3

Let f be a non-decreasing function such that

$$\begin{aligned} f\in C^{1}(-\infty ,\infty )\cap C^{2}((-\infty ,\infty )\setminus (d_{i})_{i\le m}), \end{aligned}$$

(30)

and

$$\begin{aligned}&\max \limits _{i\le m}\left( \lim \limits _{x\uparrow d_{i}}\big |f^{\prime \prime }(x)\big |\vee \lim \limits _{x\downarrow d_{i}}\big |f^{\prime \prime }(x)\big |\right) <\infty , \end{aligned}$$

(31)

with m being a non-negative integer and $0\le d_{1}<\cdots<d_{m}<\infty$. Suppose

$$\begin{aligned} f(x_{2})-f(x_{1})\ge x_{2}-x_{1}-c,\,\, f^{\prime }(x)\le \phi , \,\, x_2\ge x_1+c,\,\,x_{1},x\ge 0, \end{aligned}$$

(32)

and

$$\begin{aligned} \mathcal {A}f(x)-q f(x)\le 0,\quad x\in [0,\infty )\setminus (d_{i})_{i\le m}, \end{aligned}$$

(33)

then $(f_{n})_{n\ge 1}$ are non-decreasing and twice differentiable over $(-\infty ,\infty )$, satisfy (32) and

$$\begin{aligned} \mathcal {A}f_{n}(x)-q f_{n}(x)\le 0,\quad x\in [0,\infty ), \end{aligned}$$

(34)

and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }f_{n}(x)=f(x),\quad x\in (-\infty ,\infty ). \end{aligned}$$

(35)

Proof

It is a direct result of differentiation under the integral sign. The proof is omitted. $\square$

Now we are ready to present the following verification argument. For this purpose, let $(D^*, R^*)$ be a candidate optimal admissible IDCI strategy with value function $V_{(D^*,R^*)}(x),\,\, x\in [0,\infty )$. We extend the domain of $V_{(D^*,R^*)}$ to the entire real line by setting $V_{(D^*,R^*)}(x) = V_{(D^*,R^*)}(0)+\phi x$ for $x<0$. With a little abuse of notation, the extended function is still denoted by $V_{(D^*,R^*)}$.

Lemma 4.4

(Verification) Suppose that $\int _{1}^{\infty }y\upsilon (\mathrm {d}y)<\infty$. If the function $V_{(D^*,R^*)}$ defined over $(-\infty ,\infty )$ is non-decreasing and fulfills (30), (31), (32), and (33), then $(D^*, R^*)$ is the optimal strategy, and $V_{(D^*,R^*)}(x)\ge V_{(D,R)}(x)$ for all $(D,R)\in \mathcal {D}$ and $x\in [0,\infty )$.

Proof

By Lemma 4.2, we only need to prove that $(D^*, R^*)$ dominates all strategies among $\mathcal {D}_{1}$. For a given strategy $(D,R)\in \mathcal {D}_{1}$, recall that $U(t)=X(t)-D(t)+R(t)$ for $t\ge 0$. In order to do rigorous stochastic calculus, we follow [35] to define $\widetilde{D}(t)$ as the càdlàg version of D(t) and $\widetilde{U}(t):=X(t)-\widetilde{D}(t)+R(t)$; and follow Theorem 2.1 in [30] to denote X(t) as the sum of the independent processes $\gamma t+\sigma B(t)$, $\sum _{s\le t}\Delta X(s)\mathbf {1}_{\{{\Delta X(s)\le -1}\}}$, and $X(t)-\gamma t-\sigma B(t)-\sum _{s\le t}\Delta X(s)\mathbf {1}_{\{{\Delta X(s)\le -1}\}}$, with the latter one being a square integrable martingale. It is seen that the four processes $\widetilde{U}$, X, $\widetilde{D}$, and R are all càdlàg and adapted stochastic processes. Denote by $\{\widetilde{U}_{c}(t);t\ge 0\}$ and $\{R_{c}(t);t\ge 0\}$ as the continuous part of $\{\widetilde{U}(t);t\ge 0\}$ and $\{R(t);t\ge 0\}$, respectively.

Let $(f_{n})_{n\ge 1}$ be defined via (29) with f replaced by $V_{(D^*,R^*)}$. Hence, $f_{n}$ is twice differentiable over $[0,\infty )$, and satisfies (32) and (34). By Theorem 4.57 (Itô’s formula) in [27], we have, for $x\in (0,\infty )$ and $n\ge 1$,

$$\begin{aligned}&\mathrm {e}^{-q t}f_{n}(\widetilde{U}(t)) =f_{n}(x)-\int _{0-}^{t}q \mathrm {e}^{-q s}f_{n}(\widetilde{U}(s-))\mathrm {d}s+\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-))\mathrm {d}\widetilde{U}(s)\nonumber \\&\qquad +\frac{1}{2} \int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime \prime }(\widetilde{U}(s-))\mathrm {d}\langle \widetilde{U}_{c}(\cdot ),\widetilde{U}_{c}(\cdot )\rangle _{s} \nonumber \\&\qquad +\sum _{s\le t}\mathrm {e}^{-q s}\big (f_{n}(\widetilde{U}(s-)+\Delta \widetilde{U}(s))-f_{n}(\widetilde{U}(s-))-f_{n}^{\prime }(\widetilde{U}(s-))\Delta \widetilde{U}(s)\big ) \nonumber \\&\quad = f_{n}(x)-\int _{0-}^{t}q \mathrm {e}^{-q s}f_{n}(\widetilde{U}(s-))\mathrm {d}s+\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}(\gamma s+\sigma B(s)) \nonumber \\&\quad +\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}\big (X(s)-\gamma s-\sigma B(s) \nonumber \\&\quad -\sum _{r\le s}\Delta X(r)\mathbf {1}_{\{{\Delta X(r)\le -1}\}}\big ) \nonumber \\&\quad +\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}\big (R_{c}(s) +\sum _{r\le s}\Delta R(r)-\sum _{r\le s}\Delta \widetilde{D}(r)\big ) \nonumber \\&\quad +\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}\big (\sum _{r\le s}\Delta X(r)\mathbf {1}_{\{{\Delta X(r)\le -1}\}}\big ) +\frac{\sigma ^{2}}{2} \nonumber \\&\quad \int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime \prime }(\widetilde{U}(s-))\mathrm {d}s \nonumber \\&\qquad +\sum _{s\le t}\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-)+\Delta X(s))-f_{n}(\widetilde{U}(s-))-f_{n}^{\prime }(\widetilde{U}(s-))\Delta X(s)\big ] \nonumber \\&\qquad +\sum _{s\le t}\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-)+\Delta X(s)+\Delta R(s)) \nonumber \\&\quad \,\, -f_{n}(\widetilde{U}(s-)+\Delta X(s))-f_{n}^{\prime }(\widetilde{U}(s-))\Delta R(s)\big ] \nonumber \\&\qquad +\sum _{s\le t}\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-)+\Delta \widetilde{U}(s))-f_{n}(\widetilde{U}(s-)+\Delta X(s)+\Delta R(s)) \nonumber \\&\quad \,\, +f_{n}^{\prime }(\widetilde{U}(s-))\Delta \widetilde{D}(s)\big ] \nonumber \\= & {} f_{n}(x)-\int _{0-}^{t}q \mathrm {e}^{-q s}f_{n}(\widetilde{U}(s-))\mathrm {d}s+\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}(\gamma s+\sigma B(s))\nonumber \\&\quad +\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}\big (X(s)-\gamma s-\sigma B(s)-\sum _{r\le s}\Delta X(r)\mathbf {1}_{\{{\Delta X(r)\le -1}\}}\big ) \nonumber \\&\quad +\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}R_{c}(s) +\frac{\sigma ^{2}}{2} \int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime \prime }(\widetilde{U}(s-))\mathrm {d}s \nonumber \\&\quad +\sum _{s\le t}\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-)+\Delta X(s))-f_{n}(\widetilde{U}(s-)) \nonumber \\&\quad \,\, -f_{n}^{\prime }(\widetilde{U}(s-))\Delta X(s)\mathbf {1}_{\{{-1< \Delta X(s)<0}\}}\big ] \nonumber \\&\quad +\sum _{s\le t}\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-)+\Delta X(s)+\Delta R(s)) -f_{n}(\widetilde{U}(s-)+\Delta X(s))\big ] \nonumber \\&\quad +\sum _{s\le t}\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-)+\Delta \widetilde{U}(s))-f_{n}(\widetilde{U}(s-)+\Delta X(s)+\Delta R(s))\big ], \end{aligned}$$

(36)

where $\Delta \widetilde{D}(s)=\widetilde{D}(s)-\widetilde{D}(s-)$, $\Delta X(s)=X(s)-X(s-)$, $\Delta R(s)=R(s)-R(s-)$, and, $\Delta \widetilde{U}(s)=\widetilde{U}(s)-\widetilde{U}(s-)=\Delta X(s)+\Delta R(s)-\Delta \widetilde{D}(s)$. Due to the fact that $(D,R)\in \mathcal {D}_{1}$, one knows that $\Delta R(s)>0$ implies a jump of $N(\cdot ,\cdot )$ at time s (i.e., whenever there is a jump in R, there must be a jump in X). By (32) and the fact that $\Delta \widetilde{D}(s)>c$ whenever $\Delta \widetilde{D}(s)>0$, we have, for $s\in \left[ 0,t\right)$,

$$\begin{aligned}&f_{n}(\widetilde{U}(s-)+\Delta \widetilde{U}(s))-f_{n}(\widetilde{U}(s-)+\Delta X(s)+\Delta R(s))+ \Delta \widetilde{D}(s)-c\le 0, \end{aligned}$$

(37)

$$\begin{aligned}&f_{n}(\widetilde{U}(s-)+\Delta X(s)+\Delta R(s)) -f_{n}(\widetilde{U}(s-)+\Delta X(s))\le \phi \Delta R(s). \end{aligned}$$

(38)

Therefore, by (32), (34), (36), (37), and (38), we have

$$\begin{aligned}&\mathrm {e}^{-q t}f_{n}(\widetilde{U}(t)) \nonumber \\&\quad =f_{n}(x)+\int _{0-}^{t}\mathrm {e}^{-q s}(\mathcal {A}-q)f_{n}(\widetilde{U}(s-))\mathrm {d}s +\int _{0-}^{t}\sigma \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-))\mathrm {d}B(s) \nonumber \\&\qquad +\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}\big (X(s)-\gamma s-\sigma B(s)-\sum _{r\le s}\Delta X(r)\mathbf {1}_{\{{\Delta X(r)\le -1}\}}\big ) \nonumber \\&\qquad +\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-))\mathrm {d}R_{c}(s) +\int _{0-}^{t}\int _{0}^{\infty }\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-) -y)-f_{n}(\widetilde{U}(s-)) \nonumber \\&\qquad +f_{n}^{\prime }(\widetilde{U}(s-))y \mathbf {1}_{(0,1)}(y)\big ] \overline{N}(\mathrm {d}s,\mathrm {d}y) \nonumber \\&\qquad +\sum _{s\le t}\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-)+\Delta X(s)+\Delta R(s)) -f_{n}(\widetilde{U}(s-)+\Delta X(s))\big ] \nonumber \\&\qquad +\sum _{s\le t}\mathrm {e}^{-q s}\big [f_{n}(\widetilde{U}(s-)+\Delta \widetilde{U}(s))-f_{n}(\widetilde{U}(s-)+\Delta X(s)+\Delta R(s))\big ] \nonumber \\&\quad \le f_{n}(x)+\phi \int _{0-}^{t} \mathrm {e}^{-q s}\mathrm {d}R_{c}(s) +\phi \sum _{s\le t}\mathrm {e}^{-q s}\Delta R(s)+\int _{0-}^{t}\sigma \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-))\mathrm {d}B(s) \nonumber \\&\qquad +\int _{0-}^{t} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}\big (X(s)-\gamma s-\sigma B(s)-\sum _{r\le s}\Delta X(r)\mathbf {1}_{\{{\Delta X(r)\le -1}\}}\big ) \nonumber \\&\qquad -\sum \limits _{s\le t}\mathrm {e}^{-q s}( \Delta \widetilde{D}(s)-c)+\int _{0-}^{t}\int _{0}^{\infty }\mathrm {e}^{-q s} \big (f_{n}(\widetilde{U}(s-)-y)-f_{n}(\widetilde{U}(s-)) \nonumber \\&\qquad +f_{n}^{\prime }(\widetilde{U}(s-))y \mathbf {1}_{(0,1]}(y)\big ) \overline{N}(\mathrm {d}s,\mathrm {d}y) ,\quad x\in (0,\infty ),\quad n\ge 1. \end{aligned}$$

(39)

Define a sequence of stopping times $(T_{m})_{m\ge 1}$ that

$$\begin{aligned}&T_{m}:=m\wedge \inf \{t\ge 0; \widetilde{U}(t)\ge m\}, \quad m\ge 1. \end{aligned}$$

It follows that $T_{m}\rightarrow \infty$ almost surely as $m\rightarrow \infty$. In addition, $\widetilde{U}(t-)$ is confined in the compact set $\left[ 0,m\right]$ for $t\le T_{m}$. By the Lévy-Itô decomposition theorem (see, Theorem 2.1 in [30]) or Appendix A in [35], the stochastic integral

$$\begin{aligned} {\int _{0-}^{t\wedge T_{m}} \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-)) \mathrm {d}\big [X(s)-\gamma s-\sigma B(s)-\sum _{r\le s}\Delta X(r)\mathbf {1}_{\{{\Delta X(r)\le -1}\}}\big ]}, \, t\ge 0, \end{aligned}$$

is a martingale starting from zero. By Corollary 4.6 in [30] and the facts that $\int _{0}^{1}y^{2}\upsilon (\mathrm {d}y)<\infty$ (because $\upsilon$ is a Lévy measure) and $\int _{1}^{\infty }y\upsilon (\mathrm {d}y)<\infty$ (by assumption), the following stochastic integral with respect to the compensated Poisson random measure

$$\begin{aligned}&\int _{0-}^{t\wedge T_{m}}\int _{0}^{\infty }\mathrm {e}^{-q s}\Big [f_{n}(\widetilde{U}(s-) -y)-f_{n}(\widetilde{U}(s-)) \\&\quad +f_{n}^{\prime }(\widetilde{U}(s-))y \mathbf {1}_{(0,1]}(y)\Big ] \overline{N}(\mathrm {d}s,\mathrm {d}y),\quad t\ge 0, \end{aligned}$$

is a martingale starting from zero. Similarly, the following integration with respect to the Brownian motion (see, Page 146 in [29])

$$\begin{aligned} \int _{0-}^{t\wedge T_{m}}\sigma \mathrm {e}^{-q s}f_{n}^{\prime }(\widetilde{U}(s-))\mathrm {d}B(s),\quad t\ge 0, \end{aligned}$$

is a martingale starting from zero.

Taking expectations on both sides of (39) after localization by $T_{m}$, we have

$$\begin{aligned} f_{n}(x)\ge & {} \mathrm {E}_x\left( \mathrm {e}^{-q (t\wedge T_{m})}f_{n}(\widetilde{U}(t\wedge T_{m}))\right) -\phi \mathrm {E}_x\Big (\int _{0-}^{t\wedge T_{m}} \mathrm {e}^{-q s}\mathrm {d}R(s)\Big )\nonumber \\&\quad +\, \mathrm {E}_x\Big (\sum _{s\le t\wedge T_{m}}\mathrm {e}^{-q s}( \Delta \widetilde{D}(s)-c)\Big ) \nonumber \\\ge & {} \mathrm {E}_x\left( \mathrm {e}^{-q (t\wedge T_{m})}{f(0)}\right) -\phi \mathrm {E}_x\Big (\int _{0-}^{t\wedge T_{m}} \mathrm {e}^{-q s}\mathrm {d}R(s)\Big )\nonumber \\&\quad +\, \mathrm {E}_x\Big (\sum _{s\le t\wedge T_{m}}\mathrm {e}^{-q s}( \Delta \widetilde{D}(s)-c)\Big ),\quad x\in (0,\infty ), \end{aligned}$$

(40)

where we have used the fact that, by (29) as well as the non-decreasing property of f and $f_{n}$

$$\begin{aligned} f_{n}(\widetilde{U}(t\wedge T_{m}))\ge & {} f_{n}(0)\ge {f(0)}, \quad n\ge 1. \end{aligned}$$

By setting $n, t, m\rightarrow \infty$ in (40), and then taking use of the bounded convergence theorem (note that f(0) is bounded), we get

$$\begin{aligned} f(x)\ge & {} -\phi \mathrm {E}_x\Big (\int _{0-}^{\infty } \mathrm {e}^{-q s}\mathrm {d}R(s)\Big )+ \mathrm {E}_x\Big (\sum _{s}\mathrm {e}^{-q s}( \Delta \widetilde{D}(s)-c)\Big )\\= & {} -\phi \mathrm {E}_x\Big (\int _{0-}^{\infty } \mathrm {e}^{-q s}\mathrm {d}R(s)\Big )+ \mathrm {E}_x\Big (\sum _{s}\mathrm {e}^{-q s}( \Delta D(s)-c)\Big )\\= & {} V_{(D,R)}(x),\quad x\in (0,\infty ). \end{aligned}$$

The arbitrariness of (D, R) and the continuity of $f=V_{(D^{*},R^{*})}$ give rise to $V_{(D^{*},R^{*})}(x)\ge \sup \limits _{(D,R)\in \mathcal {D}}V_{(D,R)}(x)$ for all $x\in [0,\infty )$, the reverse inequality of which is trivial. The proof is completed. $\square$

Remark 4.5

Because $V_{(D^*,R^*)}$ lacks twice differentiability at $(d_{i})_{i\le m}$, an appropriate generalized version of the Itô’s lemma such as the Itô-Tanaka-Meyer formula (see [44] ) should be applied to prove the verification argument. In our case, we employed an alternative mollifying technique (see Lemma 4.3 and 4.4 ) to deal with the difficulty of lack of sufficient differentiability.

The mollifying arguments given in Lemma 4.3 and 4.4 are rigorous and differ from the approach adopted in [28] when proving their verification theorem. $\square$

The following Lemma 4.6 and 4.7 are useful for characterizing the optimal IDCI strategy and the associated optimal value function in Theorem 4.8. Recall that, for $x\in (0,\infty )$ where $W^{(q)}$ is not differentiable, $W^{(q)\prime }(x)$ shall be understood to be $W^{(q)\prime }_{+}(x)$, i.e., the right-derivative of $W^{(q)}$ at x.

Lemma 4.6

Given $(z_{1},z_{2})\in \mathcal {M}$, we have

$$\begin{aligned} \phi +\frac{(1-\phi Z^{(q)}(x))W^{(q)\prime }(x)}{q[W^{(q)}(x)]^{2}}\ge & {} 0,\quad x\in [z_{2},\infty ). \end{aligned}$$

(41)

Proof

It is seen that

$$\begin{aligned} \phi +\frac{(1-\phi Z^{(q)}(x))W^{(q)\prime }(x)}{q[W^{(q)}(x)]^{2}}= & {} \left[ -\frac{1-\phi Z^{(q)}(x)}{qW^{(q)}(x)}\right] ^{\prime } \nonumber \\= & {} -\frac{(\phi H(x)-1)W^{(q)\prime }(x)}{q(W^{(q)}(x))^{2}} ,\, x\in [z_{2},\infty ), \end{aligned}$$

(42)

where $H(x)=Z^{(q)}(x)-q(W^{(q)}(x))^{2}/W^{(q)\prime }(x)$. By (15) and $\lim \limits _{z_{2}\rightarrow \infty }\hat{\tau }_{z_{2}}=\infty$ we know that H(x) decreases in x with $\lim _{x\rightarrow \infty }H(x)=0$. Let $a_{0}>0$ be the unique zero of the function $\phi H(x)-1$ when $\phi H(0)>1$, then the inequality (41) is equivalent to

$$\begin{aligned} z_{2}\ge \inf \{x>0; \frac{(\phi H(x)-1)W^{(q)\prime }(x)}{q(W^{(q)}(x))^{2}} \le 0\}={\left\{ \begin{array}{ll}a_{0},\, \text{ when } \,\phi H(0)>1,\\ 0,\,\,\,\, \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Since $z_{2}\ge 0$ holds trivially, we only need to show that $z_{2}\ge a_{0}$ holds when $\phi H(0)>1$. Given $\phi H(0)>1$, by (42) and the decreasing property of H(x), the function $\frac{1-\phi Z^{(q)}(x)}{qW^{(q)}(x)}$ is increasing (decreasing) over $[0,a_{0})$ ($(a_{0},\infty )$), and attains its maximum at $a_{0}$. So, when $\frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}=\frac{1-\phi Z^{(q)}(a_{0})}{qW^{(q)}(a_{0})}$ we must have $z_{2}= a_{0}$. Further, when $\frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}<\frac{1-\phi Z^{(q)}(a_{0})}{qW^{(q)}(a_{0})}$ we should have $z_{2}>a_{0}$. Otherwise, $z_{2}$ will be in the range $(z_{1},a_{0})$, which leads to

$$\begin{aligned} \frac{\partial }{\partial z_{1}}\xi (z_{1},z_{2})= & {} \frac{qW^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})} \left( \xi (z_{1},z_{2})-\frac{1-\phi Z^{(q)}(z_{1})}{qW^{(q)}(z_{1})}\right) \\= & {} \frac{qW^{(q)}(z_{1})}{Z^{(q)}(z_{2})-Z^{(q)}(z_{1})} \left( \frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}-\frac{1-\phi Z^{(q)}(z_{1})}{qW^{(q)}(z_{1})}\right) \\> & {} 0. \end{aligned}$$

This result contradicts the fact that $\xi$ attains its maximum at $(z_{1},z_{2})$, so $z_{2}\notin (z_{1},a_{0})$. The proof is completed. $\square$

In the sequel, we extend the function $V_{z_{1}}^{z_{2}}$ to the entire real axis by setting $V_{z_{1}}^{z_{2}}(x) = V_{z_{1}}^{z_{2}}(0)+\phi x$ for $x<0$. We denote by $V_{x}(y)$ the value function of the barrier dividend and capital injection strategy with barrier level x and initial reserve y (cf., Equation (5.4) in [6]), i.e.,

$$\begin{aligned} V_{x}(y)=\left\{ \begin{array}{ll} V_{x}(0)+\phi y,&{}y<0,\\ \phi (\overline{Z}^{(q)}(y)+\frac{\psi ^{\prime }(0+)}{q})+ Z^{(q)}(y)\frac{1-\phi Z^{(q)}(x)}{qW^{(q)}(x)},&{}y\in [0,x),\\ y-x+\phi (\overline{Z}^{(q)}(x)+\frac{\psi ^{\prime }(0+)}{q})+ Z^{(q)}(x)\frac{1-\phi Z^{(q)}(x)}{qW^{(q)}(x)}, &{} y\ge x. \end{array}\right. \end{aligned}$$

(43)

Lemma 4.7

Given $(z_{1},z_{2})\in \mathcal {M}$ and $x\in (z_{2},\infty )$, define

$$\begin{aligned} h(z):=V_{z_{1}}^{z_{2}}(z)-V_{x}(z),\quad z\in (-\infty ,x]. \end{aligned}$$

Then, h(z) is non-decreasing with respect to z and $h(x)\ge 0$.

Proof

Recall that it has been assumed that, for every $x\in (0,\infty )$, $W^{(q)}$ is continuously differentiable over $[0,x]\setminus (d_{i})_{i\le m_{x}}$ with $(d_{i})_{i\le m_{x}}\subseteq [0,x]$ and $m_{x}\ge 0$ being integer valued and non-decreasing in x. For $x\in (z_{2},\infty )$, denote $w_{0}:=z_{2}$, $w_{i}:=z_{2}\vee d_{i}$ for $i\in \{1,\cdots ,m_{x}\}$, and $w_{m_{x}+1}:=x$. By the Mean Value Theorem, we have

$$\begin{aligned} h(x)= & {} V_{z_{1}}^{z_{2}}(x)-V_{x}(x) \\= & {} \sum _{i=0}^{m_{x}}\left( -y+\phi \overline{Z}^{(q)}(y) + Z^{(q)}(y)\frac{1-\phi Z^{(q)}(y)}{qW^{(q)}(y)}\right) \bigg |_{w_{i+1}}^{w_{i}}\\= & {} \sum _{i=0}^{m_{x}}Z^{(q)}(\theta _{i})\bigg [\phi +\frac{[1-\phi Z^{(q)}(\theta _{i})][W^{(q)}(\theta _{i})]^{\prime }}{q[W^{(q)}(\theta _{i})]^{2}}\bigg ](w_{i+1}-w_{i}) \ge 0, \end{aligned}$$

where, $\theta _{i}\in (w_{i},w_{i+1})$ and (41) holds true for $\theta _{i}\in (w_{i},w_{i+1})\subseteq (z_{2},x)$ as long as $w_{i}<w_{i+1}$.

By (41) and the Mean Value Theorem, we also have

$$\begin{aligned} h^{\prime }(z)= & {} qW^{(q)}(z)\left( \frac{1-\phi Z^{(q)}(z_{2})}{qW^{(q)}(z_{2})}-\frac{1-\phi Z^{(q)}(x)}{qW^{(q)}(x)}\right) \\= & {} qW^{(q)}(z)\sum _{i=0}^{m_x}\left( \frac{1-\phi Z^{(q)}(w_{i})}{qW^{(q)}(w_{i})}-\frac{1-\phi Z^{(q)}(w_{i+1})}{qW^{(q)}(w_{i+1})}\right) \\= & {} qW^{(q)}(z)\sum _{i=0}^{m_x}\left( -\phi -\frac{(1-\phi Z^{(q)}(\theta _{i}))[W^{(q)}(\theta _{i})]^{\prime }}{q[W^{(q)}(\theta _{i})]^{2}}\right) (w_{i}-w_{i+1}) \ge 0, \end{aligned}$$

for $z\in [0,z_{2})$;

$$\begin{aligned} h^{\prime }(z)= & {} 1-\phi Z^{(q)}(z)-W^{(q)}(z)\frac{1-\phi Z^{(q)}(x)}{W^{(q)}(x)}\\= & {} qW^{(q)}(z)\left( \frac{1-\phi Z^{(q)}(z)}{qW^{(q)}(z)}-\frac{1-\phi Z^{(q)}(x)}{qW^{(q)}(x)}\right) \\= & {} qW^{(q)}(z)\sum _{i=0}^{m_{x}}\left( \frac{1-\phi Z^{(q)}(y_{i})}{qW^{(q)}(y_{i})}-\frac{1-\phi Z^{(q)}(y_{i+1})}{qW^{(q)}(y_{i+1})}\right) \\= & {} qW^{(q)}(z)\sum _{i=0}^{m_{x}}\left( -\phi -\frac{(1-\phi Z^{(q)}(\eta _{i}))[W^{(q)}(\eta _{i})]^{\prime }}{q[W^{(q)}(\eta _{i})]^{2}}\right) (y_{i}-y_{i+1})\ge 0, \end{aligned}$$

for $z\in [z_{2},x)$, $y_{0}:=z$, $y_{m_{x}+1}:=x$, $y_{i}:=z\vee d_{i}$ for $i\in \{1,\cdots ,m_{x}\}$, and $\eta _{i}\in (y_{i},y_{i+1})\subseteq (z,x)$ whenever $y_{i}<y_{i+1}$; and

$$\begin{aligned} h^{\prime }(z)=\phi -\phi =0,\quad \text{ for } z\in (-\infty ,0). \end{aligned}$$

The proof is completed. $\square$

The following theorem characterizes the optimal IDCI strategy among all admissible IDCI strategies. The ideas in the proof are partly obtained from [6, 34]. This theorem shows that any IDCI strategy $(z_{1},z_{2})\in \mathcal {M}$ is optimal and dominates all admissible IDCI strategies.

Theorem 4.8

Suppose that $\int _{1}^{\infty }y\upsilon (\mathrm {d}y)<\infty$, and that $W^{(q)}$ is piece-wise continuously differentiable over all compact subsets of $[0,\infty )$. Let $(z_{1},z_{2})\in \mathcal {M}$. Then the $(z_{1},z_{2})$ strategy is optimal among all admissible IDCI strategies.

Proof

By the fact that the scale function $W^{(q)}(x)$ is left and right differentiable over $(0,\infty )$ (see for example, Lemma 1 in [42]), Remark 3.5, and the extended definition $V_{z_{1}}^{z_{2}}(x) = V_{z_{1}}^{z_{2}}(0)+\phi x$ for $x<0$, one can verify that $V_{z_{1}}^{z_{2}}$ is non-decreasing and satisfies (31). Therefore, with the help of Proposition 3.6 and Lemma 4.4, we need only to prove $\mathcal {A}V_{z_{1}}^{z_{2}}(x)-q V_{z_{1}}^{z_{2}}(x)\le 0$ for $x\in [0,\infty )\setminus (d_{i})_{i\le m_{z_{2}}}$.

Let $\sigma ^{+}_{w}$ ($\sigma ^{-}_{w}$) be the first up-crossing (down-crossing) time of the level w by the process X

$$\begin{aligned} \sigma _{w}^{+}:=\inf \{t>0;X(t)> w\},\quad \sigma _{w}^{-}:=\inf \{t>0;X(t)\le w\}. \end{aligned}$$

(44)

Put $w_0:=0$, $w_{i}:=d_{i}$ for $i\in \{1,\cdots , m_{z_2}\}$, and, $w_{m_{z_{2}}+1}:=z_{2}$. For any $x\in (0,z_{2})\setminus (d_{i})_{i\le m_{z_{2}}}$, we may assume without loss of generality that $x\in (w_{i},w_{i+1})$ for some $0\le i\le m_{z_{2}}$. Let $\sigma :=\sigma _{w_{i}}^{-}\wedge \sigma _{w_{i+1}}^{+}$ with $\sigma _{w_{i}}^{-}$ and $\sigma _{w_{i+1}}^{+}$ defined via (44). By the strong Markov property of the process X, we have

$$\begin{aligned}&\mathrm {E}_{x}\left( \int _{0-}^{\infty }\mathrm {e}^{-qt}\mathrm {d}(D_{z_{1}}^{z_{2}}(t)-\phi R_{z_{1}}^{z_{2}}(t))\bigg |\mathcal {F}_{r\wedge \sigma } \right) \\&\quad =\mathrm {E}_{x}\left( \int _{0-}^{\infty }\mathrm {e}^{-q(s+r\wedge \sigma )} \mathrm {d}(D_{z_{1}}^{z_{2}}(s+r\wedge \sigma )-\phi R_{z_{1}}^{z_{2}}(s+r\wedge \sigma ))\bigg |\mathcal {F}_{r\wedge \sigma }\right) \\&\quad =\mathrm {e}^{-q(r\wedge \sigma )}\mathrm {E}_{X(r\wedge \sigma )}\left( \int _{0-}^{\infty }\mathrm {e}^{-qs} \mathrm {d}(D_{z_{1}}^{z_{2}}(s)-\phi R_{z_{1}}^{z_{2}}(s))\right) \\&\quad =\mathrm {e}^{-q(r\wedge \sigma )}V_{z_{1}}^{z_{2}}(X(r\wedge \sigma )),\quad r\ge 0, \end{aligned}$$

which implies that the right-hand side of the above equation is a martingale.

The martingale property of the process $\left( \mathrm {e}^{-q\left( r\wedge \sigma \right) }V_{z_{1}}^{z_{2}}\left( X\left( r\wedge \sigma \right) \right) \right) _{r\ge 0}$ implies that

$$\begin{aligned} \mathcal {A}V_{z_{1}}^{z_{2}}(x)-q V_{z_{1}}^{z_{2}}(x)=0, \quad x\in (0,z_{2})\setminus (d_{i})_{i\le m_{z_2}}. \end{aligned}$$

(45)

Indeed, for $x\in (w_{i},w_{i+1})$ and $\sigma :=\sigma _{w_{i}}^{-}\wedge \sigma _{w_{i+1}}^{+}$, Itô’s formula gives

$$\begin{aligned}&\mathrm {e}^{-q(r\wedge \sigma )}V_{z_{1}}^{z_{2}}(X(r\wedge \sigma ))-V_{z_{1}}^{z_{2}}(x)\\&\quad =\int _{0-}^{r\wedge \sigma }\mathrm {e}^{-q s}(\mathcal {A}-q)V_{z_{1}}^{z_{2}}(X(s-))\mathrm {d}s+\int _{0-}^{r\wedge \sigma }\sigma \mathrm {e}^{-q s}[V_{z_{1}}^{z_{2}}]^{\prime }(X(s-))\mathrm {d}B(s) \\&\qquad +\int _{0-}^{t\wedge \sigma } \mathrm {e}^{-q s}[V_{z_{1}}^{z_{2}}]^{\prime }(X(s-)) \mathrm {d}\big (X(s)-\gamma s-\sigma B(s)-\sum _{r\le s}\Delta X(r)\mathbf {1}_{\{{\Delta X(r)\le -1}\}}\big ) \\&\qquad +\int _{0-}^{r\wedge \sigma }\int _{0}^{\infty }\mathrm {e}^{-q s}\big [V_{z_{1}}^{z_{2}}(X(s-)-y)-V_{z_{1}}^{z_{2}}(X(s-)) \\&\qquad +[V_{z_{1}}^{z_{2}}]^{\prime }(X(s-))y\mathbf {1}_{(0,1]}(y)\big ] \overline{N}(\mathrm {d}s,\mathrm {d}y),\quad r\ge 0. \end{aligned}$$

Using the same arguments as the proof of Lemma 4.4, one knows that all the terms (except for the first one) on the right-hand side of the above display are martingales starting from 0. Hence, taking expectations on both sides of the above display yields

$$\begin{aligned} 0=\mathrm {E}_{x}\left( \int _{0-}^{r\wedge \sigma }\mathrm {e}^{-q s}(\mathcal {A}-q)V_{z_{1}}^{z_{2}}(X(s))\mathrm {d}s\right) ,\quad r\ge 0. \end{aligned}$$

Dividing by r the both sides and then setting $r\downarrow 0$ in the above equation, we get (45) for $x\in (0,z_{2})\setminus (d_{i})_{i\le m_{z_2}}$ by the Mean Value Theorem together with the Dominated Convergence Theorem. For a more detailed proof of (45), we can also turn to Lemma 4.2 of [33]. Thus, it suffices to further prove

$$\begin{aligned} \mathcal {A}V_{z_{1}}^{z_{2}}(x)-q V_{z_{1}}^{z_{2}}(x)\le 0, \quad x\in (z_{2},\infty ). \end{aligned}$$

(46)

By using similar arguments as those used in proving (45) we can get

$$\begin{aligned} \mathcal {A}V_{x}(y)-q V_{x}(y)=0, \quad y\in (0,x)\setminus (d_{i})_{i\le m_x}, \quad x\in (0,\infty ), \end{aligned}$$

which implies

$$\begin{aligned} \lim \limits _{y\uparrow x}\left( \mathcal {A}V_{x}(y)-q V_{x}(y)\right) =0,\quad x\in (z_{2},\infty ), \end{aligned}$$

(47)

where $\lim \limits _{y\uparrow x}\mathcal {A}V_{x}(y)$ is well-defined due to (43), the piece-wise continuous differentiability of $W^{(q)}$ over the compact set [0, x], $\int _{0}^{1}z^{2}\upsilon (\mathrm {d}z)<\infty$, as well as $\int _{1}^{\infty }z\upsilon (\mathrm {d}z)<\infty$. Meanwhile, because the function $\mathcal {A}V_{z_{1}}^{z_{2}}-q V_{z_{1}}^{z_{2}}$ is continuous over $(z_{2},\infty )$ (Actually, we have $[V_{z_{1}}^{z_{2}}]^{\prime \prime }(x)=0$ for $x\in (z_{2},\infty )$ by Proposition 3.4, and $\int _{0}^{\infty }(z^{2}\wedge z)\upsilon (\mathrm {d}z)<\infty$.), we have

$$\begin{aligned} \lim \limits _{y\uparrow x}\left( \mathcal {A}V_{z_{1}}^{z_{2}}(y)-q V_{z_{1}}^{z_{2}}(y)\right) =\mathcal {A}V_{z_{1}}^{z_{2}}(x)-q V_{z_{1}}^{z_{2}}(x), \quad x\in (z_{2},\infty ). \end{aligned}$$

(48)

Combining (47) and (48), to prove (46) it suffices to show

$$\begin{aligned} \lim \limits _{y\uparrow x}\left( \mathcal {A}[V_{z_{1}}^{z_{2}}(y)-V_{x}(y)]-q[V_{z_{1}}^{z_{2}}(y)-V_{x}(y)]\right) \le 0,\quad x\in (z_{2},\infty ). \end{aligned}$$

For $x\in (z_{2},\infty )$, we can use the dominated convergence theorem to deduce

$$\begin{aligned}&\lim _{y\uparrow x}\left( \mathcal {A}[V_{z_{1}}^{z_{2}}(y)-V_{x}(y)]-q [V_{z_{1}}^{z_{2}}(y)-V_{x}(y)]\right) \nonumber \\&\quad =\gamma \left( [[V_{z_{1}}^{z_{2}}]^{\prime }(x)-V_{x}^{\prime }(x)]\right) +\frac{\sigma ^{2}}{2}[[V_{z_{1}}^{z_{2}}]^{\prime \prime }(x)-\lim _{y\uparrow x}V_{x}^{\prime \prime }(y)]-q[V_{z_{1}}^{z_{2}}(x)-V_{x}(x)]\nonumber \\&\qquad +\int _{(0,\infty )}\left( [V_{z_{1}}^{z_{2}}(x\!-\!y)\!-\!V_{x}(x\!-\!y)]\!-\![V_{z_{1}}^{z_{2}}(x)\!-\!V_{x}(x)] \right. \nonumber \\&\qquad \left. +[[V_{z_{1}}^{z_{2}}]^{\prime }(x)\!-\!V_{x}^{\prime }(x)] y\mathbf {1}_{(0,1)}(y)\right) \upsilon (\mathrm {d}y)\nonumber \\&\qquad =-\frac{\sigma ^{2}}{2}\lim \limits _{y\uparrow x}V_{x}^{\prime \prime }(y)-q[V_{z_{1}}^{z_{2}}(x)-V_{x}(x)]\nonumber \\&\qquad +\int _{(0,\infty )}\left( [V_{z_{1}}^{z_{2}}(x-y)-V_{x}(x-y)]-[V_{z_{1}}^{z_{2}}(x)-V_{x}(x)]\right) \upsilon (\mathrm {d}y), \end{aligned}$$

(49)

where the last equality stems from $[V_{z_{1}}^{z_{2}}]^{\prime }(x)=V_{x}^{\prime }(x)=1$ and $[V_{z_{1}}^{z_{2}}]^{\prime \prime }(x)=0$ for $x\in (z_{2},\infty )$.

Similarly, by (41), (43), and the piece-wise continuous differentiability of $W^{(q)}$ over the compact set [0, x], we have

$$\begin{aligned} \lim _{y\uparrow x}V_{x}^{\prime \prime }(y)\ge 0,\quad x\in (z_{2},\infty ) . \end{aligned}$$

By Lemma 4.7, it holds that $V_{z_{1}}^{z_{2}}(x)-V_{x}(x)\ge 0$ and

$$\begin{aligned} \left[ V_{z_{1}z}^{z_{2}}(x-y)-V_{x}(x-y)\right]- & {} \left[ V_{z_{1}}^{z_{2}}(x)-V_{x}(x)\right] \\= & {} h(x-y)-h(x)\le 0, \quad y\in [0,\infty ). \end{aligned}$$

Therefore, the right-hand side of (49) is non-positive, and this proves (46).

Now, as per Lemma 4.4, the $(z_{1},z_{2})$ strategy is optimal among all admissible IDCI strategies. The proof is completed. $\square$

5 Numerical Examples

This section aims to illustrate the results derived in the previous sections. We are interested in the value of $\xi (z_1, z_2)$ in (11), which determines the optimal $(z_1,z_2)$ strategy for the problem. The values of the optimal $z_1$, $z_2$, $z_2-z_1$ and $z_2-z_1-c$ are also quantities of interest in the understanding of the optimal lump sum dividend amount. We study two examples: Brownian motion with drift and Jump diffusion process, to study the impacts of the transaction cost parameters and other model parameters on the optimal dividend and capital injection strategies.

5.1 Brownian Motion with Drift

Brownian motion (with or without drift) is the only continuous Lévy process. When X is reduced to a Brownian motion with drift

$$\begin{aligned} X(t)=\mu t+\sigma B(t),\quad t\ge 0, \end{aligned}$$

where $\mu \in \mathbb {R}$, $\sigma >0$, and $\{B(t)\}$ is the standard Brownian motion. As per [31], the q-scale function for the above Brownian motion is

$$\begin{aligned} W^{(q)}(x)= & {} \frac{\exp \Big \{\frac{-\mu +\sqrt{ \mu ^2+2q\sigma ^2 }}{\sigma ^2} x\Big \} -\exp \Big \{\frac{-\mu -\sqrt{ \mu ^2+2q\sigma ^2 }}{\sigma ^2} x\Big \}}{\sqrt{ \mu ^2+2q\sigma ^2}}\\:= & {} \frac{1}{\sigma ^2 \delta }\left( \mathrm {e}^{(-w+\delta ) x}-\mathrm {e}^{-(w+\delta ) x}\right) ,\quad x\ge 0, \end{aligned}$$

where $\delta =\frac{\sqrt{ \mu ^2+2q\sigma ^2 } }{ \sigma ^2}$ and $w=\frac{\mu }{ \sigma ^2}$. Let $\alpha =w+\delta$ and $\beta =w-\delta$. By definition we have

$$\begin{aligned} Z^{(q)}(x)= & {} 1+q\int _{0}^{x}W^{(q)}(z)\mathrm {d}z =\frac{1}{2 \delta }\left( \alpha \mathrm {e}^{-\beta x}-\beta \mathrm {e}^{-\alpha x}\right) ,\quad x\ge 0,\\ \overline{Z}^{(q)}(x)= & {} \int _{0}^{x}Z^{(q)}(z)\mathrm {d}z =-\frac{\mu }{q}+\frac{\sigma ^2 }{4q \delta }\left( \alpha ^{2}\mathrm {e}^{-\beta x}-\beta ^{2}\mathrm {e}^{-\alpha x}\right) ,\quad x\ge 0. \end{aligned}$$

Hence, for $0<c\le z_{1}+c< z_{2}<\infty$, it holds that

$$\begin{aligned} \xi (z_{1},z_{2})= & {} \frac{2\delta (z_{2}-z_{1}-c)}{\zeta (z_1, z_2)}-\frac{\phi \mu }{q}-\frac{\phi (\mathrm {e}^{-\beta z_{2}}-\mathrm {e}^{-\beta z_{1}}-\mathrm {e}^{-\alpha z_{2}}+\mathrm {e}^{-\alpha z_{1}})}{\zeta (z_1, z_2)},\nonumber \\ \end{aligned}$$

(50)

where $\zeta (z_1, z_2)=\alpha (\mathrm {e}^{-\beta z_2}-\mathrm {e}^{-\beta z_1})-\beta (\mathrm {e}^{-\alpha z_2}-\mathrm {e}^{-\alpha z_1})$. Differentiating both sides of (50) with respect to $z_1$ we get

$$\begin{aligned} \frac{\partial }{\partial z_1}\xi (z_{1},z_{2})= & {} -\frac{2\delta +\phi (\beta \mathrm {e}^{-\beta z_1}-\alpha \mathrm {e}^{-\alpha z_1})}{\zeta (z_{1},z_{2})}-\frac{\xi (z_1,z_2)+\frac{\phi \mu }{q}}{\zeta (z_{1},z_{2})}\frac{\partial }{\partial z_1}\zeta (z_{1},z_{2}).\nonumber \\ \end{aligned}$$

(51)

By solving $\frac{\partial }{\partial z_{1}}\xi (z_{1},z_{2})=0$ we get

$$\begin{aligned} \xi (z_{1},z_{2})=-\frac{2\delta +\phi (\beta \mathrm {e}^{-\beta z_1}-\alpha \mathrm {e}^{-\alpha z_1})}{\alpha \beta (\mathrm {e}^{-\beta z_1}-\mathrm {e}^{-\alpha z_1})}-\frac{\phi \mu }{q}. \end{aligned}$$

(52)

Differentiating both sides of (50) with respect to $z_{2}$ we get

$$\begin{aligned} \frac{\partial }{\partial z_2}\xi (z_{1},z_{2})= & {} \frac{2\delta +\phi (\beta \mathrm {e}^{-\beta z_2}-\alpha \mathrm {e}^{-\alpha z_2})}{\zeta (z_{1},z_{2})}-\frac{\xi (z_1,z_2)+\frac{\phi \mu }{q}}{\zeta (z_{1},z_{2})}\frac{\partial }{\partial z_2}\zeta (z_{1},z_{2}). \end{aligned}$$

(53)

Setting $\frac{\partial }{\partial z_{2}}\xi (z_{1},z_{2})=0$ in (53) we solve

$$\begin{aligned} \xi (z_{1},z_{2})=\frac{2\delta +\phi (\beta \mathrm {e}^{-\beta z_2}-\alpha \mathrm {e}^{-\alpha z_2})}{\alpha \beta (\mathrm {e}^{-\alpha z_2}-\mathrm {e}^{-\beta z_2})}-\frac{\phi \mu }{q}. \end{aligned}$$

(54)

By (51) one can verify that $\frac{\partial }{\partial z_{1}}\xi (0,z_{2})=\frac{2\delta (\phi -1)}{\alpha (\mathrm {e}^{-\beta z_{2}}-1)-\beta (\mathrm {e}^{-\alpha z_{2}}-1)}>0$, excluding the possibility for the maximizer of $\xi$ to lie on the line $z_{1}=0$. Since it is proved (cf., Proposition 3.3) that the maximizer of $\xi$ cannot be attained on the line $z_{2}=z_{1}+c$, we claim that the $\xi$ is maximized at an interior point of the set $\{(z_{1},z_{2});z_{1},z_{2}\in [0, z_{0}],z_{1}+c\le z_{2}\}$ for some bounded $z_{0}>0$ (see the arguments immediately following (12)). Thus, if $(z_{1},z_{2})$ is the maximizer of $\xi$, then (50), (52) and (54) should hold simultaneously. Combining (52) and (54) yields

$$\begin{aligned} \mathrm {e}^{-\alpha z_2}-\mathrm {e}^{-\alpha z_1}-\mathrm {e}^{-\beta z_2}+\mathrm {e}^{-\beta z_1}+\phi (\mathrm {e}^{-\beta z_2-\alpha z_1}-\mathrm {e}^{-\alpha z_2-\beta z_1})=0. \end{aligned}$$

(55)

Similarly, combining (50) and (52) yields

$$\begin{aligned}&\alpha \beta (z_2-z_1-c)(\mathrm {e}^{-\beta z_1}-\mathrm {e}^{-\alpha z_1})+\zeta (z_1, z_2)+2\delta \phi \mathrm {e}^{-\frac{2\mu }{\sigma ^2}z_1}\nonumber \\&\quad -\alpha \phi \mathrm {e}^{-\alpha z_1-\beta z_2}+\beta \phi \mathrm {e}^{-\alpha z_2-\beta z_1}=0. \end{aligned}$$

(56)

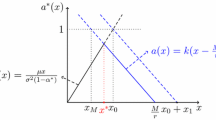
Now, we are ready to present the numerical results. First, we set $\mu =1, \sigma =0.36, q=0.05$, $c=0.1$ and $\phi =1.05$. Numerically, (55) and (56) are uniquely solved by $(z_1,z_2)=(0.02682,2.12950)$, a maximizer of $\xi$. According to the previous argument, it must be the maximizer of $\xi$. In fact, by routine calculus we can verify that, at $(z_1,z_2)=(0.02682,2.12950)$,

$$\begin{aligned} \frac{\partial ^2\xi (z_1, z_2)}{\partial z_1^2}= & {} \frac{\phi (\beta ^2 \mathrm {e}^{-\beta z_1}-\alpha ^2 \mathrm {e}^{-\alpha z_1})+\frac{2\delta +\phi (\beta \mathrm {e}^{-\beta z_1}-\alpha \mathrm {e}^{-\alpha z_1})}{\mathrm {e}^{-\beta z_1}-\mathrm {e}^{-\alpha z_1}}(\alpha \mathrm {e}^{-\alpha z_1}-\beta \mathrm {e}^{-\beta z_1})}{\zeta (z_1, z_2)}<0,\\ \frac{\partial ^2\xi (z_1, z_2)}{\partial z_2^2}= & {} \frac{\phi (\alpha ^2 \mathrm {e}^{-\alpha z_2}-\beta ^2 \mathrm {e}^{-\beta z_2})-\frac{2\delta +\phi (\beta \mathrm {e}^{-\beta z_2}-\alpha \mathrm {e}^{-\alpha z_2})}{\mathrm {e}^{-\alpha z_2}-\mathrm {e}^{-\beta z_2}}(\beta \mathrm {e}^{-\beta z_2}-\alpha \mathrm {e}^{-\alpha z_2})}{\zeta (z_1, z_2)}<0,\\ \frac{\partial ^2\xi (z_1, z_2)}{\partial z_1\partial z_2}= & {} \frac{\partial ^2\xi (z_1, z_2)}{\partial z_2\partial z_1}=0, \end{aligned}$$

and hence $\frac{\partial ^2\xi (z_1, z_2)}{\partial z_1^2}\frac{\partial ^2\xi (z_1, z_2)}{\partial z_2^2}-\frac{\partial ^2\xi (z_1, z_2)}{\partial z_1\partial z_2}\frac{\partial ^2\xi (z_1, z_2)}{\partial z_2\partial z_1}>0$, verifying that $(z_1,z_2)=(0.02682,2.12950)$ is the maximizer of $\xi$. This is also confirmed in Fig. 1. Also, as seen in Fig. 2a,

$$\begin{aligned} G(x):=\phi q[W^{(q)}(x)]^2+[1-\phi Z^{(q)}(x)]W^{(q)\prime }(x)\ge 0,\,\,x\ge z_2=2.12950. \end{aligned}$$

(57)

This verifies (41).

Fig. 1

The surface of $\xi (z_1,z_2)$ and its global maximizer

Fig. 2

The illustration of G(x) and the value function $V^{z_2}_{z_1}(x)$

With the optimal $(z_1,z_2)=(0.02682,2.12950)$ strategy, we can plot its associated value function $V^{z_2}_{z_1}(x)$. According to Proposition 3.1, we have

$$\begin{aligned} V^{z_2}_{z_1}(x)=\left\{ \begin{array}{l l} \frac{2\delta (\alpha \mathrm {e}^{-\beta x}-\beta \mathrm {e}^{-\alpha x})}{\xi (0.02682, 2.1295)}+\frac{\phi \sigma ^2 }{4q \delta }(\alpha ^{2}\mathrm {e}^{-\beta x}-\beta ^{2}\mathrm {e}^{-\alpha x}), &{}0\le x\le 2.1295,\\ x-2.1295+V^{z_2}_{z_1}(2.1295), &{}x>2.1295.\end{array}\right. \end{aligned}$$

It is observed in Fig. 2b that the segment in blue (i.e. $x\le 2.1295$) is shaped similar to a straight line, even though its underlying function is actually a combination of exponential functions.

Table 1 Maximizer of $\xi$ with respect to c when $\phi =1.05$

Next, let us examine the parameter sensitivity concerned with c and $\phi$, both playing a critical role in our model. To avoid repetitiveness, we omit the checking arguments of the maximizers of $\xi$. Also, for ease of comparison, we set $\mu =1, \sigma =0.36$, and $q=0.05$ thereafter. For $\phi =1.05$, in Table 1 of the maximizer of $\xi$ for $c= 0.01, 0.02, \ldots , 0.20$, $z_1$ is seen to have a slow but steady downward trend when c increases while $z_2$ has a solid upward trend. Further, in Fig. 3, the individual dividend amount $z_2-z_1$ and the net individual dividend amount $z_2-z_1-c$ both display a solid increasing trend when the transaction cost c increases. This is reasonable because the better way of paying dividends is to pay out more each time with a higher dividend threshold when transaction cost increases.

For $c=0.1$, Table 2 lists the maximizer $\xi$ for $\phi = 1.01, 1.02, \ldots , 1.20$. Both $z_1$ and $z_2$ are seen to have steady upward trends when $\phi$ increases. However, $z_2-z_1$ and $z_2-z_1-c$ in this case almost keep constant no matter how $\phi$ changes. As seen in Fig. 3, when the cost of capital injection goes up, it is more beneficial to have a higher dividend threshold, which partially reduces the chance of needing capital injection. Also, the increasing trend of $z_1$ upon $\phi$ lowers the negative impact of dividends on the solvency of the insurer, while at the same time helping the company to reduce the need of additional capital. On the other hand, the amount of money paid out in each dividend does not depend on $\phi$, but on the value of c which has been observed in the previous case.

Fig. 3

Optimal lump sum dividend amount w.r.t. the transaction parameters c and $\phi$

Table 2 Maximizer of $\xi$ with respect to $\phi$ when $c=0.1$

5.2 Jump Diffusion Process

The previous example considers a continuous Lévy process. In this subsection, we proceed with the case of jump diffusion process. When X is reduced to a jump-diffusion process,

$$\begin{aligned}X_{t} = x + p t + \sigma _1 {B_t} - \sum \limits _{i = 1}^{{N_{1}(t)}} {{Y_i}},\quad t\ge 0,\end{aligned}$$

where $B_t$ is a Brownian motion, $p,\sigma _1>0$, $\left\{ {{N_{1}(t)};t \ge 0} \right\}$ is a Poisson processes with arrival rate $\lambda _{1}$, $\{Y_{i}; i\ge 1\}$ is a sequence of i.i.d. random variables with Erlang$(2,\beta )$ distribution law $F(\mathrm {d}x)=\beta ^{2}x\mathrm {e}^{-\beta x}\mathrm {d}x$ for $x>0$ and $\beta >0$. The Lévy measures for X is given by $\upsilon (\mathrm {d}z)=\lambda _1 F(\mathrm {d}z)$. The scale functions associated with X are derived as

$$\begin{aligned} {W_{q}}( x ) = \sum \limits _{j = 1}^4 C_j( q )\mathrm {e}^{{\theta _j}( q )x},\,\, Z_{q}(x)=1+q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}(\mathrm {e}^{\theta _j( q )x}-1),\,\,x\ge 0, \end{aligned}$$

(58)

where

$$\begin{aligned} {C_j}\left( q \right) = \frac{{{{\left( {\beta + {\theta _j}\left( q \right) } \right) }^2}}}{{\frac{\sigma _1 ^2}{2}\prod \limits _{i = 1,i \ne j}^4 {\left( {{\theta _j}\left( q \right) - {\theta _i}\left( q \right) } \right) } }} , \end{aligned}$$

and ${\theta _j}\left( q \right)$ for $j\le 4$ are the (distinct) zeros of the polynomials

$$\begin{aligned}&(\psi (\theta )-q)(\beta +\theta )^2=\Big (\frac{1}{2}\sigma _1^2\theta ^2+p\theta -\lambda _1+\frac{\lambda _1\beta ^2}{(\beta +\theta )^2}-q\Big )(\beta +\theta )^2, \end{aligned}$$

By definition we have

$$\begin{aligned} \overline{Z}^{(q)}(x)= & {} \int _{0}^{x}Z^{(q)}(z)\mathrm {d}z =x\left( 1-q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}\right) +q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)^2}\left( \mathrm {e}^{{\theta _j}\left( q \right) x}-1\right) \end{aligned}$$

Hence, for $0<c\le z_{1}+c< z_{2}<\infty$, it holds that

$$\begin{aligned} \xi (z_{1},z_{2})= & {} \frac{z_{2}-z_{1}-c-\phi (z_2-z_1)\left( 1-q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}\right) }{\zeta (z_1,z_2)}\nonumber \\&\quad -\phi q\frac{ \sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)^2}\left( \mathrm {e}^{\theta _j(q)z_2}-\mathrm {e}^{\theta _j(q)z_1}\right) }{\zeta (z_1, z_2)}, \end{aligned}$$

(59)

where $\zeta (z_1, z_2)=q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}(\mathrm {e}^{\theta _j(q) z_2}-\mathrm {e}^{\theta _j(q) z_1})$. Differentiating both sides of (59) with respect to $z_1$ we get

$$\begin{aligned} \frac{\partial }{\partial z_1}\xi (z_{1},z_{2})= & {} \frac{-1+\phi \left( 1-q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}\right) +\phi q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}\mathrm {e}^{\theta _j(q)z_1}}{\zeta (z_{1},z_{2})}\\&+q\frac{\xi (z_1,z_2)}{\zeta (z_{1},z_{2})}\sum _{j=1}^{4}C_{j}(q)\mathrm {e}^{\theta _j(q)z_1}. \end{aligned}$$

Let $\frac{\partial }{\partial z_1}\xi (z_{1},z_{2})=0$ we have

$$\begin{aligned} \xi (z_{1},z_{2})=\frac{1-\phi \left( 1-q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}\right) }{q\sum _{j=1}^{4}C_j(q)\mathrm {e}^{\theta _j(q)z_1}}-\phi \frac{\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}\mathrm {e}^{\theta _j(q)z_1}}{\sum _{j=1}^{4}C_{j}(q)\mathrm {e}^{\theta _j(q)z_1}}. \end{aligned}$$

(60)

Similarly, we first differentiate both sides of (59) with respect to $z_2$ and then let $\frac{\partial }{\partial z_2}\xi (z_{1},z_{2})=0$ to obtain

$$\begin{aligned} \xi (z_{1},z_{2})=\frac{1-\phi \left( 1-q\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}\right) }{q\sum _{j=1}^{4}C_j(q)\mathrm {e}^{\theta _j(q)z_2}}-\phi \frac{\sum _{j=1}^{4}\frac{C_{j}(q)}{\theta _{j}(q)}\mathrm {e}^{\theta _j(q)z_2}}{\sum _{j=1}^{4}C_{j}(q)\mathrm {e}^{\theta _j(q)z_2}}. \end{aligned}$$

(61)

Numerically, we equate (59), (60) and (61) to obtain the maximizer of $\xi (z_1,z_2)$.

Let $p=8$, $\sigma _1=1.5$, $\lambda _1=3$, $\beta =2$, $c=0.2$, $\phi =1.05$ and $q=0.1$. Then the maximizer of $\xi (z_1,z_2)$ is $(z_1,z_2)=(0.1122,5.6223)$, and the corresponding second-order derivatives are $\frac{\partial ^2\xi (z_1, z_2)}{\partial z_1^2}=-2.8388<0$, $\frac{\partial ^2\xi (z_1, z_2)}{\partial z_2^2}=-0.1859<0$ and $\frac{\partial ^2\xi (z_1, z_2)}{\partial z_1 z_2}=0$, which verifies the optimality of (0.1122,5.6223). The surface of $\xi (z_1,z_2)$ is plotted in Fig. 4.

Fig. 4

The surface of $\xi (z_1,z_2)$ and its global maximizer

For the jump diffusion process, let the function G(x) be defined in the same manner as (57), where $W^{(q)}(x)$ and $Z^{(q)}(x)$ are given in (58), $\phi =1.05$, $q=0.1$, and $x\ge z_2=5.6223$. Similar to the case of Brownian motion with drift, we can also plot the curves of G(x) and $V^{z_2}_{z_1}(x)$, see Fig. 5a and b. Due to the presence of positive Gaussian coefficient $\sigma$ in the surplus process X(t), the resulting G(x) and the value function are both smooth. The trends of $z_1$, $z_2$, $z_2-z_1$ and $z_2-z_1-c$ along with the transaction cost parameters c and $\phi$ are also similar to the Brownian motion case as shown in Fig. 5a and b.

Fig. 5

The illustration of G(x) and the value function $V^{z_2}_{z_1}(x)$

Fig. 6

Optimal lump sum dividend amount w.r.t. the transaction parameters c and $\phi$

In addition to the impacts of c and $\phi$, the impacts of other model parameters also deserve to be investigated. To start with, the parameter p stands for the premium rate charged by the insurance company. The higher value of p, the corresponding surplus is more likely to achieve a higher level, which pushes the dividend paying threshold $z_2$ higher. Since in this case the company is more confident of its financial situation, more dividends are supposed to be paid out to the investors, which brings down the lower barrier $z_1$. As shown in Fig. 7, we observe a slightly decreasing value of $z_1$ and an increasing $z_2$ along with p. The lump sum dividend payments $z_2-z_1$ is also increasing.

We proceed with the volatility parameter $\sigma _1$. Higher $\sigma _1$ brings more uncertainty to the company’s financial situation, it would be wiser for the company to set up a higher dividend paying threshold $z_2$, and a higher lower barrier $z_2$ to reserve more capital in the account, which builds up more safety for the company. As for the arrival rate parameter $\lambda _1$, more frequent arrivals of claims results in a lower surplus level, then the overall dividend paying threshold $z_2$ should be lower. The reserve level $z_1$ after the payments of dividends is expected to be higher to secure the company’s financial situation. Lastly, the parameter $\beta$ describes the severity of each claim. The larger of $\beta$, the average amount of claims is smaller, which is a relief to the company’s surplus process, then the company is more likely to pay out dividends at a lower threshold $z_2$. The reserve barrier $z_1$ is also relaxed to a lower level indicating the company’s confidence of its financial situation.

Fig. 7

Optimal lump sum dividend amount w.r.t. the process parameters p, $\sigma$, $\lambda _1$ and $\beta$

6 Conclusions

This paper studies an optimal impulse dividend and capital injection problem. To imitate the real-world procedure of dividend payments, we also include the consideration of transaction costs. To describe the underlying surplus process, we use spectrally negative Lévy processes, which have been taken as good candidates to model insurance risks. Through maximizing the expected accumulated discounted net dividend payments subtracted by the accumulated discounted cost of injecting capital, we obtain the optimal IDCI strategy, which provides a useful reference for insurance companies when designing their long-term profit-sharing strategies.