1 Introduction

The application of composite material in load carrying structural components of an aircraft is rapidly gaining momentum. Three principal reasons for this can be identified. One, the continuous enhancements in the area of automated production technologies. Two, the progress in the development of computational methods to analyze and optimize composite structures to fully exploit their possible advantages. Three, the increasing confidence of designers in composite materials as a result of growing experience.

The identification of potential benefits to be achieved with composites, accordingly has entailed a considerable amount of research work. [39], for example, apply an approximation-based optimization to minimize the weight of a composite wing structure subjected to different combinations of buckling, strength, displacement and twist constraints. Although not optimizing, analyzing the effect of bending-twist coupling on the aeroelastic behavior of composites plates with various symmetric, unbalanced stacking sequences [17], demonstrate the effects induced by the coupling terms in the bending stiffness matrix. [14] investigates the influence of non-symmetric laminates on the aeroelastic behavior of high aspect ratio wings by applying an integrating matrix method to derive divergence and flutter speeds of various stacking sequences. A valuable survey on aeroelastic tailoring effects as a result of the directional stiffness in orthotropic composites is provided in [37]. They investigate possible influences of rotated fiber angles on minimum weight, twist, normal modes, flutter and aerodynamic performance for various configurations, ranging from fighter aircraft to forward swept configurations. A general overview on optimization technologies ranging from optimizations on panel level to the aeroelastic optimization of composites in aircraft wings is provided in [42]. [10] investigate the influence of layup orientation in a straight fiber design on the optimized mass of a low aspect ratio wing, constrained by strength, roll-reversal and flutter velocity.

In a more recent work [27], maximize the flutter eigenfrequency and speed of a composite plate wing with ply angles as design variables, considering symmetric and non-symmetric stackings. A related research, but for a tow-steered composite plate featuring symmetric layups is described in [40]. The effect of varying tow angles on eigenmodes, elastic axis, as well as divergence and flutter speed is investigated. [15] present a two-stage procedure, where in a first step, layer thicknesses and angles serve as the design variables in minimizing mass, subject to strength and damage tolerance constraints. The second stage focuses on a reduction of the wing’s response to a 1-cos-gust, measured by its transverse tip deflection.

Composite optimization with a focus on forward swept wings were first performed by [26], who demonstrated a considerable weight saving potential with the application of tailored stiffness distributions. [43, 44] performed detailed investigations into the effect of the spanwise stiffness distribution and bending–torsion coupling on divergence velocity, aileron effectiveness and spanwise center of pressure of forward swept wings.

Aeroelastic tailoring studies based on lamination parameters have been attempted previously. [24] using a composite plate wing demonstrated the influence of lamination parameters on the flutter and divergence characteristics. They consider a parametrization of the bending stiffness matrix only, while implying symmetric laminates. [16] demonstrate a two-step optimization scheme to minimize mass of an aeroelastically loaded wing. In a first step, lamination parameters describing symmetric but potentially unbalanced laminates in the skins and spars are used. The second step comprises a genetic algorithm-based stacking sequence optimization. Minimization of compliance of a variable stiffness slender wing represented by beam elements is demonstrated in [1]. The cross-sectional properties of the beam are parametrized using lamination parameters that define the membrane stiffnesses of the box cross section. Another two-level optimization strategy has recently been proposed by [29]. Allowing for symmetric and unbalanced laminates, a lamination parameter-based weight minimization is performed before applying genetic algorithms for the derivation of stacking sequences.

In [8], the authors describe a stiffness optimization strategy based on lamination parameters and the consideration of static aeroelastic constraints. The strategy is adopted in the stiffness optimization of a parametrically defined set of forward swept wings, [7], featuring equivalent wing area and span and variable leading edge sweep. The influence of several static aeroelastic constraints on the minimized wing skin mass is investigated, in particular focusing on potential benefits of unbalanced over balanced laminates. The present paper describes an advancement of the optimization framework by means of a correction of the aero loads adopted in the optimization, as well as a stacking sequence optimization following the continuous stiffness optimization. Correction methods, with a strong focus on doublet lattice, have received a lot of attention. [13] suggest methods that require either a correcting of DLM pressures or modifications to the downwash based on the aerodynamic influence coefficients. [32] provided a survey of the available correction techniques, focusing on unsteady aerodynamic forces. An industrial application of DLM correction is presented in [4], who suggest a least square correction method that makes use of unsteady CFD results, and a two-dimensional correction method. Both methods are aimed at correcting the aerodynamic influence coefficient matrix. In a more recent work, [9] compare gust responses obtained from DLM, CFD, and DLM that are corrected using quasi-steady CFD data.

The outline of the paper is as follows. Section 2 provides an overview of the continuous stiffness optimization framework. The aero load correction methods are introduced in Sect. 3. They are twofold, one, an adaptation of the camber line represented by the doublet lattice method that is integrated in the applied finite element solver, Sect. 3.1, and two, a correction of aero loads by means of a higher order CFD method, Sect. 3.2. An introduction to the stacking sequence optimization is provided in Sect. 4. Section 4.1 describes the methodology of stacking sequence tables, Sect. 4.2 introduces an interpolation strategy for response approximations. Results for the optimization of a forward swept wing are summarized in Sect. 5, starting with a model description, Sect. 5.1, a basic trim analysis, Sect. 5.2, a mass minimization, Sect. 5.3, and a stacking sequence optimization, Sect. 5.4.

2 Continuous stiffness optimization

For the optimization of composite structures, the problem is split into a three-step process, as detailed in [18], allowing for efficient use of suitable methods in each step. The first gradient-based design step targets optimal stiffness distribution using laminate stiffness matrices through lamination parameters as the design variables. Step one, which constitutes the central topic in the previous works on aeroelastic tailoring of composite wings, [7, 8], will briefly be introduced in this section. The second step targets an optimal stacking sequence design, with the optimization seeded from the design obtained in the first step. Details will be provided in Sect. 4. The third step deals with retrieving optimal fiber paths for manufacturing and is not part of this research.

Fig. 1
figure 1

Stiffness optimization process

Full size image

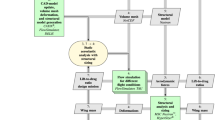
An overview of the step one optimization process is depicted in Fig. 1. The boxes featuring a gray background constitute the original process without aero correction. It corresponds to a successive convex subproblem iteration procedure, in which a gradient-based optimizer consecutively solves a local approximation problem.

The process is geared towards the optimization of the load carrying, shell-like structural components in a wing box, the properties of which can be represented as membrane A and bending stiffness matrices D, and shell thickness h. Considering only symmetric laminates, the coupling stiffness matrix B is zero and does not have to be considered.

The optimization is based on a finite element (FE) model of the wing structure that serves as an analysis model for the desired responses f, and for the evaluation of sensitivities \(\frac{\partial f}{\partial \mathbf x }\) of the responses with respect to the design variables x. In this research, the Nastran finite element solver is applied. The DLR–Institute of Aeroelasticity in-house tool ModGen [25] is used as a pre-processor to parametrically define and generate the FE model of the load carrying wing box, the aerodynamic and coupling model, as well as fuel and mass models. The responses and sensitivities serve as input for the derivation of an analogous analysis model that describes the behavior of each response in the surrounding of the analyzed design. For this purpose, each response is approximated as a function of potentially each design variable, while satisfying the essential properties of convexity, separability and conservativeness, as shown in the below equation:

$$\begin{aligned} \tilde{f} = \sum ^N_{j=1}\left( \hat{{{\varvec{\Psi }}_\mathbf{j }}}^m \big |_0 : \hat{\mathbf{A }}_\mathbf{j } + \hat{{{\varvec{\Psi }}}_\mathbf{j }}^b \big |_0 : \hat{\mathbf{D }}_\mathbf{j } + {{\varvec{\Phi }}_\mathbf{j }}^m \big |_0 : \mathbf A _\mathbf{j }^{-1} + {{\varvec{\Phi }}_\mathbf{j }}^b \big |_0 : \mathbf D _\mathbf{j }^{-1} + \alpha _j\big |_0 h_j \right) + C_0. \end{aligned}$$
(1)

The sensitivities generated with Nastran are converted to linear, \({\varvec{\Psi }}\), and reciprocal, \({\varvec{\Phi }}\), sensitivities with respect to the stiffness matrices, where superscripts \([\cdot ]^m\) and \([\cdot ]^b\) denote sensitivities with respect to membrane and bending stiffness, respectively. \(\alpha _j\) is the sensitivity with respect to the thickness design variable. The approximation model replaces the actual analysis model in the search of the optimizer for a minimum of the objective function \(f_0\), greatly accelerating the function evaluations required during the optimization. Within the optimizer, stiffness matrices A and D are represented as functions of lamination parameters, along with consideration of their feasible region as described for example in [36].

Each optimization step results in a new set of design variables that represent the global optimum of the convex approximation subproblem. Convergence is monitored by determining the change in the objective function for subsequent feasible iterations, Eq. (2). In case the change drops below a prescribed value \(\delta _\mathrm{stop}\), the optimization is stopped, otherwise the process continuous with the derivation of new responses and sensitivities:

$$\begin{aligned} \left| \frac{ f_{0}\bigr |_{(l+1)} - f_{0}\bigr |_{(l)} }{f_{0}\bigr |_{(l)}} \right| \le \delta _\mathrm{stop}. \end{aligned}$$
(2)

A detailed description of the optimization process and the components involved is provided in [6].

Aside from regular structural responses strength, buckling and mass, the aeroelastic responses aileron effectiveness, twist and divergence are considered in the optimization process. While their approximations are summarized in Table 1, the reader is referred to [6,7,8] for details on their derivation.

Table 1 Response approximations
Full size table

The process depicted in Fig. 1 is based on aeroelastic loads generated with the Nastran internal doublet lattice method. Methods for correcting those loads will be discussed in the following section.

3 Aero correction methods

The reason to perform a correction of the aeroelastic loads is the potential differences in wing surface pressures between the doublet lattice method developed for subsonic flows and presumably more correct higher order aerodynamic methods, usually designated as computational fluid dynamics (CFD). The latter types of methods allow for the consideration of flow phenomena that cannot be reproduced with DLM. Among the flow phenomena that should be considered the most important are

  1. 1.

    airfoil camber and thickness as opposed to the standard flat plate results obtained from DLM,

  2. 2.

    compressibility effects including local recompression shocks,

  3. 3.

    strongly non-linear aerodynamic lift and drag forces and sectional moments resulting from viscous flow phenomena like separation.

The doublet lattice method is also the built-in method of choice for computing steady and unsteady aerodynamic loads in Nastran, [34]. The theory is established in [3, 12], and [33]. It belongs to the potential theory methods, where potential flow singularities, distributed on a flat mesh, are superimposed with the undisturbed free stream. The strength of the singularities as a result of a linear system of equation has to be such, that the flow tangency at each box making up the mesh is fulfilled. This finally leads to a so-called aerodynamic influence coefficient matrix AIC that relates the pressure p in a box to the local downwash angle w of each box:

$$\begin{aligned} \mathbf w _j = \frac{1}{q} \mathbf {AIC} _{jj} \mathbf p _j. \end{aligned}$$
(3)

Along with a surface integration matrix S, the aeroelastic loads in each DLM box \(\mathbf f _{a}\) can be related to the pressures, Eq. (4):

$$\begin{aligned} \mathbf f _a= \mathbf S _{aj} \mathbf p _j, \end{aligned}$$
(4)
$$\begin{aligned} \mathbf f _\mathrm{DLM}= \mathbf H _{sa} \mathbf f _a, \end{aligned}$$
(5)

and ultimately to the aeroelastic loads in the structural coupling nodes \(\mathbf f _\mathrm{DLM}\) by means of a coupling matrix H, Eq. (5). Aero correction methods modifying either Eqs. (3) or (5) will be introduced in the following Sects. 3.1 and 3.2.

It should be noted that this paper does not necessarily focus on the most correct aerodynamic modeling strategy rather than on the provision of a general methodology which will allow for the consideration of all kinds of CFD-based aerodynamic fidelity levels in the aeroelastic optimization. To demonstrate the functionality of the method while maintaining reasonable modeling and computational effort, an Euler solver is applied in the present work, noting its shortcomings especially with respect to point 3 in the above listing of flow phenomena to be addressed. More details on this will be given in Sect. 3.2.

3.1 Camber correction

It is possible in Nastran to influence the geometric downwash w in Eq. (3) by a so-called W2GJ correction matrix. A detailed investigation of this contribution is provided in [23]. To this end, an individual downwash can be defined for each DLM box, corresponding to a local angle of attack change, as illustrated in Fig. 2. The required box rotations for the emulation of a camber line are shown in Fig. 2a. The chordwise constant rotation of each DLM box as shown in Fig. 2b is used to emulate a twist of the wing section.

Fig. 2
figure 2

DLM W2GJ correction illustration for a chordwise row of DLM boxes

Full size image

Both downwash types described in Fig. 2 can be varied in spanwise direction, allowing for the simulation of cambered airfoil blending and a geometric twist distribution. The parametric FE model generator ModGen by default provides three W2GJ correction matrices for camber, twist, and the combination of both, which are generated based on the wing planform and the airfoil data provided in the ModGen input file. Airfoil and planform data suffice to span the underlying aerodynamic surface.

In Sect. 5, it will be demonstrated that by a sole correction for airfoil camber and twist, an adequate agreement of pressure distributions computed with DLM and higher order aerodynamics can be achieved. This, however, only holds for lower, recompression shock-free Mach numbers. In the presence of shocks, the necessity for a correction by means of CFD is inevitable when aiming at an improvement of aeroelastic loads. Such a correction will be discussed in the following section.

3.2 CFD correction

Computational fluid dynamics, CFD, denotes methods used to solve the governing equations of a fluid flow. While the term is usually applied in conjunction with higher order volume mesh methods like Navier-Stokes solvers, strictly speaking it also applies to lower order methods. In the scientific community, as in this work, its meaning is dedicated to higher order methods exclusively.

Decision was made in favor of the DLR-German Aerospace Center unstructured CFD solver Tau, [11, 35]. It can be applied either for solving the full Navier-Stokes equations with a dedicated boundary layer and turbulence modeling, or in a simplified version, in which the viscous terms in the flow equations are neglected, hence resulting in Euler equations. Despite its inability to account for skin friction and flow separation—except at sharp corners such as trailing edges—as well as a biased shock prediction for strong shocks, [22, 45], the Euler solver is applied in the present work. The main reasons are the considerable time saving compared to a full Navier-Stokes calculation, along with faster mesh generation by avoiding the necessity for a dedicated boundary layer mesh. With respect to the consideration of recompression shocks, Euler constitutes a reasonable compromise between computational effort and the gain in accuracy of the aerodynamic loading, well suited for the application in the structural optimization process. It should be noted, however, that capturing viscous effects is still out of scope and requires the application of higher order methods.

Fig. 3
figure 3

Force vectors at the coupling nodes

Full size image

The basic idea behind the entitled CFD correction consists of rectifying aerodynamic loads obtained using the doublet lattice method by means of the supposably superior CFD results. To this end, the relevant sizing load cases are analyzed with Tau, considering an appropriate volume mesh deformation that resembles the structural displacements. With the doublet lattice forces concentrated onto the coupling nodes, compare Eq. (5), the same nodes are selected for splining the surface forces obtained from the Euler calculation. The difference between the CFD force vector and the DLM force vector at each coupling node is applied as a static amendment to the respective load case. The force vectors on a deformed wing structure are shown in Fig. 3.

3.2.1 Process

The process of correcting the aerodynamic loads obtained with DLM constitutes an addition to the existing optimization framework [8]. In Fig. 1, the CFD correction part is already incorporated. It is defined as a stand-alone module that collaborates with the optimization via well-defined interfaces.

For each load case that is to be corrected using CFD aero loads, the necessary input is generated along with the Nastran runs required for sensitivity derivation and passed to the CFD correction module. The input consists of structural displacements at the coupling nodes, utilized for the CFD mesh deformation, and the flow parameters Mach number, stagnation pressure, density and the angle of attack.

Two important notes have to be addressed at this point. One, the Euler calculation is performed for the same angle of attack as identified in the Nastran DLM trim maneuver analysis. Two, the displacements passed to the load correction process and used in the mesh deformation routines in the beginning are not necessarily converged displacements. Only throughout the structural optimization process, the loads and displacements eventually will converge, as will be shown below and be supported by computational results in Sect. 5.3.

Only symmetric maneuver and cruise load cases are designated for CFD correction, the first due to their potential to drive the structural sizing and the latter due to the evaluation and possible constraining of wing twist. In both cases, the corrected aero loading can have a significant influence on the results. The reason to consider only symmetric load cases is twofold: one, the currently limited analysis capabilities confined to symmetric steady cases and two, in lack of further information available, the effort to capture the largest loads by means of only a few load cases, see for example [6].

Once the CFD forces are generated and condensed to the coupling nodes, denoted as \(\mathbf f _\tau\) in Fig. 1, they are subtracted from the appropriate DLM forces \(\mathbf f _{\rm DLM}\), yielding the correction forces \(\Delta \mathbf f _\tau\):

$$\begin{aligned} \Delta \mathbf f _\tau ^k = \mathbf f _\tau ^k - \mathbf f _{\rm DLM}^k \; , \end{aligned}$$
(6)

where superscript \(^k\) indicates the structural iteration steps for which Tau corrections are generated.

The correction forces are grouped by load case and saved in the appropriate NastranFORCE card format. A new optimization process is initiated, this time including the correction forces during the responses and sensitivity generation. They will have a direct influence on responses such as strains and displacements, and only an indirect influence on sensitivities via the forces influence on the aeroelastic behavior. The loop of optimizing and computing new correction forces is continued until an overall convergence is achieved. Investigations have shown that a recalculation of the correction forces is not necessarily required during each, but only every \(n{\rm th}\) iteration step. Details will be provided in Sect. 5.

Usually, an aeroelastic trim calculation in Nastran ensures that the lift forces generated by the doublet lattice model exactly balance the weight vector multiplied with the vector defining the load factor. Performing a trim calculation along with the additional correction forces implies a force distribution at the coupling nodes in the trimmed solution, which exactly matches the CFD results. Since this only is true if the structural properties and, therefore, the stiffness remains unchanged, this statement strictly speaking does not apply during the optimization, where stiffness properties deliberately are modified. The reason is that during an optimization sequence, the correction forces remain constant and will only be updated after n iterations performed in the optimization block. Details on the influence on the load displacement behavior will be addressed in more detail in Sects. 5.2 and 5.3.

In the following, an examination of the convergence behavior will be given to demonstrate the acceptance of this approach. Setting up the static equilibrium equation for the \((k+n){\rm th}\) iteration leads to

$$\begin{aligned} (\mathbf K - q \mathbf K ^{A}) \mathbf u ^{k+n}_s = \mathbf f _{ie} + \Delta \mathbf f _\tau ^{k}, \end{aligned}$$
(7)

where \(\mathbf K ^{A}\) is the aerodynamic stiffness matrix, which links structural displacements to the aerodynamic forces generated by DLM according to

$$\begin{aligned} \mathbf f _{\rm DLM} = q \mathbf K ^{A} \mathbf u _s. \end{aligned}$$
(8)

Superscript \(^k\) denotes the last structural iteration step for which Tau correction forces were generated, and accordingly superscript \(^n\) is the nth subsequent structural iteration step. This notation implies that Tau corrections not necessarily have to be performed for each structural iteration. Vector \(\mathbf f _{ie}\) represents inertial and external forces. Inserting Eqs. (6) and (8) in (7) yields

$$\begin{aligned} \mathbf K \mathbf u ^{k+n}_s - \mathbf f _{\rm DLM}^{k+n} = \mathbf f _{ie} + \mathbf f _\tau ^{k} -\mathbf f _{\rm DLM}^{k}, \end{aligned}$$
(9)

and thus,

$$\begin{aligned} \mathbf K \mathbf u ^{k+n}_s = \mathbf f _{ie} + \mathbf f _\tau ^{k} + \Delta \mathbf f _{\rm res}, \end{aligned}$$
(10)

where

$$\begin{aligned} \Delta \mathbf f _{\rm res} = \left( \mathbf f _{\rm DLM}^{k+n} -\mathbf f _{\rm DLM}^{k} \right). \end{aligned}$$
(11)

Equation (10) states that in a converged solution where the residual force \(\Delta \mathbf f _{\rm res}\) vanishes, the static equilibrium is determined entirely by means of Tau aerodynamic forces \(\mathbf f _\tau\), keeping in mind that according to Eq. (6) the aerodynamic force vector is a combination of doublet lattice forces and correction forces, \(\mathbf f _\tau = \mathbf f _{\rm DLM}+ \Delta \mathbf f _\tau\). At this point, it should be stressed that the converged aeroelastic deformation \(\mathbf u\) complies with the Tau aerodynamic forces, and likewise also accounts for the displacement-dependent doublet lattice forces according to Eq. (8).

3.2.2 Implementation

The CFD correction module depicted in Fig. 1 takes over the task of computing Euler CFD forces at the coupling nodes, based on the input that is required to perform a Tau calculation on a deformed mesh. The essential steps successively performed in the module are illustrated in Fig. 4.

Fig. 4
figure 4

CFD correction module flow diagram

Full size image

Equivalent to the coupling matrix applied in Eq. (5), a coupling matrix H to map FE node deformations onto the CFD surface mesh, Eq. (12), needs to be constructed. The transpose of H can also be used to achieve the second goal of transforming CFD forces onto the structure, Eq. (13):

$$\begin{aligned} \mathbf u _{a}= & {} \mathbf H \mathbf u _{s}, \end{aligned}$$
(12)
$$\begin{aligned} \mathbf f _{s}= & {} \mathbf H ^T \mathbf f _{a}. \end{aligned}$$
(13)

In this research, the coupling method by [31] is applied. The volume mesh deformation following the surface mesh deformation is part of the Tau software suite. Details are described in [6].

The CFD meshes employed in this work were generated using the surface modeler and unstructured volume mesher sumo, [41]. Depending on the intended surface pressure resolution, result accuracy, in connection with, for example, the computed shock position, and the CFD convergence and computing time, the generated Euler meshes usually exhibit \(\approx 200{,}000\) to 300,000 triangular surface elements and tetrahedra elements ranging from \(\approx 0.7 \times 10^6\) to \(3 \times 10^6\). sumo allows for a mesh export directly in the appropriate Tau mesh format.

4 Stacking sequence optimization

In this section, the second stacking sequence design step is described using the method developed in [30]. It constitutes the next step subsequent to the continuous optimization process depicted in Sect. 2, which in turn provides the required stiffness matrix input and sensitivities. The stacking sequence design tool [30] consists of a stacking sequence table (SST)-based genetic algorithm (GA) for the design of blended structures, [21], combined with a modified Shepard’s method for improving approximation accuracy in the GA, [20].

4.1 Stacking sequence table

In an efficient variable stiffness design, usually a finite number of panels each having constant stacking sequence are considered. Laminate blending [46] is a technique that assures continuity of fiber and material content between such adjacent panels having different ply layups, thus enhancing structural integrity and manufacturability. [19, 38] present some of the successful attempts at achieving fully blended optimal designs.

A stacking sequence table is an intuitive way of representing the ply layup of panels in a blended composite structure. Each column in an SST essentially corresponds to the stacking sequence of a certain number of plies. Starting with the stack featuring the smallest thickness, plies are added successively, following several design guidelines, up to the maximum number of plies. This ensures that the plies in the thinnest stack are carried on to the thicker ones, thus inherently satisfying the requirement of blending, without enforcing it as additional constraints.

In comparison to previous works on blended composite design, [2, 19, 28], the SST-based optimizer [21] offers the following advantages:

  • implementation of several industry-standard laminate and ply-drop design guidelines;

  • explicit information of ply-drop sequence among adjacent panels for manufacturability;

  • fully blended designs according to the generalized blending definition [5].

An advantage inherent to this approach is the compact and efficient form of encoding of the entire SST using only two chromosomes. \({\rm SST}_{\rm lam}\) defines the stacking sequence of the thickest laminate and \({\rm SST}_{\rm ins}\) defines the order in which plies are inserted from the thinnest to thickest plies. By suitably optimizing for these two chromosomes and the ply numbers in the panels, an optimal blended structure can be obtained. An example of an SST having ply numbers between six and ten is shown in Fig. 5.

Fig. 5
figure 5

Example of SST with six to ten number of plies

Full size image

4.2 Successive approximations

The concept of successive approximations as introduced in Sect. 2 helps to reduce computational costs related to expensive FE analyses. This is realized by carrying out the optimization on approximations of responses, Eq. (1), rather than expensive FE responses themselves. The optimization is iteratively followed by a design update and construction of new approximations for the next optimization loop. A similar successive approximation framework is used in this stacking sequence step also.

The aeroelastic response approximations listed in Table 1 are applied also in the GA to evaluate the optimization objective and constraints. The stacking sequence optimizer presented in [30] addresses strength and buckling constraints using a modified approach. Rather than using direct approximations of strain and buckling as in [8], panel loads are directly approximated instead:

$$\begin{aligned} \tilde{N} \simeq \sum _{j}{{\varvec{\Psi }}}_{j}^{m}:\mathbf{A }_{j} + {{\varvec{\Psi }}}_{j}^{b}:\mathbf{D }_{j} + \alpha _j h_j , \end{aligned}$$
(14)

where \({{\varvec{\Psi }}}^{m}\) and \({{\varvec{\Psi }}}^{b}\) are panel load sensitivities evaluated from Nastran. The panel loads are then used to evaluate strain and buckling responses using suitable analytical tools. The benefit of such an approach is that using a direct analysis of approximated loads compensates for the increase in computational time with a higher accuracy in the buckling and strain responses themselves.

The approximations mentioned above are single-point approximations constructed at a design point and are accurate only at that particular point. A modified Shepard’s method [20] constructs multi-point approximations by interpolating previously analyzed design points, thus improving the quality of the approximations. For instance, the aileron effectiveness response is evaluated using such a multi-point approximation as

$$\begin{aligned} \tilde{\eta }_{\rm ail}(\mathbf x ) = {\frac{\sum \nolimits _{i = 1}^{n} {{w_{i}}}(\mathbf x ) \,{\tilde{\eta }_{{\rm ail}_i}}}{\sum \nolimits _{i = 1}^{n} {{w_i}}(\mathbf x ) }}, \end{aligned}$$
(15)

where \({\tilde{\eta }_{{\rm ail}_i}}\) is a single-point approximation of the aileron effectiveness response at the \(i{\rm th}\) point as in Table 1, \({{w_{i}}}(\mathbf x )\) is a weighting function defined in [20] and n is the total number of approximation points. An improvement in the quality of the approximations naturally results in a faster convergence.

4.2.1 Optimization steps

  1. 1.

    At the optimal design obtained from the continuous stiffness optimization step, response approximations are evaluated. This forms the first design point.

  2. 2.

    The optimal solution to this approximate subproblem is then found using the GA for SST, wherein response approximations are used to evaluate the objective and constraints. In this step, approximations for mass, twist, divergence and aileron effectiveness are evaluated to obtain the respective approximate responses. Panel strength and buckling are estimated analytically from the panel loads, which are approximated from the load sensitivities.

  3. 3.

    An FE analysis at the optimal design point obtained in step (2) yields new response approximations at this point.

  4. 4.

    A multi-point approximation of the responses (as in Eq. 15) is formulated using all single-point approximations obtained till the present iteration. Steps (2)–(4) are then sequentially repeated till convergence.

Two possible objective functions for the GA optimization can be utilized. In the first case, the objective function of the GA is directly chosen as the particular response to be minimized, for instance structural mass. In the second case, the objective function aims to match the stiffness of the GA design to the optimal stiffness obtained in the previous continuous optimization step. The optimizer described here and in the ensuing results utilizes the former approach.

5 Results

A stiffness optimization with corrected aero loads, followed by a stacking sequence optimization, likewise featuring aero load correction, is demonstrated in this section.

5.1 Model description

With this work following up on the research presented in [7], the same reference model for demonstration of the developed processes was adopted. An overview on the analysis model is presented in Fig. 6. In Fig. 6a, the dimensions of wing and wing box are depicted. The corresponding FE model is shown in Fig. 6b, along with non-structural masses in front and aft of the wing box and clamping at the root rib. The fuel model, featuring one concentrated mass per rib bay is shown in Fig. 6c. The DLM and aero-structural coupling model are depicted in Fig. 6d.

Fig. 6
figure 6

Reference model setup

Full size image

The coupling nodes are based on the so-called load reference axis (LRA), which consists of a virtual axis in spanwise direction that is marked by grid points in each rib plane. The grid points are attached with RBE3 multi-point connections to the corresponding circumferential rib nodes. Each LRA grid point comprises two RBE2 rigid elements, one extending to the leading edge of the underlying planform and one to the trailing edge.

All the above-mentioned models were parametrically generated with the ModGen pre-processor. A detailed description of the model generation process and the applied mass and material properties are given in [6].

Load cases applied in the optimization are listed in Table 2. They can be grouped into maneuver load cases used for sizing of the structure (1–4), a cruise load case (7), load cases for the determination of aileron effectiveness (12–15), and a divergence load case (16). The load cases are combined with five mass cases resulting from variations in fuel and passenger mass. Masses for half the fuselage and tails were attached to the clamping node on the centerline. Presumably, the most unfavorable combination of empty wing tanks and maximum passenger load was considered for sizing load cases (1–4). The cruise load case (7) was investigated for a wing fuel loading approximately corresponding to begin/mid, and end of cruise flight, and for maximum and half passenger loading, totaling four more load cases. The aileron effectiveness at a constant roll rate and divergence load case were independent of the mass distribution and could, therefore, be computed along with one of the depicted mass cases (further details on the responses can be found in [6]). It should be noted that mainly the lack of an adequate sensitivity derivation technique in a time-varying analysis did not yet allow for a consideration of gust load cases in the optimization.

Table 2 Load case definition
Full size table

The optimization model comprised in total 68 design fields, Fig. 7, where a design field specifies a group of elements that all refer to the same, unique set of stiffness matrices and shell thickness. Accordingly, the design variables are made up of 68 independent (A, D, h)-sets.

Fig. 7
figure 7

Design fields

Full size image

Approximations for strain and buckling failure, aileron effectiveness, divergence and twist were implemented according to the derivations summarized in Table 1. This included the convexification of aeroelastic responses, described in [6]. The strain allowables required for the failure envelope construction were set to \([\varepsilon _t, \ \varepsilon _c, \ \gamma _{xy}] = [0.5\%, \ -0.4\%, \ 0.4\%]\).

The CFD mesh was generated with sumo and based on the same planform and airfoil coordinate input defined for the generation of the finite element model. To determine the appropriate mesh resolution that would be required to achieve convergence of the important aerodynamic quantities such as lift and moment, a convergence study was performed. The values of lift, moment and drag coefficient, \(C_{\rm L}\), \(C_{\rm m}\) and \(C_{\rm D}\), for six meshes featuring different tetrahedra numbers are presented in Fig. 8a. As stated by the figure, the coefficients converged for meshes with element numbers above \(\approx 1.5 \times 10^6\).

Fig. 8
figure 8

Reference model CFD mesh

Full size image

The mesh that was finally selected for the aero correction process consisted of \(\approx 2.7 \times 10^6\) tetrahedra and is marked by a blue star in Fig. 8a. It comprised \(\approx 315,000\) surface triangles, a spanwise section of which is shown in Fig. 8b, to give an impression on the element density and distribution as it was achieved using diverse sumo meshing parameters.

In response to the vast amount of significant results generated by trim calculation and stiffness optimization using aero correction forces, only the most interesting results and load cases are selected for presentation. They are chosen depending on the particular structural or aerodynamic focus. The reader is referred to [6] for an in-depth discussion of the findings.

5.2 Trim application

To separate the effects of a newly applied CFD aero correction from the effects induced by a stiffness optimization, the general functionality of the CFD correction module was demonstrated using a classical static aeroelastic trim application. In doing so, the most prominent differences between the results of the applied aerodynamic methods can be highlighted.

The iterative procedure to determine the aeroelastic deformation considering Tau correction forces can be expressed as

$$\begin{aligned} \mathbf u ^{k+1}_s= \mathbf K ^{-1} \left( \mathbf f _{\rm DLM}^{k+1} + \Delta \mathbf f _{\tau }^{k} + \mathbf f _{\rm ie} \right), \end{aligned}$$
(16)

with

$$\begin{aligned} \Delta \mathbf f _{\tau }^{k}= \mathbf f _{\tau }^{k} - \mathbf f _{\rm DLM}^{k}, \end{aligned}$$
(17)

where superscript \(^k\) denotes the iteration step and \(\mathbf f _{ie}\) corresponds to the summation of constant inertial and external forces. An iterative procedure which performs deformation and aerodynamic analysis in a sequential order is referred to as a weakly coupled system, whereas in a closely coupled system the aerodynamic forces can be expressed directly as a function of displacement, thus allowing for a direct solution of the static equilibrium equation.

According to Eq. (16), convergence can be tested by monitoring either a characteristic node deflection or the iterative behavior of the aerodynamic forces. This is shown in Fig. 9, exemplarily for a sizing and a cruise load case. The load case numbering corresponds to the definition given in Table 2, where the last two digits identify the load case and the first digit the mass case.

Fig. 9
figure 9

Static trim monitoring

Full size image

The deflection shown in Fig. 9a is monitored at the outermost spanwise load reference axis grid point, representing the tip of the wing. In the finite element solution of iteration \(k=1\), Tau forces \(\mathbf f _{\tau }^{0}\) were not yet included. They are generated only afterwards, for a CFD mesh deformation which is based on the displacement results of the FE analysis. Accordingly, only DLM forces affected the deflection for iteration \(k=1\). From the second iteration onwards, Tau forces based on the previous FE analysis were included. Figure 9a shows that once the correction forces are considered from iteration two on, convergence was achieved after three to four iteration steps.

The same holds for the monitored aero loads, Fig. 9b. Depicted in the upper axis is the force development for DLM and Tau, respectively. \(|\mathbf f _{\rm aero}|\) denotes the magnitude of the sum over all aerodynamic forces in the xz-plane. Aside from quick convergence, a second very important finding is the convergence of the resulting Tau force towards exactly the same value as the DLM force in the first iteration step \(k=1\), which did not, as yet, comprise the correction forces. This implies that the combination of \(\mathbf f _{\rm DLM}\) and correction \(\Delta \mathbf f _{\tau }\) in the converged solution exactly reflects \(\mathbf f _{\tau }\), as it was stated in Eq. (17), \(\mathbf f _{\tau } = \mathbf f _{\rm DLM} + \Delta \mathbf f _{\tau }\). The corresponding force magnitude reflects the constant lift force required to balance aircraft weight multiplied by the load factor.

The lower axes in Fig. 9b depict the relative differences between the DLM and Tau force magnitudes. It was mentioned previously that the TauEuler calculation is performed for the same angle of attack as that resulting from the Nastran trim analysis. Thus, the converged difference between \(|\mathbf f _{\rm DLM}|\) and \(|\mathbf f _{\tau }|\) is based only on aerodynamic discrepancies among the two discretization and analysis methods.

To demonstrate the impact of the two aero load correction methods presented in Sect. 3, a comparison of pressure difference \(\Delta C_{\rm p}\) between upper and lower surfaces for DLM and Tau is plotted in Fig. 10.

Fig. 10
figure 10

Pressure difference \(\Delta C_{\rm p}\) for the converged trim solution

Full size image

A comparison for LC 1002, hence a sizing load case with \(n_z\,\,=\,\,+\,\,2.5\,\,{\rm g}\) and a rather low Mach number of \(M=0.597\) is shown in Fig. 10a. Evidently, the camber-corrected DLM was in good agreement with the higher order aerodynamic CFD method Tau. In all the depicted sections, DLM reproduced the main trends, although slightly downstream of the Tau results. With the DLM mesh featuring a considerably coarser discretization, no data were available at the trailing edge; the largest deviations, therefore, occurred at these positions. An entirely different behavior is revealed when looking at the second \(n_z=+\,\,{\rm g}\) sizing load case 1004, Fig. 10b. The free stream Mach number was considerably higher, resulting in a strong shock on the upper and on the lower wing surface and thus a considerable influence on the pressure difference \(\Delta C_{\rm p}\). As a result of the large negative pressure difference in the back, and a decrease in the frontal part with respect to the doublet lattice results, the Tau distribution was expected to cause a larger nose-down, thus negative twisting moment.

5.3 Numerical results: mass minimization

Having demonstrated the functionality of the aero correction process in a pure trim analysis, the application and interaction within the stiffness optimization process were tested. While the wing skin mass was defined as the objective to be minimized, the structural constraints again comprised strain and buckling failure for all shell elements belonging to the specified design fields. In terms of aeroelastic responses, only aileron effectiveness and divergence were constrained, while no constraint was defined for twist. Aileron effectiveness for the four load cases listed in Table 2 was limited by a lower bound to \(\eta _{\rm ail} \ge 0\), thus no aileron reversal. Divergence was constrained to a lower limit of \(q_{\rm div} \ge 35,000\,{\rm Pa}\) at a Mach number of \(M=0.87\), ensuring a reasonable clearance with respect to the aeroelastic stability margin (1.15 times the dive Mach number/velocity). To confirm the mass minimization results, several variations of the starting design, comprising modifications on thickness and stacking sequence, were optimized in parallel. Except for some exceptions, all the starting designs led to the same optimum in terms of minimum mass and optimized thickness and stiffness.

The minimized masses of the investigated combinations with and without aero correction as well as balanced and unbalanced laminates are listed in Table 3.

Table 3 Optimized wing skin masses
Full size table

As illustrated by the table, consideration of the aero correction did not imply a fixed impact on optimized mass, given by the fact that the mass increased for balanced, and decreased for unbalanced laminates. Anyway, the intention of the aero correction lies in the improvement of sizing loads and the enhanced determination of the aeroelastic responses. Owing to the considerable mass savings of unbalanced over balanced laminates, the sections focus will be placed on the results attained with unbalanced laminates.

Fig. 11
figure 11

Aero force development, unbalanced laminates

Full size image

In a first step, the aero force development during the stiffness optimization was reviewed to ensure convergence of the structural properties, and of the correction forces. The results for two sizing load cases are depicted in Fig. 11. In the optimization process depicted in Fig. 1, a Tau correction run was requested every five structural optimization steps. The dashed blue lines in Fig. 11 indicate a Tau correction run at the \(4{\rm th}\), \(9{\rm th}\), \(14{\rm th}\ldots\) iteration step. Accordingly, the new correction forces were only available for these iterations, while DLM forces were generated during each iteration step. The graphs state that the Tau and DLM forces for all sizing load cases converged, while in parallel, the optimization process minimized the mass objective by modifying the stiffness properties and thus the aeroelastic behavior. The trim application already proved a fast convergence with constant structural properties, and the stiffness changes during the optimization did not considerably deteriorate the convergence behavior. Nevertheless, Fig. 11 reveals a more gradual correction force change during the optimization, compared to the already good agreement seen with respect to the final state for the second Tau correction step in the trim application.

Fig. 12
figure 12

Optimized design, unbalanced laminates

Full size image

The optimized thickness and stiffness distribution are plotted in Fig. 12, where \(\hat{E}_{11}(\theta ) = 1 / \hat{A}_{11}^{-1} (\theta )\) is the polar thickness normalized engineering modulus of elasticity. It allows for a visual assessment of the directional membrane stiffness distribution. In search of a weight optimal solution, bending–torsion coupling was introduced by tilting the major stiffness direction from inner to outer wing gradually forward, thus leading to a negative twisting tendency when bending the wing up. Thereby the center of lift could be shifted inward, eventually reducing the root bending moment.

Fig. 13
figure 13

Aeroelastic constraints development, unbalanced laminates

Full size image

The optimization with aero correction led to an active divergence pressure constraint, while it was not active when optimizing with DLM only. Divergence pressure as developing throughout the iteration steps is shown in Fig. 13a. The aileron effectiveness remained clearly in the feasible domain; the lowest, still inactive response is shown in Fig. 13b.

Fig. 14
figure 14

Optimized design, sizing load case per field, unbalanced laminates

Full size image

More prominent differences when applying aero correction were revealed when looking at the load cases that accounted for the highest strength or buckling failure index in each design field, Fig. 14. Plots in the left column depict upper and lower skins of the optimized model including aero correction (denoted “DLM & Tau ”), the equivalent, but without aero correction (denoted “DLM”), is shown in the right column. While wing skin sizing for the optimization without aero correction was clearly dominated by \(n_z\,\, =\,\,+\,\,2.5\,\,{\rm g}\) LC 1002 and \(n_z\,\,=\,\,-\,\,1.0\,\,{\rm g}\) LC 1003 and only a few design fields being sized by LC 1004 and none by LC 1001, the allowance for aero correction led to a perceptibly different distribution. Distinct spanwise and chordwise regions developed, comprising all sizing load cases considered in the optimization. It should be noted that the distributions shown in Fig. 14 are only an indicator of the dominant load cases. Even a slightly lower failure index in an element resulting from another load case is not represented in this plot.

The differences in twist for an optimization with aero correction compared to an optimization without is depicted in Fig. 15, in which the spanwise twist distribution for two high Mach number sizing load cases 1003 and 1004, and for two representative cruise load cases 2007 and 5007, featuring the largest mass variation among the investigated cruise conditions, are shown.

Fig. 15
figure 15

Optimized design, twist distribution with and without aero correction, unbalanced laminates

Full size image

Unexpectedly, the \(n_z\,\,=\,\,+\,\,2.5\,\,{\rm g}\) pull-up maneuver LC 1004 in both optimizations showed a negative tip twist, differing by \(\approx 2^\circ\). The reason for this could be found in the bending–torsion coupling evoked by the variable stiffness orientation, Fig. 12b. The twist distribution promoted compliance with the divergence pressure constraint and helped to alleviate loads in the outer wing, thus supporting mass minimization. The twist being more negative when considering aero correction could be attributed to the different structural designs and to the more negative aerodynamic airfoil moment. As a result of the superposition of geometric coupling of the forward swept wing, and the negative aerodynamic twisting moment, and despite the lower inertial and, therefore, aerodynamic loading in case of the \(n_z\,\,=\,\,-\,\,1.0\,\,{\rm g}\) push-down maneuver LC 1003, the wing twisted considerably more negatively for LC 1003 compared to LC 1004. Again, the difference between the aero-corrected design and non-corrected design could mainly be attributed to the different aerodynamic moment distribution.

5.4 Numerical results: stacking sequence optimization

Fig. 16
figure 16

Distribution of independently blended regions in the upper skin

Full size image

The results from the stacking sequence optimization as described in Sect. 4 are presented here. The optimization hence constitutes the second step in the three-step design process. The results for the forward swept model are introduced above, subjected to the same load cases, objectives and constraints. The continuous stiffness optimization presented in the previous section showed an optimal wing box mass of 403.9 kg with unbalanced laminates. This mass represents the theoretical upper bound in performance that can be achieved since a lamination parameter-based continuous optimization does not impose any restriction on ply angles, ply thickness or laminate continuity. This continuous design constituted the first design point in the stacking sequence optimization, helping to efficiently find the region of interest for the GA to search.

For this step, the wing was modeled to comprise six independently blended regions—hence, six independent SSTs. This is more appealing from an industrial perspective, wherein a large structure such as an aircraft wing is manufactured as segments before being joined together. Enforcing blending over the complete wing hence only constrains the design space by combining structurally separate entities. Shown in Fig. 16 is the distribution of the independently blended regions over the upper wing surface. A similar distribution is also used for the lower surface.

The GA parameters and the design guidelines enforced are presented in Table 4. The optimal stacking sequence design was found to have a wing mass of 485.9 kg, or \(\approx\)20% higher mass than the stiffness-optimal design. Importantly, the optimal stacking design was feasible, i.e., having a safety factor for the design constraints of exactly 1.0. The increase in mass over the stiffness-based design can be attributed mainly to the following reasons: allowable thickness only in discrete steps of the ply thickness, discrete set of allowable ply angles, enforcing ply continuity through blending, inclusion of several design guidelines and the limitations of a GA search in itself.

Table 4 GA parameters and design guidelines, [21]
Full size table

The optimized thickness and stiffness distribution are plotted in Fig. 17. A direct comparison of Fig. 17b with the continuous optimization counterpart, Fig. 12b, identifies an equivalent tendency of the wing to have a forward-tilted stiffness, indicating the dominant direction of the ply angles. The discrete design, however, shows a rather smeared distribution of the stiffness with a less articulate directional alignment.

Fig. 17
figure 17

Optimized stacking design, unbalanced laminates

Full size image

A comparison of the thickness in Fig. 17a with Fig. 12a shows a more gradual decrease in the thickness of the plies from root to tip in the stacking sequence design. Some of the elements, in fact, have a lower thickness than in the theoretical continuous optimum itself. The above observations are a consequence of the blending requirement—each panel in a blended design is influenced by the ply layup in all the other panels in that blended region. This results in a smooth and ’smeared’ distribution of the thickness and ply angles, resultantly in the stiffness itself.

6 Conclusion

A detailed insight into the application and implications of a doublet lattice force correction using a higher order CFD method in an aeroelastic stiffness optimization was presented.

The trim application demonstrated the general functionality and convergence of the correction procedure, and highlighted the differences to be expected when using the two aerodynamic methods Tau and DLM. The improvements made in the doublet lattice method due to using a W2GJ camber correction and the limitations of this correction with the emergence of recompression shocks were illustrated. It was shown that the consideration of camber correction did greatly improve DLM quality when applied in shock-free conditions. The effects of aero correction consideration on mass minimization, emphasizing the differences with respect to optimizations that did not feature an aero correction, were highlighted.

The applied Euler method proved to converge reliably with the mesh generated in sumo. Nevertheless, it should be mentioned that the Euler method has a limited application range. With increasing angle of attack and thus lift coefficient, Euler predicts the shock to move more and more downstream, increasing in strength. Flow separation, other than at the sharp trailing edge, cannot be modeled. Accordingly, in the case of severe aerodynamic load conditions, the Euler results will start to deviate from what can be expected in reality. A possible solution to this problem is to increase CFD fidelity further, and thus consideration of the full Navier-Stokes equations along with viscous boundary layers and turbulence modeling. Apart from the need for a new CFD mesh topology including a prismatic sub-layer, the required changes to the developed CFD correction module are minimal.