Structural optimization of an aeroelastic wind tunnel model for unsteady transonic testing

Abstract

The reduction of loads, ultimately leading to a weight reduction and thus an increase in aircraft performance, plays an important role in the design of modern aircraft. To this end, two aeroelastic tailoring methodologies, independently developed at ONERA and DLR and aiming at load reduction by means of a sophisticated application of composite materials, were applied to a common model geometry. A choice was made in favor of the publicly available NASA Common Research Model (CRM) wing, featuring a comprehensive database with respect to geometry, as well as analytical and experimental research results. The span of the wing half to be investigated was set to 0.55 m, limited by the test section dimensions. While wind tunnel testing was part of ONERA’s workshare, the model building was performed by DLR. This paper at hand focuses on the structural, aeroelastic optimization of the DLR wing. It is based on an optimization framework developed and constantly being enhanced and extended at the DLR - Institute of Aeroelasticity (DLR-AE). The paper describes the consideration of different structural objective functions, structural and aeroelastic constraint combinations, design field considerations, as well as the application of an aero load correction applied in the course of the optimization. The final results consist of the selection of an appropriate fiber type, optimized fiber layers represented as stacking sequence tables for the upper and lower wing skins, and the corresponding optimized jig twist distribution, required for manufacturing the lamination molds; in summary, all data required to start the construction of the wind tunnel model.

1 Introduction

Research towards reducing loads in primary structural aircraft components is an ongoing subject and has been so for many decades. Its main driver clearly is a reduction in aircraft weight and thus an increased transport capacity on the one hand, and an enhancement in fuel efficiency and ultimately environmental and economic aspects on the other hand. Two major branches of load reduction techniques can be identified: passive and active load reduction [1]. The latter typically refers to the use of control surfaces in order to influence lift and/or drag, also known as aeroservoelasticity.

The research presented in this paper deals with passive load reduction techniques, which can either be achieved by geometrical measures like sweep angle and taper ratio adaption, topological variations in the load carrying structure, or by means of material considerations. Within the scope of the “DLR—ONERA Partnership in Transport Aircraft Research”, a common research program (CRP) called FIGURE—Flexible Wind Gust Response—was launched to investigate means of passive load control in the transonic regime, featuring a gust excitation via a gust generator mounted upstream of the test section.

The introduction of fiber reinforced materials along with aeroelastic tailoring techniques has led to a technology leap and in the past decades to a considerable amount of research work. Aeroelastic tailoring in this respect denotes a targeted application of fiber reinforced materials to optimally perform in the scope of a prescribed objective function. Already in the late 70’s Starnes Jr and Haftka [2] investigated the weight minimization subject to buckling, strength, displacement and twist responses. Hollowell and Dungundji [3] investigated the effect of bending torsion coupling based on composite tailoring, while the influence of non-symmetric laminates was surveyed for example by Green [4]. A general overview of aeroelastic tailoring technology is provided by Shirk et al. [5], and Vanderplaats and Weisshaar [6] show a variety of examples considering composite optimization to demonstrate its use to tailor aircraft structures. More recent work on variable stiffness composite optimization with aeroelastic responses is provided by Stodieck et al. [7] and Stanford et al. [8, 9]. The author presents a composite stiffness optimization framework with a focus on static aeroelastic constraints in [10, 11] and an aero load correction strategy—within the optimization framework—by means of a higher order computational fluid dynamics (CFD) method, [12].

An application of the optimization process with its problem-specific adaptations is described in this paper. It constitutes an enhancement and the first consideration of the framework in the optimization of a transonic wind tunnel model including the consideration of aerodynamic corrections and gust loads, and as such an advancement over the research presented in previous publications.

The paper is organised as follows. Section 2 details the wind tunnel model layout, test setup and objective, Sect. 3 describes the analysis and optimization models, and Sect. 4 details the structural optimization leading to the data required for manufacturing. Eventually, Sect. 5 provides a conclusion and outlook.

2 Wind tunnel model layout, test setup and objective

The wind tunnel test was to be carried out at the ONERA S3Ch facility in Meudon, France. The tunnel features a Mach number domain of $M=0.3 - 1.2$ along with a rectangular test section of $0.76 \times 0.80\,m$. The installation of a gust generator based on two oscillating NACA0012 airfoils, located upstream of the test section, allows for the generation of vertical velocity components and thus angle of attack changes in the range of $0.4^\circ$ at frequencies of up to $80\,\text {Hz}$ in the transonic regime.

Fig. 1

CRM wing geometry

With the availability of the tunnel, the selection of an adequate wing geometry had to be made. In view of its widespread consideration in various aerodynamic, structural and aeroelastic research works, the publicly available common research model CRM [13] was chosen. Based on the wind tunnel dimensions, the span of the wing half to be tested was set to $0.55\,m$. Figure 1 shows the scaled geometry in top and rear view. The linear extension for $y < 0.0\,m$ on the inner wing, highlighted in red in the plot, serves towards the wing mounting purely and will not be part of the analysis model later on, justified by assuming a perfectly clamped wing at the wing root, $y=0.0\,m$.

Experience gained in previous wind tunnel campaigns, [14, 15], led to the decision of building both, the ONERA and the DLR wing, with load carrying wing skins and a foam core to support the skins and prevent buckling. A more detailed description will be provided in Sect. 3. The wings are clamped with identical steel connectors designed by ONERA, Fig. 2, and glued into the wing root to guarantee an easy interchange during the test campaign. For this purpose, the wing geometry was extended five centimeter inboard in order to provide space for the outer steel clamp. The clamp also served as connector for a splitter plate, acting as a fence for the boundary layer emanating on the wind tunnel walls.

Fig. 2

Clamping design

Both wings are equipped with six accelerometers in three spanwise rows—two of which to the left and right of the kink and one in the tip region—and chordwise one sensor close to the nose and one at about $60\%$. Moreover, six pressure sensors in three spanwise rows in the outer mid-wing are installed in the upper skin. Choosing similar positions for both, the ONERA and the DLR wing allows for a straightforward comparison of the experimental results later on. Although the sensor installation is not considered in the stiffness optimization directly, the mass introduced by the sensors and their wiring should be included in the setup of the dynamic analysis model. The overall goal comprised the structural design of a wing with maximized passive load alleviation capability under gust loading, while retaining a predefined cruise twist distribution for a lift coefficient of $C_L=0.5$ and a Mach number of 0.85.

3 Numerical models

In this Section the different computational models involved in the optimization process will be addressed. It should be noted that an in-depth description of each is provided in [16].

3.1 Analysis model

The Nastran finite element (FE) model used for the computation of all structural and aeroelastic responses to be considered is generated using the DLR in-house parametric modelling software ModGen [17]. A representation of the FE model is shown in Fig. 3, left wing. It comprises load carrying wing skins, extending from leading to trailing edge, rather than the usual box design as seen on full-scale aircraft. The skins are supported by a foam core to prevent it from buckling under compressional loads. While the skins are represented by shell elements in the FE model, the foam is modelled by volumetric elements. The aerodynamics are represented by a doublet lattice model (DLM) including a camber and twist correction, available in Nastran via the so-called W2GJ correction matrix, [12]. Coupling between the structural and the aerodynamic model is achieved by a dedicated set of coupling nodes, Fig. 3, right wing. To this end, ribs connecting directly to the wing skins are introduced in nearly equidistant positions along the span. This technique is required by the ModGen modeling process, which necessitates the presence of a rib in order to generate coupling nodes. For the ribs to not add mass or stiffness, they are modelled without structural properties, as so-called dummy-ribs. Each outer node on a dummy-rib and thus wing skin is connected to an RBE3 interpolating element, the central, dependent node of which is placed in the quarter chord. Extending from the central node towards the leading and trailing edge are RBE2 rigid body elements, resulting in three nodes suitable for the aeroelastic coupling per dummy-rib. The entity of central nodes constitutes the so-called load reference axis, which will also be addressed in the monitoring of deformation and twist responses. A detailed description of the coupling model can be found in [16]. Eventually, non-structural masses can be included as point masses, attached via rigid body elements.

Fig. 3

Finite element model (left) and coupling model (right)

The geometry underlying the finite element representation is generated using ModGen and based on four airfoil control stations, placed in the wing root, the inner kink, an additional station in the outer wing, and the tip station. As mentioned before, the linear inboard extension of the wing is not part of the CRM geometry and thus also not of the finite element model. Accordingly, subsequent plots depicting spanwise distributions will start at $y=0.0\,m$ rather than $y=-0.05\,m$, compare Fig. 1.

The target cruise twist is linearized between the airfoil control stations, unlike in the original CAD geometry of the CRM wing, where the cruise twist distribution is continuous. This is illustrated in Fig. 4, comparing the original CRM CAD twist distribution, black line, and the linearized target cruise twist distribution for the wind tunnel model, red line. The reason to linearize is mainly twofold, one, the difference of linearized and original CAD twist is sufficiently small, and two, it greatly facilitates the analysis model setup as well as the mold manufacturing process, with minimal penalty in performance. It is important to note that the jig twist is not part of the optimization process and thus needs to be defined when setting up the analysis model. The jig twist distribution ultimately implemented in the wind tunnel model is plotted as solid blue line in Fig. 4. Later on in the result Sects. 4.1.3 and 4.2 it will be shown that for the optimized structure this jig twist led to a very good match of the target cruise twist and the computed cruise twist. Eventually, the dashed blue line resembles the solid blue one, only with a shift of the root twist to $0^\circ$, which was used in the finite element model.

Fig. 4

Cruise and jig twist distribution

3.2 CFD model

As mentioned before, the standard procedure to compute aerodynamic loads in Nastran is the doublet lattice method, also applied in the aeroelastic optimization process. While it is suitable for compressible subsonic flows, and in case of a camber correction also for non-symmetric airfoils, the DLM has its drawbacks when it comes to the presence of recompression shocks or other non-linearities such as flow separation arise. To cope with these drawbacks, a correction method was developed [12], which alters the doublet lattice loads by means of a higher order CFD (computational fluid dynamics) method. In the present case, the DLR in-house CFD solver TAU [18] was applied. In order to limit the computation costs, the Euler solver was employed in the present work. The unstructured mesh was generated with Sumo [19], shown in Fig. 5, right. Studies with varying mesh density showed a good convergence behavior for a mesh with $\approx 2.3e6$ tetrahedral and $\approx 165,000$ surface triangles, as shown in Fig. 5, left plot.

Fig. 5

Aero load correction: mesh convergence (left) and mesh (right)

3.3 Optimization model

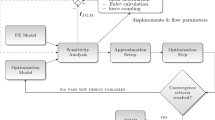
The optimization process, described in detail in [10, 16], comprises a two-step approach, successively featuring a global continuous stiffness optimization and a discrete stacking sequence optimization. Global in this context implies that the entire wing is optimized at once. The first step applies lamination parameters and laminate thicknesses as design variables in a continuous, gradient-based optimization. The second step features ply number, ply angle and ply extension throughout the design fields as design variables and targets an optimal stacking sequence design based on the results of the first step. In both steps, a Nastran finite element model is applied for the computation of all responses relevant for the aeroelastic stiffness optimization process. The objective to be minimized or maximized is subject to the optimization purpose and is addressed individually, see Sect. 4.1.

As mentioned above, the continuous optimization step implements lamination parameter as design variables, which were first introduced by Tsai et al. [20, 21]. They allow for a representation of laminate stiffness matrices in a continuous form, enabling the use of gradient based optimizers independent of the number of plies. The problem formulation however is stated in terms of membrane and bending stiffness matrices, A and D respectively, which are a direct input to the Nastran FE model. To this end, the shell elements considered in the optimization are clustered in so-called design fields, each of which comprises a dedicated set of an A and D matrix. The design field distribution chosen for the CRM wing is shown in Fig. 6. In total eight design fields are considered, four each in the upper and lower wing skin, where the second design field deliberately reaches over the kink in the planform, in order to avoid the amplification of a potential stiffness discontinuity resulting from ply drops at the design field border, and a discontinuity in the geometry. The third design field covers a majority of the main wing, followed by a fourth design field in the tip region. Investigations showed that this distribution is sufficiently detailed with only minimal drawbacks with respect to the attainable optimum, while promoting a manageable manufacturing process, which clearly benefits from its simplicity. To this end, the rather small design field in the tip region not only allows for a local decrease in thickness but also the additional flexibility to introduce a local change in the aeroelastic characteristics by means of tilting the stiffness direction.

Fig. 6

Design fields in the wind tunnel model

The responses considered in the optimization and requiring the corresponding representation in the Nastran optimization model are summarized in Table 1. In the optimization runs presented in Sect. 4, one of the responses always served as the objective to be minimized, while the other ones were implemented as constraints.

Table 1 Optimization responses

3.4 Gust analysis

The gust analysis applied in this research was developed by Handojo, a detailed description of which is provided in [22]. In order to reduce the computational cost for the presumably numerous gust cases to be investigated, a modal condensation is performed along the nodes of the load reference axis. The analysis is based on a combination of Nastran aeroelastic static trim (SOL144) and dynamic gust calculations (SOL146). The load increments for a harmonic gust excitation provided by SOL146 are superimposed with the static results from SOL144 to yield the total load. To identify the most severe loads occurring in the analyzed gusts, monitoring points are defined at which the time dependent loads of interest (shear force, bending moment) are computed. The algorithm can then identify timestamps at which each load of interest is maximum/minimum and save the load distribution at that timestamp. These quasi-steady load cases can be used in a static analysis to assess stresses and strains, eventually judging their impact on the integrity of the structure.

Another possibility to include the quasi-stead gust load cases, as applied in this research, features their implementation in an optimization-rerun. To this end, it is important to note that the gust load cases are not initially part of the static aeroelastic optimization of the wing. Instead, gust load cases are computed for the optimized design with the above mentioned procedure and subsequently included in a second optimization run based on the optimized design. Should the gust load cases lead to a violation of constraints previously optimized, the optimizer will decide to redesign the structure. If the gust load cases do not violate any constraint (meaning they are not active), the design will remain as is.

4 Optimization and results

This section depicts the results of the aeroelastic optimization, leading to the final structural layout and the data required to manufacture the wind tunnel model.

Aiming at passive load control, or rather passive load alleviation, the objective to be optimized can be described in various ways. Ultimately, objectives such as root bending moment minimization, maximization of maneuver load alleviation, bending-twist coupling maximization and so forth are mostly motivated by the search for the lightest structure, safely supporting the maximum occurring loads. For this reason, different objective functions were investigated, in order to determine the most appropriate one for the ultimate goal of demonstrating passive load alleviation. Because of its efficient gradient based setup, all investigations were performed with the first step in the optimization framework, the continuous stiffness optimization, Sect. 4.1. Only the ultimately selected design was transferred to the discrete stacking sequence optimization, Sect. 4.2. A flutter check of the final layout is shown in Sect. 4.3 and eventually, constituting the interface of the optimization to the manufacturing process, Sect. 4.4 exemplifies the data preparation for building the wing.

4.1 Continuous stiffness optimization

The continuous stiffness optimization constitutes the first step in the two-step optimization approach, concluding in an optimized stiffness distribution, expressed by membrane and bending stiffness matrices A and D for each of the design fields considered. The considered load cases are listed in Table 2 and can be grouped into three categories: fixed alpha load cases to determine maximum strains, trim load cases to determine cruise and maneuver twist / displacement distributions as well as maximum strains, and a load case considering the dynamic properties of the wing. For the trim load cases a central mass at the wing root was attached to attain a target lift coefficient of $C_L=0.5$ in cruise flight (load factor $=1.0\,g$). The atmospheric conditions in the wind tunnel test section when running at Mach 0.85 resemble the atmospheric conditions in an altitude of $3785\,m$, thus an air density of $\rho =0.834\,kg/m^3$, a temperature of $T=263^\circ \,K$ and a speed of sound of $a=325\,m/s$.

Table 2 Load case definition

The material selected for manufacturing the wing skins is an E-Glas Silenka type fiber, with an E-modulus of $74\,GPa$, which along with an Epoxy resin and a fiber volume fraction of $fvf=0.575$ results in the single ply material properties shown in Table 3. The fiber volume fraction was determined in previous test campaigns, [14, 15], for the same fiber, resin and hand layup technique, and thus also applied in the present research. In order to construct the strain failure envelope for the optimization - details on which are provided in [16] - the strain allowables $\varepsilon _t$, $\varepsilon _c$, $\gamma _s$ in Table 3 are knocked down by a safety factor of 3.0. Properties of the foam core are listed in Table 4.

Table 3 Single ply material properties

Table 4 Single ply material properties

The objective functions that were investigated in more detail are tip displacement minimization, strain failure index minimization, root bending moment minimization and mass minimization. The responses to be considered are listed in Sect. 3.3. As described in detail for example in [10], Nastran is used solely for the generation of responses and their sensitivities with respect to the design variables. The optimization itself occurs outside Nastran with a gradient based optimizer tailored towards lamination parameter optimization. All optimizations were performed with unbalanced laminates in order to maximize the load alleviation potential. In the following, only the most prominent results will be highlighted.

4.1.1 Tip deflection minimization

In order to gain some insight on the influence of constraining weight to an upper limit while minimizing the tip deflection in cruise, corresponding optimizations were performed with CFD correction. The jig twist distribution was kept constant throughout the optimizations runs and not adapted according to the procedure described in Sect. 3.1. The slightly changing cruise twist had little influence on the overall result and thus was neglected for simplicity. As shown in the resulting Pareto front in Fig. 7, with an increasing upper bound on mass, the minimized tip deflection drops (black line). Each marker represents a full optimization run with the corresponding upper bound on mass $m_{max}$. The graph also features the corresponding maximum strain failure index (red line) throughout the design fields as a function of maximum mass, where a failure index above 1.0 indicates strain failure. Above $m = 1\,kg$ the wing skins are no longer loaded up to their maximum capacity. The reason for the displacement to still increase even when reaching $fi=1.0$ is that for decreasing mass more and more areas throughout the wing reach the failure index boundary; the wing becomes increasingly loaded throughout.

Fig. 7

Cruise tip deflection minimization as function of constrained mass

4.1.2 Root bending moment minimization

In this set of optimizations, the root bending moment at a $2.5\,g$ maneuver load case (compare Table 2) was to be minimized, constrained by an upper limit on mass. The results are shown in Fig. 8. Increasing the mass constraint beyond $m_{max}=2.0\,kg$ did not bring any further advantage in terms of the objective, which plateaus beyond a constrained mass of $m_{max}=1.8,kg$. Compared to the optimization shown in the previous section, in order to reach minimum root bending moment, some area in the wing skins is at some point always loaded up to its maximum capacity, indicated by the maximum strain failure index $fi=1.0$.

Fig. 8

Root bending moment minimization as function of constrained mass

4.1.3 Mass minimization

In order to accomplish a better match with the intended cruise twist distribution for load case 1008, see Fig. 4 and Table 2, an additional airfoil station was introduced in the outer wing. Moreover, as mentioned before, the maneuver load case 1009 in consultation with ONERA was lowered from $2.5\,g$ to $2.0\,g$. The changes were considered in this set of optimizations, which eventually led to the design to be passed to the stacking sequence optimization step. It was mentioned earlier that mass minimization usually is the main driver for passive load alleviation endeavors, given that the lightest possible structure usually is achieved when simultaneously the loads are minimized. However, choosing weight minimization as an objective for a wind tunnel model can be conflicting with the robustness and safety issues that go along with wind tunnel testing. For this reason, the strain allowables mentioned in Table 3 (and divided by a safety factor of 3.0) were reduced by another $45\%$. Results for a mass minimization comprising strain constraints and incorporating a CFD correction are presented below. The underlying jig twist distribution, shown in Fig. 4, was determined by performing the mass minimization twice, with a manual adjustment of the linearized jig twist in-between. This one additional minimization proved to be sufficient for a very good match of the analysed cruise twist and the linearized target CAD cruise twist, thus superseding additional twist constraints (Fig. 9).

Fig. 9

Twist and displacement distribution for the trim load cases of the mass-minimized wing, cont. opt

Twist and displacement distributions for the trim load cases 1008 and 1009 for the optimized wing are shown in Fig. 10. Considering its linear jig twist interpolation, the CRM twist is adequately met for the cruise load case 1008. The tip displacement amounts to $34.4\,mm$ and $66.8\,mm$ for load factors $n=1.0\,g$ and $n=2.0\,g$ respectively. The optimized thickness distribution is shown in Fig. 10, resulting in a total minimized skin weight of $0.608\,kg$. In the plot, elements $1-429$ belong to the upper skin, elements $430-858$ to the lower skin, root to tip respectively. The increased chord near the root (design field 1) allows for a reduced thickness. As a result of the lower compressional strain allowable and the considered load cases, the main wing features larger thicknesses in the upper skin.

Fig. 10

Optimized thickness distribution, cont. opt

Fig. 11

Optimized stiffness distribution $\hat{E}_{11}(\theta )$ in lower (left) and upper (right) skin, cont. opt

The optimized stiffness distribution in the lower and upper wing skin is plotted in Fig. 11, showing the polar thickness-normalized engineering modulus of elasticity $\hat{E}_{11}(\theta ) = 1 / \hat{A}_{11}^{-1}(\theta )$, red line. It allows for a visual assessment of the directional membrane stiffness distribution. Indicated by the black lines is the $0.0^\circ$ fiber direction in each design field, while the blue lines indicate the maximum stiffness direction based on the red polar plot. Clearly, by increasingly tilting the main stiffness direction towards the leading edge, a bending twist coupling is achieved which supports the geometric wash-out effect when increasing the wing loading. It constitutes the most efficient way of passively reducing the loads.

Fig. 12

TAU results for cruise load case 1008, Mach distribution (upper) and $\Delta C_p$ TAU / DLM (lower) , cont. opt

An example of the need to consider a CFD correction is illustrated in Fig. 12. The presence of recompression shocks is not captured in the DLM calculation, leading essentially to an inexact computation of for example the moment coefficient. A detailed analysis of the possible implications is given in [12].

With the optimized structure, a gust analysis was performed to examine the robustness of the design and a potential re-optimization including quasi-static gust load cases (compare Sect. 3.4 for a description of the procedure). The shell model was condensed by means of a Guyan reduction available in Nastran, two samples modes of which are shown in Fig. 13, including non-structural plot-elements. To this end, the load reference axis, composed of the central nodes belonging to the coupling model, compare Fig. 3 and Sect. 3.1, were selected for stiffnesses and masses to be condensed to.

Fig. 13

Condensed optimized model sample modes

The input to the gust analysis was a harmonic, sinusoidal vertical gust velocity $u_g$ resulting from $0.25^\circ$ up- and downward flow deflection

$$\begin{aligned} u_g=sin(0.25^\circ )\,U_{cruise} sin(2 \pi f t), \end{aligned}$$

a frequency range of $f=20-80\,Hz$ and Mach number 0.85. Three monitoring points at root ($y=0.0\,m$), mid ($y=0.21\,m$), and outer wing ($y=0.41\,m$) were defined for the extraction of critical load cases. In order to provide an additional safety factor, the calculations were performed at total atmospheric conditions, thus, an air density of $\rho =1.17\,kg/m^3$. In Fig. 14 the bending moment envelope for the root section monitoring point is exemplified. It comprises gust loads, as well as the steady maneuver load cases. The plot indicates that the maneuver load case dominates the root bending moment.

Fig. 14

2D gust and maneuver envelope for the root monitoring point, cont. opt

From the analyzed gusts, the seven most severe quasi-steady gust load cases were extracted and for the optimized design included in an analysis run with the previously defined load cases, Table 2. Gust load cases in the following are numbered from 3000 onward. The failure index plot in Fig. 15 confirms that the maneuver load case 1009 clearly dominates the design compared to the gust case 3027, featuring the highest failure indices among the gust load cases. Only in the tip region and for very low failure indices the gust load dominates.

Fig. 15

Failure indices for the most severe maneuver and gut load case, cont. opt

Fig. 16

Sizing load cases on element level (left) and design field level (right) in the lower wing skin, cont. opt

Yet, also in the tip region, the wing ultimately is sized by the static load cases, as indicated in Fig. 16, which compares the sizing load cases on element and design field level, using the example of the lower skin. Eventually the design is driven by the highest failure index in a design field. This concludes the continuous stiffness optimization, the result of which was passed to the discrete stacking sequence optimization.

4.2 Discrete stacking sequence optimization

The stacking sequence optimization featuring blended laminates is based on a method developed by Meddaikar et al. [23, 24]. It features a stacking sequence table (SST)-driven genetic algorithm in combination with a modified Shepard’s method to improve the response approximation accuracy. While it allows for the specification of various manufacturing driven blending guidelines, the only constraint included in the present case was a predefined set of ply angles with fixed increments of $15^\circ$, starting at $0^\circ$. Starting from the optimized continuous design, an identical set of objective function and constraints as for the continuous optimization was applied. Apart from the single ply properties that were also required for the continuous optimization, a single ply thickness needed to be specified. For the selected $220\,g/m^2$ UD glass fiber material and a fiber volume fraction of $\text {fvf}=0.575$ this amounts to $t_{ply}=0.15\,mm$. Moreover, the minimum thickness was constrained to 10 plies ($\ge 1.5\,mm$). The main outcome of the optimization is stacking sequence tables describing the definition of each ply throughout the design fields and the fiber angle. They can be translated to a so-called ply-book, that visualizes the layup in a coherent manner, an example of which will be provided in Sect. 4.4. Despite the discrete nature of the problem, the optimizer was able to retain the performance of the continuous optimization to a large extend, the most important results of which are summarized in Table 5. The weight slightly increased for the discrete optimization, which can partly be attributed to the minimum thickness requirement. Figures 17 and 18 provide the displacement/twist and the stiffness distribution results, which directly compare to Figs. 9 and 11 from the continuous optimization step. Clearly, the cruise twist distribution adequately matches the CRM target, while the stiffness distribution resembles the one found for the continuous optimization.

Table 5 Comparison of continuous and stacking sequence optimization results

Fig. 17

Twist and displacement distribution for the trim load cases of the mass-minimized wing, stack. seq. opt

Fig. 18

Optimized stiffness distribution $\hat{E}_{11}(\theta )$ in lower (left) and upper (right) skin, stack. seq. opt

Fig. 19

Failure indices for the most severe maneuver and gut load case, stack. seq. opt

Eventually, the strain failure indices including quasi-steady gust load cases, Fig. 19, reveals a similar picture as for the continuous optimization, Fig. 15. The design is dominated by the fixed alpha and maneuver load cases, noting that as a result of the higher minimum thickness for the laminates, the failure indices dropped at the tip.

4.3 Flutter calculation

To verify a flutter free operation of the optimized stacking sequence design obtained in the previous section, a flutter analysis was performed with the Nastran PK flutter solver. The calculation was made for Mach numbers ranging from 0.1 to 0.95 and the corresponding matched densities and pressures. The results are depicted in Fig. 20. The analysis shows that for the investigated velocity range the model is free of flutter, indicated by the negative damping coefficient. The nearly constant frequency spacing between the single eigenmodes moreover implies that there is no tendency for mode-pairs to couple.

Fig. 20

Flutter curves for a matched Nastran PK analysis

4.4 Manufacturing data compilation

Depending on the envisaged manufacturing technology for the structure, appropriate tools and techniques are required, in order to realize the optimized design data into hardware to be tested. In case of the wind tunnel model a hand layup process with wet fibers was chosen, requiring among others a CNC milled lamination mold, as well as a so-called ply book for the upper and lower skin. The latter was derived from the stacking sequence tables applied in the second optimization step, Sect. 4.2, a sample of which is provided in Fig. 21 for the upper skin. The ply book constitutes a simple, yet efficient way to visualize the region and fiber angle for each single ply. The ply gauge shown in Fig. 22 was developed to facilitate a precise layout of the single plies. The gauge is transferred and cut out in a 1 : 1 scale from hardwood and then used to precisely cut the glas fiber plies under the specified angles.

Fig. 21

Ply book for the upper skin

Fig. 22

Ply gauge

5 Conclusion and outlook

The structural optimization of a wind tunnel model featuring passive load alleviation in the transonic regime was presented in this paper. Starting with a description of the analysis and optimization models involved in the response generation, an explanation of the various objective functions investigated was provided, with an in-depth review of the results achieved for the mass minimization objective. The subsequent discrete stacking sequence optimization showed to nearly preserve the theoretical optimum achieved with the continuous optimization. Eventually, a flutter analysis was performed in order to ensure a safe operation in the transonic regime.

The work represents the first application of the framework for the aeroelastic optimization of a wind tunnel model operating in the transonic regime. It could be shown that the selection of structural weight as the objective to be minimized is a meaningful choice in the quest for the load alleviation target. Eventually, the gust load cases enabled by the gust generator did not drive the design, rather than the static maneuver load case. Therefore, in a future campaign attention could be paid to an explicitly gust-driven load spectrum in order to focus on its influence on the design in terms of load reduction.

The wing was built at the end of 2020 and tested in the beginning of 2021, a representation of the wind tunnel setup including the gust generator is shown in Fig. 23. Results of the test are to be published in a next step.

Fig. 23

Wind tunnel setup