Introduction

The study of convective flow, heat and mass transfer in porous media has been an active field of research as it plays a crucial role in diverse applications, such as thermal insulation, extraction of crude oil and chemical catalytic reactors etc. Considerable work has been reported on flow and heat and mass transfer in Darcian porous media, Somers (1956), Kliegel (1959), Merkin (1969), Lloyd and Sparrow (1970) and Kafoussias (1990). The process of heat and mass transfer caused by the simultaneous effect of free and forced convection is known as mixed convection flow. Considerable attention has been paid to the theoretical and numerical study of mixed convection boundary layer flow along a vertical plate in the recent past as it plays a crucial role in diverse applications, such as electronic devices cooled by fans, nuclear reactors cooled during an emergency shutdown, a heat exchanger placed in a low-velocity environment, solar collectors and so on. In the study of fluid flow over heated surfaces, the buoyancy force is neglected when the flow is horizontal. However, for vertical or inclined surfaces, the buoyancy force exerts strong influence on the flow field. The diffusion of mass due to temperature gradient is called Soret or thermo-diffusion effects and this effect might become significant when large density differences exist in the flow regime. For example, Soret effect can be significant when species are introduced at a surface in fluid domain, with a density lower than the surrounding fluid.

Nanofluids are potential heat transfer fluids with enhanced thermophysical properties and heat transfer performance can be applied in many devices for better performances (i.e., energy, heat transfer and other performances). In this paper, a comprehensive literature on the applications and challenges of nanofluids have been compiled and reviewed. Recent researches have indicated that substitution of conventional coolants by nanofluids appears promising. Specific applications of nanofluids in engine cooling, solar water heating, cooling of electronics, cooling of transformer oil, improving diesel generator efficiency, cooling of heat exchanging devices, improving heat transfer efficiency of chillers, domestic refrigerator-freezers, cooling in machining, in nuclear reactor and defense and space have been reviewed and presented. In recent times, the flow analysis of nanofluids has been the topic of extensive research due to its characteristic in increasing thermal conductivity in heat transfer process. Several ordinary fluids including water, toluene, ethylene glycol and mineral oils, etc., in heat transfer processes have rather low thermal conductivity. The nanofluid (initially introduced by Choi 1995) is an advanced type of fluid containing nano-meter sized particles (diameter less than 100 nm) or fibers suspended in the ordinary fluid. Undoubtedly, the nanofluids are advantageous in the sense that they are more stable and have an acceptable viscosity and better wetting, spreading and dispersion properties on a solid surface (Buongiorno 2006; Kakac and Pramuanjaroenkij 2009; Kuznetsov and Nield 2010; Bachok et al. 2010; Kuznetsov and Nield 2011; Gorla 2011). Nanofluids are used in different engineering applications such as microelectronics, microfluidics, transportation, biomedical, solid-state lighting and manufacturing.

Magnetohydrodynamic has many industrial applications such as crystal growth, metal casting and liquid metal cooling blankets for fusion reactors. Sheikholeslami et al. (2014) studied the problem of MHD free convection in an eccentric semi-annulus filled with nanofluid. They showed that Nusselt number decreases with increase of position of inner cylinder at high Rayleigh number. Rashidi et al. (2013) considered the analysis of the second law of thermodynamics applied to an electrically conducting incompressible nanofluid fluid flowing over a porous rotating disk. They concluded that using magnetic rotating disk drives has important applications in heat transfer enhancement in renewable energy systems. Recently, several authors studied the effect of magnetic field on flow and heat transfer (Kandelousi 2014; Nizar Ben Salah et al. 2001; Ariel 1993; Sheikholeslami and Ganji 2014; Sampath and Zabaras 2001; Nesliturk and Tezer-Sezgin 2005; Sheikholeslami 2015; Sheikholeslami and Gorji-Bandpy 2014; Singh and Lal 1983; Ravindran 2008). From an energy saving perspective, improvement of heat transfer performance in systems is a necessary subject. Low thermal conductivity of conventional heat transfer fluids such as water and oils is a primary limitation in enhancing the performance and the compactness of systems. Solids typically have a higher thermal conductivity than liquids. For example, copper (Cu) has a thermal conductivity 700 times greater than water and 3000 times greater than engine oil. An innovative and novel technique to enhance heat transfer is to use solid particles in the base fluid (i.e., nanofluids) in the range of sizes 10–50 nm. Abu-Nada et al. (2008) investigated natural convection heat transfer enhancement in horizontal concentric annuli field by nanofluid.

Thermophoresis is an interesting consequence of the Brownian movement of particles in fluids with an externally sustained and constant temperature gradient. It becomes apparent from Eqs. (2) and (3) that particle dispersion is higher and the Brownian force is stronger when the local fluid temperature is higher. When there is a temperature gradient in the flow domain of the suspension, small particles disperse faster in hotter regions and slower in colder regions. The collective effect of the differential dispersion of the particles is their migration from hotter to colder parts of the fluid domain. That is, in the presence of a temperature gradient, particles move on the average against this gradient. The averaged motion of the particles has been known as thermophoresis. The phenomenon of thermophoresis was first observed by Tyndall, when he saw that aerosol particles in a dust-filled room were driven away from a heated surface (Tyndall 1870) but was not studied in detail until the twentieth Century. Tyndall did not connect thermophoresis to the molecular impulses on particles (Tyndall 1870). It must be noted that the particles in suspension will not fully accumulate in the colder region. Inter particle collisions in the colder regions, where the particle concentration becomes higher, would disperse the particles stronger than in the hotter regions, where the particle concentration is lower. Thus, in the absence of other dispersion mechanisms—such as turbulence, velocity fluctuations, shear forces, lift forces, etc.—a dynamic equilibrium for the particle concentration will be established, with lower particle concentrations in the hotter regions and higher concentrations in the colder regions (Michaelides 2013).

The objective of the present article is motivated by the above referenced work and the vast possible industrial applications, it is of paramount interest to consider the effect of Brownian motion of the nanoparticle on MHD mixed convective flow along a porous vertical plate in a nanofluid under convective boundary condition. The presence of convective boundary conditions makes the mathematical model of the present physical system a little more complicated leading to the complex interactions of the flow, heat and mass transfer mechanism. Consideration of the nanofluid and the convective boundary conditions enhanced the number of non-dimensional parameters analyzed in the presence of magnetic field. To examine the convergence of the numerical code written to solve the present problem, (i.e., for code validation) we compare the present results for the clear fluid mixed convection results with previously published works with convective boundary conditions, and the comparison shows that the results are in good agreement.

Mathematical formulation

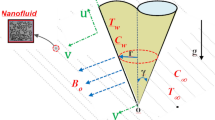
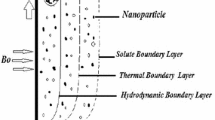
The physical model and coordinate system are shown in Fig. 1, where the x-axis is along the porous vertical plate and the y-axis normal to the plate. Consider the steady laminar two-dimensional mixed convection heat and mass transfer along a porous vertical surface embedded in a nanofluid having \( T_{\infty } \), \( C_{\infty } \), and \( \phi_{\infty } \) as the temperature, concentration and nanoparticle volume fraction, respectively, in the ambient medium. A uniform transverse magnetic field of strength \( B_{0} \) is applied parallel to the y-axis. It is assumed that the induced magnetic field, the external electric field and the electric field due to the polarization of charges are negligible. Also assume that a free stream with uniform velocity \( u_{\infty } \) goes past the porous plate. The plate is either heated or cooled from left by convection from a fluid of temperature \( T_{f} \) with \( T_{f} > T_{\infty } \) corresponding to a heated surface (assisting flow) and \( T_{f} < T_{\infty } \) corresponding to a cooled surface (opposing flow), respectively. On the wall, the solutal concentration and the nanoparticle volume fraction are taken to be constant and are given by \( C_{w} \) and \( \phi_{w} \), respectively. By employing Oberbeck–Boussinesq approximation, making use of the standard boundary layer approximations and eliminating pressure, the governing equations for the nanofluid are given by

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(1)
$$ \begin{aligned} \rho_{{f_{\infty } }} \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = & \mu \frac{{\partial^{2} u}}{{\partial y^{2} }} - \left( {\sigma \;B_{0}^{2} + \frac{{\nu \;\rho_{{f_{\infty } \;}} }}{K}} \right)u + \\ & g\rho_{{f_{\infty } }} (1 - \phi_{\infty } )\left\{ {\beta_{T} (T - T_{\infty } ) + \beta_{C} (C - C_{\infty } ) - (\rho_{p} - \rho_{{f_{\infty } \;}} )g(\phi - \phi {}_{\infty })} \right\} \\ \end{aligned} $$
(2)
$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{m} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \left[ {D_{B} \frac{\partial \phi }{\partial y}\frac{\partial T}{\partial y} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] $$
(3)
$$ u\frac{\partial \phi }{\partial x} + v\frac{\partial \phi }{\partial y} = D_{B} \frac{{\partial^{2} \phi }}{{\partial y^{2} }} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} $$
(4)
$$ u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{S} \frac{{\partial^{2} C}}{{\partial y^{2} }} + D_{CT} \frac{{\partial^{2} T}}{{\partial y^{2} }} $$
(5)
Fig. 1
figure 1

Physical model and coordinate system

Full size image

where \( u \) and \( v \) are the velocity components along the \( x \) and \( y \) axis, respectively, \( T \)  is the temperature, ϕ is the nanoparticle volume fraction, \( C \) is the solutal concentration, \( g \) is the gravitational acceleration, \( \alpha_{m} = \frac{k}{{(\rho \;c)_{f} }} \)  is the thermal diffusivity of the fluid, \( \nu = \frac{\mu }{{\rho_{{f_{\infty } }} }} \) is the kinematic viscosity coefficient and \( \tau = \frac{{(\rho \;c)_{p} }}{{(\rho \;c)_{f} }} \) is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid. Further, \( \rho_{{f_{\infty } }} \) is the density of the base fluid and \( \rho ,\mu ,k,\beta_{T} \) and \( \beta_{C} \) are the density, viscosity, thermal conductivity, volumetric thermal expansion coefficient and volumetric solutal expansion coefficient of the nanofluid, while \( \rho_{p} \) is the density of the nanoparticles, \( (\rho \;c)_{f} \) is the heat capacity of the fluid and \( (\rho \;c)_{p} \) is the effective heat capacity of the nanoparticle material. The coefficients that appear in Eqs. (3), (4) and (5) are the Brownian diffusion coefficient \( D_{B} \), the thermophoretic diffusion coefficient \( D_{T} \), the solutal diffusivity \( D_{S} \) and the Soret-type diffusivity \( D_{CT} \). For, details of the derivation of Eqs. (1)–(5), see Buongiorno (2006), Kuznetsov and Nield (2010) and Somers (1956).

The boundary conditions are

$$ \begin{aligned} u = 0,v = V_{0} , - k\frac{\partial T}{\partial x} = h_{f} (T_{f} - T),\;\phi = \phi_{w} ,C = C_{w} \,\, at\;y = 0; \hfill \\ u \to u_{\infty } ,C \to C_{\infty } ,T \to T_{\infty } ,\phi \to \phi_{\infty } \,\, as\;y \to \infty \hfill \\ \end{aligned} $$
(6)

where, \( h_{f} \) is the convective heat transfer coefficient, \( V_{0} \) is the velocity of suction/injection and the subscripts \( w \) and \( \infty \) indicate the conditions at the surface and at the outer edge of the boundary layer, respectively.

In view of the continuity Eq. (1), we introduce the stream function \( \psi \) by \( u = \frac{\partial \psi }{\partial y} \), \( v = - \frac{\partial \psi }{\partial x} \) and then using the following non-dimensional transformation

$$ \eta = \frac{y}{{\sqrt {2x} }}\text{Re}_{x}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} ,\psi = \sqrt {2\nu } \text{Re}_{x}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} f(\eta ),\theta = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }},\phi = \frac{{\phi - \phi_{\infty } }}{{\phi_{w} - \phi_{\infty } }}\;\; {\text{and}}\;\chi = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }} $$
(7)

with the local Raynold’s number \( \text{Re}_{x} = \frac{{u_{\infty } x}}{\nu } \), we get the transformed system of ordinary differential equations as

$$ f^{\prime \prime \prime } + ff^{\prime \prime } + 2\delta \left( {\theta + {\text{Nc}}\chi - {\text{Nr}}\phi } \right) - 2\left( {M + \lambda } \right)f^{\prime } = 0 $$
(8)
$$ \frac{1}{\Pr }\theta^{\prime \prime } + f\theta^{\prime } + {\text{Nb}}\theta^{\prime } \varphi^{\prime } + {\text{Nt}}\theta^{\prime 2} = 0 $$
(9)
$$ \varphi^{\prime\prime} + {\text{Lef}}\,\varphi^{\prime} + \frac{\text{Nt}}{\text{Nb}}\theta^{\prime \prime } = 0 $$
(10)
$$ \frac{1}{Sc}\chi^{\prime \prime } + S_{T} \theta^{\prime \prime } + f\chi^{\prime } = 0. $$
(11)

In usual notations, \( \Pr = \frac{\nu }{{\alpha_{m}^{{}} }} \) is the Prandtl number, \( {\text{Sc}} = \frac{\nu }{{D_{S} }} \) is the Schmidt number and \( {\text{Le}} = \frac{\nu }{{D_{B} }} \) is the Lewis number. \( {\text{Nr}} = \frac{{(\rho_{P} - \rho_{{f_{\infty } }} )(\phi_{w} - \phi_{\infty } )}}{{\rho_{{f_{\infty } }} \beta_{T} (T_{f} - T_{\infty } )(1 - \phi_{\infty } )}} \) is the nanofluid buoyancy ratio and \( N_{C} = \frac{{\beta_{C} (\phi_{w} - \phi_{\infty } )}}{{\beta_{T} (T_{f} - T_{\infty } )}} \) is the regular buoyancy ratio. Further, \( {\text{Nr}} = \frac{{(\rho c)_{P} D_{B} \;(\phi_{w} - \phi_{\infty } )}}{{(\rho c)_{f} \;\nu }} \) is the Brownian motion parameter, \( {\text{Nt}} = \frac{{(\rho c)_{P} \;D_{T} (T_{f} - T_{\infty } )}}{{(\rho c)_{f} \nu T_{\infty } )}} \) is the thermophoresis parameter, \( {\text{Gr}}_{x} = \frac{{g\beta _{T} (1 - \varphi _{\infty } )(T_{f} - T_{\infty } )x^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}{{v^{2} }} \) is the local Grashof number, \( \delta = \frac{{{\text{Gr}}_{x} }}{{\text{Re}_{x} }} \) is the mixed convection parameter, \( M = \frac{{\sigma B_{0}^{2} }}{{\rho_{{f_{\infty } }} u_{\infty } }} \) is the magnetic parameter and \( \lambda = \frac{\nu }{{{\text{Ku}}_{\infty } }} \) is the porous parameter. Finally, \( S_{T} = \frac{{D_{CT} (T_{f} - T_{\infty } )}}{{\nu (C_{w} - C_{\infty } )}} \) is the Soret number. Boundary conditions (6) in terms of \( f,\theta ,\varphi ,\chi \) become

$$ \begin{aligned} \eta = 0:f(0) = S,f^{\prime } (0) = 0,\theta^{\prime } (0) = - B(1 - \theta (0)),\varphi (0) = 1,\varphi (0) = 1; \hfill \\ \eta \to \infty :f^{\prime } (\infty ) \to 1,\theta (\infty ) \to 0,\varphi (\infty ) \to 0,\chi (\infty ) \to 0 \hfill \\ \end{aligned} $$
(12)

where \( S = - \frac{{V_{0} \sqrt {2\nu } }}{{u_{\infty } }}\text{Re} x^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \), \( S > 0 \) corresponds to suction whereas \( S < 0 \) corresponds to injection. \( B = \frac{c}{k}\sqrt {\frac{2\nu }{{u_{\infty } }}} \) is the Biot number. These boundary conditions will be free from the local variable x when we choose \( h_{f} = c\;x^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \). The Biot number \( B \) is a ratio of the internal thermal resistance of the plate to the boundary layer thermal resistance of the hot fluid at the bottom of the surface. It is important to note that this boundary value problem reduces to the classical problem of flow and heat and mass transfer due to the Blasius problem when \( Nb \) and \( {\text{Nt}} \) are zero. Most nanofluids examined to date have large values for the Lewis number \( {\text{Le}} > 1 \). For practical purposes, the non-dimensional shear stress \( C_{f} = \frac{{\tau_{w} }}{{\rho_{{f_{\infty } }} u_{\infty }^{2} }} \), the Nusselt number \( {\text{Nu}}_{x} = \frac{{q_{w} x}}{{k(T_{f} - T_{\infty } )}} \), the nanoparticle Sherwood number \( {\text{NSh}}_{x} = \frac{{q_{n} x}}{{D_{B} (\varphi_{w} - \varphi_{\infty } )}} \), and the regular Sherwood number \( {\text{Sh}}_{x} = \frac{{q_{m} x}}{{D_{B} (C_{w} - C_{\infty } )}} \) are given by

$$ \begin{aligned} C_{f} \left( {2\text{Re}_{x} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} & = f^{\prime \prime } (0),\;{\text{Nu}}_{x} = \left( {{\raise0.7ex\hbox{${\text{Re}_{x} }$} \!\mathord{\left/ {\vphantom {{\text{Re}_{x} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right)^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = - \theta^{\prime } (0), \\ {\text{NSH}}_{x} = \left( {{\raise0.7ex\hbox{${\text{Re}_{x} }$} \!\mathord{\left/ {\vphantom {{\text{Re}_{x} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right)^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} & = - \varphi^{\prime } (0),{\text{Sh}}_{x} = \left( {{\raise0.7ex\hbox{${\text{Re}_{x} }$} \!\mathord{\left/ {\vphantom {{\text{Re}_{x} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right)^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = - \chi^{\prime } (0). \\ \end{aligned} $$
(13)

Here, \( \text{Re}_{x} = \frac{{u_{\infty } \;x}}{\nu } \) is the local Raynolds number. Effect of the various parameters involved in the investigation on these coefficients is discussed in the following section.

Results and discussion

The Eqs. (8)–(11) are highly nonlinear coupled equations and cannot be solved analytically, and numerical solutions subject to the boundary conditions (12) are obtained using the very robust computer algebra software Maple 18. This software uses a fourth-fifth order Runge–Kutta–Fehlberg method as default to solve boundary value problems numerically using the dsolve command. For the benefit of the readers, the Maple worksheet is listed in “Appendix”. The transformed system of coupled nonlinear ordinary differential Eqs. (8)–(11) including boundary conditions (12) depends on the various parameters. The numerical results are represented in the form of the dimensionless velocity, temperature, nanoparticle volume fraction and concentration. During computation we choose parameters such that \( \delta = 1.0,{\text{Nr}} = {\text{Nc}} = B = \Pr = 1.0,{\text{Nb}} = {\text{Nt}} = 0.5,M = \lambda = 1.0,\;{\text{Sc}} = 0.6 \) and \( {\text{Le}} = 10.0 \) correspond physically to air (nanofluid). In order to validate our method, we have compared the results of \( - \theta^{\prime } (0) \) with those of Makinde and Olanrewaju (2010) and Subhashini et al. (2011) and found them in excellent agreement, Table 1. Thus, the present results are more accurate than their results.

Table 1 Comparison of the result of −θ′(0) for mixed convection along a vertical plate, (Makinde and Olanrewaju 2010; Subhashini 2011)
Full size table

It is also observed from the Fig. 2 that the agreement with the theoretical solution of temperature profile for different values of B and \( {\text{Nr}} \) is excellent correlates with Fig. 2a of Ram Reddy et al. (2013).

Fig. 2
figure 2

Comparison of velocity profile for B and \( {\text{Nr}} \) with a of (Ramreddy and Murthy 2013)

Full size image

Figure 3a–d displays the effect of thermophoretic particle deposition \( {\text{Nt}} \) on velocity, temperature, nanoparticle volume fraction and concentration profiles. In the presence of magnetic field (\( M = 3.0) \), it is interesting to note that the velocity decreases, the temperature decreases (\( \eta \le 0.68 \)) and then increases (\( \eta > 0.68 \)), the volume fraction of the nanoparticles and the concentration of the nanofluid increase with increase of thermophoresis particle deposition whereas \( M = 0.0 \), the velocity of the nanofluid firstly decreases and then increases, the temperature and concentration firstly increase and then decrease and the nanoparticle volume fraction increases \( 0 \le \eta \le 0.61 \) and then decreases \( \eta > 0.61 \) with increase of \( {\text{Nt}} \). It is noticed that the positive value of \( {\text{Nt}} \) indicates a cold surface, but the negative value of \( {\text{Nt}} \) to be a hot surface. For hot surfaces, thermophoresis tends to blow the nanoparticle volume fraction boundary layer away from the surface since a hot surface repels the sub-micron sized particles from it, thereby forming a relatively particle-free layer near the surface. As a consequence, the momentum, thermal and diffusion boundary layer are formed just outside. In particular, the effect of increasing the thermophoretic parameter \( {\text{Nt}} \) is limited to decreasing slightly the wall slope of the nanoparticle volume fraction profiles but increasing the nanoparticle volume fraction. This is true only for small values of Lewis number for which the Brownian diffusion effect is large compared to the convection effect. However, for large values of Lewis number, the diffusion effect is minimal compared to the convection effect and therefore the thermophoretic parameter \( {\text{Nt}} \) is expected to alter the nanoparticle volume fraction boundary layer significantly. Although thermophoresis effect is important in mixed convection of nanofluids, there are other parameters that may have effect and should be considered. These effects include decrease in effective kinematic viscosity of nanofluid due to the presence of nanoparticles and density variation due to variable volume fraction with heat capacity of the nanofluid. On the other hand, it is showed that the separation factor for common nanofluids is positive and density variation due to variable volume fraction of nanoparticles, called particulate buoyancy force, helps nanofluid to have strong convection heat transfer. These results clearly demonstrate that the magnetic field can be used as a means of controlling the flow and heat transfer characteristics including thermophoretic force of the nanoparticles. The result agrees with the expectations, since magnetic field exerts retarding force on the mixed convection flow.

Fig. 3
figure 3

Effects of \( {\text{Nt}} \) on a velocity, b temperature, c nanoparticle volume fraction and d concentration profiles

Full size image

Brownian motion of the nanoparticles is a key parameter for studying the effect of nanoparticles on flow fields temperature, nanoparticle volume fraction and concentration distributions. Thus, Fig. 4a–d presents the effect of Brownian motion on velocity, temperature, nanoparticle volume fraction and concentration of the nanofluid. When \( M = 3.0 \), it is observed that the velocity, temperature, nanoparticle volume fraction and concentration of the nanofluid decrease with increase of Brownian motion of the nanoparticles but \( M = 0.0 \), the typical temperature and concentration of the nanofluid firstly increases and then decreases with of increase of Brownian motion parameter and there is no additional thermal transport due to buoyancy effects created as a result of nanoparticle concentration gradients. It is interesting to note that the Brownian motion of nanoparticles at the molecular and nanoscale levels is a key nanoscale mechanism governing their thermal behavior with magnetic field. In nanofluid systems, due to the size of the nanoparticles, Brownian motion in the presence of magnetic field takes place which can affect the heat transfer properties. As the particle size scale approaches to the nano-meter scale, the particle Brownian motion and its effect on the surrounding liquids play an important role in heat transfer.

Fig. 4
figure 4

Effects of \( {\text{Nb}} \) on a velocity, b temperature, c nanoparticle volume fraction and d concentration profiles

Full size image

Figure 5a–d presents the velocity, temperature, nanoparticle volume fraction and concentration of the nanofluid with (M = 3.0) or without (M = 0.0) magnetic field. In the presence of uniform magnetic field, it is seen that the velocity decreases and the temperature and nanoparticle volume fraction of the nanofluid increase with increase of nanoparticle buoyancy ratio \( {\text{Nr}} \) whereas there are no significant changes in concentration profiles. This is due to the combined effect of density and thermal coefficient expansion of the base fluid with nanoparticle mass density. When \( M = 0.0 \), it is observed that the temperature, nanoparticle volume fraction and concentration of the nanofluid firstly increase and then decrease with increase of nanoparticle buoyancy ratio. In this case, the combined effect of thermophoresis and Brownian motion plays a dominant role on the flow field.

Fig. 5
figure 5

Effects of \( {\text{Nr}} \) on a velocity, b temperature, c nanoparticle volume fraction and d concentration profiles

Full size image

Figure 6a–d predicts the Soret number \( (S_{T} ) \) on velocity, temperature, nanoparticle volume fraction and concentration profile evolution through the boundary layer. The values of \( S_{T} \) have been selected to ensure that the Soret number is constant, assuming that the mean temperature is constant. These effects are defined in the Eq. (11) by the final second order derivatives, \( S_{T} \theta^{\prime \prime } \). As such the Soret term represents the effect of temperature gradients on the concentration field. In the presence of magnetic field, it is seen that the concentration of the nanofluid increases whereas the velocity, temperature and nanoparticle volume fraction of the nanofluid are uniform with increase of Soret number because of the combined effect of kinematic viscosity and distinct reduce in the concentration field throughout the boundary layer regime, i.e., for all \( \eta \) values. Concentration gradients therefore generally assist the flow and enhance thermal energy in the regime. An increase in Soret number \( (S_{T} ) \) with uniform magnetic field has a favorable effect on the concentration values in the regime. When \( M = 0.0 \), it is noticed that the temperature, nanoparticle volume fraction and concentration of the nanofluid firstly increase and then decrease with increase of Soret number. As such temperature gradients generally accentuate the concentration distributions in the porous regime.

Fig. 6
figure 6

Effects of \( S_{T} \) on a velocity, b temperature, c nanoparticle volume fraction and d concentration profiles

Full size image

Figure 7a–d depicts the influence of the suction parameter \( S \) on velocity, temperature, nanoparticle volume fraction and concentration profiles in the boundary layer when the magnetic field is uniform, i.e., \( M = 3.0 \). Increasing the value of suction (S > 0), the velocity and the temperature are found to increase (Fig. 7a, b), i.e., suction causes to increase the velocity and temperature of the nanofluid in the boundary layer region. The physical explanation for such a behavior is as follows. In case of suction, the heated fluid is pushed towards the wall where the buoyancy forces can act to enhance the nanofluid due to high influence of the viscosity. This effect acts to decrease the wall shear stress. Figure 7c and d exhibits that the nanoparticle volume fraction firstly decreases and then increases and concentration of the nanofluid decreases with increase of suction parameter. The explanation for such behavior is that the fluid is brought closer to the surface and increases the thermal and reduces the concentration boundary layer thickness in case of suction. As such then the presence of wall suction increases the momentum boundary layer thickness but increases the thermal and reduces solute boundary layers thickness, i.e., thick out the thermal and thin out the solute boundary layers. However, the exact opposite behavior is produced by imposition of wall fluid blowing or injection.

Fig. 7
figure 7

Effects of \( S \) on a velocity, b temperature, c nanoparticle volume fraction and d concentration profiles

Full size image

Figure 8a–d presents typical profiles for velocity, temperature, nanoparticle volume fraction and concentration of the nanofluid for different values of magnetic strength in the presence of uniform Brownian motion of the nanoparticles. Due to the high strength of Brownian motion of the nanoparticles \( {\text{Nb}} = 1.0 \) with uniform thermophoresis particle deposition of the nanoparticles, it is clearly shown that the velocity of the fluid decreases, the nanoparticle volume fraction and concentration of the nanofluid increase and the temperature of the fluid increases \( 0 \le \eta \le 0.37 \) and then decreases \( \eta > 0.37 \) with increase of the strength of magnetic field whereas there are some significant changes in all field (see Fig. 8a–d) for \( {\text{Nb}} = 0.1 \). The effects of a transverse magnetic field to an electrically conducting fluid give rise to a resistive-type force called the Lorentz force. This force has the tendency to slow down the motion of the fluid and to increase its temperature, nanoparticle volume fraction and concentration profiles. This result qualitatively agrees with the expectations, since magnetic field exerts retarding force on the mixed convection flow. Application of a magnetic field moving with the free stream has the tendency to induce a motive force which decreases the motion of the fluid and increases its boundary layer. This is accompanied by an increase in the nanofluid temperature, nanoparticle volume fraction and concentration field.

Fig. 8
figure 8

Effects of \( M \) on a velocity, b temperature, c nanoparticle volume fraction and d concentration profiles

Full size image

Conclusions

In this paper, the effect of Brownian motion of nanoparticles on mixed convection flow along a porous vertical plate in a nanofluid is analyzed in the presence of magnetic field under the convective boundary conditions. The numerical results are obtained for a wide range of values of the physical parameters as follows

  • It is clearly demonstrated that the magnetic field can be used as a means of controlling the flow and heat and mass transfer characteristics including thermophoretic force and Brownian motion of the nanoparticles. The result agrees with the expectations, since magnetic field exerts retarding force on the mixed convection flow.

  • Brownian motion of the nanoparticles in the presence of magnetic field takes place which can affect the temperature and nanoparticle volume fraction properties.

  • It is interesting to note that the velocity of the nanofluid decreases, the temperature firstly decreases (\( \eta \le 0.68 \)) and then increases (\( \eta > 0.68 \)), the volume fraction of the nanoparticles and the concentration of the nanofluid increase with increase of thermophoresis particle deposition.

  • In the presence of uniform magnetic field, it is seen that the velocity decreases and the temperature and nanoparticle volume fraction of the nanofluid increase with increase of nanoparticle buoyancy ratio \( {\text{Nr}} \) whereas there are no significant changes in concentration profiles.

  • It is seen that the concentration of the nanofluid increases whereas the velocity, temperature and nanoparticle volume fraction of the nanofluid are uniform with increase of Soret number because of the combined effect of kinematic viscosity and distinct reduction in the concentration with magnetic field.

  • Increasing suction causes to increase the velocity and temperature of the nanofluid in the boundary layer region because of the heated fluid is pushed towards the wall where the buoyancy forces can act to enhance the nanofluid due to high influence of the viscosity whereas the nanoparticle volume fraction firstly decreases and then increases and the concentration of the nanofluid decreases with increase of suction parameter.

  • Due to the high strength of Brownian motion of the nanoparticles with uniform thermophoresis particle deposition, it is clearly shown that the velocity of the fluid decreases, the nanoparticle volume fraction and concentration of the nanofluid increase and the temperature of the fluid increases \( 0 \le \eta \le 0.37 \) and decreases \( \eta > 0.37 \) with increase of the magnetic field. The surface temperature increases as Biot number increases because of the combined effect of kinematics viscosity and thermal conductivity of nanofluids.

The mixed convection of nanofluid in the presence of magnetic field with small-particles suspensions has been used in many applications. The present study is of immediate interest in next-generation heat exchangers technology, materials processing exploiting vertical surfaces, geothermal energy storage and all those processes which are highly affected with heat enhancement concept. The analysis has helped engineers understand the mechanisms that are most important in the deposition process. One of the technological applications of nanoparticles that hold enormous promise is the use of heat transfer fluids containing suspensions of nanoparticles to confront cooling problems in thermal systems. Hence, the combined effect of thermophoresis particle deposition with Brownian motion on nanofluids due to magnetic field is of great interest worldwide for basic and applied research.