Dual solutions of radiative MHD nanofluid flow over an exponentially stretching sheet with heat generation/absorption

Abstract

In this study, we analyzed the heat and mass transfer in thermophoretic radiative hydromagnetic nanofluid flow over an exponentially stretching porous sheet embedded in porous medium with internal heat generation/absorption, viscous dissipation and suction/injection effects. The governing partial differential equations of the flow are converted into nonlinear coupled ordinary differential equations by using similarity transformation. Runge–Kutta-based shooting technique is employed to yield the numerical solutions for the model. The effect of non-dimensional parameters on velocity, temperature and concentration profiles are discussed and presented through graphs. The physical quantities of interest local skin friction coefficient, Nusselt and Sherwood numbers are calculated and presented through tables.

Introduction

Heat and mass transfer of MHD thermophoretic flow has potential applications such as air cleaning, aerosol particles sampling, nuclear reactor safety and microelectronics manufacturing. Thermophoresis describes the migration of suspended small micron-sized particles in a non-isothermal gas to the direction with decreasing thermal gradient and the velocity acquired by the particle is known as thermophoretic velocity. The detailed discussion about this study was given by Derjaguin and Yalamov (1965). Thermophoresis of aerosol particles in laminar boundary layer on flat plate was analyzed by Goren (1977). The behavior of particles over heated surface by applying thermophoretic effect was discussed by Talbot et al. (1980). Mills et al. (1984) analyzed thermophoresis effect on aerosol particles by considering wall suction over flat plate. The similar effects were discussed by Batchelor and Chen (1985) on cold surface. MHD flow over exponential surface by considering visco-elastic fluid was given by Andersson (1992). Choi (1995) was the first person who introduced the concept of nanofluid by suspending nanometer-sized particles into base fluids. Chamka and Issa (2000) studied thermophoresis effects of the MHD flow over flat plate with heat source/sink. Elbashbeshy (2001) discussed heat transfer characteristics over stretching surface. Lin et al. (2004) discussed particle deposition through circular tube by taking wall temperature is higher than gas. A detailed note on heat transfer analysis was given by Wang and Mujumdar (2007). Thermophysical properties of nanofluids were discussed by Philip et al. (2008). A similarity solution by considering suction/injection over stretching surface was discussed by Afify (2009). Hayat and Qasim (2010) presented thermal radiation effects on MHD flow of Maxwell’s fluid by taking thermophoresis effect. Bhattacharya (2011) analyzed the flow over exponentially shrinking sheet. The boundary layer flow of a nanofluid past a stretching sheet was discussed by Makinde and Aziz (2011). They used convective boundary conditions to analyze the effects of physical parameters on the flow. Remeli et al. (2012) discussed the effects of suction/injection parameter on Marangoni boundary layer flow of a nanofluid. They gave a conclusion that increase in suction parameter leads to a decrease in velocity profiles and increase in injection parameter decreases the velocity of the nanofluid.

Thermophoresis effect by considering unsteady MHD flow past an inclined porous plate was studied by Kabir and Mahbub (2012). In this study, they used Runge–Kutta sixth-order technique with shooting technique. Rana and Bhargava (2012) used finite element and finite difference methods for nonlinear stretching sheet problem. Zaimi et al. (2014) extended the work of Rana and Bhargava and studied heat transfer and boundary layer flow of a nanofluid over a stretching/shrinking sheet. The effect of particle size on thermal conductivity of the nanofluids was studied by Baheta and Woldeyohannes (2013) and notified that the thermal conductivity enhancement will reduces with an increase in size of the nanoparticles. Researchers Sandeep et al. (2013) and Mohankrishna et al. (2013) discussed the effect of physical parameters on the flow and heat transfer behavior of nano- and dusty fluid flows. Hydromagnetic flow over inclined plate by considering thermophoretic effect with heat source or sink was analyzed by Noor et al. (2013). Motion of aerosol particles on horizontal plates by considering external pressure was discussed by Guha and Samanta (2014). Sandeep et al. (2014) analyzed aligned magnetic field effect on unsteady flow over vertical plate in porous medium. Radiation effect on MHD viscous fluid over exponentially stretching sheet in porous medium was analyzed by Ahmad et al. (2014). Brownian motion and thermophoresis effects on radiative magnetohydromagnetic flow between two horizontal rotating plates were analyzed by Sheikholeslami et al. (2015).

To the author’s knowledge, no studies has been reported on heat and mass transfer in thermophoretic radiative hydromagnetic nanofluid flow over an exponentially stretching porous sheet embedded in porous medium with internal heat generation/absorption and viscous dissipation. The governing partial differential equations of the flow are converted into nonlinear coupled ordinary differential equations by using similarity transformation. Runge–Kutta-based shooting technique is employed to yield the numerical solutions for the model. The effect of non-dimensional parameters on velocity, temperature and concentration profiles are discussed and presented through graphs.

Mathematical formulation

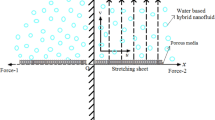
Consider a steady, incompressible, electrically conducting, two-dimensional boundary layer flow of a dissipative nanofluid over an exponentially stretching sheet in a porous medium. The x-axis is along the continuous stretching surface, and y-axis is normal to the surface. The porous medium with non-uniform permeability k is considered, and a variable magnetic field B(x) is applied along y direction. A variable heat source Q(x), suction/injection effects along with thermophoretic, is taken into account. The boundary layer equations that governs the present flow subject to the Boussinesq approximations can be expressed as

$$ \frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} = 0 $$

(1)

$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \frac{1}{{\rho_{\text{nf}} }}\left[ {\mu_{\text{nf}} \frac{{\partial^{2} u}}{{\partial y^{2} }} + g(\rho \beta )_{\text{nf}} (T - T_{\infty } ) - \sigma B^{2} (x)u - \frac{{\upsilon_{f} }}{k}u} \right] $$

(2)

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{\text{nf}} \frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{(\rho c_{p} )_{\text{nf}} }}\frac{{\partial q_{r} }}{\partial y} + \frac{Q(x)}{{(\rho c_{p} )_{\text{nf}} }}(T - T_{\infty } ) + \frac{{\mu_{\text{nf}} }}{{(\rho c_{p} )_{\text{nf}} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} $$

(3)

$$ u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{m} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{\kappa \upsilon_{f} }}{{T_{r} }}\frac{\partial T}{\partial y}\frac{\partial C}{\partial y} - C\frac{\partial C}{\partial y} $$

(4)

where u and v are the velocity components in the x, y directions, ρ _nf is the density of nanofluid, μ _nf is the dynamic viscosity of the nanofluid, g is the acceleration due to gravity, β _nf is the volumetric coefficient of thermal expansion, σ is the electrical conductivity, $B(x) = B_{0} {\text{e}}^{{{\text{Nx}}/2L}}$ is the variable magnetic field, B ₀ is the constant magnetic field, N is the exponential parameter, υ _f is the kinematic viscosity of the fluid, $k = k_{0} {\text{e}}^{{ - {\text{Nx}}/L}}$ is the non-uniform permeability of porous medium, T and T _∞ are the surface and ambient temperatures, $\alpha_{\text{nf}} = k_{\text{nf}} /(\rho c_{p} )_{\text{nf}}$ is the thermal diffusivity, $(c_{p} )_{\text{nf}}$ is the specific heat of the nanofluid, qr is the radiative heat flux, $Q(x) = Q_{0} {\text{e}}^{{{\text{Nx}}/L}}$ is the internal heat source/sink, D _m is the molecular diffusivity of species concentration, T _r is the reference temperature which is approximately equal to 300 K, and κ is the thermophoretic coefficient defined by Talbot et al. (1980).

$$ \kappa = \frac{{2.34(6\pi \mu \upsilon r)(\lambda_{\text{r}} + 4.36Kn)}}{{(1 + 6.84Kn)(1 + 8.72Kn + 2\lambda_{\text{r}} )}} $$

(5)

The range value of κ is from 0.2 to 1.2 is given by Batchelor and Chen (1985). $\lambda_{r} = \lambda /\lambda_{p}$ is the ratio of the thermal conductivity of the fluid and particles, and Kn is the Knudsen number. A thermophoretic parameter τ can be defined by Mills et al. (1984) as followsis the thermal Grashof

$$ \tau = - \frac{{\kappa (T_{w} - T_{\infty } )}}{{T_{r} }} $$

(6)

The approximate value of τ is equal to 0.1

The boundary conditions of the flow is given by

$$ \left. \begin{gathered} u = u_{w} (x),v = \pm v_{w} (x),T = T_{w} ,C = C_{w} \quad {\text{at}}\quad y = 0 \hfill \\ u \to 0,T \to T_{\infty } ,C \to C_{0} \quad {\text{as}}\quad y \to \infty \hfill \\ \end{gathered} \right\} $$

(7)

where $u = u_{w} (x) = U_{0} {\text{e}}^{{{\text{Nx}}/L}}$ is the surface velocity and $v_{w} (x) = v_{0} {\text{e}}^{{{\text{Nx}}/2L}}$ is the special type of velocity at the surface. Here $v_{w} (x) > 0$ represents suction and $v_{w} (x) < 0$ represents injection on the porous surface.

The radiative heat flux q _r under Rosseland approximation is of the form

$$ q_{r} = - \frac{{4\sigma_{1} }}{3\chi }\frac{{\partial T^{4} }}{\partial y}\, $$

(8)

where σ ₁ is the Stefan–Boltzmann constant and χ is the mean absorption coefficient. The temperature differences within the flow are assumed to be sufficiently small such that T ⁴ may be expressed as a linear function of temperature. Expanding T ⁴ using Taylor series and neglecting higher-order terms yields

$$ T^{4} \cong 4T_{\infty }^{3} T - 3T_{\infty }^{4} $$

(9)

Substituting Eqs. (8) and (9) into (3), we get

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{\text{nf}} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{16\sigma_{1} T_{\infty }^{3} }}{{3(\rho c_{p} )_{\text{nf}} \chi }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{Q(x)}{{(\rho c_{p} )_{\text{nf}} }}(T - T_{\infty } ) + \frac{{\mu_{\text{nf}} }}{{(\rho c_{p} )_{\text{nf}} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} $$

(10)

The governing Eqs. (1)–(4) and (9) can be simplified by introducing the similarity transformations

$$ \begin{gathered} \eta = y\sqrt {U_{0} /2\upsilon_{\text{nf}} L} e^{{{\text{Nx}}/2L}} ,\quad u = U_{0} e^{{{\text{Nx}}/L}} f'(\eta ),\quad C = C_{0} {\text{e}}^{{{\text{Nx}}/2L}} \phi (\eta ) \hfill \\ T = T_{w} = T_{\infty } + T_{0} {\text{e}}^{Nx/2L} \theta (\eta ),\quad v = - N\sqrt {\upsilon_{\text{nf}} U_{0} /2L} \quad {\text{e}}^{{{\text{Nx}}/2L}} \left\{ {f(\eta ) + \eta f'(\eta )} \right\} \hfill \\ \end{gathered} $$

(11)

Using (11), the governing partial differential equations are reduced to

$$ f^{{{\prime \prime \prime }}} + Nff^{{{\prime \prime }}} - 2Nf^{{{\prime 2}}} + Gr\theta - (M + K)f^{{\prime }} = 0 $$

(12)

$$ \left( {\frac{1}{\Pr } + R} \right)\theta^{{{\prime \prime }}} - 4N\theta f^{{\prime }} + Nf\theta^{{\prime }} + Ec(f^{{{\prime \prime }}} )^{2} + Q_{H} \theta = 0 $$

(13)

$$ \phi^{{{\prime \prime }}} - NSc(4f^{{\prime }} \phi - f\phi ') - \frac{Sc\tau }{\theta }\left( {\theta^{{\prime }} \phi^{{\prime }} + \theta^{{{\prime \prime }}} } \right) = 0 $$

(14)

Subject to the boundary conditions

$$ f = f_{w} ,\,f^{{\prime }} = 1,\theta = 1,\phi = 1\quad {\text{at}}\quad \eta = 0 $$

$$ f^{{\prime }} \to 0,\theta \to 0,\phi \to 0,\quad {\text{as}}\;\eta \to \infty $$

(15)

where N is the exponential parameter, $Gr = 2Lg\beta_{\text{nf}} T_{0} /U_{0}^{2}$ is the thermal Grashof number, $M = 2L\sigma B_{0}^{2} /\rho_{\text{nf}} U_{0}$ is the Hartmann number,$K = 2L\upsilon_{\text{nf}} /k_{0} U_{0}$ is the porosity parameter, $\Pr = \upsilon_{\text{nf}} /\alpha_{\text{nf}}$ is the Prandtl number, $R = 16\sigma_{1} T_{\infty }^{3} /3\chi (\mu c_{p} )_{\text{nf}}$ is the radiation parameter, $Ec = U_{0}^{2} /T_{0} (c_{p} )_{\text{nf}}$ is the Eckert number, $Q_{H} = 2LQ_{0} /(\rho c_{p} )_{\text{nf}} U_{0}$ is the internal heat source/sink, $Sc = \upsilon_{\text{nf}} /D_{m}$ is the Schmidt number, $\tau = - \kappa (T - T_{\infty } )/T_{r}$ is the thermophoretic parameter, and $f_{w} = - v_{w} (x)\sqrt {\upsilon_{\text{nf}} U_{0} /2L}$ is the permeability of the porous surface with positive value indicates suction, while negative value indicates injection.

Results and discussion

Equations (12)–(14) with the boundary conditions (15) have been solved numerically using Runge–Kutta-based shooting technique. The results obtained show the influences of the non-dimensional governing parameters, namely magnetic field parameter M, heat generation/absorption parameter Q _H , thermophoretic parameter τ, porosity parameter K, exponential parameter N, radiation parameter R, Grashof number Gr, Prandtl number Pr, Eckert number Ec and Schmidt number Sc on the velocity, temperature and concentration profiles. Also friction factor, local Nusselt and Sherwood numbers are discussed. In the present study, for numerical results, we considered the non-dimensional parameter values as $\Pr = 0.71,N = 1,Gr = 1$, $M = K = R = Q_{H} = 0.5,Sc = 0.6Ec = 0.1$ and τ = 0.1. These values are kept as constant except the varied parameters as shown in figures.

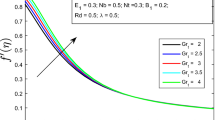
Figures 1, 2 and 3 describe the effect exponential parameter (N) on the nanofluid velocity, temperature and concentration profiles, respectively, for both suction and injection cases. It is evident from figures that an increase in exponential parameter depreciates the velocity, temperature and concentration profiles in both suction and injection cases. It is observed that the exponential parameter influence is more on suction while compared with injection. Physically, this means that increase in N value reduces the momentum, thermal and concentration boundary layer thickness and it is important to mention here that for positive exponential parameter, also the surface temperature depreciates near the boundary layer. Figures 4, 5 and 6 illustrate the effect magnetic field parameter (M) on the nanofluid velocity, temperature and concentration profiles, respectively, for both suction and injection cases. It is noticed from figures that increase in magnetic field parameter decreases the velocity profiles for both suction and injection cases, but it is reversed in temperature and concentration profiles. It is due to the fact that increase in magnetic field generates the opposite force to the flow, is called Lorentz force. This force helps to enhance the thermal and concentration boundary layers. Due to this reason, we have seen rising in the values of temperature and concentration profiles.

Fig. 1

Velocity profiles for different values of exponential parameter N

Fig. 2

Temperature profiles for different values of exponential parameter N

Fig. 3

Concentration profiles for different values of exponential parameter N

Fig. 4

Velocity profiles for different values of magnetic field parameter M

Fig. 5

Temperature profiles for different values of magnetic field parameter M

Fig. 6

Concentration profiles for different values of magnetic field parameter M

Figures 7, 8 and 9 depict the effect of thermophoretic parameter (τ) on the nanofluid velocity, temperature and concentration profiles, respectively, for both suction and injection cases. It is noticed from figures that thermophoretic parameter does not shown any influence on velocity and temperature profiles. But a rise in the value of τ opposes the concentration profiles of the flow for both suction and injection cases. We may explain this phenomenon as the enhancement in thermophoretic parameter causes the fluid particles to move away from cool surroundings. Figures 10, 11 and 12 show the effect of porosity parameter (K) on the nanofluid velocity, temperature and concentration profiles, respectively, for both suction and injection cases. It is observed from figures that rise in the value of porosity parameter declines the velocity profiles and enhances the temperature as well as concentration profiles. It is due to the fact that increases in porosity widen the porous layer and increases the momentum boundary layer thickness. But increase in porosity generates the internal heat to the flow, which will enhance the thermal and concentration boundary layers.

Fig. 7

Velocity profiles for different values of thermophoretic parameter τ

Fig. 8

Temperature profiles for different values of thermophoretic parameter τ

Fig. 9

Concentration profiles for different values of thermophoretic parameter τ

Fig. 10

Velocity profiles for different values of porosity parameter K

Fig. 11

Temperature profiles for different values of porosity parameter K

Fig. 12

Concentration profiles for different values of porosity parameter K

Figures 13, 14 and 15 represent the effect of radiation parameter (R) on the nanofluid velocity, temperature and concentration profiles, respectively, for both suction and injection cases. It is clear from figures that nanofluid velocity and temperature distributions increase with increases in radiation parameter, but it shows opposite action in concentration profiles. This agrees the physical behavior that at R ≠ 0, the radiation is more significant and it causes momentum and thermal boundary layers to become thinner. And it is negligible as R → ∞. The reason behind the depreciate in concentration profiles is similar to the fact as we explained in thermophoretic case. Figures 16, 17 and 18 display the effect of heat generation/absorption parameter (Q _H ) on the nanofluid velocity, temperature and concentration profiles, respectively, for both suction and injection cases. The results obtained in this case are similar to the results observed for radiation parameter. But it is prominent to mention here that in this case heat generation dominates the absorption; otherwise, we may have seen the results opposite to present.

Fig. 13

Velocity profiles for different values of radiation parameter R

Fig. 14

Temperature profiles for different values of radiation parameter R

Fig. 15

Concentration profiles for different values of radiation parameter R

Fig. 16

Velocity profiles for different values of heat source parameter Q _H

Fig. 17

Temperature profiles for different values of heat source parameter Q _H

Fig. 18

Concentration profiles for different values of heat source parameter Q _H

Table 1 shows the effects of various non-dimensional parameters on friction factor, heat and mass transfer coefficients. It is evident from the table that a rise in the values of Prandtl number, exponential parameter and porosity parameter depreciates the friction factor and improves the heat and mass transfer rate. Magnetic field parameter, radiation parameter and heat source/sink parameters show opposite results to the above discussion: That is, increases in magnetic field, radiation and heat source/sink parameters enhance the coefficient of skin friction but reduces the heat and mass transfer rate. Thermophoretic parameter and Schmidt number do not show any influence in friction and heat transfer coefficients. But these parameters help to enhance the Sherwood number. Grashof number is only the parameter which improves friction factor along with heat and mass transfer rate.

Table 1 Effects of non-dimensional governing parameters on skin friction, heat and mass transfer coefficients in suction case

Conclusions

This paper presents a similarity solution for the thermal radiation influenced thermophoretic MHD flow over an exponentially stretching surface with heat generation/absorption, viscous dissipation in porous medium. By means of similarity transformation, the governing mathematical equations are reduced into ordinary differential equations which are then solved numerically. The effects of governing parameters on the velocity, temperature, concentration, friction factor, heat and mass transfer coefficients are discussed and presented through graphs and tables. The findings of the numerical results are summarized as follows:

• 1. Exponential parameter improves the heat and mass transfer rate and depreciates the velocity profiles.

• 2. Thermophoretic parameter and Schmidt number do not show any influence on velocity and temperature fields, but it proves mass transfer rate.

• 3. Increase in magnetic field parameter causes increase in friction factor and depreciates in velocity profiles of the flow.

• 4. Radiation and heat generation/absorption parameters have capability to enhance the momentum and thermal boundary layers.

• 5. Grashof number has tendency to improve friction factor as well as heat mass transfer rate.