Dynamic tracking model for the reservoir water flooding of a separated layer water injection based on a well temperature log

Abstract

A dynamic tracking model for the reservoir water flooding of a separated layer water injection was established. Based on the basic principles of heat and mass transfer, the water profile was determined using a well temperature curve. The Poisson process analysis and stochastic process methods were applied to calculate the water saturation, water breakthrough time, and water cut of each layer in a water-flooded reservoir at any given time. When the oil reservoir was producing water, the water cut predicted by the models, with consideration of the micro-pore distribution, approximated the practical measurement, having an error of less than 5 %. The sample application clearly indicated that larger water injection intensity (water intake per unit thickness) could result in more drastic water saturation variation, earlier water breakthrough, and faster increase in the water cut for layers with numerous high-permeability channels, such as fractures.

Introduction

For a water-flooded reservoir, water saturation, and water cut are key indices used to evaluate the reservoir water-out behavior as well as to monitor and manage the reservoir (Guo and Sun 1998; Li et al. 2011; Kazeem et al. 2007; Yang et al. 2006).

The main water saturation measurement methods include sealing core drilling (Wang et al. 2010; Guo and Lu 1996), geophysical logging (He et al. 2010), numerical reservoir simulation, and single-well chemical tracing (Deans 1971, 1974; Deans and Mut 1997; Cockin et al. 2000). Sealing core drilling is costly, and data points are limited. Geophysical logging can hardly meet the accuracy and effectiveness of production practice requirements, because this method commonly makes predictions based on logging information obtained using empirical correlation or regression techniques. For a reservoir simulation, the workload is heavy, and the computation period is long. Obtaining the water saturation by applying single-well chemical tracer tests is based on the chromatographic separation principle of the tracer in the reservoir. This test depends on the chromatographic effect in a balanced state. The test results are highly accurate, but costly.

Water-cut prediction methods primarily comprise numerical simulation, empirical correlation, and an analytical approach. Water-cut prediction is difficult and can be significantly affected by the reservoir and fluid properties as well as other factors (Guo and Sun 1998; Qu et al. 2010). Numerical simulation is a superior forecasting method, but it consumes a great deal of time (Zhao et al. 2004). Empirical correlation is a mathematical method of data processing that lacks a specific physical ground. This method includes an established water-cut prediction model using Neural Networks (Tang and Luo 2003), Usher Model (Yang 2008), Weibull Model, Warren Model, and Rayleigh Model (Liu et al. 2009) based on the reservoir static and production dynamic data; an established formula by fitting the plot of water cut with experimental data (Liu et al. 2011); and an established quantitatively characterized model of variations in water cut based on the actual water cut and the quantitatively characterized model principles (Zhao et al. 2010). Analytical approaches embrace the water-cut prediction method based on the water saturation function and fractional flow theory (Ershagi and Omoregie 1978; Sitorus et al. 2006; Lo et al. 1990; Ershagi and Abdassah 1984), the mathematical correlation model between the water cut and time established based on making certain assumptions for the reservoir (Li et al. 2011; Kazeem et al. 2007; Jiang et al. 1999), and the analytical solution to the water cut established by calculating the complex potential and portraying flow streamlines in a flooding pattern (Xu et al. 2010). These methods are unsuitable for the prediction of the water cut for a reservoir with a separated layer water injection.

In this paper, we calculated the water saturation, water breakthrough time, and water cut of each layer at any given time based on the water injection profile derived from a well temperature curve, Poisson process analysis, and stochastic process methods. We believe that this model can provide theoretical guide for a separate layer water shutoff during the development of a water-flooded reservoir.

Model establishment and solution

Water injection profile

For a water-flooded reservoir with a separated layer water injection, the water injection profile can be determined by applying the basic principles of heat and mass transfer based on the temperature profile of the injected water and the reservoir rock in a well bore (Li et al. 1999; Fagley et al. 1982), as shown in Fig. 1.

Fig. 1

Schematic diagram of mass and heat transfer in bore hole

• 1. Heat and mass transfer equation for the water phase.

  Water temperature in the borehole varies as follows:

  $${\mathit{\rho }}_{\text{w}}{C}_{\text{w}}\frac{\mathit{\partial }{T}_{\text{w}}}{\mathit{\partial }t}={\mathit{\rho }}_{\text{w}}{C}_{\text{w}}v\frac{\mathit{\partial }{T}_{\text{w}}}{\mathit{\partial }z}+k_{\text{w}}\frac{{\mathit{\partial }}^2{T}_{\text{w}}}{\mathit{\partial }{z}^2}+\frac{2h}{r_{\text{w}}}\left[T\left(r_{\text{w}},z,t\right)-T_{\text{w}}\left(z,t\right)\right],$$

  (1)

  where the initial conditions are

  $$T_{\text{w}}\left(z,0\right)=a+bz,$$

  (2)

  and the boundary conditions are

  $$T_{\text{w}}\left(z_{\text{max}},t\right)=T_{\text{s}}\left(t\right),\text{where}0<t\le t_{\text{si}},$$

  (3)
  $$k_{\text{w}}\frac{\mathit{\partial }{T}_{\text{w}}\left(z_{\text{max}},t\right)}{\mathit{\partial }z}=0,\text{where}{t}_{\text{si}}\le t,$$

  (4)
  $$k_{\text{w}}\frac{\mathit{\partial }{T}_{\text{w}}\left(0,t\right)}{\mathit{\partial }z}=0,\text{where}0<t,$$

  (5)

  and h is

  $$h=\mathit{\alpha }{\left[T\left(r_{\text{in}},z,t\right)-T_{\text{w}}\left(z,t\right)\right]}^{1/\phantom{14}4}.$$

Equation (1) describes the variation in temperature during water phase flow in a borehole. When the convection component equals zero, i.e., ${\mathit{\rho }}_{\text{w}}{C}_{\text{w}}v\frac{\mathit{\partial }{T}_{\text{w}}}{\mathit{\partial }z}=0,$ the equation also describes a well shut.

• 2. Heat and mass transfer equation for the reservoir rock.

  The reservoir temperature variation equation can be written as follows:

  $${\mathit{\rho }}_{\text{e}}{C}_{\text{e}}\frac{\mathit{\partial }T}{\mathit{\partial }t}=\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}\left(r{k}_{\text{fe}}\frac{\mathit{\partial }T}{\mathit{\partial }r}\right)+\frac{\mathit{\partial }}{\mathit{\partial }z}\left(k_{\text{fe}}\frac{\mathit{\partial }T}{\mathit{\partial }z}\right)-\frac{q_{\text{w}}{\mathit{\rho }}_{\text{w}}{C}_{\text{w}}}{2\mathit{\pi }r}\frac{\mathit{\partial }T}{\mathit{\partial }r}+\frac{q_{\text{w}}\left(p_{\text{w}}-p_{\text{e}}\right)}{2\mathit{\pi }{r}^2{J}_{\text{c}}ln\left(r_{\text{e}}/r_{\text{w}}\right)},$$

  (6)

  where the initial conditions are

  $$T\left(r,z,0\right)=a+bz,$$

  (7)

  and the boundary conditions are

  $$T\left(r_{\text{e}},z,t\right)=a+bz,$$

  (8)
  $$T\left(r,0,t\right)=a,$$

  (9)
  $$T\left(r,z_{\text{max}},t\right)=a+b{z}_{\text{max}},$$

  (10)

  and

  $$k_{\text{fe}}\frac{\mathit{\partial }T}{\mathit{\partial }r}\left(r_{\text{w}},z,t\right)=h\left[T_{\text{w}}\left(z,t\right)-T\left(r_{\text{w}},z,t\right)\right],(0\le z\le z_1,z_2\le z\le z_{\text{max}},0<t;z_1<z<z_2,t_{\text{si}}<t);$$
  $$T\left(r_{\text{w}},z,t\right)=T_{\text{w}}\left(z,t\right),(z_1<z<z_2,0<t\le t_{\text{si}}),$$

  and J _c is the work and thermal conversion coefficient equal to 427 (m kg)/kJ.

Equation (6) describes the heat balance of the reservoir rock around the borehole as well as the water injection layer. When the radial convection and the friction heat components are equal to zero, i.e., $\frac{q_{\text{w}}{\mathit{\rho }}_{\text{w}}{C}_{\text{w}}}{2\mathit{\pi }r}\frac{\mathit{\partial }T}{\mathit{\partial }r}=0$ and $\frac{q_{\text{w}}\left(p_{\text{w}}-p_{\text{e}}\right)}{2\mathit{\pi }{r}^2{J}_{\text{c}}ln\left(r_{\text{e}}/r_{\text{w}}\right)}=0$, respectively, the equation is also applicable to the un-injection layers and water injection layers after a well shut.

The water injection volume for each layer at any given time q_w (1, j, t) can be obtained by computing the finite difference between Eqs. (1) and (6) with the initial and boundary conditions as follows: First, given an initial injection water profile q_w (1, j, t₀), the numerical solution $T_{{}_{1,j}}^t$ is calculated, the numerical solution and the actual well temperature are compared, and then the water injection profile q_w (1, j, t) is adjusted to approximate the numerical solution $T_{{}_{1,j}}^t$ to the actual well temperature. The numerical solution q_w (1, j, t) can be regarded as the actual injection water volume at time t, where q_w (1, j, t) is the water injection volume of the first radial grid and the j^th vertical grid at time t, and $T_{{}_{1,j}}^t$ is the well temperature of the first radial grid and the jth vertical grid at time t.

Water streamlines the velocity

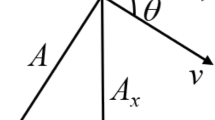
Generally, the advancing velocity of the injected water is closely related to the pore structure of the water-flooded reservoir. In a water/oil displacement experiment, we commonly use φ to denote the core porosity, A to denote the cross section area, Q to denote the water injection rate, dp/dl to denote the pressure gradient, and Q/φ to denote the water-flooded core volume per unit time. Then, the advancing velocity of the injected water in the core is Q/(Aφ) (Fig. 2).

Fig. 2

The core of water/oil displacement experiment

Assuming that the core pore diameter distribution is divided into N levels: ${\mathit{\gamma }}_1,{\mathit{\gamma }}_2,\dots ,{\mathit{\gamma }}_N$, with each proportion p(γ _j ) = p _j , where $j=1,2\dots ,N$; $p_1+p_2+\cdots +p_{\text{N}}=1$. If the number of pores in λ _j passed by a line parallel to the core axis satisfying the Poisson process (Yao et al. 1999), i.e., for a core length L, assuming that the number of pores with length l (0 ≤ l ≤ L) passing through the diameter γ _j is a random variable parameter ζ _j (l) with the following probability distribution:

$$P\left({\mathit{\zeta }}_j(l)=k\right)=\frac{{\left({\mathit{\lambda }}_{j}l\right)}^k}{k!}{e}^{{\mathit{\lambda }}_{j}l},k=0,1,2,\dots ,.$$

(11)

The total number of pores that passes through all levels with diameter of length l follows a random variable parameter $\mathit{\eta }(l)={\sum }_{j=1}^N{\mathit{\zeta }}_j(l)$. According to Poisson’s reproducibility, η(l) also satisfies the Poisson process of strength $\mathit{\lambda }={\sum }_{j=1}^N{\mathit{\lambda }}_j,$ and the probability distribution is

$$P\left(\mathit{\eta }(l)=k\right)=\frac{{\left(\mathit{\lambda }l\right)}^k}{k\text{!}}{e}^{\mathit{\lambda }l}=\frac{{\left[\left({\mathit{\lambda }}_1+{\mathit{\lambda }}_2+\cdots {\mathit{\lambda }}_N\right)l\right]}^k}{k\text{!}}{e}^{\left({\mathit{\lambda }}_1+{\mathit{\lambda }}_2+\cdots {\mathit{\lambda }}_N\right)l},k=0,1,2,\dots ,$$

(12)

The strength λ is the average total number of pores passed by any unit length straight line parallel to the core axis. λ can be obtained by observing and counting the slabbed core or the scanning electron microscopy images, and can also be determined by a mathematical derivation.

$$\mathit{\tau }=l_{\text{pore}}/\phantom{l_{\text{pore}}L=\sqrt[3]{\mathit{\varphi }}}L=\sqrt[3]{\mathit{\varphi }},$$

(13)

where τ is the linear porosity, and l_pore is the total length of the pores in the core.

The average diameter of the pore is

$$\mathit{\gamma }=\sum _{j=1}^N{\mathit{\gamma }}_j{P}_j.$$

(14)

The average number of pore passed by the unit length is

$$\mathit{\lambda }=\mathit{\tau }/\phantom{\mathit{\tau }\mathit{\gamma }}\mathit{\gamma }=\sqrt[3]{\mathit{\varphi }}/\phantom{\sqrt[3]{\mathit{\varphi }}\mathit{\gamma }}\mathit{\gamma }.$$

(15)

The average number of water-flooded pores in the water/oil displacement experiment in terms of unit time is

$$n=\mathit{\lambda }·\frac{Q}{A\mathit{\varphi }}.$$

(16)

The average distance l connected by these pores is

$$l=n·\mathit{\gamma }=\frac{\mathit{\lambda }Q\mathit{\gamma }}{A\mathit{\varphi }}.$$

(17)

The average advancing velocity of the water in the core can be expressed as

$$\overline{\mathit{\upsilon }}=\frac{\mathit{\lambda }Q\mathit{\gamma }/\phantom{Q\mathit{\gamma }\left(A\mathit{\varphi }\right)}\left(A\mathit{\varphi }\right)}{{\mathit{\varphi }}^{1/\phantom{13}3}}=\frac{\mathit{\lambda }Q\mathit{\gamma }}{A{\mathit{\varphi }}^{4/\phantom{43}3}}.$$

(18)

In an actual reservoir, the water advancing velocity along the water streamline is not always υ, but a random variable parameter U_w. Similarly, the total number of water-flooded pores along the water streamline in terms of unit time is also a random variable parameter, denoted by ζ_w, that follows the Poisson distribution

$$P\left({\mathit{\zeta }}_{\text{w}}=k\right)=\frac{{\left[\mathit{\lambda }Q/\phantom{\mathit{\lambda }Q\left(A\mathit{\varphi }\right)}\left(A\mathit{\varphi }\right)\right]}^k}{k!}{e}^{\mathit{\lambda }Q/\phantom{\mathit{\lambda }Q\left(A\mathit{\varphi }\right)}\left(A\mathit{\varphi }\right)},k=0,1,2,\dots ,,$$

(19)

and

$$U_{\text{w}}={\mathit{\zeta }}_{\text{w}}\frac{\mathit{\gamma }}{\sqrt[3]{\mathit{\varphi }}}.$$

(20)

The Poisson distribution of U_w is

$$P\left(U_{\text{w}}=k\frac{\mathit{\gamma }}{\sqrt[3]{\mathit{\varphi }}}\right)=\frac{{\left[\mathit{\lambda }Q/\phantom{\mathit{\lambda }Q\left(A\mathit{\varphi }\right)}\left(A\mathit{\varphi }\right)\right]}^k}{k!}{e}^{-\mathit{\lambda }Q/\phantom{-\mathit{\lambda }Q\left(A\mathit{\varphi }\right)}\left(A\mathit{\varphi }\right)},k=0,1,2,\dots ,.$$

(21)

Equations (20) and (21) describe the random advancing velocity of the water throughout the core, and the average velocity is

$$E\left(U_{\text{w}}\right)=\sum _{k=0}^{\infty }k\frac{\mathit{\gamma }}{\sqrt[3]{\mathit{\varphi }}}P\left(U_{\text{w}}=k\frac{\mathit{\gamma }}{\sqrt[3]{\mathit{\varphi }}}\right)=\frac{\mathit{\gamma }}{\sqrt[3]{\mathit{\varphi }}}\frac{\mathit{\lambda }Q\mathit{\gamma }}{A\mathit{\varphi }}=\frac{\mathit{\lambda }Q\mathit{\gamma }}{A{Q}^{\frac{4}{3}}}=\frac{Q}{A\mathit{\varphi }}$$

(22)

This result is consistent with the derivation result of the water macro-advancing velocity Q/(Aφ) during the water/oil displacement experiment. The corresponding variance is

$$D\left(U_{\text{w}}\right)=\frac{{\mathit{\gamma }}^2}{{\mathit{\varphi }}^{\frac{2}{3}}}\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}=\frac{\mathit{\lambda }Q{\mathit{\gamma }}^2}{A{\mathit{\varphi }}^{\frac{5}{3}}}.$$

(23)

Assuming that Y is the sum of the total number of pores that any straight line l parallel to the core axis passed through, the core and the length of one side of the core, which is random variable parameter, exhibit expectation E(Y) and variance D(Y). Y is a random variable parameter. Y _i is the sum of the lengths of the pore i in the water streamline and its unilateral rock. Y _i and Y are independent and have the same distribution; thus, the water advancing velocity U_w can be expressed as

$$U_{\text{w}}=\sum _{i=1}^{\left[\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}\right]}{Y}_i.$$

(24)

The average value of U_w is

$$E\left(U_{\text{w}}\right)=\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}E\left(Y\right).$$

(25)

The corresponding variance is

$$D\left(U_{\text{w}}\right)=\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}D\left(Y\right).$$

(26)

The water-flooded distance within any given time period t is

$$U\left(t\right)=\sum _{i=1}^{\left[\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}t\right]}{Y}_i,$$

(27)

where $\left[\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}\right]$ and $\left[\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}t\right]$ are the closest integer to $\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}$ and $\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}t$, respectively.

The average value of U(t) is

$$E\left[U\left(t\right)\right]=\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}·t·E\left(Y\right).$$

(28)

The corresponding variance is

$$D\left[U\left(t\right)\right]=\frac{\mathit{\lambda }Q}{A\mathit{\varphi }}·t·D\left(Y\right).$$

(29)

Water saturation

Figure 3 shows the water advancing process from the injection well to the production well for a high horizontal homogeneity reservoir developed by a five-spot water-flooding pattern. The coordinate system 0, x, y was established. Given its symmetry, only the triangle area below the diagonal line OB had to be analyzed

$$y=x^{\mathit{\alpha }},\left(0\le x\le 1,\mathit{\alpha }\ge 1\right),$$

(30)

$$arctg\frac{y}{x-a}-arctg\frac{y}{x+a}=c,$$

(31)

where c is constant.

Fig. 3

Schematic diagram of water streamline in five-spot water-flooding patterns

The function family curves of Eq. (30) and the streamline of Eq. (31) are similar; thus, the streamline in the triangle area can be approximated by the function y = x^α. When α = 1, y is a square diagonal of length $\sqrt{2}$; when α → ∞, y is two right-angle sides of length 2. For any value of α, the corresponding streamline length is

$$l_{\mathit{\alpha }}=\underset{0}{\overset{1}{\int }}\sqrt{1+\left[\frac{\text{d}{x}^a}{\text{d}x}\right]}\text{d}x=\underset{0}{\overset{1}{\int }}\sqrt{1+{\mathit{\alpha }}^2{x}^{2(\mathit{\alpha }\text{-}1)}\text{d}x}.$$

(32)

Selecting a batch of α values, where ${\mathit{\alpha }}_1>{\mathit{\alpha }}_2>\cdots >{\mathit{\alpha }}_n$, the n strips of the streamlines can be drawn.

$$y=x^{{\mathit{\alpha }}_i},i=1,2,\dots ,n.$$

(33)

When the injection pressure P_e and the bottom hole producing pressure P_w are stable, the pressure gradient of the injected water flowing along the streamline l_α is

$$\text{grad}{P}_{\mathit{\alpha }}=\frac{P_{\text{e}}-P_{\text{w}}}{l_{\mathit{\alpha }}}.$$

(34)

Using Darcy’s law,

$$Q=A\frac{K}{\mathit{\mu }}\text{grad}P.$$

(35)

Substituting Eq. (35) into Eq. (28), the average water-flooded distance after time period t is

$$E\left[U\left(t\right)\right]=\frac{\mathit{\lambda }Kt}{\mathit{\mu }\mathit{\varphi }}E\left(Y\right)·\text{grad}P.$$

(36)

Similarly, the corresponding variance of the water-flooded distance is

$$D\left[U\left(t\right)\right]=\frac{\mathit{\lambda }Kt}{\mathit{\mu }\mathit{\varphi }}D\left(Y\right)·\text{grad}P.$$

(37)

The water-flooded distance and the corresponding variance of the different streamlines at any given time can be calculated using Eqs. (36) and (37); thus, the water-flooded front of the different streamlines can be obtained at time t. Then, the oil–aqueous interface can be drawn by connecting the water-flooded front successively. Water saturation refers to the ratio of the area surrounded by the oil aqueous interface to the total area at time t.

Water cut

For the same layer, according to Darcy’s law, the flux rate is directly proportional to the pressure gradient. The sum of the pressure gradient of each streamline is ΔP _k and is denoted as

$$\mathit{\Delta }{P}_k=\sum _{i=1}^{n_k}\text{grad}{P}_k{\mathit{\alpha }}_i,$$

(38)

where k is the layer number, n _k is the total number of streamlines in layer k, and gradP _k α _i is the total pressure drop of streamline α _i .

Supposing that n(t) strips of the streamlines reached the well bore of the production well at time t, and these streamlines are in the water phase, The sum of the pressure gradients of these streamlines is

$$\mathit{\Delta }{P}_{kw}=\sum _{i=1}^{n_k(t)}\text{grad}{P}_k{\mathit{\alpha }}_i.$$

(39)

Then, the water cut f _kw (t) of layer k is

$$f_{kw}(t)=100\%·\frac{\mathit{\Delta }{P}_{kw}}{\mathit{\Delta }{P}_k}.$$

(40)

Calculating the water cut by applying the weighted average based on the production rate of each layer, the water cut of the production well at time t is

$$f_w(t)=\sum _{i=1}^k{q}_k·f_{kw}(t)/\phantom{\sum _{i=1}^k{q}_k·f_{kw}(t)Q_L}{Q}_L,$$

(41)

where q _k is the liquid production rate of layer k, and Q _L is the total liquid production rate of the production well.

Model application

A relatively homogeneous reservoir was developed using a five-spot water-flooding pattern. The important parameters were as follows: well depth of 3,980 m, dominating radius of 88 m, initial reservoir pressure, P_i, of 40.8 MPa, casing pressure of 43.2 MPa, casing diameter of 14.6 cm, well spacing of 200 m, injection pressure, P_e, of 45 MPa, water injection rate of 150 m³, injection time of 5610 h, and injected water temperature of 18.5 °C. The water injection layers were as follows: L₁ at 3,562.3–3,609.6 m, L₂ at 3,609.6–3,668.1 m, L₃ at 3,668.1–3,726.6 m, L₄ at 3,726.6–3,785.2 m, and L₅ at 3,785.2–3,852.2 m. Furthermore, the injection water viscosity μ_w was 1 mPa s, the crude oil viscosity μ_o was 1.5 mPa s, the initial oil saturation S_oi was 0.7, the average porosity φ was 11.25 %, and the permeability K was 32.51 × 10⁻³ μm³. The distribution of the reservoir pore system is shown in Table 1.

Table 1 Distribution of reservoir pore system

Determining the water injection profile

In “Water injection profile”, the heat and mass transfer equations of the injection water and reservoir rock were applied to determine the water injection profile, as shown in Fig. 4.

Fig. 4

Well temperature and water injection profiles of injection well

The injecting water had five layers. First, the initial injection water profiles of these layers were as follows: Q₁ = 19 m³, Q₂ = 32 m³, Q₃ = 30 m³, Q₄ = 37 m³, and Q₅ = 32 m³. The numerical solution T (red line in Fig. 4) was calculated. This solution differs from the actual well temperature (black line in Fig. 4). The water injection profile was then adjusted to obtain the new numerical solution T. The new water injection profiles were Q₁ = 24 m³, Q₂ = 28 m³, Q₃ = 35 m³, Q₄ = 32 m³, and Q₅ = 31 m³. The new numerical solution T is closer to the actual well temperature (blue line in Fig. 4).

Calculating the water saturation

Based on the water streamline velocity derivation in “Water streamlines the velocity”, the water advancing distance of the different streamlines at any time based on the determined layer water injection rates in “Determining the water injection profile” were calculated. The oil water interface at any given time was determined, and the water saturation of each layer was obtained, as shown in Figs. 5, 6, 7.

Fig. 5

Water saturation curves of each layer

Fig. 6

The development process of oil–water interface of L1

Fig. 7

The oil–water interface of each layer at the 600th day

Figure 5 shows that the water saturation in L₃ increased the fastest because of its maximum water intake per unit thickness of 0.648 m³/(d m), followed by L₄. L₁ increased the slowest because its water intake per unit thickness was 0.508 m³/(d m).

Figure 6 shows that the oil water interface of L₁ constantly expanded during the water-flooding development. The water breakthrough did not occur at the producers until the 1100th day.

Figure 7 shows that at the 600th day, the oil–water interface advanced the fastest in L₃ and the slowest in L₁. This result is consistent with Fig. 5.

Calculating the water cut

Based on the calculated results, the water breakthrough time and the water cut of each layer at any given time were calculated according to “Water cut”, as shown in Figs. 8, 9, 10.

Fig. 8

Water breakthrough time and water-cut variation for each layer

Fig. 9

Water-cut variation of each layer

Fig. 10

Variation curve of water cut for production well

The layer with the smallest water breakthrough time of 779 days was L₃, in which the water cut also increased the fastest. L₄ was second, with a water breakthrough time of 884 days. The water breakthrough time of L₁ was the longest at 1,078 days, corresponding to its water cut that grew the slowest. After 1,600 days, the water cuts of all the layers were up by 80 %.

After the water breakthrough, the water cut grew rapidly in the early stages, but then slowed down. The water cut in L₃ increased early and rose fast; its water cut was up by 98.5 % at the 1250th day, which was considered as severely water flooded. Comparatively, the water cut in L₁ increased late and rose slowly; its water cut exceeded 99.1 % at the 1850th day, which was almost completely water flooded.

The water cuts of the producers were calculated by applying the weighted average based on the production rate of each layer. The comparison results between the calculated water cut and the actual water cut are shown in Fig. 10. The initial calculations have a larger error than the later calculations. The later calculations have an error of less than 5 %. This result is attributed to the fact that water mostly comes from high-permeability channels, such as cracks, during the early breakthrough time, but the established model does not consider this effect. However, this effect is weakened when a water breakthrough gradually occurs in most of the layers, causing the calculated water cut to approximate the actual values; thus, the error decreases.

Conclusion

• 1. A dynamic tracking model for reservoir water flooding with a separated layer water injection is established. Based on the basic principles of heat and mass transfer, a well temperature curve was applied to determine the water injection profile. The Poisson process analysis and the stochastic process methods were applied to calculate the water saturation, water breakthrough time, and water cut of each layer in the water-flooded reservoir at any given time.

• 2. The dynamic watering out processes of each layer differ for a water-flooded reservoir with a separated layer water injection. A higher water intake for a layer per unit thickness with high flow channels, where water saturation increases faster results in a shorter water breakthrough time and faster increase in water cut, and vice versa.

• 3. The model prediction accuracy may vary at different development stages. For models that only consider the micro-pore distribution in a reservoir but not the high-penetration channels, such as micro-cracks, the water-cut calculation error is larger when the water mainly comes from a high-permeability channel at an early time. When the reservoir gradually becomes water flooded, the calculated water cut approximates the actual value, and the calculation error becomes less than 5 %.