Introduction

Side weirs are an overflow weir installed on the side of the main channel, which allows flow when water rises above the crest. This type of flow is considered as a spatially varied flow. Side weirs are usually used as a control structure and as head regulators in irrigation structure. Many studies deal with side weir hydraulics; some of these studies deal with sharp crested side weirs such as El-Khashab and Smith (1976), Uyumaz and Smith (1991) Swamee et al. (1994), Hager (1987), Masoud (2003), Singh et al. (1994), Rao and Pillai (2008), Delkash and Babak (2014) and other investigated deals with inclined and oblique side weir such as Mwafaq and Ahmed (2011). Honar and Javan (2007) and Amir et al. (2016). The numerical analysis on inclined side weir was investigated by Ahmed (2011), Ahmed et al. (2013) and Ahmed (2015). A powerful tool is recently used to solve complex nonlinear and multi-linear regression equations in hydraulic engineering such as artificial neural network (ANN), genetic programming (GP) and statistic’s analysis using Monte Carlo method, Kisi et al. (2012), Ahmed (2018), Hayawi et al. (2019) and Ahmed and Anna (2020). In the recent years GEP and learning machine were used to model of nonlinear problems of predicting discharge coefficient in side weir such as Isa et al. (2015) and Reza et al.(2020). The aim of this study is to estimate MLR equation and compare equation modeled from GEP for coefficient of discharge calculation from skew side weir and then compare these values with values of Cd estimated from the rectangular side weir.

Experimental methodology

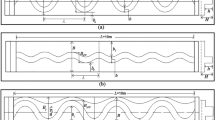
According to Al-Talib (2012), the experimental works were achieved in rectangular laboratory channel 10 m long, 0.3 m wide and 0.45 m depth, while the side channel dimensions were 0.15 m wide, 0.3 m depth and 2 m long. The discharge was measured using standard sharp crested weir (0.15 * 0.3 * 0.01) m dimensions at main channel; the side weirs were fixed at the entrance of the side channel by different angles starting from (90°) (perpendicular to the side channel) decreasing to (30°). Five different angles were taken (90°, 75°, 60°, 45° and 30°) inclined to the left of flow direction. Figure 1.

Fig. 1
figure 1

Sketch of side channel with skew side weir installed

Full size image

Five discharges were taken ranging from (7.3 to 16.5 L/s); the actual discharge for the main channel was calculated from the equation.

$$ Q_{{{\text{act}}.}} = 0.58 \times H_{1.5} $$
(1)

where Qact. = actual discharge and H = head over standard weir.

Equation (1) can be calculated by trial and error from volumetric calculations. The actual discharge was measured by closed side channel and measured depth of water over the standard weir at the end of main channel, then from Eq. 1 found Q1, then open side channel and measured water depth over the standard weir at the end of the main channel once again and from Eq. 1 found the discharge again, but discharge measured in this case (when side channel open) was Q2. Actual side channel discharge Q3 used Eq. 2.

$$ Q_{3} = Q_{1} - Q_{2} $$
(2)

where Q1 = actual discharge in main channel when side channel is closed, Q2 = actual discharge in main channel when side channel is opened, and Q3 = actual side channel discharge after subtracting Q1 and Q2.

Theoretical methodology

The general flow through the side weir derived depends on head of water over the side weir as well as the velocity of flow through it, according to specific energy assumption (De Marchi 1934).

$$ E = y + \frac{{V^{2} }}{2g} $$
(3)

where E = specific energy, y = head of water, v = flow velocity and g = gravity acceleration.

Depending on Q, Eq. 3 can be written as discharge,

$$ Q = b \times y\sqrt {2g\left( {E - P} \right)} $$
(4)

where (\( b \times y \)) = cross-sectional area, P = weir height.

Depending on De Marchi, Eq. 4 can be written as,

$$ q = - \frac{{{\text{d}}Q}}{{{\text{d}}S}} = \frac{2}{3}C_{\text{d}} \sqrt {2g} \left( {E - P} \right)^{3/2} $$
(5)

where q = discharge per unit length, S = longitudinal slope and Cd = coefficient of discharge.

Equation 5 satisfies rectangular channel and side weir perpendicular to channel bed, so in skew side weir it is not perpendicular to channel bed; the angle for inclined side weir must have taken, and then, Eq. 5 must change depending on these angles Fig. 1.

Dimensional analysis

Dimensional analysis is important to study the effects of the angle skew side weir to calculate coefficient of discharge (Cd) from standard side weir in rectangular channel. The parameters involved is calculated Cd in skew side weir as:

$$ C_{\text{d}} = f_{1} \left( {v_{1} , y_{1} , P, L, b, g, \theta } \right) $$
(6)

where Cd = coefficient of discharge, v = flow velocity, y1 = flow depth, P = weir height, L = weir length, b = channel width and g = acceleration due to gravity, \( \theta \) = side weir angle.

By using Buckingham Pi theorem, parameters on Eq. 6 can be used to develop a non-dimensional equation below:

$$ C_{\text{d}} = \emptyset \left( {F_{\text{r}} ,\frac{P}{{y_{1} }},\frac{L}{b},\theta } \right) $$
(7)

where Fr = Froude number \( \left( {\frac{v}{{\sqrt {gy} }}} \right) \).

Modeling of skew side weir using MLR

There are many applications for involved regression analysis. These applications deal with linear and nonlinear analysis, depending on variables that involve in the problem. In order to obtain a general equation for skew side weir, several trials with several equation models examined using (Statistical Package Social Sciences SPSS user guide).

According to Ahmed (2015), from Eq. 7 using several models of SPSS, Eq. 8 can be developed as MLR with a coefficient of determination R2 (0.958)

$$ C_{\text{d}} = C_{1} + C_{2} {\text{Fr}} + C_{3} P/y + C_{4} L/b + C_{5} \theta $$
(8)

where C1–C5 = constants, and \( \theta \) in radian.

GEP modeling for side weir

Gene Expression Programming was an artificial procedure to solve genotype system. This way was invented by Ferreira (2001, 2006), and GEP was similar to (GA) genetic algorithms and (GP) genetic programming; GA deals with individuals as a linear string of length fixed (chromosomes), while GP deals with individuals as nonlinear entities for different parse tree structure. In GEP, the individuals deal with encoded linear strings (chromosomes) which are expressed as nonlinear entities. In GEP, there are two important players: the tree structure (ETS) and chromosomes. The decoding of the process information is called translation that implies obviously a type of code and rules. The genetic code of GEP was simple; a relation between the symbol of the chromosomes and the node is represented in the tree. The rules of GEP determine nodes in the trees and then the type of the interaction in sub-ETS. GEP programming depends on two principal languages: the genetic language and expression trees language. This bilingual notation in GEP is named as Karva. Figure 2 shows the expression tree (ET) for an example of mathematical expressions (\( xb + \sqrt {c + d} \)) Mohd et al.(2015) and Khalid and Negm (2008), This ET is encoded in Karva language, and then, the expression is called K-expression. Each gene starts at the first left position, then scans all symbols in all directions every time when a symbol is finally added to the K-expression, and then, the K-expression mentioned above can be written as (\( + x \sqrt {ab + cd} \)).

Fig. 2
figure 2

Expression tree for expression \( x\sqrt {ab + cd} \)

Full size image

Figure 3 shown the steps of GEP, include some steps at the begin with the randomly generate of the chromosome from initial population. Then, these chromosomes were expressed and excluded the tree expression to evaluate fitness. The individual is then selected with respect to their fitness to reproduce with the modification; these individuals are subject to the same development. This process was repeated several times until a good solution is found. (Ferreira 2004) The basis of GEP is established on the structure of GEP gene. The simple structure of genes allows the encoding of thinkable program and allows their dynamic evolution due to these multilateral structural arrangements; a powerful set of genetics worker can be implemented to search efficiently solution Ferreira 2002.

Fig. 3
figure 3

GEP flow chart

Full size image

The equation obtained from GEP is given as:

$$ \begin{aligned} C_{\text{d}} & = \left( {A\tan \left( {A\tan \left( {A\tan \left( {A\tan \left( {\tan \left( {1101236493.83311 + \frac{P}{y}} \right) + \cos \left( {\exp \left\{ {\frac{L}{b}} \right\}} \right)} \right)} \right)} \right)} \right)} \right)^{4} \\ & \quad + \frac{{A\coth \left( {\left( {\left\{ {\theta \times 8173.64699339967} \right\} - 5974.47259811262} \right) \times \left( {F_{\text{r}} - \frac{P}{y}} \right)} \right)}}{{\frac{\log \left( \theta \right)}{3.22324468279425} + \frac{P}{y} - \theta + \sqrt[3]{{F_{\text{r}} }}}} \\ & \quad + A\coth \left( {\left\{ {\left\{ {\text{Csc} \left( {\frac{{{\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L b}}\right.\kern-0pt} \!\lower0.7ex\hbox{$b$}}}}{{{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P y}}\right.\kern-0pt} \!\lower0.7ex\hbox{$y$}}}}} \right) \times \left( {\frac{P}{y} + \frac{L}{b}} \right)} \right\} + \left\{ {\left( {6049.86489822289 - \frac{L}{b}} \right) - \frac{8224.16588065491}{{{\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L b}}\right.\kern-0pt} \!\lower0.7ex\hbox{$b$}}}}} \right\}} \right\} \times A\tanh \left( {F_{r} } \right)} \right) \\ & \quad + \sqrt[4]{{A\text{csch} \left( {\exp \left\{ \theta \right\} - A\tanh \left( {\frac{{\log \left( {\exp \left\{ {\frac{{{\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L b}}\right.\kern-0pt} \!\lower0.7ex\hbox{$b$}}}}{560.990764280841}} \right\}} \right)}}{{\log \left( {\text{Sech} \left\{ {\frac{{F_{r} }}{{{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P y}}\right.\kern-0pt} \!\lower0.7ex\hbox{$y$}}}}} \right\}} \right)}}} \right)} \right)}} \\ & \quad + \left( {F_{\text{r}}^{4} \times \left( {\tan \left( {\sin \left( {6378.3895352031 \times \frac{P}{y} + \theta } \right) \times \left( {\sqrt {\frac{P}{y}} - \frac{6377.3895352031}{{F_{\text{r}} }}} \right)} \right)} \right)} \right) \\ \end{aligned} $$
(9)

The corresponding expression tree for the above equation is given in Fig. 4.

Fig. 4
figure 4figure 4

Expression tree according to GEP equation

Full size image

Results and discussion

The genetic operation parameters setting is presented in Table 1, while Table 2 represents the statistics obtained from GEP after testing more than 1000 equation models and running more than 11 h. The comparison between the results of the GEP and MLR presented in this study as well as MLR for previous studies illustrated in Table 3 is presented in terms of coefficient of determination (R2), root-mean-square error (RMSE), Akaike information criteria (AIC) (AICs—which AIC with a correction for small sample sizes), mean absolute relative error (MARE) and scatter index (SI). These values are presented in Table 4, and the equations are defined below:

$$ R^{2} = \left[ {\mathop \sum \limits_{i = 1}^{n} \left( {x_{i} - \bar{x}} \right)\left( {y_{i} - \bar{y}} \right)/\sqrt {\mathop \sum \limits_{i = 1}^{n} \left( {x_{i} - \bar{x}} \right)^{2} \mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - \bar{y}} \right)^{2} } } \right]^{2} $$
(10)
$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {x_{i} - y_{i} } \right)^{2} } $$
(11)
$$ {\text{AIC}} = n \times \log \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {{\text{Fr}}_{\text{Expi}} - {\text{Fr}}_{\text{Eqi}} } \right)^{2} }}{n}} \right) + 2 \times k $$
(12)
$$ {\text{AICs}} = {\text{AIC}} + \frac{{2k^{2} + 2k}}{n - k - 1} $$
(13)
$$ {\text{MARE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\left| {x_{i} - y_{i} } \right|}}{{x_{i} }} $$
(14)
$$ {\text{SI}} = \frac{\text{RMSE}}{{\bar{x}}} $$
(15)

where xi and yi are the actual and modeled Cd values, respectively, \( \bar{x} \) and \( \bar{y} \) are the mean actual and modeled Cd values, respectively. k is the number of estimated parameters.

Table 1 GEP model parameters setting
Full size table
Table 2 Statistics obtained from GEP run
Full size table
Table 3 Equations for calculating side weir discharge coefficient in previous lecturer
Full size table
Table 4 Present work statistics comparison with previous studies
Full size table

Results in Table 4 represent statistics comparison for the present work with previous studies, and it may be seen that the GEP model refers to highest value of R2 (0.994) and the lowest value of MARE and RMSE (0.00523 and 0.00465), respectively, as well as the AIC refers to the best value (− 216.51) compared with all others equations, and all that indicate that the execution of GEP is the best with respect to other previous equations; overall, all values refer to a good agreement of equation for the present work compared with MLR according to Ahmed (2015) and all other previous equations.

Figure 5 shows a comparison between the discharge coefficients estimated using MLR models and GEP models, respectively, while Figs. 6 and 7 show the discharge coefficient estimated using an MLR model and GEP model, respectively. Compared with observed coefficient of discharge, Figs. 5, 6 and 7 show agreement between compared coefficients of discharge computed from different models and observed values having a relative error below 5%.

Fig. 5
figure 5

Comparison between Cd calculated using MLR and GEP\

Full size image
Fig. 6
figure 6

Comparison between Cd calculated using MLR and Cd observed

Full size image
Fig. 7
figure 7

Comparison between Cd calculated using GEP and Cd observed

Full size image

Figure 8 presents the discharge coefficient estimated from equations shown in Table 3 as well as that value estimated from the present model with the observed value. According to these results, all values estimated from previous equation range from 0.45 to 0.75 for vertical side weir, while in the present work, values range between 0.65 and 0.85 for the skew side weir.

Fig. 8
figure 8

Comparison of Cd calculated using GEP and that values calculated using equations in Table 3 from previous studies

Full size image

These values increased when the side angle increased; this means the discharge coefficient for skew side weir is greater than its values for vertical side weirs and these values for skew side weir increased when the side angle increased.

Conclusion

In the present study, a Gene Expression Programming (GEP) was used to predict an equation to calculate coefficient of discharge in skew side weir in a rectangular channel; this equation was compared with equation predicted from Multiple Linear Regression (MLR) which estimated from statistical tools. The two methods give a good result compared with the observed one with absolute error not exceeding 5% for both methods with correlation coefficient 0.9 and 0.996 for MLR and GEP, respectively, as well as the root-mean-square errors (RMSE) 0.0123 and 0.0046 for MLR and GEP, respectively. The results presented in this method compared with others equation calculated show that the accuracy of modeling and fitting of GEP is better than other methods. This conclusion is made by considering the fact that the AIC for the number of parameters that fitted in model where its value (− 216.51) is the best value compared with other equations, as well as the best value of the present work model for (AICs = − 918.51, MARE = 0.005234 and SI = 0.006231) compared with other values of equations is presented in this study. The values of Cd for skew side weir were greater than its values for straight vertical. Finally, the results refer to using GEP that gives more accuracy than MLR and other previous literature equations in discharge coefficient calculation and may be used as an improved alternative technique.