Application of artificial intelligence to estimate phycocyanin pigment concentration using water quality data: a comparative study

Abstract

In the present investigation, the usefulness and capabilities of four artificial intelligence (AI) models, namely feedforward neural networks (FFNNs), gene expression programming (GEP), adaptive neuro-fuzzy inference system with grid partition (ANFIS-GP) and adaptive neuro-fuzzy inference system with subtractive clustering (ANFIS-SC), were investigated in an attempt to evaluate their predictive ability of the phycocyanin pigment concentration (PC) using data from two stations operated by the United States Geological Survey (USGS). Four water quality parameters, namely temperature, pH, specific conductance and dissolved oxygen, were utilized for PC concentration estimation. The four models were evaluated using root mean square errors (RMSEs), mean absolute errors (MAEs) and correlation coefficient (R). The results showed that the ANFIS-SC provided more accurate predictions in comparison with ANFIS-GP, GEP and FFNN for both stations. For USGS 06892350 station, the R, RMSE and MAE values in the test phase for ANFIS-SC were 0.955, 0.205 μg/L and 0.148 μg/L, respectively. Similarly, for USGS 14211720 station, the R, RMSE and MAE values in the test phase for ANFIS-SC, respectively, were 0.950, 0.050 μg/L and 0.031 μg/L. Also, using several combinations of the input variables, the results showed that the ANFIS-SC having only temperature and pH as inputs provided good accuracy, with R, RMSE and MAE values in the test phase, respectively, equal to 0.917, 0.275 μg/L and 0.200 μg/L for USGS 06892350 station. This study proved that artificial intelligence models are good and powerful tools for predicting PC concentration using only water quality variables as predictors.

Introduction

Nowadays, cyanobacterial harmful algal bloom (HAB) has become a serious problem, contributes seriously to the degradation of the drinking water quality and affects human health and the aquatic life with long-lasting effects (Sivapragasam et al. 2010), including bad odors and tastes, reduction in water clarity and oxygen depletion (hypoxia or anoxia) during bloom decay (Sharaf et al. 2019). Monitoring cyanobacteria also known as blue–green algae (CBG) is of great importance for freshwater ecosystems; however, it has been very difficult over the years to ensure effective and adequate monitoring of cyanobacteria in freshwater (Backer 2002). Traditional methods used for monitoring cyanobacteria are mainly based on: (i) standard methods of chlorophyll-a determination, (ii) cell counting and (iii) direct in situ measurement of cyanotoxin (Kong et al. 2014). However, it is reported that fluorescence is a fast, real-time monitoring method to measure the concentration of phytoplankton in natural water bodies (Xiaoling et al. 2019). One of the most accessory pigment characteristics of cyanobacteria is certainly phycocyanin pigment concentration (PC), and it is considered as the main light-harvesting pigment in cyanobacteria (Simis et al. 2012). PC is more suitable for monitoring cyanobacterial blooms and toxic cyanobacteria and is a functional protein found in cyanobacteria with high intracellular variability (Yan et al. 2018). PC plays an imperative role in the energy transfer cascade by funneling the light energy toward reaction center of the photosystems (Patel et al. 2018). According to Kuo et al. (2018), cyanobacterial blooms are strongly associated with phycocyanin concentrations.

According to Gregor et al. (2007), when PC is excited by light around 590–630 nm with a maximum of 620 nm (Mishra et al. 2009), it emits red light with a maximum at 650 nm. Two methodologies were employed for assessing PC: (i) models prediction of PC utilizing satellite remotely detected data and (ii) laboratory analysis and directly in situ measurement utilizing sensors. In addition, McQuaid et al. (2011) have demonstrated that PC has the property of being soluble in water and strongly fluorescent and consequently the quantitatively detection of PC based on portable instruments is possible. However, measuring PC cannot be easily accomplished and there is no standard measurement technique (Tebbs et al. 2013). Assuming that the traditional method used for quantifying the PC is based upon laboratory analysis that is costly and time-consuming (Le et al. 2011; Kong et al. 2014; Song et al. 2013a, b), a wide variety of alternative approaches based on remote sensing have been proposed and tested to estimate PC as function of reflectance measurement at different wavelengths. In this context, depending on the magnitude of the reflectance trough around 620 nm, three different algorithms are available (Le et al. 2011): (i) semi-baseline (Dekker 1993), (ii) a single reflectance band ratio (Schalles and Yacobi 2000) and (iii) a nested band ratio semi-analytical algorithms (Simis et al. 2005). PC estimation utilizing remotely detected data has been extensively examined by the researchers (Simis et al. 2005; Li et al. 2010; Le et al. 2011).

Simis et al. (2005) introduced a basic optical model-based reflectance band ratio algorithm, for modeling PC of highly eutrophic Loosdrecht and Ijsselmeer lakes, Netherlands. They have used band settings of the MEdium Resolution Imaging Spectrometer (MERIS), and they have found a very high coefficient of determination (R²) equal to 0.94 between measured PC and predicted PC by the proposed algorithm, with measured specific absorption coefficients at 620 nm called a_pc*(620). Using hyperspectral airborne imaging spectrometer for applications (AISA) imagery from central Indiana, USA, Li et al. (2010) built up a model that linked spectral indices, called (x) to the measured PC, called (y). The authors have tested four different univariate regressions: (i) linear, (ii) exponential, (iii) power and (iv) polynomial. As a result of the study, they have demonstrated that PC concentration correlated best with the reflectance trough 628 nm (R₆₂₈), via an exponential relation, with an R² equal to 0.80 and root mean square error (RMSE) equal to 25.52 (µg L⁻¹). Le et al. (2011) compared two semi-analytical algorithms for modeling PC of Lake Taihu, China, including highly turbid water. The two algorithms are: the semi-analytical four-band algorithm already suggested by Le et al. (2009) and the nested band ratio algorithm; the two models are based upon hyperspectral reflectance measurements. The authors have obtained the following results: (i) the nested band ratio algorithm for PC modeling has provided an R² equal to 0.68 and a very high RMSE equal to 10.43 mg/m⁻³ and (ii) the semi-analytical four-band algorithm produced good predictions as compared to the first algorithm with an R² equal to 0.86 and a very low RMSE value equal to 4.83 mg/m⁻³. Song et al. (2012) proposed a new model called genetic algorithm partial least squares (GA-PLS) for PC retrieval. The model was compared to three-band algorithm (TBM), and the two were applied together in the three reservoirs, Eagle Creek, Morse and Geist reservoirs, in the Indianapolis, Indiana, USA. The authors used hyperspectral data obtained from in situ and airborne image. As a result of the study, both GA-PLS and TBA provided good accuracy, and the GA-PLS model is more accurate than the TBA. Song et al. (2013a) used data from five drinking water sources in South Australia and central Indiana, USA, for developing models using in situ hyperspectral data. The authors compared four types of algorithms, namely (i) TBM three-band, (ii) OBR optimal band ratio, (iii) SM05 Simis et al. (2005) band ratio and (iv) SY00 Schalles and Yacobi (2000) models. As a result, the four models yielded an R² in the validation phase equal to 0.95, 0.94, 0.94 and 0.12 for TBM, OBR, SM05 and SY00, respectively, and the TBM model was the best among the all others. In another study, Song et al. (2013b) compared three different models for estimating PC in the Eagle Creek reservoir, Indianapolis, Indiana, USA. The three models were: (i) three-band, (ii) two-band and (iii) optimal band models. Utilizing simulated MEdium Resolution Imaging Spectrometer (MERIS) and Hyperion spectra pooled datasets, the three models yielded an R² equal to 0.68, 0.64 and 0.74 for three-band, two-band and optimal band models, respectively. Li et al. (2012) introduced a semi-analytical method called TBBA to estimate PC using as input the absorption coefficients at 624 nm (A_PC (624)). The algorithm combines both three-band indices and the baseline algorithm. The investigation was conducted using data from in three reservoirs: Eagle Creek Reservoir (ECR), Geist Reservoir (GR) and Morse Reservoir (MR), at central Indiana, USA. Compared with the baseline and three-band algorithms, the TBBA provided better PC estimates with R² equal to 0.86.

Obviously, predicting PC concentration using remote sensing is broadly discussed in the literature and much effort has been devoted in this subject. Although the aforementioned models are robust enough, the proposition of a new kind of models is most welcome. Artificial intelligence (AI) techniques have been successfully applied in many areas of scientific researches; however, few studies have reported an application of the AI for predicting PC concentration. Sun et al. (2012) modeled PC by support vector machines (SVMs) and linear regression model utilizing band ratios as inputs. The authors have used three different reflectance forms, namely single-band, band ratio and three-band combination, and they have chosen three lakes in China as cases studies: Lake Taihu, Lake Chaohu and Lake Dianchi. To demonstrate the ability of the proposed SVM model, the authors have compared the results obtained with previous proposed algorithms, which are: (i) the baseline algorithm, (ii) the linear algorithm using band ratio, (iii) the quadratic algorithm using band ratio, (iv) the three-band combination algorithm and (v) the semi-analytical algorithm. As a result of the study, the low RMSE was found to be 38.4 (mg m⁻³), obtained from SVM model. Song et al. (2014) developed and compared three different models: (i) a partial least squares-artificial neural network (PLS-ANN) model, (ii) artificial neural network (ANN) and (iii) three-band model (TBM). The three models used the remote sensing reflectance spectra (R_rs) as input to predict the PC concentration as output. The three models were applied using data from central Indiana, USA, and South Australia. The results obtained showed that the PLS-ANN was the best, followed by TBM and the ANN ranked in the last place. Although the two studies applied AI techniques for predicting PC, they are based on the integration of the remote sensing reflectance band ratio as inputs. Recently, Heddam (2016a) proposed a new kind of models based on ANN paradigm for predicting PC utilizing water quality data as input to the model. Four water quality parameters were measured at 15-min interval of time, namely water temperature (TE), pH, specific conductance (SC) and dissolved oxygen (DO), measured at the lower Charles River Buoy, USA. The author has demonstrated that the multilayer perceptron neural network (MLPNN) satisfactorily predicted the PC with high accuracy and a coefficient of correlation equal to 0.975 in the test phase.

Therefore, the main contributions of this study are the proposition of a new kind of models based on AI for predicting PC concentration. We develop and apply four models, namely (i) feedforward neural networks (FFNNs), (ii) gene expression programming (GEP), (iii) adaptive neuro-fuzzy inference system with grid partition (ANFIS-GP) and (vi) adaptive neuro-fuzzy inference system with subtractive clustering (ANFIS-SC), for predicting PC using data from two stations operated by the United States Geological Survey (USGS).

Materials and methods

Feedforward neural network

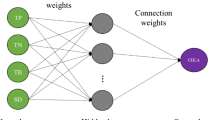
Artificial neural network (ANN) is a nonlinear model inspired from the behavior of the biological neuron. ANN is arranged in different layers, and their functioning is mainly based on the adaptation of the parameters through a learning process, generally the backpropagation algorithm (Haykin 1999). The most common architecture of ANN is the feedforward neural network (FFNN), selected in the present study. FFNN is composed of three layers: one input layer with four inputs, one hidden layer of neurons with sigmoid activation function and one output layer consisting of only one neuron corresponding to the PC. FFNN is a universal approximator (Hornik 1991; Hornik et al. 1989). The structure of the FFNN developed is shown in Fig. 1. The general equations of the FFNN from the input layer to the output layer can be presented as:

$$Y = f_{2} \left[ {\sum\limits_{{j = 1}}^{n} {w_{{jk}} \left( {f_{1} \left( {\sum\limits_{{j = 1}}^{n} {x_{i} w_{{ij}} + \delta _{j} } } \right)} \right) + \delta _{0} } } \right]$$

(1)

where x_i is the input variable, w_ij weight between the input i and the hidden neuron j and δ_j is the bias of the hidden neuron j. w_jk indicates the connection weight between the neuron j in hidden layer and the neuron k in the output layer, and δ₀ denotes the bias of the neuron k in the output layer. f₂ is the linear activation function, and f₁ the sigmoid activation function, expressed by Eq. (2).

Fig. 1

Architecture of FFNN with four input variables used for modeling PC concentration

$$f_{1} \left( x \right) = \frac{1}{{1 + e^{ - x} }}$$

(2)

Adaptive neuro-fuzzy inference system

Fuzzy inference system (FIS) is used to create nonlinear models, linking a set of inputs to an output, generally achieved in three important processes: (i) selection of membership function, (ii) applying fuzzy set operation and (iii) elaboration of the rules base (Kotti et al. 2016). These types of models use the fuzzy numbers, while the models based on statistical regression are based on the error term (Kitsikoudis et al. 2016). Adaptive neuro-fuzzy inference system (ANFIS) was first suggested by Jang (1993). ANFIS combines the learning abilities of ANN and the fuzzy logic concept (Jang 1993). ANFIS is a MLPNN based on fuzzy inference system (FIS), where each node applies a particular function on incoming signals (Jang 1993). As illustrated in Fig. 2, the ANFIS is composed of exactly six layers: (i) input layer, (ii) fuzzification layer, (iii) rules layer, (iv) normalization layer, (v) defuzzification layer and (vi) summation (output or decision) layer. In the ANFIS structure, there are only two adaptive layers, namely the fuzzification layer and the defuzzification layer. In the fuzzification layer, two modifiable parameters ({σ_i, c_i}), which are identified with the input membership functions, exist, while in the defuzzification layer there are three adjustable parameters ({p_i, q_i, r_i}) (Jang 1993). ANFIS utilizes a hybrid learning algorithm composed of the gradient descent for the premise parameters (nonlinear) parameters and the least square estimate (LSE) for the linear (consequent) parameters. The learning process is achieved into two phases: forward and backward passes. Simply assume that we have a FIS having two inputs, x and y, and one output z.

Fig. 2

Architecture of ANFIS with four input variables used for modeling PC concentration

Assume that the rule base includes two fuzzy if–then rules (Takagi and Sugeno type):

$${\text{Rule}}\, 1= {\text{If}}\;\left( {x\;{\text{is}}\;A_{1} } \right)\;{\text{and}}\;\left( {y\;{\text{is}}\; B_{1} } \right)\;{\text{Then}}\;\left( {f_{1} = p_{1} x + q_{1} y + r_{1} } \right)$$

(3)

$${\text{Rule}}\,2 = {\text{If}}\;\left( {x\;{\text{is}}\;A_{2} } \right)\;{\text{and}}\;\left( {y\;{\text{is}}\;B_{2} } \right)\;{\text{Then}}\;\left( {f_{2} = p_{2} x + q_{2} y + r_{2} } \right)$$

(4)

where x and y denote the inputs, A_i and B_i indicate the fuzzy sets, f_i are the outputs within the fuzzy region indicated by the fuzzy rule and p_i, q_i and r_i show the design parameters that are identified in the training phase. The ANFIS structure to actualize these two rules is shown in Fig. 2, in which a circle demonstrates a fixed node, whereas a square shows an adaptive node.

• Layer 1: the input layer that only fixes the input variable of the system.

• Layer 2: the fuzzification layer. Every node i in this layer is a square node with a node function:

  $${\text{O}}_{i}^{1} = \mu_{{A_{i} }} \left( x \right),\quad i = 1,\,2,$$

  (5)
  $${\rm O}_{i}^{1} = \mu_{{B_{i - 2} }} \left( y \right),\quad i = 3,4$$

  (6)

  where x (or y) is the input to node i, A_i (or B_i−2) is the linguistic label (small, large, etc.) associated with this node function and $\mu_{{ {\rm A}_{i} }} \left( x \right)$ and $\mu_{{{\rm B}_{i - 2} }} \left( y \right)$ can adopt any fuzzy membership function. Assuming a Gaussian function as a membership function, A_i can be computed as

  $$\mu _{{A_{i} }} \left( x \right) = \exp \left\lfloor { - 0.5 \times {\left\{ {\left( {x - c_{i} } \right)/\sigma _{i} } \right\}}^{2}} \right\rfloor ,$$

  (7)

  where (σ_i, c_i) denote parameter sets. Parameters in this layer are called as premise parameters.

• Layer 3: the rules layer. Each node i in this layer is a fixed node. These nodes multiply the incoming signals and outputs the product.

  $${\rm O}_{i}^{2} = w_{i} { = \mu_{{A_{i} }} \mu_{B} }_{i} ,\quad i = 1,2,$$

  (8)

  The output signal w_i indicates the firing strength of a rule. The node numbers in this layer are equal to the number of fuzzy rules in the FIS.

• Layer 4: the defuzzification layer. In this layer, the nodes are adaptive. Each node’s output of this layer is the product of the normalized firing strength and a first-order polynomial. Thus, this layer’s outputs are expressed as

  $${\rm O}_{i}^{3} = {\bar{w}}_{i} = \left( { w_{i} /\left( { w_{1} + w_{2} } \right)} \right),\quad i = 1,2,$$

  (9)

  Outputs of this layer are named as normalized firing strengths.

• Layer 5: the defuzzification layer. In this layer, the nodes are adaptive nodes. The output of each node in this layer is simply the product of the normalized firing strength and a first-order polynomial (for a first-order Sugeno model). Thus, this layer’s outputs are expressed as

  $${\rm O}_{i}^{4} = {\bar{w}}_{i} \, f_{i} = \, {\bar{w}}_{i} \, \left( { p_{i} \, x \, + q_{i} \, y + r_{i} } \right),\quad i = 1,2$$

  (10)

  where ${\bar{w}}_{i}$ is the output of Layer 3 and ({p_i, q_i, r_i}) denotes the parameter set of this node. This layer’s parameters will be called as consequent parameters.

• Layer 6: the summation (output or decision) layer. This layer’s node is a fixed node labeled Σ, which calculates the overall output as the sum of all incoming signals, i.e.,

  $${\rm O}_{i}^{5} = \sum\limits_{i = 1} {\bar{w}_{i} f_{i} } = \left( {\sum\limits_{i = 1} {w_{i} f_{i} /( w_{1} + w_{2} )} } \right).$$

  (11)

  Explicitly, this layer sums the node’s output of the previous layer to calculate the whole network’s output.

ANFIS uses two different identification approaches: the grid partition (GP) and the subtractive clustering (SC) (Sylaios et al. 2008). A detail of the methods is reported in the following.

Grid partitioning

The grid partition method (GP) separates the data into rectangular subspaces depending on the pre-defined membership functions’ number and types (Sylaios et al. 2008). Using GP method, network partitioning is uniformly utilized and with initialization (Rad et al. 2015). The major drawback of the ANFIS-GP is the so-called the curse of dimensions, which implies that the number of fuzzy rules exponentially increases when there is an increment in the number of input variables (Wei et al. 2007; Noori et al. 2009). According to the study of Jang (2016) and Jang et al. (1997), the number of input variables must be small and < 6 to apply GP. For example, in the case of building a model with high number of inputs (e.g., 10) and if it is necessary to select much membership functions (MF_s) for each input, for example, three MF_s for each input, the number of rules will be: (3¹⁰ = 2187) rules, and the calculation and optimization of this model are a difficult task, rather impossible with the actual computer machines. In the current study, modeling PC concentration was achieved using four input variables and therefore applying an ANFIS-GP model is feasible. Using ANFIS-GP, the total number of model parameters that need to be optimized is computed as follows (Heddam 2014):

Using GP method in ANFIS, the total number of modifiable parameters (Ѱ) is computed as:

$$\varPsi = \beta + \delta$$

(12)

where β is the premise parameters’ number and δ consequent parameters’ number, and β and δ are computed as:

$$\beta = N_{I} \times N_{{{\text{MF}}s}} \times N_{\text{MP}}$$

(13)

$$\delta = N_{\text{FR}} \times \left( { N_{\text{I}} + N_{\text{O}} } \right)$$

(14)

$$N_{\text{FR}} = (N_{\text{MFs}} )^{{N_{I} }}$$

(15)

where N_I is the input variable number, N_MFs MF number of each input and N_MP the number of modifiable parameters for each MF, for example, for Gaussian membership function (N_MP = 2), N_FR numbers of fuzzy rules that will be produced by all inputs and N_O system output which is equal to one (in his study, PC concentration).

Subtractive clustering

Subtractive clustering (SC) is utilized to avoid the problem of curse of dimensionality encountered when using the GP method. SC leads to a reduction in the high number of fuzzy rules and generates significantly smaller rule base depending only on one parameter: the so-called cluster radius (Vasileva-Stojanovska et al. 2015). The influential radius is very essential for calculating the number of clusters. By choosing a smaller radius, too many smaller clusters are obtained in the data space and more rules are required and vice versa (Kisi and Zounemat-Kermani 2014). SC is a modified version of the original mountain clustering approach (Yager and Filev 1994) suggested by Chiu (1994). The SC approach is utilized to decide the number of antecedent MFs and rules by taking into consideration every cluster center (D_i) as a fuzzy rule. In this method, each data point of a set of N data points {x_1… x_N} in a p-dimensional space is considered as the cluster centers’ candidate (Wei et al. 2007). Then, the density measure at data point x_i can be expressed as (Aqil et al. 2007):

$$D_{i} = \sum\limits_{j = 1}^{N} {\exp } \, \left( { - \frac{{\left\| { x_{i} - x_{j} } \right\|^{2} }}{{\left( {r_{a} /2} \right)^{2} }}} \right)$$

(16)

where r_a = a positive constant named cluster radius. A data point is marked as a cluster center when more data points are closer to it. Accordingly, the data point (x ^*₁ ) with highest density measure (D ^*₁ ) is considered as the first cluster center (Wei et al. 2007). Now removing the impact of the first cluster center, the density measure of all other data points is recalculated as:

$$D_{i} = D_{i} - D_{i}^{ * } \cdot \mu \left( { { \, x}_{i}^{ * } } \right)$$

(17)

$$\mu \left( {x_{i}^{*} } \right) = \exp \left( { - \frac{{\left\| { x_{i} - x_{j} } \right\|^{2} }}{{\left( {{\raise0.7ex\hbox{${ r_{b} }$} \!\mathord{\left/ {\vphantom {{ r_{b} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right)^{2} }}} \right)$$

(18)

where r_b (r_b > r_a) = a positive constant that yields a measurable reduction in density measures of neighborhood data points to avoid closely spaced cluster centers (Chiu 1994). Using ANFIS-SC, the total number of model parameters that need to be optimized is computed as follows (Heddam 2014):

With SC partition approach for the ANFIS model, the number of modifiable parameters (Φ) can be computed as:

$$\varphi = \alpha + \lambda$$

(19)

where α is the premise parameters’ number and λ the consequent parameters’ number, and α and λ are computed as:

$$\alpha = N_{I} \times N_{\text{MFs}} \times N_{\text{MP}}$$

(20)

$$\lambda = N_{\text{FR}} \times \left( {N_{\text{I}} + N_{\text{O}} } \right)$$

(21)

$$N_{\text{FR}} = N_{\text{C}} = N_{\text{MFs}}$$

(22)

From the above equations, it can be seen that, when fuzzy systems are designed utilizing SC approach, every cluster corresponds to a fuzzy rule. At that point, the total number of modifiable parameters is equivalent to the quantity of premise parameters in addition to the number of consequent parameters.

Gene expression programming

Gene expression programming (GEP) was introduced by Ferreira in 1999 (Ferreira 2001). This paradigm has some similarity with genetic algorithm (GA) and genetic programming (GP). In GEP similar to GA, linear and chromosomes with fixed length are used. Furthermore, in GEP similar to pars tree of GP, ramified structure is applied. GEP can be used successfully in the following situations: (i) identifying the internal relation of dependent variables is very complex, (ii) finding the size and shape of final variable is complex, (iii) common methods cannot represent the analytical solution for a given problem, (iv) an approximate solution is appropriate, (v) every small improvement in performance is measured routinely and highly valuable and (vi) the amount of data that should be evaluated and classified by computers are huge (Banzhaf et al. 1998). Some preliminary steps before implement of GEP should be considered as follows: (1) select the terminals set (i.e., problem variables and fixed stochastic numbers), (2) select the function set that required for mathematical formula creation, (3) choose the appropriate fitness function for evaluating the fitness of formulas, (4) determine the parameters that control the model evolve (i.e., population size, probability of genetic operators) and (5) determine a criterion for end of program and represent the results of model. In this study for modeling the phycocyanin pigment concentration (PC) using GEP method, various steps were considered. In the first step, the suitable fitness function was selected. In this research, root relative squared error (RRSE) was chosen as fitness function. In the second step, the input variables (i.e., pH, TE, SC and DO) and functions set were selected. In the third step, chromosomal architecture (i.e., in this study the head length and number of genes were 8 and 3, respectively) was determined. In the fourth step, linkage function for creating link between sub-expression trees was selected. Finally in the fifth step, genetic operators and theirs rates were determined. The genetic operators and theirs values are presented in Table 1. In this study for implementation of GEP, GeneXpro Tools was utilized. More details about GEP model can be found in Ferreira (2006).

Table 1 Genetic operators and their values utilized in this study for GEP model

Case studies

In the present study, historical PC concentration and four water quality data from January 1, 2015, to December 31, 2015, were utilized for developing the AI models; data can be obtained from the United States Geological Survey (USGS) Web site: http://or.water.usgs.gov. The data from two water quality stations, namely USGS 06892350 (latitude 38°59′00″, longitude 94°57′52″ NAD27) and USGS 14211720 (latitude 45°31′03″, longitude 122°40′09″ NAD83), were used in this study. The water quality data consisted of measured water temperature (TE, °C), dissolved oxygen (DO mg/L), pH (Std. unit), specific conductance (SC, μS/cm) and PC (μg/L). For USGS 06892350 station, data were measured at 15-min interval of time, while for USGS 14211720 station the data were measured at 30-min interval of time. The dataset selected had a total of 18,139 patterns for USGS 06892350 station and 17,195 for USGS 14211720. Table 2 represents the statistic parameters of water quality variables for the two stations. In the table, the terms X_mean, X_max, X_min, S_x, C_v and R indicate the mean, maximum, minimum, standard deviation, variation coefficient and the coefficient of correlation between the variable and the PC, respectively. The correlations between the water quality variables and PC are generally higher in station 06892350 than in station 14211720, except DO having the lowest correlation with PC in station 06892350. Coefficients of correlation are given in Table 3. The dataset is separated into three subsets (Table 4): (i) a training subset, (ii) a validation subset and (iii) a test subset, with a ratio of 60%, 20% and 20%, respectively. We have tested different train–test–validation splitting strategies, by changing the training ration from 20, 30, 40 and 60%. The best accuracy was obtained using 60% of the data for training.

Table 2 Statistical parameters of dataset

Table 3 Pearson’s correlation coefficients between and among physical water quality parameters and PC concentration

Table 4 Summary description of dataset

In the present study, before applying the three models, all the four input variables and the PC were normalized to contain the same scale with mean equal to 0 and standard deviation equal to 1, utilizing the Z-score by Eq. (23). Using the Z-score method, the performance of the developed models has been substantially improved (Olden et al. 2004; Heddam 2016b, c).

$$x_{{n_{i,k} }} = \frac{{x_{i,k} - m_{k} }}{{S_{dk} }}$$

(23)

where x_{ni, k} denotes the normalized value of the k variable (input or output) for every sample i. x_i, _k is the original value of the k variable. m_k and S_dk are the mean value and standard deviation of the variable k, respectively.

Application and results

In the current study, an attempt is made to estimate PC concentration using water quality variables as inputs. Several combinations of the water quality variables were selected, and in total, six scenarios were compared (Table 5), and those are: (i) TE, pH, SC and DO; (ii) TE, pH and SC; (iii) DO, pH and SC; (iv) pH and SC; (v) TE and pH; and (vi) TE and SC. The selection of the six combinations is mainly based on the correlation coefficient. In this study, three performance indices were utilized to evaluate the developed models. These three indices are: the coefficient of correlation (R), the root mean squared error (RMSE) and the mean absolute error (MAE), calculated as follows:

$$R = \left[ {\frac{{\frac{1}{\rm N}\sum\limits_{{}}^{{}} {\left( { {\rm O}_{i} - {\rm O}_{m} } \right)\left( { {\rm P}_{i} - {\rm P}_{m} } \right)} }}{{\sqrt {\frac{1}{\rm N}\sum\nolimits_{i = 1}^{n} { {\left( { {\rm O}_{i} - {\rm O}_{m} } \right)}^{2} } } \sqrt {\frac{1}{\rm N}\sum\nolimits_{i = 1}^{n} {( {\rm P}_{i} - {\rm P}_{m} )^{2} } } }}} \right]^{{}}$$

(24)

$${\text{RMSE}} = \sqrt {\frac{1}{\rm N}\sum\limits_{i = 1}^{\rm N} {\left( { {\rm O}_{i} - {\rm P}_{i} } \right)^{2} } }$$

(25)

$${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| { {\rm O}_{i} - {\rm P}_{i} } \right|}$$

(26)

where N denotes the number of data points, O_i is the measured value and P_i is the corresponding model output (prediction). O_m and P_m indicate the average values of O_i and P_i, respectively.

Table 5 Structure of the developed models

Predicting PC at USGS 06892350 station

In this section, GEP, FFNN, ANFIS_SC and ANFIS_GP were developed and compared to estimate PC concentration using four water quality variables. Results obtained in the training, validation and test stages are given in Table 6. According to Table 6, the four models achieved good accuracy with high R and low RMSE and MAE values. Table 6 clearly shows that the four models yield different accuracies for different input combinations. In the training stage as given in Table 6, the R values, respectively, range from 0.869 to 0.946, 0.872 to 0.946, 0.893 to 0.955 and 0.870 to 0.940 for the FFNN, ANFIS_GP, ANFIS_SC and GEP, highlighting high level of accuracy. In addition, the RMSE values, respectively, range 0.219–0.335, 0.222–0.334, 0.203–0.307 and 0.231–0.334 μg/L for the FFNN, ANFIS_GP, ANFIS_SC and GEP.

Table 6 Performances of the FFNN, ANFIS_SC, ANFIS_GP and GEP models in different phases for USGS 06892350 station

Finally, as given in Table 6, MAE values range 0.164–0.256, 0.167–0.258, 0.145–0.229 and 0.176–0.257 μg/L for the FFNN, ANFIS_GP, ANFIS_SC and GEP, respectively. According to Table 6, the M1 combination with TE, pH, SC and DO yielded the highest efficiency than all the others for the all four developed models, while the M4 combination with TE and SC yielded the lowest accuracy in comparison with the all other four developed models. In the training stage, the ANFIS_SC M1 model is the best among the four developed models, with an R equal to 0.955, RMSE equal to 0.203 μg/L and MAE equal to 0.145 μg/L, followed by FFNN and ANFIS_GP that lead almost the same accuracy regarding the three performances indices, and the GEP took in the third place with an R equal to 0.940, RMSE equal to 0.231 μg/L and MAE equal to 0.176 μg/L. From the six input combinations proposed, when the four AI models have included only two inputs, M5 combination with pH and TE is always the best, and ANFIS_SC M5 model performed the best with an R equal to 0.916, RMSE equal to 0.275 μg/L and MAE equal to 0.197 μg/L.

In the validation phase, as given in Table 6, the M1 combination is always the best for the four developed models. The FFNN, ANFIS_GP, ANFIS_SC and GEP M1 models used for predicting PC concentration yielded R values of 0.945, 0.946, 0.955 and 0.936, respectively, and RMSE values of 0.221, 0.220, 0.202 and 0.237 μg/L, respectively. Finally, the four models yielded MAE values of 0.165, 0.166, 0.146 and 0.179 μg/L, respectively. Similar to the results obtained in the training stage, in the validation stage ANFIS_SC M1 is always the best, followed by FFNN, and ANFIS_GP took in the third place. ANFIS_SC M1 yielded an R equal to 0.945, RMSE equal to 0.221 μg/L and MAE equal to 0.165 μg/L. Using only two input variables (pH and TE), ANFIS_SC M5 model is the best among all the others. According to Table 6, in the test stage ANFIS_SC M1 is the best model and performs superior to the FFNN, ANFIS_GP and GEP in all combinations. In the test phase as given in Table 6, the ANFIS_SC M1 improved the FFNN, ANFIS_GP and GEP M1 models of about 7.57%, 7.23% and 13.86% and 10.84%, 10.84% and 18.23% decrement in RMSE and MAE, respectively. Additionally, results were improved with respect to R statistics in the test stage by approximately 1.0%, 0.8% and 1.9%, respectively.

The cluster radius was calculated as 0.10 by trial and error. The optimal cluster number was found to be 40, and consequently, the ANFIS_SC M1 model having four input variables has a total of 40 fuzzy rules. The detailed description of the two ANFIS model parameters is reported in Table 7. As can be clearly seen from the table that the ANFIS_SC has much more parameters than the ANFIS_GP model. In Table 8, we report the testing results, different functions set and linkage function for developing GEP models. GEP model provided the best accuracy with F5 operators and addition linking function. The equation of the GEP M1 model for PC concentration using TE, pH, SC and DO as inputs is given by:

Table 7 Total number of parameters for the two ANFIS models developed for USGS 06892350 station

Table 8 Testing results of different functions set and linkage function for developing GEP for USGS 06892350 station

$${\text{PC}} = \left( \exp \left( {\sin \left( {\arctan \left( {\frac{{3.9\left( {{\text{SC}} - {\text{TE}}} \right)}}{{ {\text{TE}}^{2} }}} \right)} \right)} \right) \right) + \frac{{\cos \left( {0.8{\text{pH}}} \right)}}{{\log \left( {\exp \left( {\frac{{\text{pH}}}{{\text{DO}}}} \right)} \right)}} + \cos \left( {{\text{pH}} + \arctan \left( {1.4 + {\text{TE}} - {\text{DO}}} \right)} \right)$$

(27)

Figures 3, 4, 5 and 6 illustrate scatter plots of the computed versus measured PC for FFNN, ANFIS_GP, ANFIS_SC and GEP model M1, in the training, validation, test and all data. Comparison of the figures apparently indicates that the ANFIS_SC model M1 provides less scattered estimates with a fit line equation closer to the exact line and a higher R² value than those of the other models.

Fig. 3

Scatterplots of estimated versus measured values of PC for FFNN (M1) model: a training, b validation and c test data—station ID: 06892350

Fig. 4

Scatterplots of estimated versus measured values of PC for ANFIS_GP (M1) model: a training, b validation and c test data—Station ID: 06892350

Fig. 5

Scatterplots of estimated versus measured values of PC for ANFIS_SC (M1) model: a training, b validation and c test data—Station ID: 06892350

Fig. 6

Scatterplots of estimated versus measured values of PC for GEP (M1) model: a training, b validation and c test data—Station ID: 06892350

Predicting PC at USGS 14211720 station

The main purpose of this section is the comparison of the accuracy of the four AI models developed for predicting PC concentration using data from USGS 14211720 station. The statistics indices of performance are listed in Table 9. Firstly, from the results given in Table 9, the superiority of the ANFIS_SC model can be clearly seen, in all training, validation and test phases. Secondly, in either case, when comparing the six developed combinations (M1 to M6), ANFIS_SC is always the best among all the others. Thirdly, contrary to the results obtained in USGS 06892350 station, where the M5 combination was the best when only two input variables were included (TE and pH), herein for USGS 14211720 station, M5 combination is the worst with the lowest R and highest RMSE and MAE values. This is certainly due to the fact that the pH has a high coefficient of correlation with PC concentration in the USGS 06892350 station (0.710) and low in the other station (0.231). For the other three models, FFNN, ANFIS_GP and GEP, as given in Table 9, the three models gave relatively the similar results, especially for the M1 combination. In the training phase, ANFIS_SC M1 is the best model with R, RMSE and MAE values equal to 0.949, 0.049 μg/L and 0.031 μg/L, respectively. Comparing the ANFIS_SC with the FFNN, ANFIS_GP and GEP, ANFIS_SC has reduced RMSE by 12.50%, 14.03% and 12.50%, and MAE by 20.51%, 22.50% and 16.21% and improved the R by 1.5%, 1.8% and 1.5%, respectively.

Table 9 Performances of the FFNN, ANFIS_SC, ANFIS_GP and GEP models in different phases for USGS 14211720 station

In the validation stage as given in Table 9, ANFIS_SC M1 is always the best with R, RMSE and MAE values equal to 0.95, 0.049 μg/L and 0.032 μg/L, respectively. Comparing the ANFIS_SC with the FFNN, ANFIS_GP and GEP, ANFIS_SC has reduced RMSE by 12.50%, 15.51% and 12.50% and MAE by 17.94%, 21.95% and 15.78% and improved the R by 1.5%, 1.8% and 1.6%, respectively. In the test stage, the ANFIS_SC performed the best with the M1 combination in light of the results obtained in the training and validations phases. The corresponding R, RMSE and MAE values were 0.95, 0.050 μg/L and 0.031 μg/L. It is obvious from Table 9 that the ANFIS_SC M1 yields the best performances among the M1 to M6 input combinations. The detailed description of the two ANFIS models parameters is reported in Table 10. Similar to the previous application, here also the ANFIS_SC seems to be more complicated and has much more parameters than the ANFIS_GP. In Table 11, we report the testing results, different functions set and linkage function for developing GEP models. Similar to the previous application, the GEP model gave the best accuracy with F5 operators and addition linking function. The equation of the GEP M1 model for PC concentration using TE, pH, SC and DO as inputs is given by:

Table 10 Total number of parameters for the two ANFIS models developed for USGS 14211720 station

Table 11 Testing results of different function sets and linkage function for developing GEP for USGS 14211720 station

$${\text{PC}} = \arctan \left( {\frac{{\cos \left( {\frac{{{\text{SC}} - 6.2}}{\text{TE}}} \right)}}{{{\text{DO}} + \sin \left( {\text{SC}} \right)}}} \right) + \frac{{ {\text{pH}}^{4} }}{{ {\text{SC}}^{2} - {\text{TE}}^{2} }} + \frac{\text{pH}}{{2{\text{DO}} + {\text{pH}}^{2} + \frac{{7.3 + {\text{DO}}}}{5.5}}}$$

(28)

Figures 7, 8, 9 and 10 illustrate scatterplots of the computed versus measured PC for FFNN, ANFIS_GP, ANFIS_SC and GEP model M1, in the training, validation, test and all data. Comparison of the fit line equations and R² values shows that the ANFIS-SC model has less scattered PC estimates than the other models. The expression tree of the best GEP M1 model is shown in Fig. 10.

Fig. 7

Scatterplots of estimated versus measured values of PC for FFNN (M1) model: a training, b validation and c test data—Station ID: 14211720

Fig. 8

Scatterplots of estimated versus measured values of PC for ANFIS_GP (M1) model: a training, b validation and c test data—station ID: 14211720

Fig. 9

Scatterplots of estimated versus measured values of PC for ANFIS_SC (M1) model: a training, b validation and c test data—station ID: 14211720

Fig. 10

Scatterplots of estimated versus measured values of PC for GEP (M1) model: a training, b validation and c test data—station ID: 14211720

Conclusions

In this study, four of the most powerful artificial intelligence (AI) techniques, namely feedforward neural networks (FFNN), gene expression programming (GEP), adaptive neuro-fuzzy inference system with grid partition (ANFIS-GP) and adaptive neuro-fuzzy inference system with subtractive clustering (ANFIS-SC), have been proposed to predict the phycocyanin pigment concentration as a function of several water quality variables. Data used for developing the models were selected from two USGS water quality stations. Water temperature, pH, specific conductance and dissolved oxygen were used as predictors. From the results obtained, it can be concluded that all the AI models proposed herein are very promising and provided good results and ANFIS_SC has shown high accuracy in comparison with the all others models. Among six different combinations of the input variables, we have also demonstrated that the proposed ANFIS_SC model can predict PC concentration with high accuracy using only few inputs. Hence, the proposed models can be successfully used for estimating PC concentration in the absence of direct measurement.