Introduction

Reservoir operators must decide about volume of released water and stored water in reservoir. For this reason, several types of reservoir operating rules have been suggested. A number of studies (Shih and ReVelle 1994, 1995) have proposed various hedging schemes for modifying SOP method for mitigating great deficits in a period. Tu et al. (2003, 2008) considered a set of rule curves that is the function of the current storage level to trigger hedging for a multi-purpose multi-reservoir system. Guo et al. (2013) employed an operating rule for multi-reservoir by combining parametric rule with the hedging rule to avoid catastrophic water shortage during droughts. Taghian et al. (2014) employed a hybrid model to optimize simultaneously both the conventional rule curve and the hedging rule. In the previous studies, operation policy was determined using the rule curve and rationing factors; these factors changed from one zone to the other zone suddenly. In this regard, an alternative approach is the application of fuzzy set theory. In the past decade, a number of papers were allocated to the solution of reservoir management problems based on fuzzy set theory. Comparison of fuzzy and non-fuzzy optimal reservoir operating policies was presented by Tilament et al. (2002). Akter and Simonovic (2004) combined fuzzy sets and genetic algorithm (GA) for dealing with the uncertainties in short-term reservoir operation. Fu (2008) presented a fuzzy optimization method based on the concept of ideal and anti-ideal points to solve multi-criteria decision making problems under fuzzy environment. Deka and Chandramouli (2009) developed a hybrid model, which consists of artificial neural network and fuzzy logic in the reservoir operating policy during critical periods. Sadegh and Kerachian (2011) developed two new solution concepts for fuzzy cooperative games with crisp characteristic functions, namely fuzzy least core and fuzzy weak least core. They aimed for optimal allocation of available water resources and associated benefits to water users in a river basin. GA forms one of the most famous evolutionary algorithms (EAs) because of their flexibility and effectiveness for solving complex problems. To overcome the limitations of classical approaches, recently multi-objective evolutionary algorithms (MOEAs) have been proposed (Deb 2001). NSGA-II proposed by Deb et al. (2000, 2002) is one of the contemporary multi-objective EAs that improved the original NSGA by using a more efficient non-domination sorting algorithm, selecting an automatically sharing parameter, and making the Pareto-front by an implicitly elitist selection method (Deb 2002; Deb et al. 2000, 2002). Chang and Chang (2009) applied NSGA-II to examine the operation of a multi-reservoir system in northern Taiwan. Fallah-Mehdipour et al. (2012) employed NSGA II and multi-objective particle swarm optimization (MOPSO) as optimization tools to solve two construction project management problems and demonstrated that NSGA-II is more successful in solving these problems than the MOPSO algorithm. Ahmadi et al. (2014) employed a meta-heuristic, multi-objective optimization algorithm, named NSGA-II, to extract optimal operation policies of a single-reservoir system by maximizing the reliability and minimizing the vulnerability of hydropower generation. Ahmadianfar et al. (2016) employed MOPSO-DE algorithm to optimize a multi-reservoir and multi-purpose system in Iran. The results of this work showed that the obtained Pareto frontier by MOPSO-DE algorithm can be extremely appropriate in complex multi-reservoir systems and may help decision-makers in choosing management policies with respect to societal and political considerations that are difficult to model.

The purpose of the present study was to develop an operation policy for water supply multi-reservoir system by combining fuzzy-rationing factor with the hedging rule to avoid severe water shortage. The new hedging rule was applied to the Zohre reservoir system located in southern Iran, chosen as a case study. For solving the problem NSGA-II algorithm is coupled to the proposed hedging rule simulation. The methodology and main components of the model are described in the following.

Background of materials

Non-dominated sorting genetic algorithm (NSGA)

Srinivas and Deb (1994) introduced NSGA for multi-objective optimization problems. It is one of the most effective and efficient algorithms for solving multi-objective problems. The NSGA-II employs the non-dominated sorting and ranking selection with the crowded comparison operator (Deb et al. 2000). Three new innovations are described in the following:

  1. 1.

    Fast non-dominated sorting: The fast non-dominated sorting approach has been employed for reducing the computing time to O(MN2) (N is population size and M is the number of objective function).

  2. 2.

    Crowding Distance: In the proposed NSGA-II, the crowding distance (Deb 2001, 2002; Deb et al. 2002) is used to get an estimate of the density of solutions surrounding a particular solution i in the population.

  3. 3.

    Crowded comparison operator: The crowded comparison operator guides the selection process at the various stages of the algorithm towards a good spread of the solutions in the optimum fronts. This operator is applied between two solutions with differing non-domination ranks; it prefers the solution with better rank. Otherwise, if both solutions belong to the same front then we prefer the solution which is located in a lesser crowded region (Deb 2002; Deb et al. 2002).

The research methodology

Simulation method

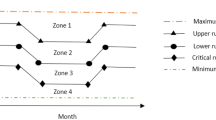
In the present study, the purpose of the simulation model was to create the monthly operation policy of a multi-reservoir system by following its fuzzification rationing factor. In previous works, the rationing factor was constant for each zone, so when the reservoir storage was near the threshold changing zone, these factors may be changed suddenly (Fig. 1). Because the rationing factor changes gradually in this research, if reservoir storage is near to rule curve, two states will occur based in the applied procedure in this study.

  1. 1.

    If reservoir storage is under the rule curve, the volume of released water will increase in comparison with conventional methods (as point A in Fig. 2).

  2. 2.

    If reservoir storage is above the rule curve, the volume of released water will decrease in comparison with conventional methods (as point B in Fig. 2).

This method prevents sudden changes of the rationing factor. To resolve this problem, the present study used of a transition zone. In this study, it considered two rule curves (upper and lower curve); thus there are three zones: normal, drought and severe drought zones. To confront limitations of conventional rule curve, the concept of fuzzy logic has been used for making a transition zone in up and down of each rule curve. Whenever the reservoir level enters into this zone, the rationing factor will be increased or decreased gradually (Fig. 2). The trapezoidal membership functions are used to determine transition zones. These transition zones are assigned by four coefficients (β 1, β 2, β 3 and β 4). Figure 3 shows membership functions and Eqs. (1)–(4) present the parameters of the each of the membership functions. Also, during each time period t, the relationship between the rule curves and the hedging rules employed in this paper and its corresponding water-supply operation rule are illustrated in Eqs. (5)–(9). In Fig. 2, there are five zones that consist of zones 1–3 and transition zone 1 and 2. How to apply simultaneously both the rule curves coupled with hedging rules is described next.

Fig. 1
figure 1

The simple hedging rules for a multipurpose reservoir

Full size image
Fig. 2
figure 2

The new hedging rules for a multipurpose reservoir

Full size image
Fig. 3
figure 3

Trapezoidal membership functions for rationing factors

Full size image
  1. 1.

    When the beginning reservoir storage is in zone 3, all target demands are met at the 100 % level.

  2. 2.

    When the beginning reservoir storage is in transition zone 1 or 2, the rationing factor depends on membership grade of reservoir storage to membership functions of fuzzy set of the rationing factors.

  3. 3.

    When the beginning reservoir storage is in zone 2, the reservoir release for meeting the planned demand must be cut back, for instance, by 30 %.

  4. 4.

    When the beginning reservoir storage is in zone 1, then the reservoir release for meeting the planned demand must be cut back, for instance, by 65 %.

In the present study, the water demand is divided into various categories, such as agriculture, public (the municipal and industrial water demands are considered as one type of demands, here called public demands) and minimum flow requirements for environmental purposes. For planning purposes, the municipal and industrial water demands are considered as one type of demands, here called public demands. These demands have the highest priority in comparison with the other demands. In this regard, the public demand will be supplied completely. Following that, minimum flow and agriculture requirements are next prioritized in this order.

$$C_{1} = S_{\hbox{min} } + (RC_{1} - S_{\hbox{min} } ) \times \beta_{1}$$
(1)
$$C_{2} = RC_{1} + (RC_{2} - RC_{1} ) \times \beta_{2}$$
(2)
$$C_{3} = C_{2} + (RC_{2} - C_{2} ) \times \beta_{3}$$
(3)
$$C_{4} = RC_{2} + (S_{\hbox{max} } - RC_{2} ) \times \beta_{4}$$
(4)
$${\text{if}}\,\,\,\,S_{t} \in \;\,{\text{zone }}3\,\,\;\,\,{\text{then}}\,\,\,R_{t} = D_{t}$$
(5)
$${\text{if}}\,\,\,\,S_{t} \in \;\,{\text{transition}}\,\,{\text{zone}}\; 2\,\,\;\,\,{\text{then}}\,\,\,R_{t} = (\mu_{3} \alpha_{2} + \mu_{4} ) \times D_{t}$$
(6)
$${\text{if}}\,\,\,\,S_{t} \in \,\,{\text{zone}}\; 2\,\,\;\,\,{\text{then}}\,\,R_{t} = \alpha_{2} \times D_{t}$$
(7)
$${\text{if}}\,\,\,\,S_{t} \in \;\,{\text{transition}}\,\,{\text{zone}}\; 1\,\,\;\,\,{\text{then}}\,\,R_{t} = (\mu_{1} \alpha_{1} + \mu_{2} \alpha_{2} ) \times D_{t}$$
(8)
$${\text{if}}\,\,\,\,S_{t} \in \,\,{\text{zone}}\; 1\,\,\;\,\,{\text{then}}\,\,R_{t} = \alpha_{1} \times D_{t}$$
(9)

where \(S_{t}\) is beginning storage of the reservoir at period t; \(D_{t}\) is planned water demand; R is water supply for \(\mathop D\nolimits_{t}\); α 1 and α 2 are rationing factors; \(\mathop S\nolimits_{\hbox{min} }\) is the minimum water storage of reservoir; \(\mathop S\nolimits_{\hbox{max} }\) is the maximum water storage of reservoir; RC 1, RC 2 are lower and upper rule curves, respectively; \(0 \le \mathop \alpha \nolimits_{1} \le \mathop \alpha \nolimits_{2} \le 1\); C 1, C 2, C 3, C 4 are the coefficients of membership functions in Fig. 3 (C 1 < C 2 < C 3 < C 4) and \(\mu_{1} ,\;\mu_{2} ,\;\mu_{3}\) and \(\mu_{4}\) are the degree of “belongingness” to a fuzzy set and depending on the reservoir storage in which the zone is appointed, for example, if the reservoir storage is belonging to transition zone 1 (Fig. 2), the release is determined based on Eq. (8). The value of rationing factors will be obtained by optimization.

Objective function

In the optimization model for the water-supply multi-reservoir operation, the water shortage index could represent the lumped water supply shortage and reflect the severity of the water shortage; the modified shortage index (MSI) of Hsu and Cheng (2002) is used in the present study, that is,

$${\text{MSI}} = \frac{100}{T}\sum\limits_{t = 1}^{T} {\left( {\frac{{{\text{TS}}_{t} }}{{{\text{TD}}_{t} }}} \right)^{2} } ,$$
(10)

where TS t is the total shortage in the tth period (month); TD t is the total demand in the tth period, and T is the total number of time periods. The MSI can be used to minimize the total water shortage of the different (minimum flow and agriculture) demands using the following objective function:

$$f_{ 1} :{\text{MSI}}_{m} = \frac{100}{T}\sum\limits_{t = 1}^{T} {\left( {\frac{{{\text{TS}}_{t} }}{{{\text{TD}}_{t} }}} \right)_{m}^{2} }$$
(11)
$$f_{ 2} :{\text{MSI}}_{\alpha } = \frac{100}{T}\sum\limits_{t = 1}^{T} {\left( {\frac{{{\text{TS}}_{t} }}{{{\text{TD}}_{t} }}} \right)_{a}^{2} } ,$$
(12)

where \({\text{MSI}}_{m}\) and \({\text{MSI}}_{a}\) are modified water shortage indexes for public, minimum flow and agriculture demands, respectively. These two objectives of the competing system are considered and both are minimized. The complete multi-objective problem is solved based on NSGA-II.

System constraints

In this paper, the number of decision variables is 82. They consist of 2 rationing factors for the agricultural demands and 2 rationing factors for the minimum flow, coefficients for determining the transition zone in the rule curves (each rule curve has 2 transition zones), 2 coefficients to specify the portion of each reservoir for supplying common demands and 72 decision variables that is 12 monthly levels for each reservoir × Two positions of hedging rule curves for each reservoir (each reservoir has 2 hedging rule curves) × 3 reservoir. This research added 4 coefficients for determining the transition zone in the rule curves to decision variables of simple hedging rule method; therefore the simple hedging rule method has 78 decision variables. Thus, there are 78 decision variables.The water balance of a reservoir system is considered as the system constraint, that is,

$$S^{j}_{t + 1} = S^{j}_{t} + Q^{j}_{t} - R^{j}_{t} - {\text{Sp}}^{j}_{t} - E^{j}_{t}$$
(13)
$$E_{{_{t} }}^{j} = f_{1} (e_{{_{t} }}^{j} ,\;\overline{A}_{{_{t} }}^{j} )$$
(14)
$$\overline{A}_{{_{t} }}^{j} = (A_{{_{t} }}^{j} + A_{{_{t + 1} }}^{j} )/2$$
(15)
$$A_{{_{t} }}^{j} = f_{2} (S_{t}^{j} )$$
(16)
$${\text{Sp}}_{{_{t} }}^{j} = \left\{ {\begin{array}{*{20}c} {S_{t}^{j} + Q_{t}^{j} - S_{\hbox{max} }^{j} \quad {\text{if}}\;(S_{t}^{j} + Q_{t}^{j} ) > \,S_{\hbox{max} }^{j} } \\ {0\quad \quad \quad \quad \quad \quad \;{\text{otherwise}}\quad \quad \quad \quad } \\ \end{array} } \right.$$
(17)

The model’s formulation is constrained by the following relation:

$$S^{j}_{\hbox{min} } \le S^{j}_{t} \le S^{j}_{\hbox{max} }$$
(18)

where \(S_{t}^{j}\) is the reservoir storage of reservoir j at period t; \(R_{t}^{j}\) is reservoir release from reservoir j at period t; \(Q_{t}^{j}\) is the water inflow to reservoir j at period t; \(E_{t}^{j}\) is the evaporation volume of reservoir j at period t, \({\text{Sp}}_{t}^{j}\) is the spilled volume water from reservoir j at period t; f 1 is function to find volume of evaporation; \(e_{{_{t} }}^{j}\) is evaporation depth in the jth reservoir at period t; \(\overline{A}_{{_{t} }}^{j}\) is average surface of the jth reservoir at period t; \(A_{{_{t} }}^{j}\) is water surface of the jth reservoir at the start of period t; f 2 linear function for transferring storage volume to water surface; \(S^{j}_{\hbox{min} }\) is the minimum storage of reservoir j and \(S^{j}_{\hbox{max} }\) is the maximum storage of reservoir j.

Hybrid of simulation and optimization model

In this study, a multi-objective NSGA-II is connected to the simulation model for optimizing simultaneously the rule curves, rationing factors and coefficients of determining the transition zone in a multi-reservoir system. Figure 4 presents the flowchart of hybrid of simulation and optimization model.

Fig. 4
figure 4

Flowchart of NSGA-II applied to the proposed and simple hedging rule

Full size image

Study basin

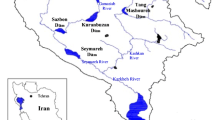
As a case study, the Zohre river system with an area of about 16,000 km2 in Iran is used. The schematic configuration of this system is shown in Fig. 5. A future planning horizon (for year 2021) is selected for this study, and the future system comprises 3 reservoir dams, 7 input stream flows, 9 irrigation networks, 3 public demand channels, 2 minimum flow channels, 9 junction nodes and some general channels. The useful storage volumes for the reservoir dams including Kosar, Chamshir and Kheirabad are, respectively, 418, 1576 and 104 million cubic meters.

Fig. 5
figure 5

Schematic configuration of the water supply system

Full size image

The basis in deriving the joint rules among the three reservoirs is indicated in the following.

Water allocation rule

For simplicity, let us consider a Y-shaped three-reservoir system as shown in Fig. 6. Reservoirs either in series or in parallel exist in the system. Demands \(D_{t}^{1} ,D_{t}^{2} ,D_{t}^{3}\) and \(D_{t}^{4}\) in period t are, respectively, \(D_{t}^{1}\) (are supplied from reservoir 1), \(D_{t}^{2}\) (are supplied from reservoir 2), \(D_{t}^{3}\) (are supplied from reservoirs 1 and 3) and \(D_{t}^{4}\) (are supplied from reservoirs 1, 2 and 3) are demands in period t. That is,

$$a^{11} D_{t}^{1} = D_{t}^{1} ,a^{11} = 1$$
(19)
$$a^{22} D_{t}^{2} = D_{t}^{2} ,a^{22} = 1$$
(20)
$$a^{13} D_{t}^{3} + a^{33} D_{t}^{3} = D_{t}^{3} ,a^{13} + a^{33} = 1$$
(21)
$$a^{14} D_{t}^{4} + a^{24} D_{t}^{4} + a^{34} D_{t}^{4} = D_{t}^{4} ,a^{14} + a^{24} + a^{34} = 1,$$
(22)

where \(a^{ij} (0 \le a^{ij} \le 1)\) is the water allocation parameter showing the percentage of required water quantity released from reservoir i to demand j in period t (Huang et al. 2002).

Fig. 6
figure 6

Schematic representation of water allocation

Full size image

Clearly, the problem is relatively complicated. However, the problem can be resolved if we decompose the multiple system into a system of three single reservoirs. The demand at a demand point is made up by a linear combination of release goals of all the upstream reservoirs utilizing the water allocation parameters. In the meantime, the planned water demand of each single reservoir is predetermined by the water allocation parameters. Each single reservoir will be handled independently.

The optimal joint operation of the original multi-reservoir system and optimal water allocation parameter values will be found by multi-objective algorithm. Namely, NSGA-II algorithm searches for the optimal decision variable values the overall functions are optimized simultaneously.

Results

In the study, the objective function is divided into two categories: (1) satisfaction of the minimum flow requirement; and (2) minimization of MSI for agricultural demands. Used inflow data for this study are obtained from historical records spanning 48 years, from 1956 to 2003. These records include severe drought periods particularly from 1958 to 1972 for nine successive years. Figure 7 shows the monthly time series for the inflow and demand in the system.

Fig. 7
figure 7

Total monthly inflows and demands in the system

Full size image

For simulating the case study on base of the hedging rule, the fuzzy-rationing factor with hedging rule has been coupled. Herein, the simulation is solved using the NSGA-II method. The main parameters of NSGA-II are population size, number of iteration, crossover ratio and mutation ratio are 200, 1000, 0.8 and 0.3–0.01, respectively. Optimal coefficients of determining the transition zones are 0.39, 0.3, 0.2 and 0.5 (β 1 = 0.39, β 2 = 0.3, β 3 = 0.2 and β 4 = 0.5). The optimum rationing factors for agricultural and minimum flow demands are shown in Table 1. The variation of fitness value through generation is shown in Fig. 8.

Table 1 Rationing factors for different demands
Full size table
Fig. 8
figure 8

Convergence curves of the fitness value through generation

Full size image

For verification of the effectiveness of the purposed hedging rule; we considered the simple rule curve following the current practical policy in Iran. According to what has already been said, minimizing of objective function of minimum flow is prioritized; in this regard, for a closer look at the proposed method, two points of Pareto front are selected, In these two points of Pareto set, the agriculture MSI value is equal for two hedging rules (simple and the proposed hedging rule). In two points, it used hybrid of the simulation hedging rule and NSGA-II; then the Pareto set presented according to Figs. 9 and 10.

Fig. 9
figure 9

Non-domination solutions with NSGA-II on the simple hedging rule

Full size image
Fig. 10
figure 10

Non-domination solutions with NSGA-II on the proposed hedging rule

Full size image

The results of the first point (Table 2) show that performance of long-term system of the proposed method is much better than the simple hedging rule.

Table 2 Long-term system performance during period 1956–2003
Full size table

In all months (but one of them and in a very few) the MSI value of the proposed method is less than the simple method (Table 3).

Table 3 Annual system performance during failure years
Full size table

Also the number of failure years in the proposed method is 13 and this number in the simple method is 19, and in Table 2 (the second point) the long-term system performance of the proposed method is better than the simple method. On the other hand, in all months (but four of them) the MSI value of the proposed method is less than the simple method (Table 3). Also the number of failure years in the proposed method is 14 and this number in the simple method is 19. For more reviews regarding the efficiency of the proposed hedging rule, diagram of rationing factors of two methods during the severe drought periods from 1958 to 1972 is shown in Fig. 11.

Fig. 11
figure 11

Diagram of variation Fuzzy-rationing factors and simple rationing factors

Full size image

Unlike conventional methods, rationing factors change gradually in the proposed method. Optimal rule curves in the proposed hedging rule are illustrated in Figs. 12, 13 and 14 for Kosar, Kheirabad and Chamshir reservoirs. Note that according to the irrigation practices in Iran, the water year begins from October.

Fig. 12
figure 12

Rule curves of the new hedging rules for Kosar reservoir

Full size image
Fig. 13
figure 13

Rule curves of the new hedging rules for Kheirabad reservoir

Full size image
Fig. 14
figure 14

Rule curves of the new hedging rules for Chamshir reservoir

Full size image

Conclusions

In this article, a hybrid model developed for simultaneously optimizing water allocation and searching the new reservoir hedging rules to minimize the impacts of droughts is shown. For this purpose, a hedging rule simulation base on fuzzy rationing factor has been connected to the multi-objective NSGA-II. The NSGA-II was used to minimize MSI values by identifying the new hedging rule. In previous studies (Tu et al. 2003, 2008; Guo et al. 2013; Taghian et al. 2014), as usual the rule curves divide reservoir storage into several zones so that the reservoir storage belongs to only one zone at each time step, whereas in the present study it applied concept of fuzzy logic to the rationing factors. According to this concept, there is an interval around each rule curve (transition zone) instead of a crisp boundary. Whenever the reservoir volume enters the transition zone the rationing factor will be changed on base of fuzzy logic concept. In order to analyze the effect of the proposed operation rule, the multi-reservoir system in Iran, namely Zohre system, is employed as a case study. According to the obtained results, the proposed hedging rule has caused marked differences in severity of shortages in comparison to applying the rule curve alone which is the usual operational policy. Table 3 shows that the proposed method has improved the results of annual system performance from 0.8 till 100 percent in comparing of the results of the simple method. Also Table 2 indicates improvement of the long-term system performance of the proposed method in comparing with the simple method from 10 till 27 percent. Table 2 shows that agriculture MSI is equal for both methods, while the proposed method improved the minimum flow MSI 63 and 46 percent in comparison with simple method for points 2 and 3, respectively. Dispersion of fuzzy-hedging factors in comparison with simple hedging factors increased the ability and flexibility of the proposed method for reducing the long-term and annual system performance during failure years. The main objective of the water resources system is reduction of MSI of minimum flow demands and the presented method can decrease it considerably.