1 Introduction

Not long ago, rather shallow wells with simple outlines were drilled in oil and gas fields. However, at the present time, deeper and more complicated trajectories of bore holes are designed in connection with exhaustion of easily accessible hydrocarbon sources. In 2015, the record 13.5 km horizontal bore hole was drilled in the Sakhalin region, Russia. According to experts’ opinions, most of the substantial achievements in the power engineering of the current century are associated with this technical direction. Particularly, some are related to the pioneering investigation of industrial extraction of shale oil and gas, whose deposits in the world essentially exceed conventional reserves. However, as a rule, drilling of such bore holes is attended by extraordinary phenomena bringing emergency situations. One of them is unstable bending buckling of a drill string (DS) in the channel of a curvilinear bore hole (Brett et al. 1989; Dawson and Paslay 1984; Kyllingstad 1995; Sawaryn et al. 2006; Gulyayev et al. 2009; Gao and Liu 2013; Huang and Gao 2014; Gao and Huang 2015). This effect is associated with deterioration of conditions of contact interaction between the DS and the bore hole wall, enlargement of friction forces, impossibility of transferring the required axial force to the bit, and the DS lockup situation. To predict these effects and exclude them in practice, computer simulation should be employed.

In parallel with the static phenomena of buckling of the DSs, there also can occur very complicated nonlinear dynamic processes accompanied by extraordinary stable and unstable changes of the DS rotation. Among them there are axial, torsional, bending, and whirl vibrations, inevitably linked with deterioration of the drilling efficiency (Liu et al. 2013, 2014a, b).

The effects of loss of equilibrium stability in these mechanical systems are manifestations of one of the most general law of nature—the law of quantitative changes transferring to qualitative ones. In different spheres of reality, these changes are realized by different ways. In mechanics, they are studied on the basis of bifurcation theory.

The problem of mechanical instability and bifurcational buckling acquires crucial urgency in the technology of long curvilinear bore hole drilling because it is specified by essential complications but is not yet understood. Current experience testifies that no well is drilled without problems. They are connected with the complexity of mechanical phenomena accompanying the drilling process and the absence of dependable methods of computer modeling providing the possibility to predict emergency situations and to exclude them in advance. In a vertical bore hole, the DS stability loss occurs at its lower part following the spiral buckling mode typical for a rod stretched, compressed, and twisted simultaneously (Lubinski et al. 1962; Gulyayev et al. 2009).

However, the problem of theoretic simulation of DS buckling in the channel of a curvilinear bore hole acquires supplementary difficulties associated with the necessity of integrating differential equations with variable coefficients in the full range of the large length of the DS. Besides, the problem possesses essential complications stemming from appearance of additional constraints, imposed on the DS by the well wall surface, and application of contact and friction distributed forces, as well as change of orientation of gravity forces compressing the DS to the well wall (Dawson and Paslay 1984; Wang and Yuan 2012; Gulyayev et al. 2014).

Comprehensive reviews of results achieved in this direction are presented in the literature (Cunha 2004; Mitchell 2008; Gao and Huang 2015). It stems from these analyses that, as a rule, the approaches used in bifurcational analysis are based on the eigenmode approximations by regular sinusoids and spirals, while the critical values of loads and buckling shapes are rather guessed. As Cunha notes apparently this circumstance is the reason of conclusions that solutions of the problem on stability loss of the DSs in curvilinear bore holes gained by different authors are in contradiction with each other and reality (Cunha 2004).

Mitchell emphasizes “that there are still challenging problems to solve and difficult questions to answer” in the domain of the DS buckling (Mitchell 2008). Among them, the fundamental unresolved questions remain:

  • What is the critical buckling load in curved, 3D bore holes?

  • What effect does friction play in DS buckling?

The last achievements in this domain are discussed by Gao and Huang (2015).

Gulyayev et al. (2014, 2015) elaborated a new mathematic model of a DS stability loss in smooth curvilinear channels. Without taking into consideration friction effects, they showed that the stated problem was singularly perturbed and so, typically, the modes of buckling were represented by boundary and localized effects in the shapes of wave packages or wavelets.

In this problem, fundamental unresolved questions remain: What role is played by the friction factor in stability loss phenomena and how to include it in the analytical or numerical model. Mitchell remarks: “Perhaps the most important force, and the force least studied in the analysis of buckling, is friction” (Mitchell 2008). The magnitude of the friction force is usually not that difficult to determine. The difficulty is determining the direction of the friction vector. We agree that this vector cannot be determined for stationary elastic systems with friction contacts because this problem is statically indeterminable (Mitchell and Samuel 2009). But if one of the contacting bodies slides on the surface of another, then the vectors of sliding velocity and friction force are collinear and the last one can be easily determined. This peculiarity facilitates the problem on the analysis of friction effects on critical buckling of the DS.

In the first place, it is necessary to point out that every balanced stationary state of the DS is preceded by its steady sliding motion associated with tripping in or out operation and drilling is accompanied by kinematic friction. As a rule, the coefficients of kinematic friction exceed their magnitudes established in static equilibrium. Besides, usually, the indicated technological procedures happen with certain ultimate longitudinal velocities, while the DS buckling occurs with very small velocities. In this case, the lateral buckling velocities (and the appropriate lateral friction forces) can be assumed to equal zero. Then, all the friction forces are axial and are oriented in one direction. Then, the moving DS experiences action of the more intensive friction forces which have deleterious effects upon the stability of its quasi-static equilibrium. Therefore, at this state, the bifurcational buckling of the DS should first of all be analyzed.

Secondly, the friction forces acting on the DS and all the functions of its total stress–strain state can be specified by rather simple calculation means.

Thirdly, with the use of these functions, the constitutive linearized homogeneous equations of critical equilibrium of the DS can be constructed. Their eigenvalues and eigenmodes determine critical loads on the DS in the bore hole channel and shapes of its bifurcational buckling.

To realize this approach, the nonlinear theory of elastic curvilinear rods is used. Its foundations are stated in monographs (Antman 2005; Gulyayev et al. 1992). A three-dimensional statement of this theory is expounded by Gulyayev and Tolbatov (2004). Its application to analysis of the DSs buckling in inclined rectilinear bore holes is described by Gulyayev et al. (2014). Below, it is formulated in a concomitant reference frame moving on the bore hole surface constraining the DS transformation. Owing to this, the total order of the differential equation is reduced to four. A two-step algorithm is proposed. At the first step, the stress–strain state of the moving DS under action of gravity and friction forces is determined; at the second step, the eigenvalue problem for linearized equations is solved. It is shown, that the buckling modes have the shapes of harmonic wavelets with localization segments depending on the friction forces.

2 Basic assumptions concerning drill string bending in a curvilinear bore hole

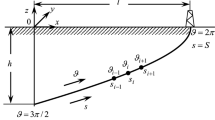
The problem about nonlinear elastic bending of a DS relative to the immovable coordinate system OXYZ inside a channel cavity of a curvilinear bore hole is considered and shown in Fig. 1. In the considered case, the DS is lowering along its axial line but the surfaces of the DS and the bore hole are in contact throughout the DS length. The DS does not rotate; hence, the distributed friction torques equal zero. Assuming that the DS movement is quasi-static, then, the inertia forces are small and can be disregarded, so only the distributed gravitational (\({\mathbf{f}}^{\text{gr}}\)), contact (\({\mathbf{f}}^{\text{cont}}\)), and frictional (\({\mathbf{f}}^{\text{fr}}\)) forces are acting on every element of the DS. As shown in Fig. 1, the \({\mathbf{f}}^{\text{gr}}\) force is vertical, \({\mathbf{f}}^{\text{cont}}\) is applied normally to the axis line at the contact point, and \({\mathbf{f}}^{\text{fr}}\) force is opposite to the axial velocity of the descending element.

Fig. 1
figure 1

Scheme of a drill string in a bore hole channel

Full size image

It is believed, also, that the DS element displacements can be comparable with the bore hole cross-sectional dimensions, but the curvature radii of its axis line L are so large that the DS strains are small and its stress–strain states are elastic. They are specified by the principal vectors of internal forces \({\mathbf{F}}(s)\) and internal moments \({\mathbf{M}}(s)\), where s is the natural parameter defined by the length of the DS axis line L measured from some initial point to the considered one.

The external and internal force factors have to satisfy the following differential equations of equilibrium (Gulyayev et al. 1992, 2014):

$$\frac{{\text{d} {\mathbf{F}}}}{{\text{d} s}} = - {\mathbf{f}}^{\text{gr}} - {\mathbf{f}}^{\text{cont}} - {\mathbf{f}}^{\text{fr}} ,\quad \frac{{\text{d} {\mathbf{M}}}}{{\text{d} s}} = - {\mathbf{t}} \times {\mathbf{F}},$$
(1)

where \({\mathbf{t}}\) is the unit vector directed along the tangent to the axis line L.

If Eq. (1) is projected on the immovable coordinate system OXYZ, it will be possible to receive six scalar equations of the element equilibrium. However, in a general case, it is more convenient to express them in axes of some movable trihedron. Usually, if elastic bending of the unconstrained curvilinear rod is studied, the Frenet trihedron with unit vectors of normal \({\mathbf{n}}\), binormal \({\mathbf{b}}\), and tangent \({\mathbf{t}}\) are used. They are calculated by the formulae:

$${\mathbf{t}} = \frac{{\text{d} {\mathbf{R}}}}{{\text{d} s}},\quad {\mathbf{n}} = r\frac{{\text{d} {\mathbf{t}}}}{{\text{d} s}},\quad {\mathbf{b}} = {\mathbf{t}} \times {\mathbf{n}}$$
(2)

where \({\mathbf{R}}(s)\) is the radius vector of the DS element in the OXYZ coordinate system; r(s) is the curvature radius of the line L.

Yet, if the DS is in contact with the well wall surface, then, the axis line L lies and slides in the channel surface Σ of radius a (Fig. 2) which is equal to half-difference

$$a = \left( {d_{1} - d_{2} } \right)/2,$$

where d 1 and d 2 are the diameters of the bore hole and DS cross sections, respectively.

Fig. 2
figure 2

Sliding of axial line L in reference surface Σ

Full size image

This surface can be parameterized by parameter u, determining the axis line T of the bore hole

$$X_{T} = X_{T} (u),\quad Y_{T} = Y_{T} (u),\quad Z_{T} = Z_{T} (u)$$
(3)

and parameter v, prescribing position of a point in the generating circle (Fig. 2). Here, \(u, \, v\) are curvilinear coordinates in the surface Σ; Σ is the channel surface of the bore hole wall; X T , Y T , Z T are the X, Y, Z coordinates of the line T.

With their use, the DS bending is preset in the 2D space of the Σ surface by equalities

$$u = u(s),\quad v = v (s )$$
(4)

Then, to describe the line L transforming, it is convenient to introduce additional right-hand reference frame oxyz with unit vectors \({\mathbf{i}}\), \({\mathbf{j}}\), \({\mathbf{k}}\), moving on the constraining surface Σ along the line L. In doing so, the unit vector \({\mathbf{i}}\) is the internal normal to the surface Σ and the vector \({\mathbf{k}}\) is tangent to the curve L.

Now, it becomes possible to introduce an analogue

$${\varvec{\upomega}} = k_{x} {\mathbf{i}} + k_{y} {\mathbf{j}} + k_{z} {\mathbf{k}}$$
(5)

of the Darboux vector (Dubrovin et al. 1992; Gulyayev et al. 1992).

In this equality, k x and k y are the appropriate components of the vector \({\varvec{\Omega}} = {\mathbf{b}}/r\) of the curvature of the line L along the ox and oy axes; k z is the value

$$k_{z} = \mathop {\lim }\limits_{\Delta s \to 0}\Delta \psi /\Delta s$$
(6)

determining rotation of the oxyz system around the vector \({\mathbf{k}}\) when this reference frame moves along the line L from the point sto the point s + Δs.

Here, Δψ is the elementary angle of vector \({\mathbf{i}}\) rotation.

Generally, if displacements of a rod are not constrained, its curvature 1/r can be calculated by the formula:

$$\frac{1}{r} = \sqrt {\frac{{\text{d}}^{2} X}{{\text{d}} s^{2} } + \left( {\frac{{\text{d}}^{2} Y}{{\text{d}} s^{2} }} \right)^{2} + \frac{{\text{d}^{2}} Z}{{\text{d}} s^{2} }}$$
(7)

and, subsequently, its components k x and k y can be determined. However, in the considered case, the rod axis L lies in the surface Σ with prescribed geometry and so it is more convenient to specify functions k x (s) and k y (s) in the terms of its geometrical parameters.

To do so, it is necessary to consider internal and external geometries of the surface Σ. Its internal geometry is defined by the first quadratic form:

$$\varPhi_{1} (u,v) = a_{11} \text{d} u^{2} + 2a_{12} \text{d} u\text{d} v + a_{22} \text{d} v^{2} ,$$
(8)

where a 11, a 12, and a 22 are parameters of the quadratic form. With their use, the geometrical objects, lying in the surface Σ, are described and calculated.

In the considered case, the surface Σ is a channel and then the coordinate lines u = const and v = const are orthogonal and a 12(u, v)=0. Owing to this, the curvature k x , coinciding with geodesic curvature k geod of the curve L, is expressed with the use of the formula (Dubrovin et al. 1992)

$$k_{x} = k^{\text{geod}} = \sqrt {a_{11} a_{22} } \left[ {a_{11} (u^{\prime } )^{2} + a_{22} (v^{\prime } )^{2} } \right]^{ - 3/2} (u^{\prime \prime } v^{\prime } - v^{\prime \prime } u^{\prime } + Av^{\prime } - Bu^{\prime } ).$$
(9)

Here, coefficients A and B are represented through the Cristoffel symbols Γ i jj by the equalities

$$A =\Gamma _{11}^{1} \left( {u^{\prime } } \right)^{2} +\Gamma _{22}^{1} \left( {v^{\prime } } \right)^{2} ,\quad B =\Gamma _{11}^{2} \left( {u^{\prime } } \right)^{2} +\Gamma _{22}^{2} \left( {v^{\prime } } \right)^{2}$$
(10)

The surface Σ shape, curvatures, and external geometry are determined by parameters b 11, b 12, b 22 of the second quadratic form:

$$\varPhi_{2} (u,v) = b_{11} \text{d} u^{2} + 2b_{12} \text{d} u\text{d} v + b_{22} \text{d} v^{2} .$$
(11)

If the surface Σ is a channel, the correlation b 12 = 0 is valid for the chosen coordinate u and v. Then, on the basis of the Euler theorem (Dubrovin et al. 1992), the curvature k y of the line L can be equalized to appropriate normal curvature k norm of the surface Σ in the direction of the curve L. In its turn, the curvature k norm is expressed through principal curvatures k 1, k 2 of the surface Σ

$$k^{\text{norm}} = k_{y} = k_{1} \cos^{2} \theta + k_{2} \sin^{2} \theta .$$
(12)

Here, θ is the angle between the directions of curve L and coordinate line u; k 1 and k 2 are the normal curvatures of lines v = const, u = const, respectively. They can be represented as follows:

$$k_{1} = b_{11} /a_{11} ,\quad k_{2} = b_{22} /a_{11}$$
(13)

The gained relations (6), (9), (12) permit one to study elastic bending of the DS in a movable reference frame (5).

3 Nonlinear constitutive equations of the drill string bending in a curvilinear channel

To deduce constitutive equations of bending, the drill string sliding along its axial line in a curvilinear bore hole Eq. (1) is represented in a moving reference frame oxyz with unit vectors \({\mathbf{i}}\), \({\mathbf{j}}\), \({\mathbf{k}}\). Then, the absolute derivatives dF/ds and dM/ds in Eq. (1) can be expressed as follows:

$$\text{d} {\mathbf{F}}/\text{d} s = \tilde{\text{d}}{\mathbf{F}}/\text{d} s + {\varvec{\upomega}} \times {\mathbf{F}},\quad \text{d} {\mathbf{M}}/\text{d} s = \tilde{\text{d}}{\mathbf{M}}/\text{d} s + {\varvec{\upomega}} \times {\mathbf{M}},$$
(14)

Here, \(\tilde{\text{d}} \ldots /\text{d} s\) is the symbol of local derivative in the oxyz system.

Vectors \({\mathbf{F}}\), \({\mathbf{M}}\), \({\mathbf{f}}^{\text{gr}}\), \({\mathbf{f}}^{\text{cont}}\), \({\mathbf{f}}^{\text{fr}}\) are resolved into their components in the \({\mathbf{i}}\), \({\mathbf{j}}\), \({\mathbf{k}}\) trihedron:

$$\begin{array}{*{20}l} {{\mathbf{F}} = F_{x} {\mathbf{i}} + F_{y} {\mathbf{j}} + F_{z} {\mathbf{k}},} \hfill & {{\mathbf{M}} = M_{x} {\mathbf{i}} + M_{y} {\mathbf{j}} + M_{z} {\mathbf{k}},} \hfill \\ {{\mathbf{f}}^{\text{gr}} = f_{x}^{\text{gr}} {\mathbf{i}} + f_{y}^{\text{gr}} {\mathbf{j}} + f_{z}^{\text{gr}} {\mathbf{k}},} \hfill & {{\mathbf{f}}^{\text{cont}} = f_{x}^{\text{cont}} {\mathbf{i}}, \, {\mathbf{f}}^{\text{fr}} = f_{{^{z} }}^{\text{fr}} {\mathbf{k}}.} \hfill \\ \end{array} \,$$
(15)

In these correlations, the advantages of the chosen approach and reference frame used are obvious. Indeed, the \({\mathbf{f}}^{\text{cont}}\) force is normal to the surface Σ, it is collinear with the vector \({\mathbf{j}}\), and has only one component. The problem on specification of friction forces is considerably harder. Assuming that the friction interaction between the DS tube and the bore hole wall obeys Coulomb’s law (Berger 2002; Mitchell and Samuel 2009; Samuel 2010)

$${\mathbf{f}}^{\text{fr}} \le \mu {\mathbf{f}}^{\text{cont}}$$
(16)

where μ is the friction coefficient.

Following Eq. (16), the fraction can be subdivided into static friction (“stiction”) between non-moving surfaces and kinetic friction generated between sliding ones (Fig. 3).

Fig.  3
figure 3

Diagram of the Coulomb friction

Full size image

The static regimes occur under conditions when the motive forces cannot overcome the resistance of cohesion forces which have some ultimate value \({\mathbf{f}}^{\text{ult}} = \mu {\mathbf{f}}^{\text{cont}}\). Once the ultimate value has been achieved, the contacting bodies begin to move relative to each other with realization of kinetic friction which does not depend on the velocity \({\mathbf{w}}\) magnitude and is equal to \({\mathbf{f}}^{\text{ult}}\). Besides, the vector \({\mathbf{f}}^{\text{fr}}\) of this force is collinear with the vector \({\mathbf{w}}\) and the equality

$${\mathbf{f}}^{\text{fr}} = - \mu \left| {{\mathbf{f}}^{\text{cont}} } \right|\frac{{\mathbf{w}}}{{\left| {\mathbf{w}} \right|}}$$
(17)

becomes valid.

This correlation permits one to investigate the processes of the DS buckling during its axial motion. Indeed, assuming that the DS is under conditions of tripping operations and internal axial force F z (s) does not achieve the critical value. Then, the DS moves along its axial line with the axial velocity w z without buckling, the friction forces \(f_{z}^{\text{fr}} \left( s \right)\) are directed along it, and lateral components of these forces equal zero. Next, when the critical axial force \(F_{z}^{\text{cr}} \left( s \right)\) is achieved and slightly exceeded, the DS begins to buckle with the small lateral velocity w y (s), generating small lateral friction forces

$$f_{y}^{\text{fr}} (s) = f_{z}^{\text{fr}} (s) \cdot w_{y} (s)/w_{z}$$
(18)

which impede the DS buckling with the induced velocity w y .

Assuming that the generated friction forces (Eq. (18)) stopped the buckling process, then w y (s) = 0 and the lateral forces \(f_{y}^{\text{fr}} \left( s \right) = 0\). However, the critical axial forces are exceeded (though slightly), the DS remains unstable, and again it begins to buckle, but this time, it selects very small velocity w y (s) in Eq. (18), inducing very small lateral forces \(f_{y}^{\text{fr}} \left( s \right)\), which cannot stop the buckling process. Therefore, it is considered that if in the DS, sliding along its axial line in the bore hole channel, the internal axial forces F z (s) exceed critical value \(F_{z}^{\text{cr}}\), the influence of induced lateral friction forces \(f_{y}^{\text{fr}} \left( s \right)\) on the buckling process can be neglected.

Therefore, the friction force is collinear with the vector \({\mathbf{k}}\) and its value constitutes (Mitchell and Samuel 2009) \(f_{z}^{\text{fr}} = \pm \mu \left| {f_{x}^{\text{cont}} } \right|\), where signs “+”, “−” are selected depending on the direction of DS movement.

Then, the system of vector correlations (1), (5), (14), and (15) can be reduced to the system of three scalar equations, describing equilibrium of internal and external forces:

$$\begin{aligned} \text{d} F_{x} /\text{d} s & = - k_{y} F_{z} + k_{z} F_{y} - f_{x}^{\text{gr}} - f_{x}^{\text{cont}} , \\ \text{d} F_{y} /\text{d} s & = - k_{z} F_{x} + k_{x} F_{z} - f_{y}^{\text{gr}} , \\ \text{d} F_{z} /\text{d} s & = - k_{x} F_{y} + k_{y} F_{x} - f_{z}^{\text{gr}} - f_{z}^{\text{fr}} , \\ \end{aligned}$$
(19)

and three equations of internal moments equilibrium

$$\begin{aligned} \text{d} M_{x} /\text{d} s & = - k_{y} M_{z} + k_{z} M_{y} + F_{y} , \\ \text{d} M_{y} /\text{d} s & = - k_{z} M_{x} + k_{x} M_{z} - F_{x} , \\ \text{d} M_{z} /\text{d} s & = - k_{x} M_{y} + k_{y} M_{x} . \\ \end{aligned}$$
(20)

Take into consideration that, according to the rod theory, bending moments M x , M y are determined by equalities

$$M_{x} = EIk_{x} ,\quad M_{y} = EIk_{y} ,$$
(21)

where E is Young’s modulus; I is the moment of inertia of the DS cross-sectional area. Then, substituting Eq. (21) into the third equation of system (20), one gains

$$\text{d} M_{z} /\text{d} s = 0.$$
(22)

Hence, M z  = const and its value can be calculated with the help of appropriate boundary conditions.

Now, with the introduction of the proposed movable reference frame oxyz and vector (5), representing an analogue of the Darboux vector, it became possible to rewrite the second equation of system (20) in the form:

$$F_{x} = - EIk^{\prime}_{y} - EIk_{x} k_{z} + M_{z} k_{x} .$$
(23)

Thereafter, contact force f cont x is found, using the first equation of system (19),

$$f_{x}^{\text{cont}} = EI\left( {k_{y}^{\prime \prime } + k_{x}^{\prime } k_{z} + k_{x} k_{z}^{\prime } } \right) + M_{z} k_{x}^{\prime } - k_{y} F_{z} + k_{z} F_{y} - f_{x}^{\text{gr}}$$
(24)

In the results, systems (19) and (20) are reduced to three equilibrium equations

$$\begin{aligned} \frac{{\text{d}} F_{y} }{{\text{d}} s} & = EIk_{x} k_{z}^{2} - M_{z} k_{x} k_{z} + EIk_{y}^{\prime } k_{z} + F_{z} k_{x} - f_{y}^{\text{gr}} , \\ \frac{{\text{d}} F_{z} }{{\text{d}} s} & = - EIk_{x} k_{x}^{\prime } - EIk_{y} k_{y}^{\prime } - f_{z}^{\text{gr}} - f_{z}^{\text{fr}} , \\ \frac{{\text{d}} k_{x} }{{\text{d}} s} & = - \frac{{M_{z} }}{EI}k_{y} + k_{y} k_{z} + \frac{1}{EI}F_{y} . \\ \end{aligned}$$
(25)

This system should be supplemented by the equations of the surface Σ, constraining displacements of the DS. They are formulated on the basis of channel surface properties with the use of Eq. (3). Generally, if the line T has a 3D geometry, the surface Σ can be represented as follows:

$$X = X(a,X_{T} ,Y_{T} ,Z_{T} ,u,v),\quad Y = {\text{Y(}}a,X_{T} ,Y_{T} ,Z_{T} ,u,v ) ,\quad Z = {\text{Z(}}a,X_{T} ,Y_{T} ,Z_{T} ,u,v )$$
(26)

However, the most overwhelming obstacle associated with this problem consists of the necessity to simulate friction forces accompanying DS deformation. These forces are statically indeterminate for elastic systems. So, it is expedient to analyze particular cases of the DS movement inside curvilinear channels of simple trajectories and to study their stability. Of particular interest in this avenue of inquiry is incipient buckling of a DS in different segments of a plane circular channel because it adequately depicts the most general regularities of friction forces impact on the buckling phenomena.

4 Bifurcational equations of DS equilibrium in a circular bore hole

Let a DS be lowering in a plane circular bore hole. Then, it slides along the bore hole bottom line and its axis line is a circle of a radius ρ + a, where ρ is the radius of the bore hole axis T and a is the system clearance. In sliding, the DS is subjected to action of gravity (f gr), contact (f cont), and friction (f fr) forces. In consequence of these forces, the DS can be compressed in some segments of its length where it can begin to buckle without losing its contact with the well wall. It is necessary to predict the critical states of the DS and to construct the modes of its stability loss.

In this case, the surface Σ is a torus described by Eq. (26) in the form:

$$X = a \sin v, \quad Y = \rho \left( {1 - \cos u} \right), \quad Z = \rho \sin u + a \sin u \cos v$$
(27)

By their application, the geometric parameters used in Eqs. (8), (11), and (13) are determined:

$$\begin{array}{*{20}l} {a_{11} = (\rho + \cos v)^{2} ,} \hfill & {a_{ 1 2} = 0,} \hfill & {a_{22} = a^{2} ,} \hfill \\ {b_{11} = (\rho + a\cos v)\cos v,} \hfill & {b_{12} = 0,} \hfill & {b_{22} = a,} \hfill \\ {k_{1} = \cos /(\rho + a\cos v),} \hfill & {k_{2} = 1/a} \hfill & {} \hfill \\ \end{array}$$
(28)

The geodesic curvature k geod = k x is calculated from Eq. (9)

$$k^{\text{geod}} = k_{x} = - a(\rho + a\cos v)\left[ {u^{\prime \prime } v^{\prime } - v^{\prime \prime } u^{\prime } - \sin vu^{\prime } \frac{{1 + a^{2} (v^{\prime } )^{2} }}{a(\rho + a\cos v)}} \right].$$
(29)

The normal curvature k norm = k y is determined by the equality

$$k^{\text{norm}} = k^{y} = \cos v\frac{{1 - a^{2} (v^{\prime } )^{2} }}{\rho + a\cos v} + a(v^{\prime } )^{2} .$$
(30)

Angle θ between directions of tangents to lines L and u at the considered point is introduced. Then, sin θ = av′, cos θ = (ρ + a cos v)u′. Here, value u′ is prescribed by the formula:

$$u^{\prime } = \text{d} u/\text{d} s = \pm \frac{{\sqrt {(1 - auv^{\prime } )^{2} } }}{\rho + a\cos v}.$$
(31)

With the use of these formulae, the appropriate components of the gravity force are constructed:

$$\begin{aligned} f_{x}^{\text{gr}} & = {\mathbf{f}}^{\text{gr}} {\mathbf{i}} = - f^{\text{gr}} \sin u\cos v, \\ f_{y}^{\text{gr}} & = {\mathbf{f}}^{\text{gr}} {\mathbf{j}} = f^{\text{gr}} (\sin u\sin v\cos \theta + \cos u\sin \theta ), \\ f_{z}^{\text{gr}} & = {\mathbf{f}}^{\text{gr}} {\mathbf{k}} = f^{\text{gr}} ( - \sin u\sin v\sin \theta + \cos u\cos \theta ). \\ \end{aligned}$$
(32)

Here, the distributed gravity force f gr is defined by the formula

$$f^{\text{gr}} = g(\gamma_{\text{st}} - \gamma_{\text{mud}} )\pi \left( {d_{1}^{2} - d_{2}^{2} } \right)/4$$

where γ st and γ mud are the densities of steel and mud; d 1 and d 2 are the external and internal diameters of the DS tube.

Now, it became possible to formulate constitutive equations of the stated problem relative to unknown variables F y , F z , k x , v, and u. They are deduced on the basis of Eqs. (25), (29), (31), and (32):

$$\left\{ {\begin{array}{*{20}l} {\frac{{\text{d}} F_{y} }{{\text{d}} s} = EIk_{x} k_{z}^{2} - M_{z} k_{x} k_{z} + EIk_{y}^{\prime } k_{z} + k_{x} F_{z} - f^{\text{gr}} (\sin u\sin v\cos \theta + \cos u\sin \theta ),} \hfill \\ {\frac{{\text{d}} F_{z} }{{\text{d}} s} = - EIk_{x} k_{x}^{\prime } - EIk_{y} k_{y}^{\prime } - f^{\text{gr}} ( - \sin u\sin v\sin \theta + \cos u\sin \theta ),} \hfill \\ {\frac{{\text{d}} k_{x} }{{\text{d}} s} = - \frac{{M_{z} }}{EI}k_{y} + k_{y} k_{z} + \frac{1}{EI}F_{y} ,} \hfill \\ {\frac{{\text{d}} v}{{\text{d}} s} = v^{\prime } ,} \hfill \\ {\frac{{\text{d}} (v^{\prime } )}{{\text{d}} s} = \frac{1}{{a(\rho + a\cos v)u^{\prime } }}k_{x} - \sin v\frac{{1 + a^{2} (v^{\prime } )^{2} }}{a(\rho + a\cos v)} + \frac{{u^{\prime \prime } v^{\prime } }}{{u^{\prime } }},} \hfill \\ {\frac{{\text{d}} u}{{\text{d}} s} = \frac{{\sqrt {1 - a^{2} (v^{\prime } )^{2} } }}{(\rho + a\cos v)}.} \hfill \\ \end{array} } \right.$$
(33)

This system with appropriate boundary conditions, determining external axial forces and torques, can be used for modeling nonlinear elastic bending of a DS in the circular channel cavity of a bore hole. Assuming that in the general case the DS can bend and take new deformed shapes remaining in contact with the bore hole wall throughout its length. If during this shape transformation small elastic displacements of the DS correspond to small increments of the external force perturbation, then the considered equilibrium state is stable. In the vicinity of this state, the linear differential equations deduced from the nonlinear system (33) with the use of linearization procedure are not degenerate and have only one solution. However, if the DS is loaded further, the coefficients of the linearized equations continue to evolve and the state can be reached when these equations become degenerate and acquire an additional (bifurcating) solution along with the initial one. Because of this, the state reached is critical (unstable) and the bifurcating solution represents the buckling mode.

The peculiarity of the nonlinear problem stated for the buckling of a DS in the circular channel is that the tube does not change its shape in the subcritical states and so the coefficients of the linearized equations of the equilibrium change owing to the step-by-step enlargement of the axial force F z (s) with the external load increase. In that event, the stated problem is analogous to the problem of Eulerian stability of a rectilinear rod because it is also associated with the eigenvalue search and eigenmode construction.

To identify the critical equilibrium and the stability loss of the DS moving along the bore hole bottom, system (33) should be linearized in the vicinity of the considered state and its eigenvalues and eigenmodes should be found. During the prescribed movement, the static and kinematic conditions F z  = F z (S), u = u 0 + s/(ρ + a), u′ = 1/(ρ + a), u′′ = 0, v = 0, v′ = 0, v′′ = 0, k x  = 0, k y  = 1/(ρ + a), k z  = 0 are satisfied. As a consequence of bifurcational deformation, the system parameters assume small variations δv, δk x , δF y . They are calculated with the help of linear homogeneous equations

$$\left\{ \begin{array}{*{20}l} {\frac{\text{d} }{{\text{d} s}}\delta F_{y} = F_{z} \delta k_{x} - f^{\text{gr}} \sin \left( {u_{0} + \frac{s}{\rho + a}} \right)\delta v + f^{\text{gr}} a\cos \left( {u_{0} + \frac{s}{\rho + a}} \right)\delta v^{\prime } ,} \hfill \\ {\frac{\text{d} }{{\text{d} s}}\delta v = \delta (v^{\prime } ),} \hfill \\ {\frac{\text{d} }{{\text{d} s}}\delta (v^{\prime } ) = - \frac{1}{a(\rho + a)}\delta v + \frac{1}{a}\delta k_{x} ,} \hfill \\ {\frac{\text{d} }{{\text{d} s}}\delta k_{x} = \frac{1}{EI}\delta F_{y} ,} \hfill \\ \end{array} \right.$$
(34)

arising from system (33) after taking into account that δu = 0, δk y  = 0, δF z  = 0.

Coefficient F z (s) in the first equation is determined with the help of the second equation of system (33). It results in

$$\frac{{\text{d}} F_{z} }{{\text{d}} s} = - f_{z}^{\text{gr}} - f_{z}^{\text{fr}} = - f^{\text{gr}} \pm \mu f^{\text{cont}} .$$
(35)

Here, signs ± are selected for the operations lowering and hoisting of the DS, contact force f cont is established through the use of the first equation of system (19) in the form:

$$f^{\text{cont}} = - \frac{1}{\rho + a}F_{z} - f_{x}^{\text{gr}} = - \frac{1}{\rho + a}F_{z} + f^{\text{gr}} \sin u$$
(36)

Substituting Eq. (36) into Eq. (35) gives the linear differential equation of the first order:

$$\frac{{\text{d}} F_{z} }{{\text{d}} u} \pm \mu F_{z} = - (\rho + a)f^{\text{gr}} \cos u \pm \mu (\rho + a)f^{\text{gr}} \sin u$$
(37)

Let u = U, s = S, then

$$F_{z} (u) = \frac{{(\rho + a)f^{\text{gr}} }}{{1 + \mu^{2} }}\left[ { \pm 2\mu (\cos u - \cos U) - (1 - \mu^{2} )(\sin u - \sin U)} \right] + F_{z} (U),$$
(38)

where F z (U) is the compressive force applied to the DS at its lower end u = U; U is the u coordinate value at s = S.

Four first-order differential Eq. (34) are equivalent to one homogeneous fourth order equation

$$\delta v^{\text{IV}} + \left[ {\frac{1}{a(\rho + a)} - \frac{{F_{z} }}{EI}} \right]\delta v^{\prime \prime } - \frac{{f^{\text{gr}} }}{EI}\cos \left( {u_{0} + \frac{s}{\rho + a}} \right)\delta v^{\prime } + \left[ {\frac{{f^{\text{gr}} }}{aEI}\sin \left( {u_{0} + \frac{s}{\rho + a}} \right) - \frac{{F_{z} }}{aEI(\rho + a)}} \right]\delta v = 0.$$
(39)

It is derived from the assumption that in buckling the friction force f fr is directed along the DS axis line. To find states of bifurcational buckling of the DS, the Sturm–Liouville problem (eigenvalue problem) should be formulated for Eq. (39). Its statement is based on the finite difference method and the construction of the corresponding matrix of algebraic equation coefficients. The matrix elements depend on multiplier F z (s) before the δv value in Eq. (39) which in its turn is determined by the boundary force F z (U) and the distributed friction force in Eq. (38). Then, the critical (bifurcational or eigen) value of the external force F z (U) applied at the end u = U (i.e., s = S) is found by its varying through the trial-and-error method application.

It is notable that the torque M z is not present in Eq. (39). This means that critical states of DSs in circular bore holes do not depend on M z values (as well as in rectilinear ones (Gulyayev et al. 2014)).

5 Critical buckling of a DS moving inside a channel of a circular bore hole

The primary objective of this paper lies in investigation of the influence of friction forces on the stability of a DS moving inside a curvilinear bore hole. Notwithstanding the fact that the simplest trajectory in the shape of a circular arc is chosen for the bore hole configuration, this example permits us to trace the principal peculiarities of the buckling processes proceeding in curve channels. It consists in the possibility to generate localized buckling wavelets in the most unexpected places of the hole length. Additional uncertainty is contributed to this situation by axial friction forces generated during lowering or hoisting the DS. It is considered that the motion is slow, and inertia forces can be disregarded. Then, the DS can be partially compressed and partially stretched by distributed variable gravity forces f gr(s), variable frictional forces f fr(s), and axial force F z (U) applied at the DS end s = S with an angular coordinate u = U. So, Eq. (39) cannot be solved by analytical methods.

To find bifurcational states of the DS, Eq. (39) was algebraized by the finite difference method for different values of F z (U) force, and the states when the matrix of linear algebraic equations became degenerate were assumed to be critical. At this state, the eigenfunction F cr z (s) and eigenmode δv(s), representing the shape of the buckling DS, were constructed.

In numerical analyses, the DS section 0 ≤ s ≤ S was divided into 500 finite difference pieces. The calculation results were tested with a doubled number of pieces. The checking confirmed the adequate precision of the computations.

In order to trace the influence of friction forces on the DS buckling, every calculation example was examined with the use of frictionless and frictional statements. The analytic results are compared.

In Fig. 4, the geometric scheme of the DS, lying inside the lower quarter of a circular channel, is presented. At its lower end, the DS axis is tangent to the horizontal, its spanning angle φ = U − u 0 and position of the top end s = 0 were varied. The DS is pinned at both its ends. Influences of the DS length S, radius ρ, clearance a, and friction force f fr on critical values F cr z (U) were examined for the next values of the system parameters: E = 2.1 × 1011 Pa, γ st = 7.8 × 103 kg/m3, γ mud = 1.3 × 103 kg/m3, d 1 = 0.1683 m, d 2 = 0.1483 m, μ = 0.2. Every example was studied for the cases f fr = 0 and f fr ≠ 0 and clearance values a = 0.5, 0.1, 0.05, 0.03 m. Although the first value of a is not practicable, it is included into analysis to reveal the trend of critical states evolving with clearance change.

Fig. 4
figure 4

Schematic of the circular DS segment

Full size image

The findings of the calculations evidence that if the DS is rather short, the clearance a is not small, and the radius ρ is large, the DS buckles similarly to the Eulerian beam under critical axial forces P cr = π 2 EI/S 2 and they are unaffected by the hole friction. However, the situation varies radically with the length S and angle φ enlargement. As it becomes longer, the system begins to exhibit properties of singularly perturbed structures and to localize unpredictably its short buckling waves in boundary layers (see Fig. 5a for frictionless case) or in inner zones with the larger values of compressive axial force (see Fig. 5b for the case of frictional interaction). In the theory of waves, such modes are termed the wave packages (Crawford 2011), in the applied mathematics they have come to known as harmonic wavelets.

Fig. 5
figure 5

Buckling of the DS in an inclined circular channel of a bore hole. a Frictionless model of the immovable DS. b Frictional model of the moving DS

Full size image

In Table 1, the calculation results for the 1200-m DS inserted into the circular bore hole with a radius ρ of 1146 m are given. The spanning angle for this example is \(\varphi = 60^{\text{o}}\). It can be seen that the DS buckling character depends on the character of the F z (s) function distribution and its external value locations. Thus, if a = 0.5 m and f fr = 0, the DS is stretched at its top end s = 0 and compressed at its lower one s = S. The critical value F cr z (S) = −98.33 kN of the external compressive axial force F z (s) applied at the pinned end s = S is maximal throughout its length. So, the buckling wavelet is localized in the boundary zone, justifying the properties of singularly perturbed systems (Chang and Howes 1984; Elishakoff et al. 2001; Gulyayev et al. 2014).

Table 1 Functions of the critical axial force F cr z (s) and buckling modes δv(s) for the case S = 1200 m, ρ = 1146 m, \(\varphi = 60^{\text{o}}\)
Full size table

The situations change if f fr ≠ 0 (see position 1 in Table 1). Then, the maximal compressive value F fr z  = −93.97 kN of the axial force shifts to the bore hole interiority and the system becomes singularly perturbed inside its length. Then, the buckling wavelet also displaces inside the DS segment.

If a ≤ 0.1 m (positions 2–4 in Table 1), the DSs buckle under the action of greater forces and the smaller a is, the more complicated is the mode of stability loss. It becomes also harder to predict the zone of the buckling localization in the presence of friction forces. Besides, the buckled zone propagates through a larger region of the DS length and at a = 0.03 m the boundary effect drifts from the right end of the diagram to its left end. As this takes place, the buckling mode pitch (λ—pitch of the eigenmode wavelet) becomes smaller and smaller. Thus, the wavelet pitch λ ≈ 26 m for a = 0.5 m and it is 10.5 m for a = 0.03 m.

Now, consider the instance when the bore hole channel arc is symmetrically disposed relative to the vertical (Fig. 6). The computations are fulfilled for the values S = 2400 m, ρ = 1146 m, \(\varphi = 120^{\text{o}}\). If the friction effects are not taken into account, then, the representative functions, determining the DS buckling, can be obtained by simple symmetric prolongations relative to the vertical of the appropriate functions represented in Table 1 for the asymmetric arc (compare Figs. 5a, 6a). As this takes place, the critical values of boundary forces F cr z (s) given in Table 1 for a frictionless asymmetric hole become equal to critical values F cr z (S/2) for the corresponding DSs in Table 2.

Fig. 6
figure 6

Buckling of DS in a symmetric circular channel of a directed bore hole. a Frictionless model of the stationary DS. b Frictional model of the moving DS

Full size image
Table 2 Functions of the critical axial force F cr z (s) and buckling modes δv(s) for the case S = 2400 m, ρ = 1146 m, φ = 120∘
Full size table

The presence of friction effects leads to shifting the buckling wavelet positions in both cases (see Figs. 5b, 6b) but the maximal values of the appropriate critical functions F cr z (S) (located in the wavelets zones) and wavelet pitches remain approximately equal, though shapes of their buckling modes acquire some distinctions.

It is of interest that if the DS length is larger than the wavelet extension, then the critical value of F cr z (s) does not depend on the DS size and with the enlargement of the spanning angle φ the noted peculiarities come into particular prominence. These conclusions are verified by Table 3 charted for \(\varphi = 180^{\text{o}}\), ρ = 1146 m, and S = 3600 m.

Table 3 Functions of the critical axial force F cr z (s) and buckling modes δv(s) for the case S = 3600 m, ρ = 1146 m, ϕ = 180°
Full size table

So then, juxtaposition of these results with the data displayed in Table 3 for \(\varphi = 180^{\text{o}}\) enables us to infer that in the case of the absence of friction the buckling wavelets are localized in the central zone of the DS length, they are identical for every value of clearance a, and are realized under similar values of axial force F cr z achieved at the middle point s = S/2. It is evident that in this case, the buckling effect does not depend on the boundary conditions at the ends s = 0 and s = S. As this takes place, the pitches λ of the eigenmode half-harmonics equal the distances between two adjacent zeros do not demonstrate essential differences. Their values at S = 2400 m and 3600 m (\(\varphi = 120^{\text{o}} {\text{ and 180}}^{\text{o}}\)) are listed in Table 4. They are seen to be invariant if the bifurcation buckling zone is small and they diminish with a decrease in a. In the cases of frictionless contact of the DS with the bore hole wall, the λ values are identical for both length S at clearance values a = 0.5 m and 0.1 m, but their distinction becomes conspicuous at a = 0.05 m and a = 0.03 m.

Table 4 Extreme values of axial force F cr z (s) and wavelet pitches λ at critical states of the DSs
Full size table

The influence of the friction forces on buckling modes is more appreciable. They cause not only the diversification of the buckling zone positioning but lead to these zones widening as well (see Table 3). Besides, in the every zone limits, the pitches of conventional harmonics become also variable (see Table 4 for f fr ≠ 0).

It is intriguing to compare the obtained results with the analytic solution deduced for the limiting case when the curvature radius ρ tends to infinity in the absence of friction effects. Then, it is valid to assume that the rectilinear bore hole is horizontal and the infinitely long DS is prestressed by the axial force F z (s) remaining unchanged throughout its length. In this event, the critical values of force F z (s) and pitch λ are determined by equalities (Cunha 2004; Mitchell 2008; Gulyayev et al. 2014):

$$F_{z}^{\text{cr}} = 2\sqrt {EIf^{\text{gr}} /a} ,\quad \lambda^{\text{cr}} = \pi \sqrt[4]{{EIa/f^{\text{gr}} }}.$$

Their bracketed values for the corresponding states are tabulated in Table 4. It can be seen that the calculated results are closely related for large values of clearance a and the difference between them grows with a reduction in a.

Summarizing obtained results, one can recognize that the found regularities of the realization of critical states and critical modes evolving are associated, in a large extent, with the circular geometry of a bore hole and invariability of its curvature radius ρ. One might expect that the considered phenomena will be far more intricate for the wells with a variable curvature both in the cases of frictionless contacts and when the frictional interactions occur.

Noteworthy also is the remark in relation to the influence of the bore hole geometry imperfections on the buckling process. The geometry imperfections entail enlargement of distributed friction forces and axial force F z (s), on the other hand, the geometry distortions result in a change of the curvature radius ρ. Both these factors imply the essential effect on the buckling process and should be specially studied.

6 Conclusions

  1. (1)

    On the basis of the theory of curvilinear elastic rods, a new statement of the problem of critical buckling of DSs in 3D curvilinear bore holes with allowance made for friction effects is suggested. It is assumed that a DS does not lose its stability in the state of its stationary equilibrium but it can buckle during its axial movement when friction forces and their directions can be easily determined.

  2. (2)

    The fourth order system of linearized differential equations of the DS buckling in a curvilinear channel is deduced with the use of differential geometry methods, theory of channel surfaces, and classical mechanics of systems with nonlinear constraints. The method of numerical solutions of this system is elaborated.

  3. (3)

    The problem is shown to belong to the singularly perturbed class, and for this reason, the buckling modes have the shapes of localized harmonic wavelets.

  4. (4)

    As an example, the phenomena of DS stability in circular channels are studied. The cases of absence and presence of friction effects are considered. It is demonstrated that the friction forces stimulate redistribution of internal axial forces in the DSs and result in essential shifting of the buckling wavelet localizations, bringing the buckling phenomenon to the less predictable type.

  5. (5)

    One might suppose that the considered phenomena will be far more complicated for the well with variable curvatures both in the cases of frictionless contacts and when the frictional interactions take place.