Nonlinear motions of a flexible rotor with a drill bit: stick-slip and delay effects

Abstract

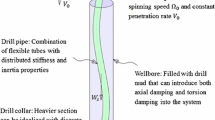
In this article, a discrete model of a drill-string system is developed taking into account stick-slip and time-delay aspects, and this model is used to study the nonlinear motions of this system. The model has eight degrees-of-freedom and allows for axial, torsional, and lateral dynamics of both the drill pipes and the bottom-hole assembly. Nonlinearities that arise due to dry friction, loss of contact, and collisions are considered in the development. State variable dependent time delays associated with axial and lateral cutting actions of the drill bit are introduced in the model. Based on this original model, numerical studies are carried out for different drilling operations. The results show that the motions can be self-exited through stick-slip friction and time-delay effects. Parametric studies are carried out for different ranges of friction and simulations reveal that when the drill pipe undergoes relative sticking motion phases, the drill-bit motion is suppressed by absolute sticking. Furthermore, the sticking phases observed in this work are longer than those reported in previous studies and the whirling state of the drill pipe periodically alternates between the sticking and slipping phases. When the drive speed is used as a control parameter, it is observed that the system exhibits aperiodic dynamics. The system response stability is seen to be largely dependent upon the driving speed. The discretized model presented here along with the related studies on nonlinear motions of the system can serve as a basis for choosing operational parameters in practical drilling operations.

Appendix: Model coefficients and development

The kinetic energy of the rotating system shown in Fig. 2 can be written as

(26)

where m ₁ and m ₂ are the respective translational disk inertias for Disks 1 and 2, and J ₁ and J ₂ are the respective rotary disk inertias for Disks 1 and 2. An overdot indicates a derivative with respect to t. Assuming linear elasticity and neglecting the buoyancy force from the drill mud, the potential energy of the rotating structure can be constructed as

(27)

where EA, GI ₀, and EI _x are the associated mechanical properties of the drill-pipe’s cross section and g=9.8 m/s² is the acceleration due to gravity. Here, a prime denotes a partial derivative with respect to z. Making use of shape functions and boundary conditions for each pipe, the spatial integrations in Eq. (27) are carried out, as detailed later in this appendix. To account for the viscous damping of the drill mud acting on each disk, the Rayleigh’s dissipation function is used and obtained as

(28)

where c _a , c _t , and c _b are the viscous damping coefficients associated with axial, bending, and torsional motions, respectively.

The discrete translational inertia mass and rotary inertia used in Eq. (26) take the forms

(29)

The corresponding geometry parameters for a cross-section of drill pipe are given in Eq. (27).

$$ \begin{cases} A=\frac{\pi}{4} (D_{p1}^2-D_{p2}^2) \\[3pt] I_0=\frac{\pi}{32} (D_{p1}^4-D_{p2}^4 )\\[3pt] I_x=\frac{\pi}{64} (D_{p1}^4-D_{p2}^4 ) \end{cases} $$

(30)

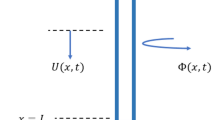
The axial displacement field u(z,t) of the drill pipe used in Eq. (27) is defined as follows

$$ u(z,t)= \begin{cases} a_1 z+a_2, & 0 \leq z \leq\frac{L_p}{2}\\[3pt] b_1 z+b_2, & \frac{L_p}{2}<z \leq L_p \end{cases} $$

(31)

where the coefficients a _i , b _i (for i=1,2) are functions of time through the displacement variables x ₁ and x ₂. The boundary conditions are then

$$ \begin{cases} EA u'(t,0)=H_0\\[3pt] u(t,z\rightarrow\frac{L_p}{2}^-)=u(t,z\rightarrow\frac {L_p}{2}^+)=x_1\\[3pt] u(t,L_p)=x_2 \end{cases} $$

(32)

On substituting these boundary conditions into Eq. (31), u′ can be obtained as follows:

$$ \frac{\partial u}{\partial z}= \begin{cases} \frac{H_0}{EA}, & 0 \leq z \leq\frac{L_p}{2}\\[3pt] \frac{z_2-z_1}{L_p/2}, & \frac{L_p}{2}<z \leq L_p \end{cases} $$

(33)

Following the same procedure as that for the axial motions, the torsional displacement field θ(z,t) of the drill pipe can be defined as

$$ \theta(z,t)= \begin{cases} a_1 z+a_2, & 0 \leq z \leq\frac{L_p}{2}\\[3pt] b_1 z+b_2, & \frac{L_p}{2}<z \leq L_p \end{cases} $$

(34)

with the associated boundary conditions being

$$ \begin{cases} \theta(t,0)=\varOmega_0 t\\[3pt] \theta(t,z\rightarrow\frac{L_p}{2}^-)=\theta(t,z\rightarrow\frac {L_p}{2}^+)=\varphi_1\\[3pt] \theta(t,L_p)=\varphi_2 \end{cases} $$

(35)

Subsequently, θ′ can be obtained as

$$ \frac{\partial\theta}{\partial z}= \begin{cases} \frac{\varphi_1-\varOmega_0 t}{L_p/2}, & 0 \leq z \leq\frac{L_p}{2}\\[3pt] \frac{\varphi_2-\varphi_1}{L_p/2}~, & \frac{L_p}{2}<z \leq L_p \end{cases} $$

(36)

The bending displacement field in the x direction can be defined by using polynomials as follows:

$$ v(z,t)= \begin{cases} a_1 z^3+a_2 z^2 +a_3 z+a_4, & 0 \leq z \leq\frac{L_p}{2}\\[3pt] b_1 z^3+b_2 z^2 +b_3 z+b_4, & \frac{L_p}{2}<z \leq L_p \end{cases} $$

(37)

Here, the coefficients a _i , b _i (for i=1,2,3,4) are functions of time through the displacement variables x ₁ and x ₂. The boundary conditions are of the form

$$ \begin{cases} v(t,0)=0\\[3pt] v''(t,0)=0\\[3pt] v(t,z\rightarrow\frac{L_p}{2}^-)=x_1\\[3pt] v(t,z\rightarrow\frac{L_p}{2}^+)=x_1\\[3pt] v'(t,z\rightarrow\frac{L_p}{2}^-)=v'(t,z\rightarrow\frac{L_p}{2}^+)\\[3pt] v''(t,z\rightarrow\frac{L_p}{2}^-)=v''(t,z\rightarrow\frac {L_p}{2}^+)\\[3pt] v(t,L_p)=x_2\\[3pt] v''(t,L_p)=0 \end{cases} $$

(38)

After substituting Eq. (38) into Eq. (37), the different coefficients are obtained and v″ can be determined as

$$ \frac{\partial^2 v}{\partial z^2}= \begin{cases} \frac{24(x_1-\frac{x_2}{2})}{L_p^3}z, & 0 \leq z \leq\frac{L_p}{2}\\[3pt] \frac{24(x_1-\frac{x_2}{2})}{L_p^3}(L_p-z), & \frac{L_p}{2}<z \leq L_p \end{cases} $$

(39)

Bending in the y direction is symmetric to that along the x direction, and on this basis, w″ can be written as

$$ \frac{\partial^2 w}{\partial z^2}= \begin{cases} \frac{24(y_1-\frac{y_2}{2})}{L_p^3}z, & 0 \leq z \leq\frac{L_p}{2}\\[3pt] \frac{24(y_1-\frac{y_2}{2})}{L_p^3}(L_p-z), & \frac{L_p}{2}<z \leq L_p \end{cases} $$

(40)

After substituting Eqs. (33) to (40) into Eq. (27) and constructing the potential energy, the result is

(41)

After making use of Lagrange’s equations

$$ \frac{d}{dt} \frac{\partial L}{\partial\dot{q_i}}-\frac{\partial L}{\partial q_i}+ \frac{\partial D}{\partial\dot{q_i}}=Q_{q_i} \\ $$

(42)

where the Lagrangian L is L=T−V and q _i , which are identified as x _i ,y _i ,z _i ,φ _i for i=1,2, are the generalized coordinates used to describe the motions of the two disks. The generalized forces $Q_{q_{i}}$ contain contributions from the centrifugal forces and contact forces as shown in Fig. 2. On substituting Eqs. (26), (28), and (41) into Eq. (42), one obtains the equations of motion as shown in Eq. (1), where the coefficients k _i are as follows

$$ k_a=\frac{2EA}{L_p},\qquad k_t= \frac{2GI_0}{L_p},\qquad k_b=\frac{48EI_x}{L_p^3} $$

(43)