Modeling the dynamics of soil erosion and vegetative control — catastrophe and hysteresis

Abstract

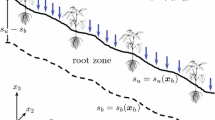
Wildfire events and anthropogenic activities such as agriculture and livestock grazing may denude the landscape from vegetation cover, resulting in systems prone to soil loss and degradation. Soil dynamics is an intricate process balanced between pedogenesis, which is a relatively slow process, and erosion which depends on many inert (e.g., soil texture, slope, precipitation, and wind) and biological factors such as vegetation properties, grazing intensity, and human disturbance. We develop here a theoretical model of the global dynamics of the interactions between vegetation and soil. Assuming a double feedback between them—plants control erosion, and soil availability facilitates plants growth—a system of nonlinear differential equations is derived, and the outcomes are investigated. The range of realistic parameter values were taken from the literature. Complex properties emerge from this model. For some ranges of parameter values, the model predicts one of two types of steady states—full recovery of vegetation cover or a degraded barren system. For another range of parameter values, bistability appears. We identify the parameter combinations which determine the qualitative behavior of the system and the threshold values beyond which the system becomes bistable. The model predicts that certain ecosystems are highly stable. Others might be bistable transitioning between these two states through perturbations. Therefore, the possibly of hysteresis as parameters vary arises, as well as the ability of the system to shift between steady states, possibly leading to sudden and dramatic changes.

Appendices

Appendix 1: Model analysis

Assumptions

We impose some assumptions on the nonlinearities f and g, which are sufficiently general to encompass any specific functional forms that one would use.

f(s) is a C¹ function on [0,∞) satisfying

$$ f(0)=0,\underset{s\to \infty }{ \lim }f(s)=1 $$

(A1)

$$ f\hbox{'}(s)>0\ \mathrm{for}\ \mathrm{all}\ \mathrm{s}>0,\kern0.5em \underset{s\to \infty }{ \lim } sf\hbox{'}(s)=0 $$

(A2)

g(v) is a C¹ function on [0,∞) satisfying

$$ g(0)=1,\underset{v\to \infty }{ \lim }g(v)=0 $$

(A3)

$$ -M<g\hbox{'}(v)<0\kern0.5em \mathrm{for}\ \mathrm{all}\ v>0 $$

(A4)

Nondimensionalization

To reduce the complexity of the model (1),(2), we define the nondimensional variables:

$$ v= cV,s= aS,\tau = rt $$

and the nondimensional parameters:

$$ \eta =\frac{\varepsilon }{r},\beta =\frac{a\sigma}{\varepsilon },\chi = cK $$

The model then becomes:

$$ \frac{d v}{d\tau}=v\cdot \left(1-\frac{v}{\chi f(s)}\right) $$

(A5)

$$ \frac{d s}{d\tau}=\eta \left(\beta -s\cdot g(v)\right) $$

(A6)

Equilibria

Equilibria of (A5),(A6) are given by equating derivatives with respect to time to zero

The vegetation-free equilibrium is given by:

$$ {v}^{*}=0,{s}^{*}=\beta $$

Nontrivial equilibria are solutions (s, v) of the algebraic system v = χf(s), g(v)s = β Substituting the first equation in to the second one, we reduce the above system to an equation for s:

$$ sg\left(\chi f(s)\right)=\beta . $$

(A7)

Defining the function

$$ F(s)= sg\left(\chi f(s)\right) $$

we can write (A7) as

$$ F(s)=\beta . $$

(A8)

We thus have

Lemma 1

Non-trivial equilibria of (A5),(A6) are in one-to-one correspondence with solutions of (A8), with each solution s ^∗ of (A8) corresponding to an equilibrium (s ^∗,v ^∗) = (s ^∗,χf(s ^∗)) of (A5),(A6).

Stability of equlibria

The Jacobian at a stationary solution (s ^∗ ,v ^∗) is given by:

$$ J=\left(\begin{array}{cc}\hfill 1-\frac{2{v}^{*}}{\chi f\left({s}^{*}\right)}\hfill & \hfill \frac{v^{*}}{\chi}\frac{f\hbox{'}\left({s}^{*}\right)}{f{\left({s}^{*}\right)}^2}\hfill \\ {}\hfill -\eta g\hbox{'}\left({v}^{*}\right){s}^{*}\hfill & \hfill -\eta g\left({v}^{*}\right)\hfill \end{array}\right) $$

For the vegetation-free equilibrium, we have

$$ J\left|{}_{v^{*}=0,{s}^{*}=\frac{\alpha }{\eta g(0)}}\right.=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ {}\hfill -\eta \beta \frac{g\hbox{'}(0)}{g(0)}\hfill & \hfill -\eta g(0)\hfill \end{array}\right) $$

with eigenvalues 1 and −ηg(0) < 0, so we have a saddle point, which is unstable (Edelstein-Keshet 2005).

For nontrivial equilibria, we have, using the relation v ^∗ = χf(s ^∗),

$$ J=\left(\begin{array}{cc}\hfill -1\hfill & \hfill \chi f\hbox{'}\left({s}^{*}\right)\hfill \\ {}\hfill -\eta g\hbox{'}\left(\chi f\left({s}^{*}\right)\right){s}^{*}\hfill & \hfill -\eta g\left(\chi f\left({s}^{*}\right)\right)\hfill \end{array}\right) $$

so that tr(J) = − 1 − ηg(v*) < 0 and det(J) = η[g(χf(s*) + χf ' (s*)g ' (χf ' (s*)s*)] = ηF ' (s*)

We then conclude that:

Lemma 2

A nontrivial stationary solution (s ^∗,v ^∗) is stable if F ' (s ^∗) > 0 and unstable if F ' (s ^∗) < 0.

Multiplicity of equilibrium solutions

Lemmas 1 and 2 reduce the study of the existence, multiplicity, and stability of stationary solutions of (A5),(A6) to the study of the zeros of the scalar function F(s), which can thus be approached by tools of elementary calculus. We show that at least one nontrivial equilibrium always exists and that the equilibrium is unique and stable when χ is sufficiently small and also when β. is either very small or very large. On the other hand, we show that multiple solutions exist for some parameter values, under certain conditions on the nonlinearities f,g.

Theorem 1

• (i) For any values of χ, β. and η, (A5),(A6) has at least one nontrivial equilibrium solution.

• (ii) For any value of χ, there exist a,b > 0 such that if β < a or β > b _, then (A5),(A6) has a unique equilibrium solution, which is stable.

• (iii) There exists a value χ ₀ such that if χ < χ ₀, then there is a unique solution of (A5),(A6) for all values of β, η _, which is stable.

• (iv) Define the quantities:

$$ A=\underset{v>0}{ \sup}\frac{v\left|g\hbox{'}(v)\right|}{g(v)} $$

$$ B=\underset{s>0}{ \inf}\frac{f(s)}{sf\hbox{'}(s)} $$

• If B ≥ A, then (A5),(A6) has a unique solution for all values of χ, β, η which is asymptotically stable.

• -If A > B, then there is a range of values of χ, β, η for which (A5),(A6) has at least three solutions, at least one of which is unstable.

Proof: (i) We note that

$$ F(0)=0 $$

(A9)

and since, using (A1) $\underset{s\to \infty }{ \lim }g\left(\chi f(s)\right)=g\left(\chi \right)>0$ _, we have

$$ \underset{s\to \infty }{ \lim }F(s)=\underset{s\to \infty }{ \lim } sg\left(\chi f(s)\right)=+\infty $$

(A10)

From (A9),(A10) and the intermediate value theorem, we have that (A8) has at least one solution for any values of α, η.

(ii) We have F ' (s) = g(χf(s)) + χsg ' (χf(s))f ' (s)_. So F ' (0) = g(χf(0)) > 0

Hence, there exists s ₁ > 0 such that

$$ s\in\ \left[0,{s}_1\right]\Rightarrow F\hbox{'}(s) > 0 $$

(A11)

Let

$$ a=\underset{s\ge {s}_1}{ \inf }F(s) $$

(A12)

Since F is positive and satisfies (A10), we have a > 0. Now if β < a and s ^∗ is a solution of (A8), then by (A12), we have s ^∗ < s ₁, and since by (A11), F is increasing on [0, s ₁], this solution must be unique. By (A11), we have F ' (s*) > 0_, so that Lemma 2 implies that the corresponding equilibrium is stable. We therefore have uniqueness and stability of the nontrivial equilibrium when β < a.

We note also that, using (A1),(A2),(A3), we have

$$ \underset{s\to \infty }{ \lim }F\hbox{'}(s)=g\left(\chi \right)+\chi g\hbox{'}\left(\chi \right)\cdot \underset{s\to \infty }{ \lim } sf\hbox{'}(s)=g\left(\chi \right)>0 $$

so there exists s ₂ such that

$$ s\in \left[{s}_2,+\infty \right)\Rightarrow F\hbox{'}(s)>0 $$

(A13)

Let

$$ b=\underset{s\in \left[0,{s}_2\right]}{ \sup }F(s) $$

(A14)

If β > a and s* is a solution of (A8), then by (A14), we have s* > s ₂ and since, by (A13), F is increasing on [s₂, +∞), this solution is unique. By (A13), we have F ' (s*) > 0_, so Lemma 2 implies that the corresponding equilibrium is stable. We therefore have uniqueness and stability of the nontrivialequilibrium when β > a.

(iii) Let

$$ {m}_1=\underset{s>0}{ \sup}\left| sg\hbox{'}\left(\chi f(s)\right)f\hbox{'}(s)\right| $$

By (A2),(A4) m ₁ is finite. Since f is increasing and g is decreasing, we have for all s ≥ 0,

$$ 0<f(s)\le 1\Rightarrow g\left(\chi f(s)\right)\ge g\left(\chi \right) $$

Hence, for all s ≥ 0,

$$ F\hbox{'}(s)\ge g\left(\chi \right)-\chi \left| sg\hbox{'}\left(\chi f(s)\right)f\hbox{'}(s)\right|\ge g\left(\chi \right)-\chi {m}_1 $$

(A15)

Since g(χ) − χm ₁ → 1 as χ → 0, we can choose χ ₀, so that g(χ) − χm ₁ > 0 for χ ∈ [0, χ ₀], so that (A15) implies F’(s) > 0 for all s ≥ 0, which implies uniqueness of the solution of (A8) for all values of β as well as, by Lemma 2, the stability of the corresponding equilibrium.

(iv) If F’(s) > 0 for all s, then the solution of (A8) is unique for all β, η, and, by Lemma 2, it is stable. On the other hand, assume F’(s ₀) < 0 for some s ₀ > 0. Since by (A11) and (A13) we know that for very small and very large values of s > 0 we have F’(s) > 0, there exist s ⁻₀  < s ₀ < s ⁺₀ such that F’(s) < 0 for s ∈ (s ⁻₀ , s ⁺₀ ) and F ' (s ⁻₀ ) = F ' (s ⁺₀ ) = 0. F is thus decreasing in the interval [s ⁻₀ , s ⁺₀ ]. Assume β ∈ (F(s ⁻₀ ), F(s ⁺₀ ))_. Then (A8) has a solution s ^* ∈ (s ⁻₀ s ⁺₀ ) which, by Lemma 2, is unstable. Since F(0) = 0 and F(s ⁻₀ ) > β, (A8) also has a solution in (0, s ⁻₀ )_, and since F(s ⁺₀ ) < β and we have (A10), (A8) also has a solution in (s ⁺₀ , ∞). Thus, we have shown that, if F ' (s ₀) < 0 for some s _{0 ,} then (A8) has at least three solutions for some range of values of β.

Let us show that, if B ≥ A, then F’(s) > 0 for all s and any value of χ. Indeed, the condition F’(s) < 0 can be written

$$ g\left(\chi f(s)\right) + \chi sg\hbox{'}\left(\chi f(s)\right)f\hbox{'}(s) < 0 $$

or equivalently

$$ \chi f(s)\frac{\left|g\hbox{'}\left(\chi f(s)\right)\right|}{g\Big(\left(\chi f(s)\right)}>\frac{f(s)}{sf\hbox{'}(s)} $$

(A16)

If B ≥ A, then we have, for all s > 0

$$ \chi f(s)\frac{\left|g\hbox{'}\left(\chi f(s)\right)\right|}{g\left(\chi f(s)\right)}\le \underset{v>0}{ \sup}\frac{v\left|g\hbox{'}(v)\right|}{g(v)}=A. $$

$$ \frac{f(s)}{sf\hbox{'}(s)}\ge \underset{s>0}{ \inf}\frac{f(s)}{sf\hbox{'}(s)}=B $$

So that B ≥ A implies that (A16) cannot hold, hence F’(s) > 0 for all s.

On the other hand, if A > B, then we can find some values of v, s > 0 such that $\frac{v\left|g\hbox{'}(v)\right|}{g(v)}>\frac{f(s)}{sf\hbox{'}(s)}$, and defining $\chi =\frac{v}{f(s)}$ _, we obtain (A16), so that for this value of χ, we have F’(s) < 0.

This concludes the proof of Theorem 1.

We demonstrate the application of part (iv) of the above theorem for two choices of the nonlinearities:

For the particular function forms (3),(4) $f(s)=1-\frac{1}{1+s},g(v)={e}^{-v}$ _, we have $A=\underset{v>0}{ \sup}\frac{v\left|g\hbox{'}(v)\right|}{g(v)}=\underset{v>0}{ \sup }v=+\infty$

$$ B=\underset{s>0}{ \inf}\frac{f(s)}{sf\hbox{'}(s)}= \inf \left(1+s\right)=1 $$

so that A > B and part (iv) of Theorem 1 implies that there are values of the parameters for which multiple stationary solutions exist. Further study of this case is made in Appendix 2.

On the other hand, if we take f as above, but take

$$ g(v)=\frac{1}{1+\sqrt{v}} $$

we get $A=\underset{v>0}{ \sup}\frac{1}{2}\frac{\sqrt{v}}{1+\sqrt{v}}=\frac{1}{2}$, so that B > A and part (iv) of Theorem 1 ensures a unique stationary solution for all values of the parameters, and thus bistability will not occur. Thus, the capacity of the model to produce bistability does depend on the functional forms f,g.

Appendix 2. Conditions of bistability for the functional form (3),(4)

We now carry out a more detailed analysis in the case of the functional forms (3),(4), which allows us to explore more explicitly the conditions under which bistability emerges. In this case,

$$ F(s)= sg\left(\chi f(s)\right)=s{e}^{-\chi \frac{s}{1+s}} $$

(B1)

Differentiating, we have:

$$ F\hbox{'}(s)={e}^{-\chi \frac{s}{1+s}}\left(1-\chi \frac{s}{{\left(s+1\right)}^2}\right) $$

and the critical points of F are obtained by solving F’(s) = 0, giving:

$$ {s}_1=\left(\chi -2-\sqrt{\chi \left(\chi -4\right)}\right),\kern1em {s}_2=\left(\chi -2+\sqrt{\chi \left(\chi -4\right)}\right) $$

We consider two cases:

(I) If χ < 4 then no critical points exist, so that F’(s) does not change sign, and since F’(0) = 1 > 0, we conclude that F’(s) > 0, for all s ≥ 0 and that F(s) is monotonically increasing. Since lim _S→∞ F(s) = +∞, we conclude that, in this case, the equation (A8) has a unique solution, hence, there exists a unique nontrivial equilibrium (s ^*,v ^*) of (A5),(A6). Moreover, by Lemma 2, this equilibrium is stable.

(II) If χ > 4, then there are two critical points s ₁ and s ₂, and it is evident that both are positive. Since F’(0) > 0, we conclude that F(s) is increasing in the interval [0,s ₁], decreasing in the interval [s ₁,s ₂] and increasing in the interval [s ₂,∞). Thus, s ₁ is a local maximum point and s ₂ a local minimum point of F(s) (Fig. 2). Therefore, if equation F(s ₂) < β < F(s ₁), then (A8) has three solutions s ^*_{1 ,} s ^*_{2 ,} and s ^*_{3 ,} satisfying:

$$ {s}_1^{*}\in \left(0,{s}_1\right),{s}_2^{*}\in \left({s}_1,{s}_2\right),{s}_3^{*}\in \left({s}_2,\infty \right), $$

so that F ' (s ^*₁ ) > 0, F ' (s ^*₂ ) < 0, F ' (s ^*₃ ) > 0. 

Therefore, by Lemma 2 of Appendix 1, the solutions s ^*₁ and s ^*₃ correspond to stable equilibria while s ^*₂ corresponds to the unstable equilibrium. The condition for bistability is thus:

$$ {\uplambda}_1<\beta <{\uplambda}_2 $$

(B2)

Where λ ₁ = F(s ₂), λ ₂ = F(s ₁) or explicitly:

$$ {\lambda}_{1,2}=\frac{1}{2}\left(\chi -2\mp \sqrt{\chi \left(\chi -4\right)}\right){e}^{-\chi \left(1-\frac{2}{\chi \mp \sqrt{\chi \left(\chi -4\right)}}\right)}. $$