Introduction

Fluid–solid reactions play a major role in many important chemical and metallurgical processes. A large amount of work has been devoted to the kinetics of fluid–solid reactions. The reader is referred to the literature[1] for a comprehensive discussion of this topic. The investigation of reaction kinetics often relies on the initial rates.[2,3,4,5,6] [Also see the numerous sources and sites found by googling with the term ‘initial rate method.’] The initial rate method is appropriate for the determination of kinetics of homogeneous reactions, often saving time and effort. But as will be shown in this paper, the initial rate should not be used for the measurement or analysis of the kinetics of a fluid–solid reaction, especially for a reaction in which the effect of pore diffusion starts appearing even moderately as the reaction proceeds. The following analysis of the initial rate of a gas–solid reaction is based on an isothermal system. The heat transfer effect, which makes the analysis even less reliable, is not taken into consideration in this analysis.

Typically, the rate of a fluid–solid reaction is measured under a fixed concentration of the fluid reactant with mass transfer effects eliminated under a sufficiently high fluid velocity. Let us consider the following general fluid–solid reaction:

$$ A\left( f \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} bB(s){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} cC(s){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} dD(f).$$
(1)

An Initially Non-Porous Solid Forming a Porous Product Layer (The Shrinking-Core System)

A schematic representation of this reaction system is shown in Figure 1.

Fig. 1
figure 1

Reprinted from Ref. [9]

Schematic representation of the reaction of an initially non-porous solid forming a porous product layer (the shrinking-core system).

Full size image

In this case, the exact conversion vs time relationship is given in the following dimensionless form for the three basis geometries (large slabs, long cylinders, and spheres)[1,8]:

$$ t^{*} = g_{{F_{\text{p}} }} \left( X \right) + \sigma_{\text{s}}^{2} \left[ {p_{{F_{\text{p}} }} \left( X \right) + 4X/Sh^{*} } \right], $$
(2)

where

$$ g_{{F_{\text{p}} }} \left( X \right){\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 1 - \left( {1 - X} \right)^{{1/F_{\text{p}} }} $$
$$ p_{{F_{\text{p}} }} (X) = 1 - \frac{{F_{\text{p}} (1 - X)^{{2/F_{\text{p}} }} - 2(1 - X)}}{{F_{\text{p}} - 2}} $$

The specific form of \( p_{{F_{\text{p}} }} \left( X \right) \) for the three basic geometries is:

$$ p_{{F_{\text{p}} }} \left( X \right) = \left\{ {\begin{array}{*{20}l} {X^{2} } \hfill & {F_{\text{p}} = 1} \hfill \\ {X + \left( {1 - X} \right){\textrm{Ln}} \left( {1 - X} \right)} \hfill & {F_{\text{p}} = 2} \hfill \\ {1 - 3\left( {1 - X} \right)^{2/3} + 2\left( {1 - X} \right)} \hfill & {F_{\text{p}} = 3} \hfill \\ \end{array} } \right. $$

with

$$ t^{ * } = \frac{bk}{{\rho_{\text{s}} }}\frac{{A_{\text{p}} }}{{F_{\text{p}} V_{\text{p}} }}\left( {C_{A0} - \frac{{C_{C0} }}{K}} \right)t $$
$$ \sigma_{\text{s}}^{2} {\kern 1pt} = \frac{k}{{2D_{\text{e}} }}\frac{{V_{\text{p}} }}{{A_{\text{p}} }}\left( {1 + \frac{1}{K}} \right) $$
$$ Sh^{*} = \frac{{h_{\text{D}} }}{{D_{\text{e}} }}\left( {2F_{\text{p}} V_{\text{p}} /A_{\text{p}} } \right) $$

here, \( \sigma_{\text{s}}^{2} \) is the shrinking-core reaction modulus, which represents a ratio of chemical reactivity and capacity for pore diffusion. A large \( \sigma_{\text{s}}^{2} \) signifies that the overall rate is diffusion-controlled, while a small \( \sigma_{\text{s}}^{2} \) represent the cases of chemical reaction control.

In Eq. [2], the \( g_{{F_{p} }} (X) \) arises from the contribution of chemical reaction and is the conversion function under chemical reaction control; the \( p_{{F_{\text{p}} }} (X) \) arises from the contribution of pore diffusion in the product layer and is the conversion function under pore diffusion control.

The rate of conversion in terms of the extent of reaction can be readily derived from Eq. [2], as follows:

$$ \frac{{d{\kern 1pt} X}}{{d{\kern 1pt} t^{*} }} = \left[ {g^{\prime}_{{F_{\text{p}} }} \left( X \right) + \sigma_{\text{s}}^{2} \left( {p^{\prime}_{{F_{\text{p}} }} \left( X \right) + \frac{4}{{Sh^{*} }}} \right)} \right]^{ - 1} $$
(3)

The initial rate is when X = 0, at which point \( g^{\prime}_{{F_{\text{p}} }} \left( X \right) = 1/F_{\text{p}} \) and \( p^{\prime}_{{F_{\text{p}} }} \left( X \right) = 0 \), thus signifying the absence of pore diffusion effect and the fact that the initial rate in the shrinking-core system is controlled by chemical reaction and external mass transfer. The initial rate is thus given by:

$$ \left. {\frac{{{\text{d}}X}}{{{\text{d}}{\kern 1pt} t}}} \right|_{t = 0} = \frac{{b{\kern 1pt} k\left( {C_{{{\text{A}}0}} - \frac{{C_{{{\text{C}}0}} }}{K}} \right)}}{{\rho_{\text{s}} \left( {1 + \frac{k}{{h_{\text{D}} }}\left( {1 + \frac{1}{K}} \right)} \right)}}\frac{{A_{\text{p}} }}{{V_{\text{p}} }} $$
(4)

In the absence of external mass transfer effect (Sh* → ∞), Eq. [4] is simplified to:

$$ \left. {\frac{{{\text{d}}X}}{{{\text{d}}{\kern 1pt} t}}} \right|_{t = 0} = \frac{{b{\kern 1pt} k\left( {C_{A0} - C_{C0} /K} \right)}}{{\rho_{\text{s}} }}\left( {\frac{{A_{\text{p}} }}{{V_{\text{p}} }}} \right) $$
(5)

Equation [5] can be further rearranged to obtain the molar rate of solid consumption per area of the sample as:

$$ R_{\text{r}} = - \frac{{\rho_{\text{s}} V_{\text{p}} }}{{A_{\text{p}} }}\left. {\frac{{{\text{d}}\left( {1 - X} \right){\kern 1pt} }}{{{\text{d}}{\kern 1pt} t}}} \right|_{t = 0} = b \cdot k{\kern 1pt} \left( {C_{{{\text{A}}0}} - C_{{{\text{C}}0}} /K} \right) $$
(6)

As expected, this equation indicates that the initial rate per unit area is independent of the shape or size of the solid.

It is shown from Eq. [6] that the rate constant obtained from the initial rate is the intrinsic value. It is noted that a first-order chemical reaction is assumed in the above derivation for convenience, but the same result applies to non-first-order fluid–solid reaction is:

$$ R_{\text{r}} = - \frac{{\rho_{\text{s}} V_{\text{p}} }}{{A_{\text{p}} }}\left. {\frac{{{\text{d}}\left( {1 - X} \right){\kern 1pt} }}{{{\text{d}}{\kern 1pt} t}}} \right|_{t = 0} = b \cdot k \cdot f\left( {C_{\text{A}}^{\text{n}} ,C_{\text{C}}^{\text{cn}} } \right) $$
(7)

In practice, the determination of the initial rate requires measurements until the solid achieves a certain degree of reaction, i.e., up to a certain value of X. This value of X will depend on the value of \( \sigma_{\text{s}}^{2} \). To evaluate this, the rate in Eq. [3] in the absence of external mass transfer effect is plotted as a function of fraction conversion X in Figure 2. It is seen that for \( \sigma_{\text{s}}^{2} \) less than 0.1, the reaction rate is not significantly affected by pore diffusion until conversion reaches 5 to 10 pct, and up to this range of conversion, the rate can still be approximated as initial rate. However, it would be very difficult to obtain the intrinsic kinetics from the initial rate when there is even a relatively moderate effect of pore diffusion (\( \sigma_{\text{s}}^{2} > 0.1 \)) in the overall rate, even though the mathematical equation, Eq. [6], indicates that the rate at X = 0 is the intrinsic rate in this system in the absence of external mass transfer effect. Further, with external mass transfer effect in place, it would be even more difficult to obtain the intrinsic rate constant, as shown in Eq. [4], especially for reactions with small equilibrium constants K.

Fig. 2
figure 2

(1/F p)dX/dt* vs X for different values of \( \sigma_{\text{s}}^{2} \) with F p = 3 for an initially non-porous solids with Sh* → ∞

Full size image

An Initially Porous Solid Forming a Porous Product Layer

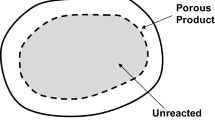
For the reaction of a porous solid, the grain model[1,7] that assumes idealized solid structure made up of individual grains will be used for the derivation of the initial reaction rate. The choice of this model is just for the purpose of illustration and the general conclusion drawn by the analysis performed in this work is valid regardless of the model used to describe the reaction of an initially porous solid with a fluid. In the grain model, the grains react according to chemically controlled shrinking-core system. Although this idealization is not necessary and can be relaxed, grain model facilitates the analysis and will not affect the conclusions made here. A schematic representation of a porous solid with unreacted grains is shown in Figure 3.

Fig. 3
figure 3

Reprinted from Ref. [9]

Schematic representation of a porous solid with unreacted grains.

Full size image

The equation that governs the fluid diffusion and chemical reaction of a porous solid is given as follows, assuming pseudo-steady state and equal effective diffusivity of gaseous species A and C:

$$ D_{\text{e}} \nabla^{2} C_{\text{A}} - v_{\text{A}} = 0 $$
(8)
$$ D_{\text{e}} \nabla^{2} C_{\text{C}} + v_{\text{A}} = 0 $$
(9)

By dividing Eq. [9] by K and subtracting from Eq. [8]:

$$ D_{\text{e}} \nabla^{2} \left( {C_{\text{A}} - C_{\text{C}} /K} \right) - v_{\text{A}} \left( {1 + 1/K} \right) = 0 $$
(10)

Although not necessary for this discussion, it is convenient to rewrite Eq. [10] in dimensionless form by introducing the following normalized variables:

$$ \begin{aligned} \psi = \left( {C_{\text{A}} - C_{\text{C}} /K} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} /\left( {C_{{{\text{A}}0}} - C_{{{\text{C}}0}} /K} \right) \hfill \\ t^{*} = \frac{bk}{{\rho_{\text{s}} }}\left( {\frac{{A_{\text{g}} }}{{F_{\text{g}} V_{\text{g}} }}} \right)\left( {C_{{{\text{A}}0}} - \frac{{C_{{{\text{C}}0}} }}{K}} \right)t{\kern 1pt} \hfill \\ \hat{\sigma }^{2} = \frac{1}{{2F_{\text{p}} }}\left( {\frac{{F_{\text{p}} V_{\text{p}} }}{{A_{\text{p}} }}} \right)^{2} \left( {\frac{{A_{\text{g}} }}{{F_{\text{g}} V_{\text{g}} }}} \right)\frac{{\left( {1 - \varepsilon } \right)k}}{{D_{\text{e}} }}\left( {1 + \frac{1}{K}} \right) \hfill \\ \xi = \frac{{A_{\text{g}} r_{\text{c}} }}{{F_{\text{g}} V_{\text{g}} }} \hfill \\ \eta = \frac{{A_{\text{p}} R}}{{F_{\text{p}} V_{\text{p}} }} \hfill \\ \end{aligned} $$
(11)

The above particular definition of \( \hat{\sigma } \), which represents a ratio of the capacities for pore diffusion and chemical reaction, has been shown to be very convenient in that it makes the numerical criteria for chemical or pore diffusion control identical for all nine combinations of F g and F p.[1,8]

Equation [10] now becomes

$$ \frac{1}{{\eta^{{F_{\text{p}} - 1}} }}\frac{\text{d}}{{{\text{d}}\eta }}\left( {\eta^{{F_{\text{p}} - 1}} \frac{{{\text{d}}\psi }}{{{\text{d}}\eta }}} \right) - 2F_{\text{g}} F_{\text{p}} \cdot \hat{\sigma }^{2} \psi \cdot \xi^{{F_{\text{g}} - 1}} = 0 $$
(12)

At t = 0, all the grains are unreacted as shown in Figure 3 and ξ is unity everywhere throughout the particle. Thus, Eq. [12] becomes:

$$ \frac{1}{{\eta^{{F_{\text{p}} - 1}} }}\frac{\text{d}}{{{\text{d}}\eta }}\left( {\eta^{{F_{\text{p}} - 1}} \frac{{{\text{d}}\psi }}{{{\text{d}}\eta }}} \right) - 2F_{\text{g}} F_{\text{p}} \cdot \hat{\sigma }^{2} \psi = 0\quad{\text{at}}\;t = X = 0 $$
(13)

This equation can be solved for different values of F p by rearranging it into a Bessel’s equation:

$$ \eta^{2} \frac{{d^{2} \psi }}{{{\text{d}}\eta^{2} }} + \left( {F_{\text{p}} - 1} \right)\eta \frac{{{\text{d}}\psi }}{{{\text{d}}\eta }} - 2F_{\text{g}} F_{\text{p}} \hat{\sigma }^{2} \cdot \eta^{2} \psi = 0\quad{\text{at}}\;t = X = 0 $$
(14)

with the following boundary conditions:

$$ {\kern 1pt} \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\psi }}{{{\text{d}}\eta }} = Sh^{*} \left( {1 - \psi } \right)/2} \hfill & {{\text{at}}\;\eta = 1} \hfill \\ {\frac{{{\text{d}}\psi }}{{{\text{d}}\eta }} = 0} \hfill & {{\text{at}}\;\eta = 0} \hfill \\ \end{array} } \right. $$

Equation [14] can be solved analytically to yield the following general solution:

$$ \psi = \eta^{{\frac{{2 - F_{\text{p}} }}{2}}} \left[ {c_{1} \cdot I_{{\frac{{\left| {2 - F_{\text{p}} } \right|}}{2}}} \left( {\sqrt {2F_{\text{p}} F_{\text{g}} } \hat{\sigma } \cdot \eta } \right) + c_{2} \cdot I_{{ - \frac{{\left| {2 - F_{\text{p}} } \right|}}{2}}} \left( {\sqrt {2F_{\text{p}} F_{\text{g}} } \hat{\sigma } \cdot \eta } \right)} \right], $$
(15)

where c 1 and c 2 are constants to be determined based on the boundary conditions. The solutions for particles of different shape factors are listed in Table I.

Table I Analytical Solutions at t = 0 with External Mass Transfer Effects
Full size table

In the absence of external mass transfer effect (Sh* → ∞), the above analytical solutions are simplified as follows:

Unlike the initial rate of a non-porous solid following the shrinking-core model, the analytical solutions for X = t = 0 in Tables I and II show general dependence on pore diffusion. Under the pseudo-steady state approximation, the overall reaction rate is equal to the rate of diffusion of fluid reactant into the particle:

$$ \frac{{\left( {1 - \varepsilon } \right)\rho_{\text{s}} V_{\text{p}} }}{b}\frac{{{\text{d}}X}}{{{\text{d}}t}} = D_{\text{e}} A_{\text{p}} \left. {\frac{{{\text{d}}C_{\text{A}} }}{{{\text{d}}R}}} \right|_{{R = F_{\text{p}} V_{\text{p}} /A_{\text{p}} }} $$
(16)

The dimensionless form of which is:

$$ \frac{{{\text{d}}X}}{{{\text{d}}t^{ * } }} = \frac{1}{{2\hat{\sigma }^{2} }}\left. {\frac{{{\text{d}}\psi }}{{{\text{d}}\eta }}} \right|_{\eta = 1} $$
(17)

The derivations of the above equations are given in the literature[1] and the reader is referred to it for details. The initial rates in Table I under the two asymptotic cases of no pore diffusion effect (\( \hat{\sigma } \to 0 \)) and pore diffusion control (\( \hat{\sigma } \to \infty \)) become:

$$ \mathop {\lim }\limits_{\sigma \to 0} \left. {\frac{{{\text{d}}X}}{{{\text{d}}t^{ * } }}} \right|_{t = 0} = F_{\text{g}} $$
(18)
$$ \left. {\mathop {\lim }\limits_{{\hat{\sigma } \to \infty }} \frac{{{\text{d}}X}}{{{\text{d}}t^{ * } }}} \right|_{t = 0} = \frac{1}{{2\hat{\sigma }}}\frac{{Sh^{*} \sqrt {2F_{\text{p}} F_{\text{g}} } }}{{Sh^{*} + 2\sqrt {2F_{p} F_{\text{g}} } \hat{\sigma }}} $$
(19)

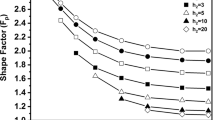
It is seen from Eq. [18] that the initial rates for particles of different shapes are independent of external mass transfer effect when pore diffusion effect is negligible. The initial rates dX/dt* in Table II (Sh* → ∞) for particles of different shapes are plotted as a function of \( \hat{\sigma }^{2} \) in Figure 4 with \( \hat{\sigma }^{2} < 1 \). It is shown that the initial rates of particles of different overall shapes become the same as \( \hat{\sigma }^{2} \) approaches 0 as indicated by Eq. [18]. The initial rates for particles of different shapes when there is a significant effect of pore diffusion and the effect of external mass transfer is negligible are presented in Figure 5. In this case, the initial rates described by Eq. [19] converge to the following asymptote:

Table II Analytical Solutions at t = 0 in the Absence of External Mass Transfer Effects
Full size table
Fig. 4
figure 4

Initial reaction rates for particles of different shapes with \( \hat{\sigma }^{2} < 1 \) and F g = 3

Full size image
Fig. 5
figure 5

Initial reaction rates for particles of different shape with \( \hat{\sigma }^{2} > 1 \) and F g = 3

Full size image
$$ \left. {\mathop {\lim }\limits_{{\hat{\sigma } \to \infty }} \frac{{{\text{d}}X}}{{{\text{d}}t^{ * } }}} \right|_{{t^{*} = 0}} = \frac{{\sqrt {2F_{\text{p}} F_{\text{g}} } }}{{2\hat{\sigma }}} $$
(20)

Further, the expressions of the asymptotic rates in terms of molar rate of solid consumption per area of the external surface in the absence of the effect of external mass transfer are given by

$$ \begin{aligned} R_{\text{r}} &= - \frac{{\rho_{\text{s}} V_{\text{p}} \left( {1 - \varepsilon } \right)}}{{A_{\text{p}} }}\left. {\frac{{{\text{d}}\left( {1 - X} \right){\kern 1pt} }}{{{\text{d}}t}}} \right|_{t = 0} \\&= b{\kern 1pt} k\left( {C_{\text{As}} - C_{\text{Cs}} /K} \right)\frac{{\left( {1 - \varepsilon } \right)A_{\text{g}} }}{{V_{\text{g}} }}\\ &= b \cdot k \cdot f\left( {C_{\text{A}} ,C_{\text{C}} } \right) \cdot S_{\text{v}} \end{aligned} $$
(21)
$$ \begin{aligned} R_{\text{r}} &= - \left. {\frac{{\rho_{\text{s}} V_{\text{p}} \left( {1 - \varepsilon } \right)}}{{A_{\text{p}} }}\frac{{{\text{d}}\left( {1 - X} \right){\kern 1pt} }}{{{\text{d}}t}}} \right|_{t = 0} = \sqrt {k \cdot D_{\text{e}} } \cdot \frac{{b{\kern 1pt} }}{{\sqrt {1 + 1/K} }}\left( {\frac{{\left( {1 - \varepsilon } \right)A_{\text{g}} }}{{V_{\text{g}} }}} \right)^{{\frac{1}{2}}} \left( {C_{\text{As}} - \frac{{C_{\text{Cs}} }}{K}} \right) \hfill \\ &= b\frac{{\sqrt {k \cdot D_{\text{e}} \cdot S_{\text{v}} } }}{{\sqrt {1 + 1/K} }} \cdot f\left( {C_{\text{A}} ,C_{\text{C}} } \right) = \frac{{b \cdot k_{\text{app}} }}{{\sqrt {1 + 1/K} }} \cdot f\left( {C_{\text{A}} ,C_{\text{C}} } \right), \hfill \\ \end{aligned} $$
(22)

where S v is the surface area per unit volume of porous solid, a quantity readily measured, e.g., by the BET method. These equations indicate that the initial rate per unit area of external surface is independent of the shape or size of the pellet.

It is noted that the initial reaction rate of porous solids will represent the intrinsic reaction rate only when \( \hat{\sigma } \to 0 \), as shown by Eq. [21]. However, the initial rate for a porous solid with some effects of pore diffusion (\( \hat{\sigma }^{2} > 0.1 \)) will be significantly affected by pore diffusion, and thus does not represent the intrinsic reaction rate, as shown in Figures 3 and 4 as well as by Eq. [22]. Moreover, the effect external mass transfer would make it even more difficult to obtain the intrinsic rate constant when the effect of pore diffusion is in place. It is of interest to note that even in the case of \( \hat{\sigma } \to \infty \) and Sh* → ∞, the initial rate of a porous solid is not controlled by pore diffusion alone; rather it is controlled equally by pore diffusivity and chemical reactivity represented by the \( \sqrt {k \cdot D_{e} } \) term.

The relationship between the apparent activation energy when \( \hat{\sigma } \to \infty \) and the true activation energy for an irreversible reaction (large K) or when K is a weak function of temperature can be derived by taking the natural logarithm of Eq. [22] (neglecting the usually weak temperature dependence of D e):

$$ { {\textrm{Ln}} }\left( {R_{\text{r}} } \right) = {\textrm{Ln}} \left( {\sqrt k } \right) + {\text{const}} = {\textrm{Ln}} \left( {k_{\text{app}} } \right) + {\text{const}} $$
(23)

Substituting the reaction rate constants in Eq. [23] with their Arrhenius expressions:

$$ \begin {aligned} &- \frac{1}{2}\frac{{E_{\text{T}} }}{RT} + \frac{1}{2}{\textrm{Ln}} \left( {A_{\text{T}} } \right) + {\text{const}}\\& \quad= - \frac{{E_{\text{app}} }}{RT} + {\textrm{Ln}} \left( {A_{\text{app}} } \right) + {\text{const}} \end {aligned} $$
(24)

It is seen from Eq. [24] that the value of the apparent activation energy when \( \hat{\sigma } \to \infty \) is related to the true activation energy by:

$$ E_{\text{app}} = \frac{1}{2}E_{\text{T}} $$
(25)

The ratio of the apparent activation energy for an intermediate value of \( \hat{\sigma }^{2} \) and the true activation energy should lie between one half and unity (for large or weakly temperature dependent K). This result is also observed in reactions in catalyst pellets[10] and also in the reactions of porous solids that produce no solid product layer.[11] Although not shown here, the apparent reaction order with respect to the fluid reactant concentration is also falsified for a non-first-order reaction.[10,11]

Concluding Remarks

To summarize, the following points should be kept in mind when considering initial rates of an isothermal fluid–solid reactions:

  1. 1.

    Mathematically, the initial rate (at X = 0) of reaction of an initially non-porous solid represents the intrinsic reaction rate, regardless of the value of \( \sigma_{\text{s}}^{2} \). Up to what extent of solid conversion this condition applies depends on the value of \( \sigma_{\text{s}}^{2} \) for the system, as shown in Figure 2. The results shown in this figure indicates that it would be very difficult to obtain the intrinsic kinetics from the initial rate when there is even a relatively moderate effect of pore diffusion (\( \sigma_{s}^{2} > 0.1 \)) in the overall rate, even though the mathematical equation indicates that the rate at X = 0 is the intrinsic rate in this system (in the absence of external mass transfer effect).

  2. 2.

    The initial rate of a porous solid is in general affected by pore diffusion. When \( \hat{\sigma }^{2} < 0.01 \), however, the initial rate (in fact the rate over the entire conversion) will equal the intrinsic rate. Even for \( \hat{\sigma }^{2} \) as small as 0.1, the initial rate of an initially porous solid is significantly affected by pore diffusion, and thus not controlled by intrinsic chemical reaction. When \( \hat{\sigma }^{2} > 10 \), the apparent rate constant for the initial rate will be \( \sqrt {k \cdot D_{\text{e}} } \). Additionally, pore diffusion alone does not control the initial rate no matter how large the ratio of k/D e becomes. (In this case, reactions that produce porous product layer will eventually be rate-controlled by pore diffusion as the product layer builds up.)

  3. 3.

    Besides fluid–solid reactions often encounter, an induction period in the initial stage of reaction, during which the reaction mechanism applicable to the main reaction is not applicable. The existence of this induction period would make it much more difficult to determine the intrinsic reaction rate constant for the main reaction based on the initial rate. Another factor that sometimes makes the measurement of the initial rate difficult is the time taken for the concentration of gas to be uniform through the reactor once the gas is switched to the reactant gas in isothermal experiments. Moreover, the transient period for the reactive gas to reach the pseudo-steady state profile inside the pores of the solid particle at the beginning of an experiment may affect the accuracy of determining the initial rates. These other factors are usually negligible for reactions with moderate rates, but can be significant for fast reactions.