1 Introduction

The covid-19 epidemic has led the vast majority of states around the world to take very strict confinement measures ranging from lockdown to partial confinement. The economic consequences of this confinement over more than two months are considerable and alarming. At a time when most states begin to lift confinement, sometimes with great reluctance, it seems very useful to develop reliable models as much as possible to estimate the risks of an excessive level of un-confinement which could give rise to a resurgence of the epidemic.

Many models have been developed very quickly to describe the evolution of the pandemic, Adam (2020). Various computer or mathematical models have been produced and show sometimes very alarming scenarios with successive phases of confinement followed by phases of restarting the epidemic, Kissler et al. (2020). While most countries are in the process of release of the confinement, it is important to develop models to assess whether the protective measures taken by the government are sufficient to prevent a restart of the epidemic.

The goal of this work is to propose a simple model allowing to estimate a threshold of release of confinement and of protection by masks below which the epidemic cannot restart. For this, we combine two approaches, our previous work, Moussaoui and Auger (2020), where we had defined a threshold for the release of confinement with that of Howard et al. (2020) where they had proposed a formula for reducing the basic reproduction rate of an epidemic in the case where the population uses masks to protect themselves from infection.

2 The SEIR Model Without Intervention

Liu et al. (2020) considered four representative places of social contacts : (H) individual households where families are living; (S) schools, college and universities; (W) various workplaces indoor and outdoor; (P) large density public places, such as stadiums, shops, markets, including public transportation. In our model, we will group two compartments (S) and (W) into one that we continue to call (W). In this way, schools, colleges and universities are included in the workplace. We therefore only consider for simplicity 3 compartments (H), (W) and (P).

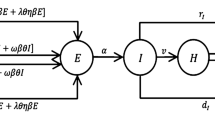
The population is structured into sub-populations associated with different places where individuals move every day. At home (H), individuals are in contact with their family members, parents, grandparents and children. At work (W), they are in contact with office colleagues inside the building or outdoors. In high-density public places (P), people can come into contact with many others and catch the disease there. Figure 1 shows the possible transitions between the different states.

Fig. 1
figure 1

Transition graph of the SEIR model with different places (Color figure online)

Full size image

The complete model takes into account daily movements in different places at the fast time scale and the dynamics of the epidemic at a slow time scale. Our variables are the proportions of susceptible individuals in household \(S_H(t)\), at work \(S_W(t)\) and in public places \(S_P(t)\) at time t. We use similar notations for exposed, infectious and removed individuals. Removed individuals are isolated people, deceased and cured. The complete model reads as follows:

$$\begin{aligned} \frac{\mathrm{d}S_H}{d\tau }&=(\frac{\gamma }{T_W} S_W + \frac{\gamma }{T_P} S_P - 2 \frac{\gamma }{T_H} S_H) - \epsilon \beta _H S_H I_H \end{aligned}$$
(1)
$$\begin{aligned} \frac{\mathrm{d}S_W}{\mathrm{d}\tau }&= ( \frac{\gamma }{T_H} S_H - \frac{\gamma }{T_W} S_W) - \epsilon \beta _W S_W I_W \end{aligned}$$
(2)
$$\begin{aligned} \frac{\mathrm{d}S_P}{\mathrm{d}\tau }&= ( \frac{\gamma }{T_H} S_H - \frac{\gamma }{T_P} S_P) - \epsilon \beta _P S_P I_P \end{aligned}$$
(3)
$$\begin{aligned} \frac{\mathrm{d}E_H}{\mathrm{d}\tau }&= (\frac{\gamma }{T_W} E_W + \frac{\gamma }{T_P} E_P - 2 \frac{\gamma }{T_H} E_H) + \epsilon ( \beta _H S_H I_H - k E_H) \end{aligned}$$
(4)
$$\begin{aligned} \frac{\mathrm{d}E_W}{\mathrm{d}\tau }&= ( \frac{\gamma }{T_H} E_H - \frac{\gamma }{T_W} E_W) + \epsilon (\beta _W S_W I_W - k E_W) \end{aligned}$$
(5)
$$\begin{aligned} \frac{\mathrm{d}E_P}{\mathrm{d}\tau }&= ( \frac{\gamma }{T_H} E_H - \frac{\gamma }{T_P} E_P) + \epsilon (\beta _P S_P I_P - k E_P) \end{aligned}$$
(6)
$$\begin{aligned} \frac{\mathrm{d}I_H}{\mathrm{d}\tau }&= (\frac{\gamma }{T_W} I_W + \frac{\gamma }{T_P} I_P - 2 \frac{\gamma }{T_H} I_H) + \epsilon (k E_H - \alpha I_H) \end{aligned}$$
(7)
$$\begin{aligned} \frac{\mathrm{d}I_W}{\mathrm{d}\tau }&= ( \frac{\gamma }{T_H} I_H - \frac{\gamma }{T_W} I_W) + \epsilon (k E_W - \alpha I_W) \end{aligned}$$
(8)
$$\begin{aligned} \frac{\mathrm{d}I_P}{\mathrm{d}\tau }&= ( \frac{\gamma }{T_H} I_H - \frac{\gamma }{T_P} I_P) + \epsilon (k E_P - \alpha I_P) \end{aligned}$$
(9)
$$\begin{aligned} \frac{\mathrm{d}R_H}{\mathrm{d}\tau }&=(\frac{\gamma }{T_W} R_W + \frac{\gamma }{T_P} R_P - 2 \frac{\gamma }{T_H} R_H) + \epsilon \alpha I_H \end{aligned}$$
(10)
$$\begin{aligned} \frac{\mathrm{d}R_W}{\mathrm{d}\tau }&= ( \frac{\gamma }{T_H} R_H - \frac{\gamma }{T_W} R_W) + \epsilon \alpha I_W \end{aligned}$$
(11)
$$\begin{aligned} \frac{\mathrm{d}R_P}{\mathrm{d}\tau }&= ( \frac{\gamma }{T_H} R_H - \frac{\gamma }{T_P} R_P) + \epsilon \alpha I_P \end{aligned}$$
(12)

We define the total proportion of susceptible individuals \(S(t) = S_H(t) + S_W(t) + S_P(t)\), exposed \(E(t) = E_H(t) + E_W(t) + E_P(t)\), infectious \(I(t) = I_H(t) + I_W(t) + I_P(t)\) and removed \(R(t) = R_H(t) + R_W(t) + R_P(t)\) at time t. Our variables are proportions and verify for any t the following expression:

$$\begin{aligned} S(t) + E(t) + I(t) + R(t) = 1. \end{aligned}$$
(13)

\(\tau \) is the fast time, \(t = {\varepsilon }\tau \) is the slow time and \(\epsilon \) is a small dimensionless parameter. For instance, we can choose \({\varepsilon }= \frac{1}{24}\). In this way, the time unit of the fast model is the hour and the time unit of the epidemic model would be the day.

With regard to epidemic models in the metapopulation domain, we refer to Arino and van den Driessche (2003), Arino and van den Driessche (2006). In our work, we assume that displacements are carried out quickly with regard to the dynamics of the epidemic. The fast part of the model is obtained when \(\epsilon =0\) and corresponds to the daily movement model. We define time slots for average occupancy per day of the different compartments, respectively, denoted \(T_H\), \(T_W\) and \(T_P\) for each compartment. The time slots verify that their sum is equal to one day:

$$\begin{aligned} T_H + T_W + T_P = D. \end{aligned}$$
(14)

where \(D=24\). \(\gamma \) is a positive parameter. \(m_{AB} = \frac{\gamma }{T_B}\) is the rate for change from place B to place A with \(B \in [H,W,P]\) and \(A \ne B\). The rate is assumed to be inversely proportional to the time slot of the departure place. Therefore, individuals are more likely to remain on places with larger time slots. The slow part of the model corresponds to all the terms of order of \(\epsilon \) and is a classic SEIR model taking into account different places. \(\beta _A\) is the transmission rate in location \(A \in [H,W,P]\). \(\frac{1}{k}\) is the average time spent in the exposed compartment before becoming infectious. \(\frac{1}{\alpha }\) is the average time spent in the infected compartment to go to the removed compartment in which the cured individuals as well as the deceased ones are found.

Let us look for the fast equilibrium of this model. A simple calculation shows that the fast equilibrium verifies the following relationships for susceptible:

$$\begin{aligned} u_H^{*} = \frac{S_H^*}{S} = \frac{T_H}{D},~~~u_W^{*} = \frac{S_W^*}{S} = \frac{T_W}{D},~~~u_P^{*} = \frac{S_P^*}{S} = \frac{T_P}{D}. \end{aligned}$$
(15)

We denote the fast equilibrium with an upper star. At the fast equilibrium, the proportion of susceptible individuals in the different places is proportional to the total proportion of susceptible. We get the same fast equilibrium formulas for the exposed, the infectious and the removed because they are supposed to move in the same way. \(u_A^{*}\) is the constant proportion of individuals in place A at equilibrium with \(A \in [H,W,P]\) which is proportional to the time slot associated with this place. We assume that exposed individuals have no symptoms and move as before they were infected. For infectious individuals, we assume that symptomatic individuals are very quickly isolated and go into compartment R. The asymptomatic infected do not know that they are infectious and continue to move as before. Such equilibrium proportions in the different places are reported in Xia et al. (2013) for the 2009 Hong Kong H1N1 Influenza Epidemic also reported in Liu et al. (2020) for the Covid-19 epidemic.

Using the methods of aggregation of variables, Auger et al. (2008a) and Auger et al. (2008b), we derive a reduced model governing global proportions in the different epidemic compartments at the slow time. For this, we replace the fast equilibrium of daily displacement in the complete model. Then, we add the 3 equations of susceptible, exposed, infectious and removed and we go back in slow time which leads us to the following reduced model which is a classic SEIR model:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&=-\beta S(t)I(t), \end{aligned}$$
(16)
$$\begin{aligned} \frac{\mathrm{d}E}{\mathrm{d}t}&=\beta S(t)I(t)-k E(t), \end{aligned}$$
(17)
$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t}&=k E(t)-\alpha I(t), \end{aligned}$$
(18)
$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}&=\alpha I(t), \end{aligned}$$
(19)
$$\begin{aligned} S(t&)+E(t)+I(t)+R(t)=1, \end{aligned}$$
(20)

where we find an overall transmission rate \(\beta \) which is expressed as a function of local transmission rates and the proportions of individuals in the different places at the fast equilibrium as follows:

$$\begin{aligned} \beta = \beta _H (u_H^{*})^2 + \beta _W (u_W^{*})^2 + \beta _P (u_P^{*})^2. \end{aligned}$$
(21)

For the example of covid-19 epidemic, the value of the transmission rate \(\beta =2.1\) was estimated using data for Algeria Moussaoui and Auger (2020) and France Bacaër (2020). Based on Linton et al. (2019), Kuniya (2020), Sun et al. (2020), we fix \(1/k=5\) , and thus, \(k = 0.2\) and we set \(1/\alpha = 1\) as the average time in compartment ”I” before isolation.

Regarding local contact parameters, based on the reference Liu et al. (2020), we estimate them to be roughly proportional to 0.4, 1.4 and 0.2, respectively, for locations H, W and P. Assuming that susceptible, exposed and asymptomatic infected individuals spend around 14 hours at home, 8 hours at work, and 2 hours in public places per day, in order to find an overall contact rate \(\beta = 2.1\) we must take the following contact rates by location, \(\beta _H = 2.87\), \(\beta _W = 10.03\) and \(\beta _P = 1.43\).

Figure 2 shows numerical simulations of the complete model. It shows the evolution over time of the proportions of individuals in the different places for various epidemiological compartments with \(1/\alpha =1\) for the example of covid-19 epidemic with \({\mathcal {R}}_0 = 2.1\) close to the value found for covid-19 for France, Bacaër (2020), \({\mathcal {R}}_0 = 2.33\) and to the one found for Algeria, Moussaoui and Auger (2020), \({\mathcal {R}}_0 = 2.1\).

Fig. 2
figure 2

Evolution of the proportions in the different places in each epidemic compartment over time. The parameters values used in the simulation are: \(\gamma =10; \beta _H=2.87; \beta _W=10.03; \beta _P=1.43; T_H=14, T_W=8; T_P=2, \alpha =1, \epsilon =0.04; k=0.2\) (Color figure online)

Full size image
Fig. 3
figure 3

Comparison between the dynamics of S, E, I and R given by the complete system (red) and that obtained with the four-dimensional aggregated system (green). We see on this figure that the reduced system solution matches quite well the complete model solution. The parameters values used in the simulation are: \(\gamma =10, \beta _H=2.87, \beta _W=10.03, \beta _P=1.43, T_H=14, T_W=8, T_P=2, \alpha =1, \epsilon =0.01, k=0.2\) (Color figure online)

Full size image

Figure 2 shows that the proportions in the different places for each epidemic compartment change over time while remaining proportional to the proportions at the fast equilibrium, i.e., \(u_H^{*} = \frac{T_H}{D} = 0.583\), \(u_W^{*} = \frac{T_W}{D} = 0.333\) and \(u_P^{*} = \frac{T_P}{D} = 0.083\). The fast equilibrium is established quickly and is verified throughout the slow trajectory. It is therefore sufficient to simulate the reduced (aggregated) model because the fast equilibrium makes it possible to know the distribution in the different places at any time.

Figure 3 compares the trajectories of the complete system taking into account the epidemic compartments by location with the reduced or aggregated system considering only 4 global epidemic compartments. The figure shows that the solutions of the two systems are extremely close. We can therefore use the aggregated model to understand the dynamics of the complete model.

3 Consideration of Intervention Strategies

After the start of the epidemic, most countries have put in place a set of measures to protect the population against the epidemic. The main measures were almost total confinement and protective measures, notably the compulsory wearing of masks and social distancing. Therefore, we will now consider three phases, a first phase corresponding to the start of the epidemic at \(t=0\) without any protective measures, followed by a second phase of severe confinement starting at time T and a third phase of partial release of confinement at time \(T^*\) by taking additional protective measures such as wearing masks and social distancing.

3.1 The Model with Confinement

In Moussaoui and Auger (2020), the first part proposed a classic SEIR epidemiological model to describe the dynamics of the Covid-19 epidemic in Algeria. The second part proposed a SEIR model taking into account confinement but without taking into account different groups of places. In this work, we consider daily movements of people in various groups of places. Therefore, we will now adapt the confinement model to the case with groups of places. After the start of the epidemic in China, in France and in most countries in the world, a very severe period of confinement was imposed on populations, especially in large cities. In the model, we will assume that a constant proportion v of the population is strictly confined. We assume that the confined people are completely removed from the chain of transmission of the epidemic. Thus, we consider total confinement as in the big cities in China where individuals stayed at home all day with a ban on going out and with deliveries of basic necessities every day at home. Confined people can no longer contaminate other people except for family members confined with them. In the case of covid-19, symptomatic people from the same family who are confined and infected are quickly taken into hospital care and can no longer infect another family. Asymptomatic people are confined to their house, cannot infect other persons outside and stop being infectious after a period of around ten days on average.

\(u = 1 - v\) represents the proportion of unconfined people. In France, as in most of the countries concerned by confinement, part of the population has not been confined. These are doctors and health personnel in hospitals, police and security personnel, persons providing minimum transport and city maintenance, etc. These people continued to move about as before. To simplify, in our model, we are going to assume that non-confined individuals move in exactly the same way as before the epidemic with the same average durations of time spent in different places. We also assume that the transmission rates remain unchanged in the various places visited. These are strong assumptions. However, if we accept these hypotheses, we get the following expressions of the fast equilibrium for susceptible as well as for exposed and infected:

$$\begin{aligned} \frac{S_H^*}{S} = u u_H^{*},~~~\frac{S_W^*}{S} = u u_W^{*},~~~\frac{S_P^*}{S} = u u_P^{*}, \end{aligned}$$
(22)

Thus, \(S_{uc} = S_H^* + S_W^* + S_P^* = u S\) corresponds to the proportion of un-confined persons. \(S_c = v S = (1 - u) S\) is the proportion of totally confined individuals removed from the contamination chain. Then, the reduced model taking into account confinement is the following, similar to the one found in Moussaoui and Auger (2020):

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&=-\beta _1 S(t)I(t), \end{aligned}$$
(23)
$$\begin{aligned} \frac{\mathrm{d}E}{\mathrm{d}t}&=\beta _1 S(t)I(t)-k E(t), \end{aligned}$$
(24)
$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t}&=k E(t)-\alpha I(t), \end{aligned}$$
(25)
$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}&=\alpha I(t), \end{aligned}$$
(26)
(27)

However, we get a different overall transmission rate \(\beta _1\):

$$\begin{aligned} \beta _1 = u^2 \beta = u^2 (\beta _H (u_H^{*})^2 + \beta _W (u_W^{*})^2 + \beta _P (u_P^{*})^2), \end{aligned}$$
(28)

\(u = 1\) corresponds to the situation before the epidemic, no confinement at all. \(u = 0\) corresponds to lockdown, total confinement of all the population. \(0<u<1\) corresponds to partial confinement situations.

Following the method in Moussaoui and Auger (2020), it is possible to calculate a threshold for the release of confinement making it possible to avoid a second epidemic peak. A simple way to find this threshold is to consider the effective reproduction rate of the epidemic \({\mathcal {R}}_0(T^*)\) at time \(T^*\) of the release of confinement of the third phase and which is given by the following expression:

$$\begin{aligned} {\mathcal {R}}_0(T^*) = (u^{*})^2{\mathcal {R}}_0 S(T^*). \end{aligned}$$
(29)

where \({\mathcal {R}}_0\) is the basic reproduction number of the epidemic and \(S(T^*)\) the proportion of susceptible individuals at the time of the release of confinement \(T^*\). Here, we note \(u^{*} = u(T^*)\) which is the constant proportion of un-confined persons fixed at \(t = T^*\). Those persons are free to move exactly as they did before the epidemic started. In order to avoid a secondary peak, we need an effective \({\mathcal {R}}_0(T^*)\) smaller than 1 which leads to the next condition:

$$\begin{aligned} u^*=\frac{1}{\sqrt{{\mathcal {R}}_0S(T^*)}}. \end{aligned}$$

This formula means that it is necessary to end the confinement with a proportion below this threshold to avoid a secondary peak of the epidemic. In Moussaoui and Auger (2020), the authors show numerical simulations for successful and unsuccessful release of confinement.

3.2 The Model with Confinement and Masks

Protective measures have also been taken such as masks including social distancing. We will now consider the additional effect of wearing masks based on the article by Howard et al. (2020) . The authors claim that wearing masks reduces \({\mathcal {R}}_0\) by a factor \((1 - p q)^2\), where q is the efficacy of trapping viral particles inside the mask and p is the percentage of the population that wears masks. Now we assume that in addition to partial release of confinement at time \(T^*\), the government decides to make the wearing of the mask compulsory in certain risky places. The SEIR model with partial confinement and using mask is given by the system:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}&=-\beta _2S(t)I(t), \end{aligned}$$
(30)
$$\begin{aligned} \frac{\mathrm{d}E}{\mathrm{d}t}&=\beta _2 S(t)I(t)-k E(t), \end{aligned}$$
(31)
$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t}&=k E-\alpha I, \end{aligned}$$
(32)
$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}&=\alpha I, \end{aligned}$$
(33)

where \(\beta _2= (u^{*})^2 (1-pq)^2\beta \).

As a consequence, combining the two models, the one for confinement, Moussaoui and Auger (2020), and the one for use of masks, Howard et al. (2020), we get the following formula for the effective basic reproduction number of the epidemic at the time of the release of confinement \(t=T^*\) with use of masks:

$$\begin{aligned} {\mathcal {R}}_0(T^*) =(1 - pq)^2 (u^{*})^2 {\mathcal {R}}_0S(T^*) \end{aligned}$$
(34)

Consequently, we find a new threshold for the release of confinement with masks in order to avoid a second epidemic peak:

$$\begin{aligned} u^{*}=\frac{1}{(1 - pq) \sqrt{{\mathcal {R}}_0 S(T^*)}}. \end{aligned}$$
(35)

Threshold formulas were presented in Moussaoui and Auger (2020), but here we generalize to the case of protection with masks.

3.3 Comparison of the Final Sizes of the Epidemic for Pure Confinement Strategy and Pure Mask Strategy

In Moussaoui and Auger (2020), the authors established the following final size relation in the case of pure confinement:

$$\begin{aligned} R_c(\infty )\simeq {\mathcal {R}}_0R(T)\frac{1-(1 - v^*)^2}{1-(1 - v^*)^2{\mathcal {R}}_0}. \end{aligned}$$
(36)

where \(v^* = 1 - u^*\) which is the constant proportion of confined individuals imposed by the government at time \(t>T^*\). When \(v^* \rightarrow 1\) (corresponding to lockdown measures), the final size of the epidemic will be:

$$\begin{aligned} R(\infty )\simeq {\mathcal {R}}_0R(T^*). \end{aligned}$$
(37)

A similar argument may be used to establish the final size of the epidemic in the case of pure mask strategy without confinement:

$$\begin{aligned} R_m(\infty )\simeq {\mathcal {R}}_0R(T^*)\frac{1-(1-pq)^2}{1-(1-pq)^2{\mathcal {R}}_0}. \end{aligned}$$
(38)

When \(pq \rightarrow 1\), corresponding to all the population uses masks of total efficacy, the final size of the epidemic will be:

$$\begin{aligned} R(\infty )\simeq {\mathcal {R}}_0R(T^*). \end{aligned}$$
(39)

The two strategies, total confinement (\(v^* \rightarrow 1\)) and \(100\%\) efficient mask worn by everybody (\(pq \rightarrow 1\)) allow to stop definitively the epidemic. Furthermore, both lead to the same final size of the epidemic, \({\mathcal {R}}_0R(T^*)\). However, it seems clear that to avoid a slowdown in economic activity, it seems preferable to use protective measures with masks rather than a total confinement of the population resulting in a major economic slowdown and a significant increase in unemployment.

3.4 The Model with Confinement, Masks and the Effect of the Proportion of Asymptomatic Infected Individuals

Let f be the constant proportion of asymptomatic infected. In Liu et al. (2020), the proportion of asymptomatic people was estimated to be \(f=0.2\). On the Charles de Gaulle French aircraft carrier, around \(60\%\) of the sailors on board were infected with the virus and around half of them were asymptomatic. Last July, the French national public health agency was able to determine that around \(24.3\%\) of positive cases did not show symptoms. Consequently, the value of the parameter f is not well known and it appears useful to study the sensitivity of the model with respect to it.

We assume that the rate of transition from the infected compartment to the removed compartment is written as follows:

$$\begin{aligned} \alpha (f) = f \alpha _1 + (1-f) \alpha _2, \end{aligned}$$
(40)

where \(\frac{1}{\alpha _1}\) represents the average infection time for an asymptomatic individual which is about 10 days, while \(\frac{1}{\alpha _2}\) represents the average infection time before isolation at hospital or quarantine for a symptomatic individual which can be estimated about 1 or 2 days because symptomatic people are in principle quickly isolated. In our model, isolated individuals go into the removed compartment because they no longer contribute to the infection cycle at all.

The travel behavior, particularly in urban areas, of people infected with a disease is generally modified. In Perkins et al. (2016), the authors study these changes in urban mobility behavior in the case of dengue. While it seems acceptable to think that asymptomatic infected people who are not in quarantine continue to move around as usual, the movement behavior of symptomatic infected individuals may be altered by the effects of the disease. In our model, we will therefore assume that asymptomatic infected move with the same rate as uninfected individuals, i.e., \(\frac{\gamma }{T_A}\) for a move from site \(A=[H,W,P]\) to any other place. The proportion at the fast equilibrium of asymptomatic individuals in the different places is therefore always given by the following formula:

$$\begin{aligned} u_H^{*} = \frac{T_H}{D},~~~u_W^{*} = \frac{T_W}{D},~~~u_P^{*} = \frac{T_P}{D}. \end{aligned}$$
(41)

However, it seems acceptable to assume that symptomatic individuals with the disease move less during the day and stay at home longer. In our model, we can represent this effect by increasing the time slot corresponding to the home and reducing the times slots corresponding to the places visited daily, work and public locations.

$$\begin{aligned} T^S_H = \theta T_H,~~~T^S_W = \phi T_W,~~~T^S_P = \psi T_P. \end{aligned}$$
(42)

with \(\theta > 1\), \(\phi < 1\) and \(\psi < 1\) and still checking:

$$\begin{aligned} D = \theta T_H + \phi T_W + \psi T_P. \end{aligned}$$
(43)

With these assumptions, symptomatic infected individuals spend more time at home and less time at work and in public places. As a result, the fast equilibrium frequencies of symptomatic infected individuals become:

$$\begin{aligned} {u^S_H}^{*} = \frac{\theta T_H}{D}, \ \ \ {u^S_W}^{*} = \frac{\phi T_W}{D}, \ \ \ {u^S_P}^{*} = \frac{\psi T_P}{D}. \end{aligned}$$
(44)

For example, if we assume that asymptomatic infected people spend 14 hours per day at home, 8 hours at work and 2 hours in public places while symptomatic spend 19 hours a day at home, 4 hours at work and 1 hour in public places. The previous parameters are equal to \(\theta = 1.36\) and \(\phi = \psi = 0.5\). This only adds two parameters as they are related by relation \(14 \theta + 8 \phi + 2 \psi = 24\).

Furthermore, the overall rate of infection is modified and will depend on the proportion f of asymptomatic infected persons. We recall that we assume that the proportion of asymptomatic infected persons remains constant for all t. Under these conditions, the global contact rate becomes \(\beta _1(f)\) :

$$\begin{aligned} \beta _1(f) = (u^{*})^2 \beta (f), \end{aligned}$$
(45)

where \(\beta (f)\) is the global rate of contact in the absence of confinement with a proportion f of asymptomatic infected persons:

$$\begin{aligned} \beta (f)= & {} f (\beta _H (u_H^{*})^2 + \beta _W (u_W^{*})^2 + \beta _P (u_P^{*})^2) \nonumber \\&+ (1-f) (\beta _H u_H^{*} {u^S_H}^{*} + \beta _W u_W^{*} {u^S_W}^{*} + \beta _W u_P^{*} {u^S_P}^{*}), \end{aligned}$$
(46)

This expression takes into account infections between sane individuals and asymptomatic infected individuals as well as those with symptomatic infected. Finally, the global rate of contact with confinement and with a proportion f of asymptomatic is written more simply as follows:

$$\begin{aligned} \beta _1(f)= & {} \frac{(u^*)^2}{D^2} \bigg (\beta _H T_H^2 (f + \theta (1 -f))\nonumber \\&+ \beta _W T_W^2 (f + \phi (1 -f)) + \beta _P T_P^2 (f + \psi (1 -f))\bigg ), \end{aligned}$$
(47)
Fig. 4
figure 4

Sensitivity analysis for system (30)–(33) taking into account the proportion of unconfined people, the masks as well as the effect of change in urban displacement behavior of the symptomatic (Color figure online)

Full size image

Finally, taking into account confinement and the masks we obtain an overall contact rate:

$$\begin{aligned} \beta _2(f) = (1 - pq)^2 \beta _1(f), \end{aligned}$$
(48)

4 Discussion of the Results

4.1 Sensitivity Analysis with Respect to Parameters

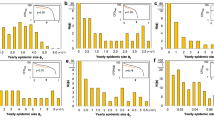
Figure 4 shows the sensitivity analysis with respect to the various parameters of the model taking into account the proportion of unconfined people, the masks as well as the effect of change in urban displacement behavior of the symptomatic. As we might expect, the effect on the population of susceptible individuals is contrary to the effect on the population of exposed, infected and removed ones. For example, a small increase in the proportion of unconfined persons, u, significantly increases the number of infections but decreases the number of susceptible persons. It is in fact normal that by reducing the number of people confined, we increase contacts and facilitate infection.

The parameters having the most effect on the infection by promoting the epidemic are the proportion of people outside confinement as well as the parameters which favor infection at work, \(T_W\), \(\beta _W\) and \(\phi \) where the contact rate is supposed to be much higher than in the other places. The parameters having the most effect in slowing the epidemic are the control parameters on the masks p and q and parameter \(\alpha _2\). A small increase in \(\alpha _2\) corresponds to a decrease in isolation time for a symptomatic person. It is understandable that by isolating symptomatic people more quickly by practicing a policy of rapid and numerous tests, this will slow down the epidemic.

4.2 Threshold in Case of Partial Release of Confinement

While most countries are reluctant to lift severe confinement in fear of seeing a secondary/third peak in the covid-19 epidemic start again, it is useful to use our model for evaluating a threshold for release of confinement and protective measures to avoid a restart of the epidemic.

We now present numerical simulations in different cases. We still mention the covid-19 epidemic with parameters values mentioned above for the simulation of the complete and aggregated models. Under these conditions, Bacaër (2020) found \({\mathcal {R}}_0=2.33\) while Moussaoui and Auger (2020) found \({\mathcal {R}}_0 = 2.1\) for Algeria. However, if infectious persons are not tested and isolated rapidly, the infectivity period can last much more than one day and can be as large as ten days or more, leading to much larger values for \({\mathcal {R}}_0\), up to 3–3.5. It is for this reason that we have tested larger values of \({\mathcal {R}}_0\).

Assuming that the lifting of confinement occurs after a severe confinement phase and that there are still approximately \(95\%\) of susceptible persons not yet infected, we obtain the following threshold values to avoid a secondary peak, with \(S(T^*) = 0.95\), for different values of \({\mathcal {R}}_0\), see Table 1.

Table 1 Threshold for the release of confinement for different \({\mathcal {R}}_0\)
Full size table

Table 1 shows that it is necessary to keep confined a large part of the population, almost \(27\%\) for an \({\mathcal {R}}_0\) of 2, and up to \(45\%\) for an \({\mathcal {R}}_0\) of 3.5. These values remain high and show that it is necessary to couple partial release of confinement with protective measures such as the wearing of masks.

4.3 Threshold in Case of Partial Release of Confinement and Use of Masks

Figure 5 illustrates the threshold for the release of confinement which allows to avoid a second peak of the epidemic in the case \({\mathcal {R}}_0 = 3\). In that example, the proportion of the population who is allowed to end confinement and to move again as before the start of the epidemic is 0.592, see table 1. It shows that below this confinement threshold \(u^* = 0.59\), there is no need to wear masks, shown in Fig. 5 upper figure. Above this threshold \(u^* = 0.60\), it is necessary to ask the population to wear masks, shown in Fig. 5 lower figure. For example, it is needed to use masks worn by \(15\%\) of the population and with efficacy almost equal to \(15\%\).

Fig. 5
figure 5

Illustration of the threshold for the release of confinement, \(u^* = 0.592\), for \({\mathcal {R}}_0 = 3\). Upper figure: Below the threshold \(u^*=0.59\), it is not even needed to use mask. Indeed, without mask \(p=q=0\), \({\mathcal {R}}_0(T^*) < 1\). Lower figure: Above the threshold \(u^*=0.60\), without mask \(p=q=0\), \({R}_0(T^*) > 1\), there is a second peak after the release of the confinement. In order to avoid it, it is needed to use mask in order to be above the level curve \({\mathcal {R}}_0(T^*) = 1\) (Color figure online)

Full size image

Figure 6 illustrates the threshold for a total release of confinement \(u^*=1\) for different \({\mathcal {R}}_0\) ranging from 2 to 3.5. In this case, all individuals are allowed to break out of confinement and behave exactly as before the epidemic. Figure  6 shows that the higher the \({\mathcal {R}}_0\), the more the level curve corresponding to \({\mathcal {R}}_0(T^*) = 1\) is shifted at the top right of each of the four sub-figures, which means that to reach the un-confinement threshold making it possible to avoid a second peak, it is necessary to ask a larger proportion of the population to wear increasingly effective masks.

Fig. 6
figure 6

Illustration of the threshold for a total release of confinement, \(u^* = 1\), for different values of \({R}_0\). Up left: \({\mathcal {R}}_0 = 2\). Up right: \({\mathcal {R}}_0 = 2.5\). Down left: \({\mathcal {R}}_0 = 3\). Down right: \({\mathcal {R}}_0 = 3.5\) (Color figure online)

Full size image

Figure 6 shows that it is possible to lift totally confinement with success for an epidemic of \({\mathcal {R}}_0 = 2\), with \(50\%\) efficacy masks worn by only \(50\%\) of the population, whereas for \({\mathcal {R}}_0 = 2.5\), we need on average \(60\%\) efficacy masks worn by \(60\%\) of the population, for \({\mathcal {R}}_0 = 3\), \(65\%\) efficacy masks worn by \(65\%\), and for \({\mathcal {R}}_0 = 3.5\), \(70\%\) efficacy masks worn by at least \(70\%\) of the population.

Fig. 7
figure 7

Illustration of the threshold for an almost total release of confinement at \(90\%\), i.e., \(u^* = 0.9\), for different values of \({R}_0\). Up left : \({\mathcal {R}}_0 = 2\). Up right : \({\mathcal {R}}_0 = 2.5\). Down left : \({\mathcal {R}}_0 = 3\). Down right : \({\mathcal {R}}_0 = 3.5\) (Color figure online)

Full size image

Figure 7 up right shows that for an epidemic with an \({\mathcal {R}}_0\) of 2.5, corresponding to the value usually reported for Covid-19, the release of confinement for \(90\%\) of the population is possible without risk, if \(80\%\) of the population wears masks in risky areas with efficacy \(40\%\) which more or less corresponds to the efficacy of masks not reserved for hospital staff but in sold in local shops for the public which seems realistic.

In addition, with teleworking, we can consider that if around \(10\%\) of people on average stay at home and are therefore not very prone to infection, this ensures successful release of confinement without a second peak with an \({\mathcal {R}}_0\) of up to 2.5. It is also obviously very important to couple protection with masks with the use of tests to trace the chains of contamination and quickly isolate infected people in areas where the epidemic starts again after lifting of confinement.

5 Conclusion and Perspectives

These results show that the coupling of a release of confinement at a almost total level \(90\%\) and even more, coupled to the use of masks by a reasonable fraction of the population in risky areas, is possible in good safety conditions. We may achieve this goal by keeping a rather small proportion of the population (\(10\%\)) in a state of total confinement. In addition, the situation could be even more favorable because of the protective measures taken in establishments for the elderly to avoid contacts as well as teleworking allowing for many people to avoid risky places such as workplaces and public transportations. Consequently, this makes it possible to reach this goal and to obtain this target rate of partial confinement more easily. An even better efficiency of the masks as well as a higher proportion of people wearing masks, which seems to be the case especially in France where the masks are compulsory in many public places, should make it possible to carry out the end of confinement still in better conditions.

In the future, we plan to develop mathematical models taking into account the daily movements of individuals in different places, schools and universities, workplaces, transport and public places, shops where the risks of infection are different, Liu et al. (2020) and human behavior Manfredi and d’Onofrio (2013). It also appears important to take into account the age structure of the populations insofar as the intensities of social contacts strongly depend on the age groups, Liu et al. (2020). Because the processes take place at different time scales, daily for travel and several months for the epidemic, it remains possible to use methods of aggregation of variables to reduce the dynamical system for which it still will be possible to obtain analytical results such as expression for confinement threshold.