An SIS model for the epidemic dynamics with two phases of the human day-to-day activity

Abstract

An SIS model is analyzed to consider the contribution of community structure to the risk of the spread of a transmissible disease. We focus on the human day-to-day activity introduced by commuting to a central place for the social activity. We assume that the community is classified into two subpopulations: commuter and non-commuter, of which the commuter has two phases of the day-to-day activity: private and social. Further we take account of the combination of contact patterns in two phases, making use of mass-action and ratio-dependent types for the infection force. We investigate the dependence of the basic reproduction number on the commuter ratio and the daily expected duration at the social phase as essential factors characterizing the community structure, and show that the dependence is significantly affected by the combination of contact patterns, and that the difference in the commuter ratio could make the risk of the spread of a transmissible disease significantly different.

1 Introduction

Since mid-December 2019, the outbreak of a febrile respiratory illness due to a novel coronavirus COVID-2019 in China is now spreading out internationally (WHO 2020). Its human-to-human transmissibility has been confirmed though the detail has been under investigation (ECDC 2020). Its exponentially increasing number of cases and large-scale spread of the emerging virus are being regarded as resulted from human-to-human transmission, initiated and promoted by the human mobility in global and local scales (Du Toit 2020; Liu and Saif 2020; Munster et al. 2020; Phan et al. 2020).

One of past well-recognized examples of such transportation-related global infection of a transmissible disease, SARS by severe acute respiratory syndrome coronavirus broke out in 2003, beginning with some infection on an airplane (Wang and Wu 2018). There have been many investigations concerning the effect of transportation (or population dispersal) on the spread of a transmissible disease, and especially conducted been many theoretical/mathematical studies taken account of such a possibility for some individuals to become infective during transportation in order to such an significant contribution of transport-related infection [as a recent review, see Walters et al. (2018) and references therein; especially for the SARS virus transmission, see Wang (2014)]. Not only the particular transportation with a long travel, but also the human quotidian mobility as a common phase of the human activity can be considered as one of relevant factors that could cause the spread of a transmissible disease such as influenza (WHO 2018). So is the case of today’s spread of COVID-2019 in each local region of every country (ECDC 2020; WHO 2020).

One choice to model such a transport-related infection is to use a disease transmission model based on the well-known patch models, which may be of so-called metapopulation model, described by ordinary differential equations or numerical network dynamics with a geographically divided population (Hethcote 1976; Rvachev and Longini 1985; Sattenspiel and Diez 1995; Sattenspiel and Herring 1998, 2003; Brauer and van den Driessche 2001; Arino and van den Driessche 2003; Wang and Mulone 2003; Wang and Zhao 2004, 2005; Cui et al. 2006; Keeling et al. 2010; Balcan and Vespignani 2011; Ball et al. 2015; Nakata and Röst 2015, and the references therein). In contrast to many of previous mathematical works focusing on the contribution of long-term migration (to cause the change in population size) or the infection during a short-term or mid-term temporal transportation between communities (e.g., the case of SARS) to a certain global scale of transmissible disease spread, we shall focus in this paper on the contribution of human quotidian activity (including only transportations as quotidian commuting) to the spread of transmissible disease within a community.

In this paper, we propose a specific model of so-called SIS type in a simplified geographical structure of a city with a central place (downtown) and some residential districts (outskirts) in the commuter belt, between which the quotidian commuting occurs (Fig. 1). At the central place, the commuters make their social activities. Falcón-Lezama et al. (2016) considered a very similar situation and analyzed a mathematical model of SEIR type with respect to the dengue epidemic dynamics and its control. Differently from theirs, the principal subject of our analysis about our model is the dependence of the spread of a transmissible disease on the community structure represented by the commuting subpopulation size, and we will try to discuss the community structure to have the smaller risk of the disease spread, that is, to have its higher resistance to the disease spread over the community. However, we shall not intend to make any discussion about the control to realize the smaller risk of the disease spread. This is because we will consider only daily activity characterizing the community structure and its contribution to the risk, so that we regard it as very hard to control any factors in such activity closely related to the daily life. Since the nature of such daily activity is gradually changing as the lifestyle becomes modified, we will try to give some arguments about the prospective change in the risk of the spread of a transmissible disease in future, and about the difference in the risk between communities different from each other in their structures.

2 Model

2.1 Private phase and social phase

Let us consider a community of which the population can be classified into two subpopulations: the subpopulation of individuals interacting to others mainly of the same residential district, for example, elders and infants (say, non-commuters); the subpopulation of individuals usually commuting the central place for their day-to-day living activities, for example, working, studying or shopping, etc. with interactions to others also from different residential districts.

Fig. 1

Schematic illustration of a typical structure of the city with residential districts (outskirts) and a central place (downtown) at which the commuters from different residential districts interact to each other in their social activities

Furthermore let us divide the commuter’s day-to-day activity into two phases: the activity in which the individual interacts to others mainly of the same residential district; the activity in which the individual interacts to others also from different residential districts. Let us call the former private phase, and the latter social phase. The non-commuters are regarded as staying at the private phase all day. The community consists of individuals at one of these two phases.

Fig. 2

Schematic examples of the structure of commuting route between residential districts and a central place. In a, the commuter can be considered to be at the private phase during commuting, because each commuter is independent of those from the other residential districts. In b or c, the commuters from different residential districts are mixed in their commuting routes, so that the commuter can be considered to be at the social phase during commuting with respect to our epidemic dynamics

The commuter is not necessarily at the social phase. If the most of commuters use their private transportation method, for example, own cars or bicycles as in a local city with a relatively small size, then the commuter can be considered to be at the private phase, because each commuter during commuting is independent of those from the other residential districts (Fig. 2a). In constrast, if the main commuting method between the residential districts and the central place is a public transportation in which the commuters from different residential districts are mixed, the commuter can be considered to be at the social phase of our modeling (Fig. 2b, c). In reality, some commuters could be considered to be at the private phase, while the other as being at the social phase. In further detail, commuting of each commuter could be considered to be at the private phase in the earlier period and at the social phase in the rest period. We remark that these two phases of our modeling are not to distinguish the commuters from the non-commuters, but to tell the situation in terms of the disease transmission dynamics, according to the detail of our modeling described in the following section.

Our modeling belongs to what is called the multitype model or the two-level mixing epidemic model in the terminology of Diekmann et al. (2013) (also see Ball et al. (1997) or the outlining review by Ball et al. (2015) and references therein), although our model is different from what is called the house hold epidemic model as described in the following sections. On the other hand, our model may be one of so-called meta-population models or two-patch spatial models, as so was in Britton and Giardina (2016), whereas our modeling does not consider the spatial patches but introduces the phases as described above.

2.2 Mobility dynamics of commuter subpopulation

In this section, we describe the modeling of the mobility dynamics for the commuter subpopulation in our model without any effect of epidemic dynamics. The commuter subpopulation is divided into two classes depending of the phase, that is, the private and the social phases, as introduced in the previous section. Let n indicate the size of commuter subpopulation at the private phase, and ${\widetilde{n}}$ at the social phase. Then we introduce the following mobility dynamics for the commuter subpopulation:

$$\begin{aligned} \begin{array}{rl} \dfrac{dn }{dt} &{}= -m_{\mathrm {rc}}n +m_{\mathrm {cr}}\widetilde{n} \\ \dfrac{d\widetilde{n}}{dt} &{}= m_{\mathrm {rc}}n -m_{\mathrm {cr}}\widetilde{n}, \end{array} \end{aligned}$$

(1)

where the rates of commuter’s phase-transition between the private and the social phases are given respectively by $m_{\mathrm {rc}}$ and $m_{\mathrm {cr}}$.

As easily seen from (1), the sum $n+{\widetilde{n}}$ is constant independently of time. This means that the size of commuter subpopulation is now assumed to be constant independently of time. Further, let us define the size of non-commuter subpopulation ${\overline{n}}$ which consists of the individuals who remain at the private phase all day.

As re-mentioned in the next section, as long as considering the epidemic dynamics for a certain time scale in this paper, we do not assume any transition between the commuter and the non-commuter. Besides, we assume that the change of population size with birth, death, and migration is negligible in the time scale for the epidemic dynamics of this paper. Hence the total population size of the community is assumed to be constant given by N, that of the commuter subpopulation is by pN, and that of the non-commuter subpopulation is by $(1-p)N$, where p is the commuter ratio, a positive constant such as $0< p < 1$. Therefore, for the mobility model given by (1), $n +\widetilde{n} = pN$ and ${\overline{n}} = (1-p)N$.

For the mobility model (1), the expected duration at the social phase is given by $1/m_{\mathrm {cr}}$, and the expected duration at the private phase by $1/m_{\mathrm {rc}}$ respectively. In the time unit of day, we can assume the following constraint about the expected durations at each phase since we focus on the day-to-day routine activity:

$$\begin{aligned} \dfrac{1}{m_{\mathrm {rc}}}+\dfrac{1}{m_{\mathrm {cr}}} = 1 \end{aligned}$$

(2)

which constrains the values of these parameters in this mobility model for the reasonability of modeling. Since the individual at the social phase necessarily comes back every day to the own residential district after a duration of stay at the central place, this constraint gives the dependence between the rates of phase-transition $m_{\mathrm {rc}}$ and $m_{\mathrm {cr}}$.

The mobility model (1) is the simplest one very popular in the modern theory of metapopulation and epidemic dynamics in a multi-patchy environment with migration process, while it may be regarded as one of so-called mover-stayer model in demographic research, in which the population consists of “mover” who changes states over time, and “stayer” who does not change states after the initial time. The mover-stayer model is essentially based on a discrete-time stochastic process with two independent Markov chains (Blumen et al. 1955; Spilerman 1972; Vermunt 2004), in contrast to our time-continuous deterministic model (1) with the system of ordinary differential equations. Note that our mobility model (1) is to govern the transition of two phases (i.e., states), not necessarily following the geographic (spatial) movement of commuters.

In the subsequent section to introduce the epidemic dynamics, we will divide each of the commuter and the non-commuter subpopulations further into susceptible and infective classes. Moreover we assume that the mobility is different between the susceptible and the infective commuters. The above-mentioned modeling will be extended to the population dynamics with an epidemic disease.

2.3 Epidemic dynamics with commuter and non-commuter subpopulations

For our modeling of an epidemic population dynamics with the day-to-day activity, we have set up the following assumptions including some already mentioned in the previous section:

• The disease is non-fatal;

• The birth, the death, and the migration are negligible in the time scale of epidemic dynamics under consideration;

• The transition between the non-commuter and the commuter is negligible in the time scale of epidemic dynamics under consideration;

• On the epidemic dynamics, the traffic of people between different residential districts has a contribution in an averaged way, with the mean-field approximation.

The first assumption means that the disease is not serious to cause the increase of death rate for the infected individual. The second and the third assumptions mean that the total population size, the sizes of non-commuter and commuter subpopulations are assumed constant independently of the time in the epidemic dynamics, as already mentioned in the previous section, given by N, $(1-p)N$, and pN. With the fourth assumption, we introduce a certain effect of the traffic of population between residential districts on the epidemic dynamics, so that individuals at the private phase are assumed to have an interaction to cause the disease transmission which is now given in a manner of the mean-field approximation.

With these assumptions, we shall consider the following mathematical model with the extension of the mobility model (1) described in the previous section, taking account of the dynamics of a disease transmission :

$$\begin{aligned} \begin{array}{rl} \dfrac{d\overline{S}}{dt} &{}= -{\varLambda } \overline{S} + \rho \overline{I} \\ \dfrac{d\overline{I}}{dt} &{}= {\varLambda } \overline{S} - \rho \overline{I} \\ \dfrac{dS }{dt} &{}= -\varLambda S +\rho I -m^{\mathrm {S}}_{\mathrm {rc}}S +m^{\mathrm {S}}_{\mathrm {cr}}\widetilde{S} \\ \dfrac{dI }{dt} &{}= \varLambda S -\rho I -m^{\mathrm {I}}_{\mathrm {rc}}I +m^{\mathrm {I}}_{\mathrm {cr}}\widetilde{I} \\ \dfrac{d\widetilde{S}}{dt} &{}= -{\widetilde{\varLambda }}\widetilde{S} +m^{\mathrm {S}}_{\mathrm {rc}}S -m^{\mathrm {S}}_{\mathrm {cr}}\widetilde{S} \\ \dfrac{d\widetilde{I}}{dt} &{}= {\widetilde{\varLambda }}\widetilde{S} +m^{\mathrm {I}}_{\mathrm {rc}}I -m^{\mathrm {I}}_{\mathrm {cr}}\widetilde{I} , \end{array} \end{aligned}$$

(3)

where symbols S and I represent respectively susceptible and infective subpopulations (see Fig. 3). The non-commuter subpopulation is given by $({\overline{S}} , {\overline{I}} )$: $\overline{n} ={\overline{S}} +{\overline{I}}$, while the commuter subpopulation is given by (S, I) and $({\widetilde{S}} , {\widetilde{I}} )$. The former (S, I) indicates the commuter at the private phase, and the latter $({\widetilde{S}} , {\widetilde{I}} )$ at the social phase: $n = S + I$ and ${\widetilde{n}} = {\widetilde{S}} +{\widetilde{I}}$. From the assumptions with respect to the population sizes, the total population size of the community, the sizes of non-commuter and commuter subpopulations are respectively given by $N={\overline{S}} +{\overline{I}} +S +I +\widetilde{S} +\widetilde{I}$, $(1-p)N = {\overline{n}} = {\overline{S}} +{\overline{I}}$, and $pN = n +{\widetilde{n}} = S +I +\widetilde{S} +\widetilde{I}$.

Fig. 3

Modelling for the system (3). See the detail in the main text

$\varLambda$ and ${\widetilde{\varLambda }}$ represent the infection forces respectively at the private phase and at the social phase. As introduced later in this section, $\varLambda$ is a function of $({\overline{S}} , {\overline{I}} , S , I )$, and ${{\widetilde{\varLambda }}}$ is a function of $(\widetilde{S},\widetilde{I})$. Positive parameter $\rho$ is the recovery rate for the infective individual only at the private phase. We do not assume the recovery at the social phase (i.e., in the central place) because it is little likely that the individual might recover from the disease during commuting and acting in the day-to-day routine out of the residential district. Moreover, we do not consider the recovery within one day after the infection, that is, the recovery is assumed to take more than one day. This means that $1/\rho > 1$ in the time unit of day, since the value of $1/\rho$ means the expected duration of the infectivity after the infection. So we shall take the constraint for $\rho$ such that $\rho < 1$ in the time unit of day. After the recovery, the individual becomes susceptible so as to be possible to get infected again. This means that the epidemic dynamics of our model is of SIS type. The social condition of the medical treatment for a transmissible disease would affect the expected duration taken for the recovery, that is, the value of $\rho$.

Following the modeling described in the previous section, the rates of commuter’s phase-transition between the private and the social phases are given respectively by $m^{\mathrm {S}}_{\mathrm {rc}}$ and $m^{\mathrm {S}}_{\mathrm {cr}}$ for the susceptible commuter, $m^{\mathrm {I}}_{\mathrm {rc}}$ and $m^{\mathrm {I}}_{\mathrm {cr}}$ for the infective commuter (Fig. 3). Hence the expected duration at the social phase is given by $1/m^{\mathrm {S}}_{\mathrm {cr}}$ and $1/m^{\mathrm {I}}_{\mathrm {cr}}$ respectively. In the same way, the expected duration at the private phase is given by $1/m^{\mathrm {S}}_{\mathrm {rc}}$ and $1/m^{\mathrm {I}}_{\mathrm {rc}}$ respectively. In the time unit of day, we can assume the following constraints about the expected durations at each phase, since we focus on the day-to-day routine activity, as already mentioned by (2) in the previous section:

$$\begin{aligned} \dfrac{1}{m^{\mathrm {S}}_{\mathrm {rc}}}+\dfrac{1}{m^{\mathrm {S}}_{\mathrm {cr}}} = 1 ;\quad \dfrac{1}{m^{\mathrm {I}}_{\mathrm {rc}}}+\dfrac{1}{m^{\mathrm {I}}_{\mathrm {cr}}} = 1 \end{aligned}$$

(4)

which will constrain the values of these parameters in our analysis on the model for the reasonability of modeling.

From the constraints of (4), we can replace at need these parameters to the following $\tau _{\mathrm {S}}$ and $\tau _{\mathrm {I}}$:

$$\begin{aligned} \dfrac{1}{m^{\mathrm {S}}_{\mathrm {cr}}}=\tau _{\mathrm {S}}; \quad \dfrac{1}{m^{\mathrm {S}}_{\mathrm {rc}}}=1-\tau _{\mathrm {S}}; \quad \dfrac{1}{m^{\mathrm {I}}_{\mathrm {cr}}}=\tau _{\mathrm {I}}; \quad \dfrac{1}{m^{\mathrm {I}}_{\mathrm {rc}}}=1-\tau _{\mathrm {I}}, \end{aligned}$$

(5)

where $0<\tau _{\mathrm {S}}< 1$ and $0< \tau _{\mathrm {I}}< 1$. Parameters $\tau _{\mathrm {S}}$ and $\tau _{\mathrm {I}}$ respectively represent the expected duration at the social phase in the time unit of day about the susceptible commuter and the infective one respectively.

2.4 Forces of infection

Infection forces $\varLambda$ and ${\widetilde{\varLambda }}$ are now assumed to satisfy the following conditions:

$$\begin{aligned} \begin{array}{ll} \left. \varLambda \right| _{({\overline{I}} ,\, I )= (0, 0)} = 0 ;\quad &{} \left. {\widetilde{\varLambda }}\right| _{\widetilde{I} = 0} = 0 ; \\ \left. \dfrac{\partial \varLambda }{\partial \overline{S}}\right| _{({\overline{I}} ,\, I )= (0, 0)} = \left. \dfrac{\partial \varLambda }{\partial {S}}\right| _{({\overline{I}} ,\, I )= (0, 0)} = 0 ;\quad &{} \left. \dfrac{\partial {{\widetilde{\varLambda }}}}{\partial \widetilde{S}}\right| _{\widetilde{I }=0} = 0 ; \\ \left. \dfrac{\partial \varLambda }{\partial \overline{I}}\right| _{({\overline{I}} ,\, I )= (0, 0)} = \left. \dfrac{\partial \varLambda }{\partial I }\right| _{({\overline{I}} ,\, I )= (0, 0)} =\lambda (\overline{S} , S )>0 ;\qquad &{} \left. \dfrac{\partial {{\widetilde{\varLambda }}}}{\partial \widetilde{I}}\right| _{\widetilde{I }=0} ={{\widetilde{\lambda }}} (\widetilde{S})>0. \end{array} \end{aligned}$$

(6)

The former four assumptions for $\varLambda$ and ${{\widetilde{\varLambda }}}$ mean that the infection never occurs with no infective individual (i.e., at the disease-free state), and the latter two do that the secondary infection necessarily occurs once some infective individuals appear in the community. Note that commuters from different residential districts at the social phase are assumed to be mixed in the central place, and the infection in the central place follows the assumption of complete mixing as the application of the mean-field approximation for the epidemic dynamics. Similarly, the infection at the private phase is assumed to follow the complete mixing, so that there is no difference in the contribution to the disease infection between non-commuter and commuter at the private phase.

In this paper, as for $\varLambda$ and ${{\widetilde{\varLambda }}}$, we will consider the mass-action and the ratio-dependent (frequency-dependent) types. The former can be regarded as a modeling for the case that the contact rate could be assumed to be proportional to the population density, while the latter can be for the case that the contact rate could be assumed constant independently of the population density. Therefore, with the above-mentioned assumption of complete mixing, we can give the following functions as each type of the infection force:

$$\begin{aligned} \text {MASS-ACTION TYPE:}&\left\{ \begin{array}{l} \varLambda ({\overline{S}}, {\overline{I}}, S, I) = \beta \,\dfrac{{\overline{I}} + I}{{\overline{S}} +{\overline{I}} + S+I}\,\kappa ({\overline{S}} +{\overline{I}} + S+I) = \beta \kappa ({\overline{I}}+I) ; \\ {{\widetilde{\varLambda }}}(\widetilde{ S},\widetilde{ I}) = \beta \dfrac{{\widetilde{I}}}{\widetilde{ S}+\widetilde{ I}}\, K(\widetilde{ S}+\widetilde{ I}) = \beta K{\widetilde{I}}. \end{array} \right. \end{aligned}$$

(7)

$$\begin{aligned} \text {RATIO-DEPENDENT TYPE:}&\left\{ \begin{array}{l} \varLambda ({\overline{S}} , {\overline{I}} , S , I ) = \beta \dfrac{{\overline{I}} +I }{{\overline{S}} +{\overline{I}} +S +I }\, \omega \, ; \\ {{\widetilde{\varLambda }}}(\widetilde{ S},\widetilde{ I}) = \beta \dfrac{{\widetilde{I}}}{{\widetilde{S}}+{\widetilde{I}}}\, \varOmega . \end{array} \right. \end{aligned}$$

(8)

Here $\beta$ is the probability of infection per contact between a susceptible and an infective, which significantly depends on the nature of the disease transmissibility. For the mass-action type, the contact rate is given by $\kappa ({\overline{S}} +{\overline{I}} + S+I)$ at the private phase and by $K(\widetilde{ S}+\widetilde{ I})$ at the social phase with positive constant coefficients $\kappa$ and K, while for the ratio-dependent type, it is given by a constant $\omega$ at the private phase and by a constant $\varOmega$ at the social phase. These positive parameters $\kappa$, K, $\omega$, and $\varOmega$ depend not only on the nature of disease transmission (e.g., route) but also on the characteristics of community (e.g., the condition of public health, the social custom/manner, and the kind of principal job if it can be identified). Then, for each type of the infection force, we can get the following formulas of $\lambda (\overline{S} , S )$ and ${{\widetilde{\lambda }}} (\widetilde{ S})$ defined in (6):

$$\begin{aligned} \text{ MASS-ACTION } \text{ TYPE: }&\qquad \lambda (\overline{S} , S ) = \beta \kappa ;\quad {{\widetilde{\lambda }}} (\widetilde{ S}) = \beta K, \end{aligned}$$

(9)

$$\begin{aligned} \text{ RATIO-DEPENDENT } \text{ TYPE: }&\qquad \lambda (\overline{S} , S ) = \dfrac{\beta \omega }{{\overline{S}} +S } ;\quad {{\widetilde{\lambda }}} (\widetilde{ S}) = \dfrac{\beta \varOmega }{{\widetilde{S}}}. \end{aligned}$$

(10)

3 Equilibrium population distribution

3.1 Disease-free equilibrium

From (3), we have the following ordinary differential equation in terms of the commuter population size at the private phase when no infective exists, that is, at the disease-free state:

$$\begin{aligned} \dfrac{dS }{dt}&= -m^{\mathrm {S}}_{\mathrm {rc}}S +m^{\mathrm {S}}_{\mathrm {cr}}\widetilde{S} = -m^{\mathrm {S}}_{\mathrm {rc}}S +m^{\mathrm {S}}_{\mathrm {cr}}(p N -S ) = (m^{\mathrm {S}}_{\mathrm {rc}}+m^{\mathrm {S}}_{\mathrm {cr}}) \Big ( \dfrac{ p N }{ 1+m^{\mathrm {S}}_{\mathrm {rc}}/m^{\mathrm {S}}_{\mathrm {cr}} } -S \Big ). \end{aligned}$$

(11)

Hence we can immediately find that the commuter population distribution necessarily approaches its equilibrium state with $(S ,\, \widetilde{S} ) =(S_0^*,\, \widetilde{S}_0^*)$ given by

$$\begin{aligned} S_0^* = \dfrac{ p N }{ 1+m^{\mathrm {S}}_{\mathrm {rc}}/m^{\mathrm {S}}_{\mathrm {cr}} } = \big (1-\tau _{\mathrm {S}}\big )p N ;\quad \widetilde{S}_0^* = \tau _{\mathrm {S}}p N , \end{aligned}$$

(12)

where we used (5). It is clearly seen that the equilibrium size of subpopulation at each phase is proportional to the expected duration at the phase. As for the non-commuter subpopulation at the disease-free equilibrium, we have $\overline{S} = \overline{S}_0^*=(1-p )N$, since every individual is susceptible.

3.2 Endemic equilibrium

The existence of the endemic equilibrium $(\overline{S} , \overline{I} , S , I , \widetilde{S} , \widetilde{I} ) {=} (\overline{S}_+^*, \overline{I}_+^*, S_+^*, I_+^*, \widetilde{S}_+^*, \widetilde{I}_+^*)$ with positive values of the infectives $\overline{I}_+^*$, $I_+^*$, and $\widetilde{I}_+^*$ depends on the detail of functions $\varLambda$ and ${\widetilde{\varLambda }}$. Even for those given by (7) or (8), the equations of these equilibrium values appear messy. Following to the aim of this paper, we shall not look into the mathematical problem of the existence of the endemic equilibrium. As demonstrated by the figures given in the following sections, numerical calculations of (3) with (7) or (8) show its existence and stability. Although it can be conjectured that, for (3) with (7) or (8), the endemic equilibrium is globally stable whenever it exists, we shall not look into the stability of the endemic equilibrium either in this paper, and shall leave these issues a mathematically open problem about the model.

4 Basic reproduction number $\varvec{{\mathscr {R}}_0}$

In the biological context, the basic reproduction number is defined as the expected number of new cases of an infection caused by an infected individual, in a population consisting of susceptible contacts only (for the recent review about the definition, the translation, and the practical application, see Delamater et al. (2019)). Following the biological definition, a mathematical theory is used to derive the basic reproduction number as the spectrum radius of a specific matrix which is called the “next generation matrix” for a system of the ordinary differential equations governing an epidemic dynamics (see Diekmann et al. (2013) for a complete reference, or see van den Driessche (2017); Lewis et al. (2019) for the recent review).

As shown in “Appendix A”, making use of the next generation matrix with the theory given by van den Driessche and Watmough (2002, 2008), we can derive the following basic reproduction number ${\mathscr {R}}_{0}$ for the model (3):

$$\begin{aligned} {\mathscr {R}}_{0}&= \dfrac{\, 1\, }{2} \Bigg \{ \frac{\lambda ^*_0\overline{S}_{0}^*}{\rho } + \frac{\lambda ^*_0{S}_{0}^*}{\rho } + \frac{\rho +m_{\mathrm {rc}}^{\mathrm {I}}}{\rho } \, \frac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{ m_{\mathrm {cr}}^{\mathrm {I}}} \nonumber \\&\quad + \sqrt{ \Big ( \frac{\lambda ^*_0\overline{S}_{0}^*}{\rho } + \frac{\lambda ^*_0{S}_{0}^*}{\rho } - \frac{\rho +m_{\mathrm {rc}}^{\mathrm {I}}}{\rho } \, \frac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{ m_{\mathrm {cr}}^{\mathrm {I}}} \Big )^2 + 4\, \frac{m_{\mathrm {rc}}^{\mathrm {I}}}{\rho } \, \frac{\lambda ^*_0{S}_{0}^*}{\rho } \, \frac{{{\widetilde{\lambda }}}^*_0\widetilde{S}_{0}^*}{ m_{\mathrm {cr}}^{\mathrm {I}}} } \ \Bigg \} , \end{aligned}$$

(13)

with $\lambda ^*_0 := \lambda (\overline{S}_{0}^*,\, S_{0}^*)$ , ${\widetilde{\lambda }}^*_0 := {\widetilde{\lambda }} (\widetilde{S}_{0}^*,\, 0)$, $\overline{S}_{0}^*=(1-p )N$, $S_{0}^* = \big (1-\tau _{\mathrm {S}}\big )pN$, and $\widetilde{S}_{0}^* = \tau _{\mathrm {S}}pN$. Then we can get the following result about the condition that ${\mathscr {R}}_0 < 1$:

Theorem 1

The following condition is necessary and sufficient for $\mathscr {R}_{0} < 1$:

$$\begin{aligned}&\dfrac{\lambda ^*_0\overline{S}_{0}^*}{\rho } + \dfrac{\lambda ^*_0{S}_{0}^*}{\rho }<1, \quad \dfrac{\rho +m_{\mathrm {rc}}^{\mathrm {I}}}{\rho } \, \dfrac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{ m_{\mathrm {cr}}^{\mathrm {I}}} < 1,\nonumber \\&\quad \text{ and } \ \Big \{ 1 - \Big ( \dfrac{\lambda ^*_0\overline{S}_{0}^*}{\rho } + \dfrac{\lambda ^*_0{S}_{0}^*}{\rho } \Big ) \Big \} \Big ( 1 - \dfrac{\rho +m_{\mathrm {rc}}^{\mathrm {I}}}{\rho } \, \dfrac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{ m_{\mathrm {cr}}^{\mathrm {I}}} \Big ) > \dfrac{m_{\mathrm {rc}}^{\mathrm {I}}}{\rho } \, \dfrac{\lambda ^*_0{S}_{0}^*}{\rho } \, \dfrac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{m_{\mathrm {cr}}^{\mathrm {I}}} . \end{aligned}$$

(14)

The outline of proof is given in the last part of “Appendix A”.

For a convenience of the subsequent analysis, let us define the following extremal values of ${\mathscr {R}}_0$:

$$\begin{aligned} {\mathscr {R}}_{00} := \lim _{p\rightarrow 0+}{\mathscr {R}}_0 ;\quad {\mathscr {R}}_{01} := \lim _{p\rightarrow 1-0}{\mathscr {R}}_0. \end{aligned}$$

Especially ${\mathscr {R}}_{00}$ is the basic reproduction number when everyone always remains at the private phase, and we can get the following simple formula from (13) with (9) and (10):

$$\begin{aligned} {\mathscr {R}}_{00} = \dfrac{\lambda ^*_0N}{\rho } = \left\{ \begin{array}{cl} \dfrac{\beta \kappa N}{\rho }&{} \text{ for } \text{ the } \text{ mass-action } \text{ type } \text{ of } \text{ infection } \text{ force };\\ \dfrac{\beta \omega }{\rho }&{} \text{ for } \text{ the } \text{ ratio-dependent } \text{ type } \text{ of } \text{ infection } \text{ force }. \end{array} \right. \end{aligned}$$

(15)

5 Dependence of $\varvec{{\mathscr {R}}_0}$ on the commuter ratio p

Fig. 4

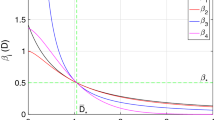
p-dependence of the basic reproduction number ${\mathscr {R}}_0$ given by (13) for each combination of (9) and (10). Numerical examples for each combination of formulas about $\varLambda$ of the private phase and ${{\widetilde{\varLambda }}}$ of the social phase, defined by (7) and (8), the mass-action and the ratio-dependent types with the following parameter values at the disease-free equilibrium: $N = 100,000$; $\tau _{\mathrm {S}} = 0.4$; $\tau _{\mathrm {I}}=0.3$; $\rho = 0.2$; $\beta \kappa = 3.0\times 10^{-6}$; $\beta K= 6.0\times 10^{-6}$; $\beta \omega = 0.3$; $\beta \varOmega = 0.6$. Commonly ${\mathscr {R}}_{00} = 1.5$, defined by (15)

Especially in this paper, we shall focus on the dependence of the basic reproduction number ${\mathscr {R}}_0$ on the commuter ratio p, and investigate how the commuter ratio p affects the value of ${\mathscr {R}}_0$ in our model. Indeed, as shown by numerical calculations of the value of ${\mathscr {R}}_0$ in Fig. 4, it is clear that the basic reproduction number ${\mathscr {R}}_0$ significantly depends on the commuter ratio p, and the p-dependence has different characteristics for different types of the infection force.

5.1 Case of only mass-action type of infection force

In this section, let us consider the case that the infection forces for two phases are only mass-action type. That is, the functions of infection force $\varLambda$ and ${{\widetilde{\varLambda }}}$ are given by (7). From (13) with $\lambda ^*_0$ and ${\widetilde{\lambda }}^*_0$ given by (9) at the disease-free equilibrium obtained in Sect. 3.1, we now have the following ${\mathscr {R}}_0$:

$$\begin{aligned} {\mathscr {R}}_0&= \dfrac{\, 1\, }{2}\, {\mathscr {R}}_{00} \Bigg [ \left( 1-\tau _{\mathrm {S}}p\right) + \big (\dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \big ) \tau _{\mathrm {S}}p \tau _{\mathrm {I}} \dfrac{K}{\kappa } \nonumber \\&\quad + \sqrt{ \Big \{ (1-\tau _{\mathrm {S}}p) - \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {S}}p \tau _{\mathrm {I}} \dfrac{K}{\kappa } \Big \}^2 + 4\,\dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}}\,\tau _{\mathrm {S}}p^2\tau _{\mathrm {I}}\dfrac{K}{\kappa } } \ \Bigg ], \end{aligned}$$

(16)

where ${\mathscr {R}}_{00}$ is given by (15) for the case of the mass-action type of infection force.

In Fig. 4, it is clearly shown that there is a case that the basic reproduction number ${\mathscr {R}}_0$ takes the smallest value at an intermediate commuter ratio. This is the case under a certain condition. In fact, numerical calculations of the value of ${\mathscr {R}}_0$ in Fig. 5 show that there is the case that the relation of ${\mathscr {R}}_0$ to the commuter ratio p appears monotonic, as in Fig. 5c. We can get the following results with respect to the existence of the extremal minimum value of ${\mathscr {R}}_0$ for an intermediate value of p (“Appendix B.1”):

Fig. 5

p-dependence of the basic reproduction number ${\mathscr {R}}_0$ given by (16) for the mass-action type of infection forces $\varLambda$ and ${{\widetilde{\varLambda }}}$ defined by (7). Numerical examples of ${\mathscr {R}}_0$ for different values of ${{\widetilde{\lambda }}}^* =\beta K$: a  $\beta K= 9.0\times 10^{-6}$; b  $\beta K= 6.0\times 10^{-6}$; c  $\beta K= 2.4\times 10^{-6}$. Commonly, $N = 100,000$; $\tau _{\mathrm {S}} = 0.4$; $\tau _{\mathrm {I}}=0.3$; $\rho = 0.2$; $\lambda ^* = \beta \kappa = 3.0\times 10^{-6}$; $\beta \omega = 0.3$; $\beta \varOmega = 0.6$; ${\mathscr {R}}_{00} = 1.5$

Theorem 2

For ${\mathscr {R}}_0$ with $\lambda ^*_0$ and ${\widetilde{\lambda }}^*_0$ of the mass-action type, it takes the extremal minimum for a unique value of $p = p^*$ such that $0< p^* < 1$, if and only if the following condition is satisfied:

$$\begin{aligned}&\Big \{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 \Big \} \sqrt{ \Big \{ (1-\tau _{\mathrm {S}}) - \tau _{\mathrm {S}} \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } \Big \}^2 + 4 \tau _{\mathrm {S}} \dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}} \tau _{\mathrm {I}} \dfrac{K}{\kappa } }\nonumber \\&\quad > \Big \{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } +1 \Big \} \Big \{ (1-\tau _{\mathrm {S}}) - \tau _{\mathrm {S}} \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } \Big \} - 4 \dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}} \tau _{\mathrm {I}} \dfrac{K}{\kappa }.\nonumber \\ \end{aligned}$$

(17)

Otherwise, it is monotonically decreasing in terms of p.

Corollary 1

Under the condition (17), ${\mathscr {R}}_0$ with $\lambda ^*_0$ and ${\widetilde{\lambda }}^*_0$ of the mass-action type takes the extremal minimum at $p = p^*$ which is given by

$$\begin{aligned} p^* = \dfrac{ \Big \{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } +1 \Big \} - \Big \{\left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 \Big \} \sqrt{ \dfrac{1-\tau _{\mathrm {S}}}{\tau _{\mathrm {S}}(1-\tau _{\mathrm {I}})\rho + 1} } }{ \tau _{\mathrm {S}} \Big \{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } +1 \Big \}^2 + 4\dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}} \tau _{\mathrm {I}} \dfrac{K}{\kappa } } . \end{aligned}$$

(18)

The condition (17) is equivalent to the condition that $0< p^* < 1$.

When such a $p^*$ exists, the basic reproduction number for $p = p^*$, that is, ${\mathscr {R}}_0^*={\mathscr {R}}_0\big |_{p = p^*}$ is expressed as the following formula (“Appendix B.1”):

$$\begin{aligned} {\mathscr {R}}_0^* = {\mathscr {R}}_{00} \left[ 1 - \dfrac{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+1+\tau _{\mathrm {S}}\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } + \tau _{\mathrm {S}} }{ \ \tau _{\mathrm {S}} \Big \{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } +1 \Big \}^2 + 4\dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}} \tau _{\mathrm {I}} \dfrac{K}{\kappa } \ } \right] . \end{aligned}$$

(19)

We note that the results given by Theorem 2 and Corollary 1 are independent of the disease-specific parameter $\beta$ and the total population size of the community N, whereas the value of ${\mathscr {R}}_0$ depends on them.

As shown by Fig. 6, the value of $K/\kappa$ is crucial for the existence of an intermediate commuter ratio $p^*$ to minimize the basic reproduction number ${\mathscr {R}}_0$. Only for relatively large value of $K/\kappa$, such $p^*$ exists:

Fig. 6

Parameter dependence about the p-dependence of the basic reproduction number ${\mathscr {R}}_0$ given by (16) for the mass-action type of infection forces. The left numerical result shows the parameter region of $(\rho , K/\kappa )$, identified by the condition (17) with $\tau _{\mathrm {S}} = 0.4$ and $\tau _{\mathrm {I}}=0.3$. For the upper region with the larger value of $K/\kappa$, ${\mathscr {R}}_0$ takes its extremal minimum for $p = p^*$ which is given by (18), while for the lower region with the smaller value of $K/\kappa$, it is monotonically decreasing in terms of p with the minimum at $p = 1$. $\xi ^*$ and $\xi _*$ are defined by (20) and (21): $\xi ^* = 0.712$ and $\xi _* = 0.590$ in this numerical calculation. The right numerical result is the contour map for the value of ${\mathscr {R}}_0$ in the $(p, K/\kappa )$-parameter space, with $N = 100,000$; $\tau _{\mathrm {S}} = 0.4$; $\tau _{\mathrm {I}}=0.3$; $\beta \kappa = 2.3\times 10^{-6}$; $\rho = 0.2$; ${\mathscr {R}}_{00} = 1.15$. The filled region of the right figure indicates that for ${\mathscr {R}}_0 < 1$

Corollary 2

There exists the following specific values $\xi ^*$ and $\xi _*$ for $K/\kappa$ such that if $K/\kappa \ge \xi ^*$, ${\mathscr {R}}_0$ takes the minimum for $p=p^*$ less than 1 independently of the recovery rate $\rho$ while if $K/\kappa \le \xi _*$, ${\mathscr {R}}_0$ is monotonically decreasing in terms of p independently of the recovery rate $\rho$:

$$\begin{aligned} \xi ^*&:= \dfrac{1-\tau _{\mathrm {I}}}{\tau _{\mathrm {I}}} \cdot \dfrac{ \sqrt{1-\tau _{\mathrm {S}}} }{ 1+\sqrt{1-\tau _{\mathrm {S}}} }; \end{aligned}$$

(20)

$$\begin{aligned} \xi _*&:= \dfrac{1}{\tau _{\mathrm {I}}} \cdot \dfrac{ (1-\tau _{\mathrm {S}}) \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\dfrac{\tau _{\mathrm {S}}}{\,\tau _{\mathrm {I}}\,} \right) }{ \dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}} \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\tau _{\mathrm {S}} \right) + \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+2\dfrac{\tau _{\mathrm {S}}}{\,\tau _{\mathrm {I}}\,} \right) + \sqrt{ \dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}} \big ( \dfrac{1}{1-\tau _{\mathrm {I}}}+\tau _{\mathrm {S}} \big ) } }. \end{aligned}$$

(21)

It can be easily found that

$$\begin{aligned} 0<\xi _*< \xi ^*<\dfrac{1-\tau _{\mathrm {I}}}{2\tau _{\mathrm {I}}} \end{aligned}$$

(22)

for any positive $\tau _{\mathrm {S}}$ and $\tau _{\mathrm {I}}$ less than 1. We note that $\xi ^* = \xi _*=({1-\tau _{\mathrm {I}}})/({2\tau _{\mathrm {I}}})$ for $\tau _{\mathrm {S}} = 0$, and $\xi ^* = \xi _*=0$ for $\tau _{\mathrm {S}} = 1$.

Fig. 7

$\tau _{\mathrm {I}}$-dependence of $\xi ^*$, $\xi _*$, and $\xi ^*-\xi _*$, defined by (20) and (21), numerically drawn with $\tau _{\mathrm {S}} = 0.4$

The reasonable value of $\tau _{\mathrm {I}}$ must be in general less than that of $\tau _{\mathrm {S}}$ from their meanings in our modeling. Further, $\xi ^*$ and $\xi _*$ are monotonically decreasing in terms of $\tau _{\mathrm {S}}$ and $\tau _{\mathrm {I}}$ as seen in Fig. 7. Supposing the value of $\tau _{\mathrm {S}}$ from 0.3 to 0.4 day (around 7 to 10 hours) as its reasonable value, we have $\xi ^*\big |_{\tau _{\mathrm {I}} = \tau _{\mathrm {S}}}$ from 0.65 to 1.06, and $\xi _*\big |_{\tau _{\mathrm {I}} = \tau _{\mathrm {S}}}$ from 0.55 to 0.91. When $\tau _{\mathrm {I}}$ is near $\tau _{\mathrm {S}}$, that is, when the disease weakly disturbs the day-to-day activity, the width of band $[\xi _*, \xi ^*]$ is rather narrow as indicated by Fig. 7, so that the existence of $p^*$ weakly depends on the recovery rate $\rho$, that is, on the period for recovery $1/\rho$.

In contrast, when the disease seriously disturbs the day-to-day activity and limits the infective individual’s day-to-day activity, that is, when $\tau _{\mathrm {I}}$ is sufficiently smaller than $\tau _{\mathrm {S}}$, the width of band $[\xi _*, \xi ^*]$ becomes significantly wider as indicated by Fig. 7. Then for a relatively wide range of the value of $K/\kappa$, the existence of $p^*$ significantly depends on the period for recovery $1/\rho$. It should be now remarked that this is the case that both values of $\xi ^*$ and $\xi _*$ are relatively large as seen from Fig. 7. For this reason, when $\tau _{\mathrm {I}}$ is sufficiently smaller than $\tau _{\mathrm {S}}$, a sufficiently large value of $K/\kappa$ is necessary for the existence of such a value $p^*$.

The ratio $K/\kappa$ can be regarded as an index to indicate the relative likelihood of contacts between the susceptible and the pathogen (or the infective individuals, especially if the disease transmission requires the direct contact between individuals) at the social phase, compared to those at the private phase. Since the reasonable values for $\xi ^*$ and $\xi _*$ estimated above are around one when $\tau _{\mathrm {I}}$ is near to $\tau _{\mathrm {S}}$, such a value $p^*$ is expected to exist if the likelihood of contacts between the susceptible and the pathogen is larger at the social phase than at the private phase. This would be a frequent situation for a variety of non-serious transmissible diseases in the reality.

As a general result from the above arguments, when the disease weakly disturbs the day-to-day activity, there could be very likely to exist a specific intermediate commuter ratio such as to minimize the basic reproduction number${\mathscr {R}}_0$. In contrast, for the disease seriously disturbing the day-to-day activity, such a value $p^*$ could exist only under the situation that the contacts between the susceptible and the pathogen is several times more likely at the social phase than at the private phase. We shall detail the dependence of ${\mathscr {R}}_0$ on the commuter ratio p and the other parameters in the rest of this section.

From the above results, we have found that the basic reproduction number ${\mathscr {R}}_0$ takes its maximal value for $p = 0$ or $p = 1$. More clearly we can get the following result (“Appendix B.1”):

Theorem 3

${\mathscr {R}}_0$ given by (16) takes the maximal value

$$\begin{aligned} \left\{ \begin{array}{ll} {\mathscr {R}}_{00} \text{ when } p=0\text{, } &{}\quad \text{ if } \;\Big ( \dfrac{1}{1-\tau _{\mathrm {I}}} + \tau _{\mathrm {S}}\rho \Big ) \tau _{\mathrm {I}} \dfrac{K}{\kappa } < 1; \\ {\mathscr {R}}_{01} \text{ when } p=1\text{, } &{}\quad \text{ if } \;\Big ( \dfrac{1}{1-\tau _{\mathrm {I}}} + \tau _{\mathrm {S}}\rho \Big ) \tau _{\mathrm {I}} \dfrac{K}{\kappa } > 1. \end{array} \right. \end{aligned}$$

(23)

Fig. 8

$K/\kappa$-dependence of ${\mathscr {R}}_{00}$, ${\mathscr {R}}_0^*$, and ${\mathscr {R}}_{01}$, given by (15) and (19) for the mass-action type of infection force, numerically calculated with $N = 100,000$; $\tau _{\mathrm {S}} = 0.4$; $\tau _{\mathrm {I}}=0.3$; $\beta \kappa = 2.3\times 10^{-6}$; $\rho = 0.2$. In this numerical calculation, ${\mathscr {R}}_{00} = 1.15$, and the ranges from the left to the right are [0, 0.973], (0.973, 1.51], (1.51, 1.92], (1.92, 2.21], and $(2.21, \infty )$. The attached graphs show the representative p-dependence of ${\mathscr {R}}_0$ for each parameter range. For the detail explanation, see the main text

Figure 8 numerically demonstrates the dependence of the maximal and the minimal values of ${\mathscr {R}}_0$ on the parameter value of $K/\kappa$, following the appearance of a specific value $p^*$. For sufficiently small $K/\kappa$, the range $([+],\,*\, ,-)$ in Fig. 8, ${\mathscr {R}}_0$ is monotonically decreasing in terms of p, where ${\mathscr {R}}_{00}> 1 > {\mathscr {R}}_{01}$. For the range $([+],\,-\, ,-)$ in Fig. 8, the extremal minimum of ${\mathscr {R}}_0$ exists, and ${\mathscr {R}}_{00}> 1> {\mathscr {R}}_{01}>{\mathscr {R}}_0^*$. Further, ${\mathscr {R}}_{00}> {\mathscr {R}}_{01}>1>{\mathscr {R}}_0^*$ for the range $([+],\,-\, ,+)$, ${\mathscr {R}}_{00}> {\mathscr {R}}_{01}>{\mathscr {R}}_0^*> 1$ for the range $([+],\,+\, ,+)$, and ${\mathscr {R}}_{01}> \mathscr {R}_{00}>{\mathscr {R}}_0^*> 1$ for the range $(+,\,+\, , [+])$.¹

For the ranges $([+],\,+\, ,+)$ and $(+,\,+\, , [+])$ in Fig. 8, ${\mathscr {R}}_0$ is beyond 1 for any commuter ratio p, so that the spread of such a transmissible disease could occur in the community independently of the commuter ratio. In contrast, as for a transmissible disease corresponding to the other ranges, $([+],\,*\, ,-)$, $([+],\,-\, ,-)$, and $([+],\,-\, ,+)$, its spread depends on the commuter ratio. It is noted that, for those ranges $([+],\,*\, ,-)$, $([+],\,-\, ,-)$, and $([+],\,-\, ,+)$, sufficiently small commuter ratio makes $\mathscr {R}_0$ beyond 1, so that a transmissible disease could be regarded as likely to spread in the community with sufficiently small commuter ratio. Interestingly for the range $([+],\,-\, ,+)$, the community with only an intermediate specific range of the commuter ratio can make ${\mathscr {R}}_0$ below 1 so as to escape from the spread of a transmissible disease. While Fig. 8 shows numerical results in the case of ${\mathscr {R}}_{00} > 1$ when the community only with the private phase has the basic reproduction number larger than 1, there are some other comparable cases as numerically shown in Fig. 9.

Fig. 9

Categorization of the parameter region of $(\rho , K/\kappa )$ with respect to the p-dependence of ${\mathscr {R}}_{00}$, ${\mathscr {R}}_0^*$, and ${\mathscr {R}}_{01}$, given by (15) and (19) for the mass-action type of infection forces. Numerical calculation with $N = 100,000$; $\tau _{\mathrm {S}} = 0.4$; $\tau _{\mathrm {I}}=0.3$; $\beta \kappa = 2.3\times 10^{-6}$. The attached graphs show the representative p-dependence of ${\mathscr {R}}_0$ for the parameter regions, additionally to those given in Fig. 8. For the detail explanation, see the main text

From those results given in Figs. 8 and 9 , ${\mathscr {R}}_0$ is less than 1 independently of p for the parameter regions indicated by $(-,\,-\, ,[-])$, $([-],\,-\, ,-)$, and $([-],\,*\, ,-)$, where $\rho$ is relatively large. So these regions correspond to a disease from which the recovery is relatively fast (e.g., $\rho = 0.5$ corresponds to the recovery expectedly two days after the infection). On the other hand, ${\mathscr {R}}_0$ is larger than 1 independent of p for the regions $(+,\,+\, ,[+])$, $([+],\,+\, ,+)$, and $([+],\,*\, ,+)$, where $\rho$ is relatively small, corresponding to a disease from which the recovery takes a relatively long period. Although the regions $(-,\,-\, ,[-])$, $([-],\,-\, ,-)$, and $([-],\,*\, ,-)$ are located for $\rho > 0.23$ in Fig. 9, they are expanded toward the smaller $\rho$ as the value of $\beta \kappa N$ gets smaller, while the regions $(+,\,+\, ,[+])$, $([+],\,+\, ,+)$, and $([+],\,*\, ,+)$ shrink at the same time. This means that, for the disease which requires the longer period for the recovery from it (that is, the smaller value of $\rho$), if some operation of the public health could succeed in decreasing enough the likelihood of the contact between the susceptible and the pathogen at the private phase, the disease spread in the community could be avoided, since such an operation could work to reduce the value of $\kappa$. Washing hands and using the mask would be examples of such operation.

The region $(-,\,-\, , [+])$ indicates the case that ${\mathscr {R}}_0$ is larger than 1 only for the larger commuter ratio, while it is smaller than 1 for the smaller commuter ratio. As seen in Fig. 9, this is only when the value of $K/\kappa$ is large and that of $\rho$ is intermediate. A large value of $K/\kappa$ can be considered as the case when there is a sufficiently higher chance of the disease transmission at the social phase than at the private phase. It might seem that, for a community in such a case of $(-,\,-\, , [+])$, the limitation of the commuting between the residential districts and the central place in order to reduce the commuter ratio could be reasonable as an intervention policy to suppress the spread of a transmissible disease. However, we remark that such an operation to limit the commuting would be in general impractical, as long as the commuting is for the day-to-day activity which provides the base of daily life of the residents in the community.

Contrarily, for the regions $([+],\,*\, ,-)$ and $([+],\,-\, ,-)$, ${\mathscr {R}}_0$ is larger than 1 only for the smaller commuter ratio. This case could occur only when the value of $K/\kappa$ is small and that of $\rho$ is intermediate. The small value of $K/\kappa$ can be considered here to mean that the chance of the disease transmission at the social phase is not much larger than that at the private phase. It is implied for such a case of $([+], * , -) \ \mathrm{or} \ ([+], -, -)$ that, when the structure of a community (e.g., the age structure, the kind of principal industry, or the working pattern) shifts to that with such a small commuter ratio, a specific disease which is rare before would emerge and spread within the community.

Fig. 10

Temporal variation of infective populations for the mass-action type of infection force. Numerical calculation of (3) with (7) about the region $([+],\,-\, ,+)$ in Fig. 9 for different commuter ratios: a $p = 0.4$ (${\mathscr {R}}_0 = 1.011$); b $p = 0.6$ (${\mathscr {R}}_0 = 0.9880$); c $p = 0.8$ (${\mathscr {R}}_0 = 1.003$). The initial condition for each numerical calculation is given by $(\overline{S}(0), \overline{I}(0), S(0), I(0), \widetilde{S}(0), \widetilde{I}(0)) = (\overline{S}_0^*-1, 1, S_0^*, 0, \widetilde{S}^*_0, 0)$ with an infective individual at the private phase, which corresponds to a perturbation from the disease-free equilibrium shown in Sect. 3.1. Commonly, $N = 100,000$; $\tau _{\mathrm {S}} = 0.4$; $\tau _{\mathrm {I}}=0.3$; $\rho =0.2$; $\beta \kappa = 2.3\times 10^{-6}$; $\beta K = 4.025\times 10^{-6}$; ${\mathscr {R}}_{00} = 1.15$

In the most interesting case of the regions $([+],\,-\, ,+)$ and $(+,\,-\, , [+])$, ${\mathscr {R}}_0$ is below 1 only for a certain intermediate range of the commuter ratio, so that it becomes beyond 1 for the ranges of sufficiently small or large commuter ratio, although such a parameter region of $(\rho , K/\kappa )$ appears rather small as indicated by Fig. 9. For a community corresponding to the regions $([+],\,-\, ,+)$ and $(+,\,-\, , [+])$, a change in the community ratio would increase the risk of the disease spread, as illustrated by some numerical calculations in Figs. 10 and 11. Such a community could be regarded as fragile against the spread of such a transmissible disease.

Fig. 11

A numerical result about the p-dependence of ${\mathscr {R}}_0$ and the equilibrium size of total infective population $\overline{I}^*+I^*+\widetilde{I}^*$ for the mass-action type of infection force, according to (3) with (7) for the region $([+],\,-\, ,+)$ in Fig. 9. The initial condition for the numerical calculation of the equilibrium size is given by $(\overline{S}(0), \overline{I}(0), S(0), I(0), \widetilde{S}(0), \widetilde{I}(0)) = (\overline{S}_0^*-1, 1, S_0^*, 0, \widetilde{S}^*_0, 0)$ with an infective individual at the private phase, which corresponds to a perturbation from the disease-free equilibrium shown in Sect. 3.1. Commonly, $N = 100,000$; $\tau _{\mathrm {S}} = 0.4$; $\tau _{\mathrm {I}}=0.3$; $\rho =0.2$; $\beta \kappa = 2.3\times 10^{-6}$; $\beta K = 4.025\times 10^{-6}$; $\mathscr {R}_{00} = 1.15$

On the whole, it is very interesting that we find a wide region of $(\rho , K/\kappa )$ such that ${\mathscr {R}}_0$ has the extremal minimum for an intermediate value of p, that is the region except for $([+],\,*\, ,+)$, $([+],\,*\, ,-)$, and $([-],\,*\, ,-)$ in Fig. 9. This implies that the social difference or change reflected to the commuter ratio could increase the risk of the spread of a transmissible disease, independently of whether such a change makes the commuter ratio larger or smaller.

5.2 Case of the mass-action and the ratio-dependent types respectively for private and social phases

In this section, we consider the case that the infection force is the mass-action type for the private phase and the ratio-dependent type for the social phase. The function of infection force $\varLambda$ is given by (7), and ${{\widetilde{\varLambda }}}$ by (8). In this case, by the arguments given in “Appendix B.2”, we can get the following result about the dependence of ${\mathscr {R}}_0$ on p:

Theorem 4

For ${\mathscr {R}}_0$ with $\lambda ^*_0$ and ${\widetilde{\lambda }}^*_0$ of respectively the mass-action type and the ratio-dependent one at the disease-free equilibrium, $\mathscr {R}_{0}$ is monotonic in terms of p as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \text{ decreasing } \text{ if } &{} \left( \dfrac{1}{1-\tau _{\mathrm {I}}} +\tau _{\mathrm {S}}\rho \right) \dfrac{\tau _{\mathrm {I}}}{\tau _{\mathrm {S}}}\dfrac{\varOmega }{\kappa N} < 1; \\ \text{ increasing } \text{ if } &{} \left( \dfrac{1}{1-\tau _{\mathrm {I}}} +\tau _{\mathrm {S}}\rho \right) \dfrac{\tau _{\mathrm {I}}}{\tau _{\mathrm {S}}}\dfrac{\varOmega }{\kappa N} > 1. \end{array} \right. \end{aligned}$$

(24)

Therefore, ${\mathscr {R}}_0$ takes its maximum for $p = 0$ when the former condition of (24) is satisfied, while it does for $p = 1$ when the latter condition of (24) is satisfied. The numerical result given in Fig. 4 corresponds to the former about this case. Indeed as numerically shown by Fig. 12, ${\mathscr {R}}_0$ is monotonically decreasing or increasing in terms of p.

Since the condition (24) in Theorem 4 depends on the total population size of the community N, it is implies in this case that the community with a sufficiently large population size would have the smaller risk of the disease spread as the commuter ratio gets larger, while the community with a sufficiently small population size would have the larger risk as the commuter ratio gets larger.

Fig. 12

$(p, \beta \varOmega )$-dependence of ${\mathscr {R}}_0$ for the ratio-dependent type of infection force at the private phase and the mass-action type at the social phase. . Numerical calculation with $N = 100,000$; $\tau _{\mathrm {S}} = 0.4$; $\tau _{\mathrm {I}}=0.3$; $\rho = 0.2$; $\lambda ^* = \beta \kappa = 3.0\times 10^{-6}$; ${\mathscr {R}}_{00} = 1.5$

5.3 Case of the ratio-dependent and the mass-action types respectively for private and social phases

Let us consider here the case that the infection force is the ratio-dependent type for the private phase and the mass-action type for the social phase. That is, the function of infection force $\varLambda$ is given by (8), and ${{\widetilde{\varLambda }}}$ by (7). In this case, as proved in “Appendix B.3”, we can get the following result about the dependence of ${\mathscr {R}}_0$ on p:

Theorem 5

For ${\mathscr {R}}_0$ with $\lambda ^*_0$ and ${\widetilde{\lambda }}^*_0$ of respectively the ratio-dependent type and the mass-action one at the disease-free equilibrium, $\mathscr {R}_{0}$ is monotonically increasing in terms of p.

See the numerical result in Fig. 4. Therefore, the risk of the spread of a transmissible disease is higher for the community with the larger commuter ratio.

5.4 Case of only ratio-dependent type of infection force

At the end, we consider the case that the infection forces are only ratio-dependent type for both phases. The functions of infection force $\varLambda$ and ${{\widetilde{\varLambda }}}$ are here given by (8). From (13) with $\lambda ^*_0$ and ${\widetilde{\lambda }}^*_0$ given by (10) at the disease-free equilibrium, we now have the following $\mathscr {R}_0$:

$$\begin{aligned} {\mathscr {R}}_0&= \dfrac{\, 1\, }{2}\, {\mathscr {R}}_{00} \Bigg [ 1 + \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}} \dfrac{\varOmega }{\omega }\nonumber \\&\quad + \sqrt{ \Big \{ 1 - \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}} \dfrac{\varOmega }{\omega } \Big \}^2 + 4\,\dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}}\, \dfrac{1}{\,\tau _{\mathrm {S}}} \left( \dfrac{1}{1-\tau _{\mathrm {S}}p}-1 \right) \tau _{\mathrm {I}}\dfrac{\varOmega }{\omega } } \ \Bigg ], \end{aligned}$$

(25)

where ${\mathscr {R}}_{00}$ is given by (15) for the case of the ratio-dependent type of infection force. From this formula of ${\mathscr {R}}_0$, we can immediately get the following result about the dependence of ${\mathscr {R}}_0$ on p:

Theorem 6

For ${\mathscr {R}}_0$ with $\lambda ^*_0$ and ${\widetilde{\lambda }}^*_0$ of the ratio-dependent type, $\mathscr {R}_{0}$ is monotonically increasing in terms of p.

See the numerical result in Fig. 4. Therefore, in this case, a transmissible disease is more likely to spread in the community with the larger commuter ratio.

6 Nontrivial contribution of the duration at the social phase

In this section, as a supplementary result to those in the previous sections about the p-dependence of ${\mathscr {R}}_0$, we consider the contribution of the duration at the social phase, that is, of $\tau _{\mathrm {S}}$ and $\tau _{\mathrm {I}}$ to the risk of the spread of a transmissible disease.

A change of the life style could affect the working hours averaged over the community. Actually some statistical data show that the working hours have a general trend to become shorter, as the life style gets modernized while the modern society respects a work–life balance more and more [for a cross-country data, see OECD (2018a)]. Besides, the average value of working hours can be observed significantly depending on the society-specific factors to determine the working pattern and structure, as discussed in Dolton (2017) with respect to the working hours for different countries [for some other detailed arguments about such factors, see Lee et al. (2007), Messenger (2018), OECD (2018b)]. Since our main purpose of this paper is to try to discuss the relation of the community structure to the risk of the spread of a transmissible disease, and since such a change in the working hours would modify it, it would be worth while showing some suggestive results about the dependence of ${\mathscr {R}}_0$ on the duration at the social phase.

Fig. 13

Contour map in the $(p, \tau _{\mathrm {S}} )$ space for the value of ${\mathscr {R}}_0$ given by (13) for each combination of the infection forces given by (9) and (10), the mass-action and the ratio-dependent types: a only mass-action; b mass-action and ratio-dependent; c ratio-dependent and mass-action; d only ratio-dependent infection forces at the private and the social phases respectively. Numerical calculation with $N = 100,000$; $\tau _{\mathrm {I}}=0.75\tau _{\mathrm {S}}$; $\beta \kappa = 2.3\times 10^{-6}$; $\beta \omega = 0.23$; $\beta K = 3.45\times 10^{-6}$; $\beta \varOmega = 0.345$; $\rho = 0.2$; ${\mathscr {R}}_{00} = 1.15$. The filled region in (a) indicates that for ${\mathscr {R}}_0 < 1$. In each contour map, the value of ${\mathscr {R}}_0$ tends to increase toward the right-up corner. For the detail, see the main text

In our model, the change or the difference of the working hours is reflected to the values of $\tau _{\mathrm {S}}$ and $\tau _{\mathrm {I}}$. Figure 13 shows a numerical result about the dependence of ${\mathscr {R}}_0$ on the duration at the social phase. In the numerical calculation of ${\mathscr {R}}_0$, we assumed $\tau _{\mathrm {I}}=0.75\tau _{\mathrm {S}}$. The numerical calculations imply that the basic reproduction number ${\mathscr {R}}_0$ would have non-trivial dependence on the duration at the social phase. Only when the infection forces are the mass-action type at the private phase and the ratio-dependent type at the social phase, that is of Fig. 13b, the dependence appears simple such that the longer duration at the social phase would make ${\mathscr {R}}_0$ larger so as to increase the risk of the spread of a transmissible disease.

As outstandingly indicated by the numerical result of Fig. 13a in the case that the infection forces are only of the mass-action type, the dependence of ${\mathscr {R}}_0$ on the duration at the social phase is monotonic only for sufficiently small value of the commuter ratio p. For the larger value of the commuter ratio p, there could be a certain intermediate range of the duration at the social phase only in which the basic reproduction number ${\mathscr {R}}_0$ becomes less than 1. In such a case, the longer or shorter duration at the social phase out of the intermediate range makes ${\mathscr {R}}_0$ greater than 1. Therefore, it is likely that the decrease of the averaged working hours would make the risk of the spread of a transmissible disease larger in such a community. In contrast, as shown in Fig. 13c, d, when the infection force at the private phase is the ratio-dependent type, there is a case that ${\mathscr {R}}_0$ becomes larger in a certain range of the duration at the social phase. In the case of Fig. 13c, the range exists only for a relatively small value of p, while in the case of Fig. 13d, it exists only for the value of p near to 1. Except for these cases, the basic reproduction number ${\mathscr {R}}_0$ becomes larger as the duration at the social phase gets longer even when the infection force at the private phase is the ratio-dependent type.

Even only from these supplementary results with some numerical calculations, it is clear that the contribution of the duration at the social phase to the risk of the spread of a transmissible disease is nontrivial, and it is implied that its contribution to the risk of the spread of a transmissible disease is significantly related to the commuter ratio, and more generally to the community structure. It is an important suggestion that the shorter duration at the social phase would not necessarily result in the smaller risk of the spread of a transmissible disease.

7 Concluding remarks

The contact pattern is one of the most important factors to determine the risk of the spread of a transmissible disease. It depends on the transmission route, the social and the cultural customs related to it, and the demographic nature of the community (see Mossong et al. 2008; Ball et al. 2015; Britton and Giardina 2016; Yin et al. 2017; Cui et al. 2018). In this paper, we considered two types of the formula for the infection force: the mass-action and the ratio-dependent (frequency-dependent). These are frequently used for the population dynamics modeling about the disease spread in a variety of contexts, especially with the system of differential equations. As discussed in Diekmann et al. (2013), the formula for the infection force should be introduced appropriately for the reasonable modeling about the contact pattern characterized by the transmissible disease considered in each research project. Our analysis of the model in this paper was not for a specific transmissible disease, whereas it gave some theoretical results clearly showing the significant difference depending on the formula for the infection force. This means that the nature of the spread of a transmissible disease in a community significantly depends on the contact pattern characterizing a relation between the community and the disease.

In most of previous mathematical models for the epidemic dynamics, the infection force was introduced by a common formula/rule specifically chosen about the model even in the case of the dynamics with a multi-group or multi-patch setup (Del Valle et al. 2013), and in the case of the dynamics with a multi-level mixing (Ball et al. 1997; Ball and Neal 2002; Aplloni et al. 2014; Falcón-Lezama et al. 2016). However, as we did for our model in this paper, some different formulas for the infection force could be appropriate to be introduced in the model as the reasonable modeling, because the contact pattern itself could be regarded as heterogeneous in the community (Britton and Giardina 2016; Yin et al. 2017; Cui et al. 2018; Goeyvaerts et al. 2018). For this reason, the results about our model with different combinations of the formulas for the infection force demonstrated that such a heterogeneity in the contact pattern could cause a significant difference in the conclusion of an epidemic dynamics, depending on communities different with respect to the characteristics about the contact pattern, for example, as discussed in Keeling et al. (2010) and Balcan and Vespignani (2011) by the network-based numerical models.

In this paper, we did focus on the commuter ratio as a factor characterizing the community. Our analysis on the model showed that the basic reproduction number significantly depends on the commuter ratio. Especially it is a meaningful result that there could be the threshold value for the commuter ratio such that the basic reproduction number becomes less than or greater than 1. The commuter ratio could significantly affect the risk of the spread of a transmissible disease within a community.

One of modern world problems is the aging of society (UNDESA 2017). It has been discussed also for Japanese society (Muramatsu and Akiyama 2011; Yamashige 2014). Social aging could be a factor to modify or change the structural characteristics of the community especially with respect to the day-to-day activity. Generally saying, since it is expected that the commuter ratio would be relatively small in the aged community, the social aging could cause a significant change for the risk of the spread of a transmissible disease, not only because of the residents’ aging but also because of the change in the community structure in terms of the day-to-day activity.

There are some other factors which would change the structural characteristics of the community with respect to the day-to-day activity. A definite example of such factors in the modern era is the teleworking or the telecommuting. Teleworking could be defined in general as a form of labor that consists of at least partial working at non-conventional workspace with a certain practical use of the information and telecommunication equipment (Sato 2013), whereas its meaning would appear still vague (Garad and Ismail 2018). It has been investigated as one of the trends and the policies about the modern working style, following the developments in information and communication technologies (ICT) (Eurofound and the International Labour Office 2017; Messenger 2018; Morikawa 2018). Although the effect of teleworking on the working pattern is open to debate (de Abreu e Silva and Melo 2018a, b), we could expect that it would contribute to the increase of the duration at the private phase defined in this paper. Therefore, such a prospective shift in the working pattern would cause the change in the risk of the spread of a transmissible disease for the community.

Since the results of this paper imply that the risk of the spread of a transmissible disease in a community significantly depends on the day-to-day working pattern of the community, such risk differs between communities with different characteristics about the day-to-day working pattern, for example, due to the difference about the major industry. Further, since the day-to-day working pattern will be forced to vary due to the social aging or the shift of working style, the risk of the spread of a transmissible disease will be changed from now to the future for the community. The practical research of public health to prevent the spread of a transmissible disease would become need a collaborative action with the researches in social sciences more and more, for example, to discuss the policy of public health for the community, as suggested by Soriano-Paños et al. (2018) with an agent-based model.

Appendices

Appendix

The basic reproduction number $\varvec{{\mathscr {R}}_{0}}$

At first, we pick up only the infective subpopulations from the 6-dimensional system with a unique residential district given by (3) as follows:

$$\begin{aligned} \dfrac{d\overline{I}}{dt}&= {\varLambda }\overline{S} - \rho \overline{I} \nonumber \\ \dfrac{dI}{dt}&= \varLambda S -\rho I -m^{\mathrm {I}}_{\mathrm {rc}}I+m^{\mathrm {I}}_{\mathrm {cr}}\widetilde{I} ;\\ \dfrac{d\widetilde{I}}{dt}&= {\widetilde{\varLambda }}\widetilde{S} +m^{\mathrm {I}}_{\mathrm {rc}}I-m^{\mathrm {I}}_{\mathrm {cr}}\widetilde{I} .\nonumber \end{aligned}$$

(26)

Next we decompose the dynamical terms into two classes in which one shows the new infection process, and the other does show the other processes of the population dynamics:

$$\begin{aligned} \dfrac{d\varvec{\varphi }}{dt}={\mathscr {F}} (\varvec{\varphi })-{\mathscr {V}}(\varvec{\varphi }), \end{aligned}$$

(27)

where $\varvec{\varphi }:= {}^{{\mathsf {T}}} \big [\, \overline{I}\ \ I\ \ \widetilde{I} \, \big ]$;

$$\begin{aligned} {\mathscr {F}}_c(\varvec{\varphi }) := \begin{bmatrix} \ {\varLambda }\overline{S} \ \\ \ {\varLambda }{S} \ \\ \ {\widetilde{\varLambda }}\widetilde{S} \ \end{bmatrix} ; \quad -{\mathscr {V}}(\varvec{\varphi }) := \begin{bmatrix} -\rho \overline{I} \\ -\rho I -m^{\mathrm {I}}_{\mathrm {rc}}I+m^{\mathrm {I}}_{\mathrm {cr}}\widetilde{I} \ \\ m^{\mathrm {I}}_{\mathrm {rc}}I-m^{\mathrm {I}}_{\mathrm {cr}}\widetilde{I} \end{bmatrix}. \end{aligned}$$

The 3-dimensional vector ${\mathscr {F}}$ is for the terms of new infection process, while $-{\mathscr {V}}$ is for the other. The Jacobian $3\times 3$ matrices of ${\mathscr {F}}$ and ${\mathscr {V}}$ about the disease-free equilibrium ${\varvec{0}} : = {}^{{\mathsf {T}}} \big [\, 0\ \ 0\ \ 0 \, \big ]$ are given by

$$\begin{aligned} {\mathcal {F}} {:=} D{\mathscr {F}}({\varvec{0}}) {=} \begin{bmatrix} \ \lambda ^*_0\overline{S}_{0}^*\ &{}\quad \lambda ^*_0\overline{S}_{0}^*\ &{}\quad 0 \ \\ \ \lambda ^*_0 {S}_{0}^*\ &{}\quad \lambda ^*_0 {S}_{0}^*\ &{}\quad 0 \ \\ \ 0\ &{}\quad 0\ &{}\quad {\widetilde{\lambda }}^*_0\widetilde{S}_{0}^* \ \end{bmatrix} ; \quad {\mathcal {V}} {:=} D{\mathscr {V}}({\varvec{0}}) {=} \begin{bmatrix} \ \rho \ &{}\quad 0\ &{}\quad 0 \ \\ \ 0&{}\quad \ \rho +m^{\mathrm {I}}_{\mathrm {rc}}\ &{}\quad -m^{\mathrm {I}}_{\mathrm {cr}}\ \\ \ 0&{}\quad \ -m^{\mathrm {I}}_{\mathrm {rc}} \ &{}\quad m^{\mathrm {I}}_{\mathrm {cr}}\ \end{bmatrix}, \end{aligned}$$

where we used (6). Then, the next generation matrix ${\mathcal {K}}$ is given by ${\mathcal {F}} {\mathcal {V}}^{-1}$, that is,

$$\begin{aligned} {\mathcal {K}} = {\mathcal {F}}{\mathcal {V}}^{-1} = \begin{bmatrix} \ \dfrac{\lambda ^*_0\overline{S}_{0}^*}{\rho } \ &{}\quad \dfrac{\lambda ^*_0\overline{S}_{0}^*}{\rho } \ &{}\quad \dfrac{\lambda ^*_0\overline{S}_{0}^*}{\rho } \ \\ \ \dfrac{\lambda ^*_0 {S}_{0}^*}{\rho } \ &{}\quad \dfrac{\lambda ^*_0 {S}_{0}^*}{\rho } \ &{}\quad \dfrac{\lambda ^*_0 {S}_{0}^*}{\rho } \ \\ \ 0 \ &{}\quad \dfrac{m^{\mathrm {I}}_{\mathrm {rc}}}{\rho } \, \dfrac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{m^{\mathrm {I}}_{\mathrm {cr}}} \ &{}\quad \dfrac{\rho +m^{\mathrm {I}}_{\mathrm {rc}}}{\rho } \, \dfrac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{m^{\mathrm {I}}_{\mathrm {cr}}} \ \end{bmatrix}. \end{aligned}$$

(28)

The theory by van den Driessche and Watmough (2002, 2008) says that the spectrum radius, that is, the maximum absolute value of the eigenvalue of ${\mathcal {K}}$ gives the basic reproduction number ${\mathscr {R}}_{0}$. The eigenvalue $\mu$ of ${\mathcal {K}}$ is the root of the following cubic equation:

$$\begin{aligned} -\mu \big ( \mu ^2 -a_1\mu +a_0 \big ) = 0, \end{aligned}$$

(29)

with

$$\begin{aligned} a_1 := \frac{\lambda ^*_0\overline{S}_{0}^*}{\rho } + \frac{\lambda ^*_0 {S}_{0}^*}{\rho } + \frac{\rho +m^{\mathrm {I}}_{\mathrm {rc}}}{\rho } \, \frac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{m^{\mathrm {I}}_{\mathrm {cr}}} ;\quad a_0 := \frac{{\widetilde{\lambda }}^*_0\widetilde{S}_{0}^*}{m^{\mathrm {I}}_{\mathrm {cr}}} \Big ( \frac{\rho +m^{\mathrm {I}}_{\mathrm {rc}}}{\rho } \, \frac{\lambda ^*_0\overline{S}_{0}^*}{\rho } + \frac{\lambda ^*_0 {S}_{0}^*}{\rho } \Big ). \end{aligned}$$

(30)

Then, it is easily found that three roots of (29) are zero and two positive values, and that the largest one is given by

$$\begin{aligned} \max \big |\mu \big | = \dfrac{a_1+\sqrt{a_1^2-4a_0}}{2}. \end{aligned}$$

Consequently, from (28), we can derive the residential basic reproduction number ${\mathscr {R}}_{0}$ given by (13). Further, since $a_1>0$ and $a_0 > 0$, the necessary and sufficient condition for ${\mathscr {R}}_{0}< 1$ is the following:

$$\begin{aligned} \dfrac{a_1}{2} < 1 \quad \text{ and }\quad 1-a_1+a_0>0. \end{aligned}$$

From this condition, we can easily find the result of Theorem 1.

${\varvec{p}}$-dependence of the basic reproduction number $\varvec{{\mathscr {R}}_{0}}$

From the derivation of ${\mathscr {R}}_0$ in “Appendix A”, the basic reproduction number ${\mathscr {R}}_0$ of (13) satisfies the following quadratic equation:

$$\begin{aligned} f({\mathscr {R}}_0) := {\mathscr {R}}_0^2 -a_1{\mathscr {R}}_0 +a_0 = 0 \end{aligned}$$

(31)

with positive constants $a_1$ and $a_0$ given by (30). From this equation, we can get the following equation for the partial derivative of ${\mathscr {R}}_0$ in terms of p:

$$\begin{aligned} \dfrac{\partial {\mathscr {R}}_0}{\partial p} = \dfrac{ \mathscr {R}_0(\partial a_1/\partial p) -(\partial a_0/\partial p) }{ 2\mathscr {R}_0 - a_1 }. \end{aligned}$$

(32)

As shown in “Appendix A”, the Eq. (31) necessarily has two positive roots, of which the larger one is ${\mathscr {R}}_0$. Thus $a_1/ 2 < {\mathscr {R}}_0$ in (31), so that the denominator of the right side of (32) is necessarily positive. Hence the sign of the partial derivative $\partial {\mathscr {R}}_0/\partial p$ is determined by that of the nominator of the right side of (32).

1.1 Case of only mass-action type of infection forces

We can easily get the following result about the sign of the partial derivative $\partial \mathscr {R}_0/\partial p$:

Lemma 1

For any parameter values,

$$\begin{aligned} \lim _{p\rightarrow 0+}\dfrac{\partial {\mathscr {R}}_0}{\partial p} < 0 \end{aligned}$$

This lemma can be easily proven by the direct calculation of the partial derivative $\partial {\mathscr {R}}_0/\partial p$. Indeed, making use of $\lambda ^*$ and ${{\widetilde{\lambda }}}^*$ given by (9) at the disease-free equilibrium in case of the mass-action type of infection forces, we can get

$$\begin{aligned} \left. \dfrac{\partial a_1}{\partial p}\right| _{p = 0} = \dfrac{{\mathscr {R}}_{00}^2}{m_{\mathrm {cr}}^{\mathrm {S}}}\, \Big ( \dfrac{\rho + m_{\mathrm {rc}}^{\mathrm {I}}}{m_{\mathrm {cr}}^{\mathrm {I}}}\,\dfrac{K}{\kappa } -1 \Big ); \quad \left. \dfrac{\partial a_0}{\partial p}\right| _{p = 0} = \dfrac{\mathscr {R}_{00}^2}{m_{\mathrm {cr}}^{\mathrm {S}}}\, \dfrac{\rho + m_{\mathrm {rc}}^{\mathrm {I}}}{m_{\mathrm {cr}}^{\mathrm {I}}}\,\dfrac{K}{\kappa } , \end{aligned}$$

where ${\mathscr {R}}_{00}$ is defined by (15) for the mass-action type of infection force. Then we find that

$$\begin{aligned} \lim _{p\rightarrow 0+} \Big ( {\mathscr {R}}_0\,\dfrac{\partial a_1}{\partial p} -\dfrac{\partial a_0}{\partial p} \Big ) = -\dfrac{\mathscr {R}_{00}^2}{m_{\mathrm {cr}}^{\mathrm {S}}}\, < 0, \end{aligned}$$

(33)

and result in the above lemma.

From Lemma 1, if there exists a value of p, say $p^*$, such that $\partial {\mathscr {R}}_0/\partial p = 0$ for positive $p= p^*$ less than 1, ${\mathscr {R}}_0$ could takes its extremal minimum, and furthermore such value $p^*$ is unique if exists. Now $a_0$ is a second order polynomial of p while $a_1$ is a first order one. Hence the Eq. (31) defines a quadratic curve (curve of second order) in $(p, \mathscr {R}_0)$-space. Thus it is impossible that there exist such extremal points more than one for a smooth curve ${\mathscr {R}}_0$ in terms of p. From this argument, we can find it necessary and sufficient for the existence of such a unique $p^*$ that the p-derivative of ${\mathscr {R}}_0$ is positive for $p = 1$:

$$\begin{aligned} \Big ( {\mathscr {R}}_0\,\dfrac{\partial a_1}{\partial p} -\dfrac{\partial a_0}{\partial p} \Big )_{p=1} > 0. \end{aligned}$$

(34)

Making use of (16), the direct calculation of the above condition (34) results in the first part of Theorem 2. If there is no extremum, $\mathscr {R}_0$ is monotonically decreasing in terms of p because of (33). This indicates the last part of Theorem 2.

Under the condition (34), ${\mathscr {R}}_0$ takes the extremal minimum at $p = p^*$ with

$$\begin{aligned} \Big ( {\mathscr {R}}_0\,\dfrac{\partial a_1}{\partial p} -\dfrac{\partial a_0}{\partial p} \Big )_{p=p^*} = 0. \end{aligned}$$

(35)

Making use of (16), the Eq. (35) is expressed as follows:

$$\begin{aligned} \Big \{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 \Big \} \sqrt{ \tau _{\mathrm {S}}c_2(p^*)^2-\tau _{\mathrm {S}}c_1p^*+1 } = \dfrac{\ c_1}{2} -c_2p^* , \end{aligned}$$

(36)

where $c_1$ and $c_2$ are defined by

$$\begin{aligned} c_1&:= 2\, \Big \{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } +1 \Big \} ;\nonumber \\ c_2&:= \tau _{\mathrm {S}} \Big \{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } +1 \Big \}^2 + 4\, \dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}} \tau _{\mathrm {I}}\dfrac{K}{\kappa } . \end{aligned}$$

(37)

It should be now noted that the condition (34) is equivalent to the inequality such that the left side of (36) with $p^* = 1$ is greater than the right side with $p^* = 1$. Then it is easily found that, under the condition (34), the Eq. (36) has a unique root $p^*$ such that $0< p^* < 1$, for example, making use of the graphs of both sides of (36). This argument shows that the condition (34) is equivalent to the condition that $0< p^* < 1$, as indicated in Corollary 1.

Squaring both sides of (36), we can get the quadratic equation $G(p^*):= c_2(p^*)^2 - c_1p^* + c_0 = 0$ with

$$\begin{aligned} c_0&:= \dfrac{\frac{1}{1-\tau _{\mathrm {I}}}+\rho }{\frac{1}{1-\tau _{\mathrm {I}}}+\tau _{\mathrm {S}}\rho } . \end{aligned}$$

(38)

It is easily found that the quadratic equation $G(\zeta ) = 0$ has always two positive roots: $\zeta _{\pm } := (c_1\pm \sqrt{c_1^2-4c_0c_2})/(2c_2)$. It should be remarked that only one of them satisfies the Eq. (36) because squaring the Eq. (36) ignores the equality of the signs for both sides of it. In fact, from the graphs of both sides of (36), we can find that two roots $\zeta _{\pm }$ respectively correspond to the root of following equation:

$$\begin{aligned}&\mp \left\{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 \right\} \sqrt{ \tau _{\mathrm {S}}c_2(p^*)^2-\tau _{\mathrm {S}}c_1p^*+1 } = \dfrac{\ c_1}{2} -c_2p^* \nonumber \\&\quad \text{ if } \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 \ge 0 ;\nonumber \\&\pm \left\{ \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 \right\} \sqrt{ \tau _{\mathrm {S}}c_2(p^*)^2-\tau _{\mathrm {S}}c_1p^*+1 } = \dfrac{\ c_1}{2} -c_2p^* \nonumber \\&\quad \text{ if } \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 <0. \end{aligned}$$

(39)

where the double sign corresponds. As a result, we can get the following expression of $p^*$:

$$\begin{aligned} p^* = \left\{ \begin{array}{cl} \ \zeta _- &{} \quad \text{ when } \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 \ge 0;\\ \ \zeta _+ &{} \quad \text{ when } \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 < 0 . \end{array} \right. \end{aligned}$$

(40)

Then, making use of the following equality, the expression (40) leads to (18) of Corollary 1:

$$\begin{aligned} \sqrt{c_1^2-4c_0c_2} = 2\Big | \left( \dfrac{1}{1-\tau _{\mathrm {I}}}+\rho \right) \tau _{\mathrm {I}}\dfrac{K}{\kappa } -1 \Big | \sqrt{ \dfrac{1-\tau _{\mathrm {S}}}{\tau _{\mathrm {S}}(1-\tau _{\mathrm {I}})\rho + 1} } . \end{aligned}$$

The formula of the basic reproduction number for $p = p^*$, that is, ${\mathscr {R}}_0^*={\mathscr {R}}_0\big |_{p = p^*}$ can be obtained by substituting (18) for (35):

$$\begin{aligned} {\mathscr {R}}_0^* = \left. \dfrac{\partial a_0/\partial p}{\partial a_1/\partial p} \right| _{p = p^*}, \end{aligned}$$

which results in (19).

Next let us consider the maximum of ${\mathscr {R}}_0$, which can be taken when $p = 0$ or $p = 1$. Now ${\mathscr {R}}_{01} := \displaystyle \lim _{p\rightarrow 1-0}{\mathscr {R}}_0$ is given by the larger positive root of the quadratic equation (31) with $p = 1$. So let us consider the following rescaled values:

$$\begin{aligned} \widehat{{\mathscr {R}}}_{00}:= \dfrac{{\mathscr {R}}_{00}}{\beta \kappa N/\rho }; \quad \widehat{{\mathscr {R}}}_{01}:= \dfrac{\mathscr {R}_{01}}{\beta \kappa N/\rho }, \end{aligned}$$

where eventually $\widehat{{\mathscr {R}}}_{00} = 1$ because of (15) for the mass-action type of infection force. Then the value $\widehat{{\mathscr {R}}}_{01}$ is given by the larger positive root of the quadratic equation $h (\zeta ):= \zeta ^2 -{\widehat{a}}_{11}\zeta +{\widehat{a}}_{01} = 0$ with

$$\begin{aligned} {\widehat{a}}_{11} = 1-\tau _{\mathrm {S}}+\left( \dfrac{1}{1-\tau _{\mathrm {I}}}\right) \tau _{\mathrm {S}}\tau _{\mathrm {I}}\dfrac{K}{\kappa } ;\quad {\widehat{a}}_{01} = (1-\tau _{\mathrm {S}})\rho \tau _{\mathrm {S}}\tau _{\mathrm {I}}\dfrac{K}{\kappa }. \end{aligned}$$

So $\widehat{{\mathscr {R}}}_{01} < \widehat{{\mathscr {R}}}_{00} = 1$ if and only if $h (1) > 0$ and ${\widehat{a}}_{11}/2 < 1$. This condition results in (23). Since the condition that $\widehat{{\mathscr {R}}}_{01} < \widehat{{\mathscr {R}}}_{00} = 1$ is equivalent to that ${\mathscr {R}}_{00} < {\mathscr {R}}_{01}$, we get the result in Theorem 3.

1.2 Case of the mass-action and the ratio-dependent types respectively for private and social phases

In this case, since the expression for $a_1$ and $a_0$ given by (30) with (9) and (10) becomes as follows:

$$\begin{aligned} a_1&= {\mathscr {R}}_{00} (1-\tau _{\mathrm {S}}p) + \left( \dfrac{1}{1-\tau _{\mathrm {I}}} +\rho \right) \dfrac{\tau _{\mathrm {I}}\beta \varOmega }{\rho } ;\nonumber \\ a_0&= {\mathscr {R}}_{00} \left[ \left( \dfrac{1}{1-\tau _{\mathrm {I}}} +\rho \right) - \left( \dfrac{1}{1-\tau _{\mathrm {I}}} +\tau _{\mathrm {S}}\rho \right) p \right] \dfrac{\tau _{\mathrm {I}}\beta \varOmega }{\rho } , \end{aligned}$$

(41)

where ${\mathscr {R}}_{00}$ is defined by (15) for the mass-action type of infection force, and

$$\begin{aligned} \eta : = \dfrac{\partial a_0/\partial p}{\partial a_1/\partial p} = \left( \dfrac{1}{1-\tau _{\mathrm {I}}} +\tau _{\mathrm {S}}\rho \right) \dfrac{\tau _{\mathrm {I}}\beta \varOmega }{\tau _{\mathrm {S}}\rho }. \end{aligned}$$

(42)

Now it is easily seen that $\partial a_0/\partial p < 0$ and $\partial a_1/\partial p < 0$ for any p. Thus, from (32), the sign of $\partial {\mathscr {R}}_0/\partial p$ is equivalent to that of $\eta -{\mathscr {R}}_0$. From the arguments in “Appendix A”, since the quadratic equation $f(x) = 0$ has two positive roots, of which the larger gives ${\mathscr {R}}_0$, the necessary and sufficient condition for $\eta > {\mathscr {R}}_0$ is such that $f(\eta ) > 0$ and $\eta > a_1/2$. Calculating with (42), we have

$$\begin{aligned} f(\eta ) = (\eta -{\mathscr {R}}_{00})\dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}}\dfrac{\tau _{\mathrm {I}}\beta \varOmega }{\tau _{\mathrm {S}}\rho }, \end{aligned}$$

and find that $f(\eta ) > 0$ if and only if $\eta > {\mathscr {R}}_{00}$. Besides, we can easily find that $\eta > a_1/2$ if $\eta >\mathscr {R}_{00}$. As a result, $\partial {\mathscr {R}}_0/\partial p$ is positive if and only if $\eta > {\mathscr {R}}_{00}$. This result implies Theorem 4.

1.3 Case of the ratio-dependent and the mass-action types respectively for private and social phases

At first, in this case, we can get the following result:

Lemma 2

For any $p > 0$, ${\mathscr {R}}_0 > {\mathscr {R}}_{00}.$

Here ${\mathscr {R}}_{00}$ is defined by (15) for the ratio-dependent type of infection force. This lemma can be proved in the following way: Now the expression for $a_1$ and $a_0$ given by (30) with (9) and (10) becomes as follows:

$$\begin{aligned} \begin{array}{cl} a_1 = {\mathscr {R}}_{00} {+} \left( \dfrac{1}{1-\tau _{\mathrm {I}}} {+}\rho \right) \dfrac{\tau _{\mathrm {I}}\beta KN}{\rho }\,\tau _{\mathrm {S}}p ;\quad a_0 {=} {\mathscr {R}}_{00} \Big ( \dfrac{1}{1-\tau _{\mathrm {I}}}\,\dfrac{1-p}{1-\tau _{\mathrm {S}}p} {+} \rho \Big ) \dfrac{\tau _{\mathrm {I}}\beta KN}{\rho }\,\tau _{\mathrm {S}}p . \end{array} \end{aligned}$$

(43)

Then we have

$$\begin{aligned} f({\mathscr {R}}_{00}) = -{\mathscr {R}}_{00} \dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}}\, \dfrac{p}{1-\tau _{\mathrm {S}}p}\, \dfrac{\tau _{\mathrm {I}}\beta KN}{\rho }\,\tau _{\mathrm {S}}p < 0 \end{aligned}$$

for any $p > 0$. From the arguments in “Appendix A”, since the quadratic equation $f(x) = 0$ has two positive roots, of which the larger gives ${\mathscr {R}}_0$, the above result means that ${\mathscr {R}}_{00} < {\mathscr {R}}_0$ for any $p > 0$.

Next, from (43), we have

$$\begin{aligned} \dfrac{\partial a_1}{\partial p}= & {} \left( \dfrac{1}{1-\tau _{\mathrm {I}}} +\rho \right) \dfrac{\tau _{\mathrm {I}}\beta KN}{\rho }\,\tau _{\mathrm {S}} ; \nonumber \\ \dfrac{\partial a_0}{\partial p}= & {} {\mathscr {R}}_{00} \, \left[ \dfrac{1}{1-\tau _{\mathrm {I}}} +\rho - \dfrac{1}{\tau _{\mathrm {S}}}\, \dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}}\, \Big \{ \dfrac{1}{(1-\tau _{\mathrm {S}}p)^2} -1 \Big \} \right] \dfrac{\tau _{\mathrm {I}}\beta KN}{\rho }\,\tau _{\mathrm {S}} . \end{aligned}$$

(44)

Then,

$$\begin{aligned} \eta : = \dfrac{\partial a_0/\partial p}{\partial a_1/\partial p} = {\mathscr {R}}_{00} \, \left[ 1 - \Big ( \dfrac{1}{1-\tau _{\mathrm {I}}} +\rho \Big )^{-1} \dfrac{1}{\tau _{\mathrm {S}}}\, \dfrac{1-\tau _{\mathrm {S}}}{1-\tau _{\mathrm {I}}}\, \Big \{ \dfrac{1}{(1-\tau _{\mathrm {S}}p)^2} -1 \Big \} \right] . \end{aligned}$$

(45)

Since $\partial a_1/\partial p > 0$, from (32), the sign of $\partial {\mathscr {R}}_0/\partial p$ is equivalent to that of $\mathscr {R}_0-\eta$. It is clear from (45) that $\eta < \mathscr {R}_{00}$ for any $p > 0$. From Lemma 2, this result immediately leads to the subsequent result that $\eta < \mathscr {R}_0$ for any $p >0$. Therefore, $\partial {\mathscr {R}}_0/\partial p > 0$ for any $p > 0$. This result implies Theorem 5.