Analysis of Malaria Control Measures’ Effectiveness Using Multistage Vector Model

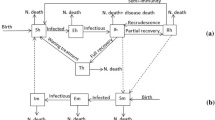
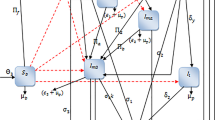
Abstract

We analyze an epidemiological model to evaluate the effectiveness of multiple means of control in malaria-endemic areas. The mathematical model consists of a system of several ordinary differential equations and is based on a multi-compartment representation of the system. The model takes into account the multiple resting–questing stages undergone by adult female mosquitoes during the period in which they function as disease vectors. We compute the basic reproduction number $\mathcal R_0$ and show that if $\mathcal R_0\le 1$, the disease-free equilibrium is globally asymptotically stable (GAS) on the nonnegative orthant. If $\mathcal R_0>1$, the system admits a unique endemic equilibrium (EE) that is GAS. We perform a sensitivity analysis of the dependence of $\mathcal R_0$ and the EE on parameters related to control measures, such as killing effectiveness and bite prevention. Finally, we discuss the implications for a comprehensive, cost-effective strategy for malaria control.

Appendices

Useful Definitions and Results

In order to make this paper self-contained, this appendix gives definitions and summarizes prior results from the literature that were used in the above discussion. Proofs of all results in this section may be found in McCluskey (2008) or Kamgang and Sallet (2008), as indicated.

1.1 Useful Definitions

Definition A1

[Metzler matrix, Metzler stable matrix (Berman and Plemmons 1994; Jacquez and Simon 1993; Luenberger 1979)] A given $n\times n$ real matrix is said to be a Metzler matrix if all its off-diagonal terms are nonnegative. The matrix is called Metzler stable if in addition all of the eigenvalues have negative real parts.

Note that a square matrix $\mathbf A$ is a Metzler matrix if and only if $-\mathbf A$ is a Z-matrix, and $\mathbf A$ is Metzler stable if and only if $-\mathbf A$ is a M-matrix. This paper makes use of the fact (which is not difficult to prove) that the positive cone is invariant for every dynamical system described by a system of ordinary differential equations whose Jacobian matrix is a Metzler matrix.

Definition A2

(Irreducible matrix) A given $n\times n$ matrix $\mathbf A$ is said to be a reducible matrix if there exists a permutation matrix $\mathbf P$ such that $\mathbf P^{\mathbf T}\,\mathbf A\,\mathbf P$ has block matrix form: $\mathbf P^{\mathbf T}\,\mathbf A\,\mathbf P=\left( \begin{array}{cc}\mathbf A_1 &{}\quad \mathbf A_{12}\\ \mathbf 0 &{}\quad \mathbf A_{2} \end{array}\right)$, where $\mathbf A_1$ and $\mathbf A_2$ are square matrices. A matrix $\mathbf A$ that is not reducible is said to be irreducible.

Irreducibility of $\mathbf A$ can be checked using the directed graph associated with $\mathbf A = (a_{k\,j} )$. This graph (denoted as $G(\mathbf A)$) has vertices ${1, 2, \dots , n}$, and the directed arc $(k,\; j)$ from k to j is in $G(\mathbf A)$ iff $a_{k\,j}\ne 0$. $G(\mathbf A)$ is said to be strongly connected if any two distinct vertices of $G(\mathbf A)$ are joined by an oriented path. The matrix $\mathbf A$ is irreducible if and only if $G(\mathbf A)$ is strongly connected (Guo et al. 2008).

1.2 Arithmetic–Geometric Means Inequality and Consequences

In demonstrating that the Lyapunov derivative is nonpositive (see Section (4.2)), a key tool is the arithmetic–geometric means inequality, stated as follows:

Lemma A1

(Weighted AM-GM) Let the positive numbers $z_1,\dots ,z_d$ and the positive weights $w_1,\dots ,w_d$ be given. Set $w = w_1+\cdots +w_d$. If $w>0$, then

$$\begin{aligned} \root w \of {z_1^{w_1}\cdots z_d^{w_d}} \le \frac{w_1z_1+\cdots +w_dz_d}{w} \end{aligned}$$

Furthermore, exact equality occurs iff $z_1=\cdots =z_d$

The classical weighted AM–GM is more general than this lemma.

An immediate consequence of weighted AM–GM is:

Corollary A1

(McCluskey 2008) Let $z_1,\dots ,z_d$ be positive real numbers such that their product is 1. Then,

$$\begin{aligned} d - z_1 -\cdots - z_d\le 0. \end{aligned}$$

Furthermore, exact equality occurs iff $z_1=\cdots =z_d$.

This is obtained from Lemma A1 by choosing $w_i=1$ for all 1.

Another useful consequence is

Corollary A2

Let the positive numbers $z_1,\dots ,z_d$ and the positive weights $w_1,\dots ,w_d$ be given. Assume for a given i, $1\le i \le d$ there is a $v\in \mathbb R$ such that ${z_i}^v=z_1^{w_1}\cdots z_{i-1}^{w_{i-1}}z_{i+1}^{w_{i+1}}\cdots z_d^{w_d}$. Set $w = w_1+\cdots +w_d$. If $w>0$ and $(z_i-1)(w+v)\le 0$, then

$$\begin{aligned} w - w_1z_1 -\cdots - w_dz_d\le 0. \end{aligned}$$

Furthermore, exact equality occurs iff $z_1=\cdots =z_d$.

Proof

For numbers and associated weights as stated in Corollary, applying Lemma A1 gives

$$\begin{aligned} z_i^{\frac{w_i+v}{w}}\le \frac{w_1z_1+\cdots +w_dz_d}{w}; \end{aligned}$$

since for given x and $\beta$ positive real numbers and $\alpha$ a real number with $|\alpha |<\beta$ we have the relation $1\le x^{\frac{\alpha }{\beta }}$ iff $x\le 1\wedge \alpha \ge 0$ or $x\ge 1\wedge \alpha \le 0$, which holds iff $(x-1)\alpha \le 0$. Thus, assuming $(z_i-1)(w_i+v)\le 1$, since this is equivalent to $1\le z_i^{\frac{w_i+v}{w}}$, the result follows straightforwardly. $\square$

1.3 Results on the Global Asymptotic Stability (GAS) of the DFE of Epidemiological Model

Theorem A1 and Proposition A1 given in this section are key tools in demonstrating Theorem 4.1 in Sect. 4.1 and Proposition 3.5 in Sect. 3.4, respectively.

Theorem 4.1 is conventionally proven by constructing an adequate Lyapunov function for the model at the equilibrium concerned. Theorem A1 establishes the existence of such a Lyapunov function in cases similar to the situation in this paper.

Theorem A1

(Kamgang and Sallet 2008) Consider the system

$$\begin{aligned} \left\{ \begin{array}{ll}\dot{\mathbf x}_S = \mathbf A_S(\mathbf x)\,.\, \left( \mathbf x_S - \mathbf x^*_S\right) + \mathbf A_{S,I}(\mathbf x)\,.\,\mathbf x_I \\ \dot{\mathbf x}_I = \mathbf A_I(\mathbf x)\,.\,\mathbf x_I \end{array}\right. \end{aligned}$$

(86)

defined on a positively invariant set $\Omega \subset \mathbb R_+^{n_S\times n_I}$. Given that:

h1:

The system is dissipative on $\Omega$;

h2:

The equilibrium $\mathbf x_S^*$ of the subsystem $\dot{\mathbf x}_S = \mathbf A_S\left( \mathbf x_S,\;\mathbf 0\right) \,.\,(\mathbf x_S-\mathbf x^*_S)$ of system (86) is globally asymptotically stable on the canonical projection of $\Omega$ on $\mathbb R_+^{n_S}$;

h3:

The matrix $\mathbf A_I(\mathbf x)$ is a Metzler matrix and irreducible for each $\mathbf x\in \Omega$;

h4:

There is an upper-bound matrix $\overline{\mathbf A}_I$ (in the sense of point-wise order) for the set of $n_I\times n_I$ square matrices $\mathfrak {M} = \{\mathbf A_I(\mathbf x)\;/\;\mathbf x\in \Omega \}$ with the property that either $\overline{\mathbf A}_I\not \in \mathfrak {M}$ or if $\overline{\mathbf A}_I \in \mathfrak {M}$, then for any $\overline{\mathbf x}\in \Omega$ such that $\overline{\mathbf A}_I = \mathbf A_I(\overline{\mathbf x})$, we have $\overline{\mathbf x}\in \mathbb R_+^{n_S}\times \{\mathbf 0\}$;

h5:

$\alpha (\overline{\mathbf A}_I)\le 0$.

Then, the DFE $\mathbf x^*$ is GAS for the system (86) in $\overline{\Omega }$.

Proposition A1 shows that the Metzler stability of matrix $\mathbf M$ is equivalent to the Metzler stability of two smaller matrices, which if properly chosen may be easier to compute with.

Proposition A1

(Kamgang and Sallet 2008) Let $\mathbf M$ be a Metzler matrix, with block decomposition $\mathbf M=\left( \begin{array}{cc} \mathbf {A} &{}\quad \mathbf {B}\\ \mathbf {C} &{}\quad \mathbf {D}\\ \end{array}\right)$, where $\mathbf {A}$ and $\mathbf {D}$ are square matrices.

Then, $\mathbf M$ is Metzler stable if and only if $\mathbf A$ and $\mathbf D - \mathbf C \mathbf A^{-1} \mathbf B$ (or $\mathbf D$ and $\mathbf A-\mathbf B \mathbf D^{-1} \mathbf C$) are Metzler stable.

The Lyapunov Function in the Proof of Theorem 4.2

The Lyapunov function technique is commonly used in the study of the stability of endemic equilibria of epidemiological systems in the literature (Guo et al. 2006, 2008; Korobeinikov 2001, 2004; Korobeinikov and Maini 2004; Korobeinikov and Wake 2002; Ma et al. 2003; McCluskey 2006, 2003, 2005; McCluskey and van den Driessche 2004; Tewa et al. 2009, 2012). For the current model, we define a function $V_{ee}$ on the space state of the model, $\left( \mathbb R_{>0}\right) ^u$:

$$\begin{aligned} V_{ee}(\mathbf x)\equiv & {} \left( S_q-S^\dagger _q\ln S_q\right) +\,\tilde{\sigma }_r\left( S_r-S^\dagger _r\ln S_r\right) +\, \sigma _r^{(1)}\left( E^{(1)}_r-E^{(1)\dagger }_r\ln E^{(1)}_r\right) \nonumber \\&+\,\displaystyle \sum _{j=1}^\ell \left( \sigma _q^{(j)}\left( E^{(j)}_q-E^{(i)\dagger }_q\ln E^{(j)}_q\right) +\sigma _r^{(j+1)}\left( E^{(j+1)}_r-E^{(j+1)\dagger }_r\ln E^{(j+1)}_r\right) \right) \nonumber \\&+\,\tau _q\left( I_q-I_q^{\dagger }\ln \,I_q\right) \nonumber \\&+\tau _r\left( I_r-I_r^{\dagger }\ln \,I_r\right) +\,\displaystyle \sum _{i=0}^{n}\vartheta _i\left( S_i-S_i^{\dagger }\ln \,S_i\right) +\,\displaystyle \sum _{i=0}^{n}\upsilon _i\left( I_i-I_i^{\dagger }\ln \,I_i\right) , \end{aligned}$$

(87)

where the coefficients $\tilde{\sigma }_r$; $\sigma _r^{(j)}$ for $j=1,2,\dots , \ell + 1$; $\sigma _q^{(j)}$ for $j=1,2,\dots , \ell$; $\tau _r$; $\tau _q$; $\upsilon _i$, $\vartheta _i$, for $i=0,1,\dots , n$ are positive constants to be determined such that the derivative of $V_{ee}$ along the trajectories of system (1) is negative. This form of the Lyapunov function and some of the techniques used in our solution were inspired by Guo et al. (2006, 2008), who use a graph-theoretic approach to compute the derivative of the Lyapunov function. In the system of Guo et al., each group has the same compartmental description, as well as the same mode of influence exchange with other groups. (Susceptible individuals of a given group are transferred to the next class of the group via contact with all infectious individuals in the system.) In our model, not all groups have the same compartmental description: host groups have an SIS structure, while the vector group is more complex. Furthermore, the mode of exchanging influence between groups is also different: there is no exchange of influence between host groups; the vector group influences host groups through contact of susceptible hosts with infectious questing vectors; and all host groups influence questing vectors.

The function $V_{ee}$ defined in (87) is $\mathcal C^\infty$ and is positive definite on $\left( \mathbb R_{>0}\right) ^u$ as long as all coefficients are positive. Its derivative along the trajectories of the system (1) is:

$$\begin{aligned} \frac{\mathrm{d}V_{ee}}{\mathrm{d}\,t}(\mathbf x(t))= & {} \left( 1-\frac{S^\dagger _q}{S_q}\right) \left( \Gamma -(d_q+r_\mathrm{suc}) S_q+\delta S_r\right) +\, \tilde{\sigma }_r\left( 1-\frac{S^{\dagger }_r}{S_r}\right) \left( \left( r_\mathrm{suc}-r_\mathrm{inf}\right) S_q-\frac{\delta }{f_r} S_r \right) \\&+\, \sigma _r^{(1)}\left( 1-\frac{E^{(1)\dagger }_r}{E^{(1)}_r}\right) \left( r_\mathrm{inf}S_q-\frac{\delta }{f_r} E^{(1)}_r \right) \\&+\,{\displaystyle \sum _{j=1}^\ell }\sigma _q^{(j)} \left( 1-\frac{E^{(j)\dagger }_q}{E^{(j)}_q}\right) \left( \delta E^{(j)}_r - \frac{r_\mathrm{suc}}{f_q}E^{(j)}_q \right) \\&+\,{\displaystyle \sum _{j=1}^\ell }\sigma _r^{(j+1)} \left( 1-\frac{E^{(j+1)\dagger }_r}{E^{(j+1)}_r}\right) \left( r_\mathrm{suc}E^{(j)}_q-\frac{\delta }{f_r}E^{(j+1)}_r \right) \\&+\,\tau _r\left( 1-\frac{I^\dagger _r}{I_r}\right) \left( r_\mathrm{suc}I_q - \frac{\delta }{f_r}I_r \right) +\,\tau _q\left( 1-\frac{I^\dagger _q}{I_q}\right) \left( \delta E^{(\ell + 1)}_r - \frac{r_\mathrm{suc}}{f_q} I_q +\delta I_r \right) \\&+\,{\displaystyle \sum _{i=0}^{n}}\vartheta _i\left( 1-\frac{S^\dagger _i}{S_i}\right) \left( \Lambda _i+\tilde{\nu _i}H_i - \left( \nu _i+a\,\varphi _i\frac{I_q}{H}\right) S_i +\gamma _i I_i\right) \\&+\,{\displaystyle \sum _{i=0}^{n}}\upsilon _i\left( 1-\frac{I^\dagger _i}{I_i}\right) \left( \frac{a}{H}\,\varphi _iS_i I_q - (\nu _i+\gamma _i)I_i \right) . \end{aligned}$$

Since according to Proposition 3.4 we may restrict ourselves to $\mathbf x \in \Omega$, we have $H_i=S_i+I_i=H^*_i$ for each i. Furthermore, from Table 3, we find that $r_\mathrm{suc}$, d and $f_q$, and $h_{i}$ are all time-independent: hence, we may write $r_\mathrm{suc}^*=r_\mathrm{suc}$, $d^*_q=d_q$, $f^*_q=f_q$. After substituting $\Gamma =(d_q+r_\mathrm{suc}^*)S_q^\dagger -\delta S_r^\dagger$, $\Lambda _i = a\varphi _i\frac{I^\dagger _q}{H^*}S^\dagger _i + (\nu _i-\tilde{\nu }_i)S^\dagger _i - (\gamma _i + \tilde{\nu }_i)I^\dagger _i$ and rearranging, we obtain

$$\begin{aligned} \dfrac{\mathrm{d}V_{ee}}{\mathrm{d}\,t}(\mathbf x(t))= & {} d_qS_q^\dagger \left( 2-\frac{S_q^\dagger }{S_q}-\frac{S_q}{S_q^\dagger }\right) +r_\mathrm{suc}^\dagger S_q^\dagger -r_\mathrm{suc}^\dagger S_q^\dagger \frac{S^\dagger _q}{S_q}-r_\mathrm{suc}S_q+r_\mathrm{suc}S_q^\dagger \\&+\, \delta S^\dagger _r \left( \frac{S^\dagger _q}{S_q}-\frac{S^\dagger _q}{S_q}\frac{S_r}{S_r^\dagger }\right) +\,\tilde{\sigma }_r\left( r_\mathrm{suc}-r_\mathrm{inf}\right) S_q \left( 1 - \frac{S^\dagger _r}{S_r} \right) \\&+\,\left( \frac{\tilde{\sigma }_r}{f_r}-1\right) \delta \left( S_r^\dagger -S_r\right) +\, \sigma _r^{(1)}r_\mathrm{inf}S_q \left( 1-\frac{E^{(1)\dagger }_r}{E^{(1)}_r}\right) \\&+\, \sigma _r^{(1)}\left( \frac{\delta }{f_r}E^{(1)\dagger }_r- \frac{\delta }{f_r}E^{(1)}_r\right) +\,{\displaystyle \sum _{i=1}^l} \sigma _q^{(i)} \delta E^{(i)}_r\left( 1-\frac{E^{(i)\dagger }_q}{E^{(i)}_q}\right) \\&+\,{\displaystyle \sum _{j=1}^{\ell }} \sigma _q^{(j)}\left( \frac{r_\mathrm{suc}}{f_q}E^{(j)\dagger }_q- \frac{r_\mathrm{suc}}{f_q}E^{(j)}_q \right) \\&+\,{\displaystyle \sum _{j=1}^{\ell }}\sigma _r^{(j+1)}E^{(j)}_qr_\mathrm{suc}\left( 1-\frac{E^{(j+1)\dagger }_r}{E^{(j+1)}_r}\right) +\,{\displaystyle \sum _{j=1}^{\ell }}\sigma _r^{(j+1)}\left( \frac{\delta }{f_r}E^{(j+1)\dagger }_r-\frac{\delta }{f_r}E^{(j+1)}_r\right) \\&+\,\tau _q\left( E^{(\ell + 1)}_r + I_r\right) \delta \left( 1-\frac{I^\dagger _q}{I_q}\right) +\,\tau _q\left( \frac{r_\mathrm{suc}}{f_q}I_q^\dagger - \frac{r_\mathrm{suc}}{f_q}I_q \right) \\&+\,\tau _r r_\mathrm{suc}I_q \left( 1- \frac{I^\dagger _r}{I_r} \right) +\,\tau _r \left( \frac{\delta }{f_r}I_r^\dagger - \frac{\delta }{f_r}I_r\right) \\&+\,{\displaystyle \sum _{i=0}^{n}}\vartheta _i\left( \nu _i - \tilde{\nu }_i\right) S^\dagger _i \left( 2-\frac{S^\dagger _i}{S_i} \right) - \,{\displaystyle \sum _{i=0}^{n}} \vartheta _i\left( \nu _i - \tilde{\nu }_i\right) H_i \\&+\,{\displaystyle \sum _{i=0}^{n}}(\upsilon _i(\nu _i+\gamma _i) - \vartheta _i\left( \gamma _i+\tilde{\nu }_i\right) ) I^\dagger _i -\,{\displaystyle \sum _{i=0}^{n}} \vartheta _i\left( \gamma _i+\tilde{\nu }_i\right) I_i\frac{S^\dagger _i}{S_i} \\&+ \,{\displaystyle \sum _{i=0}^{n}} \vartheta _i\left( \gamma _i+\tilde{\nu }_i\right) I^\dagger _i \frac{S^\dagger _i}{S_i} +\,{\displaystyle \sum _{i=0}^{n}} \vartheta _i a\,\varphi _i\frac{I^\dagger _q}{H^*} S^\dagger _i +\,{\displaystyle \sum _{i=0}^{n}} \vartheta _i a\,\varphi _i\frac{I_q}{H} S^\dagger _i-\,{\displaystyle \sum _{i=0}^{n}} \vartheta _i a\,\varphi _i\frac{I^\dagger _q}{H^*} S^\dagger _i\frac{S^\dagger _i}{S_i} \\&+\,{\displaystyle \sum _{i=0}^{n}} (\upsilon _i - \vartheta _i) \left( a\,\varphi _i\frac{I_q}{H} S_i - (\gamma _i + \nu _i)I_i\right) -\,{\displaystyle \sum _{i=0}^{n}} \upsilon _ia \varphi _i\frac{I_q}{H}S_i\frac{I^\dagger _i}{I_i} \end{aligned}$$

We may write

$$\begin{aligned} \dfrac{\mathrm{d}V_{ee}}{\mathrm{d}\,t}(\mathbf x(t)) = d_qS_q^\dagger \left( 2-\frac{S_q^\dagger }{S_q}-\frac{S_q}{S_q^\dagger }\right) + F(\mathbf x), \end{aligned}$$

(88)

where

$$\begin{aligned} F(\mathbf x)= & {} r_\mathrm{suc}^\dagger S_q^\dagger \left( 1-\frac{S^\dagger _q}{S_q}\right) -r_\mathrm{suc}S_q+r_\mathrm{suc}S_q^\dagger + \delta S^\dagger _r \left( \frac{S^\dagger _q}{S_q}+\frac{S_r}{S_r^\dagger }-\frac{S^\dagger _q}{S_q}\frac{S_r}{S_r^\dagger }-1\right) \\&+\,\tilde{\sigma }_r\left( r_\mathrm{suc}-r_\mathrm{inf}\right) S_q \left( 1 - \frac{S^\dagger _r}{S_r} \right) +\,\tilde{\sigma }_r\frac{\delta }{f_r} S^\dagger _r\left( 1-\frac{S_r}{S_r^\dagger }\right) \\&+ \, \sigma _r^{(1)}r_\mathrm{inf}S_q \left( 1-\frac{E^{(1)\dagger }_r}{E^{(1)}_r}\right) +\,\delta {\displaystyle \sum _{j=1}^\ell }\left( E^{(j)\dagger }_r \left( \frac{\sigma _r^{(1)}}{f_r}- \sigma _q^{(j)}\frac{E^{(j)}_r}{E^{(j)\dagger }_r}\frac{E^{(j) \dagger }_q}{E^{(j)}_q}\right) +\, \left( \sigma _q^{(j)} -\,\frac{\sigma _r^{(j)}}{f_r} \right) E^{(j)}_r \right) \\&+\,\delta \left( \tau _q -\,\frac{\sigma _r^{(\ell + 1)}}{f_r} \right) E^{(\ell + 1)}_r +\,\delta E^{(\ell + 1)\dagger }_r \left( \frac{\sigma _r^{(\ell + 1)}}{f_r}- \tau _q\frac{E^{(\ell + 1)}_r}{E^{(\ell + 1)\dagger }_r}\frac{I^{ \dagger }_q}{I_q}\right) \\&+\, \delta \left( \tau _q -\frac{\tau _r}{f_r} \right) I_r +\, \delta I^\dagger _r\left( \frac{\tau _r}{f_r}-\tau _q \frac{I_r}{I^\dagger _r}\frac{I^\dagger _q}{I_q}\right) \\&+\,r_\mathrm{suc}{\displaystyle \sum _{j=1}^{\ell }}\left( E^{(j)\dagger }_q \left( \frac{\sigma _q^{(j)}}{f_q}-\sigma _r^{(j+1)}\frac{E^{(j)}_q}{E^{(j)\dagger }_q}\frac{E^{(j+1)\dagger }_r}{E^{(j+1)}_r} \right) +\, \left( \sigma _r^{(j+1)}- \frac{\sigma _q^{(j)}}{f_q}\right) E^{(j)}_q\right) \\&+\, r_\mathrm{suc}I^\dagger _q \left( \frac{\tau _q}{f_q}- \tau _r\frac{I_q}{I^\dagger _q}\frac{I^\dagger _r}{I_r} \right) + \, r_\mathrm{suc}I_q\left( \tau _r- \frac{\tau _q}{f_q}\right) \\&+\,{\displaystyle \sum _{i=0}^{n}}\vartheta _i\left( \nu _i - \tilde{\nu }_i\right) S^\dagger _i \left( 2-\frac{S^\dagger _i}{S_i} \right) - \,{\displaystyle \sum _{i=0}^{n}} \vartheta _i\left( \nu _i - \tilde{\nu }_i\right) H_i +\,{\displaystyle \sum _{i=0}^{n}}(\upsilon _i\nu _i - \vartheta _i\tilde{\nu }_i ) I^\dagger _i \\&-\,{\displaystyle \sum _{i=0}^{n}} \vartheta _i\left( \gamma _i+\tilde{\nu }_i\right) I_i\frac{S^\dagger _i}{S_i} + \,{\displaystyle \sum _{i=0}^{n}} \vartheta _i\left( \gamma _i+\tilde{\nu }_i\right) I^\dagger _i \frac{S^\dagger _i}{S_i} \\&+\,{\displaystyle \sum _{i=0}^{n}} \vartheta _i a\,\varphi _i\frac{I^\dagger _q}{H^*} S^\dagger _i +\,{\displaystyle \sum _{i=0}^{n}} \vartheta _i a\,\varphi _i\frac{I_q}{H} S^\dagger _i-\,{\displaystyle \sum _{i=0}^{n}} \vartheta _i a\,\varphi _i\frac{I^\dagger _q}{H^*} S^\dagger _i\frac{S^\dagger _i}{S_i} \\&+\,{\displaystyle \sum _{i=0}^{n}} (\upsilon _i - \vartheta _i) \left( a\,\varphi _i\frac{I_q}{H} S_i - (\gamma _i + \nu _i)I_i + \gamma _iI^\dagger _i\right) -\,{\displaystyle \sum _{i=0}^{n}} \upsilon _ia \varphi _i\frac{I_q}{H}S_i\frac{I^\dagger _i}{I_i}. \end{aligned}$$

Note that $\frac{\mathrm{d}V_{ee}}{\mathrm{d}\,t}(\mathbf x(t)) \le F(\mathbf x)$, since $2-\frac{S_q^\dagger }{S_q}-\frac{S_q}{S_q^\dagger }\le 0$ for all $\mathbf x\in \left( \mathbb R_{>0}\right) ^u$.

The expression for $F(\mathbf x)$ may be simplified by choosing

$$\begin{aligned}&\tau _q =\dfrac{\tau _r}{f_r}; ~\sigma ^{(\ell + 1)}_r = f_r\tau _q ;~ \sigma ^{(j)}_q=f_q\sigma ^{(j+1)}_r, \sigma ^{(j)}_r = f_r\sigma ^{(j)}_q~ \nonumber \\&\quad \text {for}j=\ell ,~\ell -1,\dots 1,\,\text {and}\, \vartheta _i = \upsilon _i ~ \text {for} i = 0,1,\dots ,n \end{aligned}$$

(89)

from which follows

$$\begin{aligned} \sigma ^{(j)}_r= & {} \sigma ^{(1)}_r(f_qf_r)^{1-j},\;\hbox { for} \;j=1,2,\dots ,\ell + 1; \nonumber \\ \sigma ^{(j)}_q= & {} \sigma ^{(1)}_r(f_qf_r)^{1-j}f_r^{-1},\; \hbox {for}\; j=1,2,\dots ,\ell ;\nonumber \\ \tau _q= & {} \sigma ^{(1)}_rf_r^{-1}(f_qf_r)^{-\ell } ; \quad \tau _r =\sigma ^{(1)}_r(f_qf_r)^{-\ell } . \end{aligned}$$

(90)

Using these substitutions and the fact that the size of the fraction of population in the $i\mathrm{th}$ hosts group $H_i=S_i+I_i$ is constant for $i=0,\;\cdots ,\;n$, we get:

$$\begin{aligned} F(\mathbf x)= & {} r_\mathrm{suc}^\dagger S_q^\dagger \left( 1-\frac{S^\dagger _q}{S_q}\right) +\left( (\sigma _r^{(1)}-\tilde{\sigma }_r)r_\mathrm{inf}+(\tilde{\sigma }_r -1)r_\mathrm{suc}\right) S_q+r_\mathrm{suc}S_q^\dagger \\&+\, \delta S^\dagger _r \left( \frac{S^\dagger _q}{S_q}+\frac{S_r}{S_r^\dagger }-\frac{S^\dagger _q}{S_q}\frac{S_r}{S_r^\dagger } - 1\right) +\,\tilde{\sigma }_r\frac{\delta }{f_r} S_r^\dagger \left( 1-\frac{S_r}{S_r^\dagger }\right) \\&-\,\tilde{\sigma }_r\left( r_\mathrm{suc}-r_\mathrm{inf}\right) S_q \frac{S^\dagger _r}{S_r} - \, \sigma _r^{(1)}r_\mathrm{inf}S_q \frac{E^{(1)\dagger }_r}{E^{(1)}_r} +\, r_\mathrm{suc}\sigma _r^{(1)}{\displaystyle \sum _{j=1}^{\ell }}\frac{E^{(i)\dagger }_q}{(f_qf_r)^{j}} \left( 1- \frac{E^{(j)}_q}{E^{(j)\dagger }_q} \frac{E^{(j+1)\dagger }_r}{E^{(j+1)}_r}\right) \\&+\,\delta \sigma _r^{(1)}{\displaystyle \sum _{j=1}^{\ell } }\frac{ E^{(j)\dagger }_r}{f_r(f_qf_r)^{j-1}}\left( 1-\, \frac{ E^{(j)}_r}{ E^{(j)\dagger }_r}\frac{E^{(j)\dagger }_q}{E^{(j)}_q}\right) +\delta \sigma _r^{(1)} \frac{ E^{(\ell + 1)\dagger }_r}{f_r(f_qf_r)^{l}} \left( 1 - \frac{E^{(\ell + 1)}_r}{ E^{(\ell + 1)\dagger }_r} \frac{I^\dagger _q}{I_q}\right) \\&+\, \delta \sigma _r^{(1)}\frac{I_r^\dagger }{f_r(f_qf_r)^{l}} \left( 1 - \frac{I_r}{I_r^\dagger }\frac{I^\dagger _q}{I_q}\right) +\,r_\mathrm{suc}\sigma _r^{(1)} \frac{I_q^\dagger }{(f_qf_r)^{l}} \left( \frac{1}{f_rf_q}- \frac{I_q}{I_q^\dagger }\frac{I^\dagger _r}{I_r} \right) \\&+ \,r_\mathrm{suc}\sigma _r^{(1)} \frac{f_rf_q-1}{(f_qf_r)^{\ell + 1}}I_q +\,{\displaystyle \sum _{i=0}^{n}}\upsilon _i\left( \nu _i - \tilde{\nu }_i\right) S^\dagger _i \left( 2-\frac{S^\dagger _i}{S_i} \right) \\&- \,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \nu _i - \tilde{\nu }_i\right) H_i +\,{\displaystyle \sum _{i=0}^{n}}\upsilon _i(\nu _i - \tilde{\nu }_i ) I^\dagger _i -\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \gamma _i+\tilde{\nu }_i\right) I_i\frac{S^\dagger _i}{S_i} + \,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \gamma _i+\tilde{\nu }_i\right) I^\dagger _i \frac{S^\dagger _i}{S_i} \\&+\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i a\,\varphi _i\frac{I^\dagger _q}{H^*} S^\dagger _i +\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i a\,\varphi _i\frac{I_q}{H} S^\dagger _i-\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i a\,\varphi _i\frac{I^\dagger _q}{H^*} S^\dagger _i\frac{S^\dagger _i}{S_i} -\,{\displaystyle \sum _{i=0}^{n}} \upsilon _ia \varphi _i\frac{I_q}{H}S_i\frac{I^\dagger _i}{I_i} \end{aligned}$$

Using the fact that all time derivatives in system (1) are zero at the EE, we find: $r_\mathrm{suc}^\dagger I_q^\dagger = \frac{\delta }{f_r}I_r^\dagger$, $\delta S_r^\dagger =f_r\left( r_\mathrm{suc}^\dagger -r_\mathrm{inf}^\dagger \right) S_q^\dagger$, $r_\mathrm{suc}E_q^{(j)\dagger }=\frac{\delta }{f_r}E_r^{(j+1)\dagger }$ for $j = 1,2,\dots , \ell$, and $a\varphi _i\frac{I_q^\dagger }{H^*} S^\dagger _i = (\nu _i+\gamma _i)I^\dagger _i$ for $i=0,1,\dots , n$. This leads to

$$\begin{aligned} F(\mathbf x)= & {} r_\mathrm{suc}^\dagger S_q^\dagger \left( 1-\frac{S^\dagger _q}{S_q}\right) +\left( (\sigma _r^{(1)}-\tilde{\sigma }_r)r_\mathrm{inf}+(\tilde{\sigma }_r -1)r_\mathrm{suc}\right) S_q +r_\mathrm{suc}S_q^\dagger \\&+ \,\delta S^\dagger _r \left( \frac{S^\dagger _q}{S_q}+\frac{S_r}{S_r^\dagger }-\frac{S^\dagger _q}{S_q}\frac{S_r}{S_r^\dagger }-1\right) +\,\tilde{\sigma }_r\frac{\delta }{f_r} S_r^\dagger \left( 1-\frac{S_r}{S_r^\dagger }\right) \\&-\;\tilde{\sigma }_r\left( r_\mathrm{suc}-r_\mathrm{inf}\right) S_q \frac{S^\dagger _r}{S_r} - \, \sigma _r^{(1)}r_\mathrm{inf}S_q \frac{E^{(1)\dagger }_r}{E^{(1)}_r} \\&+\,\sigma _r^{(1)} \frac{\delta }{f_r} E^{(1)\dagger }_r\left( 1-\, \frac{ E^{(1)}_r}{ E^{(1)\dagger }_r}\frac{E^{(1)\dagger }_q}{E^{(1)}_q}\right) +\,r_\mathrm{suc}\sigma _r^{(1)} \frac{1-f_rf_q}{(f_qf_r)^{\ell + 1}} \left( I^\dagger _q - I_q\right) \\&+\, r_\mathrm{suc}\sigma _r^{(1)}{\displaystyle \sum _{j=1}^{\ell -1}}\frac{E^{(i)\dagger }_q}{(f_qf_r)^{i}}\left( 2- \frac{E^{(j)}_q}{E^{(j)\dagger }_q}\frac{E^{(j+1)\dagger }_r}{E^{(j+1)}_r}-\, \frac{ E^{(j+1)}_r}{ E^{(j+1)\dagger }_r}\frac{E^{(j+1)\dagger }_q}{E^{(j+1)}_q}\right) \\&+\, r_\mathrm{suc}\sigma _r^{(1)}\frac{E^{(l)\dagger }_q}{(f_qf_r)^{l}}\left( 2- \frac{E^{(l)}_q}{E^{(l)\dagger }_q}\frac{E^{(\ell + 1)\dagger }_r}{E^{(\ell + 1)}_r}- \frac{E^{(\ell + 1)}_r}{E^{(\ell + 1)\dagger }_r}\frac{I^\dagger _q}{I_q}\right) \\&+\, r_\mathrm{suc}\sigma _r^{(1)}\frac{I_q^\dagger }{(f_qf_r)^{l}} \left( 2 - \frac{I_r}{I_r^\dagger }\frac{I_q^\dagger }{I_q}- \frac{I_q}{I_q^\dagger }\frac{I^\dagger _r}{I_r}\right) +\,{\displaystyle \sum _{i=0}^{n}}\upsilon _i\left( \nu _i - \tilde{\nu }_i\right) S^\dagger _i \left( 2-\frac{S^\dagger _i}{S_i} \right) \\&- \,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \nu _i - \tilde{\nu }_i\right) H_i +\,{\displaystyle \sum _{i=0}^{n}}\upsilon _i(\nu _i - \tilde{\nu }_i ) I^\dagger _i \\&-\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \gamma _i+\tilde{\nu }_i\right) I_i\frac{S^\dagger _i}{S_i} - \,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \nu _i - \tilde{\nu }_i\right) I^\dagger _i \frac{S^\dagger _i}{S_i} \\&+\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i a\,\varphi _i\frac{I^\dagger _q}{H^*} S^\dagger _i +\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i a\,\varphi _i\frac{I_q}{H} S^\dagger _i -\,{\displaystyle \sum _{i=0}^{n}} \upsilon _ia \varphi _i\frac{I_q}{H}S_i\frac{I^\dagger _i}{I_i} \end{aligned}$$

Using relations between components of $\mathbf x^\dagger$ given in (26), we may derive

$$\begin{aligned} r_\mathrm{inf}^\dagger S^\dagger _q= & {} \frac{\delta E^{(1)\dagger }_r}{f_r} = \frac{\delta E^{(2)\dagger }_r}{f_r(f_qf_r)} = \cdots = \frac{\delta E^{(\ell + 1)\dagger }_r}{f_r(f_qf_r)^\ell } \\= & {} \frac{r_\mathrm{suc}(1-f_qf_r) I^{\dagger }_q}{(f_qf_r)^{\ell + 1}} \hbox { and } \frac{\delta E^{(j+1)\dagger }_r}{f_r(f_qf_r)^j} = \frac{r_\mathrm{suc}E^{(j)\dagger }_q}{(f_qf_r)^j},\;\;\; j=1,\dots ,l, \end{aligned}$$

and after few algebraic rearrangements, the above becomes:

$$\begin{aligned} F(\mathbf x)= & {} \left( (\sigma _r^{(1)}-\tilde{\sigma }_r)r_\mathrm{inf}+(\tilde{\sigma }_r -1)r_\mathrm{suc}\right) S_q +r_\mathrm{suc}^\dagger S_q^\dagger \left( 1-\frac{S^\dagger _q}{S_q}\right) \\&+r_\mathrm{suc}S_q^\dagger + \delta S^\dagger _r \left( \frac{S^\dagger _q}{S_q} + \frac{S_r}{S_r^\dagger }-\frac{S^\dagger _q}{S_q}\frac{S_r}{S_r^\dagger }-1\right) +\,\tilde{\sigma }_r\frac{\delta }{f_r} S^\dagger _r \left( 1-\frac{S_r}{S_r^\dagger }\right) \\&-\;\tilde{\sigma }_r\left( r_\mathrm{suc}-r_\mathrm{inf}\right) S_q \frac{S^\dagger _r}{S_r} - \, \sigma _r^{(1)}r_\mathrm{inf}S_q \frac{E^{(1)\dagger }_r}{E^{(1)}_r}\\&+\, \sigma _r^{(1)}r_\mathrm{inf}^\dagger S^\dagger _q\left( 2\ell +2- {\displaystyle \sum _{j=1}^{\ell }}\frac{E^{(j)}_q}{E^{(j)\dagger }_q}\frac{E^{(j+1)\dagger }_r}{E^{(j+1)}_r}-\, {\displaystyle \sum _{j=1}^{\ell }}\frac{ E^{(j)}_r}{ E^{(j)\dagger }_r}\frac{E^{(j)\dagger }_q}{E^{(j)}_q}- \frac{E^{(\ell + 1)}_r}{E^{(\ell + 1)\dagger }_r}\frac{I^\dagger _q}{I_q} - \frac{I_q}{I^\dagger _q}\right) \\&+\, \frac{r_\mathrm{suc}\sigma _r^{(1)}}{(f_qf_r)^{l}}I_q^\dagger \left( 2 - \frac{I_r}{I_r^\dagger }\frac{I_q^\dagger }{I_q}- \frac{I_q}{I_q^\dagger }\frac{I^\dagger _r}{I_r}\right) +\,{\displaystyle \sum _{i=0}^{n}}\upsilon _i\left( \nu _i - \tilde{\nu }_i\right) S^\dagger _i \left( 2-\frac{S^\dagger _i}{S_i} \right) \\&- \,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \nu _i - \tilde{\nu }_i\right) H_i +\,{\displaystyle \sum _{i=0}^{n}}\upsilon _i(\nu _i - \tilde{\nu }_i ) I^\dagger _i \\&-\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \gamma _i+\tilde{\nu }_i\right) I_i\frac{S^\dagger _i}{S_i}- \,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \nu _i - \tilde{\nu }_i\right) I^\dagger _i \frac{S^\dagger _i}{S_i} +\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i a\,\varphi _i\frac{I^\dagger _q}{H^*} S^\dagger _i \\&+\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i a\,\varphi _i\frac{I_q}{H} S^\dagger _i -\,{\displaystyle \sum _{i=0}^{n}} \upsilon _ia \varphi _i\frac{I_q}{H}S_i \frac{I^\dagger _i}{I_i}. \end{aligned}$$

We choose $\tilde{\sigma }_r=\sigma ^{(1)}_r=1$ to make the initial terms vanish. We also choose $\upsilon _i = \frac{a}{H}\frac{\phi _{i} }{\nu _i - \tilde{\nu }_i}S^\dagger _q$, so that $r_\mathrm{suc}S^\dagger _q = {\sum _{i=0}^n}\upsilon _i(\nu _i - \tilde{\nu }_i)H_i$. Using the fact that $r_\mathrm{inf}= \frac{a}{H}{\sum _{i=0}^n}\phi _{i} \xi _{i} I_i$ and $r_\mathrm{suc}= \frac{a}{H}{\sum _{i=0}^n}\phi _{i} \left( S_i+I_i\right)$, the above expression becomes:

$$\begin{aligned} F(\mathbf x)= & {} \delta S^\dagger _r \left( \frac{S^\dagger _q}{S_q}+\frac{S_r}{S_r^\dagger }-\frac{S^\dagger _q}{S_q}\frac{S_r}{S_r^\dagger }-1\right) +\, \frac{r_\mathrm{suc}}{(f_qf_r)^{l}} I_q^\dagger \left( 2 - \frac{I_r}{I_r^\dagger }\frac{I_q^\dagger }{I_q}- \frac{I_q}{I_q^\dagger }\frac{I^\dagger _r}{I_r}\right) \\&+\,\frac{ a}{H}{\displaystyle \sum _{i=0}^n}\phi _{i} S^\dagger _iS^\dagger _q \left( 4 - \frac{S^\dagger _q}{S_q} -\frac{S^\dagger _i}{S_i} -\frac{S_i}{S^\dagger _i} \frac{S_q}{S^\dagger _q}\frac{S^\dagger _r}{S_r}-\frac{S_r}{S^\dagger _r}\right) \\&+\,\frac{ a}{H}{\displaystyle \sum _{i=0}^n} \xi _{i} \phi _{i} I^\dagger _iS^\dagger _q\left( 2\ell +5 - \frac{S^\dagger _i}{S_i} -\frac{S^\dagger _q}{S_q} -\; \frac{I_i}{I^\dagger _i}\frac{S_q}{S^\dagger _q}\frac{E^{(1)\dagger }_r}{E^{(1)}_r}- {\displaystyle \sum _{j=1}^{\ell }}\frac{E^{(j)}_q}{E^{(j)\dagger }_q}\frac{E^{(j+1)\dagger }_r}{E^{(j+1)}_r}\right. \\&\left. -\, {\displaystyle \sum _{j=1}^{\ell }}\frac{ E^{(j)}_r}{ E^{(j)\dagger }_r}\frac{E^{(j)\dagger }_q}{E^{(j)}_q} -\frac{E^{(\ell + 1)}_r}{E^{(\ell + 1)\dagger }_r}\frac{I^\dagger _q}{I_q}- \frac{I_q}{I^\dagger _q}\frac{S_i}{S^\dagger _i} \frac{I^\dagger _i}{I_i}\right) \\&+\,\frac{ a}{H}{\displaystyle \sum _{i=0}^n}\overline{\xi _{i}} \phi _{i} I^\dagger _iS^\dagger _q\left( 4 + \frac{I_q}{I^\dagger _q} -\frac{S^\dagger _q}{S_q} - \frac{S^\dagger _i}{S_i} -\frac{I_i}{I^\dagger _i}\frac{S_q}{S^\dagger _q}\frac{S^\dagger _r}{S_r}-\,\frac{S_r}{S^\dagger _r} - \frac{I_q}{I^\dagger _q}\frac{S_i}{S^\dagger _i} \frac{I^\dagger _i}{I_i}\right) \\&-\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i\left( \gamma _i+\tilde{\nu }_i\right) I_i\frac{S^\dagger _i}{S_i} +\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i (\gamma _i+\tilde{\nu }_i)I^\dagger _i\\&+\,\frac{I_q}{I^\dagger _q}{\displaystyle \sum _{i=0}^{n}} \upsilon _i (\gamma _i+\tilde{\nu }_i)I^\dagger _i -\,\frac{I_q}{I^\dagger _q}{\displaystyle \sum _{i=0}^{n}} \upsilon _i (\gamma _i+\tilde{\nu }_i)I^\dagger _i\frac{S_i}{S^\dagger _i} \frac{I^\dagger _i}{I_i}, \end{aligned}$$

where $\overline{\xi _{i}} =1-\xi _{i}$, $i=0,\dots ,n$. Setting $\hat{\nu }_i = \nu _i - \tilde{\nu }_i$ and replacing $H_i$ by $S^\dagger _i+I^\dagger _i$ for $i=0,\dots ,n$ gives finally

$$\begin{aligned} F(\mathbf x)= & {} \delta S^\dagger _r \left( \frac{S^\dagger _q}{S_q}+\frac{S_r}{S_r^\dagger }-\frac{S^\dagger _q}{S_q}\frac{S_r}{S_r^\dagger }-1\right) +\, I_q^\dagger \frac{r_\mathrm{suc}}{(f_qf_r)^{l}} \left( 2 - \frac{I_r}{I_r^\dagger }\frac{I_q^\dagger }{I_q}- \frac{I_q}{I_q^\dagger }\frac{I^\dagger _r}{I_r}\right) \\&+\,{\displaystyle \sum _{i=0}^n}\hat{\nu }_i\upsilon _iS^\dagger _i \left( 4-\frac{S^\dagger _i}{S_i}-\frac{S^\dagger _q}{S_q}-\frac{S_i}{S^\dagger _i}\frac{S_q}{S^\dagger _q}\frac{S^\dagger _r}{S_r}-\frac{S_r}{S^\dagger _r}\right) \\&+\,{\displaystyle \sum _{i=0}^n}\hat{\nu }_i \upsilon _i\xi _{i} I^\dagger _i\left( 2\ell +5 -\frac{S^\dagger _i}{S_i}-\frac{S^\dagger _q}{S_q} -\; \frac{I_i}{I^\dagger _i}\frac{S_q}{S^\dagger _q}\frac{E^{(1)\dagger }_r}{E^{(1)}_r}- {\displaystyle \sum _{j=1}^{\ell }} \frac{E^{(j)}_q}{E^{(j)\dagger }_q} \frac{E^{(j+1)\dagger }_r}{E^{(j+1)}_r}\right. \\&\left. -\, {\displaystyle \sum _{j=1}^{\ell }}\frac{ E^{(j)}_r}{ E^{(j)\dagger }_r}\frac{E^{(j)\dagger }_q}{E^{(j)}_q} -\frac{E^{(\ell + 1)}_r}{E^{(\ell + 1)\dagger }_r}\frac{I^\dagger _q}{I_q}-\frac{I_q}{I^\dagger _q}\frac{S_i}{S^\dagger _i} \frac{I^\dagger _i}{I_i}\right) \\&+\,{\displaystyle \sum _{i=0}^n}\hat{\nu }_i\upsilon _i\overline{\xi _{i}} I^\dagger _i\left( 4 + \frac{I_q}{I^\dagger _q}-\frac{S^\dagger _i}{S_i}-\frac{S^\dagger _q}{S_q}-\frac{I_i}{I^\dagger _i}\frac{S_q}{S^\dagger _q}\frac{S^\dagger _r}{S_r}-\,\frac{S_r}{S^\dagger _r}-\frac{I_q}{I^\dagger _q}\frac{S_i}{S^\dagger _i} \frac{I^\dagger _i}{I_i}\right) \\&+\,{\displaystyle \sum _{i=0}^{n}} \upsilon _i (\gamma _i+\tilde{\nu }_i)I^\dagger _i\left( 1 - \frac{I_i}{I_i^\dagger } \frac{S_i^\dagger }{S_i}\right) \\&+\,\frac{I_q}{I^\dagger _q}{\displaystyle \sum _{i=0}^{n}} \upsilon _i (\gamma _i+\tilde{\nu }_i)I^\dagger _i\left( 1 - \frac{I^\dagger _i}{I_i} \frac{S_i}{S^\dagger _i}\right) . \end{aligned}$$

which together with (88) yields expression (41). $\square$