Abstract
We focus on discrete-time infectious disease models in populations that are governed by constant, geometric, Beverton–Holt or Ricker demographic equations, and give a method for computing the basic reproduction number, \(\mathcal {R}_{0}\). When \(\mathcal {R}_{0}<1\) and the demographic population dynamics are asymptotically constant or under geometric growth (non-oscillatory), we prove global asymptotic stability of the disease-free equilibrium of the disease models. Under the same demographic assumption, when \(\mathcal {R}_{0}>1\), we prove uniform persistence of the disease. We apply our theoretical results to specific discrete-time epidemic models that are formulated for SEIR infections, cholera in humans and anthrax in animals. Our simulations show that a unique endemic equilibrium of each of the three specific disease models is asymptotically stable whenever \(\mathcal {R}_{0}>1\).
Similar content being viewed by others
1 Introduction
The basic reproduction number (or basic reproductive number or basic reproductive ratio), \(\mathcal {R}_{0}\), is the average number of secondary cases produced by an infected individual introduced into a population of susceptible individuals, where an infected individual has acquired the disease, and susceptible individuals are healthy but are at risk of acquiring the infectious disease, see for example Diekmann et al. (1990). In a recent paper, van den Driessche (2017) reviewed the next-generation method of finding \(\mathcal {R}_{0}\) for continuous-time (ODE) infectious disease models and demonstrated how this and other reproduction numbers can be used to guide disease control strategies. A next-generation method for computing \(\mathcal {R}_{0}\) for discrete-time compartmental epidemic models was developed by Allen and van den Driessche (2008) in Theorem 3. The next-generation method entails a specification of what events are considered as “new infections” and what events are considered as “transition states.” Cushing and Diekmann (2016) used discrete-time models to show that several next-generation method “splittings” are possible and that the corresponding \(\mathcal {R}_{0}\) expressions need not be the same.
By the next-generation method, if \(\mathcal {R}_{0}<1\) then the disease-free equilibrium (DFE) is locally asymptotically stable (LAS) and the disease dies out if the initial number of infected individuals is small. However, the DFE is unstable and the disease persists if \(\mathcal {R}_{0}>1\) (Allen and van den Driessche 2008; Cushing and Diekmann 2016; van den Driessche 2017). For many compartmental epidemic models, the basic reproduction number \(\mathcal {R}_{0} \) gives a sharp threshold that completely determines their global dynamics. That is, for these epidemic models, the DFE is globally asymptotically stable (GAS) when \(\mathcal {R}_{0}<1\) and unstable when \(\mathcal {R}_{0}>1\). In Theorem 2.1, Shuai and van den Driessche (2013) provided a method for constructing a Lyapunov function for continuous-time (ODE) infectious disease models, and in Theorem 2.2 of Shuai and van den Driessche (2013) they used a matrix-theoretic method that is based on the Perron eigenvector to prove GAS of the DFE of some ODE disease models.
In this paper, we focus on discrete-time infectious disease models in populations that are governed by constant, geometric, Beverton–Holt or Ricker demographic equations. That is, our discrete-time epidemic model framework allows for the demographic population dynamics to be either asymptotically constant or under geometric growth (Castillo-Chavez and Yakubu 2001; Yakubu 2010). Others have studied discrete-time epidemic models without demographic dynamics, for example see Allen (1994) and Brauer et al. (2010). In Sect. 2, we first review the next-generation method for computing \(\mathcal {R}_{0}\) for discrete-time models (Allen and van den Driessche 2008). Secondly, we use the methods in Shuai and van den Driessche (2013) to obtain a Lyapunov function for discrete-time epidemic models (Theorem 2). Also in Sect. 2, as in Shuai and van den Driessche (2013), we use a similar matrix-theoretic method that is based on the Perron eigenvector to obtain verifiable conditions for GAS of the DFE of the discrete-time disease models (Theorem 3). The results of Sect. 2 serve as background for later sections.
To demonstrate how the results of Sect. 2 can be applied to study specific discrete-time infectious diseases, we introduce discrete-time SEIR, cholera and anthrax epidemic models in Sects. 3, 4 and 5, respectively. For each of these models, we compute \(\mathcal {R}_{0}\) and prove GAS of the DFE when \(\mathcal {R}_{0}<1\). That is, we prove that independent of initial population densities, the SEIR, cholera or anthrax disease dies out whenever \(\mathcal {R}_{0}<1\) and the demographic population dynamics is asymptotically constant or under geometric growth. Also, under this demographic assumption when \(\mathcal {R}_{0}>1\), we prove that the disease persists, and show the existence of a unique endemic equilibrium (EE) for the SEIR and cholera models. Our simulations illustrate that the EE of each of the three specific disease models is asymptotically stable whenever \(\mathcal {R}_{0}>1\). We summarize our results in Concluding Remarks section.
2 Next-Generation Method for \(\mathcal {R}_{0}\) Computation
A next-generation method for computing \(\mathcal {R}_{0}\) for discrete-time compartmental epidemic models was developed by Allen and van den Driessche (2008) in Theorem 3. To describe the method, we write a general discrete-time compartmental infectious disease model in the form
where
and
respectively, represent the population sizes in the disease and non-disease compartments. Here, \(\mathcal {F=}\left( \mathcal {F}_{1},\mathcal {F}_{2} ,\ldots ,\mathcal {F}_{n}\right) ^{T}\) and \(\mathcal {T=}\left( \mathcal {T}_{1},\mathcal {T}_{2},\ldots ,\mathcal {T}_{n}\right) ^{T}\) where for each \(i\in \left\{ 1,2,\ldots ,n\right\} \), \(\mathcal {F} _{i}\) represents the density of new infections that appear in compartment i, and \(\mathcal {T}_{i}\) represents the population size of individuals that transition between compartment i and other compartments. Also, \(\mathcal {G=}\left( \mathcal {G}_{1},\mathcal {G}_{2},\ldots ,\mathcal {G}_{m}\right) ^{T}\) where for each \(i\in \left\{ 1,2,\ldots ,m\right\} \), \(\mathcal {G}_{i}\) represents the population size in non-disease compartment i.
To ensure well-posedness of Model (1) and guarantee the existence of a DFE, we assume that for each \(i\in \left\{ 1,2,\ldots ,n\right\} \), \(\mathcal {F}_{i}\left( 0,y\left( t\right) \right) =\mathcal {T}_{i}(0,y\left( t\right) )=0\), \(\mathcal {F}_{i}\left( x\left( t\right) ,y\left( t\right) \right) \geqslant 0\) and \(\mathcal {T} _{i}(x\left( t\right) ,y\left( t\right) )\geqslant 0\). For each \(i\in \left\{ 1,2,\ldots ,m\right\} ,\) we assume that \(\mathcal {G} _{i}\left( x\left( t\right) ,y\left( t\right) \right) \geqslant 0\). Furthermore, we assume that the disease-free system
has a unique equilibrium point, \(y\left( t\right) =y_{\infty }\), that is locally asymptotically stable (LAS) in the disease-free space. Details of the underlying assumptions are given in Allen and van den Driessche (2008).
Model (1) predicts the vectors of population sizes in the disease and non-disease compartments, \(x\left( t+1\right) \) and \(y\left( t+1\right) \), at time \(\left( t+1\right) \) from knowledge of vectors of population sizes in the disease and non-disease compartments, \(x\left( t\right) \) and \(y\left( t\right) \), at time t, where \(t=0,1,2,\ldots \). The unit of time depends on the specific model application. For example, the unit of time could be a convenient time for a follow-up census. The basic reproduction number, \(\mathcal {R}_{0}\), the lifetime production of infections produced per infectious individual, is independent of the model’s timescale. We will use Model (1) to compute \(\mathcal {R}_{0}\).
Following Allen and van den Driessche (2008) and Shuai and van den Driessche (2013), we define the two \(n\times n\) matrices
Thus, F is the matrix of new infections that survive the time interval, and T is the transition matrix. Since some of the population may die, \(\rho \left( T\right) <1\), where \(\rho \) is the spectral radius (Li and Schneider 2002). From the biological meanings of F and T, it follows that F is entrywise nonnegative and \((Id-T)\) is a non-singular M-matrix, where Id is the identity matrix of order n. Since
assuming that \(T\ge 0\) and \(\rho \left( T\right) <1\) implies \((Id-T)^{-1}\) is entrywise nonnegative. Let \(\psi \left( 0\right) \) be the number of initially infected individuals. Then, \(F(Id-T)^{-1}\psi \left( 0\right) \) is an entrywise nonnegative vector that gives the expected number of new infections. The matrix \(F(Id-T)^{-1}\) has (i, j) entry equal to the expected number of secondary infections in compartment i produced by an infected individual introduced in compartment j. Consequently, the basic reproduction number for the discrete-time system is
where \(Q=\)\(F(Id-T)^{-1}\) is the next-generation matrix. Using the above next-generation matrix method notation and assumptions on F and T, we summarize the relationship between the local stability of the DFE, \((0,y_{\infty })\), and \(\mathcal {R}_{0}\) in the following result of Allen and van den Driessche (2008) (see Theorem 3.2), a corollary of the results of Cushing and Yicang (1994) and Li and Schneider (2002).
Theorem 1
(Allen and van den Driessche 2008) If \((0,y_{\infty })\) is a DFE of the system
then \((0,y_{\infty })\) is locally asymptotically stable if
but unstable if
2.1 Global Stability of the DFE
For many continuous-time ODE disease models, the DFE is globally asymptotically stable (GAS) whenever \(\mathcal {R}_{0}\le 1\). That is, LAS of \((0,y_{\infty })\) implies its GAS. Shuai and van den Driessche (2013) use a matrix-theoretic method that is based on the Perron eigenvector to prove the GAS of the DFE for continuous-time ODE disease models. We use a similar method to provide a proof for GAS of the discrete-time disease model, Model (1).
Following Shuai and van den Driessche (2013), let
and recall that \(f(0,y(t))=0\). Then, the equations for the disease compartments of the discrete-time disease model, Model (1), becomes
For each \(t\in \left\{ 0,1,2,\ldots \right\} \) and \(x(t),y(t)\ge 0\), we assume that \(f(x(t),y(t))\ge 0\) so that near the disease-free equilibrium, the nonlinear interactions are deleterious. That is, \(f(x(t),y(t))\ge 0\) implies that only negative feedbacks are present, and this forces the absence of a backward bifurcation in the model.
Since \(\rho \left( T\right) <1\) and \(Q=\)\(F(Id-T)^{-1}\) is the next-generation matrix,
Now, let x(0) be the initial vector of the population sizes of the infectious individuals, then
is the distribution of all infections accumulated during the life span of the infectious population (Allen and van den Driessche 2008). Let \(\omega ^{T}\ge 0\) be the left eigenvector of the nonnegative matrix \(\left( Id-T\right) ^{-1\text { }}F\) corresponding to the eigenvalue \(\mathcal {R}_{0}=\rho \left( \left( Id-T\right) ^{-1\text { }}F\right) =\rho \left( F\left( Id-T\right) ^{-1\text { }}\right) \). In the following result, we provide a general method for constructing a Lyapunov function for the GAS of the disease-free equilibrium of the discrete-time disease model, Model (1), when \(\mathcal {R}_{0}\le 1\).
Theorem 2
Let the \(n\times n\) matrices F, T and the function f(x(t), y(t)) be as defined in (3) and (4). If \(f\left( x(t),y(t)\right) \ge 0\) in \( \Omega \subset \mathbb {R}_{+}^{n+m}\), \(F\ge 0\), \(T\ge 0\), \(\rho \left( T^{\text { } }\right) <1\) and \(\mathcal {R}_{0}\le 1\), then the function
defined by
is a Lyapunov function for Model (1), where \( \Omega \) is an open subset of \(\mathbb {R}_{+}^{n+m}\) containing \((0,y_{\infty })\).
Proof
L is a continuous function, \(L(0)=0\) and \(L(x(t))\ge 0\) for all \(x(t)\ne 0\in \mathbb {R}_{+}^{n}\). Consider L along solutions of Model (1). Then,
Since \(\omega ^{T}\ge 0\), \(f(x(t),y(t))\ge 0\), \((Id-T)^{-1}\)\(\ge 0\) and \(\mathcal {R}_{0}\le 1\), it follows that \(\omega ^{T}\left( -1+\mathcal {R} _{0}\right) x(t)\le 0\) and \(\omega ^{T}(Id-T)^{-1}f(x(t),y(t))\)\(\ge 0.\) Consequently,
Hence, L is a Lyapunov function for Model (1) on \( \Omega \subset \mathbb {R}_{+}^{n+m}.\)\(\square \)
As in continuous-time ODE compartmental disease models (see Shuai and van den Driessche 2013), in applications to discrete-time infectious disease models, all nonnegative population orbits are bounded under iterations. As a result, we will typically choose \( \Omega \) in Theorem 2 so that closure of \( \Omega \), \(\overline{ \Omega }\), is a compact positively invariant (with respect to Model (1)) subset of \(\mathbb {R}_{+}^{n+m}\) with the unique DFE, \((0,y_{\infty })\), in \(\overline{ \Omega }\). This choice of \(\Omega \) allows us to construct the Lyapunov function L of Theorem 2 and to prove the uniform persistence result of Theorem 3.
Using the results of Cushing and Yicang (1994) and Li and Schneider (2002), Allen and van den Driessche (2008) (see Theorem 2.1) established a relationship between \(\rho \left( F+T\right) =r\) and \(\mathcal {R}_{0}\), where \(F+T\) is irreducible. The relationship between r and \(\mathcal {R}_{0}\) satisfies one of the following inequalities (Allen and van den Driessche 2008; Li and Schneider 2002):
In the following result, we establish conditions for uniform persistence of the infectious disease (see Franke and Yakubu 1996; Hofbauer and So 1987).
Theorem 3
Let the \(n\times \ n\) matrices F, T and the function f(x(t), y(t)) be as defined in (3) and (4), and let \(\overline{ \Omega }\) be a compact positively invariant (with respect to Model 1) subset of \(\mathbb {R}_{+}^{n+m}\) with the unique DFE, \((0,y_{\infty })\), in \(\overline{\Omega }\). Suppose that \(f(x(t),y(t))\ge 0\) with \(f(0,y_{\infty })=0\) in \(\overline{ \Omega }\), \(F\ge 0\), T\(\ge 0\), \(\rho \left( T^{\text { }}\right) <1\) and \((Id-T)^{-1}F\) is irreducible. Assume that the disease-free system, \(y(t+1)=\mathcal {G}(0,y(t))\), has a unique equilibrium point, \(y=y_{\infty } >0\), that is GAS in \(\mathbb {R}_{+}^{m}\). Then, the following results hold for Model (1):
- 1.
If \(\mathcal {R}_{0}<1\), then the DFE \((0,y_{\infty })\) is GAS in the interior of \(\overline{ \Omega }\).
- 2.
If \(\mathcal {R}_{0}>1\), then the DFE \((0,y_{\infty })\) is unstable, Model (1) is uniformly persistent, and the disease is endemic.
Proof
From Theorem 2, \(\mathcal {R}_{0}<1\) implies that \(L(x(t))=\omega ^{T}(Id-T)^{-1}x(t)\) is a Lyapunov function of Model (1). Since \((Id-T)^{-1}F\) is irreducible and nonnegative, it follows by Perron–Frobenius theory that \(\omega ^{T}>0\). Recall that
Hence, \(L(x(t+1))-L(x(t))=0\) and \(\mathcal {R}_{0}<1\) imply that \(x(t)=0\). Using the GAS assumption on the DFE, \((0,y_{\infty })\), and the fact that \(f(0,y_{\infty })=0\), the only invariant set in \(\mathbb {R}_{+}^{n+m}\) where \(x(t)=0\) is the singleton \(\{(0,y_{\infty })\}\). By the Lyapunov function Theorem of La Salle (see Elaydi 2000; La Salle 1976), \(\{(0,y_{\infty })\}\) is GAS in \( \Omega \).
If \(\mathcal {R}_{0}>1\), then \(\omega ^{T}(-1+\mathcal {R}_{0})x(t)>0\) provided \(x(t)>0\). Furthermore, \(f(x(t),y(t))\ge 0\) with \(f(0,y_{\infty })=0 \) in \(\overline{ \Omega \text {,}}\) and \(\omega ^{T}(Id-T)^{-1}f(x(t),y(t))\ge 0\). By continuity of f, given any \(\varepsilon >0\), there exists \(\delta >0\) such that \(0\ne x(t)<\delta \) implies that \(f(x(t),y_{\infty })<\varepsilon \). Hence, there exists \(\delta _{1}>0\) such that \(L(x(t+1))-L(x(t))>0\) for any \(x(t)>0\) in \(\delta _{1}\)-neighborhood of \((0,y_{\infty })\). Thus, initial conditions (x(t), y(t)) with \(x(t)\ne 0\) in the positive cone and sufficiently close to \((0,y_{\infty })\) move away from \((0,y_{\infty })\) under iterations. That is, \((0,y_{\infty })\) is unstable. By a uniform persistence result from Hofbauer and So (1987) and an argument as in the proof of Proposition 1 of Franke and Yakubu (1996), we obtain that instability of \((0,y_{\infty })\) implies Model (1) is uniformly persistent whenever \(\mathcal {R}_{0}>1 \). As in Shuai and van den Driessche (2013), in Model (1), the instability of \((0,y_{\infty })\) in \(\mathbb {R}_{+}^{n+m}\), uniform persistence and positive invariance of \(\overline{ \Omega }\) imply that the disease is endemic whenever \(\mathcal {R}_{0}>1\). \(\square \)
The assumption that \((Id-T)^{-1}F\) is irreducible is a technical assumption that ensures that \(\omega ^{T}>0\). In some epidemic models, the matrix \((Id-T)^{-1}F\) is reducible, so Theorem 3 cannot be used directly. However, it may still be possible to use the Lyapunov function L as defined in Theorem 2. In the next section, we formulate an SEIR discrete-time epidemic model to illustrate the next-generation method for computing \(\mathcal {R}_{0}\), and we use Theorem 3 to understand disease extinction and persistence in this SEIR model.
3 SEIR Model
Susceptible–Exposed–Infectious–Recovered (SEIR) disease epidemic models have been used to study childhood diseases including chicken pox (varicella) and for the host population in the study of vector-borne diseases (for example, malaria). To introduce a SEIR disease epidemic model, we assume that at each time \(t\in \{0,1,2,\cdots \}\), each member of a population is either susceptible (\(S_{t}\)), exposed (individuals who have the disease and are mildly infectious, \(E_{t}\)), infectious (infected with the disease, \(I_{t}\)) or recovered from the disease with lifelong immunity (\(R_{t}\)), where the total population is
That is, we let \(S_{t}\), \(E_{t}\), \(I_{t}\), \(R_{t}\) and \(N_{t}\), respectively, denote the population density of susceptible, exposed, infectious, recovered and total population of individuals at time \(t\in \{0,1,2,\)···\(\}\).
Following Yakubu (2010) and the references therein, we assume that a fraction \(\theta \in (0,1)\) of susceptible individuals who interact with the infectious become exposed with probability \(\widehat{\varphi }\left( \frac{I_{t}}{N_{t}}\right) =\left( 1-\varphi \left( \frac{I_{t}}{N_{t} }\right) \right) \) and remain susceptible with probability \(\varphi \left( \frac{I_{t}}{N_{t}}\right) \) per the time interval, where the “escape” function
is a nonlinear decreasing smooth concave-up function with \(\varphi (0)=1\). That is, \(\varphi ^{\prime }(x)<0\) and \(\varphi ^{\prime \prime }(x)>0\) for all \(x\ge 0\). For example, when infections are modeled as Poisson processes, then \(\varphi \left( \frac{I_{t}}{N_{t}}\right) =\exp \left( -\beta \frac{I_{t} }{N_{t}}\right) \) and
Since exposed individuals are mildly infectious, we assume that a fraction \((1-\theta )\in (0,1)\) of susceptible individuals who interact with the exposed become exposed with probability \(\widehat{\psi }\left( \varepsilon \frac{E_{t} }{N_{t}}\right) =\left( 1-\psi \left( \varepsilon \frac{E_{t}}{N_{t}}\right) \right) \) and remain susceptible with probability \(\psi \left( \varepsilon \frac{E_{t}}{N_{t}}\right) \) per the time interval, where the “escape” function
is a nonlinear decreasing smooth concave-up function with \(\psi (0)=1\), and \(0<\varepsilon <1\).
The probability that an exposed individual progresses to the infectious class is the constant \(\kappa \in (0,1)\) per time interval and remains in the exposed class with probability \((1-\kappa )\). Furthermore, we assume that infectious individuals recover from the infection with constant probability \(\gamma \in (0,1)\) and remain infectious with constant probability \((1-\gamma )\) per time interval. We assume that the probability of natural death for each individual in the population is \(d\in (0,1)\) per the time interval, and probability of staying alive per time interval is \((1-d)\).
To include simple demography, we let
denote the recruitment (birth or immigration) function of individuals to the susceptible class per the time interval. Below, we list examples of four recruitment functions for this study.
Constant recruitment function,
$$\begin{aligned} g(N_{t})=\Lambda >0. \end{aligned}$$Geometric recruitment function,
$$\begin{aligned} g(N_{t})=rN_{t}, \end{aligned}$$where the proportionality constant \(r>0\).
Beverton–Holt recruitment function,
$$\begin{aligned} g(N_{t})=r\frac{N_{t}}{1+bN_{t}}, \end{aligned}$$where the intrinsic growth rate \(r>0\) and the scaling parameter \(b>0\).
Ricker recruitment function,
$$\begin{aligned} g(N_{t})=rN_{t}e^{-bN_{t}}, \end{aligned}$$where the intrinsic growth rate \(r>0\) and the scaling parameter \(b>0\).
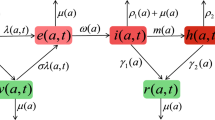
We assume that a susceptible individual has to be in the exposed class before becoming infectious. Similarly, an exposed individual must be in the infectious class before recovering, and we assume that recovered individuals have lifelong immunity. That is, we consider a disease that is not fatal so we ignore death to the disease. The flow diagram for the disease dynamics with compartments S, E, I and R is shown in Fig. 1.
Our frequency-dependent discrete-time SEIR model with \(\varphi \left( \frac{I_{t}}{N_{t}}\right) \) and \(\psi \left( \varepsilon \frac{E_{t}}{N_{t} }\right) \) implicitly assumes three distinct temporal phases. At the end of each time interval, susceptibles become exposed and exposed become infectious while infectious recover; a fraction of each class is removed; then, susceptibles, exposed, infectious and recovered reproduce into the susceptible class. These important assumptions distinguish our discrete-time SEIR epidemic model from a similar continuous-time differential equation model. Typically, continuous-time differential equation models with similar well-defined distinct temporal phases are non-autonomous. Taking into account the temporal ordering of events, we derive our SEIR model in the following three steps:
- 1.
Disease Transmission and Recovery:
$$\begin{aligned} \left. \begin{array}{lll} S_{(1)} &{} = &{} \theta S_{t}\varphi \left( \frac{I_{t}}{N_{t}}\right) +\left( 1-\theta \right) S_{t}\psi \left( \varepsilon \frac{E_{t}}{N_{t}}\right) \\ E_{(1)} &{} = &{} \theta S_{t}\widehat{\varphi }\left( \frac{I_{t}}{N_{t}}\right) +\left( 1-\theta \right) S_{t}\widehat{\psi }\left( \varepsilon \frac{E_{t} }{N_{t}}\right) +\left( 1-\kappa \right) E_{t}\\ I_{(1)} &{} = &{} \kappa E_{t}+\left( 1-\gamma \right) I_{t}\\ R_{(1)} &{} = &{} \gamma I_{t}+R_{t} \end{array} \right\} \end{aligned}$$That is, after disease transmission and recovery, \(S_{(1)}\), \(E_{(1)}\), \(I_{(1)}\) and \(R_{(1)}\) denote densities of susceptibles, exposed, infectious and recovered individuals, respectively.
- 2.
Natural Death (Survival):
$$\begin{aligned} \left. \begin{array}{lll} S_{(2)} &{} = &{} \left( 1-d\right) S_{(1)}\\ E_{(2)} &{} = &{} \left( 1-d\right) E_{(1)}\\ I_{(2)} &{} = &{} \left( 1-d\right) I_{(1)}\\ R_{(2)} &{} = &{} \left( 1-d\right) R_{(1)} \end{array}\right\} \end{aligned}$$That is, after disease transmission, recovery and natural death, \(S_{(2)}\), \(E_{(2)}\), \(I_{(2)}\) and \(R_{(2)}\) denote densities of susceptibles, exposed, infectious and recovered individuals, respectively.
- 3.
Reproduction (S, E, I and R into S):
$$\begin{aligned} \left. \begin{array}{lll} S_{(3)} &{} = &{} g\left( N_{t}\right) +S_{(2)}\\ E_{(3)} &{} = &{} E_{(2)}\\ I_{(3)} &{} = &{} I_{(2)}\\ R_{(3)} &{} = &{} R_{(2)} \end{array}\right\} \end{aligned}$$That is, after disease transmission, recovery, natural death and reproduction, \(S_{(3)}\), \(E_{(3)}\), \(I_{(3)}\) and \(R_{(3)}\) denote densities of susceptibles, exposed, infectious and recovered individuals, respectively.
These assumptions and notation lead to the following discrete-time SEIR epidemic model:

where \(t=0,1,2,\ldots \). We study Model (5) with initial conditions \(\left( S_{0},E_{0},I_{0},R_{0}\right) \in \left( [0,\infty )\times [0,\infty )\times [0,\infty )\times [0,\infty )\right) \backslash \left\{ \left( 0,0,0,0\right) \right\} .\)
Summing all the four equations of Model (5), at each time \(t\in \left\{ 0,1,2,\ldots \right\} \), the total population is governed by the equation
In Model (5) , we assume that events happen in the following order: disease transmission and recovery, survival (death) and reproduction. However, in real biological systems, these three events may happen in different orders. Cyclic permutations of the three distinct temporal phases may lead to models that are topologically conjugate to Model (5), while non-cyclic permutations of the three temporal phases typically lead to models that are not topologically conjugate to Model (5). When the exposed class is ignored \(\left( \text {that is, }\kappa =\theta =1\right) \) and there is neither recruitment nor death \(\left( \text {that is, }g\left( N_{t}\right) =d=0\right) \), then Model (5) reduces to a simple SIR model as studied by Brauer et al. (2010) and Martcheva (2015) (see Chapter 16).
Allen and van den Driessche (2008) studied a discrete-time SI Hantavirus model (see Model (9) in Allen and van den Driessche 2008), with separate compartments for males and females. Unlike Model (5), in the SEIR model of Allen and van den Driessche (2008) specific \(g\left( \cdot \right) \) and \(\varphi \left( \cdot \right) \) functions are taken, and the E class is not infectious.
3.1 Asymptotically Constant Growth Recruitment
For three of the four recruitment functions specified in the previous section, in Model (5) the total population \(N_{t}\) tends to a positive constant, denoted by \(S_{\infty }\), as \(t\rightarrow \infty \). The constant values are found from (6) and are given in Table 1 with \(\mathcal {R}_{d}=\frac{r}{d}\), and all parameters are positive. For the Ricker recruitment, if \(\mathcal {R}_{d}>e^{\frac{2}{d}}\), then demographic equation (6) undergoes period-doubling bifurcations route to chaos (Elaydi 2000; Yakubu 2010).
Equation (6), the demographic equation, is a single-variable equation of the total population. To reduce the number of variables in Model (5) by one, we assume that the total population is asymptotically constant and \(\lim _{t\rightarrow \infty }N_{t}\equiv S_{\infty }>0\). Then, Model (5) reduces to the following “limiting” system (see Best et al. 2003; Zhao 2003 for theorems on “limiting” systems).
where time \(t=0,1,2,\ldots \). The qualitative asymptotic dynamics of Model (5) and that of Model (7) are topologically conjugate when \(\lim _{t\rightarrow \infty }N_{t}\equiv S_{\infty }>0\) (Best et al. 2003).
In this case of asymptotically constant growth, \(\lim _{t\rightarrow \infty }N_{t}=S_{\infty }>0\) and \(N_{t+1}=g(N_{t})+\left( 1-d\right) N_{t}\) imply that
To consider proportions, let
Since \(s_{t}=1-e_{t}-i_{t}-r_{t}\), Model (7) reduces to the following system of three equations:
with DFE \(\left( e,i,r\right) =\left( 0,0,0\right) \).
To compute the basic reproduction number, \(\mathcal {R}_{0}\), we use the next-generation matrix method. To choose the matrix of new infections, F, we assume that a “new infection” means entry into the mildly infectious exposed class (Cushing and Diekmann 2016). As a result,
the transition matrix,
giving
where
and
The first term of \(\mathcal {R}_{0}\) gives contributions from the mildly infectious compartment E, whereas the second term gives contributions from the infectious compartment I. Therefore, mild infections from the exposed class increase the value of \(\mathcal {R}_{0}\). By Theorem 1, under the asymptotically constant growth in Model (5), the DFE, (1, 0, 0, 0), is locally asymptotically stable when \(\mathcal {R}_{0}<1\) and unstable when \(\mathcal {R}_{0}>1\). When \(\kappa =\theta =1\) (no E class) and \(d=0\) (no death) in Model (5), it becomes a simple SIR model, and \(\mathcal {R}_{0}\) reduces to \(\mathcal {R}_{0}=\frac{-\varphi ^{\prime }\left( 0\right) }{\gamma }\).
Theorem 4
If \(\mathcal {R}_{0}<1\), then the DFE of Model (8) is globally asymptotically stable. However, if \(\mathcal {R}_{0}>1\) then the DFE is unstable and Model (8 ) is uniformly persistent and has a unique endemic equilibrium.
Proof
To prove the global stability of the DFE, we will show that all the hypotheses of Theorem 3 are satisfied. Matrices F, T are nonnegative and \(\rho \left( T^{\text { }}\right) <1\). Furthermore,
is irreducible. Let
and
where \(\Psi \left( e_{t},i_{t}\right) =\)\(\theta \widehat{\varphi }\left( i_{t}\right) +\left( 1-\theta \right) \widehat{\psi }\left( \varepsilon e_{t}\right) \). Then,
Moreover,
Using the Mean Value Theorem, for all \(e_{t},i_{t}\in [0,1]\), gives
Hence, \(\left( 1-d\right) \theta \left( \varphi \left( i_{t}\right) -1-\varphi ^{\prime }\left( 0\right) i_{t}\right) \ge 0\) and \(\left( 1-d\right) \left( 1-\theta \right) \left( \psi \left( \varepsilon e_{t}\right) -1-\varepsilon \psi ^{\prime }\left( 0\right) e_{t}\right) \ge 0\), thus \(f\left( x\left( t\right) ,y\left( t\right) \right) \ge 0\).
The disease-free system,
has a unique equilibrium point, \(y_{\infty }=\left( s_{\infty },r_{\infty }\right) =\left( 1,0\right) \) that is GAS in \([0,1]\times [0,1]\), and \(f\left( 0,y_{\infty }\right) =0\). By Theorem 3, if \(\mathcal {R}_{0}<1\), then the DFE is GAS in the interior of \(\overline{ \Omega }=[0,1]\times [0,1]\times [0,1]\times [0,1]\). Furthermore, if \(\mathcal {R}_{0}>1\), then by Theorem 3, the DFE is unstable, Model (8) is uniformly persistent, and the disease is endemic.
Next, we establish that Model (8) has a unique endemic equilibrium when \(\mathcal {R}_{0}>1\). Let \(\left( e_{*},i_{*},r_{*}\right) \) denote an endemic equilibrium point of Model (8). Then,
The last two equations of (9) reduce to
Substituting for \(e_{*}\) and \(r_{*}\) in the first equation of (9) gives the equation
where
and
The endemic equilibrium exists whenever the graphs of the two smooth functions, \(M_{1}\left( i\right) \) and \(M_{2}\left( i\right) \), intersect at \(i_{*}\in \left( 0,1\right) \).
The graph of \(M_{1}\left( i\right) \) is a line through the origin with positive slope
The graph of \(M_{2}\left( i\right) \) passes through the origin. Notice that
implies for \(i\ge 0\) that
Also, \(M_{2}\left( i\right) \ge 0\) for all \(i\in [0,\frac{1}{1+\frac{\left( 1-\left( 1-\gamma \right) \left( 1-d\right) \right) }{\left( 1-d\right) \kappa }+\frac{\left( 1-d\right) \gamma }{d}}]\) and \(\lim _{i\rightarrow 1^{-}}M_{2}\left( i\right) <0\). Consequently, Model (8) has at least one endemic equilibrium whenever
That is, \(\mathcal {R}_{0}>1\) implies that Model (8) has at least one endemic equilibrium \(i_{*}\in \left( 0,1\right) \) with \(M_{1}\left( i_{*}\right) >0\). For uniqueness of the endemic equilibrium, notice that \(M_{2}^{\prime \prime }\left( i\right) <0\) for all \(i\in [0,\frac{1}{1+\frac{\left( 1-\left( 1-\gamma \right) \left( 1-d\right) \right) }{\left( 1-d\right) \kappa }+\frac{\left( 1-d\right) \gamma }{d}}]\) implies that the graph of \(M_{2}\left( i\right) \) is concave down and \(M_{2}^{\prime }\left( i\right) \) is decreasing on this interval. This establishes the uniqueness of the endemic equilibrium in the interior of \(\overline{ \Omega }=[0,1]\times [0,1]\times [0,1]\times [0,1].\)\(\square \)
When the E compartment is not infectious and \(\theta =1\), then \(\varepsilon =0\) and Model (5) reduces to
Using proportions, Model (10) becomes the following system of four equations:
with DFE \(\left( s,e,i,r\right) =\left( 1,0,0,0\right) \), where
The basic reproduction number for Model (11) is
where
and the transition matrix, T, remains unchanged. As in Model (5), under the asymptotically constant growth in Model (11), the DFE, \(\left( 1,0,0,0\right) \), is locally asymptotically stable when \(\mathcal {R}_{0}<1\) and unstable when \(\mathcal {R}_{0}>1\). However, unlike in Model (5), in this case the matrix
is reducible, so we cannot apply Theorem 3. In the next result, we establish the GAS of the DFE of Model (11).
Theorem 5
If \(\mathcal {R}_{0}<1\), then the DFE of Model (11) is globally asymptotically stable. However, if \(\mathcal {R}_{0}>1\), then the DFE is unstable, Model (11) is uniformly persistent and has a unique endemic equilibrium.
Proof
To prove the global stability of the DFE, note that F and T are nonnegative and \(\rho \left( T^{\text { }}\right) <1\). However, \((Id-T)^{-1}F\) is reducible, so we cannot use Theorem 3 directly. Instead, we use the Lyapunov function given in Theorem 2 to establish GAS. Since this is a special case of Model (5) when \(\theta =1\) and \(\varepsilon =0\), as in the proof of Theorem 4,
Moreover,
since by the Mean Value Theorem,
Thus, by Theorem 2, \(L\left( x\left( t\right) \right) =\omega ^{T}(Id-T)^{-1}x\left( t\right) \) is a Lyapunov for Model (11) if \(\mathcal {R}_{0}<1\), where \(\omega ^{T}=\left( 0,1\right) \) is the left eigenvalue of \((Id-T)^{-1}F\). Explicitly,
Computing \(L\left( x\left( t+1\right) \right) \), it follows that \(L\left( x\left( t+1\right) \right) =L\left( x\left( t\right) \right) \) implies that \(e_{t}=i_{t}=0\). The only invariant set where \(e_{t}=i_{t}=0\) is the DFE. Therefore, by La Salle’s invariance principle, the DFE is GAS if \(\mathcal {R}_{0}<1\). By arguments as in the proof of Theorem 3 , if \(\mathcal {R}_{0}>1\) the DFE is unstable and Model (11) is uniformly persistent and the disease persists. The proof of the existence of a unique endemic equilibrium of Model (11) is similar to that of Model (5) and is omitted. \(\square \)
Next, we consider an extension of Model (10). Suppose that a fraction p of individuals are vaccinated at recruitment into the susceptible population, where the E compartment is not infectious. This is an approximation for vaccination of babies against childhood diseases. In addition, suppose that the vaccine is perfectly effective, so everyone receiving the vaccine is protected from the disease. With constant, Beverton–Holt or Ricker recruitments, the total population is asymptotically constant and \(\lim _{t\rightarrow \infty }N_{t}\equiv S_{\infty }>0\). We assume that \((1-p)g(S_{\infty })\) enter the S compartment and the remaining \(pg(S_{\infty })\) enter the R compartment. The DFE becomes
and the vaccination reproduction number also called a control reproduction number, denoted by \(\mathcal {R}_{V}\), is given by
That is,
To bring \(\mathcal {R}_{V}\) below the threshold value 1, the fraction that needs to be vaccinated to give herd immunity is \(p>\)\(1-\frac{1}{\mathcal {R}_{0}}\), where either \(S_{\infty }=\frac{\Lambda }{d}\) (constant recruitment, \({\Lambda }>0\)) or \(S_{\infty }=\frac{\left( \mathcal {R}_{d}-1\right) }{b}\) (Beverton–Holt recruitment, \(\mathcal {R}_{d}>1\)) or \(S_{\infty }=\frac{\ln \mathcal {R}_{d}}{b}\) (Ricker recruitment, \(1<\mathcal {R}_{d}<e^{\frac{2}{d}}\)).
3.2 Geometric Growth Recruitment
When the recruitment function is proportional to the total population, then \(g\left( N_{t}\right) =rN_{t}\) and the demographic equation (6) reduces to
Hence,
for time \(t=1,2,3,\ldots \). When \(\mathcal {R}_{d}<1\), the total population goes extinct at geometric rate. However, when \(\mathcal {R}_{d}>1\) the total population grows at a geometric rate.
Under the geometric recruitment function, to study the disease transmission dynamics in Model (10) for \(\mathcal {R}_{d}>1\), we let
where
for \(t=0,1,2,3,\ldots .\) Since \(s_{t}=1-e_{t}-i_{t}-r_{t}\), Model (10) reduces to the following system of three equations:
where
When \(\mathcal {R}_{d}=1\), then \(\eta =1-d\) and Model (12) reduces to Model (11). In fact, Model (12) is exactly Model (11) when \(\eta \) is replaced by \(\left( 1-d\right) \). Consequently, \(\mathcal {R}_{0}\) for Model (12) is
By Theorem 1, under geometric growth in Model (10), the DFE, \(\left( 1,0,0,0\right) \), is locally asymptotically stable when \(\mathcal {R}_{d}>1\) and \(\mathcal {R}_{0}<1 \) and unstable when \(\mathcal {R}_{d}>1\) and \(\mathcal {R}_{0}>1\). Proceeding exactly as in the case of asymptotically constant recruitment function with \(\mathcal {R}_{d}>1\), the following result is immediate.
Theorem 6
Let \(\mathcal {R}_{d}>1\). If \(\mathcal {R}_{0}<1\), then the DFE of Model (12) is globally asymptotically stable. However, if \(\mathcal {R}_{0}>1\), then the DFE is unstable, Model (12) is uniformly persistent and has a unique endemic equilibrium.
3.3 Illustrative Example
\(\mathcal {R}_{0}\) for the 1913–1917 chicken pox epidemics in Maryland, USA, was estimated to be between 7 and 8 (see Chapter 4 of Barton 2016). Barton used an SIR discrete-time epidemic model with vital dynamics to obtain \(\mathcal {R}_{0}=8.960\) for the chicken pox disease, where \(\beta =0.896\), \(\gamma =0.1\), \(S_{0}\)\(=4,995\), \(I_{0}=5\) and \(R_{0}\)\(=0\) (see Example 4.9 of Barton 2016). Recall that Model (11) reduces to a SIR model when the exposed class is ignored and \(\kappa =1\). To use Model (11) to compute \(\mathcal {R}_{0}\) for the 1913–1917 chicken pox epidemics in Maryland, USA, we assume that the SEIR disease infections are modeled as Poisson processes and \(\varphi \left( i_{t}\right) =e^{-\beta i_{t}},\) where \(\kappa =0.99\), \(d=0.015\), \(\beta =0.896\), \(\gamma =0.1\) and the model’s unit of time is a year (Barton 2016).
With our choice of parameters \(\mathcal {R}_{0}=\mathcal {R}_{0I}=7.658\), where \(t=0\) corresponds to 1913 (the year of the initial chicken pox infection in Maryland) and \(t=9\) corresponds to 1922 (5 years after the 1913–1917 chicken pox epidemics). With \(0.1\%\) of the population as the initial number of infectious individuals at the onset of the epidemics in 1913, Fig. 2 shows that less than \(7\%\) of the susceptibles were infected in less than 10 years of the infection. The inclusion of the exposed class and natural death rate in Model (11) resulted in a smaller value of \(\mathcal {R}_{0}=7.658\) than \(\mathcal {R}_{0}=8.960\) calculated in Barton (2016) with an SIR model. Our computed value of \(\mathcal {R} _{0}=7.658\) is consistent with the estimated \(\mathcal {R}_{0}\) between 7 and 8 for the 1913–1917 chicken pox epidemics in Maryland. Using the above parameter values and initial condition, as predicted by Theorem 5, Fig. 2 shows that the DFE \((s_{\infty } ,e_{\infty },i_{\infty },r_{\infty })\)\(=(1,0,0,0)\) is unstable and the uniformly persistent Model (11) has a unique asymptotically stable endemic equilibrium at \((s_{*},e_{*},i_{*},r_{*})\)\(=\) (0.137, 0.013, 0.112, 0.738) that is reached at approximately \(t=100\) years (not shown in Fig. 2).
4 Cholera Model
Cholera, an infectious disease of the small intestine, is caused by some strains of the bacterium Vibrio cholerae. In most cases, cholera infection causes mild diarrhea. However, some infection cases develop to severe diarrhea and vomiting, which if not properly treated lead to death within a few hours. Cholera can be transmitted indirectly to susceptible humans via water infected with the bacterium that is shed by infected humans, or directly from infected humans to susceptible humans. Continuous-time ODE models of cholera have been used to illustrate the relative importance of the two cholera transmission pathways in designing control strategies; see for example Tien and Earn (2010).
4.1 Direct and Indirect Cholera Transmission Pathways
We use the same notation as used previously, augmented by a variable \(B_{t}\) denoting the concentration of bacterium in the water at each time \(t\in \{0,1,2,\ldots \}\), with the probability of bacterium that is removed from the water (death) per the time interval denoted by the constant \(\delta \in \left( 0,1\right) \), where cholera-infected humans shed bacterium into the water at a positive per capita rate \(\xi \) per the time interval. At the end of each time interval, a fraction of susceptible individuals, \(\theta S_{t}\), become infected via direct contact with cholera-infected humans with probability \(\widehat{\varphi }_{1}\left( \frac{I_{t}}{N_{t}}\right) =\left( 1-\varphi _{1}\left( \frac{I_{t}}{N_{t}}\right) \right) \), and a fraction of susceptible individuals, \(\left( 1-\theta \right) S_{t}\), become infected via indirect contact with cholera-infected water with probability \(\widehat{\varphi }_{2}\left( \frac{B_{t}}{N_{t}}\right) =\left( 1-\varphi _{2}\left( \frac{B_{t}}{N_{t}}\right) \right) \), where the constant \(\theta \in \left[ 0,1\right] \) and the total human population at time t is \(N_{t}=S_{t} +I_{t}+R_{t}\). The “escape from direct infection” and “escape from indirect infection” functions are, respectively, the nonlinear decreasing smooth concave-up functions
and
where \(\varphi _{1}\left( 0\right) =\varphi _{2}\left( 0\right) =1\). That is, for each \(i\in \left\{ 1,2\right\} \), \(\varphi _{i}^{\prime }<0\) and \(\varphi _{i}^{\prime \prime }>0\). These assumptions and notation lead to the following discrete-time cholera model with direct and indirect disease transmission pathways:
for time \(t\in \{0,1,2,\ldots \}\). We study Model (13) with initial conditions \((S_{0},I_{0},R_{0},B_{0})\in ([0,\infty )\times [0,\infty )\times [0,\infty )\times [0,\infty ))\backslash \{(0,0,0,0)\}\).
When the fraction \(\theta =0\), Model (13) captures only water-to-human indirect cholera transmission pathway (as assumed in some cholera models, see for example Codeço 2001), whereas \(\theta =1\) implies the model captures only human-to-human direct cholera transmission pathway, and \(\theta \in (0,1)\) implies the model captures both direct and indirect cholera transmission pathways.
Summing the first three equations of Model (13), at each time \(t\in \{0,1,2,\)···\(\}\), the total population is governed by the human demographic equation
4.2 Asymptotically Constant Growth Recruitment
When the total population is asymptotically constant, as in the SEIR model, we assume that \(\lim _{t\rightarrow \infty }N_{t}=S_{\infty }>0\). Then, Model (13) reduces to the “limiting system”
To consider proportions, let
Then, Model (14) becomes the following system of four equations:
with DFE \(\left( s,i,r,b\right) =\left( 1,0,0,0\right) \), where \(s_{t}+i_{t}+r_{t}=1\). Notice that in Model (15), \(0\le s_{t},r_{t},i_{t}\le 1\) implies the concentration of bacterium in the water is bounded.
The DFE is
We now use the next-generation matrix to compute \(\mathcal {R}_{0}\) for Model (13). Assuming that bacteria shedding is not a new infection, and proceeding exactly as before we obtain that at the DFE, the matrix of new infections that survive the time interval is
and the transition matrix is
F, T are nonnegative matrices, \(\rho \left( T\right) <1\), and
As in the continuous-time ODE cholera models, the direct and indirect routes of cholera transmission enter \(\mathcal {R}_{0}\) in an additive way. Therefore,
where
As in Model (5), under the asymptotically constant growth in Model (15), the DFE, (1, 0, 0, 0), is locally asymptotically stable when \(\mathcal {R}_{0}<1\) and unstable when \(\mathcal {R}_{0}>1\). If either direct reproduction number, \(\mathcal {R}_{0I}\), or indirect reproduction number, \(\mathcal {R}_{0B}\), is greater than 1, then \(\mathcal {R}_{0}>1\). As in the ODE models, when we assume that shedding is not a new infection, the discrete-time model confirms that both cholera transmission routes must be controlled to successfully eliminate the disease (Tien and Earn 2010; van den Driessche 2017).
If shedding is regarded as a new infection, i.e., put in matrix F instead of T, then in this case, \(\widehat{\mathcal {R}}_{0}\) is the positive root of the quadratic equation,
From the signs of the coefficients, this quadratic equation has a unique positive root, \(\widehat{\mathcal {R}}_{0}\). If \(\widehat{\mathcal {R}}_{0}<1\), then \(p(1)>0\) and \(\mathcal {R}_{0}=\mathcal {R}_{0I}+\mathcal {R}_{0B}<1\). Similarly, if \(\widehat{\mathcal {R}}_{0}>1\), then \(p(1)<0\) and \(\mathcal {R} _{0}=\mathcal {R}_{0I}+\mathcal {R}_{0B}>1\). Moreover, \(p(1)=1-\mathcal {R}_{0}\), thus \(\widehat{\mathcal {R}}_{0}\) gives the same threshold as derived for \(\mathcal {R}_{0}\).
For GAS of the DFE, observe that when shedding is not regarded as a new infection, then the matrices F and T are nonnegative with \(\rho \left( T\right) <1\). Furthermore,
is irreducible. Let
and
where \(\Delta \left( i_{t},b_{t}\right) =\)\(\theta \widehat{\varphi } _{1}\left( i_{t}\right) +\left( 1-\theta \right) \widehat{\varphi } _{2}\left( b_{t}\right) \). Then,
and as in the proof of Theorem 4, \(f\left( x\left( t\right) ,y\left( t\right) \right) \ge 0.\)
The disease-free system
has a unique equilibrium point, \(y_{\infty }=\left( s_{\infty },r_{\infty }\right) =\left( 1,0\right) \) that is GAS in \([0.1]\times [0.1]\), and \(f\left( 0,y_{\infty }\right) =0\). By Theorem 3, if \(\mathcal {R}_{0}<1\), then the DFE is GAS in the interior of \(\overline{ \Omega }=[0,1]\times [0,1]\times [0,1]\times [0,1]\). Furthermore, if \(\mathcal {R}_{0}>1\), then by Theorem 3, the DFE is unstable and Model (15) is uniformly persistent and the disease is endemic.
Next, we establish the existence of a unique endemic equilibrium. Let \(\left( i_{*},r_{*},b_{*}\right) \) denote an endemic equilibrium point of Model (15). Then,
The last two equations of (16) reduce to
Substituting for \(r_{*}\) and \(b_{*}\) in the first equation of (16) gives the equation
where
Proceeding exactly as in the proof of Theorem 4, the following result is immediate:
Theorem 7
If \(\mathcal {R}_{0}<1\), then the DFE of cholera Model (15) is globally asymptotically stable. However, if \(\mathcal {R}_{0}>1\), then the DFE is unstable, Model (15) is uniformly persistent and has a unique endemic equilibrium.
4.3 Geometric Growth Recruitment
Under the geometric recruitment function, to study cholera disease transmission dynamics in Model (13), for \(\mathcal {R}_{d}>1\) let
where
for \(t=0,1,2,3,\ldots .\) Since \(s_{t}=1-i_{t}-r_{t}\), Model (13) reduces to the following system of three equations:
where \(\eta =\frac{1-d}{1+d\left( \mathcal {R}_{d}-1\right) }\). Since \(\mathcal {R}_{d}>1\), \(0<\eta <1\) and \(0<\frac{\eta \left( 1-\delta \right) }{\left( 1-d\right) }<1\). Proceeding exactly as before, at the DFE \(\left( i,r,b\right) =\left( 0,0,0\right) \) the matrix of new infections that survive the time interval is
and the transition matrix is
F, T are nonnegative matrices, \(\rho \left( T\right) <1\), and
As in the case of constant recruitment, when the total population is under geometric growth, the direct and indirect routes of cholera transmission enter \(\mathcal {R}_{0}\) in an additive way. Therefore,
where
By Theorem 1, under geometric growth in Model (13), the DFE, \(\left( 1,0,0,0\right) \), is locally asymptotically stable when \(\mathcal {R}_{d}>1\) and \(\mathcal {R}_{0}<1 \) and unstable when \(\mathcal {R}_{d}>1\) and \(\mathcal {R}_{0}>1\).
For GAS of the DFE, observe that in this case the matrices F and T are nonnegative with \(\rho \left( T\right) <1\). Furthermore, \(\left( Id-T\right) ^{-1}F\) is irreducible, and
where \(\Delta \left( i_{t},b_{t}\right) =\)\(\theta \widehat{\varphi } _{1}\left( i_{t}\right) +\left( 1-\theta \right) \widehat{\varphi } _{2}\left( b_{t}\right) \). Proceeding exactly as in the case of asymptotically constant growth with \(\left( 1-d\right) \in \left( 0,1\right) \) replaced by \(\eta \in \left( 0,1\right) \), the following result is immediate.
Theorem 8
Let \(\mathcal {R}_{d}>1\). If \(\mathcal {R}_{0}<1\), then the DFE of cholera Model (17) is globally asymptotically stable. However, if \(\mathcal {R}_{0}>1\), then the DFE is unstable, Model (17) is uniformly persistent and has a unique endemic equilibrium.
4.4 Illustrative Example
The basic reproduction number for the 2006 cholera outbreak in Angola, as reported in Eisenberg et al. (2013), is \(\mathcal {R}_{0}=5.89\). Assuming asymptotically constant growth, to numerically show an asymptotically stable endemic equilibrium in Model (15), we assume that cholera infections are modeled as Poisson processes and \(\varphi _{1} (i_{t})=exp(-\beta _{I}i_{t})\), \(\varphi _{2}(b_{t})=exp(-\beta _{B}b_{t})\), where \(\beta _{B}=1.209\), \(\beta _{I}=0.263\), \(d=0.01\), \(\delta =0.196\), \(\xi =0.744\), \(\gamma =0.18\), \(\theta =0.8\) and the model’s unit of time is a year.
With our choice of parameters, \(\mathcal {R}_{0B}=4.780\), \(\mathcal {R} _{0I}=1.107\) and so \(\mathcal {R}_{0}=5.887\) (Eisenberg et al. 2013). With \(1\%\) of the population as the initial number of infectious individuals at the onset of the epidemic in 2006, Fig. 3 shows that less than \(20\%\) of the susceptibles were infected in 10 years of the infection. Using the above parameter values and initial condition, as predicted by Theorem 7, Fig. 3 shows that the DFE \(\left( s_{\infty },i_{\infty },r_{\infty },b_{\infty }\right) =\left( 1,0,0,0\right) \) is unstable, and the uniformly persistent Model (15) has a unique asymptotically stable endemic equilibrium at \(\left( s_{*},i_{*},r_{*},b_{*}\right) =(0.184,0.043,0.773,0.163)\) that is reached at approximately \(t=200\) years (not shown in Fig. 3). Since \(\mathcal {R}_{0I}\approx 1\), the proportion of directly infected humans is small.
5 Anthrax Model
Anthrax, an infectious disease that is known to infect both humans and animals, is caused by Bacillus anthracis, a gram-positive sporulating bacterium (Friedman and Yakubu 2013; Furniss and Hahn 1981; Hahn and Furniss 1983; Saad-Roy et al. 2017). Anthrax infections can be cutaneous, gastrointestinal or by inhalation, and may be deadly. Periodic anthrax disease outbreaks occur in animals and contact with anthrax-infected animals, or infected carcasses may spread the disease to susceptible animals or humans. Several continuous-time ODE models have been used to study the transmission of anthrax in animal populations; see for example Friedman and Yakubu (2013), Furniss and Hahn (1981), Hahn and Furniss (1983) and Saad-Roy et al. (2017).
5.1 Anthrax Epizootic
To introduce a discrete-time anthrax epidemic model in animal populations, we assume that at each time \(t\in \{0,1,2,\cdots \}\), each live animal is either susceptible (\(S_{t}\)) or infectious (infected with anthrax disease, \(I_{t}\)). That is, we let \(S_{t}\), \(I_{t}\) and \(N_{t}\)\(=\)\(S_{t}\)\(+\)\(I_{t}\), respectively, denote the population density of susceptible, infectious and total population of live animals at each time t. Furthermore, at each time t, we let \(A_{t}\) denote the grams of anthrax spores in the environment and let \(C_{t}\) denote the density of anthrax-infected carcasses.
The animals’ intrinsic birth rate per time interval is denoted by \(r>0\), and \(d\in (0,1)\) is the fraction of animals that die “naturally” per the time interval. The total animal population is assumed to follow the Beverton–Holt model. Consequently, assuming all newborn animals are susceptible,
are born into the susceptible class per time interval, where the scaling parameter \(b>0\). In the environment, anthrax spores grow on infected carcasses and decay or are washed away. Therefore, at each time t, we let \(\beta >0\) denote the constant per capita spore growth rate per carcass, and \(\alpha \in (0,1)\) denote the fraction of spores that decay per the time interval.
At time t, a fraction of live susceptible animals, \(\theta _{1}S_{t}\), become infected from grazing or inhaling anthrax spores in the environment with probability \(\widehat{\varphi }_{1}\left( A_{t}\right) \)\(=\)\((1-\varphi _{1}(A_{t}))\), a fraction of live susceptible animals, \(\theta _{2}S_{t}\), become infected via contact with anthrax-infected carcasses with probability \(\widehat{\varphi }_{2}\left( C_{t}\right) \)\(=\)\((1-\varphi _{2}(C_{t}))\), and the remaining fraction of live susceptible animals, \(\theta _{3}S_{t}\), become infected via direct contact with anthrax-infected live animals with probability \(\widehat{\varphi }_{3}\left( I_{t}\right) \)\(= \)\((1-\varphi _{3}(I_{t}))\), where the constants \(\theta _{1}\), \(\theta _{2}\), \(\theta _{3}\)\(\in [0,1]\) and \(\theta _{1}+\theta _{2}+\theta _{3}=1 \).
We assume that anthrax-infected live animals die from anthrax with constant probability \(\mu \in (0,1)\) per time interval. At each time t, the total live animal population feeds on infected carcasses with probability \((1-\varphi _{4}(N_{t}))\in [0,1]\). That is, \(\varphi _{4}(N_{t})C_{t}\) gives the remaining carcasses not consumed by live animals per time interval. For each \(i\in \{1,2,3,4\}\), we assume that each nonlinear probability function,
is a decreasing smooth concave-up function with \(\varphi _{i}(0)=1\). That is, \(\varphi _{i}^{\prime }<0\) and \(\varphi _{i}^{\prime \prime }>0\). Carcasses are organic matter and decay with probability \(\kappa \in (0,1)\) per time interval. Since some anthrax-infected animals recover from the disease, we let \(\tau \in [0,1]\) denote the probability of anthrax recovery per time interval. These assumptions and notation lead to the following discrete-time anthrax epizootic model with three disease transmission pathways.
for time \(t=0,1,2,3,\ldots \), where \(\widehat{d}=\left( 1-d\right) \), \(\widehat{\mu }=\left( 1-\mu \right) \) and \(\widehat{\tau }=\left( 1-\tau \right) .\)
Adding the equations for \(S_{t+1}\) and \(I_{t+1}\) results in
The demographic threshold parameter is
Thus, \(\mathcal {R}_{d}>1\) implies that
Assuming \(0\le N_{0}\le S_{\infty }\), if \(\mathcal {R}_{d}>1\), the feasible region \(\overline{\Omega }\left( \mathcal {R}_{d}>1\right) \) is
where \(\rho =\frac{\left( d+\mu \left( 1-\tau \right) \left( 1-d\right) \right) }{\kappa }\). If \(\mathcal {R}_{d}<1\), then
and \(N_{t}\le N_{0}\) for all \(t\ge 0\). The feasible region in this case is
5.2 Disease-Free Equilibria and \(\mathcal {R}_{0}\)
Model (18) has a trivial disease-free equilibrium, \(\left( S,I,A,C\right) =\left( 0,0,0,0\right) \). When \(\mathcal {R}_{d}>1\), the model exhibits two disease-free equilibria, the trivial equilibrium, \(P_{0-}\), and the equilibrium in which every live animal is susceptible and there are no infectious carcasses or spores, \(P_{0+}\), where
Note that \(P_{0-}\) is also a trivial equilibrium of Model (18 ) whenever the animal populations are under geometric growth or Ricker model. The following theorem addresses the stability of the trivial DFE, \(P_{0-}\).
Theorem 9
If \(\mathcal {R}_{d}<1\) and the probability of death per time interval is greater than the intrinsic per capita birth rate, then \(P_{0-}\) is LAS. However, if \(\mathcal {R}_{d}<1\) and \(d\le \frac{\mu \tau }{1+\mu \tau }\), then the probability of natural death is small and \(P_{0-}\) is GAS in interior of \(\overline{\Omega }\left( \mathcal {R}_{d}<1\right) ;\) thus, the total animal population goes extinct in Model (18). Otherwise, if \(\mathcal {R}_{d}>1\) and the probability of death per time interval is less than the intrinsic per capita birth rate, then \(P_{0-}\) is unstable; thus, the total animal population persists in Model (18).
Proof
For local stability, computing the Jacobian matrix of Model (18) about \(P_{0-}\) gives
with eigenvalues \(\lambda _{1}=r+1-d\), \(\lambda _{2}=\left( 1-\tau \right) \left( 1-\mu \right) \left( 1-d\right) \), \(\lambda _{3}=1-\alpha \) and \(\lambda _{4}=1-\kappa \). Clearly, if \(\mathcal {R}_{d}<1\), then \(0<\lambda _{j}<1\) for each \(j\in \left\{ 1,2,3,4\right\} \) and \(P_{0-}\) is LAS. However, if \(\mathcal {R}_{d}>1\), then \(\lambda _{1}=r+1-d>1\) and \(P_{0-}\) is unstable.
To prove GAS of \(P_{0-}\) in Model (18) for \(\mathcal {R} _{d}<1\), we define the Lyapunov function
by
V is a continuous function, \(V\left( P_{0-}\right) =0\), and \(V\left( S,I,A,C\right) >0\) for all \(\left( S,I,A,C\right) \ne P_{0-}\in Interior\left( \overline{\Omega }\left( \mathcal {R}_{d}<1\right) \right) \).
To show that
for all \(\left( S_{t},I_{t},A_{t},C_{t}\right) \ne P_{0-}\in Interior\left( \overline{\Omega }\left( \mathcal {R}_{d}<1\right) \right) \), it is useful to note that since by assumption \(d\le \frac{\mu \tau }{1+\mu \tau }\) it follows that
Hence, for all \(\left( S_{t},I_{t},A_{t},C_{t}\right) \ne P_{0-}\in Interior\left( \overline{\Omega }\left( \mathcal {R}_{d}<1\right) \right) ,\)
Thus, for \(\mathcal {R}_{d}<1\) GAS of \(P_{0-}\) follows using the Lyapunov function theorem of La Salle (Elaydi 2000; La Salle 1976). \(\square \)
In all that follows, we assume that \(\mathcal {R}_{d}>1\). Proceeding as in the previous sections, for stability of the non-trivial DFE, \(P_{0+}\), we use the next-generation matrix method to compute the basic reproduction number. The infected compartments are I, A and C. Taking \(\left( d+\mu \left( 1-\tau \right) \left( 1-d\right) \right) \) and \(\beta \) as transfers, we obtain that
and
Here, F, T are nonnegative matrices, \(\rho \left( T\right) <1\) and
where
Biologically, \(\mathcal {R}_{0}\) is the sum of the number of anthrax infections transmitted to the animal population from anthrax spores in the environment, \(\mathcal {R}_{0A}\), from feeding on anthrax-infected carcasses, \(\mathcal {R} _{0C}\), and from direct contact with anthrax-infected animals, \(\mathcal {R} _{0I}\).
The following result of the LAS of \(P_{0+}\) follows immediately from Theorem 1.
Theorem 10
Suppose \(\mathcal {R}_{d}>1\) in Model (18). If \(\mathcal {R} _{0}<1\), then \(P_{0+}\) is LAS; thus a small anthrax outbreak is eradicated. However, if \(\mathcal {R}_{0}>1\), then \(P_{0+}\) is unstable; thus anthrax persists.
For GAS of the DFE \(P_{0+}\), we note that we cannot use Theorems 2 and 3 since the function f is not signed correctly.
5.3 Herbivore Model
Anthrax disease is primarily a disease of herbivores. Saad-Roy et al. (2017) introduced a continuous-time ODE model of anthrax disease transmission in herbivores. Since herbivores do not feed on carcasses, to reduce Model (18) to a discrete-time anthrax model of only herbivores, we assume that \(\varphi _{2}\left( C_{t}\right) =\varphi _{4}\left( N_{t}\right) =1\). Also, since direct anthrax infections between live animals are rare, we assume that \(\varphi _{3}(I_{t})=1\). Sudden death of an anthrax disease-infected animal is by far the most common clinical sign of anthrax infection in animals, and as in Saad-Roy et al. (2017), we assume that \(\tau =0\). Consequently, \(\varphi _{2}\left( C_{t}\right) =\)\(\varphi _{3}(I_{t})=\)\(\theta _{2}=\theta _{3}=0\), \(\theta _{1}=1\), and Model (18) simplifies to the following discrete-time anthrax model of herbivores:
with DFE \(P_{0-}\) and \(P_{0+}\). By Theorem 9, \(P_{0-}\) is LAS when \(\mathcal {R} _{d}<1\) and unstable when \(\mathcal {R}_{d}>1.\)
To compute the basic reproduction number for Model (19), we use that of Model (18). By our simplification assumptions, we obtain that
Consequently, if \(\mathcal {R}_{d}>1\), then the DFE \(P_{0+}\) is LAS when \(\mathcal {R}_{0}<1\) and unstable when \(\mathcal {R}_{0}>1.\)
In this case, the matrix
is reducible, so Theorem 3 cannot be used directly to prove the GAS of the DFE \(P_{0+}\). In the next result, we establish the GAS of the DFE \(P_{0+}\) of Model (19).
Theorem 11
Let \(\mathcal {R}_{d}>1\). If \(\mathcal {R}_{0}<1\), then the DFE \(P_{0+}\) of herbivore Model (19) is GAS in the interior of \(\overline{\Omega }=[0,\infty )\times [0,\infty \times [0,\infty )\times [0,\infty )\). However, if \(\mathcal {R}_{0}>1\), then the DFE is unstable, Model (19) is uniformly persistent, and the disease is endemic.
Proof
To prove the GAS of \(P_{0+}\), we note that F, T and \(\left( Id-T\right) ^{-1}\) are nonnegative matrices. We use the Lyapunov function given in Theorem 2 to establish GAS. Let
and
Then,
Moreover,
Thus, by Theorem 2, \(L(x(t))=\omega ^{T}(Id-T)^{-1}x(t)\) is a Lyapunov function for Model (19) if \(\mathcal {R} _{0}<1\), where \(\omega ^{T}=\left( 0,1,0\right) \) is a left eigenvector of \((Id-T)^{-1}F\). Explicitly,
Computing \(L(x(t+1))\), it follows that \(L(x(t+1))=L(x(t))\) implies that \(I_{t}=A_{t}=C_{t}=0\). The only invariant LAS set where \(I_{t}=A_{t}=C_{t}=0\) is \(P_{0+}\). Therefore, by La Salle’s invariance principle, \(P_{0+}\) is GAS if \(\mathcal {R}_{0}<1\). By arguments as in the proof of Theorem 3 , if \(\mathcal {R}_{0}>1\) the DFE is unstable, Model (19) is uniformly persistent, and the disease is endemic. \(\square \)
5.4 Illustrative Example
As in the previous examples, in Model (19), we assume that anthrax infections in the herbivores are modeled as Poisson processes and \(\varphi _{1}\left( A_{t}\right) =e^{-\sigma A_{t}}\), where \(\alpha =0.997,\)\(\beta =0.1,\)\(b=1,\)\(\sigma =0.01,\)\(d=0.004,\)\(r=1,\)\(\kappa =0.2\), \(\mu =0.01\), the model’s unit of time is a year, and the total population of animals is 200. With our choice of parameters, \(\mathcal {R}_{d}>1\) and \(\mathcal {R} _{0}=1.244>1\). With about \(5\%\) of the animal population as the initial number of infectious animals at the onset of the epidemic, due to the relatively small value of \(\mathcal {R}_{0}\), Fig. 4 shows that less than \(10\%\) of the susceptible animals are infected in 10 years of the anthrax infection. Using the above parameter values and initial condition, as predicted by Theorem 11, Fig. 4 shows that the DFE \((S_{\infty },I_{\infty },A_{\infty },C_{\infty })=(249,0,0,0)\) is unstable and the uniformly persistent Model (19) has an asymptotically stable endemic equilibrium at \((S_{*},I_{*},A_{*},C_{*})=\) (200.298, 13.908, 0.097, 0.971) that is reached at approximately \(t=600\) years (not shown in Fig. 4).
6 Concluding Remarks
We use the next-generation method of Allen and van den Driessche (2008) to compute \(\mathcal {R}_{0}\) for discrete-time epidemic models in populations that are governed by constant, geometric, Beverton–Holt or Ricker demographic equations. When \(\mathcal {R}_{0}<1\) and the demographic population dynamics are asymptotically constant or under geometric growth (non-oscillatory), we prove GAS of the DFE of the disease models. That is, independent of initial population densities, the disease dies out whenever \(\mathcal {R}_{0}<1\) and the demographic population dynamics are asymptotically constant or under geometric growth. We apply our theoretical results to discrete-time epidemic models that are formulated for SEIR infections, cholera in humans and anthrax in animals. Also, under the demographic assumption when \(\mathcal {R}_{0}>1\), we prove that the disease persists, and show the existence of a unique endemic equilibrium (EE) for the SEIR and cholera models. The proof of GAS of the unique EE of our discrete-time epidemic models is an open question.
For any given disease, different models of the disease may not deliver the same \(\mathcal {R}_{0}\) expression. Thus, in using \(\mathcal {R}_{0}\) to evaluate the effect of a disease control measure on outbreaks it is necessary to link the \(\mathcal {R}_{0}\) value directly to the model assumptions (Lewis et al. 2006). Most infectious disease surveillance data are reported at discrete-time intervals; see for example CDC malaria surveillance data in USA (Mace and Arguin 2017). Our discrete-time epidemic models assume that populations are censored at discrete-time unit intervals, and reproduction occurs only once during the time interval. Consequently, our \(\mathcal {R}_{0}\) expressions typically differ from corresponding \(\mathcal {R}_{0}\) for continuous-time models.
Bacaer et al. computed \(\mathcal {R}_{0}\) for time-periodic (non-autonomous) continuous-time and discrete-time epidemic models; see Bacaer and Ait Dads (2012) and the references therein. Our discrete-time epidemic models for this study are not seasonal or time-periodic models. However, due to density dependence of the recruitment function, our model framework allows for the disease-free system to support cyclic and chaotic dynamics. For example, the disease-free system undergoes period-doubling route to chaos bifurcations when the recruitment function is the Ricker model with parameters in the period-doubling bifurcation route to chaos regimes (Yakubu 2010). When the equilibrium point of the disease-free system undergoes a period-doubling bifurcation, then the demographic equation has a locally asymptotically stable period-2 orbit coexisting with an unstable fixed point. In this case, since there is no asymptotically stable DFE in the disease-free system, the next-generation matrix method of computing \(\mathcal {R}_{0}\) for our discrete-time epidemic models is not applicable. Theorems 1–3 need the disease-free system to have a LAS DFE. Constructing methods for computing \(\mathcal {R}_{0}\) for autonomous infectious disease models when the disease-free systems have cyclic or chaotic (oscillatory) dynamics and have no LAS DFE are interesting open problems that we are now considering.
References
Allen L (1994) Some discrete-time SI, SIR and SIS epidemic models. Math Biosci 124:83–105
Allen L, van den Driessche P (2008) The basic reproduction number in some discrete-time epidemic models. J Differ Equ Appl 14(10–11):1127–1147
Bacaer N, Ait Dads EH (2012) On the biological interpretation of a definition for the parameter \(\cal{R}_{0}\) in periodic models. J Math Biol 65:601–621
Barton JT (2016) An introduction to discrete mathematical modeling with Microsoft Office Excel. Wiley, Hoboken
Best J, Castillo-Chavez C, Yakubu A-A (2003) Hierarchical competition in discrete time models with dispersal. Fields Inst Commun 36:59–86
Brauer F, Feng Z, Castillo-Chavez C (2010) Discrete epidemic models. Math Biosci Eng 7(1):1–15
Castillo-Chavez C, Yakubu A-A (2001) Dispersal, disease and life-history evolution. Math Biosci 173:35–53
Codeço CT (2001) Endemic and epidemic dynamics of cholera: the role of aquatic reservoir. BMC Infect Dis 1:1
Cushing JM, Diekmann O (2016) The many guises of \(\cal{R}_{0}\) (a diadactic note). J Theor Biol 404:295–302
Cushing JM, Yicang Z (1994) The net reproductive value and stability in matrix population models. Nat Resour Model 8:297–333
Diekmann O, Heesterbeek JAP, Metz JAJ (1990) On the definition and computation of the basic reproduction ratio \(\cal{R}_{0}\) in models for infectious diseases in heterogeneous populations. J Math Biol 28:365–382
Eisenberg MC, Robertson SL, Tien JH (2013) Identifiability and estimation of multiple transmission pathways in cholera and waterborne disease. J Theor Biol 324:84–102
Elaydi N (2000) Discrete chaos. Chapman & Hall/CRC, Boca Raton
Franke J, Yakubu A-A (1996) Extinction and persistence of species in discrete competitive systems with a safe refuge. J Math Anal Appl 203:746–761
Friedman A, Yakubu A-A (2013) Anthrax epizootic and migration: persistence or extinction. Math Biosci 241:137–144
Furniss PR, Hahn BD (1981) A mathematical model of an anthrax epizootic in the Kruger National Park. Appl Math Model 5:130–136
Hahn BD, Furniss PR (1983) A mathematical model of anthrax epizootic: threshold results. Ecol Model 20:233–241
Hofbauer J, So JW-H (1987) Uniform persistence and repellors for maps. Proc Am Math Soc 107:1137–1142
La Salle JP (1976) The stability of dynamical systems. SIAM, Philadelphia
Lewis MA, Rencławowicz J, van den Driesschen P, Wonham M (2006) A comparison of continuous and discrete-time West Nile virus models. Bull Math Biol 68:491–509
Li C-K, Schneider H (2002) Applications of Perron–Frobenius theory to population dynamics. J Math Biol 44:450–462
Mace KE, Arguin PM (2017) Malaria surveillance—United States, 2014. Surveill Summ 66(12):1–24. https://www.cdc.gov/mmwr/volumes/66/ss/ss6612a1.htm
Martcheva M (2015) An introduction to mathematical epidemiology, vol 61. Springer texts in applied mathematics. Springer, New York
Saad-Roy CM, van den Driessche P, Yakubu A-A (2017) A mathematical model of anthrax transmission in animal populations. Bull Math Biol 79(2):303–324
Shuai Z, van den Driessche P (2013) Global stability of infectious disease models using Lyapunov function. SIAM J Appl Math 70(1):1513–1532
Tien JH, Earn DJD (2010) Multiple transmission pathways and disease dynamics in a water borne pathogen model. Bull Math Biol 72(6):1506–1533
van den Driessche P (2017) Reproduction numbers of infectious disease models. Infect Dis Model 2(3):288–303
Yakubu A-A (2010) Introduction to discrete-time epidemic models. DIMACS Ser Discrete Math Theor Comput Sci 75:83–109
Zhao X-Q (2003) Dynamical systems in population biology. CMS books in mathematics. Springer, Berlin
Acknowledgements
We thank the referees for their useful comments and suggestions. This research was partially supported by NSERC, through a Discovery Grant (P.vdD.). A.-A.Y. was partially supported by DHS Center Of Excellence for Command, Control and Interoperability at Rutgers University, NSF Computational Sustainability Grant # CCF-1522054 and NSF Award # DMS-1743144.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
van den Driessche, P., Yakubu, AA. Disease Extinction Versus Persistence in Discrete-Time Epidemic Models. Bull Math Biol 81, 4412–4446 (2019). https://doi.org/10.1007/s11538-018-0426-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11538-018-0426-2