A Model for Transfer of P-Glycoproteins in MCF-7 Breast Cancer Cell Line with Multiple Transfer Rules

Abstract

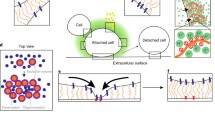
In this paper, we consider a direct protein transfer process between cells in co-culture. Assuming that cells continually encounter each other, and from some hypotheses on cell-to-cell rules of transfer, we derive discrete and continuous Boltzmann-like integro-differential equations. The novelty of this model is to take into account multiple transfer rules. This new transfer model is used to fit the experimental data of cell-to-cell protein transfer in breast cancer.

Appendix: Convergence of the Discrete Model to Continuous Model

In this section, we show the convergence of the scheme (6). It means that the difference $|u- u^\Delta |_1$ between the approximate solution $u^\Delta$ of the discrete model (6) and the solution u of the continuous model (4) tends to zero as the meshsizes $\Delta t, \Delta x$ go to zero (for simplicity we set $\Delta t=r\Delta x$). Here the approximate solution $u^\Delta$ is defined as the piecewise constant function defined on $]0, T[ \times \Omega _L$ (with $\Omega _L:=[0,L]$)

$$\begin{aligned} u^\Delta (t,x)=u^n_{i} \text{ For } \text{ all } (t,x) \in , ]t_n, t_{n+1}[\times ]x_i, x_{i+1}[, \end{aligned}$$

where the values $u^n_{i}$ are computed by (6).

Theorem 12

Let $u_0\in (L^1\cap L^\infty )(\Omega _L)$ with total variation be bounded locally in $\Omega _L$, $u_0\ge 0$ , then as the meshsize $\Delta x$ tends to zero, there is a subsequence of ${( u^{\Delta })}_{\Delta x>0}$, the family of approximate solution, converging in $L^1_{loc}([0,T]\times \Omega _L)$ to a function $u\in L^1_{loc}([0,T]\times \Omega _L)$.

The limiting function u(t, x) just obtained is a weak solution of the problem (1).

In order to prove Theorem 12, we first prove the existence of a limit u to $u^{\Delta }$ when the meshsize $\Delta x$ goes to zero. Then we prove that this limit is a solution of the continuous problem (1).

Existence of a limit for $u^\Delta$ The proof of existence of the limit u(t, x) is based on the compact canonical imbedding from $W^{1,1}(\Omega )$ into $L^{1}(\Omega )$. Let $I(u^\Delta )$, defined on $[0,T]\times \Omega _L$, be the interpolate of degree one of $u^\Delta$ at the vertices of each rectangle $[x_i,x_{i+1}]\times [t_n,t_{n+1}]$ where it is given by

$$\begin{aligned} I(u^\Delta ) (x,t)= & {} u^n_i+(u^n_{i+1}-u^n_i)\frac{\textstyle x-i\Delta x}{\textstyle \Delta x}+(u^{n+1}_i-u^n_i)\frac{\textstyle t-nr\Delta x}{ \textstyle r\Delta x}\nonumber \\&+\,(u^{n+1}_{i+1}-u^{n+1}_i-u^n_{i+1}+u^n_i)\frac{\textstyle (x-i\Delta x)(t-nr\Delta x)}{\textstyle r(\Delta x)^2}. \end{aligned}$$

(15)

$I(u^\Delta )$ is continuous with

$$\begin{aligned} | I(u^\Delta )|_{L^\infty ([0,T]\times \Omega _L)}=| u^\Delta |_{L^\infty ([0,T]\times \Omega _L)}=\sup _{n,i}|u^n_i| \end{aligned}$$

(16)

and differentiable inside each rectangle. Thus, we obtain

$$\begin{aligned} \displaystyle \int \int \left| \frac{\textstyle \partial I(u^\Delta ) }{\textstyle \partial t}\right| \hbox {d}x\hbox {d}t\le \displaystyle \sum _{n=0}^N\sum _{i\le I_L}| u^{n+1}_i-u_i^{n}|\Delta x. \end{aligned}$$

(17)

In the same way,

$$\begin{aligned} \displaystyle \int \int \left| \frac{\textstyle \partial I(u^\Delta ) }{\textstyle \partial x}\right| \hbox {d}x\hbox {d}t= \displaystyle \sum _{n=0}^N\sum _{i\le I_L}| u_{i+1}^{n}-u_i^{n}| r\Delta x. \end{aligned}$$

(18)

On the other hand, one can check that the numerical scheme (6) satisfies the following a priori estimates

$$\begin{aligned} \begin{array}{ll} \displaystyle \sup _i |u_i^{n+1}|\le (1+C_1\Delta t)\sup _i |u_i^{n}|\\ \displaystyle \sum _{i=1}^{I_L-1} | u^{n+1}_{i+1}-u^{n+1}_{i}|\le (1+C_2\Delta t)\sum _{i=1}^{I_L-1} | u^{n}_{i+1}-u^{n}_{i}|\\ \displaystyle \sum _{i=1}^{I_L-1} | u^{n+1}_i-u^{n}_{i}|\le \sum _{i=1}^{I_L-1} | u^{n}_{i+1}-u^{n}_{i}|, \end{array} \end{aligned}$$

(19)

where $C_1$ and $C_2$ are two constants independent of n.

Let $u_0\in L^\infty (\Omega _L)$, then $\sup _i|u_i^0|\le C$. It follows that $u^\Delta$ is bounded and then contains a subsequence $u^{\Delta _p}$ weakly star convergent to a limit $u\in L^\infty ([0,T]\times \Omega _L)$ bounded by $|u_0|_L^\infty (\Omega _L)$.

Let $u_0$ with the total variation $TV(u_0(x))=\sum _{i=1}^{I_L} | u_{0}(x_{i+1})-u_{0}(x_{i})|$ be bounded, we have, by applying the discrete Gronwall lemma to the estimates (19) and using successively (16) and (17), (18). It follows also that

$$\begin{aligned} | I(u^\Delta ) |_{L^\infty ([0,T]\times \Omega _L)}+\left| \frac{\textstyle \partial I(u^\Delta ) }{\textstyle \partial x}\right| _{L^1([0,T]\times \Omega _L)} +\left| \frac{\textstyle \partial I(u^\Delta )}{\textstyle \partial t}\right| _{L^1([0,T]\times \Omega _L)} \le M. \end{aligned}$$

(20)

Therefore, from $\left\{ I(u)^{\Delta }\right\}$ associated with $\left\{ u^{\Delta }\right\}$, we extract a subsequence convergent to $\left\{ I(u)^{\Delta _p}\right\}$ in $L_\mathrm{loc}^1(]0,T[\times \Omega _L)$. Then we verify that $\left\{ I(u)^{\Delta _p}- u^{\Delta _p}\right\}$ tends to zero in $L^1$ , for all bounded open sets $]0,T[\times \Omega _L$. Since the associate subsequence $u^\Delta$ weakly star converges to a function $u\in L^\infty (]0,T[\times \Omega _L)$, and since on the other hand $\left\{ I(u^{\Delta _p})\right\}$ is convergent in $L_\mathrm{loc}^1(]0,T[\times \Omega _L)$, we have

$$\begin{aligned} u^\Delta \hbox { converges to }u\hbox { in } L_\mathrm{loc}^1(]0,T[\times \Omega _L). \end{aligned}$$

(21)

This ends the proof of the existence of a limit.

Convergence of $F^{\Delta }( u^{\Delta })$ to T(u) Let us define the discrete operator acting on the piecewise constant function $u^\Delta$ by

$$\begin{aligned} F^\Delta (u^\Delta )=F_i^n \hbox { for all } (t,x) \in , ]t_n, t_{n+1}[\times ]x_i, x_{i+1}[, \end{aligned}$$

where $F^n_i$ given by (8). We have proved the following lemma

Lemma 13

The discrete transfer operator $F^{\Delta }( u^{\Delta })$ converges to the continuous transfer operator T(u) , u being the limit function of $u^{\Delta }$ as $\Delta x$ goes to zero.

Let us write

$$\begin{aligned} \left| F^{,\Delta }(u^\Delta )-T(u)\right| _{1} \le | F^{\Delta }(u^\Delta )-T(u^\Delta )|_{1}+|T(u^\Delta )-T(u)|_{1}. \end{aligned}$$

Since the transfer operator T is Lipchitz and $u^\Delta$ converges to u, the second term of the right-hand side of the above inequality $\displaystyle \int _0^1| T^{\Delta }(u^\Delta )(x)-T(u)(x)|\hbox {d}x \longrightarrow 0$ as the meshsize $\Delta x$ goes to zero.

Let us now calculate $\widehat{T}(u^\Delta )(x)$.

$$\begin{aligned} \widehat{T}(u^\Delta )(x)= & {} \displaystyle \sum _j\int _{x_j}^{x_{j+1}}\pi _1(p)u^\Delta (x_i+f_{1}(p)p)u^\Delta (x_i-(1-f_{1}(p))p)\hbox {d}p\\&+\displaystyle \sum _j\int _{x_j}^{x_{j+1}}\pi _2(p)u^\Delta (x_i+f_{2}(p)p)u^\Delta (x_i-(1-f_{2}(p))p)\hbox {d}p.\\= & {} \displaystyle \sum _j \int _{x_j}^{x_{j+1}} \pi _1(p) \hbox {d}p u^n_{i+f_{1}(p_j)j} u^n_{i-(1-f_{1}(p_j)) j}\\&+\displaystyle \sum _j\int _{x_j}^{x_{j+1}}\pi _2(p)\hbox {d}p \overline{u}^n_{i+f_{2}(p_j)j}\overline{u}^n_{i-(1-f_{2}(p_j))j}. \end{aligned}$$

In Sect. 3, we use the approximation $\pi _1$ and $\pi _2$

$$\begin{aligned} \pi _1(l_j)=\frac{\int _{x_j}^{x_{j+1}}\pi _1(p)\hbox {d}p}{\Delta x} \hbox { and } \pi _2(l_j)=\frac{\int _{x_j}^{x_{j+1}}\pi _2(p)\hbox {d}p}{\Delta x} \end{aligned}$$

(22)

we conclude that $T(u^\Delta )-F^\Delta (u^\Delta )=0$. This completes the proof of the lemma.

Weak solution Now we consider the consistency of the scheme, which means that this limit u is a weak solution of the continuous problem (1). For all smooth $\phi \in C^1([0,T]\times \Omega _L)$ with compact support in $[0,T[\times [0,1]$, we define

$$\begin{aligned} \forall (t,x) \in [x_{i-1},x_i[\times [t_n,t_{n+1}[,~~\phi ^\Delta (t,x)=\phi _i^n=\frac{1}{\Delta t\Delta x}\int _{t_n}^{t_{n+1}}\int _{x_{i-1}}^{x_i} \phi (t,x)\hbox {d}t\,\hbox {d}x. \end{aligned}$$

Multiplying scheme (6) by $\Delta x\phi _i^n$ we get,

$$\begin{aligned} \displaystyle \sum _{i,n} (u^{n+1}_i-u_{i}^{n})\phi _i^n-2 \tau \Delta t \displaystyle \sum _{i,n}F^{n}_i\phi _i^n\Delta x =0, \end{aligned}$$

(23)

then summing by part we get

$$\begin{aligned} \displaystyle \sum _{i,n}\left( u^{n+1}_i\left( \phi _i^{n}-\phi _{i}^{n+1}\right) \right) \Delta x-2 \tau \Delta t \displaystyle \sum _{i,n}F^{n}_i\phi _i^n \Delta x -\displaystyle \sum _{i}u_i^{0}\phi _i^0\Delta x=0 \end{aligned}$$

(24)

which is equivalent to

$$\begin{aligned}&\displaystyle \int _0^T\int _{\Omega _L} u^\Delta (t,x)\displaystyle \frac{\phi ^\Delta (t+\Delta t,x)-\phi ^\Delta (t,x)}{\Delta t} \hbox {d}x\,\hbox {d}t\nonumber \\&\quad +\displaystyle \int _0^T\int _{\Omega _L} 2 \tau F^\Delta (u^\Delta )(t,x)\phi ^\Delta (t,x)\hbox {d}x\,\hbox {d}t\nonumber \\&\quad +\displaystyle \int _{\Omega _L} u^\Delta (0,x)\phi ^\Delta (0,x)\hbox {d}x=0, \end{aligned}$$

(25)

we pass to the limit $\Delta x \rightarrow 0$, we obtain

$$\begin{aligned}&\displaystyle \int _0^T \int _{\Omega _L} u(t,x)\frac{\partial \phi }{\partial t}(t,x)\hbox {d}x\hbox {d}t + \displaystyle \int _0^T \int _{\Omega _L}2 \tau \left[ T(u(t,.))(x)-u(t,x) \right] \phi (t,x)\,\hbox {d}x\,\hbox {d}t\nonumber \\&\quad +\displaystyle \int _{\Omega _L} u(0,x)\phi (0,x)\hbox {d}x=0 \end{aligned}$$

(26)

which means that the limit u obtained using the discrete scheme is a weak solution of the problem (1) with the initial data $u_0(x)$.