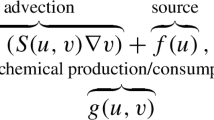The Dynamics of Root Growth: A Geometric Model

Abstract

A new model for macroscopic root growth based on a dynamical Riemannian geometry is presented. Assuming that the thickness of the root is much less than its length, the model is restricted to growth in one dimension (1D). We treat 1D tissues as continuous, deformable, growing geometries for sizes larger than 1 mm. The dynamics of the growing root are described by a set of coupled tensor equations for the metric of the tissue and velocity field of material transport in non-Euclidean space. These coupled equations represent a novel feedback mechanism between growth and geometry. We compare 1D numerical simulations of these tissue growth equations to two measures of root growth. First, sectional growth along the simulated root shows an elongation zone common to many species of plant roots. Second, the relative elemental growth rate calculated in silico exhibits spatio-temporal dynamics recently characterized in high-resolution root growth studies but which thus far lack a biological hypothesis to explain them. In our model, these dynamics are a direct consequence of considering growth as both a geometric reaction–diffusion process and expansion due to a distributed source of new materials.

Appendix: Riemannian Geometry: A Short Introduction

1.1 1. The Metric Tensor

This appendix introduces some of the fundamental concepts of Riemannian geometry those who might be unfamiliar with the subject or require a re-familiarization with the material. Reviews of Riemannian geometry and tensor analysis can be presented in one of two ways: in (1) an intrinsic coordinate free form or (2) in an explicit coordinate dependent form using index notation. Since the latter formulation provides a means for developing computational schemes and making comparisons with observation, index notation will be used throughout this review.

Although it is assumed that the geometry of root growth is described by a one-dimensional space or manifold, everything presented here will assume that there exists a set of curvilinear coordinates $\{x^i\}$ where $i=1,2, \ldots N$ in an N-dimensional space. Therefore, a vector quantity $\mathbf {A}$ will have N components represented by $A^i$ in such a manifold.

The coordinate differences between points do not necessarily give the physical separations between the points that define the coordinates. Suppose two points in the manifold P and Q are infinitesimally separated. Point P will have coordinates $x^i$, while point Q will have coordinates $x^i + \hbox {d}x^i$. The physical separation d l between the points is determined by the metric tensor $g_{ik}$ with $N^2$ components and the quadratic differential form:

$$\begin{aligned} \hbox {d}l^2 = \sum ^N_{i = 1} \sum ^N_{k = 1} g_{ik} \hbox {d}x^i \hbox {d}x^k . \end{aligned}$$

The length $\hbox {d}l$ is a scalar quantity and is invariant under arbitrary transformations of the coordinates $x^i \rightarrow \tilde{x}^i(x)$.

For Cartesian coordinates ($x^1=x$, $x^2=y$, $x^3=z$) the physical distance between P and Q in a flat 3D space is given by the standard Pythagorean relation:

$$\begin{aligned} \hbox {d}l^2 = \hbox {d}x^2 + \hbox {d}y^2 + \hbox {d}z^2 \end{aligned}$$

and the metric tensor is just the unit tensor (with 1’s along the diagonal):

In the more general case the metric tensor will have components that depend on the coordinates $x^i$ and perhaps time. In what follows, the Einstein summation notation will be used so as to simplify the expressions that appear in all subsequent computations. This convention drops the summation sign over repeated indices and simply assumes that any pair of the same index in an expression implicitly assumes a summation over that index through the range of that index from 1 to N. Therefore, the double sum in the expression for $\hbox {d}l^2$ given above can be rewritten as:

$$\begin{aligned} {\hbox {d}}l^2 = g_{ik} \hbox {d}x^i \hbox {d}x^k \end{aligned}$$

(28)

where the sum over i and k is now indicated by the fact that both indices appear in pairs. Riemannian geometries require that the metric tensor is a symmetric tensor:

$$\begin{aligned} g_{ik} = g_{ki} \end{aligned}$$

and the components of the metric tensor lead to a positive definite values of $\hbox {d}l^2$.

While scalars are mathematical quantities that remain invariant under coordinate transformations, vectors and tensors will have different components in different coordinate systems. If the different coordinate systems are curvilinear or non-orthogonal then displacement vectors will have different mathematical properties compared to vectors obtained from the gradient of scalar functions. The Jacobian matrix of the transformation $x^i \rightarrow \tilde{x}^i(x)$

$$\begin{aligned} \tilde{J}^i_j = \frac{\partial \tilde{x}^i}{\partial {x}^j} \end{aligned}$$

and its inverse:

$$\begin{aligned} {J}^j_i = \frac{\partial {x}^j}{\partial \tilde{x}^i} \end{aligned}$$

lead to the transformation rules for contravariant vector components $A^i$ (i.e. those that transform like differentials)

$$\begin{aligned} \tilde{A}^k = \tilde{J}^k_i A^i = \frac{\partial \tilde{x}^k}{\partial {x}^i} A^i \end{aligned}$$

(29)

and covariant vector components $A_i$ (i.e. those that transform like gradients)

$$\begin{aligned} \tilde{A}_k = J^i_k A_i = \frac{\partial x^i}{\partial \tilde{x}^k} A_i. \end{aligned}$$

(30)

In fact it is these transformation rules that can be used to define the difference between the contravariant and the covariant components of a vector $\mathbf {A}$. The metric tensor $g_{ik}$ and its inverse $g^{ik}$ (which obeys $g^{im}g_{mk} = \delta ^i_k$—the Kronecker delta) can be considered as an operator that transforms contravariant components into covariant components and vice versa. That is:

$$\begin{aligned} A_i = g_{ik}A^k \qquad \mathrm{and} \qquad A^i = g^{ik} A_k. \end{aligned}$$

NB: The pair of indices appearing in the Einstein summation must have one contravariant component (superscript) and one covariant component (subscript); therefore, the square of the magnitude of a vector $\mathbf {A}$ is:

$$\begin{aligned} |\mathbf {A}|^2 = A^2 = A_iA^i = g_{ik}A^kA^i. \end{aligned}$$

The rules for tensor transformations follow in a similar manner. One must associate a Jacobian matrix with each index that describes the tensors components. Since tensor requires multiple indices, one can have all contravariant components, all covariant components or a mixture of both. All the possible second-rank tensor components transform as:

$$\begin{aligned} \tilde{T}^{ik} = \frac{\partial \tilde{x}^i}{\partial {x}^m} \frac{\partial \tilde{x}^k}{\partial {x}^n} T^{mn} \end{aligned}$$

for completely contravariant components of a second-rank tensor.

$$\begin{aligned} \tilde{T}_{ik} = \frac{\partial {x}^m}{\partial \tilde{x}^i} \frac{\partial {x}^n}{\partial \tilde{x}^k} T_{mn} \end{aligned}$$

for completely covariant components of a second-rank tensor.

$$\begin{aligned} \tilde{T}^{i}_{k} = \frac{\partial \tilde{x}^i}{\partial {x}^m} \frac{\partial {x}^n}{\partial \tilde{x}^k} T^m_n \end{aligned}$$

for the mixed components of a second-rank tensor.

These transformation properties are required if the mathematical relationships between tensor quantities are to remain valid in all coordinate systems. This allows for the establishment of general laws and equations that remain invariant under the transformation of coordinates. Hence the approach taken in this article. While the components of different objects may change under coordinate transformations, the fundamental relationship between the scalars, vectors and tensors remains unchanged under a transformation of coordinates.

1.2 2. The Connection Coefficients

Higher-rank tensors can be created by taking tensor products of lower-rank tensors. For example a second-rank tensor can be constructed from two vectors $A^i$ and $B^i$ along with a scalar $\kappa$ by:

$$\begin{aligned} T^{ik} = \kappa A^i B^k \end{aligned}$$

Since there is no summation here, $T^{ik}$ consists of the ordered product of the two vectors. Alternatively higher-rank tensors can be computed by taking derivatives of lower-rank tensors. However, for a general coordinate transformation partial differentiation does not obey the tensorial transformation rules established above. Therefore, a new form of differentiation is required in order to maintain the tensorial characteristics of derivatives of tensors.

This requires the introduction of a geometric quantity that removes the non-tensorial terms from the partial derivative to yield a tensor (or covariant) derivative that has the proper transformation properties. This quantity $\varGamma ^i_{jk}$ is called a “connection coefficient”, and it creates the covariant derivative for a contravariant vector to create a mixed second-rank tensor:

$$\begin{aligned} \nabla _k A^i = \frac{\partial A^i}{\partial x^k} + \varGamma ^i_{jk}A^j. \end{aligned}$$

(31)

The covariant derivative of a covariant vector is a completely covariant second-rank tensor:

$$\begin{aligned} \nabla _k A_i = \frac{\partial A_i}{\partial x^k} - \varGamma ^j_{ik}A_j. \end{aligned}$$

(32)

A special set of connection coefficients that can be written in terms of the metric and its derivatives called Christoffel symbols of the second kind leave the metric tensor invariant to the tensor derivative, and this fact leads to:

$$\begin{aligned} \varGamma ^i_{jk} = \frac{1}{2}g^{i\ell }\left( \frac{\partial g_{j\ell }}{\partial x^k} + \frac{\partial g_{\ell k}}{\partial x^j} - \frac{\partial g_{jk}}{\partial x^\ell } \right) . \end{aligned}$$

(33)

Due to the symmetry of the metric the connection coefficients are symmetric in the covariant indices:

$$\begin{aligned} \varGamma ^i_{jk} = \varGamma ^i_{kj}. \end{aligned}$$

The connection coefficients are also important in that they define how a particle with no external forces acting on it travel along the geodesics of a curved geometry. In flat space such a particle follows a straight line with constant velocity. In a curved manifold the velocity of a particle $v^i$ obeys the “geodesic motion equation”:

$$\begin{aligned} \frac{\hbox {d}v^i}{\hbox {d}s} = - \varGamma ^{i}_{jk} v^j v^k \end{aligned}$$

(34)

where the parameter s is a scalar quantity that parameterizes the position of the particle along the geodesic.

1.3 3. Measures of Curvature

Unlike mixed partial derivatives, mixed tensor derivatives do not commute. Since the tensor derivatives are tensors it can be expected that the commutator of covariant derivatives is also a tensor. In fact it can be shown that:

$$\begin{aligned} \nabla _j \nabla _k A_i- \nabla _k \nabla _j A_i = R^{\ell }_{ijk}A_{\ell } \end{aligned}$$

where the new tensor $R^a_{bcd}$ is a quantity computed from partial derivatives of the Christoffel symbols and products of the Christoffel symbols. It is the famous “Riemann tensor” that provides an unambiguous measure of local curvature of the manifold. Explicitly it is

$$\begin{aligned} R^i_{jk\ell } = \frac{\partial \varGamma ^i_{j\ell }}{\partial x^k} -\frac{\partial \varGamma ^i_{jk}}{\partial x^\ell } +\varGamma ^m_{j\ell } \varGamma ^i_{mk} -\varGamma ^m_{jk} \varGamma ^i_{m\ell } \end{aligned}$$

(35)

obtained after much algebra. This is a fourth-rank mixed tensor and is a nonlinear functional of the metric and its first and second partial derivatives.

With this tensor Riemann was able to complete the work begun by Gauss by finding an expression for the curvature of a space from knowing its intrinsic geometric properties without reference to any embeddings of that space in a higher-dimensional manifold. This is the motivation for introducing Riemannian curvature into a growth model. The local interactions that take place in the manifold and are independent of the external space in which the manifold exists.

From the symmetries of the metric and Christoffel symbols one can show that the number of independent components of the Riemann tensor is $\frac{1}{12}N^2(N^2-1)$. Thus, a 3D manifold has six independent components to the Riemann tensor, and a 2D surface has only one independent component.

It is possible to create other tensors that measure some form of curvature. For example the Ricci curvature tensor $R_{ab}$ = $R^c_{acb}$ or:

$$\begin{aligned} R_{ik} = R^j_{ijk} = \frac{\partial \varGamma ^j_{ik}}{\partial x^j} -\frac{\partial \varGamma ^j_{ij}}{\partial x^k} +\varGamma ^j_{ik } \varGamma ^m_{jm} -\varGamma ^j_{im} \varGamma ^m_{jk} \end{aligned}$$

(36)

The Ricci tensor can be thought of as an averaged curvature measure since it does not contain all of the required local information regarding curvature. However, on a 2D surface the one component of the Riemann tensor is transferred to the Ricci tensor. For a 2D surface with coordinates $(x^1=u,x^2=v)$ the distance between points can be given by:

$$\begin{aligned} \hbox {d}\ell ^2 = f(u,v) [\hbox {d}u^2 + \hbox {d}v^2] \end{aligned}$$

where f(u, v) is a position-dependent “scale factor”. The Ricci tensor for this metric is computed to be:

$$\begin{aligned} R_{11} = R_{22} = \frac{1}{2f^2} \left[ f\frac{\partial ^2 f}{\partial u^2} + f\frac{\partial ^2 f}{\partial v^2} - \left( \frac{\partial f}{\partial u} \right) ^2 - \left( \frac{\partial f}{\partial v} \right) ^2 \right] \end{aligned}$$

(37)

Although a 1D manifold has no Riemannian curvature, the geometric KPZ operator given by Eq. (10) has the same structure as the Ricci tensor. It is linear in the second spatial derivative and quadratic in the gradient of the scale factor. Finally forming the inner product of the Ricci curvature with the metric leads to a scalar curvature measure:

$$\begin{aligned} R = g^{ab}R_{ab} \end{aligned}$$

and this quantity is often called the Ricci scalar.