The Evolutionary Dynamics of Stochastic Epidemic Model with Nonlinear Incidence Rate

Abstract

A stochastic SIRS epidemic model with nonlinear incidence rate and varying population size is formulated to investigate the effect of stochastic environmental variability on inter-pandemic transmission dynamics of influenza A. Sufficient conditions for extinction and persistence of the disease are established. In the case of persistence, the existence of endemic stationary distribution is proved and the distance between stochastic solutions and the endemic equilibrium of the corresponding deterministic system in the time mean sense is estimated. Based on realistic parameters of influenza A in humans, numerical simulations have been performed to verify/extend our analytical results. It is found that: (i) the deterministic threshold of the influenza A extinction $R^{S}_{0}$ may exist and the threshold parameter will be overestimated in case of neglecting the impaction of environmental noises; (ii) the presence of environmental noises is capable of supporting the irregular recurrence of influenza epidemic, and the average level of the number of infected individuals I(t) always decreases with the increase in noise intensity; and (iii) if $R^{S}_{0}>1$, the volatility of I(t) increases with the increase of noise intensity, while the volatility of I(t) decreases with the increase in noise intensity if $R^{S}_{0}<1$.

1 Introduction

Influenza A virus infection has been one of the most serious public health challenges globally and attained an unprecedented degree of attention in recent years. The influenza epidemics during the last few decades caused substantial morbidity and mortality in humans (see Simonsen et al. 1998; Simonsen 1999). The mathematical models have been revealed as a powerful tool to understand the mechanism that underlies the spread of influenza (e.g., Arino et al. 2008; Germann et al. 2006; Nuño et al. 2005; Wang et al. 2015).

In mathematical modeling for influenza epidemics, SIRS compartmental model is usually a reasonable qualitative description of the evolutionary dynamics of influenza A. Annually recurring of type A influenza epidemics is mainly due to continual antigenic drift of surface glycoproteins of the virus, hemagglutinin (HA) and neuraminidase (NA) (Palese and Young 1982; Webster et al. 1982). Gradual changes of influenza antigens in the drift process result in decay of host immunity and ultimately enable the new influenza virus to reinfect previously infected hosts. To incorporate antigenic drift of influenza A phenomenologically, Pease originally suggests the framework of susceptible-infected-recovered-(re)susceptible (SIRS) dynamics with viral evolution causing transition from the recovered class to the susceptible class (Pease 1987). In recent literatures, many of these SIRS or SIRS-type models have provided valuable insights into evolutionary dynamics of influenza A in humans by antigenic drift (Casagrandi et al. 2006; Dushoff et al. 2004; Hooten et al. 2010; Shaman et al. 2010; Yuan and Koelle 2012). An alternative path to incorporating antigenic drift into epidemiological influenza models is that of formulating multi-strain models (e.g., Andreasen and Sasaki 2006; Gog and Grenfell 2002; Koelle et al. 2006; Nuño et al. 2005). In this paper, we model this process of antigenic drift in the SIRS compartmental framework, by allowing recovered individuals to continuously lose their immunity to the circulating virus and hence to return to the susceptible class at a constant rate.

The incidence function of epidemic model has been considered to play a key role in ensuring that the model does give a reasonable description of the disease dynamics (Capasso 1993; Levin et al. 1989). It is traditionally supposed that the incidence rate of disease (including influenza A) transmission is bilinear with respect to the number of susceptible individuals S(t) and the number of infective individuals I(t), e.g., $\beta$ SI, where $\beta$ is the transmission rate (e.g., Anderson and May 1991; Casagrandi et al. 2006; Hethcote 1976, 2000). As a matter of fact, it is generally difficult to get the details of transmission of infectious diseases, which may vary under different conditions. In addition, choosing generalized incidence rate function may allow the data themselves to flexibly decide the function form of incidence rates in practice (Xia et al. 2005). For these reasons, there is a wide and increasing interest in studying epidemic models with nonlinear incidence rates (see, e.g., Feng and Thieme 2000; Liu et al. 1986; Ruan and Wang 2003 and the references cited therein). For instance, Capasso and Serio (1978) used a saturated incidence rate $\beta \textit{SI}/(1+\alpha I)$ to describe that incidence rates increase more gradually than linear in the infected I and susceptible S, and then to prevent the unboundedness of contact rate; Hethcote and van den Driessche (1991) used a nonlinear incidence rate given by $\beta \textit{SG}(I)$. To incorporate the impact of media coverage to the spread of infectious diseases, Cui et al. (2008a) considered the incidence rate $\beta e^{-mI}\textit{SI}$ with $m>0$. This article chooses the general nonlinear incidence rate of the form $\beta \textit{SG}(I)$ to enable our model to be more flexible in dealing with realistic data, where G(I) allows the possibility of introducing some “psychological” effects (Capasso and Serio 1978).

In the real world, biological populations exist inevitably in a noisy world of random variation in the environmental parameters that affect their dynamics. Ripa and Lundberg (1996) showed that the autocorrelation, or color, of the external noise strongly influences extinction probabilities of population dynamics. Environmental stochasticity may induce local extinction of the population (e.g., Mode and Jacobson 1987; Wissel and Stöcker 1991). Mao et al. (2002) surprisingly found the presence of even a tiny amount of white noises can suppress a potential population explosion. Therefore, it is important to investigate the effect of random fluctuations in the environment on population dynamics.

However, despite the potential importance of parameter noise, it has received relatively little attention in the epidemiology literature (Keeling and Rohani 2008). In particular, few of the existing literatures formulate mathematical models to study the effect of unpredictable fluctuations in the environment on the inter-pandemic transmission of influenza. The transmission of influenza is sensitive to random meteorological factors, such as absolute humidity, temperature and precipitation. Shaman and Kohn (2009) explored the effects of absolute humidity on influenza virus transmission and influenza virus survival (IVS), and found that absolute humidity significantly constrains both transmission efficiency and IVS. Based on experimental studies in guinea pigs, Lowen and Steel (2014) revealed influenza virus transmission is strongly modulated by temperature and humidity: Transmission is highly efficient at $5\,^{\circ }\mathrm {C}$ but is blocked or inefficient at $30\,^{\circ }\mathrm {C}$, and dry conditions (20 and 35 % relative humidity) are also found to be more favorable for spread than other humid conditions. We also refer the reader to Lowen et al. (2007), Pica and Bouvier (2012) for learning more about the effect of weather factors to transmission efficiency of influenza. Random fluctuations in temperature or humidity will therefore be translated to fluctuations in the transmission rate $\beta$ (Keeling and Rohani 2008).

In addition, some studies showed that the white noise is an appropriate representation of environmental random variability in terrestrial ecosystems, through analyzing a variety of meteorological data under the condition of removing the influence of regular diurnal, lunar and seasonal cycles (Steele 1985; Vasseur and Yodzis 2004). To consider the impact of unpredictable weather conditions to the transmission of respiratory syncytial virus (RSV), Arenas et al. (2009) formulated stochastic SIRS model with the Gaussian white noise disturbance of the transmission rate and revealed that perturbations on the transmission rate have significant effect on the transmission dynamics of RSV by numerical simulations techniques. Hence, it is reasonable to investigate the effect of environmental random fluctuations on the transmission dynamics of influenza A in human populations based on a mathematical model which introduces the Gaussian white noise disturbance in the transmission parameter of disease $\beta$.

There are mainly two types of approaches for applying modeling techniques of stochastic differential equation (SDE) to introduce environmental noises into biological systems. In the first modeling procedure, an SDE model is obtained as approximation to the continuous time Markov chain model (e.g., Lahodny and Allen 2013; Yuan and Allen 2011). The second procedure is the technique of parameter perturbation, which is the most commonly used procedure in constructing SDE models (e.g., Haque 2011; Ji et al. 2011; Li et al. 2015; Liu et al. 2011; Liu and Bai 2015; Mukhopadhyay and Bhattacharyya 2012; Øksendal 2005; Zhao et al. 2015a). In recent years, several scholars have studied the effect of environmental noise on the transmission dynamics of diseases by proposing epidemic SDE model with stochastic disturbances of $\beta$ via the second procedure above. Through analytical analysis and numerical simulations, Gray et al. (2011) obtained a threshold of disease extinction of a stochastic SIS epidemic model with bilinear incidence rate and fixed population size. Lahrouz and Settati (2014) studied a stochastic SIRS model with bilinear incidence rate and fixed population size, and when the intensity of white noise is small, they obtained the necessary and sufficient condition for extinction of disease. We also refer the readers to Cai et al. (2015a, b), Lahrouz and Omari (2013), Yang and Mao (2014), Zhao et al. (2015b) and the references therein for more similar models with stochastic disease transmission.

This article formulates a stochastic SIRS epidemic model with nonlinear incidence rate and variable population size, and our main aim is to extend results in Gray et al. (2011), Lahrouz and Settati (2014) and investigate the effect of random variability in the environments on the inter-pandemic transmission dynamics of influenza A based on realistic parameters obtained from previous literatures. Compared with previous researches, the main contributions of the present study are as follows.

• In the nonlinear incidence setting, we obtain the sufficient criteria of disease extinction and the existence of unique stationary distribution by applying comparison theorem and constructing a suitable Lyapunov function, respectively. In this sense, we extend the previous studies (Cai et al. 2015a; Gray et al. 2011; Lahrouz and Settati 2014).

• Because the total population size of our model is varying, mathematical deduction in the three-dimensional setting faces greater challenges than Cai et al. (2015a), Gray et al. (2011), Lahrouz and Settati (2014) where their system can be simplified to one or two dimensions.

• Compared with results in Liu and Chen (2015), Zhao et al. (2015b) for a stochastic SIRS epidemic model with varying population size and the fluctuation of the white noise in the transmission rate of disease, the advantages in this paper lie in: (1) the existence of endemic stationary distribution is proved in the case of persistence; (2) combining analytical results and numerical simulations, the effect of the white noise on disease spread is analyzed completely for all range of noise intensity.

• According to detailed simulation studies, we verify that Conjecture 8.1 of Gray et al. (2011) may also hold for our stochastic SIRS system with nonlinear incidence rate and variable population size, i.e., we may obtain a threshold of disease extinction.

• Through developing an SDE model, we likely first study the effect of random variability in the environments on the epidemiological consequences of the drift mechanism for influenza A viruses based on realistic parameter values.

This paper is organized as follows. In the next section, we derive our model and introduce some preliminaries used in the later parts. In Sects. 3 and 4, we investigate the disease extinction and endemic dynamics of our model in detail. In Sect. 5, we perform numerical simulations to verify/extend our analytical results based on realistic parameter values with respect to influenza A virus in human host. In the last section, we provide a brief discussion and summary of main results.

2 Model Derivation and Preliminaries

Throughout this paper, we let $(\varOmega , \mathcal {F}, \mathbb {P})$ be a complete probability space with a filtration $\{\mathcal {F}_{t}\}_{t\ge 0}$ satisfying the usual conditions (i.e., it is right continuous and increasing while $\mathcal {F}_{0}$ contains all $\mathbb {P}$-null sets), and we denote $\mathbb {R}^{3}_{+}=\big \{x\in \mathbb {R}^{3}{:}\, x_{i}>0, i=1, 2, 3 \big \}$.

If the transmission of the infection is governed by a general nonlinear incidence rate $\beta \textit{SG}(I)$, then the basic SIRS model with variable population size is

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)/\textit{dt}=A-\mu _{1}S(t)+\lambda R(t)-\beta S(t) G(I(t)), \\ d I(t)/\textit{dt}=\beta S(t) G(I(t))-\left( \mu _{2}+\delta \right) I(t), \\ d R(t)/\textit{dt}=\delta I(t)-\left( \mu _{3}+\lambda \right) R(t), \end{array} \right. \end{aligned}$$

(1)

where S, I and R denote the number of the population that are susceptible, infectious and recovered with temporary immunity, respectively. The parameter $\lambda$ is the rate constant for loss of immunity; $\delta$ is the recovery rate; $\beta$ is the transmission rate (per capita), which is the product of the rate of contact among individuals and the probability that a susceptible individual who is contacted by an infectious individual will become infected; A is a constant recruitment of susceptible individuals, and $\mu _{1}$, $\mu _{2}$ and $\mu _{3}$ represent, respectively, mortality of susceptible, infectious and recovered, and we let $\mu _{1}\le \min \{\mu _{2}, \mu _{3}\}$ because the disease may lead to the death of infectious or recovered individuals. In addition, all parameters of model (1) are assumed to be positive constants.

Following the second modeling procedure of SDE mentioned above, the SDE version of system (1) with stochastic disturbances of $\beta$ is derived as follows (e.g., see Keeling and Rohani 2008): If the parameter $\beta$ in system (1) is not completely known, but subject to some random environmental effects, then we have

$$\begin{aligned} \beta =\widetilde{\beta }+ \sigma \xi (t), \end{aligned}$$

(2)

where $\xi (t)$ is the Gaussian white noise with mean zero and variance one, $\widetilde{\beta }$ represents the average transmission rate in the stochastic setting and $\sigma >0$ denotes the white noise intensity. Here, we assume the average transmission rate $\widetilde{\beta }$ is constant. Indeed, influenza incidence exhibits strong seasonal fluctuations in temperate regions throughout the world. To include the seasonal effect in the model, many existing literatures assume the average transmission rate $\widetilde{\beta }$ varies sinusoidally according to the formula $\widetilde{\beta }(t)=\beta _{0}\left( 1+\epsilon \cos (\varpi t-\phi )\right)$, where $\beta _{0}$, $\epsilon$, $\varpi$ and $\phi$ are all constants. However, our main aim is to study the influence of the white noise in the external environments on the evolutionary dynamics of influenza epidemics. Hence, it is reasonable to ignore the seasonality of transmission rates of influenza for convenience in this article.

Substituting (2) into system (1) and rearranging it yield

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( A-\mu _{1}S(t)+\lambda R(t)-\beta S(t) G(I(t))\right) \textit{dt} -\sigma S(t) G(I(t))\xi (t)\textit{dt}, \\ d I(t)=\left( \beta S(t) G(I(t))-\left( \mu _{2}+\delta \right) I(t)\right) \textit{dt} +\sigma S(t) G(I(t))\xi (t)\textit{dt}, \\ d R(t)=\left( \delta I(t)-\left( \mu _{3}+\lambda \right) R(t)\right) \textit{dt}, \end{array} \right. \end{aligned}$$

where $\widetilde{\beta }$ is rewritten as $\beta$ for convenience. Note that $\xi (t)\textit{dt}=dB(t)$, where B(t) represents the standard Brownian motion (Øksendal 2005). We then obtain the following stochastic epidemic SIRS model to be studied in this paper:

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( A-\mu _{1}S(t)+\lambda R(t)-\beta S(t) G(I(t))\right) \textit{dt} -\sigma S(t) G(I(t))\textit{dB}(t), \\ d I(t)=\left( \beta S(t) G(I(t))-\left( \mu _{2}+\delta \right) I(t)\right) \textit{dt} +\sigma S(t) G(I(t))\textit{dB}(t), \\ d R(t)=\left( \delta I(t)-\left( \mu _{3}+\lambda \right) R(t)\right) \textit{dt}. \end{array} \right. \end{aligned}$$

(3)

The interpretation associated with the stochastic integration represented by $\textit{dB}(t)$ in (3) should also be specified, as either Stratonovich or Itô (Øksendal 2005). Here, we use the Itô interpretation rather than the Stratonovich interpretation on the ground that the specific feature of the Itô model of “not looking into the future” is a reason for choosing the Itô interpretation in biology (see, e.g., Øksendal 2005; Turelli 1977).

Throughout this paper, we further assume that

(H1) :

$G(\cdot ){:}\,\mathbb {R}_{+}\rightarrow \mathbb {R}_{+}$, and $G(0)=0$, $0< G(I)\le I$ holds for all $I>0$;

(H2) :

h(x) is Lipschitz on $[0, A/ \mu _{1}]$; namely, there exists a constant $\theta >0$, such that

$$\begin{aligned} |h(x_{1})-h(x_{2})|\le \theta |x_{1}-x_{2}|\quad for \ any \ \ x_{1}, x_{2} \in [0, A/ \mu _{1}], \end{aligned}$$

where $h(x)=G(x)/ x$;

(H3) :

$G'(0)=1$, where $G'(0)$ denotes the derivative of the function G(x) at $x=0$.

Notice that the function G(I) in this paper is not necessarily increasing function with respect to I, e.g., it may firstly increase and then decrease describing some psychological effects: For a very large number of infectives, the infection force $\beta G(I)$ may decrease as I increases, because in the presence of a very large number of infectives, the population may tend to reduce the number of contacts per unit time (Capasso and Serio 1978). Our general results can be used in some specific forms for the incidence rate that have been commonly used, for example:

• (i) linear type: $G(I)=I$;

• (ii) saturated incidence rate: $G(I)= I/(1+\alpha I)$;

• (iii) incidence rates with “media coverage” effect as shown below:

Type 1 (see Cui et al. 2008a): $G(I)=I \exp (-mI)$, where m is a positive constant.

Type 2 (see Cui et al. 2008b): $\beta G(I)=(\beta -\beta _{2}f(I))I$, where $\beta >\beta _{2}$ and the function f(I) satisfies

$$\begin{aligned} f(0)=0,\ f^{'}(I)\ge 0,\ \lim _{I\rightarrow +\infty }f(I)=1. \end{aligned}$$

The basic reproduction number $R_{0}$ is a measure of the potential for disease spread in deterministic epidemic models. Epidemiologically, $R_{0}$ is interpreted as the expected number of secondary infections produced by an index case in a completely susceptible host. This threshold parameter $R_{0}$ of deterministic system (1) can be computed by application of the next-generation matrix approach (van den Driessche and Watmough 2002, 2008) as

$$\begin{aligned} R_{0}=\frac{A\beta G'(0)}{\mu _{1}(\mu _{2}+\delta )}=\frac{A\beta }{\mu _{1}(\mu _{2}+\delta )}. \end{aligned}$$

For convenience, let us introduce some notations as follows:

$$\begin{aligned} \sigma ^{*}:=\sqrt{\frac{\beta \mu _{1}}{A}\cdot \frac{R_{0}}{2}},\ \ \ \sigma _{*}:=\sqrt{2(\mu _{2}+\delta )(R_{0}-1)\left( \frac{\mu _{1}}{A}\right) ^{2}}, \ \ \ \overline{\sigma }:=\sqrt{\frac{\beta \mu _{1}}{A}}. \end{aligned}$$

(4)

Through simple derivations, we have the following proposition:

Proposition 1

• (1) if $R_{0}\le 2$, then $\overline{\sigma }\ge \sigma ^{*}$, otherwise $\overline{\sigma }< \sigma ^{*}$;

• (2) if $R_{0}= 2$, then $\sigma ^{*}= \sigma _{*}$, otherwise $\sigma ^{*}> \sigma _{*}$.

Let us give some definitions which will be used in later sections. In general, let X(t) be a regular time-homogenous Markov process in $\mathbb {R}^{n}$ described by the stochastic differential equation

$$\begin{aligned} d X(t)=b(X)\textit{dt}+\sum _{r=1}^{k}\sigma _{r}(X)d B_{r}(t), \end{aligned}$$

(5)

and the diffusion matrix is defined as follows

$$\begin{aligned} A(x)=\left( a_{ij}(x)\right) , \ \ \ \ a_{ij}(x)=\sum _{r=1}^{k}\sigma _{r}^{i}(x)\sigma _{r}^{j}(x). \end{aligned}$$

Moreover, for any twice continuously differential real-value function V(x), define an operator $\mathcal {L}V$ by

$$\begin{aligned} \mathcal {L}V(x)=\sum _{i=1}^{n}b_{i}(x)\frac{\partial V(x)}{\partial x_{i}} +\frac{1}{2}\sum _{i, j=1}^{n}a_{ij}(x)\frac{\partial ^{2} V(x)}{\partial x_{i}\partial x_{j}}. \end{aligned}$$

For the definition of stability, we will use those introduced in Refs. Has’minskii (1980).

Definition 1

The stochastic process $X(t)=\bar{X}$ is a stationary solution of the stochastic system (5) with initial condition $X(t_{0})=\bar{X}$ if

$$\begin{aligned} b(\bar{X})=0, \quad \sigma _{r}(\bar{X})=0, \quad r=1,2,\ldots , k. \end{aligned}$$

If $\bar{X}=0$, the stationary solution is called a trivial solution.

Definition 2

The trivial solution $X(t)=0$ of system (5) is said to be:

• (i) stable in probability if for any $\varepsilon >0$

  $$\begin{aligned} \lim _{x_{0}\rightarrow 0}\mathbb {P}\left( \sup _{t\ge 0}|X(t, x_{0})|\ge \varepsilon \right) =0, \end{aligned}$$

  where $X(t, x_{0})$ denotes the solution of (5) with the initial condition $X(0)=x_{0}$.

• (ii) globally asymptotically stable in probability if it is stable in probability and for any $x_{0} \in \mathbb {R}^{n}$

  $$\begin{aligned} \mathbb {P}\left( \lim _{t \rightarrow +\infty }X(t, x_{0})=0 \right) =1. \end{aligned}$$

To study the dynamics of model (3), we then present two lemmas.

Using the Khasminskii–Mao theorem (Khasminskii 2012; Mao 2002) and appropriate Lyapunov functions, we show that the stochastic differential equation associated with our model has a unique global positive solution.

Lemma 1

For any given initial value $(S(0), I(0), R(0))\in \mathbb {R}^{3}_{+}$, there is a unique solution (S(t), I(t), R(t)) of system (3) on $t\ge 0$ and the solution will remain in $\mathbb {R}^{3}_{+}$ with probability 1, namely $(S(t), I(t), R(t))\in \mathbb {R}^{3}_{+}$ for all $t \ge 0$ almost surely.

Proof

Since the argument is similar to that of Lahrouz and Omari (2013), Theorem 2.1, we here only sketch the proof to point out the difference with it. Define the stopping time $\tau ^{+}$ by

$$\begin{aligned} \tau ^{+}=\inf \Big \{t \in [0, +\infty ): S(t)\le 0\ \ or\ \ I(t)\le 0\ \ or\ \ R(t)\le 0\Big \}. \end{aligned}$$

To show this solution is positive globally in the first octant, we only need to show that $\tau ^{+} = +\infty$ a.s. Assume that there exists a $T > 0$ such that $\mathbb {P}(\tau ^{+} < T ) > 0$. Let $\widetilde{\varOmega }=\{\omega \in \varOmega {:}\,\tau ^{+} < T\}$, where $\omega$ represents a sample point (i.e., a possible outcome of the sample space $\varOmega$). Introduce $C^{2}$ function $V{:}\,\mathbb {R}^{3}_{+}\rightarrow \mathbb {R}$ by $V(t)=V(S,I,R) =\log (SIR)$. Applying the Itô’s formula to V, we obtain that for all $t \in [0, \tau ^{+})$ and $\omega \in \widetilde{\varOmega }$

$$\begin{aligned} d V= & {} \Big [\frac{A}{S}+\frac{\lambda R}{S}-\beta G(I)-\frac{\sigma ^{2}}{2}(G(I))^{2} +\beta S\Big (\frac{G(I)}{I}\Big )-\big (\mu _{1}+\mu _{2}+\mu _{3}+\lambda +\delta \big ) \nonumber \\&\quad -\,\frac{\sigma ^{2}}{2}\Big (\frac{S G(I)}{I}\Big )^{2}+ \frac{\delta I}{R}\Big ]dt -\sigma \Big [G(I)-S\Big (\frac{ G(I)}{I}\Big )\Big ]d B(t), \nonumber \\\ge & {} \Big [-\beta I-\frac{\sigma ^{2}}{2}(I^{2}+S^{2}) -\big (\mu _{1}+\mu _{2}+\mu _{3}+\lambda +\delta \big )\Big ]dt \nonumber \\&\quad -\,\sigma \Big [G(I)-S\Big (\frac{ G(I)}{I}\Big )\Big ]d B(t), \end{aligned}$$

(6)

where the last inequality is obtained by using the fact that $0<G(I)\le I$ and $S, I, R >0$ for all $t \in [0, \tau ^{+})$. we can integrate both sides of (6) from 0 to $\tau ^{+} \wedge t$ to get

$$\begin{aligned} V(\tau ^{+} \wedge t)\ge & {} V(0) + \int _{0}^{\tau ^{+} \wedge t}\Big [-\beta I-\frac{\sigma ^{2}}{2}\left( I^{2}+S^{2}\right) \\&\quad -\,\left( \mu _{1}+\mu _{2}+\mu _{3}+\lambda +\delta \right) \Big ]\textit{ds} \\&\quad -\,\int _{0}^{\tau ^{+} \wedge t} \sigma \Big [G(I)-S\left( \frac{ G(I)}{I}\right) \Big ]\textit{dB}(s). \end{aligned}$$

Recall that $0< G(I)/I \le 1$ for all $t \in [0, \tau ^{+})$. Let $t\rightarrow +\infty$ in both sides of the above inequality, we obtain from the definition of $\tau ^{+}$ that

$$\begin{aligned} -\infty > -\infty , \end{aligned}$$

which is a contradiction. This completes the proof of Lemma 1. $\square$

Lemma 2

For any given initial value $(S(0), I(0), R(0))\in \mathbb {R}^{3}_{+}$, the solution (S(t), I(t), R(t)) of system (3) has the property that

$$\begin{aligned} \lim _{t\rightarrow + \infty } (S(t)+I(t)+R(t))\le \frac{A}{\mu _{1}} \end{aligned}$$

for all $\omega \in \varOmega$.

Proof

Summing up the three equations in (3) and denoting $N(t)=S(t)+I(t)+R(t)$, we obtain from Lemma 1 that

$$\begin{aligned} \frac{\textit{dN}}{\textit{dt}}= & {} A-\mu _{1}S-\mu _{2}I-\mu _{3}R \\\le & {} A-\mu _{1}N, \end{aligned}$$

where the last inequality is obtained by using the fact that $\mu _{1}\le \min \{\mu _{2}, \mu _{3}\}$. By comparison theorem, we obtain the required assertion. $\square$

3 Stochastic Disease-Free Dynamics

In this section, we will discuss the disease-free dynamics under each one of the following conditions.

• (C1) $R_{0}^{S}< 1$ and $\sigma <\overline{\sigma }=\sqrt{\frac{\beta \mu _{1}}{A}}$,

• (C2) $\sigma >\sigma ^{*}=\sqrt{\frac{\beta \mu _{1}}{A}\cdot \frac{R_{0}}{2}}$,

where

$$\begin{aligned} R_{0}^{S}:=R_{0}-\frac{A^{2}\sigma ^{2}}{2 \mu _{1}^{2} (\mu _{2}+\delta )}. \end{aligned}$$

(7)

From Lemmas 1 and 2, we get that $\varGamma =\{x\in (0, A/\mu _{1})^{3}| x_{1}+x_{2}+x_{3}\le A/\mu _{1}\}$ is an almost surely positively invariant set of system (3), which is attracting in the first octant. For convenience and simplicity, we therefore assume that $(S(0), I(0), R(0))\in \varGamma$ in the proof of Theorem 1 without loss of generality.

Theorem 1

Suppose that (C1) or (C2) holds, then the solution (S(t), I(t), R(t)) of system (3) with any initial value $(S(0), I(0), R(0))\in \mathbb {R}^{3}_{+}$ has the property that

$$\begin{aligned} \lim _{t\rightarrow +\infty }S(t)= & {} \frac{A}{\mu _{1}}\quad a.s., \end{aligned}$$

(8)

$$\begin{aligned} \lim _{t\rightarrow +\infty }I(t)= & {} 0\quad a.s., \end{aligned}$$

(9)

$$\begin{aligned} \lim _{t\rightarrow +\infty }R(t)= & {} 0\quad a.s. \end{aligned}$$

(10)

Proof

Using the Itô’s formula to $\log I(t)$ yields

$$\begin{aligned} d\log I(t)= & {} \Big [\frac{1}{I}\left( \beta \textit{SG}(I)-\left( \mu _{2}+\delta \right) I\right) -\frac{\sigma ^{2}}{2}\left( \frac{\textit{SG}(I)}{I}\right) ^{2}\Big ]\textit{dt}\nonumber \\&\quad +\,\sigma \left( \frac{\textit{SG}(I)}{I}\right) \textit{dB}(t) \nonumber \\= & {} \Big [\beta \left( \frac{\textit{SG}(I)}{I}\right) -\left( \mu _{2}+\delta \right) -\frac{\sigma ^{2}}{2}\left( \frac{\textit{SG}(I)}{I}\right) ^{2}\Big ]\textit{dt} +\sigma \left( \frac{\textit{SG}(I)}{I}\right) \textit{dB}(t) \nonumber \\= & {} \varPsi \left( \frac{\textit{SG}(I)}{I}\right) \textit{dt}+\sigma \left( \frac{S G(I)}{I}\right) \textit{dB}(t), \end{aligned}$$

(11)

where $\varPsi (x)=-\frac{1}{2}\sigma ^{2}x^{2}+\beta x-(\mu _{2}+\delta )$.

Let us consider separately the two cases:

Case 1. Suppose that (C1) holds. Firstly, we will prove that the assertion (9) holds. Noting that $\varPsi (x)$ is monotone increasing for $x\in [0, \beta /\sigma ^{2}]$ and $\sigma ^{2}< \beta \mu _{1}/A$ in the condition (C1) yields

$$\begin{aligned} \varPsi \left( \frac{\textit{SG}(I)}{I}\right) \le \varPsi \left( S\right) \le \varPsi \left( \frac{A}{\mu _{1}}\right) , \end{aligned}$$

where we make use of the fact that $G(I)\le I$ and $S \le A/\mu _{1}$. Substituting this inequality into (11), we have

$$\begin{aligned} d\log I(t)\le & {} \varPsi \left( \frac{A}{\mu _{1}}\right) \textit{dt}+\sigma \left( \frac{\textit{SG}(I)}{I}\right) \textit{dB}(t). \end{aligned}$$

Integrating the above inequality via t along [0, t] and using the strong law of large numbers for local martingales, we have

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{\log I(t)}{t}\le & {} \varPsi \left( \frac{A}{\mu _{1}}\right) \quad a.s. \end{aligned}$$

Noting that $R_{0}^{S}<1$ implies $\varPsi (A/\mu _{1})<0$, we therefore have

$$\begin{aligned} \lim _{t\rightarrow +\infty }I(t)= & {} 0\quad a.s. \end{aligned}$$

(12)

This is the required assertion (9).

Secondly, we shall prove that the assertion (10) holds. Let $\overline{\varOmega }=\{\omega \in \varOmega {:}\,\lim _{t\rightarrow +\infty }I(t)= 0\}$, then (12) implies $\mathbb {P}(\overline{\varOmega })=1$. Note that the stochastic process I(t) in the SDE (3) in fact is the abbreviation of the symbol $I(\omega , t)$, which can be regarded as a function of two variables: sample point $\omega \in \varOmega$ and time $t\in [0, \infty )$; For each $\omega \in \varOmega$ fixed $I(\omega , t)$ can be viewed as a function with respect to $t\in [0, \infty )$ which is usually called a sample path of I(t) (Øksendal 2005). For different selections of sample point $\omega \in \overline{\varOmega }$, the sample path $I(\omega , t)$ may have different convergence speeds with respect to time t. Hence, for any $\omega \in \overline{\varOmega }$ and any constant $\varepsilon >0$, there exists a constant $T(\omega , \varepsilon )>0$ such that

$$\begin{aligned} I(\omega , t)\le \varepsilon \end{aligned}$$

for all $t>T$. Substituting this into the third equation of the SDE (3), we get

$$\begin{aligned} dR(\omega , t)\le \big [\delta \varepsilon -\left( \mu _{3}+\lambda \right) R(\omega , t)\big ]\textit{dt}\quad for \ all\ \omega \in \overline{\varOmega }, t>T, \end{aligned}$$

which implies by comparison theorem that

$$\begin{aligned} \limsup _{t\rightarrow +\infty }R(\omega , t)\le \frac{\delta \varepsilon }{\mu _{3}+\lambda } \end{aligned}$$

for all $\omega \in \overline{\varOmega }$. Noting that $R(\omega , t)>0$ for all $\omega \in \varOmega$ and $t>0$, by arbitrariness of $\varepsilon$, we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }R(\omega , t)= 0,\quad \omega \in \overline{\varOmega }. \end{aligned}$$

Recalling that $\mathbb {P}( \overline{\varOmega })=1$, we therefore have

$$\begin{aligned} \lim _{t\rightarrow +\infty }R(t)= 0,\quad a.s., \end{aligned}$$

(13)

this is the required assertion (10).

Finally, we shall prove the assertion (8) holds. Let $N(t)=S(t)+I(t)+R(t)$. From the system (3), we have

$$\begin{aligned} \frac{\textit{dN}(t)}{\textit{dt}}= & {} A-\mu _{1}S(t)-\mu _{2}I(t)-\mu _{3}R(t) \\= & {} A-\mu _{1}N(t)-(\mu _{2}-\mu _{1})I(t)-(\mu _{3}-\mu _{1})R(t). \end{aligned}$$

From the well-known variation of constants formula, we have

$$\begin{aligned} N(t)= & {} y(t)\Big (N(0)+\int _{0}^{t}y^{-1}(s)\big (A-(\mu _{2}-\mu _{1})I(s)\nonumber \\&\quad -\,(\mu _{3}-\mu _{1})R(s)\big ) ds\Big ), \end{aligned}$$

(14)

where $y(t)=\exp \Big \{-\int _{0}^{t}\mu _{1}\textit{ds} \Big \}=\exp \{-\mu _{1} t\}$.

Let $F=\{\omega \in \varOmega {:}\, \lim _{t\rightarrow +\infty }I(t)=\lim _{t\rightarrow +\infty }R(t)= 0\}$, then (12) and (13) imply that $\mathbb {P}(F)=1$. Hence, for any $\omega \in F$ and any constant $\varepsilon _{1} >0$, there exists a constant $T_{1}(\omega , \varepsilon _{1})>0$ such that

$$\begin{aligned} I(\omega , t)\le \varepsilon _{1}, \ \ R(\omega , t)\le \varepsilon _{1}, \quad \forall t>T_{1}. \end{aligned}$$

(15)

Since $\mu _{1}\le \min \{\mu _{2}, \mu _{3}\}$ implies $\mu _{2}-\mu _{1}\ge 0$ and $\mu _{3}-\mu _{1}\ge 0$. This, combining with (14) and (15), yields

$$\begin{aligned} N(\omega , t)\ge & {} y(t)\Big (N(0)+\int _{0}^{t}y^{-1}(s)\big [A-(\mu _{2}+\mu _{3}-2\mu _{1})\varepsilon _{1}\big ] ds\Big )\\= & {} N(0)\exp \{-\mu _{1} t\}+ \big [A-(\mu _{2}+\mu _{3}-2\mu _{1})\varepsilon _{1}\big ] \int _{0}^{t}\exp \Big \{-\mu _{1}(t-s)\Big \}d s \\= & {} N(0)\exp \{-\mu _{1} t\}+ \frac{A-(\mu _{2}+\mu _{3}-2\mu _{1})\varepsilon _{1}}{\mu _{1}} \Big (1-\exp \{-\mu _{1} t\}\Big ), \end{aligned}$$

which implies

$$\begin{aligned} \liminf _{t\rightarrow +\infty }N(\omega , t)\ge \frac{A-(\mu _{2}+\mu _{3}-2\mu _{1})\varepsilon _{1}}{\mu _{1}},\quad \forall \ \omega \in F. \end{aligned}$$

From the arbitrariness of $\varepsilon _{1}$, this implies

$$\begin{aligned} \liminf _{t\rightarrow +\infty }N(\omega , t)\ge \frac{A}{\mu _{1}},\ \ \ \ for\ all\ \omega \in F, \end{aligned}$$

which, together with $\mathbb {P}(F)=1$, proves

$$\begin{aligned} \liminf _{t\rightarrow +\infty }N(t)\ge \frac{A}{\mu _{1}}\quad a.s. \end{aligned}$$

On the other hand, by Lemma 2, we get $\limsup _{t\rightarrow +\infty } N(t)\le A/\mu _{1}$. Hence, we have $\lim _{t\rightarrow +\infty }N(t)=A/\mu _{1}$ a.s. Recalling that $N(t)=S(t)+I(t)+R(t)$, from (12) and (13), we therefore have

$$\begin{aligned} \lim _{t\rightarrow +\infty }S(t)= \frac{A}{\mu _{1}}\quad a.s., \end{aligned}$$

this is the required assertion (8).

Case 2. Suppose that (C2) holds. Since

$$\begin{aligned} \varPsi (x)= & {} -\frac{1}{2} \sigma ^{2}\left( x-\frac{\beta }{\sigma ^{2} }\right) ^{2} +\frac{\beta ^{2}}{2\sigma ^{2}}-\left( \mu _{2}+\delta \right) \\\le & {} -\left( (\mu _{2}+\delta )-\frac{\beta ^{2}}{2\sigma ^{2}}\right) , \end{aligned}$$

we get that if $\sigma ^{2}> \frac{\beta \mu _{1}}{A}\cdot \frac{R_{0}}{2}$,

$$\begin{aligned} \varPsi \left( \frac{\textit{SG}(I)}{I}\right) \le -\left( (\mu _{2}+\delta )-\frac{\beta ^{2}}{2\sigma ^{2}}\right) < 0. \end{aligned}$$

Substituting this inequality into (11) yields

$$\begin{aligned} d\log I(t) \le -\left( (\mu _{2}+\delta )-\frac{\beta ^{2}}{2\sigma ^{2}}\right) \textit{dt} +\sigma \left( \frac{\textit{SG}(I)}{I}\right) \textit{dB}(t). \end{aligned}$$

Integrating both sides, from the strong law of large numbers for local martingales, we derive that

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{\log I(t)}{t}\le & {} -\left( (\mu _{2}+\delta )-\frac{\beta ^{2}}{2\sigma ^{2}}\right) <0\quad a.s. \end{aligned}$$

Then using the similar arguments to those given in Case 1, we can also get the required assertion (8), (9) and (10). This completes the proof of Theorem 1. $\square$

Remark 1

In Theorem 1, we extend the results of Cai et al. (2015a), Gray et al. (2011), Lahrouz and Settati (2014) by considering a stochastic SIRS model with a general incidence rate and variable population size. Because total population size is dynamic, the mathematical deduction here faces bigger challenges than that of Gray et al. (2011), although the proof also use comparison theorem of SDE as authors in Gray et al. (2011) do. If we let $A=\mu _{1}=\mu _{2}=\mu _{3}=\mu$ and $G(I)=I$, the system (3) is reduced to the system (7) in Lahrouz and Settati (2014); Theorem 3.1 in Lahrouz and Settati (2014) shows that if $\sigma \le \sqrt{\beta \mu _{1}/A}=\sqrt{\beta }$ and

$$\begin{aligned} \mathcal {R}_{S}=\frac{\beta }{\mu +\delta +\sigma ^{2}/2}<1, \end{aligned}$$

(16)

then the solution $(A/\mu _{1},0,0)=(1,0,0)$ of system (7) in Lahrouz and Settati (2014) will be globally asymptotically stable in probability. From the proof procedure of Theorem 1, it is obvious to see that any positive solution of system (3) will tend to ($A/\mu _{1},0,0$) exponentially with probability one, which implies the asymptotically stable in probability in Definition 2. Note that (16) is equivalent to $R_{0}^{S}<1$ in this article. Hence, our results for the disease extinction are stronger than that given in Lahrouz and Settati (2014), Theorem 3.1.

Remark 2

Comparing with Theorem 3.1 of Lahrouz and Settati (2014), here we also show that the infection will be eradicated a.s. when $\sigma > \sigma ^{*}$. This indicates that the large environmental noises may help to bring about extinction of diseases.

4 Stochastic Endemic Dynamics

In studying epidemic modelings, we are usually interested in two issues: One is the occurring of extinction, which has been shown in Sect. 3; another is the disease persistence in a host population. In this section, we will first prove that the disease is persistent when $R^{S}_{0}>1$, and next we show that under the same condition, a unique stationary distribution exists for the solution of system (3), which implies the disease is recurrent. Finally, we explore the relations of the stochastic solution to the interior deterministic stationary point when the stochastic effects are not too strong.

4.1 Persistence of the Disease

Let us first consider the disease persistence, which corresponds to the stochastic strong persistence in the mean defined by Wang (2010) and Zhao et al. (2015a). The following theorem shows that the disease will be almost surely persistent in the time mean sense when $R^{S}_{0}>1$.

Theorem 2

If $R^{S}_{0}>1$, then for any initial value $(S(0), I(0), R(0))\in \mathbb {R}^{3}_{+}$, the solution (S(t), I(t), R(t)) of system (3) has the property that

$$\begin{aligned}&(\mathrm{i}) \liminf _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}S(s)\textit{ds} \ge \frac{A\mu _{1}}{\mu _{1}^{2}+A\beta }\quad a.s., \\&(\mathrm{ii}) \liminf _{t\rightarrow +\infty } \frac{1}{t}\int _{0}^{t}I(s) \textit{ds} \ge \frac{\mu _{1}^{2}\varPsi \left( \frac{A}{\mu _{1}} \right) }{ A(\mu _{1}\theta + \beta )\left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) } \quad a.s., \\&(\mathrm{iii}) \liminf _{t\rightarrow +\infty } \frac{1}{t}\int _{0}^{t}R(s) \textit{ds} \ge \frac{\delta \mu _{1}^{2}\varPsi \left( \frac{A}{\mu _{1}} \right) }{ A (\mu _{3}+\lambda )(\mu _{1}\theta + \beta )\left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) }\quad a.s., \end{aligned}$$

where $\varPsi (x)=-\frac{1}{2}\sigma ^{2}x^{2}+\beta x-(\mu _{2}+\delta )$.

Proof

Let (S(t), I(t), R(t)) be a solution of system (3) with any initial value (S(0), I(0), R(0)) $\in$ $\mathbb {R}^{3}_{+}$. By Lemma 2, it holds that $\limsup _{t\rightarrow +\infty }I(t)\le A/\mu _{1}$ for all $\omega \in \varOmega$. This yields that, for any $\omega \in \varOmega$ and any $\varepsilon >0$ sufficiently small, there exists a $T^{\omega }=T^{\omega }(\varepsilon )>0$ such that $I(\omega , t)\le A/\mu _{1}+\varepsilon$ for all $t>T^{\omega }$. Then, noting that $0<G(I)\le I$, from the first equation of system (3), we derive that for all $t>T^{\omega }$,

$$\begin{aligned} d S(t)\ge & {} \left( A-\mu _{1}S-\beta S \left( \frac{A}{\mu _{1}}+\varepsilon \right) \right) \textit{dt} -\sigma \textit{SG}(I)\textit{dB}(t) \\= & {} \Big [A-\left( \mu _{1}+\beta \left( \frac{A}{\mu _{1}}+\varepsilon \right) \right) S\Big ]\textit{dt} -\sigma \textit{SG}(I)\textit{dB}(t), \end{aligned}$$

where $\omega$ is omitted. For the sake of convenience, we assume that the above inequality holds for all $t>0$ without loss of generality. Integrating the above inequality and dividing both sides by t, we get

$$\begin{aligned} \Big (\mu _{1}+\beta \Big (\frac{A}{\mu _{1}}+ & {} \varepsilon \Big )\Big )\frac{1}{t}\int _{0}^{t}S(s)ds \nonumber \\\ge & {} A-\frac{S(t)-S(0)}{t}-\frac{\sigma }{t}\int _{0}^{t} S G(I)d B(s). \end{aligned}$$

(17)

From $\limsup _{t\rightarrow +\infty }N(t)=\limsup _{t\rightarrow +\infty }\left( S(t)+I(t)+R(t)\right) \le A/\mu _{1}$ for all $\omega \in \varOmega$ and the strong law of large numbers for local martingales, we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }\left( \frac{S(t)-S(0)}{t}+\frac{\sigma }{t}\int _{0}^{t} \textit{SG}(I)\textit{dB}(s)\right) =0\quad a.s., \end{aligned}$$

which, together with (17), implies

$$\begin{aligned} \liminf _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}S(s)\textit{ds} \ge \frac{A}{\mu _{1}+\beta \left( \frac{A}{\mu _{1}}+\varepsilon \right) }\quad a.s. \end{aligned}$$

As this holds for arbitrary $\varepsilon >0$, it follows that

$$\begin{aligned} \liminf _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}S(s)\textit{ds} \ge \frac{A\mu _{1}}{\mu _{1}^{2}+A\beta }\quad a.s., \end{aligned}$$

this is the required assertion (i).

Next, we will prove that (ii) holds. By the Itô’s formula, it can be seen from the second equation of system (3) that

$$\begin{aligned} d\log I(t)= & {} \Big [\frac{1}{I}\left( \beta \textit{SG}(I)-\left( \mu _{2}+\delta \right) I\right) -\frac{\sigma ^{2}}{2}\left( \frac{\textit{SG}(I)}{I}\right) \Big ]\textit{dt} \\&\quad +\,\sigma \left( \frac{\textit{SG}(I)}{I}\right) \textit{dB}(t) \\= & {} \varPsi \left( \frac{\textit{SG}(I)}{I}\right) \textit{dt}+\sigma \left( \frac{\textit{SG}(I)}{I}\right) \textit{dB}(t). \end{aligned}$$

Integrating both sides yields

$$\begin{aligned} \log I(t)= & {} \log I(0)+\int _{0}^{t}\varPsi \left( \frac{\textit{SG}(I)}{I}\right) d s+\sigma \int _{0}^{t} \frac{\textit{SG}(I)}{I}\textit{dB}(s). \end{aligned}$$

(18)

We compute

$$\begin{aligned}&\varPsi \left( \frac{\textit{SG}(I)}{I}\right) -\varPsi \left( \frac{A}{\mu _{1}} \right) \nonumber \\&\quad =\frac{\sigma ^{2}}{2}\left( \frac{A}{\mu _{1}} \right) ^{2}\Big [1-\left( \frac{\mu _{1}}{A}\cdot \frac{S G(I)}{I}\right) ^{2}\Big ] - \frac{A\beta }{\mu _{1}}\Big [1-\left( \frac{\mu _{1}}{A}\cdot \frac{S G(I)}{I}\right) \Big ]. \end{aligned}$$

(19)

By Lemma 2, we get $\limsup _{t\rightarrow +\infty }S(t)\le A/\mu _{1}$. For the sake of convenience, we may assume that $S(t)\le A/\mu _{1}$ for all $t>0$. Hence, $G(I)\le I$ implies $\mu _{1}\textit{SG}(I)/(AI)\le 1$, which yields from (19) that

$$\begin{aligned} \varPsi \left( \frac{\textit{SG}(I)}{I}\right)\ge & {} \varPsi \left( \frac{A}{\mu _{1}} \right) - \left( \frac{A\beta }{\mu _{1}}- \frac{\sigma ^{2}}{2}\left( \frac{A}{\mu _{1}} \right) ^{2}\right) \Big [1-\left( \frac{\mu _{1}}{A}\cdot \frac{\textit{SG}(I)}{I}\right) \Big ] \\= & {} \varPsi \left( \frac{A}{\mu _{1}} \right) - \left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) \left( \frac{A}{\mu _{1}}- \frac{\textit{SG}(I)}{I}\right) . \end{aligned}$$

Substituting this inequality into (18) yields

$$\begin{aligned} \log I(t)\ge & {} \log I(0)+\varPsi \left( \frac{A}{\mu _{1}}\right) t -\left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) \int _{0}^{t} \left( \frac{A}{\mu _{1}}- \frac{\textit{SG}(I)}{I}\right) d s \nonumber \\&\quad +\,\sigma \int _{0}^{t}\frac{\textit{SG}(I)}{I}\textit{dB}(s). \end{aligned}$$

(20)

On the other hand, from the first equation of system (3), we have

$$\begin{aligned} \textit{dS}\ge & {} \left( A-\mu _{1} S-\beta \textit{SG}(I)\right) \textit{dt} -\sigma \textit{SG}(I)\textit{dB}(t) \nonumber \\= & {} \Big [\mu _{1} \left( \frac{A}{\mu _{1}}-\frac{S G(I)}{I}\right) -\mu _{1} S\left( 1-\frac{G(I)}{I}\right) -\beta S G(I)\Big ]\textit{dt} \nonumber \\&\quad -\,\sigma \textit{SG}(I)\textit{dB}(t). \end{aligned}$$

(21)

Let $f(I)=1-G(I)/I$. By the hypotheses (H2) and (H3), we derive that there exists a constant $\theta >0$, such that

$$\begin{aligned} f(I)-f(0)\le \theta (I-0), \end{aligned}$$

namely,

$$\begin{aligned} 1-\frac{G(I)}{I}\le \theta I. \end{aligned}$$

(22)

Substituting this inequality into (21) and recalling that $G(I)\le I$ and $S\le A/\mu _{1}$, we have

$$\begin{aligned} d S \ge \Big [\mu _{1}\left( \frac{A}{\mu _{1}}-\frac{\textit{SG}(I)}{I}\right) -\left( \mu _{1}\theta + \beta \right) \frac{A}{\mu _{1}}I \Big ]\textit{dt} -\sigma \textit{SG}(I)\textit{dB}(t), \end{aligned}$$

which implies

$$\begin{aligned}&\mu _{1}\int _{0}^{t}\left( \frac{A}{\mu _{1}}-\frac{\textit{SG}(I)}{I}\right) d s \le S(t)-S(0) +\left( \mu _{1}\theta + \beta \right) \frac{A}{\mu _{1}}\int _{0}^{t}I(s) \textit{ds} \nonumber \\&\quad +\,\sigma \int _{0}^{t}\textit{SG}(I)\textit{dB}(s). \end{aligned}$$

(23)

Combining (20) with (23) and rearranging, we get

$$\begin{aligned} \log I(t)\ge \varPsi \left( \frac{A}{\mu _{1}} \right) t - \frac{A(\mu _{1}\theta + \beta )}{\mu ^{2}_{1}}\left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) \int _{0}^{t}I(s) \textit{ds}+ Y(t), \end{aligned}$$

(24)

where

$$\begin{aligned} Y(t)= & {} \log I(0) -\frac{1}{\mu _{1}}\left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) \left( S(t)-S(0) +\sigma \int _{0}^{t} S G(I)\textit{dB}(s)\right) \\&\quad +\,\sigma \int _{0}^{t}\frac{\textit{SG}(I)}{I}\textit{dB}(s). \end{aligned}$$

By Lemma 2 and the strong law of large numbers for local martingales, we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }\frac{Y(t)}{t}= 0 \quad a.s.,\ \ \ and \quad \hbox {limsup}_{t\rightarrow +\infty }\frac{\log I(t)}{t}\le 0. \end{aligned}$$

This, together with (24), yields by Lemma 2 that

$$\begin{aligned} \liminf _{t\rightarrow +\infty } \frac{1}{t}\int _{0}^{t}I(s) \textit{ds} \ge \frac{\mu _{1}^{2}\varPsi \left( \frac{A}{\mu _{1}} \right) }{ A(\mu _{1}\theta + \beta )\left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) } \quad a.s. \end{aligned}$$

(25)

This is the required assertion (ii).

Finally, we shall prove the assertion (iii). Integrating the third equation of the system (3) and dividing both sides by t, we get

$$\begin{aligned} (\mu _{3}+\lambda ) \frac{1}{t}\int _{0}^{t}R(s)\textit{ds} \ge \frac{\delta }{t}\int _{0}^{t}I(s)\textit{ds} -\frac{R(t)-R(0)}{t}, \end{aligned}$$

which, together with (25), yields by Lemma 2 that

$$\begin{aligned} \liminf _{t\rightarrow +\infty } \frac{1}{t}\int _{0}^{t}R(s) \textit{ds} \ge \frac{\delta \mu _{1}^{2}\varPsi \left( \frac{A}{\mu _{1}} \right) }{ A (\mu _{3}+\lambda )(\mu _{1}\theta + \beta )\left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) } \quad a.s. \end{aligned}$$

This completes the proof of Theorem 2. $\square$

From Theorem 2, it can be seen that persistence in mean implies the following stochastic weak persistence in the mean that was defined by Wang (2010) and (Zhao et al. 2015a, Definition 2.1).

Corollary 1

If $R^{S}_{0}>1$, then for any initial value $(S(0), I(0), R(0))\in \mathbb {R}^{3}_{+}$, the solution (S(t), I(t), R(t)) of system (3) has the property that

$$\begin{aligned} \limsup _{t\rightarrow +\infty } I(t)\ge \frac{\mu _{1}^{2}\varPsi \left( \frac{A}{\mu _{1}} \right) }{ A(\mu _{1}\theta + \beta )\left( \beta - \frac{A \sigma ^{2}}{2\mu _{1}}\right) }>0 \quad a.s. \end{aligned}$$

4.2 Stationary Distribution and Positive Recurrence

Before giving the main results, we first present a lemma, which is a useful criterion for positive recurrence in terms of Lyapunov function (see Zhu and Yin 2007).

Lemma 3

(Zhu and Yin 2007) The system (5) is positive recurrent if there is a bounded open subset D of $\mathbb {R}^{n}$ with a regular (i.e., smooth) boundary, and

• (i) there exist some $\iota =1,2, \ldots , n$ and a positive constant $\kappa$ such that

  $$\begin{aligned} a_{\iota \iota }(x)\ge \kappa \ \ \ for\ any\ \ x\in D, \end{aligned}$$

• (ii) there exists a nonnegative function $V{:}\,D^{c}\rightarrow R$ such that V is twice continuously differentiable and that for some $\theta > 0$,

  $$\begin{aligned} \mathcal {L}V(x)\le - \theta , \ \ \ for\ any\ \ x\in D^{c}. \end{aligned}$$

Moreover, the positive recurrent process X(t) has a unique stationary distribution $\mu (\cdot )$ with density in $\mathbb {R}^{n}$ such that for any Borel set $B \in \mathbb {R}^{n}$

$$\begin{aligned} \lim _{t\rightarrow +\infty }\mathbb {P}(t, x, B)=\mu (B), \end{aligned}$$

and

$$\begin{aligned} \mathbb {P}_{x}\bigg \{\lim _{T\rightarrow +\infty }\frac{1}{T}\int _{0}^{T}f(X(t))\textit{dt}=\int _{\mathbb {R}^{n}}f(x)\mu (dx)\bigg \}=1, \end{aligned}$$

for all $x \in \mathbb {R}^{n}$ and $f{:}\,\mathbb {R}^{n}\rightarrow \mathbb {R}$ be a function integrable with respect to the measure $\mu$.

In the following theorem, we show that $R_{0}^{S}>1$ is also a sufficient condition for the positive recurrence and the existence of stationary distribution for system (3).

Theorem 3

If $R_{0}^{S}>1$, then the solution (S(t), I(t), R(t)) of system (3) with any positive initial value $(S(0), I(0), R(0))\in \varGamma$ is positive recurrent and admits a unique ergodic stationary distribution in $\varGamma$, where $\varGamma =\{x\in (0, A/\mu _{1})^{3}| x_{1}+x_{2}+x_{3}\le A/\mu _{1}\}$.

Proof

Define the following bounded open subset of $\varGamma$

$$\begin{aligned} D=\Big \{x \in \varGamma \ \Big |\ \frac{1}{\alpha _{1}}< x_{1}, x_{2} < 1-\frac{1}{\alpha _{1}}, \ \frac{1}{\alpha _{2}}< x_{3} < 1-\frac{1}{\alpha _{2}} \ and\quad \alpha _{1}<\alpha _{2}\Big \}, \end{aligned}$$

where $\alpha _{1}$ and $\alpha _{2}$ are sufficiently large positive constants to be chosen in the following. The diffusion matrix associated with the system (3) is given by

$$\begin{aligned} A(S,I,R)= (\sigma \textit{SG}(I))^{2}\left[ \begin{array}{ccc} 1 &{}\quad -1 &{}\quad 0 \\ -1 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{array} \right] . \end{aligned}$$

Since $\overline{D} \in \mathbb {R}^{3}_{+}$, then

$$\begin{aligned} a_{11}(S,I,R)=(\sigma \textit{SG}(I))^{2}\ge \min _{(S,I,R)\in \overline{D}} (\sigma \textit{SG}(I))^{2}\ge \eta , \end{aligned}$$

where $\eta$ is a positive constant. This implies the condition (i) in Lemma 3 is satisfied. It therefore remains for us to verify the condition (ii) in Lemma 3. Define the following nonnegative function

$$\begin{aligned} g(S,I,R)=V_{1}(S,I)+V_{2}(I)+V_{3}(R), \end{aligned}$$

where

$$\begin{aligned} V_{1}(S,I)= & {} \frac{1}{S}+\frac{1}{\nu }I^{-\nu }\left( \frac{A}{\mu _{1}}-S\right) ,\\ V_{2}(I)= & {} \frac{1}{\nu }I^{-\nu }, \ \ \ V_{3}(R)= R-\log R+\rho , \end{aligned}$$

and $\nu$ is a positive constant to be chosen later and $\rho >0$ is so large that $V_{3}(R)\ge 0$ for all $R>0$. Using similar arguments to that given in Lahrouz and Settati (2014), Theorem 5.1, we have

$$\begin{aligned} \mathcal {L}V_{1}(S,I)\le & {} \left[ -\frac{\mu _{1}}{\nu }+\mu _{2}+\delta +\frac{1}{2}(1+\nu )\left( \frac{A\sigma }{\mu _{1}}\right) ^{2}\right] I^{-\nu }\left( \frac{A}{\mu _{1}}-S\right) +\frac{A\beta }{\nu \mu _{1}}I^{1-\nu } \nonumber \\&\quad -\,\frac{A}{2S^{2}}+\frac{1}{2A}\left[ \mu _{1} +\frac{A\beta }{\mu _{1}}+\left( \frac{A\sigma }{\mu _{1}}\right) ^{2}\right] . \end{aligned}$$

(26)

Compute that

$$\begin{aligned} \mathcal {L}V_{2}(I)= & {} -I^{-\nu -1}\big [-(\mu _{2}+\delta )I+\beta S G(I)\big ]+\frac{\sigma ^{2}}{2}(1+\nu )I^{-\nu }\left( \frac{\textit{SG}(I)}{I}\right) ^{2}\\= & {} I^{-\nu }\Big [(\mu _{2}+\delta )-\beta \left( \frac{\textit{SG}(I)}{I}\right) +\frac{\sigma ^{2}}{2}(1+\nu )\left( \frac{\textit{SG}(I)}{I}\right) ^{2}\Big ] \\\le & {} I^{-\nu }\Big [(\mu _{2}+\delta )-\frac{A \beta }{\mu _{1}} +\frac{\sigma ^{2}}{2}(1+\nu )\left( \frac{A}{\mu _{1}}\right) ^{2}+\beta \left( \frac{A}{\mu _{1}}-\frac{\textit{SG}(I)}{I}\right) \Big ] \\= & {} I^{-\nu }\Big [-\varPsi \left( \frac{A}{\mu _{1}}\right) +\frac{\nu }{2}\left( \frac{A \sigma }{\mu _{1}}\right) ^{2}\Big ] +\beta I^{-\nu }\left( \frac{A}{\mu _{1}}-S\right) \\&+\beta I^{-\nu } S\left( 1-\frac{G(I)}{I}\right) . \end{aligned}$$

From (22), there exists a positive constant $\theta$, such that

$$\begin{aligned} \mathcal {L}V_{2}(I)\le & {} I^{-\nu }\Big [-\varPsi \left( \frac{A}{\mu _{1}}\right) +\frac{\nu }{2}\left( \frac{A \sigma }{\mu _{1}}\right) ^{2}\Big ] +\beta I^{-\nu }\left( \frac{A}{\mu _{1}}-S\right) +\beta \theta S I^{1-\nu } \nonumber \\\le & {} I^{-\nu }\Big [-\varPsi \left( \frac{A}{\mu _{1}}\right) +\frac{\nu }{2}\left( \frac{A \sigma }{\mu _{1}}\right) ^{2}\Big ] +\beta I^{-\nu }\left( \frac{A}{\mu _{1}}-S\right) + \frac{A \beta \theta }{\mu _{1}} I^{1-\nu }.\nonumber \\ \end{aligned}$$

(27)

We also compute that

$$\begin{aligned} \mathcal {L}V_{3}(R)= & {} \left( 1-\frac{1}{R}\right) [\delta I-(\mu _{3}+\lambda )R] \nonumber \\\le & {} -\frac{\delta I}{R}+\left( \mu _{3}+\lambda +\frac{A\delta }{\mu _{1}}\right) . \end{aligned}$$

(28)

Let us chose $\nu$ sufficiently small such that

$$\begin{aligned} -\frac{\mu _{1}}{\nu }+\mu _{2}+\delta +\beta +\frac{1}{2}(1+\nu )\left( \frac{A\sigma }{\mu _{1}}\right) ^{2}<0, \end{aligned}$$

and

$$\begin{aligned} -\varPsi \left( \frac{A}{\mu _{1}}\right) +\frac{1}{2}\nu \left( \frac{A\sigma }{\mu _{1}}\right) ^{2}<0 , \end{aligned}$$

where the second choice is allowed by the condition $R_{0}^{S}>1$. Therefore, combining (26), (27), and (28), we have

$$\begin{aligned} \mathcal {L}g(S,I, R)\le \Big [-\varPsi \left( \frac{A}{\mu _{1}}\right) +\frac{1}{2}\nu \left( \frac{A\sigma }{\mu _{1}}\right) ^{2}\Big ]I^{-\nu } -\frac{A}{2S^{2}}-\frac{\delta I}{R}+\xi , \end{aligned}$$

(29)

where $\xi$ is some positive constant.

It is obvious to see from (29) that there exists a sufficiently large $\alpha _{1}>0$, such that

$$\begin{aligned} \mathcal {L}g(S,I, R)\le -1,\quad for\ all\ \ S\le \frac{1}{\alpha _{1}} \ or \ I\le \frac{1}{\alpha _{1}}. \end{aligned}$$

It remains to consider the case where $S> 1/\alpha _{1}$, $I> 1/\alpha _{1}$ and $R\le 1/\alpha _{2}$. Since $I> 1/\alpha _{1}$, we get

$$\begin{aligned} \mathcal {L}g(S,I, R)\le -\left( \frac{\delta }{\alpha _{1}}\right) \cdot \frac{1}{R}+ \xi . \end{aligned}$$

This shows that there exists a sufficiently large $\alpha _{2}> \alpha _{1}>0$, such that

$$\begin{aligned} \mathcal {L}g(S,I, R)\le -1,\ \ \ for\ all\ S> \frac{1}{\alpha _{1}}, I> \frac{1}{\alpha _{1}} \ and \ R\le \frac{1}{\alpha _{2}}. \end{aligned}$$

Altogether, we have shown that $\mathcal {L}g(x)\le -1$ for all $x \in D^{c}$. So the condition (ii) of Lemma 3 is met. This completes the proof of Theorem 3. $\square$

Remark 3

Due to variable population size, the dimensionality of system (3) can not be reduced as authors in Gray et al. (2011), Lahrouz and Settati (2014) do. However, in case of higher dimension, we establish the ergodic property of system (3) by constructing a suitable Lyapunov function.

4.3 Stochastic Asymptotic Stability

The preceding theorem illustrates the cycling phenomena of recurrent diseases and provides a biological insight of recurrent diseases (see Ref. Yang and Mao 2013 for more biological meanings). We next investigate the behavior of the solution to system (3) near a nontrivial stationary point $E^{*}$ of the corresponding deterministic equation. In contrast to the deterministic solutions, from Theorem 3, we have the stochastic solutions do not converge to $E^{*}$. However, we shall prove a stability result which shows that the time mean of the solutions to system (30) will be close to stationary point $E^{*}$, provided the noise intensity $\sigma$ are sufficiently small.

Next, we consider the following simplified version of the system (3):

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( A-\mu _{1}S(t)+\lambda R(t)-\beta S(t) G(I(t))\right) \textit{dt} -\sigma S(t) G(I(t))\textit{dB}(t), \\ d I(t)=\left( \beta S(t) G(I(t))-\left( \mu _{1}+\delta \right) I(t)\right) \textit{dt} +\sigma S(t) G(I(t))\textit{dB}(t), \\ d R(t)=\left( \delta I(t)-\left( \mu _{1}+\lambda \right) R(t)\right) \textit{dt}. \end{array} \right. \end{aligned}$$

(30)

where $\mu _{1}=\mu _{2}=\mu _{3}$, which implies the size of the total population is fixed.

Denoting by N(t) the size of the total population, i.e., setting $N(t) = S(t) + I(t) + R(t)$, from (26), we get: $d N(t)/\textit{dt}=A-\mu _{1}N$, so that for any initial $N(0)>0$ it follows: $\lim _{t\rightarrow +\infty }N(t) = A/\mu _{1}$. Hence, the plane $S(t) + I(t) + R (t)= A/\mu _{1}$ is an invariant manifold of system (30), which is attracting in the first octant. We here assume that the population is in equilibrium and investigate the dynamics of system (30) on such plane. Therefore, the existence of the invariant manifold allows us to refer to the following reduced system:

$$\begin{aligned} \left\{ \begin{array}{ll} &{} d S(t)=\left( \frac{A(\mu _{1}+\lambda )}{\mu _{1}}-(\mu _{1}+\lambda )S(t)-\beta S(t) G(I(t))-\lambda I(t)\right) \textit{dt} \\ &{}-\sigma S(t) G(I(t))\textit{dB}(t), \\ &{} d I(t)=\left( \beta S(t) G(I(t))-\left( \mu _{1}+\delta \right) I(t)\right) \textit{dt} +\sigma S(t) G(I(t))\textit{dB}(t). \end{array} \right. \end{aligned}$$

(31)

Theorem 4

Suppose that the function x / G(x) is monotone increasing on $(0, +\infty )$. Let (S(t), I(t)) be the solution of the system (31) with any initial value $(S(0), I(0))\in (0, A/\mu _{1})\times (0,A/\mu _{1})$. If $R_{0}^{S}>1$ and $\sigma < \mu _{1} \sqrt{\mu _{1}+\lambda }/A$, then

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{1}{t}\mathbb {E}\int _{0}^{t}\bigg (m_{1} \left( S(s)-\frac{\mu _{1}+\lambda }{\mu _{1}+\lambda -(A\sigma /\mu _{1})^{2}}S^{*}\right) ^{2} +m_{2}(I(s)-I^{*})^{2}\bigg )\textit{ds} \le \eta , \end{aligned}$$

where $(S^{*}, I^{*})$ is the unique endemic equilibrium $E^{*}$ of the corresponding deterministic equation of the system (31), and

$$\begin{aligned} m_{1}= & {} \mu _{1}+\lambda -(A\sigma /\mu _{1})^{2},\quad m_{2}=\mu _{1}+\lambda +\delta , \\ \eta= & {} \bigg [\frac{(\mu _{1}+\lambda )(AS^{*}/\mu _{1})^{2}}{\mu _{1}+\lambda -(A\sigma /\mu _{1})^{2}} +\frac{\left( 2(\mu _{1}+\lambda )+\delta \right) (I^{*})^{2}}{2 \beta G(I^{*})}\bigg ]\sigma ^{2}. \end{aligned}$$

Proof

It is obvious that $R_{0}^{S}>1$ implies $R_{0}>1$. Since x / G(x) is monotone increasing on $(0, +\infty )$, by [Enatsu et al. (2012), Lemma 4.1], we have that the corresponding deterministic version of the system (31) has a unique endemic equilibrium $E^{*}$ satisfying

$$\begin{aligned} \left\{ \begin{array}{ll} &{} \frac{A(\mu _{1}+\lambda )}{\mu _{1}}-(\mu _{1}+\lambda )S^{*}-\beta S^{*} G(I^{*})-\lambda I^{*}=0, \\ &{} \beta S^{*} G(I^{*})-\left( \mu _{1}+\delta \right) I^{*}=0. \end{array} \right. \end{aligned}$$

(32)

Define $C^{2}$ functions as follows

$$\begin{aligned} V_{1}(S,I)=\frac{(S-S^{*}+I-I^{*})^{2}}{2}, \ \ \ V_{2}(I)=I-I^{*}-I^{*}\log \left( \frac{I}{I^{*}}\right) . \end{aligned}$$

Applying the Itô’s formula, (32) implies

$$\begin{aligned} \mathcal {L}V_{1}= & {} (S-S^{*}+I-I^{*})\Big (\frac{A(\mu _{1}+\lambda )}{\mu _{1}}-(\mu _{1}+\lambda )S\nonumber \\&\quad -\,\big (\mu _{1}+\delta +\lambda \big )I\Big )+\sigma ^{2}S^{2}(G(I))^{2} \nonumber \\= & {} (S-S^{*}+I-I^{*})\Big (-(\mu _{1}+\lambda )(S-S^{*})\nonumber \\&\quad -\,\big (\mu _{1}+\delta +\lambda \big )(I-I^{*})\Big ) +\sigma ^{2}S^{2}(G(I))^{2} \nonumber \\= & {} -(\mu _{1}+\lambda )(S-S^{*})^{2}-\big (\mu _{1}+\delta +\lambda \big )(I-I^{*})^{2} \nonumber \\&\quad -\,\big (2(\mu _{1}+\lambda )+\delta \big )(S-S^{*})(I-I^{*})+\sigma ^{2}S^{2}(G(I))^{2}, \end{aligned}$$

(33)

and

$$\begin{aligned} \mathcal {L}V_{2}= & {} \frac{I-I^{*}}{I}\big [\beta \textit{SG}(I)-\left( \mu _{1}+\delta \right) I\big ]+\frac{I^{*}\sigma ^{2}}{2}\left( \frac{\textit{SG}(I)}{I}\right) ^{2} \\= & {} (I-I^{*})\Big [\beta \frac{\textit{SG}(I)}{I}-\beta \frac{S^{*} G(I^{*})}{I^{*}}\Big ]+\frac{I^{*}\sigma ^{2}}{2}\left( \frac{\textit{SG}(I)}{I}\right) ^{2} \\= & {} (I-I^{*})\Big [\beta S\left( \frac{ G(I)}{I}-\frac{ G(I^{*})}{I^{*}}\right) + \frac{\beta G(I^{*})}{I^{*}}(S-S^{*})\Big ]\\&\quad +\,\frac{I^{*}\sigma ^{2}}{2}\left( \frac{\textit{SG}(I)}{I}\right) ^{2}. \end{aligned}$$

Noting that $G(I)\le I$, $S\le A/\mu _{1}$ and x / G(x) is monotone increasing function, by the hypothesis (H2), we derive that

$$\begin{aligned} \mathcal {L}V_{2}\le \frac{\beta G(I^{*})}{I^{*}}(I-I^{*})(S-S^{*})+\frac{I^{*}(A\sigma )^{2}}{2\mu _{1}^{2}}. \end{aligned}$$

(34)

Now, we define $C^{2}$ function $V{:}\,\mathbb {R}^{2}_{+}\rightarrow \mathbb {R}_{+}$ as follows

$$\begin{aligned} V(S,I)=V_{1}(S,I)+ \frac{\left( 2(\mu _{1}+\lambda )+\delta \right) I^{*}}{\beta G(I^{*})}V_{2}(I). \end{aligned}$$

Combining (33) with (34), this implies

$$\begin{aligned} \mathcal {L}V\le & {} -(\mu _{1}+\lambda )(S-S^{*})^{2}-\left( \mu _{1}+\delta +\lambda \right) (I-I^{*})^{2} +\sigma ^{2}S^{2}(G(I))^{2} \\&\quad +\,\frac{\left( 2(\mu _{1}+\lambda )+\delta \right) (A I^{*}\sigma )^{2}}{2 \beta G(I^{*})\mu _{1}^{2}} \\\le & {} -(\mu _{1}+\lambda )(S-S^{*})^{2}-\left( \mu _{1}+\delta +\lambda \right) (I-I^{*})^{2} +(\frac{A\sigma }{\mu _{1}})^{2}S^{2}\\&\quad +\,\frac{\left( 2(\mu _{1}+\lambda )+\delta \right) (A I^{*}\sigma )^{2}}{2 \beta G(I^{*})\mu _{1}^{2}}\\\le & {} -(\mu _{1}+\lambda -(A\sigma /\mu _{1})^{2})\left( S-\frac{\mu _{1}+\lambda }{\mu _{1} +\lambda -(A\sigma /\mu _{1})^{2}}S^{*}\right) ^{2}\\&\quad -\,\left( \mu _{1}+\delta +\lambda \right) (I-I^{*})^{2} +\frac{(\mu _{1}+\lambda )(A\sigma /\mu _{1})^{2}}{\mu _{1}+\lambda -(A\sigma /\mu _{1})^{2}}(S^{*})^{2}\\&\quad +\,\frac{\left( 2(\mu _{1}+\lambda )+\delta \right) (A I^{*}\sigma )^{2}}{2 \beta G(I^{*})\mu _{1}^{2}} \end{aligned}$$

It then follows from Kushner (1967), Theorem 6, p. 50 that

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{1}{t}\mathbb {E}\int _{0}^{t}\bigg (m_{1} \left( S(s)-\frac{\mu _{1}+\lambda }{\mu _{1}+\lambda -(A\sigma /\mu _{1})^{2}}S^{*}\right) ^{2} +m_{2}(I(s)-I^{*})^{2}\bigg )\textit{ds} \le \eta , \end{aligned}$$

this is the required assertion. $\square$

Remark 4

Assume that system (1) has a unique positive equilibrium $E^{*}$. From Theorem 3, global asymptotic stability of the endemic equilibrium $E^{*}$ can be obtained. In fact, it can be seen from (7) that $R_{0}^{S}$ infinitely close to $R_{0}$ as the intensity of white noise $\sigma$ is small sufficiently. For any $R_{0}>1$, a positive noise intensity $\sigma _{0}$ exists such that $R_{0}^{S}>1$ for all $\sigma <\sigma _{0}$. From Theorem 3, this implies that the solution (S(t), I(t), R(t)) of system (3) has a unique ergodic stationary distribution. Let $\sigma \rightarrow 0$, then the stationary distribution will infinitely concentrate on the small neighborhood of positive equilibrium $E^{*}$, i.e., the unique positive equilibrium $E^{*}$ of system (1) is globally asymptotically stable for $R_{0}>1$.

Finally, from the preceding results, we shall summary a useful criterion for endemic and disease extinction of system (3). Noting the denote of $\sigma ^{*},\sigma _{*},\overline{\sigma }$ in (4), let us start with discussing the relationship between $R_{0}^{S}$ and $R_{0}$ for different values of white noise intensity $\sigma$.

• Case of $R_{0} \le 1$: By the definition $R_{0}^{S}$ in (7), it is easy to see that the inequality $R_{0}^{S}<1$ always holds for any $\sigma >0$ when $R_{0} \le 1$. Note that $\overline{\sigma }\ge \sigma ^{*}$ when $R_{0}\le 2$ by Proposition 1. Hence, when $R_{0} \le 1$, at least one of conditions (C1) and (C2) in Theorem 1 holds.

• Case of $1 < R_{0} \le 2$: By Proposition 1, we have $\sigma _{*}< \sigma ^{*} \le \overline{\sigma }$ for $1 < R_{0} \le 2$. Note that $R_{0}^{S}<1$ is equivalent to $\sigma > \sigma _{*}$. Hence, the condition (C1) of Theorem 1 holds when $\sigma _{*}< \sigma < \overline{\sigma }$. This, together with condition (C2) of Theorem 1, implies the disease will be extinct for the range of $\sigma > \sigma _{*}$.

• Case of $R_{0} > 2$: By Proposition 1, we have $\sigma _{*}< \sigma ^{*}$ and $\overline{\sigma }< \sigma ^{*}$.

Therefore, noting that $R_{0}^{S}>1$ is equivalent to $\sigma < \sigma _{*}$, we obtain the following corollary from Theorems 1,2,3.

Corollary 2

For any initial value $(S(0), I(0), R(0))\in \mathbb {R}^{3}_{+}$, the solution $(S(t), I(t), R(t))$ of system (3) has the property

• (i) if $R_{0} \le 1$, then for any $\sigma >0$, the disease dies out with probability one;

• (ii) if $1 < R_{0} \le 2$, then $R_{0}^{S}$ is the threshold parameter, i.e., the infection may become almost surely persistent in the time mean and positive recurrent if $R_{0}^{S}>1$, whereas if $R_{0}^{S}<1$, the disease dies out with probability one;

• (iii) if $R_{0} > 2$, then the disease is almost surely persistent in the time mean and positive recurrent if $\sigma < \sigma _{*}$ (i.e., $R_{0}^{S}>1$), while if $\sigma > \sigma ^{*}$, the disease dies out with probability one.

Remark 5

From (ii) and (iii) in Corollary 2, it is found when $R_{0} > 1$, if the noise intensity in the environments $\sigma$ is small ($\sigma < \sigma _{*}$), the disease may always persistent a.s. and positively recurrent; if $\sigma$ is large enough, then the infected and recovered hosts will die out a.s. From the perspective of biology significance, this implies the small environmental noises can generate the cycling phenomena of recurrent diseases, while the large noises may contribute to disease eradication.

Remark 6

From Corollary 2, it is can be seen that we do not obtain analytical results only for the range of noise intensity $\sigma _{*}\le \sigma \le \sigma ^{*}$ when $R^{S}_{0}<1$. However, by using numerical simulations, we also investigate the dynamic behavior of system (3) in this case, i.e., when $R^{S}_{0}<1$ and $\sigma _{*}\le \sigma \le \sigma ^{*}$, the disease may be persistent with some positive probability during several decades (see, Figs. 7, 9). In this sense, we illustrate the effect of the white noise in the environments on the transmission dynamics of the disease in system (3) in detail. Hence, the results obtained in this article extend that in Gray et al. (2011), Lahrouz and Settati (2014). In addition, by numerical simulations studies in detail, we find the quantity $R^{S}_{0}$ may be threshold of disease extinction, which supports Conjecture 8.1 in Gray et al. (2011).

5 Numerical Simulations

In this section, we make simulations to verify / extend our analytical results based on realistic parameter values of influenza A in human host. In order to avoid differentiation difficulty, we will apply the following improved Milstein’s method, proposed by Kloeden et al. (1992), to simulate the positive solution to system (3) with the given initial positive value and parameters.

Define vector-valued functions $g_{i}{:}\, \mathbb {R}^{3}_{+}\rightarrow \mathbb {R}^{3}$, $i=0,1$ as follows

$$\begin{aligned} g_{0}(x)=\left[ \begin{array}{c} A-\mu _{1}x_{1}+\lambda x_{3}-\beta x_{1} G(x_{2}) \\ \beta x_{1} G(x_{2})-\left( \mu _{2}+\delta \right) x_{2} \\ \delta x_{2}-\left( \mu _{3}+\lambda \right) x_{3} \end{array} \right] ,\ \ \ g_{1}(x)=\left[ \begin{array}{c} -\sigma x_{1} G(x_{2}) \\ \sigma x_{1} G(x_{2}) \\ 0 \end{array} \right] \end{aligned}$$

for all $x=(x_{1}, x_{2}, x_{3})^{T}\in \mathbb {R}^{3}_{+}$. Let $X_{k}=(S_{k}, I_{k}, R_{k})^{T}$. The corresponding discretization equations are

$$\begin{aligned} X_{k+1}=X_{k}+ g_{0}(X_{k}) \varDelta t+g_{1}(X_{k})\xi _{k}\sqrt{\varDelta t} + V_{k}(g_{1}(Y_{k})-g_{1}(X_{k})), \end{aligned}$$

(35)

where

$$\begin{aligned} V_{k}=\frac{1}{2}\sqrt{\varDelta t}(\xi _{k}^{2}-1), \quad Y_{k}=X_{k}+\sqrt{\varDelta t}g_{1}(X_{k}), \end{aligned}$$

and $\xi _{k}$, $k=1, 2, \ldots , n$, are independent Gaussian random variables with distribution N(0, 1).

Then, we shall verify the feasibility of our analytical results for the following stochastic epidemic model with the saturated incidence rate $\beta SI/(1+\alpha I)$ proposed by Capasso and Serio (1978) and used by a number of authors for which we refer the readers to Liu et al. (1986), Ruan and Wang (2003) and the references therein:

$$\begin{aligned} \left\{ \begin{array}{l} \textit{dS}(t)=\left( A-\mu _{1}S(t)+\lambda R(t)-\frac{\beta S(t)I(t)}{1+\alpha I(t)}\right) \textit{dt} - \frac{\sigma S(t)I(t)}{1+\alpha I(t)}\textit{dB}(t), \\ \textit{dI}(t)=\left( \frac{\beta S(t)I(t)}{1+\alpha I(t)}-\left( \mu _{1}+\delta \right) I(t)\right) \textit{dt} +\frac{\sigma S(t)I(t)}{1+\alpha I(t)}\textit{dB}(t), \\ \textit{dR}(t)=\left( \delta I(t)-\left( \mu _{1}+\lambda \right) R(t)\right) \textit{dt}, \end{array} \right. \end{aligned}$$

(36)

where $\alpha$ is a positive saturation constant and all parameters are defined in Table 1 (in this section the unit of time is one week). The corresponding deterministic system of (36) has a basic reproduction number

$$\begin{aligned} R_{0}=\frac{A\beta }{\mu _{1}(\mu _{1}+\delta )}. \end{aligned}$$

(37)

In Korobeinikov (2007), Korobeinikov has proved that properties of this corresponding deterministic system depend on the basic reproduction number $R_{0}$:

• If $R_{0} \le 1$, then the unique infection-free equilibrium state $E_{0} = (A/\mu _{1}, 0, 0)$ is globally asymptotically stable.

• If $R_{0}> 1$, then there is an unique and globally asymptotically stable positive equilibrium $E^{*} = (S^{*}, I^{*},R^{*})$.

Table 1 Parameter values in numerical simulations for system (36)

In (36), according to the World Bank data, we choose $\mu _{1}=1/(70\times 52)$ week$^{-1}$ which suggests the average life expectancy is 70 years. For simplicity, we assume that there is no death due to the disease, and hence $\mu _{2}=\mu _{3}=\mu _{1}$. We also assume the total population size is $N=10{,}000$, then the birth rate is $A=\mu _{1} N=10{,}000/(70\times 52)$ week$^{-1}$. The value of the infectious period can be estimated to range from 2 to 7 days for flu on the basis of clinical observations only (Douglas 1975; Frank et al. 1981), so we choose the mean recovery rate of infected individuals is $\delta =7/7$ week$^{-1}$ $=1$ week$^{-1}$.

In our SIRS model of an evolutionary epidemic of influenza A, causing previously immune hosts to become susceptible from epidemic to epidemic is mainly due to the progressive antigenic drift of influenza virus, which results in evasion of host immunity; for this reason, we assume the rate of host immunity loss equals the rate of virus’s mutations. The studies of Plotkin et al. (2002), Hay et al. (2001) have shown that the new antigenic variants can rise with a frequency of one per 1–2 years, so we here choose the average rate of host immunity loss $\lambda =1/(1.5\times 52)$ week$^{-1}$.

Next, by MATLAB software and the method of discretization (35), we simulate the solution of system (36) with different values of $\sigma$ to investigate the effect of the white noise on the transmission dynamics of influenza virus. Since $\mu _{1}=\mu _{2}=\mu _{3}$ in (36), by the arguments given in (31), we only need to plot S(t) and I(t) to verify our results below. In addition, we always assume that the initial value of system (36) is $(S(0), I(0), R(0))=(9980, 20, 0)$ except for the other specification. We then divide our simulations into two cases according to the range of $R_{0}$.

Case 1: $1 < R_{0}\le 2$.

By using daily case notification data in Guangdong Province, China, Yang et al. (2013) estimated the possible range of basic reproduction number for pandemic influenza A H1N1 was preliminarily between 1.05 and 1.46. We here assume the basic reproduction number $R_{0}=1.45$, then the average transmission rate $\beta =1.450398\times 10^{-4}$ week$^{-1}$ from (37), and

$$\begin{aligned} \sigma _{*}= 9.488136 \times 10^{-5}. \end{aligned}$$

(38)

Hence for the corresponding deterministic SIRS model of (36), we have

$$\begin{aligned} I^{*}=\lim _{t\rightarrow +\infty }I(t)=27.74 \end{aligned}$$

for the initial value $(S(0), I(0), R(0))=(9980, 20, 0)$. To see the effect of the white noise intensity, we consider three different values of $\sigma$: $3.162712\times 10^{-5}$, $5.831753\times 10^{-5}$ and $1.157743 \times 10^{-4}$. The corresponding values of $R_{0}^{S}$ are 1.40, 1.28 and 0.78, respectively. By (ii) in Corollary 2, we see that the disease is persistent in the first two cases, while the disease is extinctive in the last case. The computer simulations shown in Figs. 1 and 2 clearly support these results.

Fig. 1

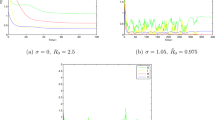
a The mean evolution of infected individuals of the stochastic model (36) is graphed for various values of $\sigma$, where $\sigma _{1} < \sigma _{2}<\sigma _{*}<\sigma _{3}$. b The corresponding standard deviation evolution of infected individuals of the stochastic model (36) (Color figure online)

Fig. 2

a The evolution of a single path of I(t) for system (36) and its corresponding deterministic model. b Probability densities of the values of the path I(t) for system (36) based on 10,000 stochastic simulations (Color figure online)

Figure 1 shows trends of the evolution of the mean and standard deviation of I(t). It is observed that when $\sigma < \sigma _{*}$ (i.e., $R_{0}^{S}>1$), both the mean and the standard deviation ultimately tend to a constant; however, both the mean and the standard deviation quickly decline and tend to 0 for $\sigma > \sigma _{*}$ (noting that $\sigma > \sigma _{*}$ is equivalent to $R_{0}^{S}<1$). We can also see that when the environmental noises exist, the mean of I(t) is always less than the corresponding deterministic solution for all case of $\sigma$, and the mean is reduced gradually with the increase in white noise intensity $\sigma$. This shows that white noise perturbations of the transmission rate $\beta$ can be beneficial to control the spread of influenza virus on average. However, as shown in (b) of Fig. 1, when the intensity of environmental noises is small (i.e., $\sigma < \sigma _{*}$), the standard deviation of I(t) increases with the increase in noise intensity $\sigma$. This suggests that the higher the volatility of the environmental noises, the more difficult the prediction of the peak size and occurring time of influenza epidemics, though the average level of the evolution of I(t) is reduced in case of the presence of environmental noises.

(b) of Fig. 2 shows histograms of the approximate stationary distribution of each case of $\sigma$ chose above. The evolution trends of the mean and standard deviation of I(t) in Fig. 1 illustrate that for each case of $\sigma$, the stationary distribution of I(t) exits and in the simulations the probability distributions of I(t) have more or less reached their stationary distributions. As can be seen in (b) of Fig. 2, for first two cases (i.e., $R_{0}^{S}>1$), both appear skew to the right and the skewness becomes larger as the intensity $\sigma$ of the white noise increases; in the last case ($R_{0}^{S}<1$), the mass of the distribution of I(t) is concentrated on the small neighborhood of zero. In addition, (a) and (b) of Fig. 2 indicate that the small environmental perturbations can generate the irregular cycling phenomena of recurrent diseases, while the large ones will eradicate diseases. This means the small perturbations of the white noise can sustain the irregular recurrence of influenza A in humans between two pandemics, and larger ones may be beneficial, leading to the extinction of influenza.

Case 2: $2 < R_{0}< 4$.

By using daily case notifications during the autumn wave of the influenza pandemic (Spanish flu) in the city of San Francisco, California, from 1918 to 1919, Chowell et al. (2007) found the reproduction number for pandemic influenza (Spanish flu) at the city level can be robustly assessed to lie in the range of 2.0–3.0. In this case, we assume the basic reproduction number $R_{0}=2.38$, which is the estimate of the second method in Chowell et al. (2007), then we have the average transmission rate $\beta = 2.380654\times 10^{-4}$ week$^{-1}$ from (37), and

$$\begin{aligned} \sigma ^{*}= 1.683145 \times 10^{-4}, \quad \sigma _{*}=1.661553 \times 10^{-4}. \end{aligned}$$

(39)

Hence for the corresponding deterministic SIRS model of (36), we have

$$\begin{aligned} I^{*}=\lim _{t\rightarrow +\infty }I(t)=58.94 \end{aligned}$$

for the initial value $(S(0), I(0), R(0))=(9980, 20, 0)$. We first verify (iii) in Corollary 2 with three different values of $\sigma$: $1.20 \times 10^{-4}$, $1.45 \times 10^{-4}$ and $1.87 \times 10^{-4}$. For the first two cases, $\sigma < \sigma _{*}$ (i.e., $R_{0}^{S}>1$), while $\sigma > \sigma ^{*}$ for the last case. By (iii) in Corollary 2, we see that the disease is persistent in the first two cases, while the disease is extinctive in the last case. The computer simulations shown in Figs. 3 and 4 clearly support these results.

Fig. 3

a The mean evolution of infected individuals of the stochastic model (36) is graphed for various values of $\sigma$, where $\sigma _{1} < \sigma _{2}<\sigma _{*}$ and $\sigma _{3} > \sigma ^{*}$. b The corresponding standard deviation evolution of infected individuals of the stochastic model (36) (Color figure online)

Fig. 4

a The evolution of a single path of I(t) for system (36) and its corresponding deterministic model. b Probability densities of the values of the path I(t) for system (36) based on 10,000 stochastic simulations (Color figure online)

(a) and (b) in Fig. 3 show trends of the evolution of the mean and standard deviation of I(t), respectively. It is observed that when $\sigma < \sigma _{*}$, both the mean and standard deviation ultimately tend to a constant; however, both the mean and standard deviation quickly decline and tend to 0 for $\sigma > \sigma ^{*}$. As shown in Fig. 3, when the noise intensity is small ($\sigma < \sigma _{*}$), with the increase in environmental noises intensity, the average level of the evolution of I(t) will decline and the standard deviation of I(t) will increase; when the noise intensity is large ($\sigma > \sigma ^{*}$), the disease will be die out.

By the similar arguments to that of Case 1, we can claim from Fig. 3 that histograms of the approximate stationary distribution in (b) of Fig. 4 have almost reached their stationary distributions. As shown in (b) of Fig. 4, for first two cases (i.e., $\sigma < \sigma _{*}$), both appear skew to the right and the skewness becomes larger as the intensity $\sigma$ of the white noise increases; in the last case ($\sigma > \sigma ^{*}$), the mass of the distribution of I(t) is concentrated almost on the small neighborhood of zero. In addition, (a) and (b) of Fig. 4 also indicate that the small environmental perturbations ($\sigma < \sigma _{*}$) can generate the irregular cycling phenomena of recurrent epidemics of influenza, while the large ones ($\sigma > \sigma ^{*}$) will be helpful to the eradication of influenza epidemics.

Next, we discuss in detail the effect of environmental noises on the evolution of I(t) in the case of $\sigma _{*}< \sigma < \sigma ^{*}$ ($R_{0}^{S}<1$), where we do not give analytical results.

For environmental noises intensity $\sigma =1.665 \times 10^{-4}$ satisfying $\sigma _{*}<\sigma <\sigma ^{*}$, Figs. 5 and 6 give the evolution dynamic of I(t) in a relatively short term (300 weeks). From Fig. 6, it is observed that for different initial values $(S(0), I(0), R(0))=(9980, 20, 0)$ and (9800, 200, 0), the mean and standard deviation of I(t) tend to be uniform quickly. This, together with (c) of Fig. 5, implies when $\sigma _{*}<\sigma <\sigma ^{*}$, the probability distribution of the values of the path of I(t) for system (36) do not depend on the initial value of I(t). As shown in (a) and (b) of Fig. 5, both the disease persistence and extinction are observed when $\sigma _{*}<\sigma <\sigma ^{*}$. At $t=300$ weeks, it is seen from (c) of Fig. 5 that the probability of the recurrence of influenza epidemic may be positive during several years. Based on 10,000 stochastic simulations, we can estimate that

$$\begin{aligned} \mathbb {P}\{I(300)\le 10^{-4}\}\approx 0.4321 ,\ \ \ \mathbb {P}\{I(300)\ge 20\}\approx 0.159 \end{aligned}$$

at $t=300$ weeks (about 5.77 years). This implies that in the short term, both the persistence and extinction of influenza virus may occur in the case of $\sigma _{*}<\sigma <\sigma ^{*}$.

Figure 7 describes the long-run evolutionary behavior of I(t) for $\sigma _{*}<\sigma <\sigma ^{*}$, including the mean and standard deviation. For two different noise intensities $\sigma _{1}=1.665 \times 10^{-4}$ and $\sigma _{2}=1.675 \times 10^{-4}$, the evolutions of the mean and standard deviation of I(t) during 3000 weeks (about 57.6 years) are graphed in Fig. 7. It is observed that the mean level decreases with the increase in the noise intensity, and that both the mean level and the standard deviation level decrease very slowly along with time; however, it is found surprisingly that the standard deviation level decreases with the increase in the noise intensity, which is very similar to the case of $\sigma >\sigma ^{*}$. Figure 8 describes the evolutions of the mean and standard deviation of I(t) in the case of $\sigma >\sigma ^{*}$, where from (iii) in Corollary 2, we obtain analytical results that the disease will go extinct ultimately. Note that as shown in Figs. 1 and 3, the standard deviation level increases with the increase in the noise intensity for $\sigma < \sigma _{*}$. Hence, by comparing Fig. 7 with 8, we find there is a strong possibility that $\sigma _{*}$ is the threshold of environmental noises, i.e., $R_{0}^{S}$ is the threshold of disease persistence or extinction. This also suggests that Conjecture 8.1 of Gray et al. (2011) may hold for our stochastic SIRS system with nonlinear incidence rate and variable population size. However, it is noteworthy that when $\sigma >\sigma _{*}$ (but not too large), the probability of disease outbreak is always a positive value for a relatively longer period of time.

Fig. 5

a, b The evolution of a single path of I(t) for system (36) and its corresponding deterministic model. c Probability densities of the values of the path I(t) for system (36) based on 10,000 stochastic simulations. The initial values are 20 and 200 for the first-line graph and the second-line graph, respectively. In all cases, we choose $\sigma =1.665 \times 10^{-4}$ satisfying $\sigma _{*}<\sigma <\sigma ^{*}$ (Color figure online)

Fig. 6

a The mean evolution of infected individuals of the stochastic model (36) is graphed for $\sigma =1.665\times 10^{-4}$, where $\sigma _{*} < \sigma <\sigma ^{*}$. b The corresponding standard deviation evolution of infected individuals of the stochastic model (36) (Color figure online)

Fig. 7

a The mean evolution of infected individuals of the stochastic model (36) is graphed with $\sigma _{*} < \sigma _{1}<\sigma _{2}<\sigma ^{*}$. b The corresponding standard deviation evolution of infected individuals of the stochastic model (36) (Color figure online)

Fig. 8

a The mean evolution of infected individuals of the stochastic model (36) is graphed with $\sigma _{2}>\sigma _{1}>\sigma ^{*}$. b The corresponding standard deviation evolution of infected individuals of the stochastic model (36) (Color figure online)

Indeed, as studied in Simonsen (1999), pandemics of influenza in humans recur every 30 years or so since the mid-eighteenth century and of course it may also be only a few years before the next pandemic occurs. Hence, from the point of epidemiology view, it is very significant to investigate the probability of reappearance of influenza epidemics during several decades for $\sigma _{*}<\sigma <\sigma ^{*}$, though the influenza virus will likely be eradicated ultimately when $\sigma > \sigma _{*}$. Figure 9 gives the long-run evolutionary behavior of the probability of disease outbreak for $\sigma _{*}<\sigma <\sigma ^{*}$. Here, the disease outbreak means the number of infected individuals I(t) is more than the stationary level $I^{*}$ of the corresponding deterministic model. As shown in Fig. 9, the probability of disease outbreak decreases very slowly along with time, although it decreases with the increase in the noise intensity. For instance, based on 10,000 stochastic simulations, we can estimate for the noise intensity $\sigma _{*}<\sigma =1.675 \times 10^{-4}<\sigma ^{*}$ that

$$\begin{aligned} \mathbb {P}\{I(300)\ge I^{*}\}\approx & {} 0.0874,\quad \mathbb {P}\{I(600)\ge I^{*}\}\approx 0.0586,\\ \mathbb {P}\{I(1500)\ge I^{*} \}\approx & {} 0.0363. \end{aligned}$$

at $t=300$ weeks (about 5.77 years), $t=600$ weeks (about 11.54 years) and $t=1500$ weeks (about 28.85 years), respectively.

So far, by combining analytical results with numerical techniques, we have comprehensively analyzed the influence of the white noise on the spread dynamics of influenza for all kinds of values of the noise intensity $\sigma$. In the end, we give an example of Case 1 with the relatively realistic noise intensity. In fact, the white noise intensity may be less than the critical intensity $\sigma _{*}$ in the real word. In Gu et al. (2011), authors formulated stochastic SIR epidemic model with the transmission rate $\beta$ disturbed by white Gaussian noise in the similar form to (2) (see, P. 3685 in Gu et al. 2011); the real data of SARS in Beijing in 2003 are nicely fitted by their model with the white noise intensity $\sigma =2.31 \times 10^{-5}< \sigma _{*}$, which has been converted into the time unit (week$^{-1}$) in this paper. This realistic noise intensity does not exceed the critical intensity $\sigma _{*}$ for both cases above in (38) and (39). It is found that the distance between this noise intensity and the critical intensity $\sigma _{*}$ becomes larger with the increase in the basic reproduction number $R_{0}$ of the corresponding deterministic model.

Fig. 9

The evolution of probability of disease outbreak is graphed for the parameters $\sigma _{1}=1.665 \times 10^{-4}$ (red line) and $\sigma _{2}=1.675 \times 10^{-4}$ (green line), where $\sigma _{*}<\sigma _{1}< \sigma _{2}<\sigma ^{*}$ and the disease outbreak means $I(t)\ge I^{*}=58.94$ (Color figure online)

For this realistic noise intensity, we compute that $R_{0}-R_{0}^{S}=0.026673$ from (7), and the mean and the standard deviation of infected individuals are $\mathbb {E}(I(t))=26.977< I^{*}=27.24$ and Var$(I(t))=8.47$ at $t=300$ weeks, respectively. Compared with the corresponding deterministic model, both the threshold parameter of disease extinction $R_{0}^{S}$ and the average level of infecteds decrease slightly. However, it is seen from Fig. 10 that the white noise increases the volatility of infecteds (i.e., the standard deviation). In particular, $\mathbb {P}\{I(300)\ge I^{*} \}\approx 0.4512$. Therefore, the presence of the white noise may pose more challenges to the prediction and control of the endemic of influenza.

Fig. 10

a The evolution of a single path of I(t) for system (36) and its corresponding deterministic model. b Probability densities of the values of the path I(t) for system (36) based on 10,000 stochastic simulations (Color figure online)

6 Summary and Discussion

As stochastic environmental factors in the real world, such as absolute humidity, temperature and precipitation, have an appreciable impact on the infection force of the disease such as influenza A, incorporating stochastic effects into the model gives us a more realistic way of modeling epidemic models. In this paper, we have considered a stochastic SIRS epidemic model with the external variability in the transmission rate $\beta$ and applied our theoretical results to the inter-pandemic evolution dynamic of influenza A based on realistic parameter values.

Combining analytical results with numerical simulations, we have discussed in detail the effect of environmental noises on the transmission dynamics of influenza A epidemics. A deterministic threshold quantity $R_{0}^{S}$ is established: The disease dies out almost surely when $R_{0}^{S}<1$ ($\sigma >\sigma _{*}$) and persists when $R_{0}^{S}>1$ ($\sigma <\sigma _{*}$), where $R_{0}^{S}<1$ is equivalent to $\sigma >\sigma _{*}$. We found that the presence of environmental noises can sustain the irregular recurrence of influenza epidemics and the average level of the number of infected individuals I(t) always decreases with the increase in noises intensity $\sigma$; however, the standard deviation of I(t) increases with increase in noises intensity when $\sigma <\sigma _{*}$, and the contrary case occurs when $\sigma >\sigma _{*}$. We also found that when $\sigma _{*} <\sigma <\sigma ^{*}$, the disease will take very long time to be eradicate completely, which implies that the probability of disease outbreak is always a positive value for a relatively long term, such as several decades.

In this article, the white noise is used to describe small-scale time environmental fluctuations such as daily or weekly variations of meteorological factors, which produce rapid fluctuations of the transmission rate compared to the evolution of influenza epidemics. However, climate conditions usually experience random switching between different environments such as dry and wet. The average values of some critical parameters of epidemic model may switch between different levels with the switching of environments, while only the transmission rate $\beta$ fluctuates around its average level between two switches of the environments, which is caused by the perturbation of the white noise. Hence, it is very interesting to consider the impact of the large-scale time disturbance of the switching of environments to the evolution of influenza epidemics.

Additionally, we neglect the seasonal effect for the transmission of influenza A. It is worthwhile to study the combined effects of seasonal variation and environmental noises, which we leave as our future work.