A Mathematical Model of Water and Nutrient Transport in Xylem Vessels of a Wheat Plant

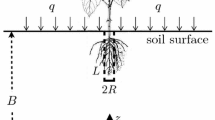
Abstract

At a time of increasing global demand for food, dwindling land and resources, and escalating pressures from climate change, the farming industry is undergoing financial strain, with a need to improve efficiency and crop yields. In order to improve efficiencies in farming, and in fertiliser usage in particular, understanding must be gained of the fertiliser-to-crop-yield pathway. We model one aspect of this pathway; the transport of nutrients within the vascular tissues of a crop plant from roots to leaves. We present a mathematical model of the transport of nutrients within the xylem vessels in response to the evapotranspiration of water. We determine seven different classes of flow, including positive unidirectional flow, which is optimal for nutrient transport from the roots to the leaves; and root multidirectional flow, which is similar to the hydraulic lift process observed in plants. We also investigate the effect of diffusion on nutrient transport and find that diffusion can be significant at the vessel termini especially if there is an axial efflux of nutrient, and at night when transpiration is minimal. Models such as these can then be coupled to whole-plant models to be used for optimisation of nutrient delivery scenarios.

Appendices

Appendix A: Xylem Dimensions in Roots and Leaves

Table 4 Calculations of $\hat{k}_{z}$ and 1/Pe in the root zone based on number and radii of xylem vessels in wheat from Percival (1921) (pp. 39–40). The number of vessels $\hat{v}$ is given by the number of vessels per bundle multiplied by the number of bundles

Table 5 Calculations of $\hat{k}_{z}$ and 1/Pe in the leaf zone based on number and radii of xylem vessels in the stout bundles of wheat from Percival (1921) (pp. 57–59). The number of vessels $\hat{v}$ is given by the number of vessels per bundle multiplied by the number of bundles

Appendix B: Range of p ⁰ that Would Give Rise to Unidirectional Flow for p ⁰≠p ^ext and G≠0

$$\begin{aligned} p^{0L}_{|z=0} =& p^\mathrm{ext}+\frac{\sqrt{M^R}(p^\mathrm{soil}-p^\mathrm{ext})\kappa_1}{f(z_1, z_2)}+ \frac{G}{f(z_1,z_2)} \biggl(-2e^{\sqrt{M^R}(1+z_2)} \\ &{}+ \bigl(\kappa_2\!+\sqrt{M^R}(z_1\!-z_2) \kappa_1 \bigr)\cos \bigl(\sqrt{M^L}z_1\bigr)\!- \frac{\!\sqrt{M^R}\kappa_1\sin (\sqrt{M^L}z_1 )\!}{\sqrt{M^L}} \biggr), \end{aligned}$$

(31)

$$\begin{aligned} p^{0R}_{\mathrm{crit}|z=1} =& p^\mathrm{ext}+\cos\bigl( \sqrt{M^L}z_1\bigr) \bigl(p^\mathrm{soil}-p^\mathrm{ext} \bigr) + \frac{\mathit{Ge}^{-\sqrt{M^R}(z_2+1)}}{2} \\ &{}\times \biggl(\cos\bigl(\sqrt{M^L}z_1 \bigr) \biggl(\frac{\kappa_1}{\sqrt{M^R}}+\kappa_2(z_1-z_2) \biggr)-\frac{\kappa_2\sin (\sqrt{M^L}z_1 )}{\sqrt{M^L}} \biggr), \end{aligned}$$

(32)

where

$$\begin{aligned} f(z_1, z_2) =&\sqrt{M^R} \kappa_1\cos \bigl(\sqrt{M^L}z_1 \bigr) \\ &{}+\sqrt{M^L} \bigl(\kappa_2+ \sqrt{M^R}(z_1-z_2)\kappa_1\bigr)\sin \bigl(\sqrt{M^L}z_1 \bigr). \end{aligned}$$

(33)

Appendix C: Analytical Solution for Nutrient Transport by Convection and Diffusion

We seek an analytical solution for the transport of phosphate, n, due to both convection and diffusion, but consider that diffusion is only important near the boundaries z=0, z ₁, z ₂, 1. In the main bulk, convection dominates and we can neglect diffusion, but near the boundaries we expect the presence of boundary layers as the solution rapidly adjusts to the boundary conditions. For an introduction into boundary layer methods, see Hinch (1991). For simpler analytical progress we neglect the effect of gravity as its effect is small, and as an example assume that F is constant.

3.1 C.1 Root Zone

We first consider the root zone and the boundary near z=1. We let ϵ=1/Pe, which is small, such that the nutrient transport equation and boundary condition become

$$\begin{aligned} &\frac{d}{dz} \biggl(n^{R} \biggl(\frac{dp^{R}}{dz}-G \biggr) +\epsilon\frac{dn^{R}}{dz} \biggr)=-F^R, \end{aligned}$$

(34)

$$\begin{aligned} &\epsilon\frac{dn^{R}}{dz}=-f\quad\mbox{at}\ z=1. \end{aligned}$$

(35)

We scale $n^{R}=\epsilon^{-1} f \bar{n}^{R}$, and integrate (34) to give

$$\begin{aligned} &\epsilon^{-1}\bar{n}^{R} \biggl(\frac{dp^{R}}{dz}-G \biggr) +\frac{d\bar{n}^{R}}{dz}=-\frac{F^R}{f}z+k_0, \end{aligned}$$

(36)

$$\begin{aligned} &\frac{d\bar{n}^{R}}{dz}=-1\quad \mbox{at}\ z=1, \end{aligned}$$

(37)

where k ₀ is determined from the boundary condition (37) to be $\frac{F^{R}-f}{f}$. We define the boundary layer coordinate x and let 1−z=ϵ ^α x, such that

$$\begin{aligned} &\epsilon^{-1}\bar{n}^{R} \tilde{R}_1- \epsilon^{-\alpha}\frac{d\bar{n}^{R}}{dx}=-\frac{F^R}{f}\bigl(1- \epsilon^{\alpha}x\bigr)+\frac{F^R-f}{f}, \end{aligned}$$

(38)

$$\begin{aligned} &\epsilon^{-\alpha}\frac{d\bar{n}^{R}}{dx}=1\quad\mbox{at}\ x=0, \end{aligned}$$

(39)

where $\tilde{R}_{1}$ is $\frac{dp^{R}}{dz}-G$ as a function of (1−ϵ ^α x), which we expand as follows:

$$\begin{aligned} \tilde{R}_1 =&\sqrt{M^R} \bigl(A_5e^{\sqrt{M^R}z}-A_6e^{-\sqrt{M^R}z}\bigr)-G \\ =&\sqrt{M^R} \biggl( \bigl(A_5e^{\sqrt{M^R}}-A_6e^{-\sqrt{M^R}}\bigr) \biggl(1+\frac{M^R\epsilon^{2\alpha}x^2}{2!}+O\bigl(\epsilon^{4\alpha}\bigr) \biggr) \\ &{}- \bigl(A_5e^{\sqrt{M^R}}+A_6e^{-\sqrt{M^R}} \bigr) \biggl(\sqrt{M^R}\epsilon^{\alpha}x+\frac{{M^R}^{\frac{3}{2}}\epsilon^{3\alpha}x^3}{3!}+O\bigl( \epsilon^{5\alpha}\bigr) \biggr) \biggr) \\ &{}-G. \end{aligned}$$

(40)

Setting G=0, we find that $A_{5}e^{\sqrt{M^{R}}}-A_{6}e^{-\sqrt{M^{R}}}=0$ and

$$\begin{aligned} &A_5e^{\sqrt{M^R}}+A_6e^{-\sqrt{M^R}} \\ &\quad =\frac{2\sqrt{M^L}e^{\sqrt{M^R}(z_2+1)} (p^\mathrm{ext}-p^0 +\cos(\sqrt{M^L}z_1)(p^\mathrm{soil}-p^\mathrm{ext}) )}{\sqrt{M^R}\kappa_1\sin(\sqrt{M^L}z_1) -\sqrt{M^L} (\sqrt{M^R}(z_1-z_2)\kappa_1+\kappa_2 )\cos(\sqrt{M^L}z_1)}, \end{aligned}$$

(41)

which is negative for the parameter values considered (values of M ^L below those given by Eq. (22)). Therefore, with G=0, we find

$$\begin{aligned} &\tilde{R}_1=-\sqrt{M^R} \bigl(A_5e^{\sqrt{M^R}}+A_6e^{-\sqrt{M^R}}\bigr) \biggl(\sqrt{M^R}\epsilon^{\alpha}x+\frac{{M^R}^{\frac{3}{2}}\epsilon^{3\alpha}x^3}{3!}+O \bigl(\epsilon^{5\alpha}\bigr) \biggr), \end{aligned}$$

(42)

which we rewrite as $\tilde{R}_{1}=\tilde{R}_{11}\epsilon^{\alpha}x+\tilde{R}_{13} \epsilon^{3\alpha}x^{3}+O(\epsilon^{5\alpha})$, and whose coefficients are positive and are given by

$$\begin{aligned} &\tilde{R}_{11}=-M^R \bigl(A_5e^{\sqrt{M^R}}+A_6e^{-\sqrt{M^R}}\bigr), \end{aligned}$$

(43)

$$\begin{aligned} &\tilde{R}_{13}=-\frac{{M^R}^{2}}{3!} \bigl(A_5e^{\sqrt{M^R}}+A_6e^{-\sqrt{M^R}}\bigr). \end{aligned}$$

(44)

Note that if G≠0 then $A_{5}e^{\sqrt{M^{R}}}+A_{6}e^{-\sqrt{M^{R}}}=G/\sqrt{M^{R}}$ and hence the series would become $\tilde{R}_{1}=\tilde{R}_{11}\epsilon^{\alpha}x+G\frac{M^{R}\epsilon^{2\alpha}x^{2}}{2!} +\tilde{R}_{13}\epsilon^{3\alpha}x^{3}+O(\epsilon^{4\alpha})$ which makes analytical progress more complicated. Therefore, with G=0, Eq. (38) becomes

$$\begin{aligned} &\epsilon^{-1}\bar{n}^{R} \bigl(\tilde{R}_{11} \epsilon^{\alpha}x+\tilde{R}_{13}\epsilon^{3\alpha}x^3+O \bigl(\epsilon^{5\alpha}\bigr) \bigr)-\epsilon^{-\alpha} \frac{d\bar{n}^{R}}{dx}=-\frac{F^R}{f}\bigl(1-\epsilon^{\alpha}x\bigr)+ \frac{F^R-f}{f}. \end{aligned}$$

(45)

In order for the viscous terms to balance the convective terms, we choose $\alpha=\frac{1}{2}$ which leads to

$$\begin{aligned} &\bar{n}^{R} \bigl(\tilde{R}_{11}x+\tilde{R}_{13} \epsilon x^3+O\bigl(\epsilon^{2}\bigr) \bigr)- \frac{d\bar{n}^{R}}{dx}=-\frac{F^R}{f}\bigl(\epsilon^{\frac{1}{2}}-\epsilon x \bigr)+ \biggl(\frac{F^R-f}{f} \biggr)\epsilon^{\frac{1}{2}}, \end{aligned}$$

(46)

$$\begin{aligned} &\frac{d\bar{n}^{R}}{dx}=\epsilon^{\frac{1}{2}}\quad\mbox{at}\ x=0. \end{aligned}$$

(47)

We expand $\bar{n}^{R}=\bar{n}^{R}_{0}+\epsilon^{\frac{1}{2}}\bar{n}^{R}_{1}+\epsilon \bar{n}^{R}_{2}+O(\epsilon^{\frac{3}{2}})$ and solve Eq. (46) at successive orders of ϵ subject to the boundary condition (47). The O(ϵ ⁰) terms of Eqs. (46) and (47) are

$$\begin{aligned} &\bar{n}^{R}_0\tilde{R}_{11}x- \frac{d\bar{n}^{R}_0}{dx}=0, \end{aligned}$$

(48)

$$\begin{aligned} &\frac{d\bar{n}^{R}_0}{dx}=0\quad\mbox{at}\ x=0, \end{aligned}$$

(49)

which have the solution $\bar{n}^{R}_{0}=C_{0}e^{\frac{1}{2}\tilde{R}_{11}x^{2}}$, where C ₀ is a free constant found by matching with the bulk solution. Since this solution grows as x increases, the only choice of C ₀ is C ₀=0, such that $\bar{n}^{R}_{0}=0$.

The $O(\epsilon^{\frac{1}{2}})$ terms of Eqs. (46) and (47) are

$$\begin{aligned} &\bar{n}^{R}_1\tilde{R}_{11}x- \frac{d\bar{n}^{R}_1}{dx}=-\frac{F^R}{f}+\frac{F^R-f}{f}, \end{aligned}$$

(50)

$$\begin{aligned} &\frac{d\bar{n}^{R}_1}{dx}=1\quad\mbox{at}\ x=0, \end{aligned}$$

(51)

which have the solution $\bar{n}^{R}_{1}= \Bigl( \frac{1}{2} \sqrt{\frac{2\pi}{\tilde{R}_{11}}}\,\mbox{erf}\bigl(\frac{1}{2}\sqrt{2\tilde{R}_{11}}x\bigr) +C_{1} \Bigr) e^{\frac{1}{2}\tilde{R}_{11}x^{2}}$, where C ₁ is a free constant found by matching with the bulk solution. To ensure a non-growing solution, we choose $C_{1}=-\frac{1}{2}\sqrt{\frac{2\pi}{\tilde{R}_{11}}}$, such that

$$\begin{aligned} \bar{n}^{R}_1=\frac{1}{2}\sqrt{ \frac{2\pi}{\tilde{R}_{11}}}e^{\frac{1}{2}\tilde{R}_{11}x^2} \biggl(\mbox{erf} \biggl(\frac{1}{2} \sqrt{2\tilde{R}_{11}}x \biggr)-1 \biggr). \end{aligned}$$

(52)

The O(ϵ) terms of Eqs. (46) and (47) are

$$\begin{aligned} &\bar{n}^{R}_2\tilde{R}_{11}x- \frac{d\bar{n}^{R}_2}{dx}=\frac{F^R}{f}x, \end{aligned}$$

(53)

$$\begin{aligned} & \frac{d\bar{n}^{R}_2}{dx}=0 \quad \mbox{at}\ x=0, \end{aligned}$$

(54)

which have the solution $\bar{n}^{R}_{2}=\frac{F^{R}}{\tilde{R}_{11}f}+C_{2}e^{\frac{1}{2}\tilde{R}_{11}x^{2}}$, where C ₂ is a free constant found by matching with the bulk solution. To ensure a non-growing solution, we choose C ₂=0, such that $\bar{n}^{R}_{2}=\frac{F^{R}}{\tilde{R}_{11}f}$. A summary of the boundary layer solution near z=1 is

$$\begin{aligned} n^{R}=&\epsilon^{-1}f \bigl(\epsilon^{\frac{1}{2}} \bar{n}^{R}_1+\epsilon \bar{n}^{R}_2+O \bigl(\epsilon^{\frac{3}{2}}\bigr) \bigr)=f \bigl(\epsilon^{-\frac{1}{2}} \bar{n}^{R}_1+\epsilon^0\bar{n}^{R}_2+O \bigl(\epsilon^{\frac{1}{2}}\bigr) \bigr). \end{aligned}$$

(55)

The boundary layer solution has to match with the bulk solution which is governed by

$$\begin{aligned} {n}^{R} \biggl(\frac{dp^{R}}{dz} \biggr) +\epsilon \frac{dn^{R}}{dz}=-F^Rz+C_4, \end{aligned}$$

(56)

where C ₄ is an unknown constant. Similarly we let $n^{R}=\epsilon^{0} n_{0}^{R}+O(\epsilon^{\frac{1}{2}})$ and find $n^{R}_{0}=\frac{-F^{R}z+C_{4}}{\frac{dp^{R}}{dz}}$ which is equivalent to the convection-only solution. Matching the bulk with the boundary layer solution we find that $\bar{n}_{1}$ matches with zero, and $\bar{n}_{2}$ matches with the bulk solution to give C ₄=F ^R. Following a similar procedure near the stem–root boundary, we find that the boundary layer solution near z=z ₂ is

$$\begin{aligned} n_0^R=k_1e^{-\tilde{R}_{20}\mathit{Pe}(z-z_2)}+ \frac{F^R(1-z_2)}{\tilde{R}_{20}}, \end{aligned}$$

(57)

where $\tilde{R}_{20}=\sqrt{M^{R}} (A_{5}e^{\sqrt{M^{R}}z_{2}}-A_{6}e^{-\sqrt{M^{R}}z_{2}} )$ and k ₁ is an unknown constant. Therefore, the composite solution in root is

$$\begin{aligned} n^{R}=& \frac{F^R(1-z)}{\frac{dp^{R}}{dz}} +k_1e^{-\tilde{R}_{20}\mathit{Pe}(z-z_2)} \\ &{}+f\sqrt{\mathit{Pe}}\frac{1}{2}\, \sqrt{\frac{2\pi}{\tilde{R}_{11}}} e^{\frac{1}{2}\tilde{R}_{11}\mathit{Pe}(1-z)^2} \biggl(\mbox{erf} \biggl(\frac{1}{2}\sqrt{2\tilde{R}_{11}\mathit{Pe}}(1-z) \biggr)-1 \biggr) +O\bigl(\epsilon^{\frac{1}{2}}\bigr). \end{aligned}$$

(58)

The constant k ₁ will be determined by applying the continuity boundary conditions, but first the solutions in the stem and leaf regions have to be calculated.

3.2 C.2 Stem Zone

Since p ^S=A ₃ z+A ₄, the nutrient transport in the stem zone is governed by

$$\begin{aligned} {n}^{S}A_3 +\epsilon\frac{dn^{S}}{dz}=-F^Sz+k_2, \end{aligned}$$

(59)

where k ₂ is an unknown constant. We expand $n^{S}=n^{S}_{0}+O(\epsilon^{\frac{1}{2}})$ and seek boundary layer solutions near z=z ₁ and z=z ₂ to match with the central bulk region. We find that a boundary layer exists only near z=z ₁, such that the composite solution in the stem region is given by

$$\begin{aligned} n^{S}=\frac{-F^Sz+k_2}{A_3} +k_3e^{-A_3\mathit{Pe}(z-z_1)}+O\bigl( \epsilon^{\frac{1}{2}}\bigr), \end{aligned}$$

(60)

where k ₃ is also an unknown constant, which, together with k ₂, will be determined from the continuity boundary conditions.

3.3 C.3 Leaf Zone

The nutrient transport in the leaf zone is governed by

$$\begin{aligned} {n}^{L} \biggl(\frac{dp^{L}}{dz} \biggr) +\epsilon \frac{dn^{L}}{dz}=-F^Lz+k_4, \end{aligned}$$

(61)

where k ₄ is an unknown constant. We expand $n^{L}=n^{L}_{0}+O(\epsilon^{\frac{1}{2}})$ and seek boundary layer solutions near z=0 and z=z ₁ to match with the central bulk region. We find that a boundary layer exists only near z=0 where the boundary condition n=ϕ at z=0 has to be satisfied. We solve for this boundary layer by defining a boundary layer variable y and letting z=ϵ ^β y, such that

$$\begin{aligned} n^{L} \tilde{L}+\epsilon^{1-\beta}\frac{dn^{L}}{dy}=-F^L \epsilon^{\beta}y+k_4, \end{aligned}$$

(62)

where $\tilde{L}=\frac{dp^{L}}{dz}$ as a function of ϵ ^β y, which we expand as follows:

$$\begin{aligned} \tilde{L} =& \sqrt{M^L} \bigl(A_1\cos\bigl( \sqrt{M^L}\epsilon^{\beta}y\bigr)-A_2\sin\bigl( \sqrt{M^L}\epsilon^{\beta}y\bigr) \bigr) \\ =&\sqrt{M^L} \biggl(A_1 \biggl(1-\frac{M^L\epsilon^{2\beta}y^2}{2!}+O \bigl(\epsilon^{4\beta}\bigr) \biggr)-A_2 \bigl( \sqrt{M^L}\epsilon^{\beta}y+O\bigl(\epsilon^{3\beta} \bigr) \bigr) \biggr). \end{aligned}$$

(63)

We rewrite $\tilde{L}$ as $\tilde{L}=\tilde{L}_{1}+\epsilon^{\beta}y\tilde{L}_{2}+O(\epsilon^{2\beta})$, whose coefficients are positive and are given by

$$\begin{aligned} \tilde{L}_1=A_1\sqrt{M^L}, \qquad \tilde{L}_2=-A_2 M^L. \end{aligned}$$

(64)

We expand $n^{L}=\epsilon^{0} n_{0}^{L}+O(\epsilon^{\frac{1}{2}})$ and choose β=1, such that

$$\begin{aligned} &n^{L} \bigl( \tilde{L}_1+\epsilon y \tilde{L}_2+O\bigl(\epsilon^{2}\bigr) \bigr)+ \frac{dn^{L}}{dy}=-F^L\epsilon y+k_4, \end{aligned}$$

(65)

$$\begin{aligned} &n^{L}=\phi\quad\mbox{at}\ y=0. \end{aligned}$$

(66)

The leading order terms of Eqs. (65) and (66) are

$$\begin{aligned} &n^{L}_0\tilde{L}_1+\frac{dn^{L}_0}{dy}=k_4, \end{aligned}$$

(67)

$$\begin{aligned} &n^{L}_0=\phi\quad\mbox{at}\ y=0, \end{aligned}$$

(68)

which have the solution $n_{0}^{L}=\frac{k_{4}}{\tilde{L}_{1}}+ \bigl(\phi-\frac{k_{4}}{\tilde{L}_{1}}\bigr)e^{-\tilde{L}_{1}y}$, and which match with the bulk solution near y=0. The composite leaf solution is

$$\begin{aligned} n^{L}=\frac{-F^Lz+k_4}{\frac{dp^{L}}{dz}} + \biggl(\phi-\frac{k_4}{\tilde{L}_1}\biggr)e^{-\tilde{L}_1\mathit{Pe}\,z} +O\bigl(\epsilon^{\frac{1}{2}}\bigr). \end{aligned}$$

(69)

3.4 C.4 Applying Continuity Boundary Conditions

The solutions (58), (60), and (69) represent the leading order composite solutions of n in the root, stem and leaf zones, respectively. The unknown constants k ₁, k ₂, k ₃, and k ₄ are determined by applying the continuity boundary conditions and retaining only the leading order terms: terms up to, but not including, those at $O(\epsilon^{\frac{1}{2}})$. At leading order, the continuity of flux condition at z=z ₁ reduces to

$$\begin{aligned} &-\tilde{L}_1 \biggl(\phi-\frac{k_4}{\tilde{L}_1} \biggr)e^{-\tilde{L}_1\mathit{Pe}\,z_1}=-A_3k_3. \end{aligned}$$

(70)

Since the terms on the left-hand side are asymptotically zero, this results in k ₃=0. Similarly, the continuity of flux condition at z=z ₂ at leading order reduces to

$$\begin{aligned} -A_3k_3e^{-A_3\mathit{Pe}(z_2-z_1)} =& -\tilde{R}_{20}k_1-f+ \frac{1}{2}f \sqrt{2\pi\tilde{R}_{11}\mathit{Pe}}(1-z_2)e^{\frac{1}{2}\tilde{R}_{11} \mathit{Pe}(1-z_2)^2} \\ &{}\times \mbox{erfc} \biggl(\frac{1}{2}\sqrt{2\tilde{R}_{11}\mathit{Pe}}(1-z_2)\biggr). \end{aligned}$$

(71)

Since k ₃=0, we find that

$$\begin{aligned} k_1=\frac{f}{\tilde{R}_{20}} \biggl(\frac{\sqrt{2\pi\tilde{R}_{11}\mathit{Pe}}}{2}(1-z_2) e^{\frac{1}{2}\tilde{R}_{11}\mathit{Pe}(1-z_2)^2} \mbox{erfc} \biggl(\frac{1}{2}\sqrt{2\tilde{R}_{11}\mathit{Pe}}(1-z_2) \biggr)-1 \biggr). \end{aligned}$$

(72)

Using the asymptotic structure of erfc we find that k ₁ is also zero to leading order with a correction at O(1/Pe). Applying continuity of n at z=z ₁ and z=z ₂, we find that the remaining constants to leading order are

$$\begin{gathered} k_2=F^R(1-z_2)+F^Sz_2+A_3\chi, \qquad k_4=z_1\bigl(F^L-F^S \bigr)+k_2 \end{gathered}$$

(73)

where $\chi=-\frac{f}{2} \sqrt{\frac{2\pi Pe}{\tilde{R}_{11}}}e^{\frac{1}{2}\tilde{R}_{11}\mathit{Pe}(1-z_{2})^{2}} \mbox{erfc} (\frac{1}{2}\sqrt{2\tilde{R}_{11}\mathit{Pe}}(1-z_{2}) )$.