Upscaling of Non-isothermal Reactive Porous Media Flow with Changing Porosity

Abstract

Motivated by rock–fluid interactions occurring in a geothermal reservoir, we present a two-dimensional pore scale model of a periodic porous medium consisting of void space and grains, with fluid flow through the void space. The ions in the fluid are allowed to precipitate onto the grains, while minerals in the grains are allowed to dissolve into the fluid, and we take into account the possible change in pore geometry that these two processes cause, resulting in a problem with a free boundary at the pore scale. We include temperature dependence and possible effects of the temperature both in fluid properties and in the mineral precipitation and dissolution reactions. For the pore scale model equations, we perform a formal homogenization procedure to obtain upscaled equations. A pore scale model consisting of circular grains is presented as a special case of the porous medium.

1 Introduction

Geochemical reactions can affect the permeability in a geothermal reservoir. As the injected water and the in situ brine have different temperatures and chemical composition, reservoir rock properties can develop dynamically with time as the fluids flow through the reservoir. Mineral dissolving and precipitating onto the reservoir matrix can change the porosity and hence the permeability of the system. As mineral solubility is affected by the cooling of the rock and by the different ion content in the saturating fluids, large changes in permeability can occur. The interaction between altering temperature, solute transport with mineral dissolution and precipitation and fluid flow is highly coupled and challenging to model appropriately as the relevant physical processes jointly affect each other (Bringedal et al. 2014). The effect of changing porosity and hence permeability through the production period may have severe impact on operating conditions.

The ion content of the injected cold water is normally different than the original groundwater, affecting the equilibrium state of the system. Also, as the solubility of minerals generally depends on temperature, the cooling itself will affect the equilibrium state. As reported from field studies and simulations, porosity and permeability changes due to precipitation and dissolution of minerals as silica, quartz, anhydrite, gypsum and calcite can be observed (McLin et al. 2006; Mroczek et al. 2000; Pape et al. 2005; Sonnenthal et al. 2005; Wagner et al. 2005; White and Mroczek 1998). Modeling of the mineral precipitation and dissolution is important in order to understand the processes and to better estimate to which extent the chemical reactions can affect the permeability of the porous medium.

When investigating porosity and permeability changes, it is important to understand the underlying processes at the pore scale. The pore geometry affects the reaction rates as the reactive surface is changed, and the permeability is depending on how the geometry changes. To achieve equations that quantify how the reaction rates and permeability depend on the pore scale effects, we start with a pore scale model and derive the Darcy scale model by homogenization. Pore scale models incorporating mineral precipitation and dissolution have been studied earlier in (van Duijn and Pop 2004; van Noorden et al. 2007), and the corresponding Darcy scale models have been investigated further in (van Duijn and Knabner 1997; Knabner et al. 1995). These papers assume that the pore geometry is not changed by the chemical reactions, which is a valid assumption when the deposited or dissolved mineral layer is thin compared to the pore aperture. Investigations honoring the porosity changes may be found in (Kumar et al. 2011; van Noorden 2009a, b), where mineral precipitation and dissolution have been considered on either circular grains or in a thin strip. In these papers, the position of the interface between grain and void space is tracked, giving a problem with a free boundary. Similar models can also be obtained for biofilm growth (van Noorden et al. 2010), for drug release from collagen matrices (Ray et al. 2013), and on an evolving microstructure (Peter 2009). These models do not include any temperature dependence.

The present work builds on (Bringedal et al. 2015), where mineral precipitation and dissolution are considered in a thin strip. There, the freely moving interface between the mineral layer and the void space is modeled as an unknown function depending on time and the location along the pore axis. Here we extend the results to a more general geometry with many solid grains periodically distributed in the medium. The geometry is as considered by van Noorden (2009a), but as we include temperature effects in fluid flow and chemical reactions, the resulting model is much more complex. Including temperature effects requires two new model equations at the pore scale: energy conservation in void space and in the grain space. The coupling between these two equations raises several issues in the upscaling process that are to be elaborated on. For geothermal systems, the temperature dependence is essential. We assume there is no phase change, but mention that Duval et al. (2004) upscale two-phase flow with phase change using volume averaging. Recently, Radu et al. (2013) proposed a mass conservative mixed finite element scheme for reactive transport with varying porosity for saturated/unsaturated porous media. Other applications of non-isothermal reactive transport models can be combustion models, and we refer to Lu and Yortsos (2005) who consider a pore-network model including filtration combustion.

The structure of this paper is as follows. In Sect. 2, we describe the pore scale model, while in Sect. 3, we perform formal homogenization on the model equations and obtain upscaled equations. The paper ends with a summary with some comments on applications and a presentation of a special case of the model equations in Sect. 4, together with some concluding remarks.

2 Pore Scale Model

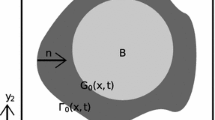
We consider a two-dimensional domain $\varOmega$ with boundary $\varGamma$. The domain is inside a square $x=(x_1,x_2)\in (0,L)^2$ for some positive number L. The domain is perforated, consisting of a connected pore space $\varOmega ^{\epsilon }(t)$ and grain space $G^{\epsilon }(t)$, and the boundary between them $\varGamma ^{\epsilon }(t)$. As we have two length scales, the domain size L and the typical pore size l, we use the superscript $\epsilon =l/L$ to emphasize dependency on both length scales. The grain space consists of some non-reactive solid surrounded by minerals. These minerals are the result of a precipitation process and may dissolve. The pore and grain space are given in a periodic manner, where the grains are assumed not to touch each other, see Fig. 1. The grains are assumed not to touch each other to simplify the upscaling as less precautionary steps are then needed, but also to avoid clogging.

Fig. 1

Model of perforated porous medium. Typical length sizes L and l are indicated

Figure 2 shows the zoomed-in pore structure. We consider a square Y having local variables $y=(y_1,y_2)\in (0,l)^2$, where l is much smaller than L. The region Y consists of grain space $G_{ij}(t)$, void space $\varOmega _{ij}(t)$ and the moving boundary between them $\varGamma _{ij}(t)$, where the outward unit normal of the void space is denoted ${\mathbf {n}}^{\epsilon }$. The indices i, j denote which subdomain in the total domain $\varOmega$ we consider, and the set of indices $\{i,j\}$ is such that the whole domain is covered. As the subdomains Y are given in a periodic manner, we have periodicity in the variable y. The microscopic variable y and macroscopic variable x are related through $x=(\epsilon i,\epsilon j)+\epsilon y$.

Fig. 2

Local model of pore

This way, $\varOmega ^{\epsilon }(t) = \cup \varOmega _{ij}(t)$, $G^{\epsilon }(t)=\cup G_{ij}(t)$ and $\varGamma ^{\epsilon }(t)=\cup \varGamma _{ij}(t)$. Note that $\varGamma \cap \varGamma ^{\epsilon }(t) = \emptyset$. Further, the total domain is $\varOmega =\varOmega ^{\epsilon }(t)\cup \varGamma ^{\epsilon }(t)\cup G^{\epsilon }(t)$. We use the level set function $S^{\epsilon }(x,t)$ to describe the position of the interface $\varGamma _{ij}(t)$ and is given as

$$\begin{aligned} S^{\epsilon }(x,t) = {\left\{ \begin{array}{ll} <0 &{} \text { if } x \in \varOmega ^{\epsilon }(t), \\ 0 &{} \text { if } x \in \varGamma ^{\epsilon }(t), \\ >0 &{} \text { if } x \in G^{\epsilon }(t). \end{array}\right. } \end{aligned}$$

This choice of $S^{\epsilon }(x,t)$ assures that the gradient of $S^{\epsilon }$ points into the grain space and is parallel to ${\mathbf {n}}^{\epsilon }$, hence

$$\begin{aligned} {\mathbf {n}}^{\epsilon } = \frac{\nabla S^{\epsilon }}{|\nabla S^{\epsilon }|}, \end{aligned}$$

where the notation $|\cdot |$ means the length when applied to a vector and the size when applied to a set. The level set function tracks the position of the interface, hence also the size and geometry of void and grain space as time evolves. As will result from below, the evolution of $S^{\epsilon }$ depends on unknowns of the model, leading to a porous medium where the size and geometry of the void space are in evolution. In particular, this evolution leads to a non-periodic structure, although the grains are assumed periodically distributed.

The boundary $\varGamma _{ij}(t)$ moves with some normal velocity $v_n$ due to the mineral precipitation and dissolution. The Rankine–Hugoniot condition guarantees conservation of quantities across a moving boundary (Fasano 2005):

$$\begin{aligned} {\mathbf {n}}^{\epsilon }\cdot [{\mathbf {j}}] = v_n[u], \end{aligned}$$

(1)

where u is the preserved quantity (e.g., mass or energy) and ${\mathbf {j}}$ is the flux of this quantity. The use of square brackets means the jump of the quantities and is the difference between the quantities at each side of the interface. The condition states that the net loss (or gain) rate of the preserved quantity u equals the difference in fluxes transporting u across the interface (Fasano 2005).

We apply the level set equation together with conservation of ions, mass, momentum and energy to form a complete set of equations at the pore scale and refer readers to, e.g., Patankar (1980) for justification of the conservation equations and to (Osher and Fedkiw 2003) for a detailed treatment of the level set equation. We prescribe boundary conditions at the internal boundary $\varGamma ^{\epsilon }(t)$. For a complete model to be used for computer simulations, boundary conditions at the external boundary $\varGamma$ are required, as well as initial conditions, but as these are not necessary for the upscaling process, they will not be specified. The model equations are briefly presented in this paper, and we refer to (Bringedal et al. 2015) for more details on the model.

2.1 Interface Evolution and the Level Set Equation

As discussed, the medium is covered by translations of a square as presented in Fig. 2, with periodicity across the external boundary $\partial Y$. The solid part $G_{ij}(t)$ consists of a non-reactive part denoted $B_{ij}$ located in the center of the square and is surrounded by a mineral part that can dissolve and precipitate. A mineral molecule consists of two ions $u_1$ and $u_2$. We assume for simplicity that $u_1$ and $u_2$ have the same initial and boundary conditions and will hence be equal. We denote their concentration with u in the following. The interface $\varGamma _{ij}(t)$ moves as mineral molecules dissolve or precipitate, and the normal velocity is proportional to the difference between the reaction rates (Knabner et al. 1995; van Noorden 2009b):

$$\begin{aligned} \rho _Cv_n = -(f_p-f_d) \text { on } \varGamma ^{\epsilon }(t), \end{aligned}$$

(2)

where $\rho _C$ is the molar density of the mineral and is assumed constant, and $f_p$ and $f_d$ are the precipitation and dissolution rates of the chemical reaction, respectively. The rates are (Chang and Goldsby 2014; van Noorden 2009a)

$$\begin{aligned} f_p(T_f,u)= k_0e^{-\frac{E}{RT_f}}\frac{u^2}{K_m(T_f)} \text { and } f_d(T_f,u,x) = k_0e^{-\frac{E}{RT_f}}w(\hbox {dist}(x,B^{\epsilon }),T_f,u), \end{aligned}$$

where $k_0$ is a positive rate constant, E is the activation energy, R is the gas constant, $T_f$ is the fluid temperature, and $K_m(T_f)$ is the equilibrium constant for the mineral. Dissolution takes place as long as there are minerals present: The union of the non-reactive solid parts is denoted $B^{\epsilon }=\cup B_{ij}$. Hence, $\hbox {dist}(x,B^{\epsilon })$ is the distance from the present point to the non-reactive solid and can be thought of as the thickness of the mineral part. The function $w(\hbox {dist}(x,B^{\epsilon }),T_f,u)$ ensures that the dissolution rate cannot exceed the precipitation rate when there are no minerals left, and is given by

$$\begin{aligned} w(\hbox {dist}(x,B^{\epsilon }),T_f,u) = {\left\{ \begin{array}{ll} 0 &{} \text {if } \hbox {dist}(x,B^{\epsilon })<0, \\ \min \left( \frac{ u^2}{K_m(T_f)},1\right) &{} \text {if } \hbox {dist}(x,B^{\epsilon })=0 ,\\ 1 &{} \text {if } \hbox {dist}(x,B^{\epsilon })>0. \end{array}\right. } \end{aligned}$$

(3)

We will denote $f=f_p-f_d$ as the net rate for increasing mineral width. This particular choice of reaction rates is inspired from (van Duijn and Pop 2004; Knabner et al. 1995; van Noorden 2009a, b), where the isothermal case is considered. Other rates can be adapted straightforwardly. Note that the reaction kinetics are assumed to be slow, as fast kinetics will require other considerations in the upscaling process; see, e.g., Kechagia et al. (2002) which shows a case where upscaling brakes down. We refer to (Mikelic et al. 2006) for upscaling of reactive flow through a thin strip for dominant Damköhler number.

The evolution of the pore structure is described by the level set equation:

$$\begin{aligned} \frac{D}{Dt}S^{\epsilon }(x,t) = \partial _t S^{\epsilon } + v_n{\mathbf {n}}^{\epsilon }\cdot \nabla S^{\epsilon } = \partial _tS^{\epsilon }+v_n|\nabla S^{\epsilon }| = 0. \end{aligned}$$

Combining the above equation with (2), we get

$$\begin{aligned} \partial _tS^{\epsilon } = \frac{f}{\rho _C}|\nabla S^{\epsilon }| \text { for } x\in \varOmega . \end{aligned}$$

(4)

Note that the level set equation and the level set function are defined in the entire domain $\varOmega$. This is handled by defining a continuous extension of the reaction rates to $\varOmega$.

2.2 Conservation of Ions

There are two active ions in the fluid, both having molar concentration u. They satisfy the convection–diffusion in the void space:

$$\begin{aligned} \partial _t u = \nabla \cdot (D\nabla u - {\mathbf {q}} u) \text { for } x\in \varOmega ^{\epsilon }(t). \end{aligned}$$

(5)

In the above equation, D is the diffusion coefficient which we assume to be constant, and ${\mathbf {q}}$ is the fluid velocity. The Rankine–Hugoniot condition (1) for conserving ions across the moving interface is

$$\begin{aligned} {\mathbf {n}}^{\epsilon }\cdot (D\nabla u - {\mathbf {q}} u) = v_n(\rho _C-u) \text { on } \varGamma ^{\epsilon }(t). \end{aligned}$$

(6)

As the minerals have zero flux, only the ion flux appears on the left-hand side. The difference on the right-hand side is the jump of the conserved quantity u. A mineral molecule consists of one of each type of the two ions; hence, the difference $(\rho _C-u)$ represents the jump across the interface for each of the ions.

2.3 Conservation of Mass

As the fluid consists mainly of water, the fluid molar density $\rho _f$ is assumed to not be affected by the chemical reactions, but depends on temperature. Hence, the mass conservation equation is

$$\begin{aligned} \partial _t\rho _f + \nabla \cdot (\rho _f{\mathbf {q}}) =0 \text { for } x\in \varOmega ^{\epsilon }(t). \end{aligned}$$

(7)

As we include the temperature effects on fluid density, density differences are accounted for and we cannot use the incompressible mass conservation equation as in van Noorden (2009a). At the boundary, ions can leave the fluid and become part of the grain space instead. The Rankine–Hugoniot boundary condition applied to mass is

$$\begin{aligned} {\mathbf {n}}^{\epsilon }\cdot (-\rho _f{\mathbf {q}}) = v_n(2\rho _C-\rho _f) \text { on } \varGamma ^{\epsilon }(t). \end{aligned}$$

(8)

The difference on the right-hand side is the jump of the mass across the moving boundary. As a mineral molecule consists of the mass from two ions, the molar density $\rho _C$ is multiplied with the factor 2.

2.4 Conservation of Momentum

We assume the fluid is Newtonian, that the stress tensor is a linear function of the strain rates, that the fluid is isotropic, and that the body forces are such that the fluid is at rest at hydrostatic pressure. Hence,

$$\begin{aligned} \partial _t(\rho _f{\mathbf {q}}) +\nabla \cdot (\rho _f\mathbf {qq}) =&-\nabla p + \nabla \cdot \left( \mu (\nabla {\mathbf {q}}+(\nabla {\mathbf {q}})^T)\right) \nonumber \\&-\frac{2}{3}\nabla (\mu \nabla \cdot {\mathbf {q}}) \text { for } x\in \varOmega ^{\epsilon }(t), \end{aligned}$$

(9)

where p is pressure and $\mu$ is viscosity of the fluid. No-penetration conditions are assumed at the boundary, meaning that ${\mathbf {q}}$ has no tangential component at the interface, but is parallel to the normal vector ${\mathbf {n}}^{\epsilon }$. Combining with Eq. (8), the new boundary condition becomes

$$\begin{aligned} {\mathbf {q}} = \frac{\rho _f-2\rho _C}{\rho _f}v_n{\mathbf {n}}^{\epsilon } \text { on } \varGamma ^{\epsilon }(t). \end{aligned}$$

(10)

2.5 Conservation of Energy

We distinguish between two temperatures, the fluid temperature $T_f$ and grain temperature $T_g$. We assume no viscous dissipation; hence, energy transfer in the fluid phase can happen through diffusion and convection:

$$\begin{aligned} \partial _t(\rho _fc_fT_f) = \nabla \cdot (k_f\nabla T_f-\rho _fc_f{\mathbf {q}} T_f) \text { in } \varOmega ^{\epsilon }(t). \end{aligned}$$

(11)

In the grain space, flow is not possible, hence

$$\begin{aligned} \partial _t(\rho _C c_gT_g)=\nabla \cdot (k_g\nabla T_g) \text { in } G^{\epsilon }(t). \end{aligned}$$

(12)

In the above equations, $c_f$ and $c_g$ are specific heats, and $k_f$ and $k_g$ are heat conductivities, of fluid and mineral, respectively, and are all assumed constant. The Rankine–Hugoniot condition for conservation of energy across the moving interface is

$$\begin{aligned} {\mathbf {n}}^{\epsilon } \cdot (k_f\nabla T_f-\rho _fc_f{\mathbf {q}}T_f - k_g\nabla T_g) = v_n(\rho _Cc_gT_g-\rho _fc_fT_f) \text { on } \varGamma ^{\epsilon }(t), \end{aligned}$$

(13)

and we also assume temperature continuity at the interface:

$$\begin{aligned} T_g=T_f \text { on } \varGamma ^{\epsilon }(t). \end{aligned}$$

(14)

The temperature continuity condition comes from the assumption of local thermodynamic equilibrium, and this second boundary condition at $\varGamma ^{\epsilon }(t)$ is needed to link the two energy conservation equations properly.

2.6 Non-dimensional Model Equations

To achieve non-dimensional quantities, we introduce $t_\mathrm{ref}$, $x_\mathrm{ref}=L$, $u_\mathrm{ref}$, $q_\mathrm{ref}=L/t_\mathrm{ref}$, $p_\mathrm{ref}=L^4u_\mathrm{ref}/t_\mathrm{ref}^2l^2$, $\mu _\mathrm{ref}=l^2p_\mathrm{ref}t_\mathrm{ref}/L^2$, $T_\mathrm{ref}$ and let $\epsilon =l/L$. Non-dimensional variables and quantities are denoted with a hat and are defined as

$$\begin{aligned} \hat{t}&=t/t_\mathrm{ref},&\hat{x}&=x/L,&\hat{y}&=y/l,&\hat{u}^{\epsilon }&= u/u_\mathrm{ref}, \\ \hat{{\mathbf {q}}}^{\epsilon }&={\mathbf {q}}/q_\mathrm{ref},&\hat{p}^{\epsilon }&=p/p_\mathrm{ref},&\hat{\rho }_f&=\rho _f/u_\mathrm{ref},&\hat{\rho }&=\rho _C/u_\mathrm{ref}, \\ \hat{k}&=k_0t_\mathrm{ref}/u_\mathrm{ref}l,&\hat{D}&=Dt_\mathrm{ref}/L^2,&\hat{\mu }&=\mu /\mu _\mathrm{ref},&\hat{T}^{\epsilon }&=T/T_\mathrm{ref}. \end{aligned}$$

We emphasize dependence on the small variable $\epsilon$ by denoting our main variables with $\epsilon$ as a superscript. Observe that the dimensionless viscosity scales with $\epsilon ^2$, which is a natural assumption leading to non-trivial upscaled flows. Since we will only use non-dimensional variables in the following, we skip the hat. Due to the scaling of y, the local square Y is now a unit square.

The non-dimensional level set Eq. (4) becomes

$$\begin{aligned} \partial _t S^{\epsilon }=\epsilon \frac{f}{\rho }|\nabla S^{\epsilon }| \text { for } x\in \varOmega , \end{aligned}$$

(15)

The non-dimensional reaction rates are

$$\begin{aligned} f(T_f^{\epsilon },u^{\epsilon },x) = ke^{-\alpha /T_f^{\epsilon }}\left( \frac{(u^{\epsilon })^2}{K_m(T_f^{\epsilon })}-w^{\epsilon }(\hbox {dist} (x,B^{\epsilon }),T_f^{\epsilon },u^{\epsilon })\right) , \end{aligned}$$

(16)

where $\alpha =E/RT_\mathrm{ref}$ and where $K_m(T_f^{\epsilon })$ is non-dimensional as it has been scaled with $u_\mathrm{ref}^2$. The Damköhler number k is assumed to be independent of $\epsilon$, which means that the reaction rates are at the same timescale as the convective timescale. This assumption is applicable for most rock–fluid interactions as this branch of chemical reactions is known to be slow (Bundschuh and Zilberbrand 2011). Including fast kinetics would require extra care, as discussed by Kechagia et al. (2002), Mikelic et al. (2006).

The convection–diffusion Eq. (5) becomes

$$\begin{aligned} \partial _tu^{\epsilon }=\nabla \cdot (D\nabla u^{\epsilon }-{\mathbf {q}}^{\epsilon }u^{\epsilon }) \text { in } \varOmega ^{\epsilon }(t), \end{aligned}$$

(17)

with the boundary condition (6) now written as

$$\begin{aligned} {\mathbf {n}}^{\epsilon }\cdot (D\nabla u^{\epsilon }-{\mathbf {q}}^{\epsilon } u^{\epsilon })= -\epsilon \frac{\rho -u^{\epsilon }}{\rho }f\text { on } \varGamma ^{\epsilon }(t), \end{aligned}$$

(18)

when (2) is inserted. Note that an underlying assumption is that the dimensionless diffusion coefficient D is not depending on $\epsilon$; hence, diffusion and convection occur at the same timescale, which is a valid assumption in the context of geothermal energy production when the injection rate is not too large.

The mass conservation Eq. (7) transforms into

$$\begin{aligned} \partial _t\rho _f+\nabla \cdot (\rho _f{\mathbf {q}}^{\epsilon })=0 \text { in } \varOmega ^{\epsilon }(t). \end{aligned}$$

(19)

The corresponding Rankine–Hugoniot boundary Eq. (8) has the dimensionless form

$$\begin{aligned} \rho _f{\mathbf {q}}^{\epsilon }\cdot {\mathbf {n}}^{\epsilon }=-\epsilon \frac{\rho _f-2\rho }{\rho }f \text { on } \varGamma ^{\epsilon }(t). \end{aligned}$$

(20)

The momentum balance Eq. (9) becomes

$$\begin{aligned}&\epsilon ^2\bigg (\partial _t(\rho _f{\mathbf {q}}^{\epsilon })+\nabla \cdot (\rho _f\mathbf {q^{\epsilon }q^{\epsilon }})\bigg ) \nonumber \\&\quad =-\nabla p^{\epsilon }+\epsilon ^2\bigg (\nabla \cdot \Big (\mu (\nabla {\mathbf {q}}^{\epsilon }+(\nabla {\mathbf {q}}^{\epsilon })^T)\Big )-\frac{2}{3}\nabla (\mu \nabla \cdot {\mathbf {q}}^{\epsilon })\bigg ) \text { in } \varOmega ^{\epsilon }(t), \end{aligned}$$

(21)

while the boundary condition (10) is

$$\begin{aligned} \rho _f{\mathbf {q}}^{\epsilon }=-\epsilon \frac{\rho _f-2\rho }{\rho }f{\mathbf {n}}^{\epsilon } \text { on } \varGamma ^{\epsilon }(t). \end{aligned}$$

(22)

The non-dimensional form of the energy conservation Eqs. (11) and (12) is

$$\begin{aligned} \partial _t(\rho _fT_f^{\epsilon })+\nabla \cdot (\rho _f{\mathbf {q}}^{\epsilon }T_f^{\epsilon })=\kappa _f\nabla ^2T_f^{\epsilon } \text { in } \varOmega ^{\epsilon }(t) \end{aligned}$$

(23)

and

$$\begin{aligned} \partial _t(\varsigma \rho T_g^{\epsilon })=\kappa _g\nabla ^2T_g^{\epsilon } \text { in } G^{\epsilon }(t), \end{aligned}$$

(24)

where $\kappa _f = k_ft_\mathrm{ref}/L^2u_\mathrm{ref}c_f$, $\kappa _g = k_gt_\mathrm{ref}/L^2u_\mathrm{ref}c_f$ and $\varsigma = c_g/c_f$ . These three constants are all assumed to not depend on $\epsilon$, but are of order 1. Hence, heat diffusion in grain and fluid space is at the same timescale as the convective timescale, which is a valid assumption when the injection rate is not too large. The boundary condition (13) is written

$$\begin{aligned} {\mathbf {n}}^{\epsilon }\cdot (\kappa _f\nabla T_f^{\epsilon }&-\rho _f{\mathbf {q}}^{\epsilon }T_f^{\epsilon }-\kappa _g\nabla T_g^{\epsilon }) = -\epsilon \frac{\varsigma \rho T_g^{\epsilon }-\rho _fT_f^{\epsilon }}{\rho }f \text { on } \varGamma ^{\epsilon }(t), \end{aligned}$$

(25)

and the continuity condition (14) is

$$\begin{aligned} T_g^{\epsilon }=T_f^{\epsilon } \text { on } \varGamma ^{\epsilon }(t). \end{aligned}$$

(26)

The fluid density and viscosity are assumed to depend linearly on the fluid temperature $T_f^{\epsilon }$, hence

$$\begin{aligned} \rho _f(T_f^{\epsilon })=\rho _0 - \beta _{\rho _f}T_f^{\epsilon } \end{aligned}$$

(27)

and

$$\begin{aligned} \mu (T_f^{\epsilon })=\mu _0-\beta _{\mu }T_f^{\epsilon }, \end{aligned}$$

(28)

for some positive constants $\beta _{\rho _f}$ and $\beta _{\mu }$. The assumption of linear relationship is a common simplification, but using other continuous relationships between density/viscosity and temperature is straightforward.

3 Asymptotic Expansions

We incorporate explicit dependence of the microscopic variable $y=(y_1,y_2)$ into the main variables by introducing the asymptotic expansions

$$\begin{aligned} S^{\epsilon }(x,t) = S_0(x,y,t)+\epsilon S_1(x,y,t) + \epsilon ^2S_2(x,y,t) + \cdots \end{aligned}$$

and similarly for the other unknowns. Due to periodicity, all the functions $S_i$ are periodic in y. The separation between x and y enables to capture both slow, macroscopic variations (variations in x) and fast, microscopic variations (variations in y).

3.1 Preliminaries

Due to the relation between x and y, the gradient of a function $f(x,\frac{x}{\epsilon })$ is

$$\begin{aligned} \nabla f = \nabla _x f + \frac{1}{\epsilon }\nabla _y f. \end{aligned}$$

Since ${\mathbf {n}}^{\epsilon }=\nabla S^{\epsilon }/|\nabla S^{\epsilon }|$, we assume ${\mathbf {n}}^{\epsilon }={\mathbf {n}}_0+\epsilon {\mathbf {n}}_1+O(\epsilon ^2)$ and find the expressions for ${\mathbf {n}}_0$ and ${\mathbf {n}}_1$ by inserting the expansion for $S^{\epsilon }$:

$$\begin{aligned} {\mathbf {n}}^{\epsilon }&= \frac{(\nabla _x+\frac{1}{\epsilon }\nabla _y)(S_0+\epsilon S_1)+O(\epsilon )}{|(\nabla _x+\frac{1}{\epsilon }\nabla _y)(S_0+\epsilon S_1)+O(\epsilon )|} \\&=\frac{\frac{1}{\epsilon }\nabla _y S_0 +(\nabla _x S_0+\nabla _y S_1)+O(\epsilon )}{\frac{1}{\epsilon }|\nabla _y S_0|\sqrt{1+2\epsilon \nabla _yS_0\cdot (\nabla _xS_0+\nabla _yS_1)/|\nabla _yS_0|^2+O(\epsilon ^2)}} \\&=\frac{\frac{1}{\epsilon }\nabla _yS_0+(\nabla _xS_0+\nabla _yS_1)+O(\epsilon )}{\frac{1}{\epsilon }|\nabla _yS_0|} \left( 1-\epsilon \frac{\nabla _yS_0\cdot (\nabla _xS_0+\nabla _yS_1)}{|\nabla _yS_0|^2}+O(\epsilon ^2)\right) \\&=\frac{\nabla _yS_0}{|\nabla _yS_0|} +\epsilon \left( \frac{\nabla _xS_0+\nabla _yS_1}{|\nabla _yS_0|} -\frac{\nabla _yS_0}{|\nabla _yS_0|} \frac{\nabla _yS_0\cdot (\nabla _xS_0+\nabla _yS_1)}{|\nabla _yS_0|^2}\right) +O(\epsilon ^2). \end{aligned}$$

Above we used the Taylor expansion for the expression in the square root. This means,

$$\begin{aligned} {\mathbf {n}}_0 = \frac{\nabla _yS_0}{|\nabla _yS_0|} \text { and } {\mathbf {n}}_1=\frac{\nabla _xS_0+\nabla _yS_1}{|\nabla _yS_0|}-\frac{\nabla _yS_0}{|\nabla _yS_0|}\frac{\nabla _yS_0\cdot (\nabla _xS_0+\nabla _yS_1)}{|\nabla _yS_0|^2}. \end{aligned}$$

By introducing $\mathbf \tau _0$, the unit vector that is orthogonal to ${\mathbf {n}}_0$, we can write ${\mathbf {n}}_1$ as

$$\begin{aligned} {\mathbf {n}}_1 = \mathbf \tau _0\frac{\tau _0\cdot (\nabla _xS_0+\nabla _yS_1)}{|\nabla _yS_0|}. \end{aligned}$$

In the upscaling process, we need to be able to formulate boundary conditions at the zero level of the moving boundary; that is, for those values of y such that $S_0(x,y,t)=0$. The boundary conditions in the previous section are formulated at $\varGamma ^{\epsilon }(t)$, i.e., at every x where $S^{\epsilon }(x,t)=0$. To overcome this challenge, we need to assume the existence of a parameterization of $\varGamma _{ij}^{\epsilon }(t)$ and that $S_0(x,y,t)$ and $S_1(x,y,t)$ have Taylor expansions, which also means assuming the boundary to have some regularity. These assumptions are necessary to perform the upscaling procedure, but excludes some pore geometries. At the boundary $\varGamma _{ij}^{\epsilon }(t)$, the level set function $S^{\epsilon }$ is zero, so we assume there exists a parameterization $k^{\epsilon }(s,t)$ such that

$$\begin{aligned} S^{\epsilon }(k^{\epsilon }(s,t),t)=0. \end{aligned}$$

We further assume that $k^{\epsilon }(s,t)$ has the asymptotic expansion

$$\begin{aligned} k^{\epsilon }(s,t)=x+\epsilon k_0(s,t)+\epsilon ^2 k_1(s,t)+O(\epsilon ^3), \end{aligned}$$

where $x=(\epsilon i,\epsilon j)$. Using the asymptotic expansion for $S^{\epsilon }$, the periodicity of $S_i$ in y, and the Taylor expansions for $S_0$ and $S_1$ around $(x,y)=(x,k_0)$, we obtain

$$\begin{aligned} 0&=S^{\epsilon }(k^{\epsilon }(s,t),y)\\&=S_0(x,k_0,t)+\nabla _xS_0\cdot (\epsilon k_0+\epsilon ^2k_1)+\nabla _yS_0\cdot (\epsilon k_1+\epsilon ^2k_2)\\&\quad \ + \frac{1}{2}(\epsilon k_0,\epsilon k_1)\cdot D_{\xi }^2S_0\cdot (\epsilon k_0,\epsilon k_1) \\&\quad \ +\epsilon \left( S_1(x,k_0,t)+\nabla _xS_1\cdot \epsilon k_0+\nabla _yS_1\cdot \epsilon k_1\right) + \epsilon ^2S_2(x,k_0,t) + O(\epsilon ^3) , \end{aligned}$$

where $D_{\xi }^2$ is the second-order differentiation matrix with respect to x and y and all derivatives are evaluated in $(x,k_0)$. Collecting lowest order terms yields

$$\begin{aligned} S_0(x,k_0,t) = 0, \end{aligned}$$

meaning that $k_0$ parameterizes locally the zero level set of $S_0$. Second lowest order terms are

$$\begin{aligned} S_1(x,k_0,t)+k_0\cdot \nabla _xS_0+k_1\cdot \nabla _yS_0=0. \end{aligned}$$

We search for a $k_1$ that is aligned with ${\mathbf {n}}_0$; hence, $k_1=\lambda _1{\mathbf {n}}_0$, where $\lambda _1=-\frac{1}{|\nabla _yS_0|}(S_1+k_0\cdot \nabla _xS_0)$. Third lowest order terms are

$$\begin{aligned}&S_2(x,k_0,t) +k_0\cdot \nabla _xS_1+k_1\cdot \nabla _yS_1\\&\quad +\frac{1}{2}(k_0,k_1)\cdot D_{\xi }^2S_0\cdot (k_0,k_1)+k_1\cdot \nabla _xS_0+k_2\cdot \nabla _yS_0=0, \end{aligned}$$

resulting in $k_2$ being $k_2=\lambda _2{\mathbf {n}}_0$, where $\lambda _2=-\frac{1}{|\nabla _yS_0|}(S_2+k_0\cdot \nabla _xS_1+k_1\cdot \nabla _yS_1+\frac{1}{2}(k_0,k_1)\cdot D_{\xi }^2S_0\cdot (k_0,k_1)+k_1\cdot \nabla _xS_0)$.

We convert the boundary conditions given for $x\in \varGamma ^{\epsilon }(t)$ such that these are given at $y\in \varGamma _0(x,t)$ where $\varGamma _0(x,t) = \{y\ | \ S_0(x,y,t) = 0\}$, and which is parameterized by $y=k_0(s,t)$. Assuming the boundary condition is given as

$$\begin{aligned} K(x,x/\epsilon ,t)=0 \text { for } x\in \varGamma ^{\epsilon }(t), \end{aligned}$$

we use that $x=k^{\epsilon }(s,t)$ at $\varGamma ^{\epsilon }(t)$ and then expand K(x, y, t) around $(x,k_0)$:

$$\begin{aligned} 0&=K(x,k_0,t)+\epsilon (k_0\cdot \nabla _xK+\lambda _1{\mathbf {n}}_0\cdot \nabla _yK)\nonumber \\&\quad \ +\epsilon ^2(\lambda _1{\mathbf {n}}_0\cdot \nabla _xK+\lambda _2{\mathbf {n}}_0\cdot \nabla _yK+\frac{1}{2}(k_0,\lambda _1{\mathbf {n}}_0)\cdot D_{\xi }^2K\cdot (k_0,\lambda _1{\mathbf {n}}_0))\nonumber \\&\quad \ +O(\epsilon ^3) \text { for } y\in \varGamma _0(x,t), \end{aligned}$$

(29)

where we have inserted $k_1$ and $k_2$ when applicable.

We use the two following results proved in (van Noorden 2009a).

Lemma 1

(Lemma 3.1 van Noorden 2009a) Let g(x, y, t) be a scalar function such that $g(x,y,t)=0$ for $y\in \varGamma _0(x,t)$, then it holds that

$$\begin{aligned} \nabla _xg=\frac{{\mathbf {n}}_0\cdot \nabla _yg}{|\nabla _yS_0|}\nabla _xS_0 \text { for } y\in \varGamma _0(x,t). \end{aligned}$$

Lemma 2

(Lemma 3.2 van Noorden 2009a) Let F(x, y, t) be a vector-valued function such that $\nabla _y\cdot F=0$ in $Y_0(x,t)=\{y\ |\ S_0(x,y,t)<0\}$ and ${\mathbf {n}}_0\cdot F=0$ on $\varGamma _0(x,t)$. Then

$$\begin{aligned} \int _{\varGamma _0(x,t)}\left( \frac{\tau _0\cdot \nabla _yS_1}{|\nabla _yS_0|}\tau _0\cdot F-\frac{S_1}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}} _0\cdot F)\right) \hbox {d}\sigma =0. \end{aligned}$$

A result similar to Lemma 2 will be used for the energy equations. As only model equations in the void space are included in (van Noorden 2009a), the following result, considering coupled model equations in the void space and grain space, is developed and proved:

Lemma 3

Let $F_Y(x,y,t)$ and $F_G(x,y,t)$ be vector-valued functions such that $\nabla _y\cdot F_Y=0$ in $Y_0(x,t)$ and $\nabla _y\cdot F_G=0$ in $G_0(x,t)=\{y \ | \ S_0(x,y,t) > 0\}$, and suppose that ${\mathbf {n}}_0\cdot (F_Y-F_G)=0$ on $\varGamma _0(x,t)$. Then

$$\begin{aligned} \int _{\varGamma _0(x,t)}\left( \frac{\tau _0\cdot \nabla _y S_1}{|\nabla _y S_0|}\tau _0\cdot (F_Y-F_G) - \frac{S_1}{|\nabla _y S_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0 \cdot (F_Y-F_G))\right) \hbox {d}\sigma = 0. \end{aligned}$$

Proof

The proof is quite similar to the proof of Lemma 3.2 in (van Noorden 2009a), but requires some extra care on how the grain space is treated. We split $S_1$ into its positive and negative parts and focus on the positive part denoted $[S_1]_+$. We define $Y^{\delta }_+(x,t)=\{y \ | \ S_0+\delta [S_1]_+ <0\}$ and $G^{\delta }_+(x,t)=\{y \ | \ S_0-\delta [S_1]_+>0\}$ for some nonnegative number $\delta$. We use opposite sign for the $S_1$ term to assure that $G^{\delta }_+(x,t)$ is included in $G_0(x.t)$. Note that the boundaries of $Y^{\delta }_+(x,t)$ and $G^{\delta }_+(x,t)$, denoted by $\varGamma ^{\delta +}_Y(x,t)$ and $\varGamma ^{\delta +}_G(x,t)$, are not the same. These boundaries are, however, equal for $\delta =0$ as they both reduce to $\varGamma _0(x,t)$. We parameterize the two boundaries with $k^+_Y(s,\delta )$ and $k^+_G(s,\delta )$ such that $S_0(x,k^+_Y,t)+\delta [S_1]_+(x,k^+_Y,t)=0$ and $S_0(x,k^+_G,t)-\delta [S_1]_+(x,k^+_G,t)=0$ for $0\le s\le 1$. By differentiating these two equations with respect to $\delta$ using the chain rule and product rule, and then evaluating the resulting equations at $\delta =0$, we obtain

$$\begin{aligned} \nabla _yS_0\cdot \partial _{\delta }k^+_Y|_{\delta =0}&=-[S_1]_+|_{\delta =0}, \text { for } y\in \varGamma _0(x,t),\\ \nabla _yS_0\cdot \partial _{\delta }k^+_G|_{\delta =0}&= [S_1]_+|_{\delta =0} \text { for } y\in \varGamma _0(x,t). \end{aligned}$$

The unit normal vectors of $\varGamma ^{\delta +}_Y(x,t)$ and $\varGamma ^{\delta +}_G(x,t)$ are denoted ${\mathbf {n}}^{\delta +}_Y$ and ${\mathbf {n}}^{\delta +}_G$. For convenience, both are oriented to be pointing into the grain space; hence, both are equal to ${\mathbf {n}}_0$ when $\delta =0$. The integrals of $\nabla _y\cdot F_Y$ and $\nabla _y\cdot F_G$ over $Y^{\delta }_+(x,t)$ and $G^{\delta }_+(x,t)$, respectively, are zero, and the derivatives of the integrals with respect to $\delta$ are also zero. Hence,

$$\begin{aligned} 0 =&\, \partial _{\delta } \int _{Y^{\delta }_+(x,t)}\nabla _y\cdot F_y\hbox {d}y|_{\delta =0} + \partial _{\delta }\int _{G^{\delta }_+(x,t)}\nabla _y\cdot F_G\hbox {d}y|_{\delta =0} \\ =&\, \partial _{\delta } \int _{\varGamma ^{\delta +}_Y(x,t)}{\mathbf {n}}^{\delta +}_Y\cdot F_Y \hbox {d}\sigma |_{\delta =0} + \partial _{\delta }\int _{\varGamma ^{\delta +}_G(x,t)}{\mathbf {n}}^{\delta +}_G\cdot F_G\hbox {d}y|_{\delta =0} \\ =&\, \partial _{\delta } \int _0^1 {\mathbf {n}}^{\delta +}_Y\cdot F_Y(x,k^+_Y(s,\delta ),t)|\partial _sk^+_Y(s,\delta )|\hbox {d}s|_{\delta =0}\\&+ \partial _{\delta }\int _0^1 {\mathbf {n}}^{\delta +}_G\cdot F_G(x,k^+_G(s,\delta ),t)|\partial _sk^+_G(s,\delta )|\hbox {d}s|_{\delta =0} \\ =&\, \int _0^1 \Big (\partial _{\delta }{\mathbf {n}}^ {\delta +}_Y\cdot F_Y|\partial _sk^+_Y|+\nabla _y({\mathbf {n}}^{\delta +}_Y\cdot F_Y)\cdot \partial _{\delta }k^+_Y|\partial _sk^+_Y| \\&\quad +\,{\mathbf {n}}^{\delta +}_Y\cdot F_Y\partial _{\delta }(|\partial _sk^+_Y|)\Big )|_{\delta =0}\hbox {d}s + \int _0^1\Big (\partial _{\delta }{\mathbf {n}}^{\delta +}_G\cdot F_G|\partial _sk^+_G| \\&\quad +\,\nabla _y({\mathbf {n}}^{\delta +}_G\cdot F_G)\cdot \partial _{\delta }k^+_G|\partial _sk^+_G|+{\mathbf {n}}^{\delta +}_G\cdot F_G\partial _{\delta }(|\partial _sk^+_G|)\Big )|_{\delta =0}\hbox {d}s. \end{aligned}$$

We now evaluate each of the terms in both integrals at $\delta =0$. For the last terms in the integrals, we use that $\partial _{\delta }(|\partial _sk^+_Y|)|_{\delta =0}=-\partial _{\delta }(|\partial _sk^+_G|)|_{\delta =0}$ since the variations in $\delta$ were made with opposite sign. Since ${\mathbf {n}}^{\delta +}_Y|_{\delta =0}={\mathbf {n}}^{\delta +}_G|_{\delta =0}={\mathbf {n}}_0$, we get that the last terms in the two integrals cancel out as ${\mathbf {n}}_0\cdot (F_Y-F_G)=0$ at $\varGamma _0(x,t)$. For the middle terms in the two integrals, we use that ${\mathbf {n}}_0\cdot \partial _{\delta }k^+_Y|_{\delta =0}=-[S_1]_+/|\nabla _yS_0|$ and ${\mathbf {n}}_0\cdot \partial _{\delta }k^+_G|_{\delta =0}=[S_1]_+/|\nabla _yS_0|$. Finally, calculating the derivatives of the unit normals with respect to $\delta$, gives that $\partial _{\delta }{\mathbf {n}}^{\delta +}_Y|_{\delta =0}=\frac{\tau _0\cdot \nabla _y[S_1]_+}{|\nabla _yS_0|}\tau _0$ and $\partial _{\delta }{\mathbf {n}}^{\delta +}_G|_{\delta =0}=-\frac{\tau _0\cdot \nabla _y[S_1]_+}{|\nabla _yS_0|}\tau _0$. Inserting this into the above equation results in

$$\begin{aligned} \int _{\varGamma _0(x,t)} \left( \frac{\tau _0\cdot \nabla _y[S_1]_+}{|\nabla _yS_0|}\tau _0 \cdot (F_Y-F_G) - \frac{[S_1]_+}{|\nabla _yS_0|}{\mathbf {n}}_0 \cdot ({\mathbf {n}}_0\cdot (F_Y-F_G))\right) \hbox {d}y = 0. \end{aligned}$$

Repeating the same steps for $[S_1]_-$ and subtracting the two parts complete the proof. $\square$

Note that even though we consider a two-dimensional pore scale model, the model equations defined in Sect. 2 could easily be defined in a three-dimensional setting. However, the previous lemmas depend on the tangent vector of the interface $\varGamma _0(x,t)$, which would need to reformulated into a tangent plane. Also, the unit tangent vector $\tau _0$ would not be uniquely defined in a three-dimensional setting.

3.2 The Level Set Equation

For the asymptotic expansion, we need Lipschitz continuous reaction rates. Therefore, we replace (3) by its Lipschitz approximation:

$$\begin{aligned} w_{\delta }(\hbox {dist}(\epsilon y,B^{\epsilon })) = {\left\{ \begin{array}{ll} 0 &{} \text {if } \hbox {dist}(\epsilon y,B^{\epsilon })<0, \\ \hbox {dist}(\epsilon y,B^{\epsilon })/\delta &{} \text {if } 0\le \hbox {dist}(\epsilon y,B^{\epsilon })<\delta , \\ 1 &{} \text {if } \hbox {dist}(\epsilon y,B^{\epsilon })\ge \delta , \end{array}\right. } \end{aligned}$$

for some small $\delta >0$. As proved in (Kumar et al. 2013), in the limit as $\delta$ approaches zero, one ends up with the original (3). Thus, by $f_{\delta }(T_f^{\epsilon },u^{\epsilon },y)$, we mean the reaction rate f where $w^{\epsilon }(\hbox {dist}(x,B^{\epsilon }),T_f^{\epsilon },u^{\epsilon })$ is replaced with $w_{\delta }(\hbox {dist}(\epsilon y,B^{\epsilon }))$. The level set Eq. (15) becomes

$$\begin{aligned} \partial _t(S_0+O(\epsilon ))&= \epsilon \frac{1}{\rho }f_{\delta }(T_{f0}+O(\epsilon ),u_0+O(\epsilon ),y)|(\nabla _x+\frac{1}{\epsilon }\nabla _y)(S_0+O(\epsilon ))| \\&=\frac{1}{\rho }f_{\delta }(T_{f0},u_0,y)|\nabla _yS_0|+O(\epsilon ). \end{aligned}$$

We collect the lowest order terms and then let $\delta$ approach zero, giving back the original $w(\hbox {dist}(\epsilon y,B^{\epsilon }),T_f^{\epsilon },u^{\epsilon })$; leading to

$$\begin{aligned} \partial _t S_0=\frac{1}{\rho }f(T_{f0},u_0,y)|\nabla _yS_0|. \end{aligned}$$

(30)

3.3 Conservation of Ions

We insert the asymptotic expansions for $u^{\epsilon }$ and ${\mathbf {q}}^{\epsilon }$ into (17) and into the boundary condition (18) and apply Eq. (29) to obtain a boundary condition valid on $\varGamma _0(t)$. The lowest order terms are

$$\begin{aligned} D\nabla _y^2u_0&=0 \text { in } Y_0(x,t),\\ {\mathbf {n}}_0\cdot D\nabla _yu_0&=0 \text { at } \varGamma _0(x,t). \end{aligned}$$

Recall that $u_0$ is periodic in y. This means $u_0$ cannot depend on y; hence, $u_0=u_0(x,t)$. The second lowest order terms are

$$\begin{aligned} \nabla _y\cdot F_u&=0 \text { in } Y_0(x,t), \end{aligned}$$

(31)

$$\begin{aligned} {\mathbf {n}}_0\cdot F_u&=0 \text { at } \varGamma _0(x,t), \end{aligned}$$

(32)

where we have introduced the notation $F_u=D\nabla _xu_0+D\nabla _yu_1-{\mathbf {q}}_0u_0$. Finally, the third lowest order terms are

$$\begin{aligned}&\partial _tu_0 = \nabla _x\cdot F_u +\nabla _y\cdot (D\nabla _xu_1+D\nabla _yu_2-{\mathbf {q}}_0u_1 -{\mathbf {q}}_1u_0) \text { in } Y_0(x,t), \end{aligned}$$

(33)

$$\begin{aligned}&{\mathbf {n}}_0\cdot (D\nabla _xu_1+D\nabla _yu_2-{\mathbf {q}}_0u_1 -{\mathbf {q}}_1u_0) + {\mathbf {n}}_1\cdot F_u +\frac{1}{\rho }f(T_{f0},u_0,y)(\rho -u_0)\nonumber \\&\quad + y\cdot \nabla _x({\mathbf {n}}_0\cdot F_u) +\lambda _1{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_u) = 0\text { at } \varGamma _0(x,t). \end{aligned}$$

(34)

We integrate (33) over $Y_0(x,t)$ and apply the boundary condition (34):

$$\begin{aligned}&|Y_0(x,t)|\partial _tu_0=\nabla _x\cdot \int _{Y_0(x,t)}F_u\hbox {d}y + \int _{\varGamma _0(x,t)}\Big (\frac{\nabla _xS_0}{|\nabla _yS_0|}\cdot F_u\hbox {d}\sigma -\big ({\mathbf {n}}_1\cdot F_u\\&\quad +\frac{1}{\rho }f(T_{f0},u_0)(\rho -u_0)+y\cdot \nabla _x({\mathbf {n}}_0\cdot F_u)+\lambda _1{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_u)\big )\Big )\hbox {d}\sigma . \end{aligned}$$

The reactive term $f(T_{f0},u_0)$ can be rewritten using the level set Eq. (30) and its relation to the normal velocity. Since $G_0(x,t)$ has volume $(1-|Y_0(x,t)|)$, we can rewrite the reactive term using Reynolds transport theorem such that $-\int _{\varGamma _0(x,t)}\frac{1}{\rho }f(T_{f0},u_0)(\rho -u_0)\hbox {d}\sigma = -\rho \partial _t|G_0(x,t)| - u_0\partial _t|Y_0(x,t)|$. Hence,

$$\begin{aligned}&\partial _t(|Y_0(x,t)|u_0+|G_0(x,t)|\rho ) = \nabla _x\cdot \int _{\varGamma _0(x,t)}F_u\hbox {d}y + \int _{\varGamma _0(x,t)}\frac{\nabla _xS_0}{|\nabla _yS_0|}\cdot F_u\hbox {d}\sigma \\&\quad -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _xS_0}{|\nabla _yS_0|}\tau _0\cdot F_u\hbox {d}\sigma -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _yS_1}{|\nabla _yS_0|}\tau _0\cdot F_u\hbox {d}\sigma \\&\quad -\int _{\varGamma _0(x,t)}y\cdot \nabla _x({\mathbf {n}}_0\cdot F_u)\hbox {d}\sigma + \int _{\varGamma _0(x,t)}\frac{S_1}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_u)\hbox {d}\sigma \\&\quad +\int _{\varGamma _0(x,t)}\frac{y\cdot \nabla _xS_0}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_u)\hbox {d}\sigma . \end{aligned}$$

The last six integrals add up to zero;

• $\int _{\varGamma _0(x,t)}\frac{\nabla _xS_0}{|\nabla _yS_0|}\cdot F_u\hbox {d}\sigma -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _xS_0}{|\nabla _yS_0|}\tau _0\cdot F_u\hbox {d}\sigma =0$ because $F_u=(\tau _0\cdot F_u)\tau _0$, as $F_u$ has zero normal component at $\varGamma _0(x,t)$.

• $\int _{\varGamma _0(x,t)}\frac{y\cdot \nabla _xS_0}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_u)\hbox {d}\sigma -\int _{\varGamma _0(x,t)}y\cdot \nabla _x({\mathbf {n}}_0\cdot F_u)\hbox {d}\sigma =0$ by Lemma 1 when applied to $g={\mathbf {n}}_0\cdot F_u$.

• $\int _{\varGamma _0(x,t)}\frac{S_1}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_u)\hbox {d}\sigma -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _yS_1}{|\nabla _yS_0|}\tau _0\cdot F_u\hbox {d}\sigma =0$ by Lemma 2.

We are therefore left with

$$\begin{aligned} \partial _t(|Y_0(x,t)|u_0+|G_0(x,t)|\rho ) = \nabla _x\cdot \int _{\varGamma _0(x,t)}(D\nabla _xu_0+D\nabla _yu_1-{\mathbf {q}}_0u_0)\hbox {d}y. \end{aligned}$$

(35)

3.4 Conservation of Energy

Upscaling the two energy conservations (23) and (24) follows similar steps as in the previous section, but requires some extra care as the grain space plays an explicit role. Following (27), the leading order term in the fluid density reads

$$\begin{aligned} \rho _{f0}=\rho _f(T_{f0}). \end{aligned}$$

(36)

Inserting the relevant asymptotic expansions into (23) and (24) and into the internal boundary conditions (25) and (26) while applying (29), the lowest order terms will be

$$\begin{aligned} \nabla ^2_yT_{f0}&=0 \text { in } Y_0(x,t),\\ \nabla ^2_yT_{g0}&=0\text { in } G_0(x,t),\\ {\mathbf {n}}_0\cdot \nabla _y(T_{f0}-T_{g0})&=0 \text { at } \varGamma _0(x,t), \\ T_{f0}-T_{g0}&=0 \text { at } \varGamma _0(x,t). \end{aligned}$$

As $T_{f0}$ and $T_{g0}$ are periodic in y, the only solution to this problem is that $T_{f0}$ and $T_{g0}$ do not depend on y, which together with the continuity condition implies $T_{f0}=T_{g0}=T_0(x,t)$. The second lowest order terms are

$$\begin{aligned} \nabla _y\cdot (\kappa _f\nabla _yT_{f1}-\rho _{f0}{\mathbf {q}}_0T_{f0})= & {} 0 \text { in } Y_0(x,t), \end{aligned}$$

(37)

$$\begin{aligned} \nabla _y^2T_{g1}= & {} 0 \text { in } G_0(x,t), \end{aligned}$$

(38)

$$\begin{aligned} {\mathbf {n}}_0\cdot F_T= & {} 0\text { at } \varGamma _0(x,t), \end{aligned}$$

(39)

$$\begin{aligned} T_{f1}-T_{g1}= & {} 0 \text { at } \varGamma _0(x,t), \end{aligned}$$

(40)

where $F_T=\kappa _f\nabla _xT_{f0}+\kappa _f\nabla _yT_{f1}-\rho _{f0}{\mathbf {q}}_0T_{f0}-\kappa _g\nabla _xT_{g0}-\kappa _g\nabla _yT_{g1}$. Finally, the third lowest order terms are

$$\begin{aligned} \partial _t&(\rho _{f0}T_{f0})+\nabla _x\cdot (\rho _{f0}{\mathbf {q}}_0T_{f0})+\nabla _y\cdot (\rho _{f0}{\mathbf {q}}_0T_{f1}+\rho _{f0}{\mathbf {q}}_1T_{f0}-\beta _{\rho _f}T_{f1}{\mathbf {q}}_0T_{f0})\nonumber \\&= \kappa _f\nabla _x\cdot (\nabla _xT_{f0}+\nabla _yT_{f1}) \quad +\,\kappa _f\nabla _y\cdot (\nabla _xT_{f1}+\nabla _yT_{f2}) \text { in } Y_0(x,t),\end{aligned}$$

(41)

$$\begin{aligned} \partial _t&(\varsigma \rho T_{g0})= \kappa _g\nabla _x\cdot (\nabla _xT_{g0}+\nabla _yT_{g1})\nonumber \\&\qquad \qquad \qquad \!\!\!+\kappa _g\nabla _y\cdot (\nabla _xT_{g1}+\nabla _yT_{g2}) \text { in } G_0(x,t),\end{aligned}$$

(42)

$$\begin{aligned} {\mathbf {n}}_1&\cdot F_T+{\mathbf {n}}_0\cdot \Big (\kappa _f\nabla _xT_{f1}+\kappa _f\nabla _yT_{f2} -(\rho _{f0}{\mathbf {q}}_0T_{f1}+\rho _{f0}{\mathbf {q}}_1T_{f0}\nonumber \\&-\beta _{\rho _f}T_{f1}{\mathbf {q}}_0T_{f0}) -\kappa _g\nabla _xT_{g1}-\kappa _g\nabla _yT_{g2}\Big ) +\frac{1}{\rho }f(T_{f0},u_0)(\varsigma \rho T_{g0}-\rho _{f0}T_{f0}) \nonumber \\&+ y\cdot \nabla _x({\mathbf {n}}_0\cdot F_T)+\lambda _1{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_T)=0 \text { at } \varGamma _0(x,t), \end{aligned}$$

(43)

$$\begin{aligned} T_{f2}&-T_{g2}+y\cdot \nabla _x(T_{f1}-T_{g1})+\lambda _1{\mathbf {n}}_0\cdot \nabla _y(T_{f1}-T_{g1})=0\text { at } \varGamma _0(x,t). \end{aligned}$$

(44)

We integrate (41) over $Y_0(x,t)$ and (42) over $G_0(x,t)$ and sum the integrals. In the integrals involving a divergence with respect to x, we interchange the order of integration and differentiation. In the integrals involving a divergence with respect to y, we apply Gauss’ theorem. We rewrite boundary terms using (43) and insert the expressions for ${\mathbf {n}}_1$ and $\lambda _1$ where applicable. We then get

$$\begin{aligned} |&Y_0(x,t)|\partial _t(\rho _{f0}T_{f0})+|G_0(x,t)|\partial _t(\varsigma \rho T_{g0}) + \nabla _x\cdot \int _{Y_0(x,t)}\rho _{f0}{\mathbf {q}}_0T_{f0}\hbox {d}y \\&=\nabla _x\cdot \int _{Y_0(x,t)}\kappa _f(\nabla _xT_{f0}+\nabla _yT_{f1})\hbox {d}y+\nabla _x\cdot \int _{G_0(x,t)}\kappa _g(\nabla _xT_{g0}+\nabla _yT_{g1})\hbox {d}y \\&-\int _{\varGamma _0(x,t)}\frac{1}{\rho }f(T_{f0},u_0)(\varsigma \rho T_{g0}-\rho _{f0}T_{f0})\hbox {d}\sigma + \int _{\varGamma _0(x,t)}\frac{\nabla _xS_0}{|\nabla _yS_0|}\cdot F_T\hbox {d}\sigma \\&-\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _xS_0}{|\nabla _yS_0|}\tau _0\cdot F_T\hbox {d}\sigma -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _yS_1}{|\nabla _yS_0|}\tau _0\cdot F_T\hbox {d}\sigma \\&- \int _{\varGamma _0(x,t)}y\cdot \nabla _x({\mathbf {n}}_0\cdot F_T)\hbox {d}\sigma +\int _{\varGamma _0(x,t)}\frac{S_1}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_T)\hbox {d}\sigma \\&+\int _{\varGamma _0(x,t)}\frac{y\cdot \nabla _xS_0}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_T)\hbox {d}\sigma . \end{aligned}$$

As before, the last six integrals add up to zero;

• $\int _{\varGamma _0(x,t)}\frac{\nabla _xS_0}{|\nabla _yS_0|}\cdot F_T\hbox {d}\sigma -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _xS_0}{|\nabla _yS_0|}\tau _0\cdot F_T\hbox {d}\sigma =0$ as $F_T$ has zero normal component at $\varGamma _0(x,t)$.

• $\int _{\varGamma _0(x,t)}\frac{y\cdot \nabla _xS_0}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_T)\hbox {d}\sigma -\int _{\varGamma _0(x,t)}y\cdot \nabla _x({\mathbf {n}}_0\cdot F_T)\hbox {d}\sigma =0$ by Lemma 1 when applied to $g={\mathbf {n}}_0\cdot F_T$.

• $\int _{\varGamma _0(x,t)}\frac{S_1}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_T)\hbox {d}\sigma -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _yS_1}{|\nabla _yS_0|}\tau _0\cdot F_T\hbox {d}\sigma =0$ by Lemma 3 with $F_Y=\kappa _f\nabla _x T_{f0}+\kappa _f\nabla _x T_{f1}-\rho _{f0}{\mathbf {q}}_0T_{f0}$ and $F_G=\kappa _g\nabla _xT_{g0}+\kappa _g\nabla _xT_{g1}$.

The reactive term can be rewritten using the level set equation as earlier. We therefore end up with

$$\begin{aligned}&\partial _t(|Y_0(x,t)|\rho _{f0}T_{f0}+|G_0(x,t)|\varsigma \rho T_{g0}) + \nabla _x\cdot \int _{Y_0(x,t)}\rho _{f0}{\mathbf {q}}_0T_{f0}\hbox {d}y \nonumber \\&\quad =\nabla _x\cdot \int _{Y_0(x,t)}\kappa _f(\nabla _xT_{f0} +\nabla _yT_{f1})\hbox {d}y+\nabla _x\cdot \int _{G_0(x,t)}\kappa _g(\nabla _xT_{g0} +\nabla _yT_{g1})\hbox {d}y, \end{aligned}$$

(45)

where $\rho _{f0}$ is given by (36).

3.5 Conservation of Mass

While van Noorden (2009a) could incorporate the incompressible mass conservation equation into the upscaling of the momentum equation, the compressible mass conservation Eq. (19) must be explicitly accounted for in the upscaling process due to the varying density. We insert the asymptotic expansions into (19) and (20) and apply (29) as before. To show the similarities with conservation of ions and energy, we introduce the notation $F_m=-\rho _{f0}{\mathbf {q}}_0$. The lowest order terms are

$$\begin{aligned} \nabla _y\cdot F_m&=0 \text { in } Y_0(x,t),\end{aligned}$$

(46)

$$\begin{aligned} {\mathbf {n}}_0\cdot F_m&=0 \text { at } \varGamma _0(x,t). \end{aligned}$$

(47)

Since $\rho _{f0}$ does not depend on y, the first equation can also be read as $\nabla _y\cdot {\mathbf {q}}_0=0$ in $Y_0(x,t)$. The second lowest order terms are

$$\begin{aligned}&\partial _t\rho _{f0}=\nabla _x\cdot F_m+\nabla _y\cdot (-\rho _{f0}{\mathbf {q}}_1+\beta _{\rho _f}T_{f1}{\mathbf {q}}_0) \text { in } Y_0(x,t), \end{aligned}$$

(48)

$$\begin{aligned}&{\mathbf {n}}_1\cdot F_m+{\mathbf {n}}_0\cdot (-\rho _{f0}{\mathbf {q}}_1 +\beta _{\rho _f}T_{f1}{\mathbf {q}}_0)+\frac{1}{\rho }f(T_{f0},u_0) (2\rho -\rho _{f0})\nonumber \\&\quad +y\cdot \nabla _x({\mathbf {n}}_0\cdot F_m)+\lambda _1{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_m)=0 \text { at } \varGamma _0(x,t). \end{aligned}$$

(49)

We integrate (48) over $Y_0(x,t)$, replacing the order of integration and differentiation where the integrand involves $\nabla _x$ and apply Gauss’ theorem when the integrand involves $\nabla _y$. We apply (49) and insert expressions for ${\mathbf {n}}_1$ and $\lambda _1$ at the same time, obtaining

$$\begin{aligned} |&Y_0(x,t)|\partial _t\rho _{f0} = \nabla _x\cdot \int _{Y_0(x,t)}F_m\hbox {d}y + \int _{\varGamma _0(x,t)}\frac{\nabla _xS_0}{|\nabla _yS_0|}\cdot F_m \hbox {d}\sigma \\&-\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _xS_0}{|\nabla _yS_0|}\tau _0\cdot F_m\hbox {d}\sigma -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _yS_1}{|\nabla _yS_0|}\tau _0\cdot F_m\hbox {d}\sigma \\&- \int _{\varGamma _0(x,t)}\frac{1}{\rho }f(T_{f0},u_0)(2\rho -\rho _{f0})\hbox {d}\sigma -\int _{\varGamma _0(x,t)}y\cdot \nabla _x({\mathbf {n}}_0\cdot F_m)\hbox {d}\sigma \\&+\int _{\varGamma _0(x,t)}\frac{S_1}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_m)\hbox {d}\sigma +\int _{\varGamma _0(x,t)}\frac{y\cdot \nabla _xS_0}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_m)\hbox {d}\sigma . \end{aligned}$$

As earlier, we rewrite the reactive term using the level set equation and Reynolds transport theorem. The six remaining boundary integrals add up to zero;

• $\int _{\varGamma _0(x,t)}\frac{\nabla _xS_0}{|\nabla _yS_0|}\cdot F_m\hbox {d}\sigma - \int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _xS_0}{|\nabla _yS_0|}\tau _0\cdot F_m\hbox {d}\sigma =0$ as $F_m$ has zero normal component at $\varGamma _0(x,t)$.

• $\int _{\varGamma _0(x,t)}\frac{y\cdot \nabla _xS_0}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_m)\hbox {d}\sigma -\int _{\varGamma _0(x,t)}y\cdot \nabla _x({\mathbf {n}}_0\cdot F_m)\hbox {d}\sigma =0$ by Lemma 1 when applied to $g={\mathbf {n}}_0\cdot F_m$.

• $\int _{\varGamma _0(x,t)}\frac{S_1}{|\nabla _yS_0|}{\mathbf {n}}_0\cdot \nabla _y({\mathbf {n}}_0\cdot F_m)\hbox {d}\sigma -\int _{\varGamma _0(x,t)}\frac{\tau _0\cdot \nabla _yS_1}{|\nabla _yS_0|}\tau _0\cdot F_m\hbox {d}\sigma =0$ by Lemma 2.

We are therefore left with

$$\begin{aligned} \partial _t(|Y_0(x,t)|\rho _{f0}+|G_0(x,t)|2\rho ) + \nabla _x\cdot \int _{\varGamma _0(x,t)}\rho _{f0}{\mathbf {q}}_0\hbox {d}y = 0. \end{aligned}$$

3.6 Conservation of Momentum

We insert the necessary asymptotic expansions into (21) and (22) and apply (29). Following (28), the leading order term in the fluid viscosity is

$$\begin{aligned} \mu _{f0}=\mu (T_{f0}). \end{aligned}$$

(50)

We collect the lowest order terms from the model equation and the boundary condition, obtaining

$$\begin{aligned} \nabla _y p_0&= 0 \text { in } Y_0(x,t), \nonumber \\ {\mathbf {q}}_0&= 0 \text { at } \varGamma _0(x,t). \end{aligned}$$

(51)

As $\nabla _y p_0 =0$ in $Y_0(x,t)$, we conclude that $p_0=p_0(x,t)$. The second lowest order terms from the model equation are

$$\begin{aligned} 0=-\nabla _xp_0-\nabla _yp_1+\nabla _y\cdot \Big (\mu _{f0}(\nabla _y{\mathbf {q}}_0+(\nabla _y{\mathbf {q}}_0)^T)\Big )-\frac{2}{3}\nabla _y(\mu _{f0}\nabla _y\cdot {\mathbf {q}}_0). \end{aligned}$$

It is known from (46) that $\nabla _y\cdot {\mathbf {q}}_0=0$ in $Y_0(x,t)$; hence, the last term disappears. Since $\mu _{f0}$ is independent of y and $\nabla _y\cdot (\nabla _y{\mathbf {q}}_0)^T=\nabla _y(\nabla _y\cdot {\mathbf {q}}_0)$, we can rewrite the above equation into

$$\begin{aligned} 0=-\nabla _xp_0-\nabla _yp_1+\mu _{f0}\nabla _y^2{\mathbf {q}}_0, \end{aligned}$$

(52)

with the fluid viscosity given by (50).

3.7 Cell Problems

Here we eliminate $u_1$ from (35). We make use of the second lowest order Eq. (31) and boundary condition (32). Since this problem is linear, $u_1$ can be written as a linear combination of the derivatives of $u_0$ with respect to x,

$$\begin{aligned} u_1(x,y,t) = \sum _{j=1,2}v^j(y)\partial _{x_j}u_0(x,t) \end{aligned}$$

for unknown functions $v^1(y)$ and $v^2(y)$. Rewriting (31), using $\nabla _y\cdot {\mathbf {q}}_0=0$ and inserting the above expansion for $u_1$ yield

$$\begin{aligned} 0=\nabla _y^2\left( \sum _{j=1,2}v^j(y)\partial _{x_j}u_0(x,t) \right) = \sum _{j=1,2}\nabla _y^2v^j(y)\partial _{x_j}u_0(x,t), \end{aligned}$$

which means that

$$\begin{aligned} \nabla _y^2v^j(y)=0\text { in } Y_0(x,t) \text { for } j=1,2. \end{aligned}$$

(53)

Doing the same for the boundary condition (32), recalling that ${\mathbf {n}}_0\cdot {\mathbf {q}}_0=0$ from (47), we get

$$\begin{aligned} {\mathbf {n}}_0\cdot \left( \sum _{j=1,2}\partial _{x_j} u_0(x,t){\mathbf {e}}_j+\nabla _yv^j(y)\partial _{x_j}u_0(x,t)\right) =0. \end{aligned}$$

From this equation, we obtain

$$\begin{aligned} {\mathbf {n}}_0\cdot ({\mathbf {e}}_j+\nabla _yv^j(y))=0 \text { at } \varGamma _0(x,t) \text { for } j=1,2. \end{aligned}$$

(54)

The two functions $v^1(y)$ and $v^2(y)$ are determined by Eqs. (53) and (54) together with requiring periodicity in y. This model problem is called the cell problem for u. Inserting the series expression for $u_1$ into the model problem (35) results in

$$\begin{aligned} \partial _t(|Y_0(x,t)|u_0+|G_0(x,t)|\rho ) +\nabla _x\cdot (\bar{{\mathbf {q}}}_0u_0)= D\nabla _x\cdot ({\mathcal {A}}_u\nabla _xu_0) \end{aligned}$$

where ${\mathcal {A}}_u=\{a^u_{ij}\}$ is a matrix with components

$$\begin{aligned} a^u_{ij}=\int _{Y_0(x,t)}(\delta _{ij}+\partial _{y_i}v^j(y))\hbox {d}y. \end{aligned}$$

We follow similar steps to eliminate $T_{f1}$ and $T_{g1}$ from (45). We assume $T_{f1}$ and $T_{g1}$ can be written as a sum of the derivatives with respect to x of $T_{f0}$ and $T_{g0}$, respectively,

$$\begin{aligned} T_{f1}&= \sum _{j=1,2}\theta ^j_f(y)\partial _{x_j}T_{f0}(x,t)\ \ y\in Y_0(x,t), \\ T_{g1}&= \sum _{j=1,2}\theta ^j_g(y)\partial _{x_j}T_{g0}(x,t)\ \ y\in G_0(x,t), \end{aligned}$$

for unknown functions $\theta ^j_f(y)$ and $\theta ^j_g(y)$. We insert the expression for $T_{f1}$ into (37) and the expansion for $T_{g1}$ into (38) and obtain

$$\begin{aligned} \nabla _y^2\theta ^j_f(y)&=0\ \ y\in Y_0(x,t) \text { for } j=1,2; \\ \nabla _y^2\theta ^j_g(y)&=0\ \ y\in G_0(x,t) \text { for } j=1,2. \end{aligned}$$

Inserting the two expressions for $T_{f1}$ and $T_{g1}$ into the boundary conditions (39) and (40) yields

$$\begin{aligned} \kappa _f{\mathbf {n}}_0\cdot ({\mathbf {e}}_j+\nabla _y\theta ^j_f(y))&=\kappa _g{\mathbf {n}}_0\cdot ({\mathbf {e}}_j+\nabla _y\theta _g^j(y))\ \ y\in \varGamma _0(x,t)\text { for } j=1,2,\\ \theta _f^j(y)&= \theta _g^j(y)\ \ y\in \varGamma _0(x,t) \text { for } j=1,2. \end{aligned}$$

Due to the continuity condition, we define $\theta ^j(y)$ to be equal to either $\theta _f^j$ or $\theta _g^j$;

$$\begin{aligned} \theta ^j(y)={\left\{ \begin{array}{ll} \theta _f^j(y) &{} \text {if } y\in Y_0(x,t), \\ \theta _g^j(y) &{} \text {if } y\in G_0(x,t). \end{array}\right. } \end{aligned}$$

We then have that $\theta ^j(y)$ is the solution of the cell problem

$$\begin{aligned} \nabla _y^2\theta ^j(y)=0 \ \ y\in Y_0(x,t)\cup G_0(x,t) \\ {\mathbf {n}}_0\cdot ({\mathbf {e}}_j+\nabla _y\theta ^j(y))=0 \text { at } \varGamma _0(x,t), \end{aligned}$$

where we also demand periodicity in y. Inserting the series expressions into (45) results in

$$\begin{aligned} \partial _t(|Y_0(x,t)|\rho _{f0}T_0 + |G_0(x,t)|\varsigma \rho T_0) +\nabla _x\cdot (\rho _{f0}\bar{{\mathbf {q}}}_0T_0)=\nabla _x\cdot \Big ((\kappa _f{\mathcal {A}}_f+\kappa _g{\mathcal {A}}_g)\nabla _x T_0\Big ), \end{aligned}$$

where ${\mathcal {A}}_f=\{a^f_{if}\}$ and ${\mathcal {A}}_g=\{a^g_{ij}\}$ are matrices given by

$$\begin{aligned} a_{ij}^f&=\int _{Y_0(x,t)}(\delta _{ij}+\partial _{y_i}\theta ^j(y))\hbox {d}y, \\ a_{ij}^g&= \int _{G_0(x,t)}(\delta _{ij}+\partial _{y_i}\theta ^j(y))\hbox {d}y. \end{aligned}$$

We combine (46) and (52) with boundary condition (51) into one cell problem to obtain an equation including only ${\mathbf {q}}_0$ and $p_0$. We assume that $p_1$ and ${\mathbf {q}}_0$ can be written as linear combinations of the derivatives of $p_0$ with respect to x, namely

$$\begin{aligned} p_1(x,y,t)&= \sum _{j=1,2}\varPi ^j(y)\partial _{x_j}p_0(x,t); \\ {\mathbf {q}}_0(x,y,t)&= -\frac{1}{\mu _{f0}}\sum _{j=1,2}\omega ^j(y)\partial _{x_j}p_0(x,t), \end{aligned}$$

for unknown functions $\varPi ^j(y)$ and vector functions $\omega ^j(y)$. Inserting the expressions for $p_1$ and ${\mathbf {q}}_0$ into (52) yields

$$\begin{aligned} {\mathbf {e}}_j+\nabla _y\varPi ^j(y)=-\nabla _y^2\omega ^j(y) \ \ y\in Y_0(x,t) \text { for } j=1,2, \end{aligned}$$

while (46) results in

$$\begin{aligned} \nabla _y\cdot \omega ^j(y)=0 \ \ y\in Y_0(x,t) \text { for } j=1,2. \end{aligned}$$

The boundary condition (51) gives us that

$$\begin{aligned} \omega ^j(y)=0 \ \ y\in \varGamma _0(x,t)\text { for } j=1,2. \end{aligned}$$

Through $\omega ^j(y)$, we get that the integral of the lowest order velocity can be written as

$$\begin{aligned} \bar{{\mathbf {q}}}_0(x,t)=\int _{Y_0(x,t)}{\mathbf {q}}_0(x,y,t)\hbox {d}y = -\frac{1}{\mu _{f0}}{\mathcal {K}}\nabla _xp_0, \end{aligned}$$

where ${\mathcal {K}}=\{k_{ij}\}$ is the matrix given by

$$\begin{aligned} k_{ij} = \int _{Y_0(x,t)}\omega ^j_i(y)\hbox {d}y, \end{aligned}$$

where $\omega ^j_i(y)$ is the i’th component of the vector function $\omega ^j(y)$.

4 Summary and Discussion

We summarize the derived effective equations, without making any assumptions on the grain geometry and hence the shape of the level set function. Since we only use the lowest order expansions, we skip the subscript 0 from the variables. We have five unknowns: S(x, y, t), u(x, t), T(x, t), $\bar{{\mathbf {q}}}(x,t)$ and p(x, t). All but the first depend only on spatial variable x and are defined for all $x\in \varOmega$, while the level set function S(x, y, t) also depends on the microscopic variable $y\in [0,1]^2$. The five upscaled equations are $(x\in \varOmega , t>0)$

$$\begin{aligned} \partial _t&\Big (\rho S(x,y,t)\Big ) = f(T,u,y)|\nabla _y S(x,y,t)|, \\ \partial _t&\Big (|Y_0(x,t)|u(x,t)+|G_0(x,t)|\rho \Big )+\nabla _x\cdot \Big (\bar{{\mathbf {q}}}(x,t)u(x,t)\Big )\\&=\nabla _x\cdot \Big (D{\mathcal {A}}_u(x,t)\nabla _xu(x,t)\Big ), \\ \partial _t&\Big (|Y_0(x,t)|\rho _f(T)T(x,t)+|G_0(x,t)|\varsigma \rho T(x,t)\Big )+\nabla _x\cdot \Big (\rho _f(T)\bar{{\mathbf {q}}}(x,t)T(x,t)\Big ) \\&= \nabla _x\cdot \Big (\kappa _f{\mathcal {A}}_f(x,t)\nabla _xT(x,t)+\kappa _g{\mathcal {A}}_g(x,t)\nabla _x T(x,t)\Big ), \\ \partial _t&\Big (|Y_0(x,t)|\rho _f(T)+|G_0(x,t)|2\rho \Big )+\nabla _x\cdot \Big (\rho _f(T)\bar{{\mathbf {q}}}(x,t)\Big ) =0, \\ \bar{{\mathbf {q}}}(&x,t) =-\frac{1}{\mu _f(T)}{\mathcal {K}}(x,t)\nabla _xp(x,t). \end{aligned}$$

The matrices ${\mathcal {A}}_u$, ${\mathcal {A}}_f$, ${\mathcal {A}}_g$ and ${\mathcal {K}}$ have components given by

$$\begin{aligned} a^u_{ij}(x,t)&=\int _{Y_0(x,t)}(\delta _{ij}+\partial _{y_i}v^j(y))\hbox {d}y,\\ a_{ij}^f(x,t)&=\int _{Y_0(x,t)}(\delta _{ij}+\partial _{y_i}\theta ^j(y))\hbox {d}y, \\ a_{ij}^g(x,t)&= \int _{G_0(x,t)}(\delta _{ij}+\partial _{y_i}\theta ^j(y))\hbox {d}y, \\ k_{ij}(x,t)&= \int _{Y_0(x,t)}\omega ^j_i(y)\hbox {d}y, \end{aligned}$$

while the functions $v^j(y)$, $\theta ^j(y)$ and $\omega ^j(y)$ are solutions to the cell problems $(x\in \varOmega ,t>0)$

$$\begin{aligned}&\nabla _yv^j(y)=0 \text { in } Y_0(x,t) \text { and } {\mathbf {n}}\cdot ({\mathbf {e}}_j+\nabla _y v^j(y))=0 \text { at } \varGamma _0(x,t), \\&\nabla ^2_y\theta ^j(y) = 0 \text { in } Y_0(x,t)\cup G_0(x,t) \text { and } {\mathbf {n}}\cdot ({\mathbf {e}}_j+\nabla _y\theta ^j(y))=0 \text { at } \varGamma _0(x,t), \\&{\mathbf {e}}_j+\nabla _y\varPi ^j(y)=-\nabla _y^2\omega ^j(y) \text { and } \nabla _y\cdot \omega ^j(y) = 0 \text { in } Y_0(x,t)\\&\text { and } \omega ^j(y)=0 \text { at } \varGamma _0(x,t), \end{aligned}$$

together with the periodicity in y for $v^j(y)$, $\theta ^j(y)$, $\varPi ^j(y)$ and $\omega ^j(y)$, $j=1,2$.

We observe that the three upscaled conservation equations for ions, mass and energy show similarities in the first term; the time derivative consists of a volume-weighted sum of the preserved quantity in void and grain space. Hence, we take the time derivative of the total quantity occurring in the unit square. The upscaled diffusive terms include a matrix with components arising from cell problems, instead of a volume factor as in the case of a thin strip (Bringedal et al. 2015). This way we take into account the geometry of the pore space and not only the size. Same happens for Darcy’s law where the permeability tensor ${\mathcal {K}}$ depends on pore geometry through the cell problems. While the thin strip case in (Bringedal et al. 2015) reduced to a one-dimensional model, the present model remains two-dimensional also in the upscaled version, which is honored through the diffusion and permeability tensors.

Compared to the reactive transport model TOUGHREACT (Xu et al. 2012), which is well used for geothermal reservoirs, the upscaled model equations found here are similar to the model equations that are applied in TOUGHREACT. The conservation equations for mass, ions and energy have the same structure with porosity-weighted averages in the time derivative, convective term with an average volume flux, and a porosity-weighted diffusive term that includes heat transfer in the grains. Hence, the upscaled model we have found behaves as expected compared to well-known models, but introduces also the pore scale effects: While TOUGHREACT (Xu et al. 2012) uses a simple equation for the porosity evolution due to mineral precipitation and dissolution, we include an explicit equation through the level set equation. Further, TOUGHREACT (Xu et al. 2012) uses only scalar diffusion and permeability, while we find that the permeability and diffusion will in general be tensors. TOUGHREACT (Xu et al. 2012) uses similar reaction rates for kinetic mineral precipitation and dissolution as considered here, but relies on estimates on the reactive surface, which in our upscaled model is handled explicitly through the level set formulation. The upscaled model contains a discontinuous reaction rate, and Agosti et al. (2015a, b) show well posedness for a similar model and suggest a numerical strategy for the implementation of such a reaction rate.

The porosity is not explicitly used in the upscaled system of equations, but the void and grain space volumes are present and are defined through the level set function. The derivatives of the void and grain space volumes are handled through the level set equation which connects these derivatives with the reaction rates. The upscaled equations are computationally cheaper than the original model problem as the two scales x and y are separated, and the microscopic variable y only appears through the cell problems and the level set equation. Redeker and Eck (2013) proposed an adaptive solution strategy for a model with two-scale dependence through a similar separation of the micro- and macroscale as considered here, and they showed that the scheme was convergent. Note that the upscaled model is not capable of describing cases with clogging as we assumed the presence of a connected pore space in Sect. 2. Hence, in numerical simulations, caution must be made to avoid situations where clogging could occur and abort the simulation if clogging were to take place.

Compared to the work of van Noorden (2009a) who considers the isothermal case, the present model includes compressible flow due to temperature-dependent fluid density and honors heat transfer in both fluid and grain space, which is expressed through a single energy conservation equation in the upscaled model due to the assumption of local thermal equilibrium at the pore scale. Temperature effects are also found in the varying fluid viscosity in Darcy’s law. We can note that at isothermal conditions, the present model reduces to the one by van Noorden (2009a).

The upscaled system of equations introduces some useful results in how the permeability and diffusion tensors of the coupled system evolve due to the chemical reactions that can be incorporated into simulator codes. TOUGHREACT (Xu et al. 2012) incorporates permeability changes based on the work by Verma and Pruess (1988) by utilizing a simple power law relationship between the scalar permeability and the porosity. Only scalar solute diffusion and heat conduction are considered in TOUGHREACT, but as shown by the present upscaling process, these will in general be tensors. The upscaled system of equations formulated here includes permeability and diffusion tensors based on cell problems, giving a more detailed and accurate description of the transport processes.

Using mass conservative mixed finite element methods (MFEM), Frank (2013) implemented a Stokes–Nernst–Planck–Poisson system based on upscaled pore scale equations, taking into account the permeability and diffusion tensors depending on pore scale effects through cell problems. Frank (2013) considered several grain shapes in the fixed geometry case and applied circular grains for varying porosity. Numerical computations using MFEM on circular grains with varying radii were also considered by Ray et al. (2013) for drug release from collagen matrices. Ray et al. (2013) derived approximate solutions of the corresponding cell problems and found good correspondence with experimental results. van Noorden (2009a) implemented his upscaled pore scale equations for reactive transport on circular grains with altering grain radius, fitting the effective diffusion and permeability with a rational polynomial function. Both Frank (2013) and van Noorden (2009a) consider incompressible flow, but extending to compressible flow should be straightforward by replacing the mass conservation equation. As the upscaled temperature equation has the same structure as the upscaled solute transport equation, it can be implemented using similar steps as performed by Frank (2013), Ray et al. (2013) or van Noorden (2009a).

If we make assumptions on the pore geometry and hence the shape of the level set function, our model equations can be further simplified. For special choices of the level set function, e.g., circular geometry, we obtain a system of equations only depending on the macroscopic variable (van Noorden 2009a). Specifically, assuming that the grains are circular and centered in the middle of the unit square, we can use the level set function $S(x,y,t)=R^2(x,t) -(y_1-1/2)^2-(y_2-1/2)^2$, where R(x, t) is the radius of the grain. Using this level set function and pore geometry, we reformulate the above equations in terms of R(x, t). All the five unknowns R(x, t), u(x, t), T(x, t), $\bar{{\mathbf {q}}}(x,t)$ and p(x, t) are now defined for $x\in \varOmega$ and do not depend on the microscopic variable y. The equations read now $(x\in \varOmega ,t>0)$:

$$\begin{aligned} \partial _t&\Big (\rho R(x,t)\Big ) = f(T,u,R), \\ \partial _t&\Big ((1-\pi R^2)u(x,t)+\pi R^2 \rho \Big ) + \nabla _x\cdot \Big (\bar{{\mathbf {q}}}(x,t)u(x,t)\Big )\\&= \nabla _x\cdot \Big (D{\mathcal {A}}_u(R)\nabla _x u(x,t)\Big ), \\ \partial _t&\Big ((1-\pi R^2)\rho _f(T)T(x,t)+\pi R^2\varsigma \rho T(x,t)\Big ) + \nabla _x\cdot \Big (\rho _f(T)\bar{{\mathbf {q}}}(x,t)T(x,t)\Big ) \\&= \nabla _x\cdot \Big (\kappa _f{\mathcal {A}}_f(R)\nabla _x T(x,t)+\kappa _g{\mathcal {A}}_g(R)\nabla _x T(x,t)\Big ), \\ \partial _t&\Big ((1-\pi R^2)\rho _f(T)+\pi R^22\rho )+\nabla _x\cdot \Big (\rho _f(T)\bar{{\mathbf {q}}}(x,t)\Big ) = 0, \\ \bar{{\mathbf {q}}}(&x,t) = -\frac{1}{\mu _f(T)}{\mathcal {K}}(R)\nabla _xp(x,t). \end{aligned}$$

The reaction rate f uses the distance between R and $R_\mathrm{min}$, where $R_\mathrm{min}$ is the radius of the non-reactive part, to calculate the width of the mineral layer. The matrices ${\mathcal {A}}_u$, ${\mathcal {A}}_f$, ${\mathcal {A}}_g$ and ${\mathcal {K}}$ depend only on R(x, t) as the integration area is determined by the radius alone. The cell problems are defined as before, but where $Y_0(x,t) = \{y\in [0,1]^2 \ | \ (y_1-1/2)^2+(y_2-1/2)^2 > R^2(x,t)\}$, $G_0(x,t)= \{y\in [0,1]^2 \ | \ (y_1-1/2)^2+(y_2-1/2)^2 < R^2(x,t)\}$ and $\varGamma _0(x,t)= \{y\in [0,1]^2 \ | \ (y_1-1/2)^2+(y_2-1/2)^2 = R^2(x,t)\}$. Note that assuming radial symmetry simplifies the level set equation, no y dependence is needed. The model equations are also simplified through the tensors ${\mathcal {A}}_u$, ${\mathcal {A}}_f$, ${\mathcal {A}}_g$ and ${\mathcal {K}}$ being cheaper to compute.

To summarize, we have considered a model for fluid flow combined with mineral precipitation and dissolution in a perforated domain. The model is non-isothermal and includes changes in the geometry of the pores, arising due to dissolution and precipitation. This leads to a model involving free boundaries at the pore scale, which are described by a level set formulation. We have applied a formal homogenization procedure and obtained upscaled effective equations for an idealized porous medium. The upscaled model describes the average behavior of the coupled system at the Darcy scale, but still honors the pore scale effects through effective parameters and cell problems. For a general pore geometry, the upscaled equations still depend on the microscopic variable through the level set equation. Assuming particular pore geometries may simplify the problem, but may result in less realistic models.