1 Introduction

Network thermodynamics (NT), created by Leonardo Peusner (Peusner 1970, 1986a) and George Oster, Alan Perelson, and Aharon Katchalsky (Oster et al. 1971; Perelson 1975) have introduced mathematical formalisms constituting one of many tools for analogical modeling of properties of complex systems functioning in different disciplines of science, technology, and medicine (Alhama et al. 2012; Bristow and Kennedy 2013; Imai 1996, 2003; Mikulecky 1990, 2005; Moya and Horno 2001, 2004; Peusner 1983a, b, 1985a, b, 1988, 2002; Peusner et al. 1985; Jamnik and Maier 2001; López-Garcia et al. 1996). A version of NT worked out by Oster, Perelson and Katchalsky uses symbols of connectivity graphs (Oster et al. 1971), whereas the NT version worked out by Peusner (PNT) uses non-equilibrium thermodynamics and theory of electric circuits (Peusner 1970, 1986a). Despite different symbols, the both of versions are of equal importance (Peusner 1986a). One of the PNT use is the mathematical modeling of membrane transport (Batko et al. 2013a, b, c; Horno et al. 1989, 1990, 1992; Imai 1989, 1996, 2003; Imai et al. 1989; Horno and Castilla 1994; Szczepański et al. 2012; Szczepański and Wódzki 2013; Ślęzak et al. 2012; Wódzki et al. 2004) and micro-flows (Biscombe et al. 2014).

The original papers of Peusner (1983a, b, 1985a, b, 1986a) as well as papers of followers of his idea (Ślęzak et al. 2012; Batko et al. 2013a, b, c) show that PNT enables the symmetric or hybrid transformation of the membrane transport Kedem–Katchalsky (K–K) equations from the classic form into the network form. The network form of the equations includes new types of coefficients, called the Peusner’s tensor coefficients (Ślęzak et al. 2012; Batko et al. 2013a, b, c, 2014). The coefficients may be calculated by means of transport parameters determined experimentally, i.e., the coefficients of hydraulic permeability (\(L_\mathrm{p}),\) solution permeability (\(\omega \)), and reflection (\(\sigma \)) (Ślęzak et al. 2012; Batko et al. 2013a, 2014). In the case of binary non-electrolyte solutions, the transformation results in two symmetric and two hybrid forms of the K–K equations (Peusner 1983a, 1985a, 1986a). Under conditions of concentration polarization involving creation of concentration boundary layers (CBLs) at the both sides of the membrane (Barry and Diamond 1984; Kargol 1999, 2000; Ślęzak 1989), the symmetric network forms of the K–K equations contain the Peusner’s tensor coefficients \(R_{ij}^{*}\) or \(L_{ij}^{*},\) whereas the hybrid network forms contain the Peusner’s tensor coefficients \(H_{ij}^{*}\) or \(P_{ij}^{*}\,(i,\,j \in \{1,\,2\})\) (Ślęzak et al. 2012; Batko et al. 2014). The network form of the K–K equations containing the Peusner’s coefficients \(R_{ij}^{*}\,(i,\,j \in \{1,\,2\})\) may be written in the following way (Ślęzak et al. 2012):

$$\begin{aligned} \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {\frac{\Delta \pi }{\overline{{C}}}} \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c} {R_{11} ^{*}}&{} {R_{12} ^{*}} \\ {R_{21} ^{*}}&{} {R_{22} ^{*}} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {J_\mathrm{vs} } \\ {J_\mathrm{ss} } \\ \end{array} }} \right] =[R^{*}] \left[ {{\begin{array}{c} {J_\mathrm{vs} } \\ {J_\mathrm{ss} } \\ \end{array} }} \right] , \end{aligned}$$
(1)

where \([R^{*}]\) is the matrix of Peusner’s coefficients \(R_{ij}^{*}\,(i,\, j \in \{1,\,2\})\) given by

$$\begin{aligned} {[R^{*}]}=\left[ {{\begin{array}{c@{\quad }c} {\frac{\zeta _\mathrm{s} \omega +\zeta _\mathrm{p} L_\mathrm{p} \overline{{C}}(1-\zeta _\mathrm{v} \sigma )(1-\zeta _\mathrm{a} \sigma )}{\zeta _\mathrm{p} L_\mathrm{p} \zeta _\mathrm{s} \omega }}&{} {-\frac{1}{\zeta _\mathrm{s} \omega }\left( 1-\zeta _\mathrm{v} \sigma \right) } \\ {-\frac{1}{\zeta _\mathrm{s} \omega }\left( 1-\zeta _\mathrm{a} \sigma \right) }&{} {\frac{1}{\overline{{C}}\zeta _\mathrm{s} \omega }} \\ \end{array} }} \right] , \end{aligned}$$
(1a)

where \(\Delta P-\Delta \pi ,\,\Delta \pi _{1}/\overline{{C}}\) are thermodynamic forces, \(\Delta P=P_\mathrm{h} -P_\mathrm{l}\) is the hydrostatic pressure difference (\(P_\mathrm{h},\,P_\mathrm{l}\) is the higher and lower value of hydrostatic pressure), \(\Delta \pi = RT\Delta C\) is the osmotic pressure difference generated by the concentration difference \(\Delta C =C_\mathrm{h}-C_\mathrm{l}\,(C_\mathrm{h},\,C_\mathrm{l}\) are the higher and the lower value of concentration), \(J_\mathrm{v}\) is the volume flux, \(J_\mathrm{ss}\) is the dissolved substance flux, RT is the product of gas constant and absolute temperature, \(\sigma \) is the reflection coefficient, \(\omega \) is the solution permeability coefficient, \(\overline{{C}} = (C_\mathrm{h} - C_\mathrm{l})[\ln (C_\mathrm{h}C_\mathrm{l}^{-1})]^{-1 }\) is the average solution concentration in the membrane, \(J_\mathrm{vs}\) and \(J_\mathrm{ss}\) are the volume and solution fluxes, \(\zeta _\mathrm{p},\,\zeta _\mathrm{v},\,\zeta _\mathrm{s}\), and \(\zeta _\mathrm{a}\) are, respectively, coefficients of hydraulic, osmotic, diffusive, and advective concentration polarization (Table 1).

Under the conditions of homogeneity of solutions separated by the membrane, i.e., when the condition \(\zeta _\mathrm{p}=\zeta _\mathrm{v}=\zeta _\mathrm{s}=\zeta _\mathrm{a} =1\) is fulfilled, Eqs. (1) and (1a) are simplified to the following expression (Peusner 1985a, 1986a)

$$\begin{aligned} \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {\frac{\Delta \pi }{\overline{{C}}}} \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c} {R_{11} }&{} {R_{12} } \\ {R_{21} }&{} {R_{22} } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {J_\mathrm{v} } \\ {J_\mathrm{s} } \\ \end{array} }} \right] =[R] \left[ {{\begin{array}{c} {J_\mathrm{v} } \\ {J_\mathrm{s} } \\ \end{array} }} \right] , \end{aligned}$$
(2)

where [R] is the matrix of Peusner’s coefficients \(R_{ij}\,(i,\,j\in \{1,\,2\})\) given by

$$\begin{aligned} {[R]}=\left[ {{\begin{array}{c@{\quad }c} {\frac{\omega +L_\mathrm{p} \overline{{C}}(1-\sigma )^{2}}{L_\mathrm{p} \omega }}&{} {-\frac{1}{\omega }(1-\sigma )} \\ {-\frac{1}{\omega }(1-\sigma )}&{} {\frac{1}{\overline{{C}}\omega }} \\ \end{array} }} \right] . \end{aligned}$$
(2a)

In Eq. (3), \(J_\mathrm{v}\,(J_\mathrm{v}> J_\mathrm{vs})\) and \(J_\mathrm{s}\,(J_\mathrm{s}>J_\mathrm{ss})\) stand for respectively the volume flux and the solution flux through the membrane under the conditions of homogeneity of solutions separated by the membrane. Determinants of the square matrix of Peusner’s coefficients \(R_{ij}^{*}\) and \(R_{ij}\) are equal to det \([R^{*}] =(\overline{{C}}\zeta _\mathrm{p}\zeta _\mathrm{s}L_\mathrm{p}\omega )^{-1}\) and det\([R]=(\overline{{C}}L_\mathrm{p}\omega )^{-1},\) whereas the quotient of the determinants is equal to det \([R^{*}]/\det [R]=(\zeta _\mathrm{p}\zeta _\mathrm{s})^{-1}.\)

Transforming Eq. (1) we get (Batko et al. 2014)

$$\begin{aligned} \left[ {{\begin{array}{c} {J_\mathrm{vs} } \\ {J_\mathrm{ss} } \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c} {L_{11} ^{*}}&{} {L_{12} ^{*}} \\ {L_{21} ^{*}}&{} {L_{22} ^{*}} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {\frac{\Delta \pi }{\overline{{C}}}} \\ \end{array} }} \right] =[L^{*}] \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {\frac{\Delta \pi }{\overline{{C}}}} \\ \end{array} }} \right] , \end{aligned}$$
(3)

where \([L^{*}]\) is the matrix of Peusner’s coefficients \(L_{ij}^{*}\,(i,\, j \in \{1,\, 2\})\) given by

$$\begin{aligned} {[L^{*}]}=\left[ {{\begin{array}{l@{\quad }l} {\zeta _\mathrm{p} L_\mathrm{p} }&{} {\overline{{C}}\left( 1-\zeta _\mathrm{v} \sigma \right) \zeta _\mathrm{p} L_\mathrm{p} } \\ {\overline{{C}}\left( 1-\zeta _\mathrm{a} \sigma \right) \zeta _\mathrm{p} L_\mathrm{p} }&{} {\overline{{C}}\left[ \zeta _\mathrm{s} \omega +\overline{{C}}\left( 1-\zeta _\mathrm{a} \sigma \right) \left( 1-\zeta _\mathrm{v} \sigma \right) \zeta _\mathrm{p} L_\mathrm{p}\right] } \\ \end{array} }} \right] . \end{aligned}$$
(3a)

If the condition \(\zeta _\mathrm{p}=\zeta _\mathrm{v}=\zeta _\mathrm{s}=\zeta _\mathrm{a} = 1\) is fulfilled, then Eqs. (3) and (3a) are simplified to the following expression (Peusner 1985a, 1986a)

$$\begin{aligned} \left[ {{\begin{array}{c} {J_\mathrm{v} } \\ {J_\mathrm{s} } \\ \end{array} }} \right] =\left[ {{\begin{array}{l@{\quad }l} {L_{11} }&{} {L_{12} } \\ {L_{21} }&{} {L_{22} } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {\frac{\Delta \pi }{\overline{{C}}}} \\ \end{array} }} \right] =[L] \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {\frac{\Delta \pi }{\overline{{C}}}} \\ \end{array} }} \right] , \end{aligned}$$
(4)

where [L] is the matrix of Peusner’s coefficients \(L_{ij}\,(i,\, j \in \{1,\,2\})\) given by

$$\begin{aligned} {[L]}=\left[ {{\begin{array}{l@{\quad }l} {L_\mathrm{p} }&{} {\overline{{C}}(1-\sigma )L_\mathrm{p} } \\ {\overline{{C}}(1-\sigma )L_\mathrm{p} }&{} {\overline{{C}}\left[ \omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p}\right] } \\ \end{array} }} \right] . \end{aligned}$$
(4a)

Determinants of the square matrix of Peusner’s coefficients \(L_{ij}^{*}\) and \(L_{ij}\) are equal to det \([L^{*}]=\overline{{C}}\zeta _\mathrm{p}\zeta _\mathrm{s}L_\mathrm{p}\omega \) and det\([L]=\overline{{C}}L_\mathrm{p}\omega \) (Peusner 1985a, 1986a; Batko et al. 2014), whereas the quotient of the determinants is equal to det\([L^{*}]/\det [L]=\zeta _\mathrm{p}\zeta _\mathrm{s}.\)

Equations (1)–(4) may be derived by the symmetric transformation of the classic K–K equations using the methods of PNT (Peusner 1983a, 1985a, 1986a). In the case of homogenous non-electrolyte solutions, PNT implements four tensor coefficients into the study of membrane transport: \(L_{ij},\,R_{ij},\,P_{ij}\) and \(H_{ij}\) (Peusner 1983a, 1985a, 1986a). For non-homogenous solutions, the tensor coefficients are as follows: \(L_{ij}^{*},\,R_{ij}^{*},\,P_{ij}^{*}\) and \( H_{ij}^{*}.\) The coefficients \(P_{ij}^{*}\) are derived when in Eq. (1) places of \(\Delta P-\Delta \pi \) and \(J_\mathrm{v}\) are swapped, whereas the coefficients \(H_{ij}^{*}\) are derived when places of \(\Delta \pi /\overline{{C}}\) and \(J_\mathrm{ss}\) are swapped.

It results from Eqs. (1a) and (2a) that for the tensor Peusner’s coefficients of the second degree \(R_{ij}^{*}\) and \(R_{ij}\,(i,\,j\in \{1,\,2\})\) we have \(R_{12}^{*} =-(1 -\zeta _\mathrm{v}\sigma )\zeta _\mathrm{s}^{-1}\omega ^{-1} \ne R_{21}^{*} =-(1-\zeta _\mathrm{a}\sigma )\zeta _\mathrm{s}^{-1}\omega ^{-1},\,R_{12}= -(1 -\sigma )\omega ^{-1} \ne R_{21}\) (Ślęzak et al. 2012). By contrast, Eqs. (3a) and (4a) show that for the tensor Peusner’s coefficients \(L_{ij}^{*}\) and \(L_{ij}\, (i,\,j\in \{1,\,2\})\) we have \(L_{12}^{*}=\overline{{C}}(1-\zeta _\mathrm{v}\sigma )\zeta _\mathrm{p}L_\mathrm{p} \ne L_{21}^{*}=\overline{{C}}(1-\zeta _\mathrm{a}\sigma )\zeta _\mathrm{p}L_\mathrm{p},\,L_{12}=\overline{{C}}(1 -\sigma )L_\mathrm{p}=L_{21}\) (Batko et al. 2014).

In the previous papers (Ślęzak et al. 2012; Batko et al. 2014), using the symmetric transformation of the classic K–K equations, the network form of the K–K equations was derived. The network equations contain the tensor coefficients \(R_{ij}^{*}\) or \(L_{ij}^{*},\) constituting the combination of the practical transport coefficients of membrane (\(L_\mathrm{p},\,\sigma ,\,\omega \)) and the average concentration of solutions in the membrane (\(\overline{{C}}).\) The equations were used to describe the membrane transport of aqueous glucose solution through a hemodialysis Nephrophan membrane under conditions of diffusion, and diffusion and convection simultaneously. The latter study includes the Rayleigh concentration number (\(R_\mathrm{C})\) used in equations describing the coefficients \(R_{ij}^{*}\) and \(L_{ij}^{*}.\) In the following paper, we are presenting the further network form of the K–K equations which were derived by the hybrid transformation of the classic K–K equations. The transformations were made by the methods of PNT. The equations derived contain the tensor coefficients \(P_{ij}^{*}\,(i,\, j\in \{1,\,2\}).\) Similar to previous experiments, the derived equations are used for the study of the membrane transport of aqueous glucose solutions through the polymeric membrane under the conditions of diffusion, and diffusion and convection simultaneously. The coefficients \(P_{11}^{*},\,P_{12}^{*},\,P_{21}^{*}\) and \(P_{22}^{*}\) are calculated for aqueous glucose solutions and for the hemodialysis Nephrophan membrane. Values of the coefficients are compared to values of the coefficients \(P_{11},\,P_{12},\,P_{21}\) and \(P_{22}\) calculated for the conditions of solution homogeneity and the same solution concentration but different configurations of the membrane system. The concentration dependence of the determinant of matrix quotient \([P^{*}]\) and [P] is calculated.

2 Theory

The source of coefficients \(P_{ij}^{*}\,(i,\,j\in \{1,\,2\})\) under the conditions of concentration polarization, for a two-directional two-port of PNT with a single input for the flux \(J_{1}^{*}\) and the flux-coupled force \(X_{1},\) as well as a single input for the flux \(J_{2}^{*}\) and the flux-coupled force \(X_{2},\) is a hybrid equation (Ślęzak 2011a, b)

$$\begin{aligned} \left[ {{\begin{array}{c} {J_{1} ^{*}} \\ {X_{2} } \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c} {P_{11} ^{*}}&{} {P_{12} ^{*}} \\ {P_{21} ^{*}}&{} {P_{22} ^{*}} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {X_{1} } \\ {J_{2} ^{*}} \\ \end{array} }} \right] . \end{aligned}$$
(5)

For the conditions of homogeneity of solutions separated by the membrane, the above equation is written as follows (Peusner 1983a, 1985a, 1986a)

$$\begin{aligned} \left[ {{\begin{array}{c} {J_{1} } \\ {X_{2} } \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c} {P_{11} }&{} {P_{12} } \\ {P_{21} }&{} {P_{22} } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {X_{1} } \\ {J_{2} } \\ \end{array} }} \right] . \end{aligned}$$
(6)

For the conditions of concentration polarization, the K–K equations may be written in the following way (Ślęzak et al. 2012)

$$\begin{aligned} J_\mathrm{vs}&= \zeta _\mathrm{p} L_\mathrm{p} \Delta P-\zeta _\mathrm{p} L_\mathrm{p} \zeta _\mathrm{v} \sigma \Delta \pi ,\end{aligned}$$
(7)
$$\begin{aligned} J_\mathrm{ss}&= L_\mathrm{p} \zeta _\mathrm{p} \left( 1-\zeta _\mathrm{a} \sigma \right) \overline{{C}}\Delta P+\left[ \zeta _\mathrm{s} \omega -L_\mathrm{p} \zeta _\mathrm{p} \sigma \zeta _\mathrm{v} \left( 1-\sigma \zeta _\mathrm{a}\right) \right] \Delta \pi . \end{aligned}$$
(8)

In the above equations \(J_\mathrm{vs}\) is the volume flux, and \(J_\mathrm{ss}\) is the solution flux under the conditions of concentration polarization. By contrast, \(\zeta _\mathrm{p},\,\zeta _\mathrm{v},\,\zeta _\mathrm{a}\) and \(\zeta _\mathrm{s}\) are respectively hydraulic, osmotic, advective and diffusive coefficient of Katchalsky (Ślęzak et al. 2012).

Employing simple algebra, Eqs. (7) and (8) may be transformed into the following ones:

$$\begin{aligned} J_\mathrm{vs}&= \frac{L_\mathrm{p} \zeta _\mathrm{ps}}{\omega \zeta _\mathrm{s} +L_\mathrm{p} \zeta _\mathrm{p}(1-\sigma \zeta _\mathrm{v} )(1-\sigma \zeta _\mathrm{a} )\overline{{C}}}\left[ {\omega \zeta _\mathrm{s} (\Delta P-\Delta \pi )+\left( 1-\sigma \zeta _\mathrm{s} \right) J_\mathrm{ss} } \right] ,\end{aligned}$$
(9)
$$\begin{aligned} \frac{\Delta \pi }{\overline{{C}}}&= \frac{1}{\omega \zeta _\mathrm{s} +L_\mathrm{p} \zeta _\mathrm{p} (1-\sigma \zeta _\mathrm{v})(1-\sigma \zeta _\mathrm{a})\overline{{C}}}\left[ {-L_\mathrm{p} \zeta _\mathrm{p} \left( 1-\sigma \zeta _\mathrm{v} \right) (\Delta P-\Delta \pi )+\frac{1}{\overline{{C}}}J_\mathrm{ss} } \right] .\nonumber \\ \end{aligned}$$
(10)

The above system of equations is the further version (hybrid version) of the K–K transformed equations for the conditions of concentration polarization, which may be written in a form of matrix equation

$$\begin{aligned} \left[ {{\begin{array}{c} {J_\mathrm{vs} } \\ {\frac{\Delta \pi }{\overline{{C}}}} \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c} {P_{11} ^{*}}&{} {P_{12} ^{*}} \\ {P_{21} ^{*}}&{} {P_{22} ^{*}} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {J_\mathrm{ss} } \\ \end{array} }} \right] =[P^{*}] \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {J_\mathrm{ss} } \\ \end{array} }} \right] , \end{aligned}$$
(11)

where \([P^{*}]\) is the matrix of Peusner’s coefficients \(P_{ij}^{*}\,(i,\,j\in \{1,\,2\})\) given by

$$\begin{aligned} {[P^{*}]}=\left[ {{\begin{array}{c@{\quad }c} {\frac{L_\mathrm{p} \zeta _\mathrm{p} \omega \zeta _\mathrm{s} }{\xi }}&{} {\frac{L_\mathrm{p} \zeta _\mathrm{p} \left( 1-\sigma \zeta _\mathrm{v}\right) }{\xi }} \\ {-\frac{L_\mathrm{p} \zeta _\mathrm{p} \left( 1-\sigma \zeta _\mathrm{v}\right) }{\xi }}&{} {\frac{1}{\overline{{C}}\xi }} \\ \end{array} }} \right] , \end{aligned}$$
(11a)

where \(\xi =[\omega \zeta _\mathrm{s} +L_\mathrm{p} \zeta _\mathrm{p} (1-\zeta _\mathrm{v} \sigma )(1-\zeta _\mathrm{a} \sigma )\overline{{C}}].\)

It results from Eq. (11a) that for non-diagonal coefficients \(P_{12}^{*} \ne P_{21}^{*}\) and \(P_{12}^{*}/P_{21}^{*} = (\zeta _\mathrm{v} \sigma - 1)/(1- \zeta _\mathrm{a}\sigma \)). Moreover, the matrix determinant \([P^{*}]\) is equal to

$$\begin{aligned} \det [P^{*}]=P_{11}^{*}P_{22} ^{*}-P_{12} ^{*}P_{21} ^{*}=\frac{\zeta _\mathrm{p} L_\mathrm{p} }{\overline{{C}}[\zeta _\mathrm{s} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} (1-\zeta _\mathrm{v} \sigma )(1-\zeta _\mathrm{a} \sigma )]}. \end{aligned}$$
(12)

For the conditions of homogeneity of solutions separated by a selective membrane, i.e., when the condition \(\zeta _\mathrm{p}=\zeta _\mathrm{v}=\zeta _\mathrm{s}=\zeta _\mathrm{a}= 1\) is fulfilled, Eq. (4) is taking the following form (Peusner 1983a, 1985a, 1986a)

$$\begin{aligned} \left[ {{\begin{array}{c} {J_\mathrm{v} } \\ {\frac{\Delta \pi }{\overline{{C}}}} \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c} {P_{11} }&{} {P_{12} } \\ {P_{21} }&{} {P_{22} } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {J_\mathrm{s} } \\ \end{array} }} \right] =[P] \left[ {{\begin{array}{c} {\Delta P-\Delta \pi } \\ {J_\mathrm{s}} \\ \end{array} }} \right] , \end{aligned}$$
(13)

where [P] is the matrix of Peusner’s coefficients \(P_{ij}\,(i,\, j\in \{1,\,2\})\) given by (Peusner 1983a, 1985a, 1986a)

$$\begin{aligned} {[P]}=\left[ {{\begin{array}{c@{\quad }c} {\frac{L_\mathrm{p} \omega \zeta _\mathrm{s} }{\omega +L_\mathrm{p} (1-\sigma )^{2}\overline{{C}}}}&{} {\frac{L_\mathrm{p} (1-\sigma )}{\omega +L_\mathrm{p} (1-\sigma )^{2}\overline{{C}}}} \\ {-\frac{L_\mathrm{p} (1-\sigma )}{\omega +L_\mathrm{p} (1-\sigma )^{2}\overline{{C}}}}&{} {\frac{1}{\overline{{C}}[\omega +L_\mathrm{p} (1-\sigma )^{2}\overline{{C}}}} \\ \end{array} }} \right] . \end{aligned}$$
(13a)

The determinant of the matrix [P] is equal to

$$\begin{aligned} \det [P]=P_{11} P_{22} -P_{12} P_{21} =\frac{L_\mathrm{p}}{\overline{{C}}[\omega +\overline{{C}}L_\mathrm{p} (1-\sigma )^{2}]}. \end{aligned}$$
(14)

Considering Eqs. (11a) and (13a), we are deriving the following expression for the selective membrane

$$\begin{aligned}&\displaystyle \frac{P_{11} ^{*}}{P_{11} }=\frac{\zeta _\mathrm{p} \zeta _\mathrm{s} [\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}{\zeta _\mathrm{s} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} (1-\zeta _\mathrm{v} \sigma )(1-\zeta _\mathrm{a} \sigma )},\end{aligned}$$
(15)
$$\begin{aligned}&\displaystyle \frac{P_{12} ^{*}}{P_{12} }=\frac{\zeta _\mathrm{p} L_\mathrm{p} (1-\zeta _\mathrm{v} \sigma )[\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}{(1-\sigma )[\zeta _\mathrm{s} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} (1-\zeta _\mathrm{v} \sigma )(1-\zeta _\mathrm{a} \sigma )]},\end{aligned}$$
(16)
$$\begin{aligned}&\displaystyle \frac{P_{21} ^{*}}{P_{21} }=\frac{\zeta _\mathrm{p} L_\mathrm{p} (1-\zeta _\mathrm{a} \sigma )[\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}{(1-\sigma )[\zeta _\mathrm{s} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} (1-\zeta _\mathrm{v} \sigma )(1-\zeta _\mathrm{a} \sigma )]},\end{aligned}$$
(17)
$$\begin{aligned}&\displaystyle \frac{P_{22} ^{*}}{P_{22} }=\frac{\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} }{\zeta _\mathrm{s} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} (1-\zeta _\mathrm{v}\sigma )(1-\zeta _\mathrm{a} \sigma )}. \end{aligned}$$
(18)

For a non-selective membrane (\(L_\mathrm{p}=L_\mathrm{pmax},\,\sigma = 0\) and \(\omega = \omega _{\max }),\) Eqs. (15)–(18) are written in the following forms

$$\begin{aligned} \frac{P_{11} ^{*}}{P_{11} }=\frac{\zeta _\mathrm{p} \zeta _\mathrm{s} [\omega _{\max } +\overline{{C}}L_\mathrm{pmax } ]}{\zeta _\mathrm{s} \omega { }_{\max }+\overline{{C}}\zeta _\mathrm{p} L_\mathrm{pmax } }, \end{aligned}$$
(15a)
$$\begin{aligned} \ \ \frac{P_{12} ^{*}}{P_{12} }=\frac{\zeta _\mathrm{p} L_\mathrm{pmax } [\omega _{\max } +\overline{{C}}L_\mathrm{pmax } ]}{\zeta _\mathrm{s} \omega _{\max } +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{pmax } }=\frac{P_{12} ^{*}}{P_{12} }, \end{aligned}$$
(16a)
$$\begin{aligned} \frac{P_{22} ^{*}}{P_{22} }=\frac{\omega _{\max } +\overline{{C}}L_\mathrm{pmax } }{\zeta _\mathrm{s} \omega _{\max } +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{pmax } }. \end{aligned}$$
(18a)

This results in \(P_{11}^{*}/P_{11}=\zeta _\mathrm{s}P_{12}^{*}/L_\mathrm{pmax}P_{12},\,P_{11}^{*}/P_{11}=\zeta _\mathrm{p}\zeta _\mathrm{s}P_{22}^{*}/P_{22}\) and \(P_{12}^{*}/P_{12}=\zeta _{p}L_\mathrm{pmax}P_{22}^{*}/P_{22}.\) By contrast, for a partially selective membrane (\(L_\mathrm{p }> 0,\,\sigma = 1\) and \(\omega = 0)\) we have \(P_{11}^{*}/P_{11}=P_{22}^{*}/P_{22} \rightarrow 0\) and \(P_{12}^{*}/P_{12}=P_{21}^{*}/P_{21} \rightarrow +\infty .\)

In order to make Eqs. (6)–(9) sensitive to hydrodynamic conditions, we may implement into them the Rayleigh concentration number (\(R_\mathrm{C}).\) The number controls the processes of turning from diffusive state into convective state in the membrane systems (Ślęzak et al. 1985, 2010): when the number value is becoming critical, then turning from diffusive (stable) state into convective (non-stable) state is noticed. In the previous paper (Ślęzak et al. 2010) it was shown that the critical value of \(R_\mathrm{C}\) is reached at a bifurcation point of the coordinates: \(\overline{{C}} = 5.41\,\mathrm{mol\,m }^{-3},\,(R_\mathrm{C})_\mathrm{crit.}= 1,709.3.\) To implement \(R_\mathrm{C}\) into Eqs. (6)–(9), we are using procedure presented in a previous paper (Ślęzak et al. 2012). The paper showed that with a sufficient approximation, we may write as follows

$$\begin{aligned} \zeta _\mathrm{p}&= \zeta _\mathrm{a} =1,\end{aligned}$$
(19)
$$\begin{aligned} \zeta _\mathrm{v}&= \zeta _\mathrm{p} =\zeta _\mathrm{i}. \end{aligned}$$
(20)

By contrast, the coefficient \(\zeta _{i}\) may be written with the equation (Katchalsky and Curran 1965; Ślęzak et al. 2012)

$$\begin{aligned} \zeta _{i} =D_{i}\left( D_{i} +2RT\omega \delta _{i}\right) ^{-1}, \end{aligned}$$
(21)

where \(D_{i}\) is the diffusion coefficient, RT is the product of gas constant and thermodynamic temperature, \(\delta _{i}\) is the thickness of CBL. For the diffusive conditions \(i=d,\) whereas for the convective conditions \(i=k.\)

Including Eq. (21) into Eqs. (15)–(18), we are deriving

$$\begin{aligned}&\displaystyle \frac{P_{11} ^{*}}{P_{11} }=\left( {1+\frac{2RTL_\mathrm{p} \omega \overline{{C}}(1-\sigma )\delta _{i} }{D_{i} [\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}} \right) ^{-1},\end{aligned}$$
(22)
$$\begin{aligned}&\displaystyle \frac{P_{12} ^{*}}{P_{12} }=\left( {1+\frac{2RT\omega \delta _{i} }{D_{i} (1-\sigma )}} \right) \left( {1+\frac{2RTL_\mathrm{p} (1-\sigma )\omega \overline{{C}}\delta _{i} }{D_{i} [\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}} \right) ^{-1},\end{aligned}$$
(23)
$$\begin{aligned}&\displaystyle \frac{P_{21} ^{*}}{P_{21} }=\left( {1+\frac{2RT\omega \delta _{i} }{D_{i} }} \right) \left( {1+\frac{2RTL_\mathrm{p} (1-\sigma )\omega \overline{{C}}\delta _{i} }{D_{i} [\omega +\overline{{C}}(1-\sigma )^{2}L_{p} ]}} \right) ^{-1}=\frac{P_{22} ^{*}}{P_{22} }. \end{aligned}$$
(24)

To derive Eqs. (16)–(18) for the diffusive conditions, the equations may be written assuming that \(i=d.\) Under non-convective (diffusive) conditions, the thickness of CBLs (\(\delta _\mathrm{d})\) for \(\overline{{C}} > (\overline{{C}})_{\mathrm{crit.}}\) is larger than that one under the convective conditions (\(\delta _\mathrm{k})\) and it depends on the solution concentration (Ślęzak et al. 2012). The diffusion coefficient value under the diffusive conditions (\(D_\mathrm{d})\) is approximately constant, i.e., it does not depend on the concentration of non-electrolyte solutions diluted and is lower than the diffusion coefficient value under the convective conditions (\(D_\mathrm{k}).\) Moreover, \(D_\mathrm{k}\) depends on the solution concentration. The equation for the diffusion coefficient under convective conditions (\(D_\mathrm{k})\) may be written as follows (Ślęzak et al. 2012)

$$\begin{aligned} D_\mathrm{k} =\frac{g\alpha _\mathrm{C} \delta _\mathrm{k} ^{3}(J_\mathrm{v} -J_\mathrm{vs} )}{2L_\mathrm{p} \sigma RT\nu R_\mathrm{C} }. \end{aligned}$$
(25)

Including Eq. (25) in Eqs. (22)–(24), we are deriving

$$\begin{aligned}&\displaystyle \frac{P_{11} ^{*}}{P_{11} }=\left( {1+\frac{4(RT)^{2}L_\mathrm{p} ^{2}\omega \sigma (1-\sigma )\overline{{C}}\nu R_\mathrm{C} }{g\alpha _\mathrm{C}\delta _\mathrm{k} ^{2}(J_\mathrm{v} -J_\mathrm{vs} )[\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}} \right) ^{-1},\end{aligned}$$
(26)
$$\begin{aligned}&\displaystyle \frac{P_{12} ^{*}}{P_{12} }=\left( {1+\frac{4(RT)^{2}L_\mathrm{p} \sigma \omega \nu R_\mathrm{C} }{g\alpha _\mathrm{C} (1-\sigma )\delta _\mathrm{k} ^{2}(J_\mathrm{v} -J_\mathrm{vs})}} \right) \left( {1+\frac{(RT)^{2}L_\mathrm{p} ^{2}\sigma \omega \overline{{C}}(1-\sigma )\nu R_\mathrm{C} }{g\alpha _\mathrm{C} \delta _\mathrm{k} ^{2}(J_\mathrm{v}-J_\mathrm{vs} )[\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}} \right) ^{-1},\nonumber \\\end{aligned}$$
(27)
$$\begin{aligned}&\displaystyle \frac{P_{21} ^{*}}{P_{21} }=\left( {1+\frac{4(RT)^{2}L_\mathrm{p} \sigma \omega \nu R_\mathrm{C} }{g\alpha _\mathrm{C} \delta _\mathrm{k} ^{2}(J_\mathrm{v} -J_\mathrm{vs} )}}\right) \left( {1+\frac{4(RT)^{2}L_\mathrm{p} ^{2}\sigma \omega \overline{{C}}(1-\sigma )\nu R_\mathrm{C} }{g\alpha _\mathrm{C} \delta _\mathrm{k} ^{2}(J_\mathrm{v}-J_\mathrm{vs} )[\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}} \right) ^{-1}=\frac{P_{22} ^{*}}{P_{22} }.\nonumber \\ \end{aligned}$$
(28)

The equation for the diffusion coefficient under convective conditions (\(D_\mathrm{k})\) may also be written in the following form

$$\begin{aligned} D_\mathrm{k} =\frac{g\alpha _\mathrm{C} \delta _\mathrm{k} ^{3}(J_\mathrm{s} -J_\mathrm{ss} )}{2\omega RT\nu R_\mathrm{C} }. \end{aligned}$$
(29)

Including Eq. (29) in Eqs. (22)–(24), we are deriving

$$\begin{aligned}&\displaystyle \frac{P_{11} ^{*}}{P_{11} }=\left( {1+\frac{4(RT)^{2}L_\mathrm{p} \omega ^{2}(1-\sigma )\overline{{C}}\nu R_\mathrm{C} }{g\alpha _\mathrm{C} \delta _\mathrm{k} ^{2}(J_\mathrm{s}-J_\mathrm{sm} )[\omega +\overline{{C}}(1-\sigma )L_\mathrm{p} ]}} \right) ^{-1},\end{aligned}$$
(30)
$$\begin{aligned}&\displaystyle \frac{P_{12} ^{*}}{P_{12} }=\frac{[g\alpha _\mathrm{C} (1-\sigma )(J_\mathrm{s}-J_\mathrm{sm} )\delta _\mathrm{k} ^{2}+4(RT)^{2}\omega ^{2}\nu R_\mathrm{C} ][\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}{(1-\sigma )\{g\alpha _\mathrm{C} \delta _\mathrm{k} ^{2}(J_\mathrm{s} -J_\mathrm{sm} )[\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p}]+4(RT)^{2}\omega ^{2}L_\mathrm{p} \overline{{C}}(1-\sigma )\nu R_\mathrm{C} \}},\nonumber \\\end{aligned}$$
(31)
$$\begin{aligned}&\displaystyle \frac{P_{21} ^{*}}{P_{21} }=\frac{P_{22} ^{*}}{P_{22}}=\frac{[g\alpha _\mathrm{C} \delta _\mathrm{k} ^{2}(J_\mathrm{s} -J_\mathrm{sm} )+4(RT)^{2}\omega ^{2}\nu R_\mathrm{C} ][\omega +\overline{{C}}(1-\sigma )^{2}L_\mathrm{p} ]}{g\alpha _\mathrm{C}\delta _\mathrm{k} ^{2}(J_\mathrm{s} -J_\mathrm{sm} )[\omega +\overline{{C}}(RT)^{2}L_\mathrm{p}]+4(RT)^{2}\omega ^{2}L_\mathrm{p} \overline{{C}}\nu R_\mathrm{C} }. \end{aligned}$$
(32)

Equations for \(\delta _\mathrm{d}\) and \(\delta _\mathrm{k}\) may be calculated using the equations below (Ślęzak et al. 2012)

$$\begin{aligned}&\displaystyle \delta _\mathrm{d} =-\frac{D_\mathrm{d} }{2RT\omega _\mathrm{m} }\left( {1-\frac{J_\mathrm{v} }{J_\mathrm{vs} }} \right) ,\end{aligned}$$
(33)
$$\begin{aligned}&\displaystyle \delta _\mathrm{k} =\frac{RT}{2(J_\mathrm{v} -J_\mathrm{vm} )}\left( {\frac{L_\mathrm{p} \sigma \omega \nu R_\mathrm{C} }{g\alpha _\mathrm{C} }} \right) ^{0.5}, \end{aligned}$$
(34)

or

$$\begin{aligned} \delta _\mathrm{d}&= -\frac{D_\mathrm{d} }{2RT\omega _\mathrm{m} }\left( {1-\frac{J_\mathrm{s} }{J_\mathrm{ss} }} \right) ,\end{aligned}$$
(35)
$$\begin{aligned} \delta _\mathrm{k}&= \frac{\omega RT}{2(J_\mathrm{s} -J_\mathrm{sm} )}\left( {\frac{\nu R_\mathrm{C} }{g\alpha _\mathrm{C} }} \right) ^{0.5}. \end{aligned}$$
(36)

In the equations above \(J_\mathrm{v},\,J_\mathrm{vs}\,(J_\mathrm{v} >J_\mathrm{vs}),\,J_\mathrm{s},\,J_\mathrm{ss}\,(J_\mathrm{s} > J_\mathrm{ss})\) may be determined in a series of independent experiments (Ślęzak et al. 2012). By contrast, the values \(\delta _\mathrm{d}\) and \(\delta _\mathrm{k}\) may be determined by optical methods (Dworecki et al. 2003; Dworecki et al. 2005). The Peusner’s coefficients \(P_{ij}^{*}\) and \(P_{ij}\) in the matrixes \([P^{*}]\) and [P] may be linked by the determinant of matrix quotient, which may be written in the following way

$$\begin{aligned} \frac{\det [P^{*}]}{\det [P]}=\det \frac{[P^{*}]}{[P]}=\frac{P_{11} ^{*}P_{22} ^{*}-P_{12}^{*}P_{21} ^{*}}{P_{11} P_{22} -P_{12} P_{21}}=\frac{\zeta _\mathrm{p} [\omega +\overline{{C}}L_\mathrm{p} (1-\sigma )^{2}]}{\zeta _\mathrm{s} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} (1-\zeta _\mathrm{v} \sigma )(1-\zeta _\mathrm{a}\sigma )}.\quad \quad \end{aligned}$$
(37)

Assuming that \(\zeta _\mathrm{p}=\zeta _\mathrm{a} = 1\) and \(\zeta _\mathrm{v}=\zeta _\mathrm{s}=\zeta ,\) and including Eqs. (21) and (25), then Eq. (37) can be written for the diffusive and convective state, respectively

$$\begin{aligned}&\displaystyle \left( {\det \frac{[P^{*}]}{[P]}} \right) _\mathrm{d} =\frac{[\omega +\overline{{C}}L_\mathrm{p} (1-\sigma )^{2}][D_\mathrm{d} +2RT\omega \delta _\mathrm{d} )]}{D_\mathrm{d} [\omega +\overline{{C}}L_\mathrm{p} (1-\sigma )^{2}]+2RT\overline{{C}}L_\mathrm{p}\omega (1-\sigma )\delta _\mathrm{d} },\end{aligned}$$
(38)
$$\begin{aligned}&\displaystyle \det \left( {\frac{[P^{*}]}{[P]}} \right) _\mathrm{k} =\left[ {1+\frac{4(RT)^{2}L_\mathrm{p} \sigma \omega \nu R_\mathrm{C} }{g\alpha _\mathrm{C} \delta _\mathrm{k}^{2}(J_\mathrm{v} -J_\mathrm{vs} )}} \right] \left[ {1+\frac{4\overline{{C}}(RT)^{2}L_\mathrm{p} ^{2}\sigma \omega \nu (1-\sigma )R_\mathrm{C} }{g\alpha _\mathrm{C} \delta _\mathrm{k} ^{2}(J_\mathrm{v} -J_\mathrm{vs} )[\omega +\overline{{C}}L_\mathrm{p} (1-\sigma )^{2}]}} \right] ^{-1}.\nonumber \\ \end{aligned}$$
(39)

3 Calculations Results and Discussion

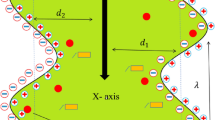
In order to calculate the coefficients \(P_{11}^{*},\,P_{12}^{*},\,P_{21}^{*},\,P_{22}^{*}P_{11},\,P_{12}=P_{21},\,P_{22}^{*},\,P_{11}^{*}/P_{11},P_{12}^{*}/P_{12},\,P_{21}^{*}/P_{21},\,P_{22}^{*}/P_{22},\) as well as det(\([P^{*}]/[P]\)) we are using the following data: \(L_\mathrm{p}= 4.9 \times 10^{-12}\,\hbox {m}^{3}\,\hbox {N}^{-1}\,\hbox {s }^{-1},\,\sigma = 0.068,\,\omega = 0.8 \times 10^{-9}\,\hbox {mol}\,\hbox {N}^{-1}\,\hbox {s}^{-1},\,C_\mathrm{h}= 2.6\,\mathrm{mol\, m}^{-3}\) do \(C_\mathrm{h}= 101\,\mathrm{mol\,m}^{-3},\,C_\mathrm{l} = 2.6\,\mathrm{mol\,m}^{-3},\,D_\mathrm{d} = 0.69\times 10^{-9}\,\hbox {m}^{2}\,\hbox { s}^{-1},\,\alpha _\mathrm{C}=\rho _\mathrm{l}^{-1 }\partial \rho /\partial C = 6.01\times 10^{-5}\,\hbox { m }^{3}\, \hbox { mol}^{-1},\,\nu _\mathrm{h}=\nu _\mathrm{l}(1 + \gamma _{1}C_\mathrm{h})\) when coefficients \(\gamma _{1}=\nu _\mathrm{l}^{-1}\partial \nu /\partial C = 3.95 \times 10^{-4}\, \hbox { m} ^{3}\, \hbox { mol }^{-1},\,\nu _\mathrm{l}= 1.012 \times 10^{-6}\, \hbox { m} ^{2}\, \hbox { s }^{-1}\) and (\(R_\mathrm{C})_\mathrm{crit. }=1,709.3\) (Ślęzak et al. 2010; Ślęzak et al. 2012). The coefficient values \(L_\mathrm{p},\,\sigma \) and \(\omega \) were determined under conditions of intensive stirring of solutions (Katchalsky and Curran 1965; Ślęzak 1989). Therefore, their values are independent of the membrane configuration, i.e., setup of the membrane and solutions separated by the membrane relative to a gravitation vector. According to Fig. 1, in the case of single-membrane system in which the membrane is placed horizontally, two configurations are distinguished, namely A and B (Ślęzak 1989). In the configuration A, the solution with the concentration \(C_\mathrm{l}\) is in a compartment above the membrane, and with the concentration \(C_\mathrm{h}\)—under the membrane. The diverse placement of solutions towards the membrane mounted horizontally is provided in the configuration B.

Table 1 Values of the volume fluxes of homogeneous solution \((J_\mathrm{v}),\) volume fluxes of non-homogeneous solution in diffusive–convective state \((J_\mathrm{vs}),\) osmotic \((\zeta _\mathrm{v})\) and diffusive \((\zeta _\mathrm{s})\) concentration polarization coefficient in configurations A \((\zeta _\mathrm{vA},\,\zeta _\mathrm{sA})\) and B \((\zeta _\mathrm{vB},\,\zeta _\mathrm{sB}),\) and thicknesses of concentration boundary layers \((\delta _{i})\) in diffusive \((\delta _\mathrm{d})\) and convective \((\delta _\mathrm{k})\) states for various mean concentrations of glucose \((\overline{{C}};\)Ślęzak et al. 2012)
Full size table

Under conditions of concentration polarization, i.e., when solutions separated by the membrane are not stirred mechanically, at the both sides of the membrane the CBLs are created limiting the volume and diffusive flows of the solution (Abu-Rjal et al. 2014; Barry and Diamond 1984; Jasik-Ślęzak et al. 2011; Kargol 1999, 2000; Ślęzak 1989; Wang et al. 2014). The CBLs are created as a result of molecular diffusion of a dissolved substance from the solution with the higher concentration into the solution with the lower concentration (Dworecki et al. 2003; Nikonenko et al. 2010; Wang et al. 2014). That fact may be included in equations introducing the additional/supporting coefficients \(\zeta _\mathrm{p},\,\zeta _\mathrm{v},\,\zeta _\mathrm{s}\) and \(\zeta _\mathrm{a}.\) For the haemodialysis Nephrophan membrane and aqueous glucose solutions, the coefficients \(\zeta _\mathrm{v}\) and \(\zeta _\mathrm{s}\) determined under the conditions of concentration polarization depend on the concentration of solutions separated by the membrane as well as on the configuration of membrane system (Ślęzak et al. 2012). By contrast, the coefficients \(\zeta _\mathrm{p}\) and \(\zeta _\mathrm{a}\) fulfill the condition \(\zeta _\mathrm{p }=\zeta _\mathrm{a}= 1\) under conditions of solution homogeneity as well as conditions of concentration polarization (Ślęzak et al. 2012). The dependences \(\zeta _\mathrm{v}=f(\overline{{C}})\) and \(\zeta _\mathrm{s}=f(\overline{{C}}),\,J_\mathrm{v}=f(\overline{{C}}),\,J_\mathrm{vs}=f(\overline{{C}}),\,\delta _\mathrm{d}=f(\overline{{C}})\) and \(\delta _\mathrm{k}=f(\overline{{C}})\) were already presented (Ślęzak et al. 2012). The calculations results of the dependence \(P_{11}^{*}=f(\overline{{C}}),\,P_{12}^{*}=f(\overline{{C}}),\,P_{21}^{*}=f(\overline{{C}}),\,P_{22}^{*}=f(\overline{{C}}),P_{11}=f(\overline{{C}}),\,P_{12}=P_{21}=f(\overline{{C}}),\,P_{22}^{*}=f(\overline{{C}}),\,P_{11}^{*}/P_{11}=f(\overline{{C}}),\,P_{12}^{*}/P_{12}=f(\overline{{C}}),\,P_{21}^{*}/P_{21}=f(\overline{{C}}),\,P_{22}^{*}/P_{22}=f(\overline{{C}})\) and det\([P^{*}]/\det [P] = f(\overline{{C}})\) are presented in Figs. 2, 3, 4, 5, 6, 7, 8, and 9.

Fig. 1
figure 1

Configurations A and B of a single-membrane system: M membrane, \(l_{l}\) and \(l_{h}\) the concentration boundary layers (CBLs), \(P_{h}\) and \(P_{l}\) mechanical pressures, \(C_{l}\) and \(C_{h}\) concentrations of solutions outside the boundaries, \(C_{e}\) and \(C_{i}\) the concentrations of solutions at boundaries \(l_\mathrm{l}/{M}\) and \(M/l_\mathrm{h},\,J_{vm}\) the volume fluxes through membrane \(M,\, J_{vs}\) the volume fluxes through complex \(l_\mathrm{l}/M/l_\mathrm{h},\,J_{sl},\,J_{sh}\) and \(J_{sm}\) the solute fluxes through layers \(l_\mathrm{l},\,l_\mathrm{h}\) and membrane, respectively, \(J_{ss}\) the solute fluxes through complex \(l_\mathrm{l}/M/l_\mathrm{h}\) (Ślęzak et al. 2012)

Full size image
Fig. 2
figure 2

The graphic illustration of dependence \(P_{11}^{*}=f(\overline{{C}})\) for aqueous glucose solutions in a concentration polarization conditions for the configuration A (graph 1), and B (graph 2) of the membrane system. The graph 3 illustrates the dependence \(P_{11}=f(\overline{{C}})\) in conditions of homogeneous solutions separated by the membrane. The values of the coefficients \(P_{11}^{*}\) and \(P_{11 }\) were calculated on the basis of Eq. (11) and of Eq. (13), respectively

Full size image
Fig. 3
figure 3

The graphic illustration of dependence \(P_{12}^{*}=f(\overline{{C}})\) for aqueous glucose solutions in a concentration polarization conditions for the configuration A (graph 1), and B (graph 2) of the membrane system. The graph 3 illustrates the dependence \(P_{12}=f(\overline{{C}})\) in conditions of homogeneous solutions separated by the membrane. The values of the coefficients \(P_{12}^{*}\) and \(P_{12}\) were calculated on the basis of Eq. (11) and of Eq. (13), respectively,

Full size image
Fig. 4
figure 4

The graphic illustration of dependence \(P_{21}^{*}=f(\overline{{C}})\) for aqueous glucose solutions in a concentration polarization conditions for the configuration A (graph 1), and B (graph 2) of the membrane system. The graph 3 illustrates the dependence \(P_{21}=f(\overline{{C}})\) in conditions of homogeneous solutions separated by the membrane. The values of the coefficients \(P_{12}^{*}\) and \(P_{12}\) were calculated on the basis of Eq. (11) and of Eq. (13), respectively,

Full size image

The calculations results of the coefficient dependence \(P_{11}^{*}=f(\overline{{C}})\) and \(P_{11}=f(\overline{{C}})\) for the configurations A and B of the membrane system within Eqs. (11) and (13) are depicted in Fig. 2. Figure shows that the values of coefficient \(P_{11}\) are decreasing linearly together with the increase in the value \(\overline{{C}}.\) By contrast, the values of coefficient \(P_{11}^{*}\) for \(\overline{{C}}\) fulfilling the condition 0 \(\le \overline{{C}}\le 5.41\,\mathrm{mol\,m}^{-3}\) are decreasing linearly and do not depend on the configuration of the membrane system. For \(\overline{{C}} > 5.41\,\mathrm{mol\,m }^{-3},\) the value of coefficient \(P_{11}^{*}\) depends on both the value \(\overline{{C}}\) and the configuration of the membrane system. Moreover, from the comparison of the value \(P_{11}^{*}\) for the same values \(\overline{{C}}> 5.41\,\mathrm{mol\,m }^{-3}\) and the configurations A and B of the membrane system, it is resulting that (\(P_{11}^{*})_\mathrm{A} < (P_{11}^{*})_\mathrm{B}.\) Within the whole range of \(\overline{{C}},\) the following condition (\(P_{11}^{*})_{\mathrm{A}} < (P_{11}^{*})_{\mathrm{B}} < P_{11}\) is fulfilled.

Fig. 5
figure 5

The graphic illustration of dependence \(P_{22}^{*}=f(\overline{{C}})\) for aqueous glucose solutions in a concentration polarization conditions for the configuration A (graph 1), and B (graph 2) of the membrane system. The graph 3 illustrates the dependence \(P_{22}=f(\overline{{C}})\) in conditions of homogeneous solutions separated by the membrane. The values of the coefficients \(P_{22}^{*}\) and \(P_{22}\) were calculated on the basis of Eq. (11) and of Eq. (13), respectively

Full size image
Fig. 6
figure 6

The graphic illustration of dependence \(P_{11}^{*}/P_{11}= f(\overline{{C}})\) for the configuration A (graphs 1 and 1 \(^{\prime }\)) and B (graphs 2 and 2 \(^{\prime }\)) of the membrane system. Graphs 1 and 2 were calculated on the basis of Eq. (15), graph 1 \(^{\prime }\) on the basis of Eq. (22), and graph 2\(^{\prime }\) on the basis of Eq. (26)

Full size image
Fig. 7
figure 7

The graphic illustration of dependence \(P_{ij}^{*}/P_{ij}= f(\overline{{C}})\,(i,\,j\in \{1,\,2\})\) for aqueous glucose solutions in condition a concentration polarization for configuration A (graphs 1, 1 \(^{\prime }\), 3, 3 \(^{\prime }\)) and B (graphs 2, 2 \(^{\prime }\), 4, 4 \(^{\prime }\)) of the membrane system. The graphs 1, 1 \(^{\prime }\), 2 and 2 \(^{\prime }\) illustrates the dependence \(P_{12}^{*}/P_{12}=f(\overline{{C}})\) and graphs 3, 3 \(^{\prime }\), 4 and 4 \(^{\prime }\)—the dependence \(P_{21}^{*}/P_{21}= P_{22}^{*}/P_{22}=f(\overline{{C}}).\) Graphs 1 and 2 were calculated on the basis of Eq. (16), graphs 3 and 4 on the basis of Eqs. (17) and (18), graph 1 \(^{\prime }\) on the basis of Eq. (23), and graph 2 \(^{\prime }\) on the basis of Eq. (27), graph 3 \(^{\prime }\) on the basis of Eq. (24) and graph 4 \(^{\prime }\) on the basis of Eq. (28)

Full size image
Fig. 8
figure 8

The graphic illustration of dependence det(\([P^{*}]/[P])=f(\overline{{C}})\) for aqueous glucose solutions in a concentration polarization conditions for the configuration A (graphs 1 and 1 \(^{\prime }\)), and B (graphs 2 and 2 \(^{\prime }\)) of the membrane system. Graphs 1 and 2 were calculated on the basis of Eq. (37), graph 1 \(^{\prime }\) on the basis of Eq. (38), and graph 2 \(^{\prime }\) on the basis of Eq. (39)

Full size image
Fig. 9
figure 9

The graphic illustration of dependence \(\kappa _{ij}= f(\overline{{C}})\, (i,\, j\in \{1,\,2\})\) for aqueous glucose solutions in a concentration polarization conditions. Graphs 1–3 were calculated on the basis of Eqs. (41)–(43), graph 1 \(^{\prime }\) on the basis of Eq. (44), graph 2 \(^{\prime }\) on the basis of Eq. (45) and graph 3 \(^{\prime }\) on the basis of Eq. (46)

Full size image

The calculations results of the coefficient dependence \(P_{12}^{*}=f(\overline{{C}})\) and \(P_{12 }=f(\overline{{C}})\) for the configurations A and B of the membrane system are depicted in Fig. 3. Figure shows that together with the increase in value \(\overline{{C}},\) the values of coefficients \(P_{12}\) are decreasing linearly and are the same in the configurations A and B of the membrane system. By contrast, the values of coefficient \(P_{12}^{*}\) for \(0 \le \overline{{C}}\le 5.41\,\mathrm{mol\,m}^{-3}\) are decreasing approximately linearly. Similar to the coefficient \(P_{11}^{*},\) the coefficient value \(P_{12}^{*}\) does not depend on the configuration of the membrane system. For \(\overline{{C}} > 5.41\,\mathrm{mol\,m }^{-3},\) the coefficient value \( P_{12}^{*}\) depends on both the value \(\overline{{C}}\) and the configuration of the membrane system. The comparison of values \(P_{12}^{*}\) for the same values \(\overline{{C}}> 5.41\,\mathrm{mol\,m } ^{-3}\) and the configurations A and B of the membrane system showed that (\(P_{12}^{*})_\mathrm{A} >(P_{12}^{*})_\mathrm{B}.\) Within the whole range of \(\overline{{C}},\) the following condition (\(P_{12}^{*})_\mathrm{A} > (P_{12}^{*})_\mathrm{B} > P_{12}\) is fulfilled.

The dependences \(P_{21}^{*}=f(\overline{{C}})\) and \(P_{21}=f(\overline{{C}})\) for the configurations A and B of the membrane system are presented in Fig. 4. Figure shows that together with the increase in value \(\overline{{C}},\) the values of coefficient \(P_{21 }\) are increasing linearly and are the same in both configurations of the membrane system. By contrast, the values of coefficient \(P_{21}^{*}\) for \(0 \le \overline{{C}}\le 5.41\,\mathrm{mol\, m }^{-3}\) are increasing linearly and are the same in the configurations A and B of the membrane system. For \(\overline{{C}} > 5.41\,\mathrm{mol\, m }^{-3},\) the coefficient value \(P_{21}^{*}\) depends on both the value \(\overline{{C}}\) and the configurations A and B of the membrane system. From the comparison of values \(P_{21}^{*}\) for the same values \(\overline{{C}}\) it is resulting that for \(\overline{{C}}>5.41\,\mathrm{mol\, m} ^{-3}\) and the configurations A and B of the membrane system, the following condition (\(P_{21}^{*})_\mathrm{A} < (P_{21}^{*})_\mathrm{B}\) is fulfilled. Moreover, within the whole range of \(\overline{{C}}\) the following condition (\(P_{21}^{*})_\mathrm{A} < (P_{21}^{*})_\mathrm{B} < P_{21}\) is fulfilled.

The dependences depicted in Fig. 5 \(P_{22}^{*}=f(\overline{{C}})\) and \(P_{22 }=f(\overline{{C}})\) are hyperbolas. The dependences \(P_{22}^{*}=f(\overline{{C}})\) illustrated by a graph 1 (for configuration A) and a graph 2 (for configuration B) were obtained under conditions of concentration polarization. The comparison of the curves present that for 0 \(\le \overline{{C}}\le 5.41\,\mathrm{mol\, m }^{-3}\) we have (\(P_{22}^{*})_\mathrm{A} = (P_{22}^{*})_\mathrm{B},\) whereas for \(\overline{{C}}> 5.41\,\mathrm{mol\, m }^{-3}\) we have (\(P_{22}^{*})_\mathrm{A} > (P_{22}^{*})_\mathrm{B}.\) The dependence \(P_{22 }=f(\overline{{C}})\) on a graph 3 shows that under the conditions of homogeneity of solutions separated by the membrane, the values \(P_{22}\) are equal, i.e., (\(P_{22}^{*})_\mathrm{A} = (P_{22}^{*})_\mathrm{B}.\) Figure shows as well that for \(\overline{{C}}> 5.41\,\mathrm{mol\, m }^{-3}\) we have (\(P_{22}^{*})_\mathrm{A} < (P_{22}^{*})_\mathrm{B} < P_{22}.\)

Considering the results showed in Fig. 2, it is possible to spot particular quantity differences between the concentration dependences of coefficients \(P_{11}^{*}\) and \(P_{11}\) and the dependence of coefficient value \(P_{11}^{*}\) on the configuration of the membrane system. Therefore, Fig. 6 presents the dependence \(P_{11}^{*}/P_{11}=f(\overline{{C}})\) for the configuration A (graph 1) and the configuration B (graph 2) of the membrane system. The dependences were calculated using Eqs. (15), (22), (26) and (30). Figure shows that \(P_{11}^{*}/P_{11}\) depend on \(\overline{{C}},\) and for \(\overline{{C}} > 5.41\,\mathrm{mol\, m}^{-3 }\)—they depend on the configuration of the membrane system, too. Moreover, from figure it results that for \(\overline{{C}} > 5.41\,\mathrm{mol\,m } ^{-3 }\) we have the following values of relation (\(P_{11}^{*}/P_{11})_\mathrm{B} >(P_{11}^{*}/P_{11})_\mathrm{B}.\) It may be noticed that the point with coordinates \(P_{11}^{*}/P_{11 }= 0.898\) and \(\overline{{C}}=5.41\, \mathrm{mol\, m }^{-3 }\) is a last joint point of the graphs 1 and 2. The point may be treated as the bifurcation point. It means that crossing the bifurcation point and reaching by \(P_{11}^{*}\) the value belonging to the graphs 1or 2 are constituting the choice between convective state (B) and non-convective state (A) of the membrane system.

Data depicted in Figs. 3, 4 and 5 allow to make the quantity analysis of the concentration dependences \(P_{12}^{*}\) and \(P_{12},\,P_{21}^{*}\) and \(P_{21},\, P_{22}^{*}\) and \(P_{22}\) on the configuration of the membrane system. Therefore, Fig. 7 presents the dependences \(P_{12}^{*}/P_{12}=f(\overline{{C}})\) and \(P_{21}^{*}/P_{21}=P_{22}^{*}/P_{22}=f(\overline{{C}})\) for the configuration A (graphs 1, 1\(^{\prime }\), 3 and 3\(^{\prime }\)) and the configuration B (graphs 2, 2\(^{\prime }\), 4 and 4\(^{\prime }\)) of the membrane system. The dependences were calculated using Eqs. (16)–(18), (23), (24), (27) and (28). The graphs depicted in Fig. 7 indicate that for \(\overline{{C}} \le 5.41\,\mathrm{mol\, m}^{-3},\) the values \(P_{12}^{*}/P_{12},\,P_{21}^{*}/P_{21}\) and \(P_{22}^{*}/P_{22}\) depend on \(\overline{{C}}\) but do not depend on the configuration of the membrane system. By contrast, for \(\overline{{C}} > 5.41\,\mathrm{mol\, m }^{-3 }\) the values \(P_{12}^{*}/P_{12},\,P_{21}^{*}/P_{21}\) and \(P_{22}^{*}/P_{22}\) depend on both \(\overline{{C}}\) and the configuration of the membrane system. Moreover, it may be noticed that points with the coordinates \(P_{12}^{*}/P_{12 }= 4.55\) (for graphs 1 and 2), \(P_{12}^{*}/P_{12 }= 4.7\) (for graphs 1\(^{\prime }\) and 2\(^{\prime }\)), \(P_{21}^{*}/P_{21 }=P_{22}^{*}/P_{22} = 4.27\) (for graphs 3 and 4), and \(P_{21}^{*}/P_{21 }=P_{22}^{*}/P_{22} = 4.42\) (for graphs 3\(^{\prime }\) and 4\(^{\prime }\)) as well as \(\overline{C}= 5.41\,\mathrm{mol\, m }^{-3 }\) are the last joint point of the graphs. The point has the properties of the bifurcation point. What is more, the graphs show that for \(\overline{{C}} > 5.41\,\mathrm{mol\, m}^{-3}\) we have (\(P_{12}^{*}/P_{12})_\mathrm{B} < (P_{12}^{*}/P_{12})_\mathrm{A},\,(P_{21}^{*}/P_{21})_\mathrm{B} < (P_{21}^{*}/P_{21})_\mathrm{A}\) and (\(P_{22}^{*}/P_{22})_\mathrm{B} < (P_{22}^{*}/P_{22})_\mathrm{A}.\) Figure shows as well that \((P_{12}^{*}/P_{12})_\mathrm{A} >(P_{21}^{*}/P_{21})_\mathrm{A}=(P_{22}^{*}/P_{22})_\mathrm{A}\) and \((P_{12}^{*}/P_{12})_\mathrm{B} >(P_{21}^{*}/P_{21})_\mathrm{B}=(P_{22}^{*}/P_{22})_\mathrm{B}.\)

Figure 8 depicts the calculations results of the dependence det(\([P^{*}]/[P]) =f(\overline{{C}})\) for the configuration A (graphs 1 and 1\(^{\prime }\)) and the configuration B (graphs 2 and \(2^{*}).\) The graphs 1 and 2 were calculated on the basis of Eq. (37), graph 1\(^{\prime }\) on the basis of Eq. (38), and graph 2\(^{\prime }\) on the basis of Eq. (39). From the curves presented it results that for \(\overline{{C}} \le 5.41\,\mathrm{mol\, m }^{-3},\) the values det(\([P^{*}]/[P]\)) depend on \(\overline{{C}}\) but do not depend on the configuration of the membrane system. By contrast, for \(\overline{{C}} > 5.41\,\mathrm{mol\, m} ^{-3 }\) the values det(\([P^{*}]/[P]\)) depend on both \(\overline{{C}}\) and the configuration of the membrane system. Moreover, it may be noticed that points with the coordinates det(\([P^{*}]/[P]) = 4.27\) (for graphs 1 and 2) and det(\([P^{*}]/[P]) = 4.41\) (for curves 1 and 2) as well as \(\overline{{C}}= 5.41\,\mathrm{mol\, m }^{-3 }\) are the last joint point of the graphs. Similar to the cases discussed above, the point has the properties of the bifurcation point (Ślęzak et al. 2012). What is more, the graphs show that for \(\overline{{C}} > 5.41\, \mathrm{mol\, m }^{-3 }\) we have \((\det [P^{*}]/[P])_\mathrm{A} < (\det [P^{*}]/[P])_\mathrm{B}.\)

For coefficients \(P_{ij }\) and \(P_{ij}^{*}\, (i,\, j \in \{1,\, 2\})\) with the same indices, units are the same and values differ; whereas for these coefficients with different indices, units are different and values differ even by several orders of magnitude. Quotients \(P_{ij}^{*}/P_{ij}\) are dimensionless and their values have, at least for a Nephrophan membrane and water glucose solutions, the same order of magnitude. This facilitates analysis of the results obtained under conditions of concentration polarization or homogeneity of solutions. Calculation of det(\([P^{*}]/[P]\)) provides basis to reduce number of parameters needed to characterize transport properties of the membrane.

The experiments carried out previously indicate that if the coefficient values \(P_{11}^{*},\,P_{12}^{*},\,P_{21}^{*}\) and \(P_{22}^{*}\) do not depend on the configuration of the membrane system, then the CBLs setting is symmetric towards the horizontal surface in which the membrane is placed separating solutions with the concentrations \(C_\mathrm{l}\) and \(C_\mathrm{h}.\) In order to show the relationship between the coefficients \(P_{11}^{*},\,P_{12}^{*},\,P_{21}^{*}\) and \(P_{22}^{*}\) in the configurations A and B of the membrane system, we are calculating the quotients (\(P_{11}^{*})_\mathrm{B}/(P_{11}^{*})_\mathrm{A},\, (P_{12}^{*})_\mathrm{B}/(P_{12}^{*})_\mathrm{A},\, (P_{21}^{*})_\mathrm{B}/(P_{21}^{*})_\mathrm{A},\, (P_{22}^{*})_\mathrm{B}/(P_{22}^{*})_\mathrm{A}.\) The quotients may be generalized and the definition of asymmetry coefficient \(\kappa _{ij}\, (i,\,j\) = 1,  2) may be introduced as follows

$$\begin{aligned} \kappa _{ij} =\frac{(P_{ij} ^{*})_\mathrm{B} }{(P_{ij} ^{*})_\mathrm{A} }. \end{aligned}$$
(40)

It results from the definition that the absence of asymmetry means \(\kappa _{ij} = 1,\) whereas the asymmetry \(\kappa _{ij} > 1\) and \(\kappa _{ij} < 1.\)

The calculations results of the dependence \(\kappa _{11}=f(\overline{{C}}),\,\kappa _{12 }=f(\overline{{C}}),\,\kappa _{21 }=f(\overline{{C}})\) and \(\kappa _{22 }=f(\overline{{C}})\) are point. For \(\overline{{C}} > 5.41\,\mathrm{mol\, m }^{-3 }\) the values of coefficients \(\kappa _{11},\,\kappa _{12},\, \kappa _{21}\) and \(\kappa _{22}\) depend on the concentration of solutions separated by the membrane. Moreover, the graphs in Fig. 9 show that for \(\overline{{C}} > 5.41\) the course of the graph \(\kappa _{11 }=f(\overline{{C}})\) differs from the course of graphs \(\kappa _{12 }\approx \kappa _{21 }=\kappa _{22}=f(\overline{{C}}).\) The latter graphs showing the dependence overlie. What is more, for \(\overline{{C}} > 5.41\) the conditions \(\kappa _{11 }> 1\) and \(\kappa _{12}\approx \kappa _{21}=\kappa _{22} < 1\) are fulfilled for each \(\overline{{C}}.\)

Using Eq. (11), then Eq. (40) for the coefficients \(\kappa _{11},\,\kappa _{12},\,\kappa _{21}\) and \(\kappa _{22}\) depicted in Fig. 9. The calculations were made using Eq. (31). Figure shows that for \(\overline{{C}} \le 5.41\,\mathrm{mol\, m }^{-3}\) the values of coefficients \(\kappa _{11},\,\kappa _{12},\,\kappa _{21}\) and \(\kappa _{22}\) do not depend on the solution concentration. Their value, similar to the value of the last joint point of the graphs 1–3, is equal to \(\kappa _{11 }= \kappa _{12 }=\kappa _{21} =\kappa _{22 }= 1.\) The point has the properties of the bifurcation may be written in the following way

$$\begin{aligned}&\displaystyle \kappa _{11} =\frac{(P_{11} )_\mathrm{B} }{(P_{11} )_\mathrm{A} }=\frac{(\zeta _\mathrm{s} )_\mathrm{B} \{(\zeta _\mathrm{s} )_\mathrm{A} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} [1-(\zeta _\mathrm{v} )_\mathrm{A} \sigma ](1-\zeta _\mathrm{a} \sigma )\}}{(\zeta _\mathrm{s} )_\mathrm{A} \{(\zeta _\mathrm{s} )_\mathrm{B} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} [1-(\zeta _\mathrm{v})_\mathrm{B} \sigma ](1-\zeta _\mathrm{a} \sigma )\}},\end{aligned}$$
(41)
$$\begin{aligned}&\displaystyle \kappa _{12} =\frac{(P_{12} )_\mathrm{B} }{(P_{12} )_\mathrm{A}}=\frac{[1-(\zeta _\mathrm{v} )_\mathrm{B} \sigma ]\{(\zeta _\mathrm{s} )_\mathrm{A} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} [1-(\zeta _\mathrm{v} )_\mathrm{A} \sigma ](1-\zeta _\mathrm{a}\sigma )\}}{[1-(\zeta _\mathrm{s} )_\mathrm{A} \sigma ]\{(\zeta _\mathrm{s} )_\mathrm{B} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} [1-(\zeta _\mathrm{v} )_\mathrm{B} \sigma ](1-\zeta _\mathrm{a}\sigma )\}},\end{aligned}$$
(42)
$$\begin{aligned}&\displaystyle \kappa _{21} =\frac{(P_{21} )_\mathrm{B} }{(P_{21} )_\mathrm{A} }=\frac{(\zeta _\mathrm{s})_\mathrm{A} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} [1-(\zeta _\mathrm{v} )_\mathrm{A} \sigma ](1-\zeta _\mathrm{a} \sigma )}{(\zeta _\mathrm{s} )_\mathrm{B} \omega +\overline{{C}}\zeta _\mathrm{p} L_\mathrm{p} [1-(\zeta _\mathrm{v} )_\mathrm{B} \sigma ](1-\zeta _\mathrm{a} \sigma )}=\kappa _{22}. \end{aligned}$$
(43)

Using Eqs. (21), (25), (34) and (35), then Eqs. (41)–(43) may be written in the following way

$$\begin{aligned}&\displaystyle \kappa _{11} =\left[ {1+\overline{{C}}a_1 \left( 1+a_2 \delta _\mathrm{d}\right) }\right] \left[ {1+\overline{{C}}a_1 \left( {1+\frac{a_3 R_\mathrm{C} }{\delta _\mathrm{k} ^{2}(J_\mathrm{v} -J_\mathrm{vs} )}} \right) } \right] ^{-1},\end{aligned}$$
(44)
$$\begin{aligned}&\displaystyle \kappa _{12} =\left[ 1+a_1 \left( 1+a_2 \delta _\mathrm{d}\right) \right] \left( {1+\frac{a_3 R_\mathrm{C} }{\delta _\mathrm{k} (J_\mathrm{v}-J_\mathrm{vs} )}} \right) \left[ {\left( 1+a_2 \delta _\mathrm{d}\right) \left( 1+a_1\right) \left( {1+\frac{a_4 R_\mathrm{C} \overline{{C}}}{\delta _\mathrm{k} ^{2}(J_\mathrm{v} -J_\mathrm{vs} )}} \right) } \right] ^{\!-1}\!,\nonumber \\ \end{aligned}$$
(45)
$$\begin{aligned}&\displaystyle \kappa _{21} =\frac{D_\mathrm{d}[1+a_1 (1+a_2 \delta _\mathrm{d} )]}{D_\mathrm{d} +2RT\omega \delta _\mathrm{d} }\left( {1+\frac{a_3 (1-\sigma )R_\mathrm{C} }{\delta _\mathrm{d} ^{2}(J_\mathrm{v} -J_\mathrm{vs} )}} \right) \left[ {1+a_1 \overline{{C}}\left( {1+\frac{a_3 R_\mathrm{C} }{\delta _\mathrm{k} ^{2}(J_\mathrm{v} -J_\mathrm{vs} )}} \right) } \right] ^{-1}=\kappa _{22},\nonumber \\ \end{aligned}$$
(46)

where \(a_{1}=L_\mathrm{p}(1 - \sigma )^{2}\omega ^{-1},\,a_{2} =2RT\omega [D_\mathrm{d}(1 - \sigma )]^{-1},\,a_{3} =4(RT){2}L_\mathrm{p}\sigma \omega \nu [g\alpha _\mathrm{C} (1-\sigma )]^{-1},\,a_{4 }=a_{3}(1 - \sigma )^{2}L_\mathrm{p}\omega ^{-1}(1+\overline{{C}}a_{1})^{-1}.\)

According to theory of functionally graded materials (Shen 2009; Woźniak et al. 2001; Woźniak 2007), contact of two objects, i.e., solutions with different concentrations and/or composition, causes conflicts. In the case of solutions, the conflict is eliminated quickly due to the transport processes such as diffusion or convection. The processes are generated by concentration gradients of substance. Therefore, the situation discussed is a non-conflict one when the concentrations and compositions of both solutions are homogenous within the space and time. By contrast, the membrane placement (as an additional object) between homogenous solutions is slowing down the transport processes due to extended in time retention of concentration gradients of particular solutions flowing across the membrane, and consequently it is defusing the conflict. It has to be emphasized that the homogeneity of solutions separated by the membrane may be provided solely by intensive mechanical stirring. Under real conditions (the absence of mechanical stirring), at the both sides of the membrane the CBLs (diffusive ones) are created. They may be treated as two additional objects between the membrane and solutions, created spontaneously. The objects defuse the conflict by the reduction of concentration gradients and become units of functionally graded materials.

4 Conclusion

Considering the study above, we may be conclude that:

  1. (1)

    The network form of the K–K equations introduced in the following paper, containing the Peusner’s coefficients \(P_{ij}^{*}\,(i,\, j\in \{1,\, 2\})\) creating the second degree matrix of the Peusner’s coefficients \([P^{*}],\) is the new tool in the study on the membrane transport under conditions of concentration polarization.

  2. (2)

    The calculated dependences of the Peusner’s coefficients \(P_{ij}^{*}\) and \(P_{ij}\, (i,\, j\in \{1,\, 2,\, 3\})\) and the quotients of the coefficients for the conditions of non-homogeneity (\(P_{ij}^{*})\) and homogeneity (\(P_{ij})\) of solutions depend on the average glucose concentration in the membrane (\(\overline{{C}}).\)

  3. (3)

    Above the threshold value \(\overline{{C}}= 5.41\,\mathrm{mol\, m }^{-3}\) we have the coefficients \(P_{11}^{*},\,P_{12}^{*}=-P_{21}^{*} \,\mathrm{and}\, P_{22}^{*},\) consequently the relations \(P_{11}^{*}/P_{11},\,P_{12}^{*}/P_{12} \,\mathrm{and}\, P_{22}^{*}/P_{22}\) depend as well on the configuration of the membrane system.

  4. (4)

    For the same values \(\overline{{C}} > 5.41\,\mathrm{mol\, m } ^{-3},\) the coefficient value \(P_{11}^{*}\) in convective state is higher than in non-convective state, whereas the values of coefficients \(P_{12}^{*}= -P_{21}^{*}\) and \(P_{22}^{*}\) in convective state are lower than in non-convective state.