Properties of Magnetic Tongues over a Solar Cycle

Abstract

The photospheric spatial distribution of the main magnetic polarities of bipolar active regions (ARs) present during their emergence deformations are known as magnetic tongues. They are attributed to the presence of twist in the toroidal magnetic-flux tubes that form the ARs. The aim of this article is to study the twist of newly emerged ARs from the evolution of magnetic tongues observed in photospheric line-of-sight magnetograms. We apply the procedure described by Poisson et al. (Solar Phys. 290, 727, 2015a) to ARs observed over the full Solar Cycle 23 and the beginning of Cycle 24. Our results show that the hemispherical rule obtained using the tongues as a proxy of the twist has a weak sign dominance (53 % in the southern hemisphere and 58 % in the northern hemisphere). By defining the variation of the tongue angle, we characterize the strength of the magnetic tongues during different phases of the AR emergence. We find that there is a tendency of the tongues to be stronger during the beginning of the emergence and to become weaker as the AR reaches its maximum magnetic flux. We compare this evolution with the emergence of a toroidal flux-rope model with non-uniform twist. The variety of evolution of the tongues in the analyzed ARs can only be reproduced when using a broad range of twist profiles, in particular having a large variety of twist gradients in the direction vertical to the photosphere. Although the analytical model used is a special case, selected to minimize the complexity of the problem, the results obtained set new observational constraints to theoretical models of flux-rope emergence that form bipolar ARs.

Appendix A: Twisted Flux Tube Model

1.1 A.1 Geometry of the Model

In this section, we describe a simple model to describe the main properties of magnetic tongues in terms of the emergence of an $\Omega$-shaped twisted flux tube. The flux-tube shape is half a torus with a main radius $R$ (Figure 11). The torus center is located at the depth $z=-d$ below the photosphere, which is located at $z=0$. Progressively decreasing $d\geq0$ simulates a very simplified emergence, i.e. the FR is emerging without any deformation (in contrast to the results of numerical simulations). Our aim is to illustrate the global, and expected to be robust, implications of the FR twist on the magnetic-tongue evolution; therefore, this very simple model is selected with this purpose.

Figure 11

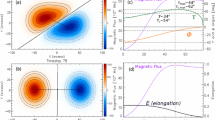
Model of a twisted flux tube having a half-torus shape with a main radius $R$ and a center located at $z=-d$ below the photospheric level ($z=0$). The twist is positive and uniform ($N_{\mathrm{t}} =0.5$ turn in half a torus, $h=g=0$ in Equations (13) and (14)). The photospheric magnetogram of $B_{\mathrm{z}}$ is shown with isocontours and color levels as for observations (Figure 1) and the superposed brown ellipses (continuous/dashed lines) show the intersection of the FR with $z=-d$ and $z=0$. The torus is outlined for a minor radius $\rho$. The red line is an example of a magnetic-field line (drawn with an enhanced twist by a factor ${\approx}\,6$ to better outline the FR structure). $\phi$ and $\theta$ are the angular coordinates along and around the axis, respectively.

Cartesian coordinates $\{x,y,z \}$ are adopted to describe the model magnetogram located at $z=0$. However, the natural coordinates for the torus are $\{\rho, \phi, \theta\}$, where $\rho$ is the distance to the torus axis, $\phi$ defines the location along the flux-tube axis, and $\theta$ corresponds to the rotation angle around the flux-tube axis (Figure 11). These are the toroidal curved cylindrical coordinates that we simply call torus coordinates below. In the axis plane, the unit vector normal to the axis is denoted as $\widehat{\boldsymbol{u}}_{\mathrm{R}}$ and the unit vector along the axis (toroidal direction) is denoted as $\widehat{\boldsymbol{u}}_{\phi}$. Finally, the unit vector around the FR (poloidal direction) is noted $\widehat{\boldsymbol{u}}_{\theta}$ and the unit vector along the $\rho$-direction, so both normal to the axis and to $\widehat{\boldsymbol{u}}_{\theta}$, is noted $\widehat {\boldsymbol{u}}_{\rho}$. Their $\{x,y,z \}$ components are

$$\begin{aligned} \begin{aligned} \widehat{\boldsymbol{u}}_{\mathrm{R}} &{} = \{ \cos\phi, 0 , \sin\phi\} , \\ \widehat{\boldsymbol{u}}_{\phi} &{} = \{-\sin\phi, 0 , \cos \phi\}, \\ \widehat{\boldsymbol{u}}_{\rho}&{} = \{ \cos\phi\cos\theta, \sin\theta, \sin\phi\cos\theta\}, \\ \widehat{\boldsymbol{u}}_{\theta} &{} = \{-\cos\phi\sin\theta , \cos \theta,-\sin\phi\sin\theta\}. \end{aligned} \end{aligned}$$

(9)

The torus coordinates need to be transformed to Cartesian ones to obtain synthetic photospheric magnetograms. A point $M$ in the torus is located at $\boldsymbol{OM} = R \widehat{\boldsymbol{u}}_{\mathrm{R}}+ \rho\widehat{\boldsymbol{u}}_{\rho}-d \widehat{\boldsymbol{u}}_{\mathrm{z}}$ (with $O$ being at the torus center). Then, in Cartesian coordinates,

$$\begin{aligned} \boldsymbol{OM} = & \{x,y,z \} \\ = &\bigl\{ (R+\rho\cos\theta) \cos\phi , \rho\sin\theta , (R+\rho\cos\theta) \sin\phi-d \bigr\} , \end{aligned}$$

(10)

which provides the transformation of torus coordinates to Cartesian ones and the reverse transformation after some algebraic computations.

1.2 A.2 Definition of the Magnetic Field

The magnetic field [$\boldsymbol{B}$] satisfies $\boldsymbol{\nabla} \cdot\boldsymbol{B} =0$. In torus coordinates, this is written as

$$\begin{aligned} \boldsymbol{\nabla} \cdot\boldsymbol{B} =& \biggl( \frac{\partial \rho (R+\rho\cos\theta) B_{\rho}}{\partial\rho} + \frac{\partial(R+\rho\cos\theta) B_{\theta}}{\partial \theta} + \rho\frac{\partial B_{\phi}}{\partial\phi} \biggr) \\ &{} / \bigl( \rho ( R+\rho\cos\theta ) \bigr) = 0. \end{aligned}$$

(11)

In order to derive a simple analytical model we do not specify a force balance. We rather assume that field lines are located on torus shapes with $\rho$ independent of $\phi$. This implies $B_{\rho}=0$. Next, we cancel separately the two remaining terms in $\boldsymbol{\nabla} \cdot\boldsymbol{B} =0$, so $B_{\theta}\widehat{\boldsymbol{u}}_{\theta}$ and $B_{\phi}\widehat{\boldsymbol{u}}_{\phi}$ are both divergence-free. This separate cancellation is only a special case selected to minimize the complexity of the following analytical derivation that poses certain limitations and implications discussed in Sections 4.3 and 5. This implies $B_{\theta}= f_{\theta} (\rho,\phi) / (R+\rho\cos\theta)$ and $B_{\phi}= f_{\phi} (\rho,\theta)$ where $f_{\theta}$ and $f_{\phi}$ are two general functions.

The dependence on $f_{\theta}$ in $\phi$ would introduce an asymmetry between the two legs, but we do not consider this asymmetry here, so $f_{\theta} (\rho)$. If $f_{\phi}$ is only a function of $\rho$, the integration of field lines implies $B_{\theta} = 2 \rho N_{\mathrm{t}}(\rho) B_{\phi}/(R+\rho\cos\theta)$ where $N_{\mathrm{t}}(\rho)$ is the number of turns in half the torus of small radius $\rho$. Following previous studies (see, e.g., Emonet and Moreno-Insertis, 1998) the axial field is typically defined as $B_{\phi} = B_{0} \exp(-(\rho/a)^{2})$, where $a$ defines the FR thickness and $B_{0}$ the field strength on the axis, then the azimuthal field is defined as

$$ B_{\theta}(\rho,\theta) = 2 \rho N_{\mathrm{t}}(\rho) B_{0} \mathrm{e}^{-(\rho/a)^{2}}/ (R+\rho\cos\theta). $$

(12)

We explore the effect of a non-uniform twist profile by defining

$$ N_{\mathrm{t}}(\rho) = N_{\mathrm{t},0} \max \bigl(1+h( \rho/a)^{2},0\bigr), $$

(13)

where $h$ is a parameter. For $h=0$, the FR is uniformly twisted. A value of $h>0$ implies a twist more concentrated at the edge; as an example, if $h=1$ the twist at $\rho=a$ duplicates its value at the center. Similarly, $h<0$ implies a twist decreasing from the axis to the FR border. Taking the maximum of the parenthesis in Equation (13) avoids the change of sign of $N_{\mathrm{t}}(\rho)$ within the FR, which would produce strong magnetic tongues with opposite sign to that in the core, a case typically not observed. We further set $h\geq-1$ so that the strong field, within $\rho< a$, is not affected.

For the axial component [$B_{\phi}$] Equation (11) allows a general form with a $\theta$-dependence (with $f_{\phi} (\rho,\theta)$). Since $B_{\theta}$ and $B_{\phi}$ are independent (no force balance is solved), we exploit this possibility by introducing the simplest $\theta$-dependence needed for our purpose:

$$\begin{aligned} &B_{\phi}(\rho,\theta) = B_{0} \mathrm{asy}(\theta) \mathrm{e}^{-(\rho/a)^{2}}, \\ &\quad{}\mbox{with } \mathrm{asy}(\theta) = (1+g \cos\theta), \end{aligned}$$

(14)

where $g$ is a parameter controlling the non-axisymmetric level of $B_{\phi}$. The term in $\cos\theta$ introduces a linear spatial variation of $B_{\phi}$ in the direction $\widehat{\boldsymbol {u}}_{\mathrm{R}}$ (orthogonal to the FR axis). It has also the property of preserving the total flux of $B_{\phi}$; therefore, changing the value of $g$ only redistributes $B_{\phi}$ within the FR.

A field line is defined by the curve tangent to $\boldsymbol{B}$, so where ${\mathrm {d}} \boldsymbol{OM}$ is parallel to $\boldsymbol{B}$, with:

$$ {\mathrm {d}} \boldsymbol{OM} = {\mathrm {d}} \rho\widehat{ \boldsymbol {u}}_{\rho}+ \rho{\mathrm {d}} \theta\widehat{\boldsymbol {u}}_{\theta} + (R+\rho\cos\theta) {\mathrm {d}} \phi\widehat{ \boldsymbol{u}}_{\phi}. $$

(15)

Then the field-line equation can be written

$$ \frac{{\mathrm {d}} \theta}{{\mathrm {d}} \phi} = \frac{R+\rho\cos\theta}{\rho} \frac{B_{\theta}}{B_{\phi}} = \frac{2 N_{\mathrm{t}}(\rho)}{1+g \cos\theta} . $$

(16)

This implies that the local twist [${\mathrm {d}} \theta/{\mathrm {d}} \phi$] is lower in the top part ($\theta\approx0$) than in the bottom one ($\theta\approx\pi$) of the FR for $g>0$ and the reverse for $g<0$.

1.3 A.3 Synthetic Magnetogram

The model magnetogram is defined at the height $z=0$ as:

$$ B_{z}(x,y) = B_{0} (x \mathrm{asy}- 2 y N_{\mathrm{t}}d/u) \mathrm{e}^{-(\rho/a)^{2}} /u , $$

(17)

with $u=\sqrt{x^{2}+d^{2}}$. As $d$ decreases from $d \approx R+a$ to $d \approx0$, $B_{z}(x,y)$ describes the evolution of a theoretical magnetogram where a twisted $\Omega$-shaped flux tube is emerging without deformation.

From Equation (17) the PIL of $B_{z}$ is

$$ x = 2 y N_{\mathrm{t}}d /\bigl(\mathrm{asy} \sqrt{x^{2}+d^{2}}\bigr) . $$

(18)

For the central part of the magnetogram, so for $|x|\ll d$, Equation (18) is approximately

$$ x \approx2 y N_{\mathrm{t},0}\bigl(1+h\rho^{2}/a^{2} \bigr) / (1+g \cos\theta) , $$

(19)

where $\rho$ and $\theta$ can be expressed in function of $(x,y,d)$ (and $z=0$). The PIL equation further simplifies to

$$ x \approx2 y N_{\mathrm{t},0} \quad\mbox{or } \tan \tau_{\mathrm{c}}= 2 N_{\mathrm{t},0}, $$

(20)

for a uniform twist [$h=g=0$]. This limit corresponds to the model used in Luoni et al. (2011). For a uniform twist, the PIL is straight and $\tau_{\mathrm{c}}$ is constant during the emergence (Equation (18) implies $x \propto y$ for $|x| \ll d$, so around the central part of the bipole with a spatial extension decreasing with $d$, then during the emergence). For a non-uniform twist [$h \ne0$] and/or an asymmetric twist [$g \ne 0$] across the FR, the PIL is curved according to the twist profile as described by Equation (19). It is also function of $d$, Equation (18), so the PIL evolves during the emergence. The model results are described in Section 4.