Experimental evidence on valuation with multiple priors

Abstract

Popular models for decision making under ambiguity assume that people use not one but multiple priors. This paper is a first attempt to experimentally elicit the min and the max of multiple priors directly. In an ambiguous scenario we measure a participant’s single prior, her min and max of multiple priors, and the valuation of an ambiguous asset with the same underlying states as the ambiguous scenario. We use the min and the max of multiple priors to directly test two popular multiple priors models: the maxmin model and the α maxmin model. We find more support for the α maxmin model: although people put about twice the weight on the minimum of multiple priors, they also consider the maximum. Furthermore, we indirectly elicit confidence weights over the whole set of multiple priors and test two additional models: variational preferences and the smooth model of ambiguity. Two particular versions of the variational preferences model explain less than the α maxmin but more than the maxmin model. Overall, the smooth model of ambiguity performs best among all models tested.

1 Introduction

In many real world situations there is too little information to form a unique prior that individuals feel confident enough to use as a sole base for decision making. In such situations of ambiguity, people may have not one but a set of priors, or ‘multiple priors’, which they consider in their decision making process. Some of the most popular models for decision making under ambiguity, which are used to explain the valuation of ambiguous assets, explicitly consider multiple priors: the maxmin model of Gilboa and Schmeidler (1989), the α maxmin model of Ghirardato et al. (2004), the variational preferences model of Maccheroni et al. (2006), and the smooth models of ambiguity by Klibanoff et al. (2005). In the quest to find out which of these models best explains real decision making, a substantial body of the pertinent literature provides empirical tests (see, e.g., Ahn et al. 2014, Hey et al. 2010, Cubitt et al. 2014 and the references therein). The results are mixed, however. We argue that one reason for this is that the predictions of the models were tested, but their underlying mechanisms were not. The latter would involve the elicitation and characterization of multiple priors, which has not been done yet. Hence, in order to understand how people use multiple priors in decisions under ambiguity, this paper attempts to measure beliefs with multiple priors and then uses these multiple priors to test the above mentioned models of decision making under ambiguity.

Characterizing beliefs under ambiguity when it is possible to have multiple priors is tricky as it calls for higher orders of beliefs. Consider, for example, an ambiguous Ellsberg urn (Ellsberg 1961) with ten balls that are either white or black. A first-order belief refers to the overall (expected) probability of a drawn ball being white or black.¹ If we want to study beliefs involving multiple priors, we need to elicit an individual’s second-order beliefs, that is her confidence weights for all potential priors.² Such a procedure can be complicated and counter-intuitive. While it is difficult enough to properly elicit one prior, it appears to be impossible to elicit more than one prior from the same individual. Even if such a procedure could be implemented, it would be difficult to find an incentive compatible mechanism for it. Note that, to properly incentivize individuals to report their multiple priors and their respective confidence weights, we need to make sure that at least one of the multiple priors actually occurs; otherwise individuals cannot benefit from reporting sincere beliefs (or lose when reporting fake ones). In almost all real world scenarios, however, only a potential state in a prior is realized but never a prior itself.

As a first objective, this paper attempts to elicit the min and the max of multiple priors. To measure beliefs with multiple priors we construct an ambiguous scenario for which we first elicit experimental participants’ ‘single prior’. For an incentive compatible elicitation of multiple priors, we exploit the uncertainty about other participants’ single priors to indirectly elicit a subject’s own perception of uncertainty in the ambiguous scenario. Explicitly, we ask each participant, without any additional information, to state her confidence weights over all other experimental participants’ single priors. As the real distribution of other subjects’ single priors can be easily obtained from the experimental data, the elicitation of confidence weights for these priors can be properly incentivized. We argue that the confidence statements of a participant about others’ priors indirectly reflect her own perception of uncertainty in the ambiguous scenario. Note that, when having to guess the priors of other experimental participants in the absence of any additional information, the best participants can do is to use their own set of multiple priors. This claim is essentially the “impersonally informative” assumption of Prelec (2004). Given the participants’ own set of multiple priors, in particular the min and the max of priors, and being uncertain about other participants’ decision models of ambiguity, a participant — whatever her own decision model is — knows that there is some possibility that her own min and max of multiple priors will be reported by others. We define the min (max) of multiple priors of a participant as the most pessimistic (optimistic) prior that receives a positive confidence weight. Having obtained the min and the max of priors, we go one step further and explore the possibility that the confidence statements of a participant about others’ priors might indirectly reflect her own perception of uncertainty in the ambiguous scenario. Hence, a participant’s confidence statements can be interpreted as her ‘confidence weight distribution’ of (multiple) priors. Although this interpretation requires a leap of faith, it is not far-fetched. Note that it is cognitively very demanding to think of other participants’ single priors. For this, each participant would have to imagine and compute multiple alternative processes and decision rules according to which a set of multiple priors is aggregated into a single prior. In comparison, it is much more intuitive and straightforward for participants to simply state their own confidence weight distribution. This idea has been explored in some studies implicitly and indirectly. Ilut and Schneider (2014) point out that the distribution of survey forecasters is often used as a measure of ambiguity since disagreement of experts plausibly reflects uncertainty about what the right model of the future is. Here we use participants’ own uncertainty about others’ opinions as a measure of ambiguity. We make a first attempt to systematically apply this idea to elicit a confidence weight distribution of multiple priors. To examine the validity of this claim, we analyze the role of the confidence weight distributions of multiple priors in the participants’ perception of the constructed ambiguous scenario, e.g. in the evaluation of ambiguous assets.

Eliciting an individual’s beliefs about others’ behavior is nothing new. It is frequently done in experiments with strategic games, (see Crawford et al. 2013 for a recent review). However, our purpose of belief elicitation is entirely different: in experiments with strategic games beliefs are used to check the consistency of strategies and beliefs or to investigate the depth of an individual’s strategic deliberation of her opponents, whereas here the elicited beliefs are used to gain a deeper understanding of the individual’s perception of an ambiguous scenario, not of her opponents.

As a second objective, this paper tests four popular ambiguity models of multiple priors: the maxmin model, the α maxmin model, the variational preferences model, and the smooth ambiguity model. In contrast to previous studies, the elicited min and max of multiple priors, together with the confidence weight distribution of multiple priors, allows us to test these models more directly.

Our results suggest that, when comparing the maxmin model and the α maxmin model, subjects consider both the max and the min of multiple priors in the evaluation of the ambiguous asset. Although they seem to place more weight on the minimum, we find more support for the α maxmin model than the maxmin model. The estimated weight on the minimium, α, is about 2/3. A likelihood ratio test suggests that the improvement in the explanatory power is statistically significant. We tested two particular versions of the variational preferences model. The explanatory power of our specifications of the variational preferences model stand between the maxmin and the α maxmin model. We find that participants’ confidence statements about others’ priors have significant explanatory power for their own valuation of the ambiguous asset. This result provides strong support for the interpretation of confidence statements as a participant’s confidence weight distribution of own priors. Encouraged by this result, we performed a test of the smooth model of ambiguity and find that it performs best among the four multiple priors models. Furthermore, we find that the estimated coefficients of the priors are generally increasing in confidence weights, a pattern that is consistent with the prediction of the smooth model of ambiguity.

The paper complements a growing literature that experimentally tests various models of ambiguity by developing and analyzing competing predictions that discriminate between the different approaches (see, e.g., Hey et al. 2010; Cubitt et al. 2014). Many of these studies explicitly use the complete set of probability measures over states as the set of multiple priors, and, hence, the support of the probability measures as the minimum (min) and maximum (max) of multiple priors. The problem with this approach is, however, that the set of priors does not need to be equal to the complete set of probability measures (Baillon et al. 2011). Furthermore, previous studies did not account for a confidence weight distribution of priors, although the smooth model of ambiguity explicitly calls for it.

The rest of this paper is organized as follows. Section 2 summarizes the four models of multiple priors and presents the experimental design. Section 3 reports and discusses the experimental results and Section 4 concludes.

2 Experimental design

The core of our experiment consisted of four parts: (1) the construction of several ambiguous scenarios; (2) the elicitation of a single prior for each ambiguous scenario; (3) the elicitation of confidence weights for all potential priors in each ambiguous scenario; and, finally, (4) the elicitation of certainty equivalents for ambiguous assets with the same underlying states as the ambiguous scenarios. Each part was administered in several rounds. In the subsections below we provide detailed design information on each part.

The experiment was conducted in the Experimental Laboratory for Sociology and Economics (ELSE) at Utrecht University in October 2013. In total, we ran four sessions with altogether 111 participants. All sessions were computerized via zTree (Fischbacher 2007) and recruitment was done with ORSEE (Greiner 2004). Each session lasted around 120 minutes. In the experiment we used ECU (experimental currency unit) instead of euro, with 200 E C U=1 e u r o. At the end of the experiment, we randomly chose one round for paying the single prior, a different round for paying the confidence weights over the priors, and a further different round for paying the certainty equivalent task. This procedure was communicated to all participants at the beginning of the experiment. The average payment was 13.43 euro.

2.1 Four popular models of decision making under ambiguity with multiple priors

Before we start with our experimental design, we briefly summarize the four models of decision making under ambiguity with multiple priors: the maxmin model (Gilboa and Schmeidler 1989), the α maxmin model (Ghirardato et al. 2004), the variational preferences model (Maccheroni et al. 2006), and the smooth models of ambiguity (Klibanoff et al. 2005). Let S denote the set of all possible states of nature, and s∈S be a state in this set. An event E is then a collection of some s∈S. Let △(S) denote the set of all possible first-order beliefs over S, i.e., △(S) is the set of priors, and δ∈△(S) be one prior. An act is a function f that assigns a monetary outcome to each s∈S. The expected utility of act f when the decision maker has prior δ(S) is then denoted as U _δ (f). The maxmin preferences (Gilboa and Schmeidler 1989) can then be written as

$$ MEU(f)=Min_{\delta\in C}\,U_{\delta}(f), $$

where C⊆△(S) is called the set of relevant priors, and, in general, C is a strict subset of △(S), i.e., not all priors in △(S) are relevant for the decision maker. The α maxmin model (Ghirardato et al. 2004) is a generalization of the maxmin model and can be summarized as

$$\alpha MEU(f)=\alpha Min_{\delta\in C}\:U_{\delta}(f)+(1-\alpha)Max_{\delta\in C}\,U_{\delta}(f), $$

where α is a constant capturing ambiguity attitudes, and when α=1 we have the maxmin model. The variational preferences by Maccheroni et al. (2006) can then be represented by

$$VP(f)=Min_{\delta\in\triangle(s)}\:\left\{ U_{\delta}(f)+c(\delta)\right\} , $$

where c(δ) is an index of ambiguity aversion assigned to prior δ. The maxmin model is a special case of the variational preferences when c(δ)=0 if δ∈C and c(δ) = ∞ if δ∉C. Finally, the smooth models of ambiguity (Klibanoff et al. 2005) can be written as

$$SA(f)={\int}_{\triangle(s)}\phi(U_{\delta}(f))d\mu(\delta), $$

where μ(δ) is the second-order probability distribution, capturing the decision maker’s confidence weights over the priors, and the ambiguity attitudes are captured by the curvature of ϕ(⋅). When there are only two acts and two outcomes (one either wins or loses), as constructed by us below, we could normalize the utility of winning to be one and that of losing to be zero. Let E denote the event of winning, X be the payoff in case of winning (f(s) = X for all s∈E), and Y the payoff in case of losing (f(s) = Y for all $s\in S\smallsetminus E$). With X>Y and the normalization u(X)=1 and u(Y)=0, we have U _δ (f) = δ(E). When no confusion is possible, δ(E) can be reduced to δ. Accordingly, the above representations can be simplified to

$$\begin{array}{@{}rcl@{}} MEU(f)&=&Min_{\delta\in C}\,\delta, \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} \alpha MEU(f)&=&\alpha Min_{\delta\in C}\:\delta+(1-\alpha)Max_{\delta\in C}\,\delta, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} VP(f)&=&Min_{\delta\in\triangle s}\:\left\{ \delta+c(\delta)\right\}, \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} SA(f)&=&{\int}_{\triangle (s)}\phi(\delta)d\mu(\delta). \end{array} $$

(4)

2.2 Construction of the ambiguous scenario

We wanted to make sure that the procedure of constructing the ambiguous scenario was transparent, while the scenario itself would be ambiguous. We therefore implemented the following procedure. One day before the experiment, we prepared 100 chips, of which 10 chips had the letter A, 10 chips had the letter B, and so forth until letter J. We then wrapped each chip with kitchen aluminum foil and asked the son of one of the authors (a 4-year-old boy) to fill five bags with 10 chips each. We used 50 chips out of 100 to make sure that the chip compositions in different bags are not correlated, e.g. the chip composition in one bag cannot be used to predict the chip composition in another bag. As the experimental assistant was very young, we controlled the bags to make sure that there were exactly 10 chips in each bag. In the lab, the above procedure was explained to the participants. Additionally, to make things more explicit, we explained that not all bags contained all letters, but that any bag could contain several chips with the same letter and some letters not at all.

The experiment consisted of 5 rounds. Each of the 5 bags was used for one round, with Bag 0 for the trial round, Bag 1 for Round 1, Bag 2 for Round 2, etc. The trial round was not payoff relevant. It served to give subjects an opportunity to become familiar with all experimental steps. The following 4 rounds were formal experimental rounds and relevant for experimental payments. In each of the 5 rounds, we went through the three decision tasks as explained in more detail in the following three subsections 2.3, 2.4, and 2.5.

Previous literature shows that subjects’ ambiguity attitudes differ with winning probabilities (see, e.g., Abdellaoui et al. 2011). In particular, subjects can be ambiguity seeking with small winning probabilities and ambiguity averse with large winning probabilities. For this reason we varied the winning probabilities across rounds, with an ambiguity-neutral winning probability of 0.4 in the trial round, 0.1 in Round 1, 0.3 in Round 2, 0.5 in Round 3, and 0.7 in Round 4. We implemented the variation in the ambiguity-neutral winning probability using the following procedure: before each round, participants were allowed to pick a certain amount of ‘winning letters’ from the 10 letters mentioned above. Depending on the round, participants could pick 4 winning letters (out of 10) for the trial round, 1 winning letter for Round 1, 3 winning letters for Round 2, 5 winning letters for Round 3, and 7 winning letters for Round 4. At the end of the experiment, we picked one of the rounds at random and played the lottery for real: a participant won 1000 ECU if a randomly drawn chip out of the bag matched (one of) the chosen winning letter(s) and 0 ECU otherwise. Hence, the amount of winning letters directly determined the ambiguity-neutral probability of winning 0 ECU.

2.3 Elicitation of single priors

At the beginning of each round, we elicited every participant’s subjective estimation of the probability — the single prior — that the drawn chip matched her chosen winning letters. There are various methods available for such a belief elicitation: non-incentivized introspection, outcome matching, the probability matching method, quadratic scoring rules, and corrections of quadratic scoring rules and the outcome matching method. Introspection is rarely used as the main method in economic experiments and outcome matching is not incentive compatible. The probability matching method is incentive compatible, relatively simple in its experimental implementation, and easy to understand.³ As shown in subsection 2.4, the simplicity and minimal cognitive demand of the single prior elicitation is crucial in this study because single priors form the basis for the elicitation of multiple priors and the confidence weight distribution. If the elicitation of single priors is already cognitively demanding, the elicitation of multiple priors becomes overwhelming. Based on these considerations, we have chosen to administer the probability matching method as our main mechanism to elicit first-order beliefs. Quadratic scoring rules are not entirely incentive compatible due to the assumption of risk neutrality, and the correction of quadratic scoring rules are procedurally complicated and not very efficient. However, quadratic scoring rules have the advantage that they elicit expectations by aiming directly at subjective beliefs and not indirectly through an asset that is constructed on the same states. As a robustness check, we therefore also conducted an experiment with a quadratic scoring rule as the primary elicitation mechanism for the single prior.⁴ The main results reported in the current paper are robust to both elicitation methods. Therefore, in the following, we focus on the probability matching method.

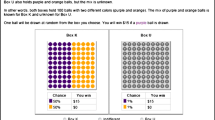
Figure 1 shows the screenshot of the elicitation of single priors with the probability matching method. Option A is the ambiguous lottery described in the previous section. It stays the same in all rows. Option B is a risky lottery paying 1000 ECU with probability p and 0 otherwise. Option B becomes more attractive when moving down the rows as the probability p of receiving 1000 ECU increases from 0.1 to 1. We asked participants to report their switching point, at which they started to prefer Option B over Option A.⁵ We then inferred their single priors from this switching point. The single prior was computed as the midpoint between the probabilities that corresponded with the row at which subjects switched and the previous row. For example, if a subject switched at Row 4, we computed a single prior of $\frac {1}{2}(0.3+0.4)=0.35$.

Fig. 1

Screenshot of the elicitation of single priors with the probability matching method. Option A is an ambiguous lottery building on the states of the ambiguous scenario

We interpret the inferred probability as one prior δ (see subsection 2.1). A prior in this setup is, strictly speaking, a first-order probability distribution $\left (p_{i}\right )_{^{i=1}}^{11}$ on the 11 possible combinations of each bag. The probability distribution over the set of priors, then, is a second-order probability distribution in which each probability is a confidence weight on a possible probability distribution. Our measure is thus a simplification, which is common in the literature. For example, Garlappi et al. (2007) use the estimated expected returns of assets as δ. A further justification is that our setup has binary outcomes allowing us to normalize u(1000)=1 and u(0)=0. With the normalization, it can be shown that $U_{\delta }(f)=U_{\left (p_{i}\right )_{i=1}^{11}}(f)=\delta .$ Finally, as shown in subsection 2.4, this simplification is also helpful to keep the elicitation of multiple priors cognitively and operationally tractable.

2.4 Elicitation of confidence weights for priors

For an incentive compatible elicitation of the probability distribution over the set of priors ΔS, we exploit a participant’s uncertainty of other participants’ priors to indirectly elicit her own perception of uncertainty in the ambiguous scenario. Note that there are 11 possible choice patterns in the elicitation of single priors in Fig. 1: ‘Possible Choice 1’ where Option B is always preferred, ‘Possible Choice 2’ where Option A is preferred in the first row while Option B is preferred in all other rows, ..., and ‘Possible Choice 11’ where Option A is always preferred. Each pattern of possible choices represents one prior δ, and we have 11 possible priors in this setup. As shown in Fig. 2, we asked subjects to estimate, for each possible choice pattern, what percentage of all subjects in the session decided for Possible Choice 1, Possible Choice 2, ..., Possible Choice 10 in the previous decision task.⁶ Strictly speaking, confidence weights refer to second-order probability distributions. We asked subjects to report the proportions instead of probabilities. This was mainly done for practical reasons, because subjects might not find it intuitive to state probabilities. To make sure that the interpretation of proportions is meaningful we included a relatively large group of subjects in each session.⁷

Fig. 2

Screenshot of the elicitation of the confidence weight distribution of priors. Each possible choice pattern represents a possible prior. The elicitation is incentivized via the following payoff function: $\text {payoff}=Max\{0,1000-0.2\times {\sum }_{i=1}^{10}(w_{\delta _{i}}-\pi _{i})^{2}\}$, where $w_{\delta _{i}}$ denotes the proportion of points that an individual assigned to the prior δ _i , i=1,2,…,10, and π _i is the realized proportion of individuals who report the prior δ _i , i=1,2,…,10

The payoff for this task was determined by the following function:

$$\text{payoff}=Max\{0,1000-0.2\times{\sum}_{i=1}^{10}(w_{\delta_{i}}-\pi_{i})^{2}\}, $$

where $w_{\delta _{i}}$ denotes the proportion of points that an individual assigned to the prior δ _i , i=1,2,…,10, and π _i is the realized proportion of individuals who report the prior δ _i , i=1,2,…,10.⁸

Note that δ is the reported prior of an individual, and we interpret the most pessimistic (optimistic) prior δ _i with $w_{\delta _{i}}>0$ as the min (the max) of the multiple priors. To be precise, $(w_{\delta _{i}})_{i=1}^{10}$ is not the confidence weight distribution of the individual’s own priors but the perception of an individual of the distribution of δ at the population level. Yet, as explained in the introduction, and in line with the ‘impersonally informative’ assumption of Prelec (2004), when having to guess the reported single priors (δ) of the rest of the population without additional information, the best one can do is to use one’s own set of multiple priors as a starting point.⁹ We examine the validity of this claim in the results section.

Our payoff mechanism does not induce hedging of $w_{\delta _{i}}$ across π _i s. One might think that, for example, a risk averse individual would report a flatter $(w_{\delta _{i}})_{i=1}^{10}$ than her subjective estimations to hedge across choice possibilities, but this should not be the case. To explain this, let us consider possible effects of risk attitudes on the reporting of $(w_{\delta _{i}})_{i=1}^{10}$ in two scenarios. In the first scenario, individuals have a point belief distribution over π _i , i=1,2,…,10. Here the payoff mechanism is incentive compatible as it is optimal to report $w_{\delta _{i}}=\pi _{i},\:i=1,\:2,\:...,\:10$. In the second scenario, individuals do not have a degenerated belief distribution over some π _i s, e.g., individuals believe that there is a probability distribution f(p|π _i ) over certain π _i s. Here risk attitudes could influence how subjects report a single $w_{\delta _{i}}$ out the f(p|π _i ), but not hedging across π _i s. To see this, note that the optimal choice of $w_{\delta _{i}}$ depends on the curvature of the utility function. For example, a risk neutral individual would report the mean of the belief distribution f(p|π _i ) over the π _i , while a risk averse individual would report something other than the mean. However, such an optimal choice of $w_{\delta _{i}}$, given a certain f(p|π _i ), occurs within the belief distribution f(p|π _i ) but not across π _i s. One would not deliberately lower a particular $w_{\delta _{i}}$ and increase another particular $w_{\delta _{j}}$ in order to increase the payoff. Hence, risk attitudes would not induce hedging of $w_{\delta _{i}}$ across π _i s and would not increase the dispersion of reported $w_{\delta _{i}}$s. For example, a risk averse subject would never assign a positive $w_{\delta _{i}}$ to a δ _i if she believes that π _i equals zero.

2.5 Elicitation of asset values

So far we have elicited the single prior and the confidence weight distribution of multiple priors. The ambiguity models we set out to test attempt to explain how multiple priors enter the evaluation of an ambiguous asset. Therefore, we must also elicit the values of ambiguous assets that are based on the same states as our ambiguous scenarios. By relating these values to the corresponding confidence weight distribution of multiple priors, we are then able to provide a direct test of different ambiguity models.

As an ambiguous asset we used the same bag from the previous two decision tasks in the same round, generating 1000 ECU if a random draw matched a winning letter and 0 ECU otherwise. We elicited the values of the ambiguous assets with the certainty equivalent method. As shown in Fig. 3, we constructed a table with 10 rows, each of which contained two options. Option A was an ambiguous lottery. It paid 1000 ECU if the drawn chip matched one of the winning letters and 0 ECU otherwise. Option A therefore directly referred to the states of the ambiguous scenario. Option C was a sure payment. Moving from Row 1 to Row 10, Option C’s sure payment increased and thus became more attractive, while Option A (the ambiguous lottery) did not change. We obtained the switching point by asking each participant to state the first row where she preferred Option C over Option A.¹⁰

Fig. 3

Screenshot of the elicitation of values of the ambiguous assets with the certainty equivalent method. The number of winning letters in Option A and hence the winning probability changes across rounds as explained in subsection 2.2. Option C is adjusted according to the winning probability of Option A in different rounds

The certainty equivalent method can be rather lengthy to achieve an accurate value. The range in this procedure should be wide enough to include possible certainty equivalent values, and it should be narrow enough for an accurate inference. We used the ambiguity-neutral winning probability p _N as a reference to compute the potential values of each row as follows:

$$\left[1000\times p_{N}\times q[n]\right], $$

where n is the row number, and q[1]=0.6,q[2]=0.7,q[3]=0.75,q[4]=0.8,q[5]=0.85,q[6]=0.9,q[7]=0.95,q[8]=1.0,q[9]=1.2,q[10]=1.4. The value of the ambiguous asset is then computed as the mean of the values in the switching row and in the previous row (analogous to the procedure in subsection 2.3).

2.6 Controls

As explained in the introduction and in subsection 2.4, an important element of our design is that the elicitation of participants’ multiple priors is based on the estimation of the other participants’ behavior. For this estimation to be reliable, a participant has to believe that not only she herself but also all others in the room fully understand the experimental procedure. Otherwise, the estimation of the others’ behavior would be confounded by a participant’s uncertainty perception of the others’ rationality. We therefore made a few efforts to reduce this noise. First, we introduced an extensive trial round. In it we went through each decision with subjects and explained the implication of each decision. Subjects were encouraged to ‘play around’ and try different decisions during the trial round. Second, after the trial round we administered three exercise questions to check subjects’ understanding of the experimental procedure. Subsequently, we administered three incentivized test questions. For each correct answer we paid subjects 200 ECU.¹¹ Finally, after subjects had answered the three incentivized test questions, we publicly displayed the proportion of students who answered all test questions correctly. The proportions of correct answers for the first, second, and third test question were, on average, 92.40%, 91.23%, and 96.50%, respectively. The public information on the high performance in the test questions not only established a common level of subjects’ perception of others’ rationality but also manifested that almost all participants had a similar understanding of the experiment.

We acknowledge that, despite our efforts to reduce individuals’ uncertainty regarding others, the confidence weight distributions (discussed in subsection 2.4) may still contain not only subjects’ own perception of uncertainty in the ambiguous scenario but also their uncertainty regarding the capability of others to understand the experiment. In principle, information on the uncertainty of others should not play any role when one deliberates an own valuation of the ambiguous asset. More importantly, if the confidence weight distributions primarily reflected the uncertainty about others rather than one’s own uncertainty about the ambiguous scenario, the elicited confidence weight distributions should not have any explanatory power for subjects’ valuations of the ambiguous assets. The results in Section 3 show that this is clearly not what we observe. Another possibility is that confidence weight distributions may capture risk attitudes, and risk attitudes, in turn, explain subjects’ valuation of the ambiguous assets. We cannot exclude this possibility, although it is neither theoretically founded nor empirically supported.¹² We are therefore confident that our measure provides genuinely useful information about subjects’ multiple priors.

3 Results

With the min and max of priors at hand and by interpreting confidence weight distributions as probability measures over the set of multiple priors we can analyze how participants’ valuations of ambiguous assets relate to their multiple priors and to their confidence weight distributions over the priors.¹³ This allows us to test multiple priors decision models directly as each model implies different relationships between multiple priors or the confidence weight distributions and the corresponding certainty equivalent (CE) for the ambiguous asset.

Specification 5 empirically replicates the maxmin model (1) by including the minimum of the multiple priors (δ _{m i n} ) as the only explanatory variable in a random effects regression:

$$ CE=\text{Intercept}+\phi_{i}+\beta_{1}\times\delta_{min}+\epsilon, $$

(5)

where CE is the certainty equivalent of the ambiguous asset, δ _{m i n} is the min of multiple priors, and ϕ _i are individual random effects on the intercept. Model ‘MEU’ in Table 1 shows the estimation results of specification 5 above. We find that the coefficient of the min of priors is positive and statistically significant. Thus, the valuation of the ambiguous asset increases in the minimum of a participant’s multiple priors, δ _{m i n} .

Table 1 Random effects regressions which predict asset values with (combinations of) multiple priors

Although we find support for the maxmin model, it may not be the best description of the data. We therefore compare the maxmin model with the α maxmin model (2) by additionally considering the max of multiple priors (δ _{m a x} ) in the following empirical specification 6:

$$ CE=\text{Intercept}+\phi_{i}+\beta_{1}\times\delta_{min}+\beta_{2}\times\delta_{max}+\epsilon. $$

(6)

Our results show, in line with the α maxmin model, that both the min and max of multiple priors play a statistically and economically important role with coefficients of 5.4834 and 2.6877, respectively (see Table 1, Model ‘ α MEU’). With these two coefficients, we obtain an α of 0.6711, indicating that individuals put more weight on the minimum of priors when evaluating an ambiguous asset.¹⁴ In fact, individuals seem to place about twice the weight on the min of priors (5.4834/2.6877=2.04). However, with an α of 0.6711, subjects clearly consider not only the minimum but also the maximum of their multiple priors. Hence, in a direct comparison between the maxmin model and the α maxmin model, the results provide more support for the latter. In line with this, Log likelihood, Akaike information criterion (AIC) and Bayesian information criterion (BIC) also show that the overall explanatory power and informational efficiency of Model ‘ α MEU’ in Table 1 are greater than those of Model ‘MEU’, providing further support for the α maxmin model compared with the maxmin model. The improvement in the explanatory power is statistically significant according to a likelihood ratio test (p<0.01).

The test of the variational preferences model is less straightforward. In the variational preferences model c(δ) can be interpreted as the relative entropy (or the Kullback–Leibler divergence) of δ from a reference belief. A direct test would therefore require the specification of participants’ reference belief, which we do not know. We do know, however, participants’ confidence weights for their priors, which provides us with an intuitive indication of their most likely reference. Below we provide two specifications of c(δ). In the first specification, note that c(δ) can also be interpreted as the cost of considering the prior δ. Such a cost should be related to the confidence weight on the prior δ. The priors with higher confidence weights should have a lower cost of considering them and, accordingly, would be more likely to be considered. In other words, it would be more costly to ignore a prior that one regards as highly likely. Thus, an approximative but informative specification of c(δ) can be:

$$\begin{array}{@{}rcl@{}} c(\delta_{i})=\left\{\begin{array}{c} \begin{array}{c} 0\\ \infty \end{array} \begin{array}{c} if w_{\delta_{i}}=max_{i}(w_{\delta_{i}})\\ otherwise. \end{array}\end{array}\right. \end{array} $$

Namely, one only considers the most likely prior. This reduces the variational preferences model to the expected utility theory with the expectation taken on the most likely prior. Specification 7 represents such a test of the variational preferences model under the assumption that participants focus on the prior they are most confident about:

$$ CE=\text{Intercept}+\phi_{i}+\beta_{1}\times\delta_{mass}+\epsilon, $$

(7)

where δ _{m a s s} denotes the prior with the highest confidence weight. In the second specification we let $c(\delta _{i})=\theta R(\delta _{i}|\delta _{mass})=\theta [\delta _{i}ln\frac {\delta _{i}}{\delta _{mass}}+(1-\delta _{i})ln\frac {1-\delta _{i}}{1-\delta _{mass}}]$, the relative entropy of prior δ _i given the reference prior δ _{m a s s} , subjects’ most confident prior, where 𝜃 is the sensitivity to the cost of considering prior δ _i . Accordingly the statistical model becomes

$$ CE=\text{Intercept}+\phi_{i}+Min_{i}\:\left\{ \delta_{i}+\theta[\delta_{i}ln\frac{\delta_{i}}{\delta_{mass}}+(1-\delta_{i})ln\frac{1-\delta_{i}}{1-\delta_{mass}}]\right\} +\epsilon. $$

(8)

We let 𝜃 vary from 0 to 100 in steps of 0.1 and choose the 𝜃 that maximizes the log-likelihood (𝜃=4.8). As we can see from the random effects regression results in Table 1, the explanatory power of both specifications of the variational preferences model (Model ‘VP(1)’ and Model ‘VP(2)’ ) — measured by Log likelihood, AIC and BIC — is superior to the maxmin model but lower than the α maxmin model.

Finally, we examine the smooth model of ambiguity. For this, we conduct two tests. In a first, simple specification we estimate an empirical model that includes a confidence weighted average of all priors:

$$ CE=\text{Intercept}+\phi_{i}+\beta_{1}\times\delta_{weighted}+\epsilon. $$

(9)

The confidence weighted prior δ _{w e i g h t e d} in specification 9 is a proxy for the right hand side of Eq. 4. It does not ignore any of the multiple priors but pools them into one explanatory variable. As we can see in Table 1, the coefficient of δ _{w e i g h t e d} in Model ‘SA’ is statistically significant and relatively close to 1. Hence, it seems the confidence weighted prior gives a good explanation of variations in the valuation of the ambiguous asset. Furthermore, comparing all four regression models, the last specification provides the best fit, as evident from the comparisons of AIC, BIC, and Log likelihood. This result also provides support for the interpretation of $(w_{\delta _{i}})_{i=1}^{10}$ as a confidence weight distribution of a participant’s priors δ _i . As discussed in the introduction, this interpretation is more realistic than first intuition might suggest.

The results in Table 1 give most support to the smooth model of ambiguity. Encouraged by this result, in a second test, we go one step further and, based on Eq. 4, use individual weights for each prior with the following specification:

$$ CE=\text{Intercept}+\phi_{i}+\beta_{1}\times w_{\delta_{1}}+...+\beta_{9}\times w_{\delta_{9}}+\epsilon. $$

(10)

This allows us to investigate the curvature of ϕ(⋅) in Eq. 4. Note that, according to the smooth model of ambiguity, β _i = ϕ(δ _i ), where ϕ(⋅) is assumed to be increasing and concave in δ _i . The regression result is reported in Table 2.

Table 2 Random effects regression which tests the smooth model of ambiguity with individual confidence weights

The smooth model of ambiguity predicts that the coefficients β _i , i=1,2,…,9 in Table 2 should increase monotonically. The result of the random effects regression is largely consistent with this prediction: the coefficient starts with small and with negative values for δ ₁ (−1.7666, p<0.01), then increases to approximately zero for δ ₅ and δ ₆(−0.5226 and 0.3321, respectively, not significantly different from zero, p>0.10), and subsequently enters positive territory with δ ₇ and δ ₈ (2.0463 and 3.1756, respectively, both with p<0.01).¹⁵ To check the increasing pattern of coefficients more concretely we run eight Wald tests to compare the pairs of β _i and β _i+1, i=1,2,..,8. The test results confirm that the general pattern is increasing: there are four significant increases, one insignificant increase, three significant decreases, and increases are stronger than decreases. Again, the AIC, BIC, and Log likelihood indicate a greater explanatory power of this model than of any other multiple prior model in previous regressions (see corresponding values of Models ‘MEU’, ‘ α MEU’, and ‘VP’ in Table 1).Thus, although the smooth model of ambiguity is not perfectly consistent with individuals’ behavior, it both organizes the data very well and also fits the predicted general pattern for the coefficients. In conclusion, our experimental results provide more support for Klibanoff et al.’s (2005) smooth model of ambiguity than for the maxmin model, the α maxmin model, or the variational preferences model.

4 Conclusion

This study is a first step toward understanding the evaluation of ambiguous assets in ambiguous scenarios by eliciting both the min and the max of multiple priors and the confidence weight distribution over multiple priors. We have experimentally elicited each subject’s prior regarding the states of ambiguous scenarios. To examine the possibility of multiple priors, in addition to each subject’s single prior, we elicited each subject’s expectation of other participants’ priors and the confidence weight distribution over those priors. We then used participants’ multiple priors and confidence weight distributions to explain their valuations of an ambiguous asset, which was constructed using the same underlying states as the ambiguous scenarios.

We find that, in the valuation of the ambiguous asset, people consider both the maximum and the minimum of multiple priors. Although people place about twice the weight on the minimum, in support of the maxmin model, our results provide more evidence for the α maxmin model. Our two empirical specifications of the variational preferences model has less explanatory power than the α maxmin but more than the maxmin model. Overall, we find that the smooth model of ambiguity performs best among the four multiple priors models.

Our finding that the smooth model of ambiguity explains our data best is in line with Cubitt et al. (2014), who provide a qualitative test of α MEU and the smooth model of ambiguity and find greater support for the latter. These results, together with findings from recent, mostly neuroscientific studies that suggest many processes in the brain are Bayesian (Friston 2003, 2005; Doya et al. 2007), point to a surprisingly high level of probabilistic sophistication in subjects.

Appendix: Test questions and correct answers