Abstract
In this paper, we consider the sample average approximation (SAA) approach for a class of stochastic nonlinear complementarity problems (SNCPs) and study the corresponding convergence properties. We first investigate the convergence of the SAA counterparts of two-stage SNCPs when the first-stage problem is continuously differentiable and the second-stage problem is locally Lipschitz continuous. After that, we extend the convergence results to a class of multistage SNCPs whose decision variable of each stage is influenced only by the decision variables of adjacent stages. Finally, some preliminary numerical tests are presented to illustrate the convergence results.
Similar content being viewed by others
1 Introduction
Uncertainty is an important ingredient in modern optimization problems and practical applications [1, 24, 28]. The stochastic complementarity problem (SCP) is to consider the complementarity problem under uncertainty, which can be derived from the Karush-Kuhn-Tucker condition for a large class of stochastic programming problems and/or the equilibrium of stochastic multi-player games.
According to the structure (or levels) of uncertainty, SCPs can be roughly divided into single-stage SCPs, two-stage SCPs, and multistage SCPs. Single-stage and two-stage SCPs use random parameters to describe the uncertainty. Multistage SCPs model the uncertainty by stochastic processes. Since the multistage SCP reveals uncertainty more elaborately, it is expected to obtain better solutions compared with the single-stage or two-stage case, especially in a relatively long decision-making period. Of course, it is also challenging in both theoretical analysis and numerical algorithms because of the complexity of uncertainty.
Deterministic variational inequalities and complementarity problems have been extensively discussed; see monographs [11, 12] and the references therein for more details. In the last decade, stochastic variational inequalities (SVIs) have received more and more attention [19, 25]. In [2], by rewriting the single-stage stochastic linear complementarity problem through a nonlinear complementarity problem (NCP) function, the quasi-Monte Carlo method was adopted to solve the reformulated problem. Xu employed in [30] the SAA approach to analyze the discretization of single-stage SVIs. In [7], Chen et al. adopted the expected residual minimization (ERM) approach to formulate the single-stage SVI and a smoothing SAA approach was proposed to solve the ERM formulation. In [3], Chen et al. extended the ERM procedure to general two-stage nonlinear SVIs. In [23], Rockafellar and Wets first proposed the formulation of multistage SVIs and lay the foundation for the further investigation of two-stage or multistage SVIs. Next to [23], Rockafellar and Sun adopted in [22] the progressive hedging method (PHM) to solve the multistage SVIs when the support set is discrete. Inspired by [3, 20, 22, 23], Chen et al. investigated in [6] a discretization scheme for two-stage stochastic linear complementarity problems. In [4], Chen et al. considered the SAA approach for two-stage stochastic generalized equations and its application in two-stage nonlinear SVI-SCP problems. In [17], Jiang et al. adopted the regularized SAA approach to solve a class of two-stage SVIs and applied them to the crude oil market. In [5], Chen et al. modeled crude oil market share under the COVID-19 pandemic using two-stage stochastic equilibrium. In [16], Jiang et al. discussed the quantitative stability as well as the rate of convergence for a class of two-stage linear SVI-SCP problems. For a comprehensive review of recent development in two-stage and multistage SVIs, we refer to [29].
The SAA approach is an important approximation method for single-stage and two-stage stochastic optimization problems [28, 30]. Compared with the single-stage or two-stage case, the convergence analysis results of the SAA of multistage cases are quite limited. The existing results concentrate on multistage stochastic programming problems; see [21, 26, 27]. To the best of our knowledge, there are few results about the SAA approach and corresponding convergence analysis for multistage SCPs. According to these existing results, there are mainly two possible approaches to sample from a random process. The first one is to view the random process as a whole and sample from its (joint) distribution; the other is the conditional sampling. In this paper, from the viewpoint of practical calculation, we adopt the conditional sampling method and focus on the SAA convergence analysis of multistage SCPs.
There are mainly two contributions of this paper.
-
We establish the strong monotonicity assertion for a class of multistage SNCPs, which extends existing results from the two-stage case to the multistage case. Specifically, we weaken the continuously differentiable condition of strong monotonicity assertion in [4, Theorem 3.9] for two-stage nonlinear SVI-SCP problems to the locally Lipschitz continuity (Theorem 2), and then extend it to the multistage case (Theorem 3).
-
Under the strong monotonicity assumption, we consider the conditional sampling method for a three-stage SNCP. The asymptotic convergence assertion is derived (Theorem 4). The convergence analysis of the SAA approach for T-stage SNCPs (T > 3) can be derived similarly.
The rest of this paper is organized as follows. In Section 2, we introduce models and some useful properties of multistage SNCPs. In Section 3, we investigate the convergence analysis results of the SAA approach to multistage SNCPs. In Section 4, some preliminary numerical results are given by PHM. Finally, we conclude the whole paper in Section 5.
2 Models and properties of multistage SNCPs
In this section, we first introduce models of multistage SNCPs. After that, some useful properties are given for the further discussion.
2.1 Models of multistage SNCPs
To describe a T-stage SNCP model, we need further the following statement. Denote by ξ1,ξ2,⋯ ,ξT the discrete stochastic process with time horizon \(2\leq T\in \mathbb {N}\). For simplicity of statement and without loss of generality, we assume that ξt, t = 1,2⋯ ,T are all \(\mathbb {R}^{s}\)-valued. Furthermore, we assume that ξ1 is deterministic and random vectors ξt, t = 2⋯ ,T are defined on probability space \(({\varOmega },\mathcal {F},\mathbb {P})\), i.e., \(\xi _{t}:{\varOmega }\rightarrow {\varXi }_{t}\) with Ξt being the support set of ξt. Denote ξ[t] = (ξ1,⋯ ,ξt) supported on \({\varXi }_{[t]}\subseteq {\Xi }_{1}\times \cdots \times {\varXi }_{t}\). Then we use \(\mathcal {F}_{t}\) to denote the σ-field induced by ξ[t], i.e., \(\mathcal {F}_{t}:=\sigma (\xi _{[t]})\). Thus, ξ[t] is a random vector on the probability space \(({\varOmega },\mathcal {F}_{t},\mathbb {P})\). Specially, without the confusion, we neglect the subscript when t = T, namely, ξ = ξ[T], Ξ = Ξ[T] and \(\mathcal {F}=\mathcal {F}_{T}\). Moreover, we have the inclusion that \(\{\emptyset , {\varOmega }\}=\mathcal {F}_{1}\subseteq \mathcal {F}_{2}\subseteq {\cdots } \subseteq \mathcal {F}_{T}=\mathcal {F}\), which forms the so-called filtration. Analogously, to simplify the description, we again assume that decision variables xt, t = 1,2,⋯ ,T are all \(\mathbb {R}^{n}\)-valued. Of course, the t th stage decision variable xt is assumed to depend only on the available information until time t, i.e., ξ[t]. Or, equivalently, xt = xt(ξ[t]). This is the well-known nonanticipativity condition, which is an essential property in multistage stochastic optimization.
With the above notation, the general T-stage SNCP model can be written as:
where \(\mathbb {E}_{\xi |\xi _{[t]}}[\cdot ]\) means the conditional expectation of ξ for giving ξ[t] for t = 1,⋯ ,T − 1; \(\mathcal {N}_{\mathbb {R}_{+}^{n}}(x_{1})\) is the normal cone of \(\mathbb {R}_{+}^{n}\) at x1 and so on in a similar fashion; \({\varPhi }_{t}:\mathbb {R}^{nT} \times {\varXi }\rightarrow \mathbb {R}^{n}\) for t = 1,⋯ ,T. Sometimes, for simplification, we also write x2 = x2(ξ[2]),⋯ ,xT = xT(ξ[T]) in what follows.
Strategies of multistage SNCP (1) are a series of tuples (x1,x2(⋅),⋯ ,xT(⋅)) satisfying (1). Another important concept for two-stage or multistage SNCPs is the so-called relatively complete recourse condition. We say the multistage SNCP (1) satisfies the relatively complete recourse condition, if
has solutions for any given ξ[t+ 1] ∈Ξ[t+ 1] and \((x_{1},x_{2},\cdots ,x_{t})\in \mathbb {R}^{tn}_{+}\).
Note that model (1) is a very general form of multistage SNCPs. However, each stage may be decided only by the adjoining decision variables, e.g., multistage stochastic inventory problems. Given this, we will focus on the following specific multistage SNCP:
In general, it is more interesting to consider the behavior of the first-stage solution x1. Intuitively, we only need to determine x1 at the present stage, and x2,⋯ ,xT are scenario-dependent (or wait and see) solutions and new information can be employed for more accurate estimate in future stages. In view of this, as well as by convention (see, e.g., [26]), we will focus on the first stage solutions of the multistage SNCP (2). Throughout this paper, we assume that Φ1(⋅,⋅,ξ2) for a.e. ξ[2] ∈Ξ[2], Φt(⋅,⋅,⋅,ξt+ 1) for a.e. ξ[t+ 1] ∈Ξ[t+ 1] with t = 2,⋯ ,T − 1 and ΦT(⋅,⋅,ξT) for a.e. ξ[T] ∈Ξ[T] are continuous.
Our analysis is based on strong monotonicity properties of multistage SNCPs. To this end, we first consider strong monotonicity properties of two-stage SNCPs, and then extend them to multistage SNCPs.
2.2 Strong monotonicity of two-stage SNCPs
Two-stage SNCP is a special case of T-stage SNCPs (with T = 2) and can be formulated as:
where ξ is a s-dimensional random vector defined on probability space \(({\varOmega },\mathcal {F},\mathbb {P})\), \(\mathbb {E}_{\xi }[\cdot ]\) denotes the expectation operator with respect to (w.r.t.) random vector ξ, \({\varPhi }:\mathbb {R}^{n}\times \mathbb {R}^{m}\times {\varXi }\rightarrow \mathbb {R}^{n}\) and \({\varPsi }:\mathbb {R}^{n}\times \mathbb {R}^{m}\times {\varXi }\rightarrow \mathbb {R}^{m}\), \({\varXi }\subseteq \mathbb {R}^{s}\) denotes the support set of random vector ξ, and y(ξ) denotes the value of y(⋅) at ξ. We assume that both Φ(⋅,⋅,ξ) and Ψ(⋅,⋅,ξ) are continuous for a.e. ξ ∈Ξ.
We first give the definition of the strong monotonicity.
Definition 1
A mapping \(f: \mathbb {R}^{n}\to \mathbb {R}^{n}\) is strongly monotone with a positive scalar γ, if \(\left \langle f(x)-f(y),x-y\right \rangle \geq \gamma \left \Vert x-y\right \Vert ^{2}\) for any \(x,y\in \mathbb {R}^{n}\).
We have from [10, p. 75, Corollary] that the following chain rule property for Clarke generalized Jacobian, which is useful in the following discussion.
Lemma 1
[10] Let \(G:\mathbb {R}^{m}\rightarrow \mathbb {R}^{k}\) and \(F:\mathbb {R}^{n}\rightarrow \mathbb {R}^{m}\). Assume that G and F are locally Lipschitz continuous. Then, for any \(v\in \mathbb {R}^{n}\), we have
where ∂(GF)(x), ∂G(F(x)) and ∂F(x) denote the Clarke generalized Jacobian of GF at x, G at F(x) and F at x, respectively.
Proposition 1
Let \(f:\mathbb {R}^{n}\rightarrow \mathbb {R}^{n}\) be locally Lipschitz continuous. Then, f is strongly monotone with a positive constant γ if and only if, for any \(x\in \mathbb {R}^{n}\) and J(x) ∈ ∂f(x), it has that \( v^{\top } J(x) v \geq \gamma \left \Vert v\right \Vert ^{2}\) for any \(v\in \mathbb {R}^{n}\).
Proposition 1 can be considered as a simple corollary of [9, Corollary 3.10], but the Jacobian is defined in the sense of Clarke, rather than Mordukhovich.
Lemma 2
Consider the following parametric variational inequality:
where \({\varTheta }:\mathbb {R}^{k}\times \mathbb {R}^{l}\rightarrow \mathbb {R}^{k}\) and \(C\subseteq \mathbb {R}^{k}\) is a closed convex set. Assume that Θ(⋅,p) is strongly monotone and locally Lipschitz continuous for every fixed p. Then, there exists a unique solution for problem (4), denoted by \(\hat {z}(p)\), and it is locally Lipschitz continuous w.r.t. p.
The result follows by Proposition 1, parametrically CD regularity, and [15, Theorem 4] directly. Thus, we neglect the proof.
To proceed, we define the following inner product in \(\mathbb {R}^{n}\times \mathcal {Y}\), where \(\mathcal {Y}\) is the collection of measurable mappings from Ξ to \(\mathbb {R}^{m}\). Let \((x,y(\cdot )),(\tilde {x},\tilde {y}(\cdot ))\in \mathbb {R}^{n}\times \mathcal {Y}\). Define \(\langle {(x,y(\cdot )),(\tilde {x},\tilde {y}(\cdot ))}\rangle = x^{\top } \tilde {x} + \mathbb {E}_{\xi }[y(\xi )^{\top } \tilde {y}(\xi )]\).
According to the definition of the inner product above, we can define the strong monotonicity (see [6]) for problem (3): there exists a positive number \(\bar {\kappa }\) such that
holds for any \((x,y(\cdot )), (\tilde {x},\tilde {y}(\cdot )) \in \mathbb {R}^{n}\times \mathcal {Y}\).
We make the following assumption.
Assumption 1
There exists a positive continuous function \(\kappa :{\varXi }\rightarrow \mathbb {R}_{++}\) with \(\mathbb {E}_{\xi }[\kappa (\xi )]<+\infty \), such that
holds for any \((u,z),(\bar {u},\bar {z})\in \mathbb {R}^{n}\times \mathbb {R}^{m}\) and a.e. ξ ∈Ξ, where \(\mathbb {R}_{++}\!:=\!\{x\in \mathbb {R}\!:\!x>0\}\).
For any fixed pair (x,ξ), under Assumption 1 and the continuity of Ψ(x,⋅,ξ), the second-stage problem of (3) has a unique solution because of the strong monotonicity with constant κ(ξ) [12, Theorem 2.3.3 (b)]. We denote by \(\hat {y}(x,\xi )\) the unique solution. Then, we take it into the first-stage problem and obtain
We also use \(\hat {{\varPhi }}(x, \xi )\) to denote \({\varPhi }(x, \hat {y}(x,\xi ), \xi )\), which stresses that the latter one depends only on x and ξ.
Now we are ready to present the main results of this part.
Theorem 1
Suppose that Ψ(x,⋅,ξ) in the second-stage problem of (3) is strongly monotone for any fixed x and a.e. ξ ∈Ξ, and Ψ(⋅,⋅,ξ) is locally Lipschitz continuous for a.e. ξ ∈Ξ.
-
For any fixed x and a.e. ξ ∈Ξ, the second-stage problem of (3) has a unique solution, denoted by \(\hat {y}(x,\xi )\), and \(\hat {y}(x,\xi )\) is locally Lipschitz continuous w.r.t. x for a.e. ξ ∈Ξ.
-
Moreover, if \(\hat {y}(x,\xi )\) is differentiable at x, then for any \(v\in \mathbb {R}^{m}\),
$$ \nabla_{x} \hat{y}(x,\xi) v \in \bigcup_{(\mathbf{C},\mathbf{D})\in \partial {\varPsi}(x,\hat{y}(x,\xi),\xi) } -(I - \mathcal{D}_{\mathcal{L}} + \mathcal{D}_{\mathcal{L}} \mathbf{D})^{-1} \mathcal{D}_{\mathcal{L}} \mathbf{C} v, $$(6)where \(\partial {\varPsi }(x,\hat {y}(x,\xi ),\xi )\) is the Clarke generalized Jacobian w.r.t. (x,y), \({\mathscr{L}}\) is a subset contained in {1,⋯ ,m} and \(\mathcal {D}_{{\mathscr{L}}}\) is a diagonal matrix with its diagonal elements defining as \( \mathcal {D}_{ll}= \begin {cases} 1 & l\in {\mathscr{L}},\\ 0 & \text {otherwise}. \end {cases} \)
Proof
The first assertion follows from Lemma 2 straightforwardly. In the following proof, we concentrate on the second assertion.
Since \(\hat {y}(x,\xi )\) is locally Lipschitz continuous, it is differentiable almost everywhere. For any fixed x with \(\hat {y}(\cdot ,\xi )\) being differentiable at x, we consider the following partition of the index set:
If index \(j\in \mathcal {J}\), \((\hat {y}(x,\xi ))_{j} = ({\varPsi }(x,\hat {y}(x,\xi ),\xi ))_{j} = 0\). There are two possible cases.
-
(a)
If there exists a sequence \(\{x^{k}\}_{k\in \mathbb {N}}\) with xk≠x and \(x^{k}\rightarrow x\) as \(k\rightarrow \infty \) such that \((\hat {y}(x^{k},\xi ))_{j} = 0\), based on the definition of differential, we have
$$ \left\Vert \nabla_{x}(\hat{y}(x,\xi))_{j} \right\Vert = \lim_{k\rightarrow\infty}\frac{\left\vert (\hat{y}(x^{k},\xi))_{j} - (\hat{y}(x,\xi))_{j} \right\vert}{\left\Vert x^{k}-x\right\Vert } = \frac{\left\vert0-0\right\vert}{\left\Vert x^{k}-x\right\Vert } = 0. $$ -
(b)
If there exists a sequence \(\{x^{k}\}_{k\in \mathbb {N}}\) with xk≠x and \(x^{k}\rightarrow x\) as \(k\rightarrow \infty \) such that \(({\varPsi }(x^{k},\hat {y}(x^{k},\xi ),\xi ))_{j} = 0\), we have
$$ \begin{array}{@{}rcl@{}} \left\Vert \nabla_{x} ({\varPsi}(x,\hat{y}(x,\xi),\xi))_{j} \right\Vert = \lim_{k\rightarrow\infty}\frac{\left\vert ({\varPsi}(x^{k},\hat{y}(x^{k},\xi),\xi))_{j} - ({\varPsi}(x,\hat{y}(x,\xi),\xi))_{j} \right\vert}{\left\Vert x^{k}-x\right\Vert } = 0. \end{array} $$
Thus, we use notation \(\mathcal {J}_{1}\) and \(\mathcal {J}_{2}\) to denote these indexes satisfying (a) and (b), respectively. Thus, \(\mathcal {J}=\mathcal {J}_{1} \cup \mathcal {J}_{2}.\) Then, we denote \({\mathscr{L}}=\mathcal {I}\cup \mathcal {J}_{2}\) and \({\mathscr{M}}=\mathcal {K}\cup \mathcal {J}_{1}\).
If index \(i\in {\mathscr{M}}\), \((\hat {y}(x,\xi ))_{i} = 0\), which obviously indicates that \(\nabla _{x}(\hat {y}(x,\xi ))_{{\mathscr{M}}} = 0\).
If index \(i\in \mathcal {I}\), we have \(({\varPsi }(x,\hat {y}(x,\xi ),\xi ))_{i} =0\). Actually, we have that
in a neighborhood of x due to \(\hat {y}(x,\xi )> 0\) and the locally Lipschitz continuity of \(\hat {y}(\cdot ,\xi )\) w.r.t. x. This obversion together with (b) indicates
where \(({\varPsi }(x,\hat {y}(x,\xi ),\xi ))_{{\mathscr{L}}}\) is the subvector of \({\varPsi }(x,\hat {y}(x,\xi ),\xi )\) with entries in \({\mathscr{L}}\).
For any vector \(v\in \mathbb {R}^{m}\), we have
where 1) follows from the chain rule of Clarke generalized Jacobian, i.e., Lemma 1; 2) follows from the convexity and compactness of \(\partial ({\Psi }(x,\hat {y}(x,\xi ),\xi ))_{{\mathscr{L}}}\) by [10, Proposition 2.6.2, (a)]. Then, we obtain
where \(\mathbf {C}_{{\mathscr{L}}}\) and \(\mathbf {D}_{{\mathscr{L}}}\) denote sub-matrices of C and D with row indexes included in \({\mathscr{L}}\), respectively.
Note that \((\nabla _{x} \hat {y}(x,\xi ))_{{\mathscr{M}}=0}\), which implies that
where \(\mathbf {D}_{{\mathscr{L}} {\mathscr{L}}}\) denotes the sub-matrix of D with row index and column index contained in \({\mathscr{L}}\). Then we have
According to Proposition 1, the strong monotonicity of Ψ(x,⋅,ξ) implies the strongly positive definiteness of \(\mathbf {D}_{{\mathscr{L}}{\mathscr{L}}}\). Thus, the inverse of \(\mathbf {D}_{{\mathscr{L}}{\mathscr{L}}}\) is well-defined. Finally, we obtain
Combining \((\nabla _{x}\hat {y}(x,\xi )v)_{{\mathscr{M}}}\) with \((\nabla _{x}\hat {y}(x,\xi )v)_{{\mathscr{L}}}\) together, we have (6) by using the same reformulation techniques in [6, 8]. □
Remark 1
In Theorem 1, we weaken the conditions in existing results in [18, Corollary 2.1] from continuous differentiability of Ψ(⋅,⋅,ξ) to locally Lipschitz continuity of Ψ(⋅,⋅,ξ).
With the above preparation, we now give the strong monotonicity assertion for the two-stage SNCP where the second-stage problem is only locally Lipschitz continuous. This will lay the foundation for the multistage case.
Theorem 2
Suppose that: (i) Assumption 1 holds; (ii) Φ(⋅,⋅,ξ) is continuously differentiable and Ψ(⋅,⋅,ξ) is locally Lipschitz continuous for a.e. ξ ∈Ξ. Then \(\hat {{\varPhi }}(\cdot , \xi )\) is strongly monotone for a.e. ξ ∈Ξ with constant κ(ξ) and thus \(\mathbb {E}_{\xi }[\hat {{\varPhi }}(\cdot , \xi )]\) is strongly monotone with constant \(\mathbb {E}_{\xi }[\kappa (\xi )]\).
Proof
According to Lemma 2, \(\hat {y}(x,\xi )\) is locally Lipschitz continuous w.r.t. x and thus \({\varPhi }(x, \hat {y}(x,\xi ), \xi )\) is locally Lipschitz continuous w.r.t. x. Then, its Clarke generalized Jacobian w.r.t. x is well-defined. We first verify that \(\hat {{\varPhi }}(x, \xi ) := {\varPhi }(x, \hat {y}(x,\xi ), \xi )\) is strongly monotone w.r.t. x for a.e. ξ ∈Ξ. Equivalently, we show that any \(J(\xi )\in \partial _{x} \hat {{\varPhi }}(x, \xi )\) is strongly positive definite (see Proposition 1). Based on the definition of Clarke generalized Jacobian, we have that, for any \(v\in \mathbb {R}^{n}\), that
where \(\mathfrak {D}_{\hat {y}(\cdot ,\xi )}\) denotes the collection of differentiable points of \(\hat {y}(\cdot ,\xi )\); \(\mathbf {A}(x^{\prime },\xi ):=\nabla _{1} {\varPhi }(x^{\prime }, \hat {y}(x^{\prime },\xi ), \xi )\), \(\mathbf {B}(x^{\prime },\xi ):=\nabla _{2} {\varPhi }(x^{\prime }, \hat {y}(x^{\prime },\xi ), \xi )\), ∇1 is the differential at the first position and ∇2 is the differential at the second position. Note that (a) follows from the definition of Clarke generalized Jacobian, and (b) follows from (6).
It knows from the strong monotonicity in Assumption 1 and Proposition 1 that any
is strongly positive definite with constant κ(ξ). Then by [6, Lemma 2.1] and Assumption 1,
for any \(z\in \mathbb {R}^{n}\) and \(x^{\prime }\in \mathfrak {D}_{\hat {y}(\cdot ,\xi )}\). This implies that each element in
is strongly positive definite with constant κ(ξ). Then, the strong monotonicity of \(\hat {{\varPhi }}(\cdot ,\xi )\) with constant κ(ξ) follows from Proposition 1.
Furthermore, we have \(\mathbb {E}_{\xi }[\hat {{\varPhi }}(\cdot ,\xi )]\) is strongly monotone with constant \(\mathbb {E}_{\xi }[\kappa (\xi )]\). □
2.3 Strong monotonicity of multistage SNCPs
In this part, we consider the strong monotonicity of the T-stage SNCP (2). It can be viewed as an extension of [6] from two-stage to multistage and linear case to nonlinear case. Analogously, we need to define the following inner product in \(\mathbb {R}^{n}\times \mathcal {Y}_{2}\times \cdots \times \mathcal {Y}_{T}\), where \(\mathcal {Y}_{t}, t=2,\cdots ,T\) stand for the set of all n-dimensional measurable mappings on Ξ[t]. For
we define
Then, we have the corresponding norm
Denote
and
Then, we can give the definition of the strong monotonicity for \(\mathcal {G}: \mathbb {R}^{n}\times \mathcal {Y}_{2}\times \cdots \times \mathcal {Y}_{T} \rightarrow \mathbb {R}^{n}\times \mathcal {Y}_{2}\times \cdots \times \mathcal {Y}_{T}\) as follows: there exists a positive number \(\bar {\eta }\) such that
for any \((x_{1},x_{2}(\cdot ),\cdots ,x_{T}(\cdot )),(y_{1},y_{2}(\cdot ),\cdots ,y_{T}(\cdot ))\in \mathbb {R}^{n}\times \mathcal {Y}_{2}\times \cdots \times \mathcal {Y}_{T}\).
Assumption 2
For any (u1,u2,⋯ ,uT), \((z_{1}, z_{2},\cdots ,z_{T})\in \mathbb {R}^{Tn}\), there exists \(\eta :{\varXi }\rightarrow \mathbb {R}_{++}\) satisfying \(\mathbb {E}_{\xi }[\eta (\xi )]<+\infty \), such that
holds for a.e. ξ ∈Ξ.
It is easy to know from (7) that
for t = 1,2,⋯ ,T. Then,
which implies Γ(x1,x2,⋯ ,xT,ξ) is strongly monotone.
Proposition 2
Let Assumption 2 hold. For any given \(x_{[t]}\in \mathbb {R}^{tn}\) and a.e. ξ[t+ 1] ∈Ξ[t+ 1], the last (T − t)-stage problem
has a unique solution \((\hat {x}_{t+1},\cdots ,\hat {x}_{T})\).
Similar to the previous discussion, we know from [14, Theorem 12.2 and Lemma 12.2] that (9) has a unique solution. Specifically, when t = 0, problem (2) has a unique solution under Assumption 2.
Theorem 3
Suppose that: (i) Assumption 2 holds; (ii) Φ1(⋅,⋅,ξ2), Φt(⋅,⋅,⋅,ξt+ 1) for t = 2,⋯ ,T − 1 and ΦT(⋅,⋅,ξT) are continuously differentiable almost surely. Then
and the following problem
for t = 2,⋯ ,T − 1 are strongly monotone with constant \(\mathbb {E}_{\xi }[\eta (\xi )]\), where \(\hat {x}_{t+1}(x_{t},\xi _{[t+1]})\) is the unique solution of the (t + 1)th stage for given x[t] and ξ[t+ 1] in Proposition 2.
Proof
We give the proof recursively. Denote
and
for t = 2,⋯ ,T − 1, where \(\hat {x}_{t+1}(x_{t},\xi _{[t+1]})\) is the unique (t + 1)th stage solution in Proposition 2.
Then, we first verify t = T − 1 for problem (11). According to Proposition 2, we have for given xT− 1 and a.e. ξ ∈Ξ that the last-stage problem
has a unique solution, denoted by \(\hat {x}_{T}(x_{T-1},\xi )\). Moreover, by Lemma 2, we know that \(\hat {x}_{T}(x_{T-1},\xi )\) is locally Lipschitz continuous w.r.t. xT− 1. By viewing
as two parts, we can obtain from Theorem 2 that \(\tilde {{\varLambda }}_{T-1}(x_{1},\cdots ,x_{T-1},\xi _{[T]})\) satisfies Assumption 2 in \(\mathbb {R}^{(T-1)n}\) with constant η(ξ). Moreover, by a similar procedure, we can obtain
for any \((x_{1}, x_{2}(\cdot ),\cdots ,x_{T-1}(\cdot )), (y_{1}, y_{2}(\cdot ),\cdots ,y_{T-1}(\cdot )) \in \mathbb {R}^{n}\times \mathcal {Y}_{2}\times \cdots \times \mathcal {Y}_{T-1}\). Thus, problem (11) is strongly monotone with constant \( \mathbb {E}_{\xi }[\eta (\xi )]\) for t = T − 1.
Now, we assume that for T − 1,T − 2,⋯ ,t + 1 (t ≥ 2) that problem (11) is strongly monotone with constant \( \mathbb {E}_{\xi }[\eta (\xi )]\) and \(\hat {x}_{t+1}(x_{t},\xi _{[t+1]})\) is locally Lipschitz continuous w.r.t. xt. Analogously, we view \(\tilde {\Lambda }_{t}(x_{1},\cdots ,x_{t},\xi _{[t+1]})\) as the following two parts:
Then, by Lemma 2 and Theorem 2, we have that \(\hat {x}_{t}(x_{t-1},\xi _{[t]})\) is locally Lipschitz continuous w.r.t. xt− 1 and \(\tilde {{\varGamma }}_{t}(x_{1},\cdots ,x_{t},\xi _{[t]})\) is strongly monotone with constant \(\mathbb {E}_{\xi }[\eta (\xi )]\).
Finally, we obtain
is strongly monotone with constant \(\mathbb {E}_{\xi }[\eta (\xi )]\), and \(\hat {x}_{3}(\cdot , \xi _{[3]})\) is locally Lipschitz continuous. By directly using Theorem 2, we verify (10). Then we complete the proof. □
Theorem 3 can be viewed as a multistage extension of Theorem 2. The following corollary directly follows from the proof of Theorem 3.
Corollary 1
Let assumptions in Theorem 3 hold. For t = 2,⋯ ,T, \(\hat {x}_{t}(x_{t-1},\xi _{[t]})\), which is the t th stage solution in Proposition 2, is locally Lipschitz continuous w.r.t. xt− 1 for a.e. ξ[t] ∈Ξ[t].
3 Conditional sampling for multistage SNCPs
To simplify the presentation as well as by convention [26, 27], we only discuss the case of the SAA approach to solve problem (2) when T = 3. That is
or equivalently
where \(\hat {x}_{3}(x_{2}(\xi _{[2]}),\xi _{[3]})\) is the unique solution of the third-stage problem for given x2(ξ[2]) and ξ[3].
Let \(\{{\xi _{2}^{1}}, {\xi _{2}^{2}},\cdots ,\xi _{2}^{N_{1}}\}\) be N1 i.i.d. random samples according to random vector ξ2. Further, we have according to \({\xi _{2}^{i}}\) for 1 ≤ i ≤ N1 the following conditional N2 i.i.d. random samples \(\{\xi _{3}^{i1},\xi _{3}^{i2},\cdots ,\xi _{3}^{iN_{2}}\}\) of ξ3. Thus, we have total N := N1N2 scenarios or sample paths. Then, we obtain the conditional sampling SAA problem of (13):
where \(\xi _{[3]}^{jk}:=(\xi _{1},{\xi _{2}^{j}},\xi _{3}^{jk})\) for j = 1,2,⋯ ,N1 and k = 1,2,⋯ ,N2. Since ξ1 is deterministic, we also neglect ξ1 and write \(\xi _{[2]}^{j}\) as \({\xi _{2}^{j}}\). Similar to the notation in the preceding context, we use \(\hat {x}_{2}(x_{1},\xi _{2})\) and \(x_{1}^{*}\) to denote the optimal solution of the second-stage problem of (13) for given x1 and ξ2 and the optimal solution of the first-stage problem of (13), respectively. Moreover, according to Theorem 3, we have that the SAA problem (14) has the unique solution by viewing that the underlying probability distributions are discrete. We use \(\tilde {x}_{1}^{N_{1},N_{2}}\) to denote the first-stage solution of problem (14) and \(\tilde {x}_{2}^{N_{2}}(x_{1},{\xi _{2}^{j}})\) to denote the second-stage solution of problem (14) for given x1 and \({\xi _{2}^{j}}\).
It should be mentioned that the convergence analysis of SAA of three-stage SNCPs (between problems (13) and (14)) is not a trivial extension from SAA of two-stage SNCPs. The main reason is that the second-stage problem in (13) changes when the SAA procedure is conducted (see (14)), which makes the SAA convergence of the first-stage problem of (14) to that of (13) harsh. To derive the convergence result, we need the following standard assumption.
Assumption 3
Let the following assertions hold:
(A1) There exist two compact and convex sets \(X_{1},X_{2}\subseteq \mathbb {R}^{n}\) such that \(x_{1}^{*}\cup \tilde {x}_{1}^{N_{1},N_{2}} \subseteq X_{1}\) for any \(N_{1},N_{2}\in \mathbb {N}\) and \(\hat {x}_{2}(x_{1},\xi _{2}) \cup \{\tilde {x}_{2}^{N_{2}}(x_{1},{\xi _{2}^{j}})\}_{j=1}^{N_{1}} \subseteq X_{2}\) for any x1 ∈ X1, \(\xi _{2}, {\xi _{2}^{j}}\in {\varXi }_{2}\) and \(N_{1}, N_{2}\in \mathbb {N}\), j = 1,2,⋯ ,N1;
(A2) For each ξ2 ∈Ξ2, the following conditional expectation
is finite.
The following lemma is a uniform convergence result.
Lemma 3
Let \(f:X\subseteq \mathbb {R}^{n}\rightarrow \mathbb {R}^{m}\) be a continuous mapping with X being a compact set and \(f_{k}: \mathbb {R}^{n}\times {\varOmega }\to \mathbb {R}^{m}\) for \(k\in \mathbb {N}\). Suppose that: (i) \(\left \Vert {f_{k}(x,\omega )-f_{k}(y,\omega )}\right \Vert \leq L_{k}(\omega ) \left \Vert {x-y}\right \Vert \) for any x,y ∈ X and \(k\in \mathbb {N}\) with \(L_{k}(\omega )\rightarrow L\) with probability 1 (w.p.1) as \(k\rightarrow \infty \), where L is a positive constant; (ii) for any fixed x ∈ X, \(f_{k}(x,\omega )\rightarrow f(x)\) w.p.1 as \(k\rightarrow \infty \). Then \(f_{k}(x,\omega )\rightarrow f(x)\) w.p.1 uniformly w.r.t. x over X as \(k\rightarrow \infty \), i.e.,
Proof
Choose now a point \(\bar {x}\in X\). For any 𝜖 > 0, due to assumption (i), there exists a neighborhood W of \(\bar {x}\) such that w.p.1 for sufficiently large k,
where \(\textup {diam}(W):=\sup _{w_{1},w_{2}\in W}\left \Vert w_{1}-w_{2}\right \Vert \) is the diameter of W.
Due to the compactness of X, by finite covering theorem, we can select finite points x1,⋯ ,xq and corresponding neighborhoods W1,⋯ ,Wq covering X such that w.p.1 for large enough k, we have
Since f is continuous, neighborhoods of xj, j = 1,⋯ ,q can be chosen in such a way that
We also know from assumption (ii) that w.p.1 for sufficiently large k,
For any x ∈ X, denote by j(x) ∈{1,⋯ ,q} the index such that x ∈ Wj(x). Then we have from (16) to (18) that w.p.1 for sufficiently large k,
Due to the arbitrariness of x and 𝜖, we complete the proof. □
Proposition 3
Suppose that: (i) Assumptions 2 and 3 hold; (ii) Φ2(⋅,⋅,⋅,ξ3) and Φ3(⋅,⋅,ξ3) are continuously differentiable and Lipschitz continuous with Lipschitz moduli L2(ξ3) and L3(ξ3) respectively for a.e. ξ3 ∈Ξ3.
-
For each \({\xi _{2}^{j}}\in {\varXi }_{2}\),
$$ \begin{array}{@{}rcl@{}} &&\sup_{x_{1}\in X_{1},x_{2}\in X_{2}}\Bigg(\frac{1}{N_{2}}\sum\limits_{k=1}^{N_{2}} {\varPhi}_{2}(x_{1}, x_{2} ,\hat{x}_{3}(x_{2},\xi_{[3]}^{jk}), \xi_{3}^{jk}) \\ &&~~~~~~~~~~~~~~~~~~~~- \mathbb{E}_{\xi_{3}|{\xi_{2}^{j}}}\left[{\varPhi}_{2}(x_{1},x_{2},\hat{x}_{3}(x_{2},\xi_{[3]}), \xi_{3}) \right ] \Bigg) \rightarrow 0 \end{array} $$w.p.1 as \(N_{2}\rightarrow \infty \),
-
If, in addition, (iii) for every \({\xi _{2}^{j}}\in {\varXi }_{2}\),
$$ \mathbb{E}_{\xi_{3}|{\xi_{2}^{j}}}[L_{2}(\xi_{3})]<\infty, ~\mathbb{E}_{\xi_{3}|{\xi_{2}^{j}}}[\eta(\xi_{[3]})]<\infty~ \text{ and }~ \mathbb{E}_{\xi_{3}|{\xi_{2}^{j}}}\left[ \frac{L_{2}(\xi_{3})L_{3}(\xi_{3})}{\eta(\xi_{[3]})} \right]<\infty, $$then for every \({\xi _{2}^{j}}\in {\varXi }_{2}\), we have
$$ \sup_{x_{1}\in X_{1}}\left\Vert \tilde{x}_{2}^{N_{2}}(x_{1},{\xi_{2}^{j}})-\hat{x}_{2}(x_{1},{\xi_{2}^{j}})\right\Vert \rightarrow 0 $$w.p.1 as \(N_{2}\rightarrow \infty \).
Proof
We know from Corollary 1 that \(\hat {x}_{3}(\cdot ,\xi _{3})\) is locally Lipschitz continuous. This together with the locally Lipschitz continuity of Φ2(⋅,⋅,⋅,ξ3) and the compactness of X1 and X2 result in (a) by directly using [28, Theorem 7.53].
In the rest of the proof, we focus on part (b). We prove it based on Lemma 3. Thus, we first verify the pointwise convergence. Let \(\{\tilde {x}_{2}^{N_{2}}(x_{1},{\xi _{2}^{j}})\}\) be the solution sequence of the second-stage problem of (14) with given x1, \({\xi _{2}^{j}}\) and samples \(\{\xi _{3}^{jk}\}_{k=1}^{N_{2}}\) and \(\bar {x}_{2}\) be any accumulation point of \(\{\tilde {x}_{2}^{N_{2}}(x_{1},{\xi _{2}^{j}})\}\) due to (A1) of Assumption 3. According to part (a), we have, for fixed x1 ∈ X1 and \({\xi _{2}^{j}}\in {\varXi }_{2}\), that
w.p.1 as \(N_{2}\rightarrow \infty \). This implies, for fixed x1 ∈ X1 and \({\xi _{2}^{j}}\in {\varXi }_{2}\), that \(\tilde {x}_{2}^{N_{2}}(x_{1},{\xi _{2}^{j}}) \rightarrow \hat {x}_{2}(x_{1},{\xi _{2}^{j}})\) w.p.1 as \(N_{2}\rightarrow \infty \) (see, e.g., [30, Proposition 2.1]). Next, we verify this pointwise convergence is uniform w.r.t. x1 over X1.
To this end, we first consider the Lipschitz modulus of \(\hat {x}_{3}(\cdot , \xi _{3}^{jk})\), which
is the upper bound of the Clarke generalized Jacobian \(\partial _{x_{2}}\hat {x}_{3}(x_{2}, \xi _{3}^{jk})\).
By directly using (6) in Theorem 1, we have
for any \(v\in \mathbb {R}^{n}\). It means that
We know from Proposition 1 and Assumption 2 that D is strongly monotone (positive definite) w.r.t. \(\eta (\xi _{[3]}^{jk})\). Then we obtain from [6, Lemma 2.1] that
Note also that \(\left \Vert \mathbf {C}\right \Vert \) is bounded from above by the Lipschitz modulus of \({\varPhi }_{3}(\cdot , \cdot ,\xi _{3}^{jk} )\) based on the definition of Clarke generalized Jacobian. Then \(\hat {x}_{3}(\cdot ,\xi _{3}^{jk})\) is Lipschitz continuous with modulus \(\frac {L_{3}(\xi _{3}^{jk})}{\eta (\xi _{[3]}^{jk})}\). Since X2 is convex and compact, we have \(\hat {x}_{3}(x_{2},\xi _{3}^{jk})\) is Lipschitz continuous over X2 with modulus \(\frac {L_{3}(\xi _{3}^{jk})}{\eta (\xi _{[3]}^{jk})}\).
According to the Lipschitz continuity of \({\varPhi }_{2}(\cdot ,\cdot ,\cdot ,\xi _{[3]}^{jk})\), a Lipschitz modulus of term
is \( \frac {1}{N_{2}}{\sum }_{k=1}^{N_{2}} L_{2}(\xi _{3}^{jk})\left (1 + \frac {L_{3}(\xi _{3}^{jk})}{\eta (\xi _{[3]}^{jk})}\right ). \)
Moreover, by Assumption 2, \(\frac {1}{N_{2}}{\sum }_{k=1}^{N_{2}} {\varPhi }_{2}(x_{1}, x_{2}, \hat {x}_{3}(x_{2}, \xi _{3}^{jk}), \xi _{3}^{jk})\) is strongly monotone with positive constant \(\frac {1}{N_{2}}{\sum }_{k=1}^{N_{2}} \eta (\xi _{[3]}^{jk})\). Finally, by the same procedure as above, we obtain a Lipschitz modulus of \(\tilde {x}_{2}^{N_{2}}(\cdot ,{\xi _{2}^{j}})\) is
which can be bounded from above by
w.p.1 as \(N_{2}\rightarrow \infty \). Then by directly using Lemma 3, we conclude (b). □
Proposition 4
Suppose that: (i) Assumptions 2 and 3 hold; (ii) Φ1(⋅,⋅,ξ2), Φ2(⋅,⋅,⋅,ξ3) and Φ3(⋅,⋅,ξ3) are continuously differentiable and Lipschitz continuous for a.e. ξ2 ∈Ξ3 and ξ3 ∈Ξ3 with Lipschitz moduli L1(ξ2), L2(ξ3) and L3(ξ3) respectively, and
Then we have
w.p.1 as \(N_{2}\rightarrow \infty \) and \(N_{1}\rightarrow \infty \).
Proof
We prove pointwise convergence firstly. For any fixed x1 ∈ X1,
For the first term of the right-hand side of (20), we have
It knows from Proposition 3 that
w.p.1 as \(N_{2}\rightarrow \infty \), and
where diam(X2) denotes the diameter of X2. Then, by Lebesgue’s dominated convergence theorem, we have
Thus, by law of large numbers (LLN), as \(N_{1}\to \infty \) and \(N_{2}\to \infty \), it holds pointwisely that
Analogously, by LLN,
as \(N_{1}\to \infty \) pointwisely. Then for any fixed x1 ∈ X1,
as \(N_{1}\to \infty \) and \(N_{2}\to \infty \).
Note that \(\frac {1}{N_{1}}{\sum }_{i=1}^{N_{1}}{\varPhi }_{1}(\cdot , \tilde {x}_{2}^{N_{2}}(\cdot ,{\xi _{2}^{i}}), {\xi _{2}^{i}})\) is Lipschitz continuous with Lipschitz modulus being
which converges to a finite number w.p.1 due to LLN. Then we complete the proof by quoting Lemma 3. □
Immediately, we can derive the following asymptotic convergence result by using Proposition 4 (see, e.g., [30, Proposition 2.1]).
Theorem 4
Under the same conditions of Proposition 4, we have
w.p.1 as \(N_{1}\rightarrow \infty \) and \(N_{2}\rightarrow \infty \).
We make the following remarks.
Remark 2
From the above discussion, it can be observed that the extension of convergence analysis of two-stage SNCPs to that of three-stage SNCPs is not trivial. The key reason is that the second-stage problem in (13) changes when the conditional SAA procedure is conducted (see (14)), which makes the SAA convergence of the first-stage problem of (14) to that of (13) unusual.
We consider the convergence analysis of the SAA approach of three-stage SNCP for the following reasons: (1) Similar to multistage stochastic optimization [26], the extension of the convergence analysis from two-stage SNCPs to three-stage SNCPs already demonstrates the main difficulties of extending the convergence analysis from two-stage SNCPs to multistage SNCPs. It is not difficult to extend our results to the general T-stage SNCPs for T > 3 by a similar procedure. (2) The discussion of three-stage SNCPs simplifies the notation.
Remark 3
In this section, we concentrate on convergence properties of the SAA approach for a class of multistage SNCPs (three-stage SNCPs whose decision variable of each stage is influenced only by the decision variables of adjoining stages). This is mainly motivated by some practical problems, like inventory problems, and multistage stochastic optimization problems (see, e.g., [28, Chapter 3]). It should be pointed out that there are some challenges to extend our results to the case of the general multistage SNCPs (1).
We use the following general three-stage SNCP (by letting T = 3 in (1)) to explain these challenges:
Under certain conditions (see, e.g., Lemma 2), we have the third-stage problem of (21) with given (x1,x2,ξ[3]) has a unique and locally Lipschitz continuous solution \(\hat {x}_{3}(x_{1},x_{2},\xi _{[3]})\). Taking it into the first and second stages, we rewrite problem (21) as
By a similar procedure as that in Theorem 1, the second-stage problem of (22) can have a unique and locally Lipschitz continuous solution \(\hat {x}_{2}(x_{1},\xi _{[2]})\). Submitting it into the first sage of (22), we obtain
It can observe from problem (23) that the mapping in problem (23) is highly composite w.r.t. x1. Moreover, our analysis can not apply to this problem directly, and it will become more complicated as the number of stages increases.
4 Numerical results
In this section, we extend the two-stage stochastic non-cooperative game problem [6, 16, 20, 31] to a three-stage case, and apply PHM to solve it. The numerical results are used to illustrate the theoretical results.
Let \(\xi _{2}:{\varOmega }_{2}\to {\varXi }_{2}\subseteq \mathbb {R}^{2}\) and \(\xi _{3}:{\varOmega }_{3}\to {\varXi }_{3}\subseteq \mathbb {R}^{2}\) be two independent random vectors. For i = 1,2, \(x_{i}\in \mathbb {R}^{n_{i}}\), \(y_{i}: {\varXi }_{2}\to \mathbb {R}^{m_{i}}\) and \(z_{i}: {\varXi }_{2}\times {\varXi }_{3}\to \mathbb {R}^{l_{i}}\) be the decision variables of the i th player at the first, second, and third stages, respectively, with ni = mi = li = 3. Denote n = n1 + n2, m = m1 + m2 and l = l1 + l2. By convention, we also use x−i,y−i and z−i to denote the rival’s decisions for i = 1,2. In this game, the i th (i = 1,2) player solves the following optimization problem:
where \(\theta _{i}:\mathbb {R}^{n_{i}}\times \mathbb {R}^{n_{-i}}\rightarrow \mathbb {R}\), \(\psi _{i}:\mathbb {R}^{n_{i}} \times \mathbb {R}^{m_{-i}}\times {\varXi }_{2} \rightarrow \mathbb {R}\) is defined as
here \(\phi _{i}:\mathbb {R}^{m_{i}}\times \mathbb {R}^{n_{i}}\times \mathbb {R}^{m_{-i}}\times {\varXi }_{2} \rightarrow \mathbb {R}\) and \(\varphi _{i}:\mathbb {R}^{m_{i}}\times \mathbb {R}^{l_{-i}}\times {\varXi }_{2} \times {\varXi }_{3} \rightarrow \mathbb {R}\) is the optimal value function of the third-stage problem, that is
with \({\varsigma }_{i}:\mathbb {R}^{l_{i}}\times \mathbb {R}^{m_{i}}\times \mathbb {R}^{l_{-i}}\times {\varXi }_{2} \times {\varXi }_{3} \rightarrow \mathbb {R}\).
To proceed, we consider the strongly convex quadratic game (see also [4, 31]), that is
where \(H_{i}\in \mathbb {R}^{n_{i}\times n_{i}}\), \({Q^{1}_{i}}(\xi _{2})\in \mathbb {R}^{m_{i}\times m_{i}}\) and \({Q^{2}_{i}}(\xi _{2},\xi _{3})\in \mathbb {R}^{l_{i}\times l_{i}}\) are symmetric positive definite matrices, \(q_{i}\in \mathbb {R}^{n_{i}}\), \(P_{i}\in \mathbb {R}^{n_{i} \times n_{-i}}\), \({c^{1}_{i}}(\xi _{2})\in \mathbb {R}^{m_{i}}\), \(S^{1}_{ij}(\xi _{2})\in \mathbb {R}^{m_{i} \times n_{j}}\), \({O^{1}_{i}}(\xi _{2})\in \mathbb {R}^{m_{i} \times m_{-i}}\), \({c^{2}_{i}}(\xi _{2},\xi _{3})\in \mathbb {R}^{l_{i}}\), \(S^{2}_{ij}\in \mathbb {R}^{l_{i} \times m_{j}}\), \(S^{2}_{ij}\in \mathbb {R}^{l_{i}\times m_{j}}\) and \({O^{2}_{i}}(\xi _{2}, \xi _{3})\in \mathbb {R}^{l_{i} \times l_{-i}}\).
Denote x = (x1,x2), y(⋅) = (y1(⋅),y2(⋅)) and z(⋅,⋅) = (z1(⋅,⋅),z2(⋅,⋅)). Due to the strong convexity, problems (25) and (26) have unique solutions, denoted by \(\bar {y}_{i}(\xi _{2})\) and \(\bar {z}_{i}(\xi _{2},\xi _{3})\) respectively.
By [13, Theorem 5.3 and Corollary 5.4],
are continuously differentiable w.r.t. xi and yi, respectively, and their gradients are
and
Hence, the three-stage stochastic game problem can be reformulated as a three-stage SVI (it can be rewritten as a three-stage stochastic linear complementarity problem): for i = 1,2,
where
Moreover, if there exists a positive continuous function κ(ξ2,ξ3) such that \(\mathbb {E}[\kappa (\xi _{2}, \xi _{3})]<\infty \) and for a.e.(ξ2,ξ3) ∈Ξ2 ×Ξ3,
then for each \((\tau ^{\top },u^{\top },k^{\top })^{\top }\in \mathbb {R}^{m+n+l}\), the three-stage SVI (27) satisfies Assumption 2. Moreover, if Ξ2 ×Ξ3 is compact, by Assumption 2, the conditions in Theorem 4 hold.
In this example, we consider a stage-wise independent case, that is ξ2 and ξ3 are independent. Let \(\{{\xi _{2}^{i}}\}_{i=1}^{N_{1}}\) be an i.i.d sample of the second-stage random variable ξ2 and \(\{{\xi _{3}^{j}}\}_{j=1}^{N_{2}}\) be an i.i.d sample of the third stage of ξ3 when given the value \({\xi _{2}^{i}}\). Then the SAA problem of problem (27) is
4.1 Generation of matrices satisfying condition (28)
We first generate i.i.d. samples \(\{{\xi _{2}^{i}}\}_{i=1}^{N_{1}}\subset [0, 1]^{2}\) of random variable \(\xi _{2}\in \mathbb {R}^{2}\) and \(\{{\xi _{3}^{j}}\}_{j=1}^{N_{2}}\subset [0,1]^{2}\) of random variable \(\xi _{3} \in \mathbb {R}^{2}\) from uniform distributions over Ξ2 = [0,1]2 and Ξ3 = [0,1]2, respectively.
Note that PHM converges to a solution of (29) if condition (28) holds. To this end, for any given (ξ2,ξ3), we generate matrices A1, B1(ξ2), L2(ξ2), A2(ξ2), B2(ξ2), L3(ξ2,ξ3), A3(ξ2,ξ3) by the following procedure. To simplify notation, we use A1,B1,L2,A2,B2,L3,A3 to denote them. Let
and
Then
Since E is nonsingular when K is positive definite, condition (28) holds.
Let \(U_{2}:=2H_{2}-(P_{2}+P_{1}^{\top })^{\top }\frac {1}{2}H_{1}^{-1}(P_{2}+P_{1}^{\top })\). Then
We first randomly generate a symmetric positive definite matrix \(H_{1}\in \mathbb {R}^{n_{1}\times n_{1}}\) and matrices \(P_{1} \in \mathbb {R}^{n_{1}\times n_{2}}\), \(P_{2}\in \mathbb {R}^{n_{2}\times n_{1}}\) with entries within [− 1,1]. Set \(H_{2}=\frac {1}{4}H_{1}(P_{1}^{\top }+P_{2})H_{1}^{-1}(P_{1}+P_{2}^{\top })+\alpha I_{n_{2}},\) where α is a positive number (we set α = 1 in the numerical tests). Then \(\left (\begin {array}{ccc} 2H_{1} & 0 \\ 0 & U_{2} \end {array}\right )\) is positive definite and then A1 + (A1)⊤ is positive definite.
We then randomly generate two matrices \({O_{1}^{2}}\in \mathbb {R}^{l_{1}\times l_{2}}\) and \({O_{2}^{2}}\in \mathbb {R}^{l_{2}\times l_{1}}\) with entries within [− 1,1] and a symmetric matrix \(\bar {Q}_{1}^{2} \in \mathbb {R}^{m_{2}\times m_{2}}\) with diagonal entries greater than \(\max \limits (m-1+\alpha ,l-1+\alpha )\) and off-diagonal entries belonging to [− 1,1]. Let
and
where \(\xi _{2}^{i(k)}\) and \(\xi _{3}^{j(k)}\) denote the k th component of vector \({\xi _{2}^{i}}\) and vector \({\xi _{3}^{j}}\), respectively. Then
is positive definite.
Finally, we generate a positive definite U1. We randomly generate matrices
with entries belonging to [− 1,1], and two symmetric matrices \(\bar {Q}_{1}^{1}\in \mathbb {R}^{m_{1}\times m_{1}}\) and \(\bar {Q}_{2}^{1} \in \mathbb {R}^{m_{2}\times m_{2}}\) with diagonal entries greater than \(\max \limits (m-1+\alpha ,l-1+\alpha )\) and off-diagonal entries belonging to [− 1,1], respectively. Set
and
Then
and \(\left (\begin {array}{ccc} 2\bar {Q}_{1}^{1} & {O_{1}^{1}}+({O_{2}^{1}})^{\top }\\ {O_{2}^{1}}+({O_{1}^{1}})^{\top } & 2\bar {Q}_{2}^{1} \end {array}\right )\) is diagonally dominant and positive definite. Moreover, for any \(y\in \mathbb {R}^{m_{1}+m_{2}}\),
Let U4 = A2 + (A2)⊤− U1. Note that
and
We have
and
which implies
Thus, U1 is positive definite. Combining the above analysis, K is positive definite and condition (28) holds.
We also set h1 = (− 1,− 1,− 1,− 3,− 3,− 3)⊤, h2(ξ2) = (− 1,− 1,− 1,− 1, − 1,− 1)⊤ and h3(ξ2,ξ3) = (− 1,− 1,− 1,− 1,− 1,− 1)⊤ for all \(\xi ^{2}\in {\varXi }_{2}\) and \(\xi ^{3}\in {\varXi }_{3}\).
4.2 Numerical results
For each sample size (N1,N2) = (25,25),(35,35),(50,50),(100,100),(200,200), we randomly generate 30 test problems and solve problem (29) by PHM as follows (see [22] for more details).
We set the parameter r = 4 in Algorithm 1, run the algorithm using Matlab 2018b on a desktop computer with two Intel Core i7 3.40GHz CPUs and 8GB RAM, and stop the iteration when the residual
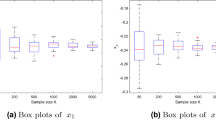
where \(y(x, {\xi _{2}^{i}})\) is the solution of the second-stage problem. Figure 1 shows the convergence tendency of x1, x2, x3, x4, x5 and x6, respectively.

5 Concluding remarks
In this paper, the strong monotonicity of two-stage and multistage SNCPs has been investigated under weaker conditions compared with the existing works, such as [4, 6]. Moreover, the conditional sampling approach has been adopted to discretize the multistage SNCPs and the asymptotic convergence results have been established. Finally, some numerical tests have been presented through PHM to illustrate our theoretical results.
There are still several questions that need to be addressed. We just analyze the asymptotic convergence of the conditional sampling approach for multistage SNCPs. What is the rate of convergence of the conditional sampling approach for multistage SNCPs? We leave this as our further research. Moreover, based on our numerical experience, the cost of solving three-stage SNCPs in PHM is relatively expensive with large sample sizes.
However, large sample size and multistage T ≥ 3 may be necessary for some real applications. How to improve the performance of PHM or propose more effective algorithms is our another further research direction.
References
Birge, J. R., Louveaux, F.: Introduction to Stochastic Programming. Springer, Berlin (2011)
Chen, X., Fukushima, M.: Expected residual minimization method for stochastic linear complementarity problems. Math. Oper. Res. 30(4), 1022–1038 (2005)
Chen, X., Pong, T. K., Wets, R. J. B.: Two-stage stochastic variational inequalities: an erm-solution procedure. Math. Program. 165(1), 71–111 (2017)
Chen, X., Shapiro, A., Sun, H.: Convergence analysis of sample average approximation of two-stage stochastic generalized equations. SIAM J. Optim. 29(1), 135–161 (2019)
Chen, X., Shi, Y., Wang, X.: Equilibrium oil market share under the COVID-19 pandemic To preprint on. arXiv (2020)
Chen, X., Sun, H., Xu, H.: Discrete approximation of two-stage stochastic and distributionally robust linear complementarity problems. Math. Program. 177(1-2), 255–289 (2019)
Chen, X., Wets, R. J. B., Zhang, Y.: Stochastic variational inequalities: residual minimization smoothing sample average approximations. SIAM J. Optim. 22(2), 649–673 (2012)
Chen, X., Xiang, S.: Newton iterations in implicit time-stepping scheme for differential linear complementarity systems. Math. Program. 138(1-2), 579–606 (2013)
Chieu, N. H., Trang, N.: Coderivative and monotonicity of continuous mappings. Taiwan. J. Math. 16(1), 353–365 (2012)
Clarke, F. H.: Optimization and Nonsmooth Analysis, Volume 5 of Classics in Applied Mathematics. SIAM, Philadelphia (1990)
Cottle, R. W., Pang, J. S., Stone, R. E.: The linear complementarity problem. SIAM, Philadelphia (2009)
Facchinei, F., Pang, J. S.: Finite-dimensional variational inequalities and complementarity problems. Springer Science & Business Media, New York (2007)
Gauvin, J., Dubeau, F.: Differential properties of the marginal function in mathematical programming. Math. Programm. Stud. 21, 199–212 (1984)
Hadjisavvas, N., Komlósi, S., Schaible, S.S: Handbook of Generalized Convexity and Generalized Monotonicity, vol. 76. Springer, New York (2006)
Izmailov, A. F.: Strongly regular nonsmooth generalized equations. Math. Program. 147(1-2), 581–590 (2014)
Jiang, J., Chen, X., Chen, Z.: Quantitative analysis for a class of two-stage stochastic linear variational inequality problems. Comput. Optim. Appl. 76(2), 431–460 (2020)
Jiang, J., Shi, Y., Wang, X., Chen, X.: Regularized two-stage stochastic variational inequalities for Cournot-Nash equilibrium under uncertainty. J. Comput. Math. 37(6), 813–842 (2019)
Kyparisis, J.: Solution differentiability for variational inequalities. Math. Program. 48(1-3), 285–301 (1990)
Lin, G., Fukushima, M.: Stochastic equilibrium problems and stochastic mathematical programs with equilibrium constraints: a survey. Pac. J. Optim. 6, 455–482 (2010)
Pang, J. S., Sen, S., Shanbhag, U. V.: Two-stage non-cooperative games with risk-averse players. Math. Program. 165(1), 235–290 (2017)
Reaiche, M.: A note on sample complexity of multistage stochastic programs. Oper. Res. Lett. 44(4), 430–435 (2016)
Rockafellar, R. T., Sun, J.: Solving monotone stochastic variational inequalities and complementarity problems by progressive hedging. Math. Program. 174(1-2), 453–471 (2019)
Rockafellar, R. T., Wets, R. J. B.: Stochastic variational inequalities: single-stage to multistage. Math. Program. 165(1), 331–360 (2017)
Ruszczyński, A., Shapiro, A.: Stochastic programming models. Handb. Oper. Res. Manag. Sci. 10, 1–64 (2003)
Shanbhag, U. V.: Stochastic variational inequality problems: applications, analysis, and algorithms. INFORMS Tutor. Oper. Res, 71–107 (2013)
Shapiro, A.: Inference of statistical bounds for multistage stochastic programming problems. Math. Methods Oper. Res. 58(1), 57–68 (2003)
Shapiro, A.: On complexity of multistage stochastic programs. Oper. Res. Lett. 34(1), 1–8 (2006)
Shapiro, A., Dentcheva, D., Ruszczyński, A.: Lectures on Stochastic Programming: Modeling and Theory, 2nd edn. SIAM, Philadelphia (2014)
Sun, H., Chen, X.: Two-stage stochastic variational inequalities: theory, algorithms and applications. J. Oper. Res. Soc. China 9, 1–32 (2021)
Xu, H.: Sample average approximation methods for a class of stochastic variational inequality problems. Asia-Pac. J. Oper. Res. 27(01), 103–119 (2010)
Zhang, M., Sun, J., Xu, H.: Two-stage quadratic games under uncertainty and their solution by progressive hedging algorithms. SIAM J. Optim. 29(3), 1799–1818 (2019)
Acknowledgements
The authors would like to thank Professor Alexander Shapiro for his enlightening discussion of this topic. They also thank two anonymous referees for their insightful and detailed comments, which improve this paper significantly.
Funding
This work was supported by Postdoctoral Science Foundation of China (Grant No. 2020M673117) and National Natural Science Foundation of China (Grant No. 11871276).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jiang, J., Sun, H. & Zhou, B. Convergence analysis of sample average approximation for a class of stochastic nonlinear complementarity problems: from two-stage to multistage. Numer Algor 89, 167–194 (2022). https://doi.org/10.1007/s11075-021-01110-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-021-01110-z
Keywords
- Two-stage
- Multistage
- Stochastic complementarity problems
- Sample average approximation
- Convergence analysis